Solidum alginate gated oxide dendritic transistor for spatiotemporal arithmetic application

Abstract

As a novel computing paradigm that transcends traditional von Neumann architectures, neuromorphic computing integrates learning and memory functions. The ability to mimic multi-input spatiotemporal integration is crucial for achieving efficient neuromorphic computing. In this work, we fabricated a multi-gate solid-state amorphous (SA) electrolyte-gated oxide dendritic transistor, which exhibits in-plane-gate modulatory behaviors and dendritic neural functions. Leveraging unique proton migration, we successfully simulated Ebbinghaus memory forgetting. By applying spatiotemporal dendritic inputs, we mimicked temporal integration and coincidence detection. Additionally, we demonstrated neural multiplication operations using frequency-encoded signals. Furthermore, spatially correlated sensitization and desensitization behaviors of pain perception were implemented on the multi-gate dendritic transistors. Collectively, these results indicate that the present oxide dendritic transistors could serve as fundamental building blocks for advanced cognitive neuromorphic platforms.

Graphical abstract

Keywords

oxide dendrite transistor / dendritic multiplication operation / spatially correlated sensitization and desensitization

1 Introduction

The von Neumann architecture plays an important role in solving structural computing problems. However, the separation of computing units and storage units leads to a significant increase in power consumption [1, 2]. In contrast, our brain is an intricate network consisted of ~10¹¹ neurons and ~10¹⁵ synapses [3]. It demonstrates superior performance by solving complex problems at high energy efficiency. Inspired by brain computing mode, efforts have been made to develop memristor based neuromorphic devices aiming at energy-efficient neuromorphic systems [4−6]. However, existing studies are mostly limited to homosynaptic structures, making it difficult to simulate spatiotemporal integration and dendrite algorithm. Three-terminal and multi-terminal based devices are suitable for simulating synaptic behaviors and addressing neuromorphic computing. Multi-terminal neuromorphic devices allow to simulate multi-channel communication, helping to promote the developments of efficient neuromorphic information processing and complex synaptic interaction functions. Recently, several achievements have been made on multi-terminals memristor based neuromorphic devices, demonstrating important neural functions, such as synaptic competition and synaptic cooperation [7], associative learning [8], pattern recognition [9], and visual recognition [10].

Morphologically, multi-gate neuromorphic transistors are attractive for mimicking multi-dendritic neurons. It can execute gate input summation and process complex signals efficiently. Multi-gates not only enhance the signal processing capability, but also simulate the complex interactions between neurons. The gates receive and integrate signals as the way the dendrites do, improving the processing accuracy. Unfortunately, with the limitation of electrostatic modulation for conventional gate dielectric, there is great challenge to design transistors with multi-gates. The ionic-conductive electrolyte gated transistors pose interesting possibilities for mimicking multi-dendritic neurons. Recently, several achievements have been made on multi-terminal neuromorphic transistor, demonstrating some advanced neural functions, such a as hetero-synaptic functions [11, 12], spatiotemporal dendritic algorithms [13, 14], nonlinear integration [15], linear classification [16, 17], and cooperative learning [18]. Despite these achievements, more spatiotemporal signal patterns are still needed to be mimicked. For spatial data, it can deal with information about physical location. For temporal data, it can deal with information which will change over time. While for spatiotemporal information, it will deal spatial phenomena changes over time. Since the branched dendrites in biological neurons can collect, integrate, and modulate the presynaptic inputs, the neuron can integrate such inputs and transmit output spikes carrying spatiotemporal characteristics. Thus, spatiotemporal arithmetic can be triggered. It refers to the multiplicative or additive modulation on input−output (I–O) relationship. Moreover, coincidence detection involves the verification and consolidation of information from various synaptic inputs, being crucial for reliable neural communication and effective decision-making [19]. Additionally, neural multiplication operation is also the basis for neural computation [20]. It scales and combines signals in biological synaptic weight adjustment. In addition, pain-perceptual nociceptor (PPN) is capable of perceiving noxious stimuli [21]. These stimuli can be converted into neural impulses, being transmitted through the peripheral nerves to the central nervous system, resulting in the perception of pain. After the noxious stimuli are removed, the biological nociceptor starts the relaxation process. During relaxation, whether nociception occurs depends on the interval of time between noxious and non-noxious stimuli. If the interval is too long, nociception may not be retriggered, i.e., desensitization effect. PPN is critical for survival and protective behaviors. Thus, the mimicking of these specific biological functions highlights areas for future research and innovation.

It is well known that electronic pollution is becoming a serious challenge in our daily lives and environments. Thus, adopting biodegradable materials for “green” electronic applications is interesting. As a representative “green” material, sodium alginate (SA) has been widely used in tissue engineering, drug delivery, proton exchange membranes, and so on. Here, SA gated indium tin oxide (ITO) dendrite transistors were fabricated. The device demonstrates strong proton interfacial coupling effects, exhibiting in-plane-gate modulatory behaviors. The characteristic protonic gating time is in the order of several tens of ms, inducing rich neuromorphic functions and dendrite neural functions. With extremely strong proton coupling, the present device demonstrates low energy consumptions of ~0.59 fJ with high sensitivity of ~11 dB. With unique proton migration, Ebbinghaus memory forgetting is simulated. With multi-gate configuration, spatiotemporal integration and coincidence detection are mimicked. Neural multiplication operations of frequency-encoded signals have also been demonstrated. Additionally, spatially correlated sensitization and desensitization behavior of pain perception have been implemented on the multi-gate dendrite transistors. Thus, the present oxide dendrite transistors could act fundamental building blocks for cognitive neuromorphic platforms.

2 Experiment

Fig.1(a) schematically shows the device processing. Firstly, 0.6 g SA powder was dissolved in 29.4 mL deionized water by stirring at room temperature for 6 h to obtain ~2 wt% SA solutions. Secondly, the SA solution was dip-coated on the ITO glass substrate. After dried at 50 °C for 6 h, a SA based solid state electrolyte film was obtained. Thirdly, patterned ITO electrodes were sputtered onto the SA film in pure Ar ambient with a one-step mask process. An ITO ceramic target (In₂O₃:SnO₂ = 90:10 wt%) was adopted. During sputtering, Ar flow rate, working pressure, DC power, and sputtering time were set to 40 sccm, 0.8 Pa, 80 W, and 15 min, respectively. Due to the reflection of ITO nanoparticles at the mask edge, a thin channel layer can be formed between source and drain electrodes. The channel length and width are 80 μm and 1000 μm, respectively. The size of the electrodes is 1000 μm × 150 μm. Additionally, isolated ITO patterns can also be deposited. Such isolated ITO patterns can be deemed as coplanar gate electrodes (G₁, G₂, ... , G_m). Thus, ITO dendrite transistors with multi-gates have been obtained. Figure S1 in the Electronic Supplementary Materials (ESM) shows the top view photograph of the ITO dendrite transistor.

Fig.1 (a) Schematic diagram of the device processing for ITO dendrite transistor. (b) AFM surface morphology image of SA film. (c) Cross-sectional SEM image of the SA film. (d) FTIR spectrum of SA film. (e) Frequency-dependent specific capacitance of the SA electrolyte film. (f) Output curves and (g) transfer curves of the SA gated ITO dendrite transistor operated at coplanar gate (G1) mode.

Full size|PPT slide

The surface morphology of the SA films was characterized using atomic force microscopy (AFM: 3100 SPM). Scanning electron microscopy (SEM: SU-70) was used to obtain the thickness of the SA film. Fourier-transform infrared spectra (FTIR: Nicolet 6700) was adopted to analyze molecular bond structure of the SA film. Frequency dependent capacitances of SA based electrolyte film were characterized by an IM3533 Impedance Analyzer. Electrical performances and synaptic plasticity of the device were measured by a semiconductor parameter analyzer (Keithley 4200A SCS) at room temperature.

3 Results and discussion

Fig.1(b) shows AFM surface morphology of the SA film coated on a glass substrate. The root-mean-square (rms) value is ~1.6 nm, indicating good flatness. The SA film can be peeled off from the substrate. Then, it was cooled in liquid nitrogen and gently pressed with tweezers to obtain film fragments. Fig.1(c) shows the cross-sectional SEM image of the SA film fragment. The thickness is estimated to be ~19 μm. Fig.1(d) shows FTIR spectrum of the SA electrolyte film coated on the glass substrate. Peak at 3266 cm⁻¹ is related to the stretching vibration of −OH [22]. Peaks at 1585 cm⁻¹ and 1409 cm⁻¹ are related to asymmetric and symmetric −COO−, respectively [23]. Peak at 1022 cm⁻¹ is related to the stretching vibrations of the −C−O−C− bond [24]. Fig.1(e) shows specific capacitance of the SA electrolyte film as a function of frequency. A high specific capacitance of ~4.0 μF/cm² is obtained at 1.0 Hz for coplanar ITO/electrolyte/ITO sandwich structure. Under external field, protons within SA-based electrolyte will hop among −OH bonds through Grotthuss mechanism. These protons will get accumulated at SA/ITO interface, resulting in the formation of electric-double-layer (EDL) with extremely big capacitance (C_EDL). We have taken long-term operation tests and environmental stability studies, as shown in Fig. S2 of the ESM. Both temperature and humidity will affect the C_EDL values. While at fixed temperature and humidity, the C_EDL values are quite stable, indicating good stabilities. Figure S3(a) of the ESM compares the C_EDL values of the present electrolyte with the previously reported ones. The present C_EDL value is the biggest, indicating the priorities for the present electrolyte.

Fig.1(f) shows the output curves of the ITO dendrite transistor. A good linearity is obtained at low V_ds region, indicating good Ohmic contact. A good saturation behavior is observed at high V_ds, confirming strong electrostatic modulation. Fig.1(g) shows double-sweep transfer curve of the ITO dendrite transistor. V_ds is fixed at 1.5 V. The sweep rate is 0.1 V/s. The gate leakage current is below 10 nA. The I_ON/I_OFF ratio, threshold voltage (V_th), subthreshold swing (SS) and field-effect mobility (μ) are estimated to be ~4.8 × 10⁵, ~1.0 V, ~216 mV/decade and ~0.9 cm²·V⁻¹·s⁻¹, respectively. A clear anticlockwise hysteresis of ~0.7 V can be observed, as could be attributed to the migration of protons within the electrolyte. Table S1 summaries the main electrical parameters of the reported neuromorphic transistors. The parameters of the present device are comparable to those of the previously reported works.

Fig.2(a) schematically shows biological neurons, which are dendrites, soma and axon [25]. Upon the neural spikes, neurotransmitters will be released from multiple presynaptic membranes. They will migrate across the synaptic cleft and bind to postsynaptic receptors at the dendrites. This activation opens ion channels linked to the receptors, regulating the postsynaptic current. Fig.2(b) schematically shows the ITO dendrite transistor. Coplanar ITO gates (G₁, G₂, ... ,G_m) can be considered as multiple pre-synapses. Here, three basic forms of short-term plasticities (STP) are mimicked, including excitatory postsynaptic current (EPSC), paired-pulse facilitation (PPF) and post-tetanic potentiation (PTP). They play important roles in decoding temporal information in sensory nervous systems, e.g., vision, touch and hearing [26−28]. Fig.2(c) shows a typical EPSC response on a spike (1.5 V, 10 ms) loaded on G₁. A peak EPSC value of ~0.58 μA is observed. When the spike ends, the EPSC will gradually decay back to a resting current of ~0.03 μA. The decay is related to the diffusion back of protons to their initial equilibrium position. Figure S4(a) of the ESM shows repeated EPSC responses. The curves approach with each other quite well. Figure S4(b) shows the extracted EPSC values. The results indicate good stabilities. For EPSC in Fig.2(c), the energy consumption is estimated to be ~5.8 nJ. It is possible to decrease the energy consumption by decreasing spike amplitude and the read voltage. Figure S4(c) shows the EPSC response triggered by a pre-synaptic spike (1 mV, 50 ms) loaded on G₁. The peak EPSC value is only ~11.51 pA, while the energy consumption (P) is only ~0.59 fJ. Table S2 of the ESM illustrates the P values for different neuromorphic devices. The present device shows the lowest energy consumption.

Fig.2 (a) Schematic diagram of biological neurons. (b) Schematic diagram of the ITO dendrite transistor. (c) A typical EPSC response trigged with a gate spike (1.5 V, 10 ms). Vds is set to 1 V. (d) PPF index as a function of Δt. Inset: A typical EPSC response triggered with paired spikes (1.5 V, 10 ms) with Δt of 20 ms. (e) EPSC responses triggered by spikes (1.5 V, 10 ms) with different frequencies. (f) PTP index as a function of spike frequency.

Full size|PPT slide

EPSC response can also be triggered with paired gate spikes (1.5 V, 10 ms), as shown in the inset of Fig.2(d) with interval time (Δt) of 20 ms. The first and the second absolute EPSC values are ~0.59 μA (A₁) and ~0.71 μA (A₂), respectively. Thus, PPF index, defined as (A₂/A₁) × 100%, is estimated to be ~120%. The increased A₂ value as compared to A₁ value is due to the increased number of accumulated protons at the electrolyte/channel interface. Fig.2(d) shows PPF index as a function of Δt. With the increased Δt value, the PPF index value decreases gradually. As is consistent with those in biological synapses [29]. Post-tetanic potentiation (PTP) is a key STP phenomenon in biological nervous systems. It is characterized as a transient enhancement of synaptic transmission after experiencing a short period of intense synaptic activity. This phenomenon mainly results from increased neurotransmitter release probability due to residual intracellular Ca²⁺ in presynaptic terminals during intense synaptic activity [30, 31]. It plays a crucial role in the formation of short-term memory in biological nervous systems. PTP can also be mimicked on the ITO dendrite transistor. Fig.2(e) shows EPSC responses on 10 spikes (1.5 V, 10 ms) with different frequencies. The spiking frequency ranges from 2 to 50 Hz. It can be seen that the EPSC values increase with the increased spike number, indicating PTP effects. Here, PTP index can be defined as (A_n/A₁) × 100%. Fig.2(f) shows PTP index as a function of spike frequency. With the increased frequency from 2 to 50 Hz, the tenth PTP indexes (A₁₀/A₁) increases from 100.04% to 157.41%.

In the brain, information will be forgotten over time following the famous Ebbinghaus forgetting curve proposed by Hermann Ebbinghaus in 1885 [32, 33]. Ebbinghaus found that initial information would be lost very quickly after it was initially learnt. The speed of the loss was significantly influenced by factors such as the way the information was learned and the frequency of its review. The forgetting curve can also be mimicked on the present oxide dendrite transistor. The “learning” conditions, i.e., the spiking conditions, can be adjusted by modulating the spike numbers, spike durations and spike amplitudes. Here, spikes were loaded on G₁. The conductance ($G_t$) was read out with a constant V_ds of 1 V. Figure S5(a) of the ESM shows the EPSC responses on spikes (5 V, 10 ms) with different numbers. Here, changes in conductance are defined as

(1)$\eta ={\displaystyle \frac{\mathrm{\Delta }G}{{\mathrm{\Delta }G}_{max}}}={\displaystyle \frac{G_t-G_0}{G_{max}-G_0}},$

where G₀ and G_max are the initial conductance and the peak conductance, respectively. Fig.3(a) shows the decayed η values. In order to catch the results more directly, the times (t₀) when spikes end are regulated to 0 s. When spikes end, the η value gradually decays to a final value η_∞. Moreover, the η_∞ increases with the increased spike number. Here, the decayed η values can be fitted with relation:

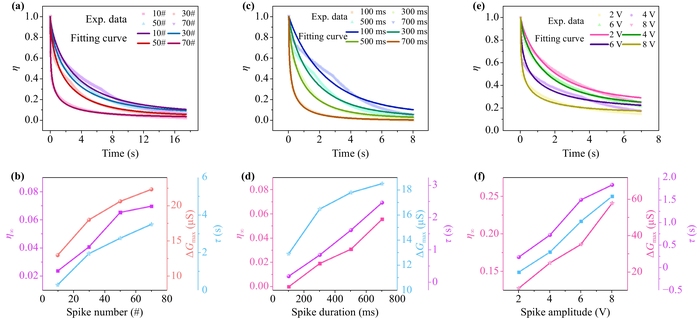
Fig.3 (a) Decayed channel conductance (η) at different number spikes. (b) η∞, τ and ΔGmax values as a function of spike number extracted from (a). (c) Decayed η at different spike duration. (d) η∞, τ and ΔGmax values as a function of spike duration. (e) Decayed η at different spike amplitude. (f) η∞, τ and ΔGmax values as a function of spike amplitude.

Full size|PPT slide

(2)$\eta ={\eta }_{\mathrm{\infty }}+(1-{\eta }_{\mathrm{\infty }})\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left({\displaystyle \frac{t}{\tau }}\right)}^{\beta }\right],$

where β is the stretching exponent. Good fitting is obtained, as shown in Fig.3(a). Fig.3(b) shows η_∞ value, τ value and ΔG_max value as a function of spike number. The τ value increases from ~0.30 to ~4.32 s with the increased spike number from 10 to 70. Correspondingly, η_∞ value and ΔG_max value increase from ~0.023 to ~0.069 and from ~12.9 to ~22.2 μS, respectively. Similarly, we have taken EPSCs for spikes with different duration times, as shown in Fig. S5(b). Fig.3(c) shows the extracted η values. Fig.3(d) shows η_∞ value, τ value and ΔG_max value as a function of spike duration. η_∞, τ and ΔG_max values increase with spike duration, accounting for the alteration in the memory strength under varied spike duration. Figure S5(c) shows EPSCs for spikes with different amplitudes. Fig.3(e) shows the extracted η values. Fig.3(f) shows the extracted η_∞ value, τ value and ΔG_max value. These behaviors are quite similar to that in psychological forgetting. The increased η_∞ value and τ value well mimic the transition from STM to LTM transition. Here, STM activities are related to EDL effects at the electrolyte/channel interface. While under LTM activities, protons within electrolyte will not only get accumulated at electrolyte/ITO interface but also penetrate into ITO channel, inducing an electrochemical doping. Thus, nonvolatile increase in channel conductance will be triggered.

Additionally, coincidence detection is particularly important in human visual auditory system [34−36]. It helps people possess the ability of spatial localization of objects. During coincidence detection, neurons detect temporal synchronization or correlation between multiple inputs. Based on the interval time (ΔT) between inputs loaded on dendrites, neuronal operational modes can be divided into temporal integration and coincidence detection. If the inputs are highly consistent in time, the neuron may produce a strong response. Thus, the processing of the inputs is expressed as coincidence detection. If the interval time between inputs is too big, the neural responses may be weak or mutually unaffected. Thus, processing of inputs is expressed as temporal integration. Previously, Yan et al. [37] proposed two-dimensional Bi₂O₂Se ferroelectric field-effect transistors to mimic coincidence detection. They used visible light and infrared light as inputs. John et al. [38] demonstrated emulation of coincidence in a single neuristor via a dual-gated architecture. Spikes were applied at two physically separate local and global gates with a delay created symmetric short-term plasticity behavior, enabling higher order temporal correlations at a unitary level. Interestingly, the present SA-gated ITO dendrite transistor possesses multi-gates (G₁, G₂, ..., G_m). Thus, temporal integration and coincidence detection functions could be mimicked. Fig.4(a) schematically shows multiple inputs for mimicking such functions. Three spatiotemporally correlated dendritic spikes, i.e., V₁ (2 V, 10 ms), V₂ (2 V, 10 ms) and V₃ (2 V, 10 ms), are loaded on dendrite 1 (G₁), dendrite 2 (G₂) and dendrite 3 (G₃), respectively. The interval times, i.e., ΔT_3-2 and ΔT_1-2 can be modulated. V_ds is fixed at 2 V to read out the EPSC response. The last triggered absolute EPSC amplitude is deemed as P_i. Fig.4(b) shows a typical EPSC response with ΔT_3-2 and ΔT_1-2 of −30 ms and 30 ms, respectively. Inputs on G₃ and G₂ precede inputs on G₁. Because of the temporal coupling effect, the EPSC will increase. The first absolute EPSC amplitude is ~6.1 μA. While the P_i, i.e., P₁, is ~11.72 μA. Here, coincidence detection can be triggered by loading spikes on two or three gates simultaneously. Fig.4(c) shows P_i as a function of ΔT_1-2 at fixed ΔT_3-2 of −50 ms.The pre-synaptic spike 3 leads pre-synaptic spike 2 of 50 ms. When ΔT_1-2 < 0, P_i, i.e., P₂, increases with the decreased |ΔT_1-2| value. Here, both inputs loaded on G₁ and G₃ will facilitate the output triggered by spike loaded on G₂. When ΔT_1-2 is 0, the P_i value arrives at the maximum value due to the coincidence detection between G₁ and G₂. When ΔT_1-2 > 0, P_i, i.e., P₁, decreases gradually due to the attenuated temporal coupling. It is worth noting that the P₁ value is greater than the P₂ value. As is due to the smaller gate-to-channel distance for G₁ than G₂, i.e., the greater coupling strength for G₁ than G₂. Fig.4(d) shows P_i as a function of ΔT_1-2 at fixed ΔT_3-2 of 0 ms. The presynaptic spike 3 and presynaptic spike 2 arrive at the same time. When ΔT_1-2 < 0, P_i, i.e., P₂ or P₃, increases with the decreased |ΔT_1-2|. Input loaded on G₁ will facilitate the output triggered by spike loaded on G₂. With the decreased |ΔT_1-2| value, the facilitation will get important, resulting in the increased P₂ value. At ΔT_1-2 of 0 ms, spikes on G₁, G₂ and G₃ are loaded simultaneously, resulting in a maximum P₂ valve. As indicates the coincidence detection among G₁, G₂ and G₃. When ΔT_1-2 > 0, P_i, i.e., P₁, decreases gradually due to the attenuated temporal coupling. Fig.4(e) shows P_i as a function of ΔT_1-2 at fixed ΔT_3-2 of 50 ms. The pre-synaptic spike 2 leads pre-synaptic spike 3 for 50 ms. It is observed that the P_i value arrives at the maximum value at ΔT_1-2 of 50 ms. At this spiking condition, spikes on G₁ and G₃ are loaded simultaneously. The result expresses the coincidence detection between G₃ and G₁. For ΔT_1-2 < 50 ms or ΔT_1-2 > 50 ms, P₁ is greater than P₃ due to the stronger coupling weight for G₁ than G₃. Fig.4(f) shows P_i as a function of ΔT_3-2 at different ΔT_1-2. The maximum P_i is ~24.99 μA when all inputs are loaded simultaneously. When ΔT_1-2 and ΔT_3-2 are 0 ms and −50 ms, respectively, spike 1 and spike 2 are loaded simultaneously. P_i, i.e., P₁, is estimated to be ~18.56 μA. When ΔT_1-2 and ΔT_3-2 are 50 ms and 50 ms, respectively, spike 1 and spike 3 are loaded simultaneously. Now, P_i, i.e., P₁, decreases to ~16.42 μA. The difference is due to the stronger coupling weight for G₂ than G₃. In summary, the temporal integration and coincidence detection are successfully implemented in the present oxide dentrite transistor. It provides an interesting direction for advanced applications of neuromorphic devices in neuromorphic platforms.

Fig.4 (a) Schematic diagram of spikes for mimicking coincidence detection. V1 (2 V, 10 ms), V2(2 V, 10 ms) and V3 (2 V, 10 ms) are loaded on G1, G2 and G3, respectively. (b) Typical EPSC response with ΔT3-2 and ΔT1-2 of −30 ms and 30 ms, respectively. Pi as a function of ΔT1-2: (c) ΔT3-2 = −50 ms, (d) ΔT3-2=0 ms, (e) ΔT3-2 = 50 ms. (f) Pi as a function of ΔT3-2 at different ΔT1-2.

Full size|PPT slide

In biological neurons, the axon output reflects the integrated sum of all inputs conveyed through the dendrites. This allows neurons to perform advanced intelligent behaviors. Fig.2(a) schematically illustrates that a neuron with branched dendrites can collect and integrate the presynaptic inputs and subsequently transmit the output spikes to other neurons through axon. Neuronal arithmetic refers to the multiplicative or additive modulation on I–O relationship. In Ref. [39], Wan et al. proposed graphene oxide-coupled neuron transistors to realize multiplicative operation. Spikes with different rates were applied on multi-gates as driving inputs. And a bias voltage was applied on modulatory terminal. The EPSC amplitude is defined as neuronal output. Thus, algebraic transformation on the neural I–O relationships was observed to be multiplicative operation. In our previous work [40], polyvinyl alcohol/chitosan electrolyte gated oxide dendrite transistors were fabricated. Spikes with different amplitudes loaded on dendrites were deemed as inputs. EPSC amplitudes were defined as outputs. Thus, additive operations were obtained. Here, neuromorphic computing can also be implemented by processing frequency-coded spike stimuli. G₁ and G₂ are deemed as synapse 1 and synapse 2, respectively. Spatiotemporally correlated frequency encoded spikes (1 V, 10 ms) were loaded on G₁ and G₂. The duration time for each frequency encoded spike train was 810 ms. Fig.5(a) shows the recorded EPSC with V_ds of 1.0 V for different frequencies f₁ and f₂. EPSC gain (R) was defined as the ratio between the last absolute EPSC peak (A₁) and the first absolute EPSC peak (A₀). When f₁ and f₂ are 25 Hz and 10 Hz, respectively, the R value is ~2.17. When f₁ and f₂ are 5 Hz and 50 Hz, respectively, the R value is ~1.70, suggesting an effective coupling between G₁ and G₂. Fig.5(b) shows R values at different f₁ and f₂ values. The results clearly indicate the high sensitivity to frequency space. Here, the data can be fitted with a function:

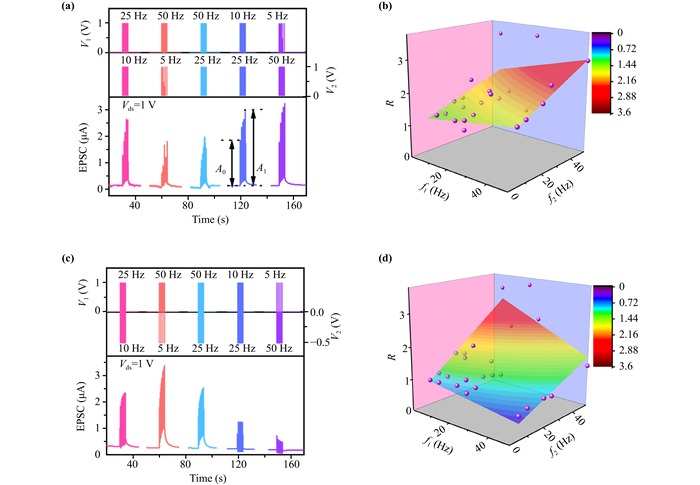
Fig.5 (a) EPSC responses triggered by spatiotemporally correlated frequency encoded V1 and V2 spikes (1 V, 10 ms) loaded on G1 and G2. (b) EPSC gain (R) at different f1 and f2 values for V1 and V2 spikes. (c) EPSC responses triggered by spatiotemporally correlated frequency encoded V1 spike (1 V, 10 ms) and V2 spike (−0,5 V, 10 ms) loaded on G1 and G2. (d) EPSC gain (R) at different f1 and f2 values for V1 and V2 spikes.

Full size|PPT slide

(3)$R\left(f_1,f_2\right)=A\cdot \left(1+B{f}_1\right)\cdot \left(1+C{f}_2\right),$

where A, B, and C are the constants for the polynomial. The fitting gives A, B and C of ~1.07, ~0.018/Hz, and 0.008/Hz, respectively. Therefore, the relationship can be written as a function of f₁ multiplied by a function of f₂, i.e., F(f₁)·F(f₂). Here, F(f₁) and F(f₂) are (1+Bf₁) and (1+Cf₂), respectively. The result indicates that multiplicative operation is implemented based on the spatiotemporally correlated frequency encoded spikes. Spatiotemporally correlated frequency encoded spikes (1 V, 10 ms) and (−0.5 V, 10 ms) can also be loaded on G₁ and G₂. The duration time for each frequency encoded spike train was still 810 ms. Fig.5(c) shows the recorded EPSC. When f₁ and f₂ are 25 Hz and 10 Hz, respectively, the R value is ~1.76. When f₁ and f₂ are 5 Hz and 50 Hz, respectively, the R value is ~0.7. Fig.5(d) shows R values at different f₁ and f₂ values. The fitted A, B, and C are ~0.72, ~0.066/Hz, and ~−0.009/Hz, respectively. The results also indicate multiplicative operation. It should be noted here that multiplicative operation is thought to be the fundamental mechanism for a wide range of neural processes, such as translation-invariant object recognition, visually guided reaching, and collision avoidance [41, 42]. Thus, the mimicking of neural algorithms on multi-gate dendrite transistors offers the potential for advanced neuromorphic computing.

Pain-perceptual nociceptor (PPN) is one of the most important sensory receptors among the various sensory neurons. It generates pain signals that allow the body to avoid external dangers [43, 44]. The three main features of the PPN are threshold, sensitization and desensitization. Fig.6(a) depicts a schematic diagram of a biological nociceptive system. When the skin is stimulated externally, the stimulus signal is converted into a nerve impulse. Then, it is sent to nociceptor. The nociceptor will determine whether to transmit the signal further through the spinal cord to the brain. Eventually it generates an action potential. The present oxide dendrite transistor can also be deemed as an artificial nociceptor. Spikes loaded on G₁ are deemed as external stimuli. An EPSC of 6 μA is defined as pain threshold (I_th). Fig.6(b) shows pain perception behavior in response to spikes with different amplitudes and durations. Contour map is extracted for catching the relations between EPSC values and spike amplitudes or durations. Fig.6(c) shows EPSC response on spikes with different spike amplitudes at fixed spike duration of 10 ms. The spikes were loaded on G₁. For spikes with amplitudes below 1.9 V, the EPSC values are below 6 μA. Conversely, for spikes with amplitudes above 2.2 V, the EPSC value exceeds 6 μA, mimicking the perception of pain. Thus, the pain threshold (V_th) for artificial nociceptor is determined to be 2.2 V. Fig.6(d) shows EPSC response on spikes with different durations at fixed spike amplitudes of 1.5 V. As the duration time increases, the EPSC value gradually rises and eventually exceeds the I_th at 30 ms. 100 consecutive spikes are also loaded on G₁. The interval time and the duration time are set at 20 ms and 10 ms, respectively. Fig.6(e) shows the EPSC responses. It is observed that the EPSC value will increase greatly in the initial and then get saturated. For spikes with amplitudes of 0.5 V, the EPSC values are below I_th, indicating that the nociception has not been triggered. When spike amplitude is 1 V, 33 spikes will trigger the nociception. When spike amplitude is 2 V and 3 V, only 2 spikes and 1 spikes are enough to trigger the nociception, respectively.

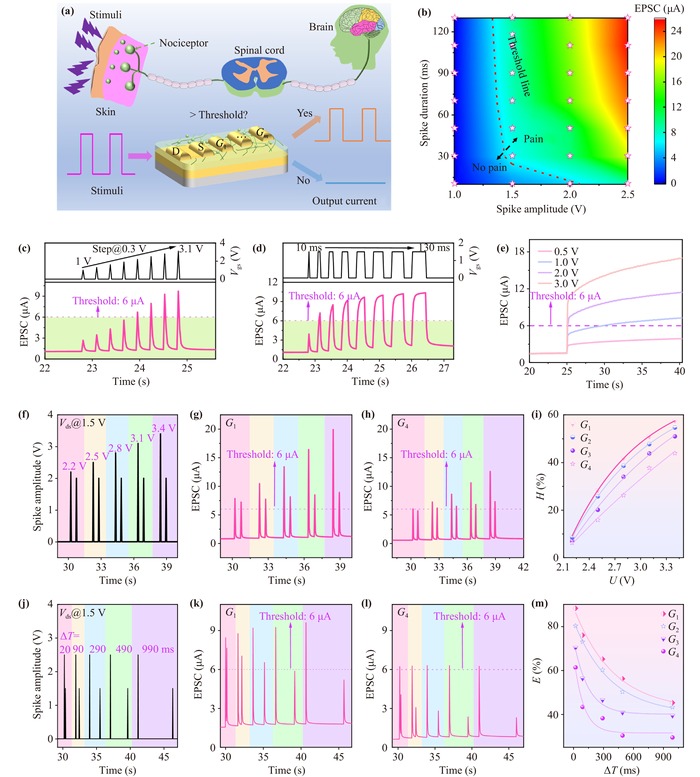
Fig.6 (a) Schematic diagram of a biological nociceptive system. (b) EPSC values with different spike amplitudes and durations. (c) EPSC response on spikes with different spike amplitudes at fixed spike duration of 10 ms. (d) EPSC response on spikes with different durations at fixed spike amplitudes of 1.5 V. (e) EPSC responses on 100 consecutive spikes with different amplitudes. Spike interval and duration time are 20 ms and 10 ms, respectively. (f) Noxious spikes followed by non-noxious spike. The interval time between noxious stimulus and non-noxious stimulus (2 V) is 90 ms. The spike duration time is 10ms. (g) EPSC responses on spikes in (f) loaded on G1. (h) EPSC responses on spikes in (f) loaded on G4. (i) H vs. U value at different dendrites, i.e., G1, G2, G3, and G4. (j) Noxious spikes (2.5 V, 10 ms) followed by non-noxious spike (1.5 V, 10 ms) with different spike interval time. (k) EPSC responses on spikes in (j) loaded on G1. (l) EPSC responses on spikes in (j) loaded on G4. (m) E vs. ΔT value at different dendrites, i.e., G1, G2, G3, and G4.

Full size|PPT slide

Sensitization is a mechanism by which the injured area is protected. It is affected by the damage degree and spatial location [45]. Here, a series of noxious spikes with amplitude above 2.2 V were applied on the dendrite transistor, followed by a non-noxious spike with amplitude of 2 V, as shown in Fig.6(f). The spike duration is fixed at 10 ms. Fig.6(g) shows EPSC responses when the spikes were loaded on G₁. The EPSC value induced by the non-noxious stimulus increase from ~7.21 to ~8.82 μA for noxious spikes with amplitudes increase from 2.2 to 3.4 V. Fig.6(h) shows EPSC responses when the spikes were loaded on G₄. The EPSC value induced by the non-noxious stimulus increase from ~5.67 to ~7.30 μA for noxious spikes with amplitudes increase from 2.2 to 3.4 V. The results indicate that noxious stimuli and spatial location can effectively modulate sensitization. Figures S6(a) and (b) show the EPSC responses when the spikes are applied on G₂ and G₃, respectively. To further investigate the sensitization feature of the artificial nociceptor, sensitization index H is defined as: H = (A₁−A₂)/A₁×100%, where A₁ and A₂ represent the absolute EPSC amplitude triggered by the noxious spike and the non-noxious spike, respectively. The relationships between H and spike amplitude (U) of the noxious stimulus are shown in Fig.6(i). For spikes loaded on G₁, H increases from ~9.1% to ~57.5% as the U value increases from 2.2 to 3.4 V. While for spikes loaded on G₄, H increases from ~6.1% to ~43.8% as the U value increases from 2.2 to 3.4 V. The sensitization process can be well fitted using the following exponential function [46]:

(4)$H=H_1{\mathrm{e}}^{\frac{-U}{U_0}}+H_0,$

where H₀ and H₁ are two sensitization constants. As shown in Table S3 of the ESM, H₀, H₁, and U₀ increase with the increased gate-to-channel distances. The results indicate that the spike amplitude required for a nociceptive response will increase with the increased gate-to-channel distances.

De-sensitization can also be mimicked by altering spike interval time (ΔT) between noxious spike (2.5 V, 10 ms) and non-noxious spike (1.5 V, 10 ms), as shown in Fig.6(j). Fig.6(k) shows EPSC responses when the spikes were loaded on G₁. The EPSC value induced by the second non-noxious spike was greater than I_th value when ΔT is below 290 ms. Fig.6(l) shows EPSCs response when the spikes were loaded on G₄. The EPSC value by the non-noxious stimulus is below I_th. Figures S7(a) and S4(b) show the EPSCs response when the spikes are loaded on G₂ and G₃, respectively. Here, desensitization index can be defined as E = A₂/A₁ × 100%, where A₂ and A₁ are absolute EPSC amplitude triggered by the non-noxious and noxious spike, respectively. Fig.6(m) shows E vs. ΔT function. For spikes loaded on G₁, E decreases from ~88.26% to ~45.23% for ΔT increases from 20 to 990 ms. For spike loaded on G₄, E decreases from ~61.32% to ~29.43% for ΔT increases from 20 to 990 ms. The desensitization process can be well fitted using the following exponential function [47]:

(5)$E=E_1{\mathrm{e}}^{\frac{-\mathrm{\Delta }T}{\tau }}+E_0,$

where E₀, E₁ and τ are the desensitization constant, the desensitization factor and the relaxation time, respectively. As shown in Table S4 of the ESM, E₀, E₁, and τ decrease with increased gate-to-channel distances. The results suggest that the artificial nociceptor will trigger desensitization behavior for ΔT>τ.

4 Conclusion

In summary, SA-gated indium tin oxide (ITO) dendrite transistors were fabricated with low-cost processing. Ebbinghaus forgetting curve is mimicked by loading spikes with different durations, numbers and amplitudes. Temporal integration and coincidence detection were successfully mimicked on the dendrite transistors by loading spikes on lateral dendrite gates with different coupling strength. Furthermore, neural multiplication operations of frequency-encoded signals have been demonstrated on a single dendrite transistor. Additionally, spatially correlated sensitization and desensitization behavior of pain perception have been implemented on the multi-gate dendrite transistors. These results pave the way for the developments of brain-inspired neuromorphic systems that are capable of advanced sensory processing.

References

[1] J. Backus, Can programming be liberated from the Von Neumann style? A functional style and its algebra of programs, Commun. ACM 21(8), 613 (1978)

[2] C. K. Machens, Building the human brain, Science 338(6111), 1156 (2012)

[3] G. Indiveri,E. Chicca,R. Douglas, A VLSI array of low-power spiking neurons and bistable synapses with spike-timing dependent plasticity, IEEE Trans. Neural Netw. 17(1), 211 (2006)

[4] W. Xiong, L. Q. Zhu, C. Ye, Z. Y. Ren, F. Yu, H. Xiao, Z. Xu, Y. Zhou, H. Zhou, and H. L. Lu, Flexible poly (vinyl alcohol)–graphene oxide hybrid nanocomposite based cognitive memristor with pavlovian‐conditioned reflex activities, Adv. Electron. Mater. 6(5), 1901402 (2020)

[5] Z. L. Dong, Q. L. Hua, J. G. Xi, Y. H. Shi, T. C. Huang, X. H. Dai, J. A. Niu, B. J. Wang, Z. L. Wang, and W. G. Hu, Ultrafast and low-power 2D Bi₂O₂Se memristors for neuromorphic computing applications, Nano Lett. 23(9), 3842 (2023)

[6] Z. Xu, Y. X. Li, Y. Xia, C. Y. Shi, S. J. Chen, C. L. Ma, C. Zhang, and Y. Li, Organic frameworks memristor: An emerging candidate for data storage, artificial synapse, and neuromorphic device, Adv. Funct. Mater. 34(16), 2312658 (2024)

[7] X. J. Zhu, D. Li, X. G. Liang, and W. D. Lu, Ionic modulation and ionic coupling effects in MoS₂ devices for neuromorphic computing, Nat. Mater. 18(2), 141 (2019)

[8] J. L. Meng, J. R. Song, Y. Q. Fang, T. Y. Wang, H. Zhu, L. Ji, Q. Q. Sun, D. W. Zhang, and L. Chen, Ionic diffusive nanomemristors with dendritic competition and cooperation functions for ultralow voltage neuromorphic computing, ACS Nano 18(12), 9150 (2024)

[9] U. Y. Won, Q. An Vu, S. B. Park, M. H. Park, V. Dam Do, H. J. Park, H. Yang, Y. H. Lee, and W. J. Yu, Multi-neuron connection using multi-terminal floating-gate memristor for unsupervised learning, Nat. Commun. 14(1), 3070 (2023)

[10] Y. H. Lin, W. X. Wang, R. L. Li, J. Kim, C. W. Zhang, H. Kan, and Y. Li, Multifunctional optoelectronic memristor based on CeO₂/MoS₂ heterojunction for advanced artificial synapses and bionic visual system with nociceptive sensing, Nano Energy 121, 109267 (2024)

[11] T. Y. Long, L. Q. Zhu, Z. Y. Ren, and Y. B. Guo, Global modulatory heterosynaptic mechanisms in bio-polymer electrolyte gated oxide neuron transistors, J. Phys. D Appl. Phys. 53(43), 435105 (2020)

[12] X. Liu,C. Sun,Z. Guo,Y. Zhang,Z. Zhang, J. Shang,Z. Zhong,X. Zhu,X. Yu,R. W. Li, A flexible dual-gate hetero-synaptic transistor for spatiotemporal information processing, Nanoscale Adv. 4(11), 2412 (2022)

[13] Y. L. He, S. Nie, R. Liu, S. S. Jiang, Y. Shi, and Q. Wan, Spatiotemporal information processing emulated by multiterminal neuro-transistor networks, Adv. Mater. 31(21), 1900903 (2019)

[14] W. N. Hu, J. Jiang, D. D. Xie, S. T. Wang, K. X. Bi, H. G. Duan, J. L. Yang, and J. He, Transient security transistors self-supported on biodegradable natural-polymer membranes for brain-inspired neuromorphic applications, Nanoscale 10(31), 14893 (2018)

[15] W. T. Gao, L. Q. Zhu, J. Tao, D. Y. Wan, H. Xiao, and F. Yu, Dendrite integration mimicked on starch-based electrolyte-gated oxide dendrite transistors, ACS Appl. Mater. Interfaces 10(46), 40008 (2018)

[16] J. M. Guo, Y. H. Liu, F. C. Zhou, F. Z. Li, Y. T. Li, and F. Huang, Linear classification function emulated by pectin-based polysaccharide-gated multiterminal neuron transistors, Adv. Funct. Mater. 31(33), 2102015 (2021)

[17] Y. Li, Y. J. Huang, X. L. Chen, W. S. Wang, X. Huang, H. Xiao, and L. Q. Zhu, Multi-terminal pectin/chitosan hybrid electrolyte gated oxide neuromorphic transistor with multi-mode cognitive activities, Front. Phys. (Beijing) 19(5), 53204 (2024)

[18] C. Y. Zheng, Y. Liao, Z. Y. Xiong, Y. Zhou, and S. T. Han, Mimicking the competitive and cooperative behaviors with multi-terminal synaptic memtransistors, J. Mater. Chem. C 8(18), 6063 (2020)

[19] D. H. Edwards, S. R. Yeh, and F. B. Krasne, Neuronal coincidence detection by voltage-sensitive electrical synapses, Proc. Natl. Acad. Sci. USA 95(12), 7145 (1998)

[20] R. A. Silver, Neuronal arithmetic, Nat. Rev. Neurosci. 11(7), 474 (2010)

[21] A. E. Dubin and A. Patapoutian, Nociceptors: The sensors of the pain pathway, J. Clin. Invest. 120(11), 3760 (2010)

[22] S. Mohanapriya, S. D. Bhat, A. K. Sahu, A. Manokaran, R. Vijayakumar, S. Pitchumani, P. Sridhar, and A. K. Shukla, Sodium-alginate-based proton-exchange membranes as electrolytes for DMFCs, Energy Environ. Sci. 3(11), 1746 (2010)

[23] P. Kanti, K. Srigowri, J. Madhuri, B. Smitha, and S. Sridhar, Dehydration of ethanol through blend membranes of chitosan and sodium alginate by pervaporation, Separ. Purif. Tech. 40(3), 259 (2004)

[24] Q. P. Fu, J. Hu, and S. Q. Zhou, Adsorption properties of graphene oxide@sodium alginate composite for Pb(II), J. Iran. Chem. Soc. 21(2), 399 (2024)

[25] C. Müller, H. Beck, D. Coulter, and S. Remy, Inhibitory control of linear and supralinear dendritic excitation in CA₁ pyramidal neuron, Neuron 75(5), 851 (2012)

[26] D. V. Buonomano, Decoding temporal information: A model based on short-term synaptic plasticity, J. Neurosci. 20(3), 1129 (2000)

[27] C. C. Wang, C. Weyrer, M. Paturu, D. Fioravante, and W. G. Regehr, Calcium-dependent protein kinase C is not required for post-tetanic potentiation at the hippocampal CA₃ to CA₁ synapse, J. Neurosci. 36(24), 6393 (2016)

[28] S. Kusakari, F. Saitow, Y. Ago, K. Shibasaki, M. Sato-Hashimoto, Y. Matsuzaki, T. Kotani, Y. Murata, H. Hirai, T. Matsuda, H. Suzuki, T. Matozaki, and H. Ohnishi, Shp2 in forebrain neurons regulates synaptic plasticity, locomotion, and memory formation in mice, Mol. Cell. Biol. 35(9), 1557 (2015)

[29] R. S. Zucker and W. G. Regehr, Short-term synaptic plasticity, Annu. Rev. Physiol. 64(1), 355 (2002)

[30] J. H. Xu, L. He, and L. G. Wu, Role of Ca²⁺ channels in short-term synaptic plasticity, Curr. Opin. Neurobiol. 17(3), 352 (2007)

[31] W. G. Regehr, Short-term presynaptic plasticity, Cold Spring Harb. Perspect. Biol. 4(7), a005702 (2012)

[32] H. Ebbinghaus, Memory: A contribution to experimental psychology, Ann. Neurosci. 20(4), 155 (2013)

[33] J. M. Murre and J. Dros, Replication and analysis of Ebbinghaus’ forgetting curve, PLoS One 10(7), e0120644 (2015)

[34] S. A. Roy and K. D. Alloway, Coincidence detection or temporal integration? What the neurons in somatosensory cortex are doing, J. Neurosci. 21(7), 2462 (2001)

[35] H. Agmon-Snir, C. E. Carr, and J. Rinzel, The role of dendrites in auditory coincidence detection, Nature 393(6682), 268 (1998)

[36] A. K. Engel, P. Fries, and W. Singer, Dynamic predictions: Oscillations and synchrony in top-down processing, Nat. Rev. Neurosci. 2(10), 704 (2001)

[37] J. M. Yan, J. S. Ying, M. Y. Yan, Z. C. Wang, S. S. Li, T. W. Chen, G. Y. Gao, F. Y. Liao, H. S. Luo, T. Zhang, Y. Chai, and R. K. Zheng, Optoelectronic coincidence detection with two-dimensional Bi₂O₂Se ferroelectric field-effect transistors, Adv. Funct. Mater. 31(40), 2103982 (2021)

[38] R. A. John, N. Tiwari, Y. Y. Chen, and N. Ankit, Ultralow power dual-gated subthreshold oxide neuristors: An enabler for higher order neuronal temporal correlations, ACS Nano 12(11), 11263 (2018)

[39] C. J. Wan, L. Q. Zhu, Y. H. Liu, P. Feng, Z. P. Liu, H. L. Cao, P. Xiao, Y. Shi, and Q. Wan, Proton-conducting graphene oxide-coupled neuron transistors for brain-inspired cognitive systems, Adv. Mater. 28(18), 3557 (2016)

[40] Y. J. Huang, W. S. Wang, X. Huang, J. K. Di, H. Xiao, and L. Q. Zhu, Oxide dendrite transistors gated with polyvinyl alcohol/chitosan hybrid electrolyte for spatiotemporal integration, J. Alloys Compd. 1010, 177938 (2025)

[41] M. J. Tovee, E. T. Rolls, and P. Azzopardi, Translation invariance in the responses to faces of single neurons in the temporal visual cortical areas of the alert macaque, J. Neurophysiol. 72(3), 1049 (1994)

[42] R. A. Andersen, G. K. Essick, and R. M. Siegel, Encoding of spatial location by posterior parietal neurons, Science 230(4724), 456 (1985)

[43] A. E. Dubin and A. Patapoutian, Nociceptors: The sensors of the pain pathway, J. Clin. Invest. 120(11), 3760 (2010)

[44] A. I. Basbaum, D. M. Bautista, G. Scherrer, and D. Julius, Cellular and molecular mechanisms of pain, Cell 139(2), 267 (2009)

[45] T. Hucho and J. D. Levine, Signaling pathways in sensitization: Toward a nociceptor cell biology, Neuron 55(3), 365 (2007)

[46] Z. H. Xu, G. B. Chen, S. B. Chen, and H. H. Xu, Mimicking pain conditioning using an electrolyte-gated organic synaptic transistor, Adv. Mater. Technol. 9(11), 2302047 (2024)

[47] Y. T. Xu, D. P. Liu, S. L. Dai, J. Y. Zhang, Z. Y. Guo, X. Liu, L. Z. Xiong, and J. Huang, Stretchable and neuromorphic transistors for pain perception and sensitization emulation, Mater. Horiz. 11(4), 958 (2024)

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

Data will be made available on request.

Electronic supplementary materials

The online version contains supplementary material available at https://doi.org/10.15302/frontphys.2025.034205.

Acknowledgements

This work was supported by Ningbo Key Scientific and Technological Project (No. 2021Z116) and the National Natural Science Foundation of China (No. U22A2075).

RIGHTS & PERMISSIONS

2025 Higher Education Press