

Development of a novel hand−eye calibration for intuitive control of minimally invasive surgical robot
Received date: 01 Dec 2021
Accepted date: 21 Apr 2022
Published date: 15 Sep 2022
Copyright
Robotic-assisted surgical system has introduced a powerful platform through dexterous instrument and hand−eye coordination intuitive control. The knowledge of laparoscopic vision is a crucial piece of information for robot-assisted minimally invasive surgery focusing on improved surgical outcomes. Obtaining the transformation with respect to the laparoscope and robot slave arm frames using hand−eye calibration is essential, which is a key component for developing intuitive control algorithm. We proposed a novel two-step modified dual quaternion for hand−eye calibration in this study. The dual quaternion was exploited to solve the hand−eye calibration simultaneously and powered by an iteratively separate solution. The obtained hand−eye calibration result was applied to the intuitive control by using the hand−eye coordination criterion. Promising simulations and experimental studies were conducted to evaluate the proposed method on our surgical robot system. We extensively compared the proposed method with state-of-the-art methods. Results demonstrate this method can improve the calibration accuracy. The effectiveness of the intuitive control algorithm was quantitatively evaluated, and an improved hand−eye calibration method was developed. The relationship between laparoscope and robot kinematics can be established for intuitive control.
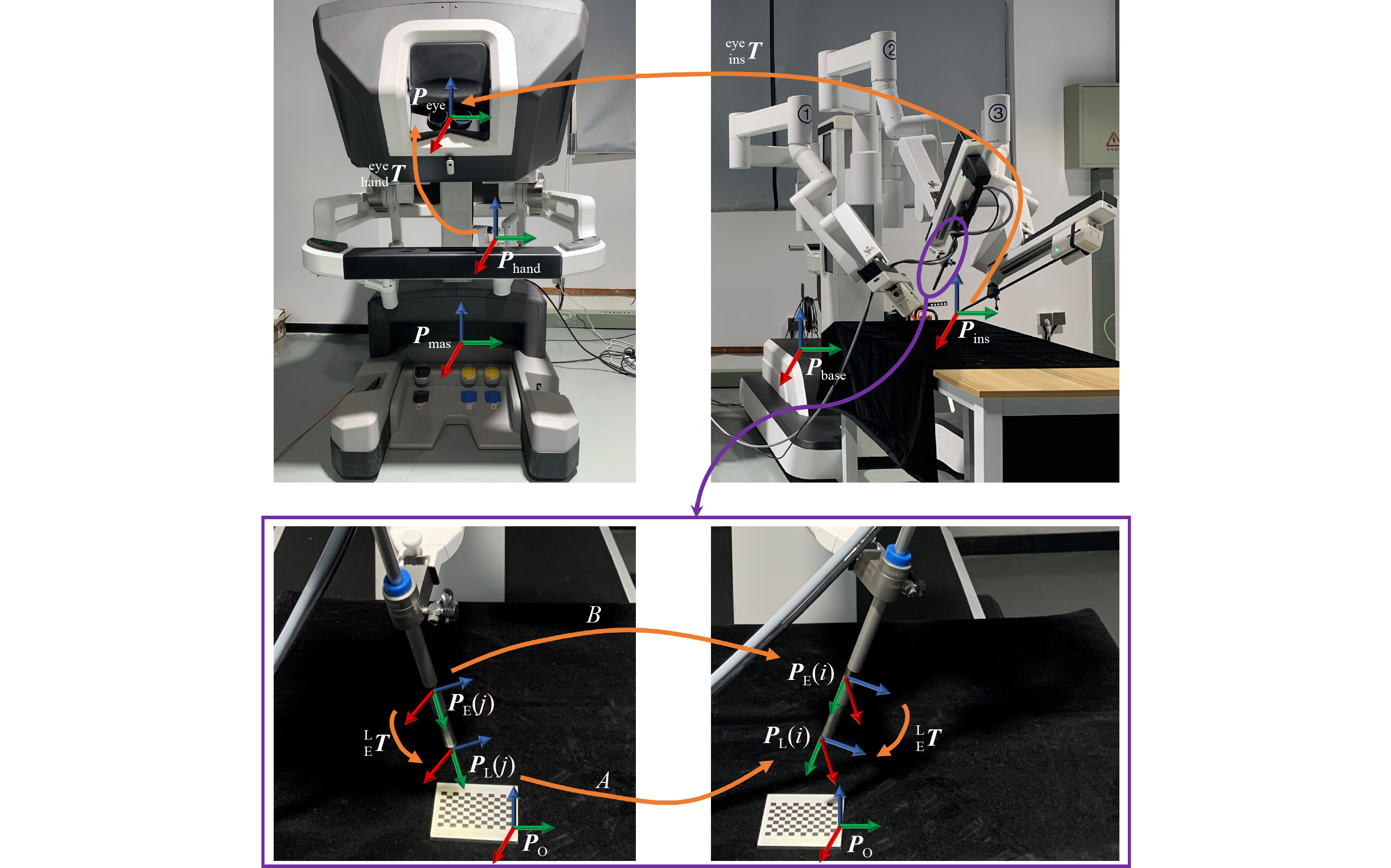
Yanwen SUN , Bo PAN , Yili FU . Development of a novel hand−eye calibration for intuitive control of minimally invasive surgical robot[J]. Frontiers of Mechanical Engineering, 2022 , 17(3) : 42 . DOI: 10.1007/s11465-022-0698-y
| A | Matrix of laparoscope motion |
| B | Matrix of robot motion |
| K | Matrix for solving hand‒eye equation |
| L | Modified matrix for hand‒eye equation solution |
| M | Matrix vector |
| N | Number of experimental test data groups |
| Robot laparoscope slave arm base frame | |
| Robot laparoscope slave arm end-effector frame | |
| Laparoscope frame | |
| Calibration object frame | |
| Translation vector from surgical robot slave instrument arm base frame to the instrument frame | |
| Position of surgical instrument in the surgeon eye frame in time step i | |
| Instrument position with respective with the laparoscope camera image frame | |
| Position of surgeon hand in the surgeon eye frame in time step i | |
| Translation vector from master system base frame to the surgeon hand frame | |
| , , | Dual quaternion representations of Eq. (2) |
| qAR, qXR, qBR | Rotation components |
| qAR0, qBR0 | Components of the and , respectively |
| qAt, qXt, qBt | Translation components |
| Rotation matrix component of | |
| Rotation matrix component of homogeneous transformation matrix from master system base frame to the surgeon hand frame | |
| Rotation matrix component of homogeneous transformation matrix from surgical robot slave instrument arm base frame to the instrument frame | |
| Rotation matrix component of homogeneous transformation matrix from laparoscope camera image frame to robot laparoscope slave arm end tool frame | |
| Rotation matrix component of | |
| , , | Translation component of the homogeneous transformation matrix in AX = XB |
| Ground-truth value | |
| Transformation matrix from robot laparoscope end tool frame to robot instrument slave arm base frame | |
| Transformation between and | |
| Homogeneous transformation from surgeon eye frame to surgeon hand frame | |
| Homogeneous transformation matrix from master system base frame to the surgeon hand frame | |
| Transformation matrix from surgeon eye frame to the laparoscope camera image frame | |
| Homogeneous transformation matrix from surgical robot slave instrument arm base frame to the instrument frame | |
| Homogeneous transformation from surgeon eye frame to instrument frame | |
| Homogeneous transformation from laparoscope camera image frame to instrument frame | |
| Transformation matrix from laparoscope camera image frame to robot laparoscope slave arm end tool frame | |
| Homogeneous transformation from surgeon eye frame to master system base frame | |
| Motion i of transformation between robot laparoscope slave arm base frame and the robot laparoscope slave arm end-effector frame | |
| Motion i of transformation between calibration object frame and the laparoscope frame | |
| X | Target homogeneous transformation matrix |
| , , | Rotation component of the homogeneous transformation matrix in AX = XB |
| Ground-truth value | |
| , | Parameters for dual quaternion solution |
| , | Parameters for dual quaternion solution of Eq. (9) |
| Defined ratio variable for solving equation | |
| , , , | Lie group members of the transformation |
| Master–slave position mapping scale factor | |
| Rotation matrix error | |
| Translation vector error | |
| Translation error between calculated value and ground-truth value | |
| Rotation error between calculated value and ground-truth value |
| 1 |
Zhong F X, Wang Z R, Chen W, He K J, Wang Y Q, Liu Y H. Hand-eye calibration of surgical instrument for robotic surgery using interactive manipulation. IEEE Robotics and Automation Letters, 2020, 5(2): 1540–1547
|
| 2 |
Gao Y Q, Wang S X, Li J M, Li A M, Liu H B, Xing Y. Modeling and evaluation of hand‒eye coordination of surgical robotic system on task performance. The International Journal of Medical Robotics and Computer Assisted Surgery, 2017, 13(4): e1829
|
| 3 |
Su H, Hu Y B, Karimi H R, Knoll A, Ferrigno G, Momi E D. Improved recurrent neural network-based manipulator control with remote center of motion constraints: experimental results. Neural Networks, 2020, 131: 291–299
|
| 4 |
Zhang W, Li H Y, Cui L L, Li H Y, Zhang X Y, Fang S X, Zhang Q J. Research progress and development trend of surgical robot and surgical instrument arm. The International Journal of Medical Robotics and Computer Assisted Surgery, 2021, 17(5): e2309
|
| 5 |
Zhang Z Q, Zhang L, Yang G Z. A computationally efficient method for hand–eye calibration. International Journal of Computer Assisted Radiology and Surgery, 2017, 12(10): 1775–1787
|
| 6 |
Su H, Qi W, Yang C G, Sandoval J, Ferrigno G, Momi E D. Deep neural network approach in robot tool dynamics identification for bilateral teleoperation. IEEE Robotics and Automation Letters, 2020, 5(2): 2943–2949
|
| 7 |
Wang Z Y, Zi B, Ding H F, You W, Yu L T. Hybrid grey prediction model-based autotracking algorithm for the laparoscopic visual window of surgical robot. Mechanism and Machine Theory, 2018, 123: 107–123
|
| 8 |
Allan M, Ourselin S, Hawkes D J, Kelly J D, Stoyanov D. 3-D pose estimation of articulated instruments in robotic minimally invasive surgery. IEEE Transactions on Medical Imaging, 2018, 37(5): 1204–1213
|
| 9 |
Kassahun Y, Yu B B, Tibebu A T, Stoyanov D, Giannarou S, Metzen J H, Vander Poorten E. Surgical robotics beyond enhanced dexterity instrumentation: a survey of machine learning techniques and their role in intelligent and autonomous surgical actions. International Journal of Computer Assisted Radiology and Surgery, 2016, 11(4): 553–568
|
| 10 |
Du X F, Kurmann T, Chang P L, Allan M, Ourselin S, Sznitman R, Kelly J D, Stoyanov D. Articulated multi-instrument 2-D pose estimation using fully convolutional networks. IEEE Transactions on Medical Imaging, 2018, 37(5): 1276–1287
|
| 11 |
Wang Z R, Liu Z W, Ma Q L, Cheng A, Liu Y H, Kim S, Deguet A, Reiter A, Kazanzides P, Taylor R H. Vision-based calibration of dual RCM-based robot arms in human‒robot collaborative minimally invasive surgery. IEEE Robotics and Automation Letters, 2018, 3(2): 672–679
|
| 12 |
Tsai R Y, Lenz R K. A new technique for fully autonomous and efficient 3D robotics hand/eye calibration. IEEE Transactions on Robotics and Automation, 1989, 5(3): 345–358
|
| 13 |
Shiu Y C, Ahmad S. Calibration of wrist-mounted robotic sensors by solving homogeneous transform equations of the form AX = XB. IEEE Transactions on Robotics and Automation, 1989, 5(1): 16–29
|
| 14 |
Chou J C K, Kamel M. Finding the position and orientation of a sensor on a robot manipulator using quaternions. The International Journal of Robotics Research, 1991, 10(3): 240–254
|
| 15 |
Horaud R, Dornaika F. Hand‒eye calibration. The International Journal of Robotics Research, 1995, 14(3): 195–210
|
| 16 |
Park F C, Martin B J. Robot sensor calibration: solving AX = XB on the Euclidean group. IEEE Transactions on Robotics and Automation, 1994, 10(5): 717–721
|
| 17 |
Daniilidis K. Hand‒eye calibration using dual quaternions. The International Journal of Robotics Research, 1999, 18(3): 286–298
|
| 18 |
Lu Y C, Chou J C K. Eight-space quaternion approach for robotic hand‒eye calibration. In: Proceedings of 1995 IEEE International Conference on Systems, Man and Cybernetics. Intelligent Systems for the 21st Century. Vancouver: IEEE, 1995,
|
| 19 |
Zhao Z J, Liu Y C. A hand‒eye calibration algorithm based on screw motions. Robotica, 2009, 27(2): 217–223
|
| 20 |
Li W, Dong M L, Lu N G, Lou X P, Sun P. Simultaneous robot–world and hand–eye calibration without a calibration object. Sensors, 2018, 18(11): 3949
|
| 21 |
Andreff N, Horaud R, Espiau B. On-line hand–eye calibration. In: Proceedings of the Second International Conference on 3-D Digital Imaging and Modeling. Ottawa: IEEE, 1999,
|
| 22 |
Pachtrachai K, Vasconcelos F, Dwyer G, Hailes S, Stoyanov D. Hand‒eye calibration with a remote centre of motion. IEEE Robotics and Automation Letters, 2019, 4(4): 3121–3128
|
| 23 |
Mao J F, Huang X P, Jiang L. A flexible solution to AX = XB for robot hand‒eye calibration. In: Proceedings of the 10th WSEAS International Conference on Robotics, Control and Manufacturing Technology. Hangzhou: World Scientific and Engineering Academy and Society (WSEAS), 2010,
|
| 24 |
Schmidt J, Vogt F, Niemann H. Robust hand–eye calibration of an endoscopic surgery robot using dual quaternions. In: Michaelis B, Krell G, eds. Pattern Recognition. DAGM 2003. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer, 2003,
|
| 25 |
Zhao Z J. Hand‒eye calibration using convex optimization. In: Proceedings of 2011 IEEE International Conference on Robotics and Automation (ICRA). Shanghai: IEEE, 2011,
|
| 26 |
Enebuse I, Foo M, Ibrahim B S K K, Ahmed H, Supmak F, Eyobu O S. A comparative review of hand‒eye calibration techniques for vision guided robots. IEEE Access, 2021, 9: 113143–113155
|
| 27 |
Pachtrachai K, Vasconcelos F, Edwards P, Stoyanov D. Learning to calibrate—estimating the hand‒eye transformation without calibration objects. IEEE Robotics and Automation Letters, 2021, 6(4): 7309–7316
|
| 28 |
Pachtrachai K, Allan M, Pawar V, Hailes S, Stoyanov D. Hand‒eye calibration for robotic assisted minimally invasive surgery without a calibration object. In: Proceedings of 2016 IEEE/ RSJ International Conference on Intelligent Robots and Systems (IROS). Daejeon: IEEE, 2016,
|
| 29 |
Thompson S, Stoyanov D, Schneider C, Gurusamy K, Ourselin S, Davidson B, Hawkes D, Clarkson M J. Hand–eye calibration for rigid laparoscopes using an invariant point. International Journal of Computer Assisted Radiology and Surgery, 2016, 11(6): 1071–1080
|
| 30 |
Pachtrachai K, Vasconcelos F, Chadebecq F, Allan M, Hailes S, Pawar V, Stoyanov D. Adjoint transformation algorithm for hand–eye calibration with applications in robotic assisted surgery. Annals of Biomedical Engineering, 2018, 46(10): 1606–1620
|
| 31 |
Su H, Li S, Manivannan J, Bascetta L, Ferrigno G, Momi E D. Manipulability optimization control of a serial redundant robot for robot-assisted minimally invasive surgery. In: Proceedings of 2019 International Conference on Robotics and Automation (ICRA). Montreal: IEEE, 2019,
|
| 32 |
Morgan I, Jayarathne U, Rankin A, Peters T M, Chen E C S. Hand‒eye calibration for surgical cameras: a procrustean perspective-n-point solution. International Journal of Computer Assisted Radiology and Surgery, 2017, 12(7): 1141–1149
|
| 33 |
Malti A, Barreto J P. Hand–eye and radial distortion calibration for rigid endoscopes. The International Journal of Medical Robotics and Computer Assisted Surgery, 2013, 9(4): 441–454
|
| 34 |
Peng J Q, Xu W F, Wang F X, Han Y, Liang B. A hybrid hand–eye calibration method for multilink cable-driven hyper-redundant manipulators. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1–13
|
| 35 |
Niu G J, Pan B, Ai Y, Fu Y L. Intuitive control algorithm of a novel minimally invasive surgical robot. Computer Assisted Surgery, 2016, 21(sup1): 92–101
|
| 36 |
Niu G J, Pan B, Fu Y L, Qu C C. Development of a new medical robot system for minimally invasive surgery. IEEE Access, 2020, 8: 144136–144155
|
| 37 |
Zuo S Y, Wang Z, Zhang T C, Chen B J. A novel master–slave intraocular surgical robot with force feedback. The International Journal of Medical Robotics and Computer Assisted Surgery, 2021, 17(4): e2267
|
| 38 |
Dimitrakakis E, Lindenroth L, Dwyer G, Aylmore H, Dorward N L, Marcus H J, Stoyanov D. An intuitive surgical handle design for robotic neurosurgery. International Journal of Computer Assisted Radiology and Surgery, 2021, 16(7): 1131–1139
|
| 39 |
Zhang Z. A flexible new technique for camera calibration. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330–1334
|
/
| 〈 |
|
〉 |