Meshing stiffness property and meshing status simulation of harmonic drive under transmission loading

Abstract

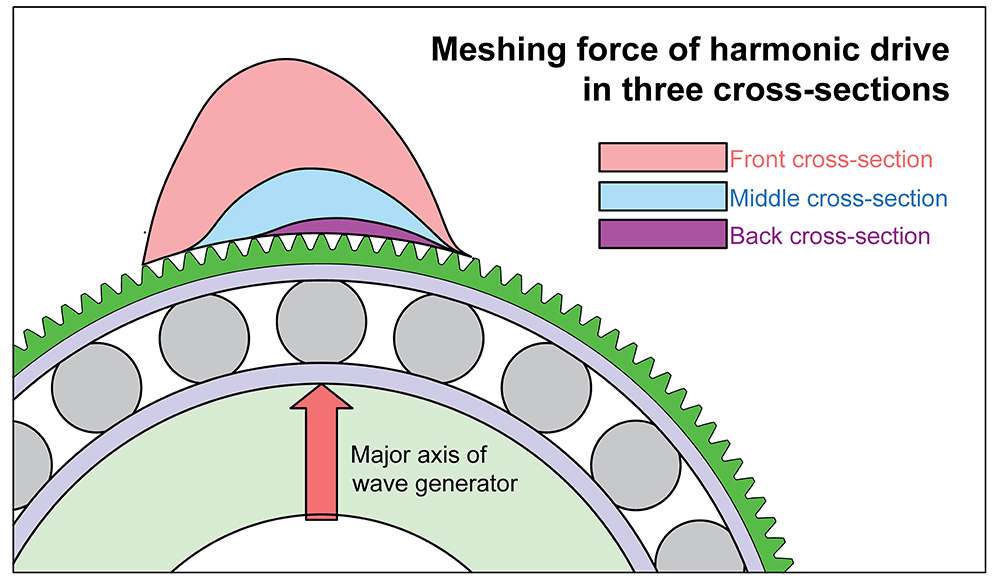
The multitooth meshing state of harmonic drive (HD) is an important basic characteristic of its high transformation precision and high bearing capacity. Meshing force distribution affects the load sharing of the tooth during meshing, and theoretical research remains insufficient at present. To calculate the spatial distributed meshing forces and loading backlashes along the axial direction, an iterative algorithm and finite element model (FEM) is proposed to investigate the meshing state under varied transmission loading. The displacement formulae of meshing point under tangential force are derived according to the torsion of the flexspline cylinder and the bending of the tooth. Based on the relationship of meshing forces and circumferential displacements, meshing forces and loading backlashes in three cross-sections are calculated with the algorithm under gradually increased rotation angles of circular spline, and the results are compared with FEM. Owing to the taper deformation of the cup-shaped flexspline, the smallest initial backlash and the earliest meshing point appear in the front cross-section far from the cup bottom, and then the teeth in the middle cross-section of the tooth rim enter the meshing and carry most of the loading. Theoretical and numerical research show that the flexibility is quite different for varied meshing points and tangential force amplitude because of the change of contact status between the flexspline and the wave generator. The meshing forces and torsional stiffness of the HD are nonlinear with the torsional angle.

Key words： harmonic drive; meshing flexibility matrix; meshing force; loading backlash; flexspline; contact analysis

Acknowledgements

The authors were grateful for support from the National Natural Science Foundation of China (Grant No. 51575390), and the Natural Science Key Foundation of Tianjin, China (Grant Nos. 19JCZDJC38700 and 18JCZDJC39000).

Nomenclature

b	Width of tooth rim
ci	Minimum initial backlash
dij (j = 1, 2, …, n)	Circumferential displacement on tooth j produced by the tangential force on tooth i
drim	Hole diameter of the disk model
D	Meshing flexibility matrix
{d}	Circumferential displacement array
e	Eccentric distance of the disk
E	Young’s modulus
F	Tangential force applied on meshing point
{F}	Meshing force array
G	Shear modulus of elasticity
GAP	Loading backlash in finite element model
haf	Tooth height from tooth tip to neutral curve
i	Number of a tooth
Ip	Inertia moment of the cross-section
Jt	Backlash between FS and CS
k	Meshing tooth number
K1, K2	Meshing point on FS tooth and CS tooth, respectively
K	Meshing stiffness matrix
l	Cylinder length from the diaphragm to the open edge of cup-shaped FS
lc	Length of the cylinder
m	Gear modulus
n	Number of the meshing points
{N}	Array of tooth number in the meshing region
PRES	Normal contact pressure in finite element model
r	Any radius on the disk model
r1	Radius of FS pitch circle
raf	Radius of the FS addendum circle
ri	Inner radius of the cylinder
rm	Radius of the tooth rim neutral circle
R	Radius of the disk in double-disk WG
Rd	Out radius of disk model
sh	Tooth thickness at x = haf/2
sp	Tooth thickness on pitch circle
Sc, Sf, Sw	Coordinate system connected with CS, FS, and WG, respectively
stp	Rotate step
tw	Width of the disk
T	Torsional moment applied on the disk model
u	Radial displacement of the neutral line
u0	Maximum radial displacement of the neutral line
u1, u2	Radial displacements of the neutral line within wrap angle and out of wrap angle, respectively
v	Circumferential displacement of the neutral line
v1, v2	Circumferential displacements of the neutral line within wrap angle and out of wrap angle, respectively
vaf	Circumferential displacement of meshing point due to the rotation of the tooth root
vb	Circumferential displacement of the cup bottom at the outside
vc	Circumferential displacement corresponding to the twist of cylinder
vr	Circumferential displacement at any radius r
vR	Circumferential displacement of meshing point due to torsional deformation of tooth rim
vT	Circumferential displacement of meshing point under bending moment of tangential force
vθ	Circumferential displacement of the disk with torsional moment
x1, x2	Tooth modification coefficients of FS and CS, respectively
z0	Tooth number of the inserted blade
z1, z2	Tooth numbers of the FS and the CS, respectively
Tk	Total torsional torque
α0	Tooth profile angle
αk	Pressure angle at any point of involute
αG2	Cutting angle of the slotting cutter when machining the CSTP
β	Wrap angle of the tooth rim to the disk
γ	Shear strain at any radius r of the disk model
λ	Involute parameter
δ1	Thickness of the tooth rim
δ2	Thickness of the cylinder
δr	Thickness of disk model
ε	Iteration accuracy
θ	Deflection angle of the neutral line normal
θ1, θ2	Deflection angles of the neutral line normal within wrap angle and out of wrap angle
θk	Circumferential displacement on the meshing point of CS
θr	Rotation angle at the tooth root
ρ(φ, z)	Polar radius of neutral layer
τ	Shear stress at any radius r of the disk model
φ	Polar angle between the major axis of WG and the point on undeformed neutral circle
φ1	Polar angle between the major axis of WG and the point on deformed neutral line
φc	Twist angle of the cylinder
φf	Rotation angle of OwOf in Fig. 5
φF	Rotation angle of FS
φi	Index angle of the CS tooth symmetry line
φw	Rotation angle of WG
ψ	Half of the corresponding center angle of a pitch
Δ	Coefficient of tooth thickness on pitch circle
Φ	Angle between yf and yc in Fig. 5
μ	Angle between OwOf (polar radius ρ) and axis yc

References

1 Musser C W. US Patent, 2906143, 1955-3-21

2 Salahshoor E , Ebrahimi S , Zhang Y Q . Frequency analysis of a typical planar flexible multibody system with joint clearances. Mechanism and Machine Theory, 2018, 126 : 429– 456

3 Karimi Eskandary P , Angeles J . The translating Π-joint: design and applications. Mechanism and Machine Theory, 2018, 122 : 361– 370

4 López-Martínez J , Blanco-Claraco J L , García-Vallejo D , Giménez-Fernández A . Design and analysis of a flexible linkage for robot safe operation in collaborative scenarios. Mechanism and Machine Theory, 2015, 92 : 1– 16

5 Ismail M A A , Windelberg J , Liu G J . Simplified sensorless torque estimation method for harmonic drive based electro-mechanical actuator. IEEE Robotics and Automation Letters, 2021, 6( 2): 835– 840

6 Li X Z , Song C S , Yang Y , Zhu C C , Liao D L . Optimal design of wave generator profile for harmonic gear drive using support function. Mechanism and Machine Theory, 2020, 152 : 103941

7 Yague-Spaude E , Gonzalez-Perez I , Fuentes-Aznar A . Stress analysis of strain wave gear drives with four different geometries of wave generator. Meccanica, 2020, 55( 11): 2285– 2304

8 Mahanto B S , Sahoo V , Maiti R . Effect of cam insertion on stresses in harmonic drive in industrial robotic joints. Procedia Computer Science, 2018, 133 : 432– 439

9 Maiti R . A novel harmonic drive with pure involute tooth gear pair. Journal of Mechanical Design, 2004, 126( 1): 178– 182

10 Kayabasi O , Erzincanli F . Shape optimization of tooth profile of a flexspline for a harmonic drive by finite element modelling. Materials & Design, 2007, 28( 2): 441– 447

11 Chen X X , Liu Y S , Xing J Z , Lin S Z , Xu W . The parametric design of double-circular-arc tooth profile and its influence on the functional backlash of harmonic drive. Mechanism and Machine Theory, 2014, 73 : 1– 24

12 Kalina A , Mazurkow A , Witkowski W , Wierzba B , Oleksy M . Properties of elasto-hydrodynamic oil film in meshing of harmonic drive gears. Materials, 2021, 14( 5): 1194

13 Gravagno F , Mucino V H , Pennestrì E . The mechanical efficiency of harmonic drives: a simplified model. Journal of Mechanical Design, 2021, 143( 6): 063302

14 Pacana J . The impact of the structural form on the stress distribution in a flexspline of a hermetic harmonic driver. Journal of Theoretical and Applied Mechanics, 2020, 58( 4): 1049– 1060

15 Abakumov A N , Zakharova N V . Determination of load capacity for flexible spline of harmonic drive. Journal of Physics: Conference Series, 2019, 1210( 1): 012001

16 Dong H M , Ting K L , Wang D L . Kinematic fundamentals of planar harmonic drives. Journal of Mechanical Design, 2011, 133( 1): 011007

17 Dong H M , Wang D L , Ting K L . Kinematic effect of the compliant cup in harmonic drives. Journal of Mechanical Design, 2011, 133( 5): 051004

18 Jia H , Li J Y , Xiang G , Wang J X , Xiao K , Han Y F . Modeling and analysis of pure kinematic error in harmonic drive. Mechanism and Machine Theory, 2021, 155 : 104122

19 Lyuminarsky I , Lyuminarsky S . Kinematic error of a harmonic drive. MATEC Web of Conferences, 2018, 224 : 01039

20 Ma D H , Wu J N , Yan S Z . A method for detection and quantification of meshing characteristics of harmonic drive gears using computer vision. Science China Technological Sciences, 2016, 59( 9): 1305– 1319

21 Ma D H , Wang R , Rao P F , Sui R M , Yan S Z . Automated analysis of meshing performance of harmonic drive gears under various operating conditions. IEEE Access: Practical Innovations, Open Solutions, 2018, 6 : 68137– 68154

22 Ma D H , Wu J N , Liu T , Yan S Z . Deformation analysis of the flexspline of harmonic drive gears considering the driving speed effect using laser sensors. Science China Technological Sciences, 2017, 60( 8): 1175– 1187

23 Xu L Z , Qin L , Zhu C . Displacements for an electromechanical integrated electrostatic harmonic drive. The Journal of Strain Analysis for Engineering Design, 2006, 41( 2): 101– 111

24 Xu L Z , Qin L , Zhu C R . Forces for electromechanical integrated electrostatic harmonic drive. Mechanism and Machine Theory, 2007, 42( 3): 334– 351

25 Hu Q S , Liu Z F , Yang C B , Xie F G . Research on dynamic transmission error of harmonic drive with uncertain parameters by an interval method. Precision Engineering, 2021, 68 : 285– 300

26 Dong H M , Zhu Z D , Zhou W D , Chen Z . Dynamic simulation of harmonic gear drives considering tooth profiles parameters optimization. Journal of Computers, 2012, 7( 6): 1429– 1436

27 Tjahjowidodo T , Al-Bender F , Van Brussel H . Theoretical modelling and experimental identification of nonlinear torsional behaviour in harmonic drives. Mechatronics, 2013, 23( 5): 497– 504

28 Strelnikov V N , Sukov M G . Teeth interference in harmonic drives intended for heavy engineering. Journal of Physics: Conference Series, 2019, 1333( 5): 052025

29 Chen X X Lin S Z Xing J Z Liu Y S. Simulation on gear backlash and interference check of harmonic drive with circular-arc teeth profile. Computer Integrated manufacturing Systems, 2011, 17(3): 643− 648 (in Chinese)

30 Chen Z G , Zhou Z W , Zhai W M , Wang K Y . Improved analytical calculation model of spur gear mesh excitations with tooth profile deviations. Mechanism and Machine Theory, 2020, 149 : 103838

31 Chen Z G , Ning J Y , Wang K Y , Zhai W M . An improved dynamic model of spur gear transmission considering coupling effect between gear neighboring teeth. Nonlinear Dynamics, 2021, 106( 1): 339– 357

32 Xie C Y , Hua L , Han X H , Lan J , Wan X J , Xiong X S . Analytical formulas for gear body-induced tooth deflections of spur gears considering structure coupling effect. International Journal of Mechanical Sciences, 2018, 148 : 174– 190

33 Li S T . Diaphragm stress analysis and fatigue strength evaluation of the flex-spline, a very thin-walled spur gear used in the strain wave gearing. Mechanism and Machine Theory, 2016, 104 : 1– 16

34 Chen X X , Liu Y S , Xing J Z , Lin S Z , Ma M . A novel method based on mechanical analysis for the stretch of the neutral line of the flexspline cup of a harmonic drive. Mechanism and Machine Theory, 2014, 76 : 1– 19

35 Ma J F Li C Luo Y C Cui L L. Simulation of meshing characteristics of harmonic reducer and experimental verification. Advances in Mechanical Engineering, 2018, 10(3): 1687814018767494

36 Chen X X Yang P P Xing J Z Yao Y P. Research on distribution of loading backlash and meshing force of harmonic drive. Journal of Xi’an Jiaotong University, 2018, 52(7): 9− 17 (in Chinese)

37 Sahoo V , Maiti R . Load sharing by tooth pairs in involute toothed harmonic drive with conventional wave generator cam. Meccanica, 2018, 53( 1): 373– 394

38 Sahoo V , Maiti R . Evidence of secondary tooth contact in harmonic drive, with involute toothed gear pair, through experimental and finite element analyses of stresses in flex-gear cup. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2018, 232( 2): 341– 357

39 Xu L Z , Liang Y L . Torque for an electromagnetic harmonic movable tooth drive system. Mechanism and Machine Theory, 2016, 98 : 190– 198