1 Introduction
High-energy physics (HEP) is an attracting and delicate branch of physics that manifests at the microscopic scale and which explores the fundamental building blocks of the universe and forces that govern their interactions at incredibly high energies under extremely intense conditions [
1,
2]. In this field many sophisticated instruments and tools with large particle accelerators, like the current CERN-LHC (located near the French and Swiss border), to study matter at energy levels that are otherwise unattainable to reach with conventional methods. These gigantic machines accelerate subatomic particles at nearly the speed of light and then smash them together, creating energy densities analogous of the early moments after the Big Bang [
3,
4]. By studying the collisions generated in these accelerators setups, it could be possible to track and evaluate rare particles that have a very short life time. This important study with the accumulated big data at higher collider luminosity values offers an improved understanding of the basic anatomy of different physics process and their topologies [
5,
6].
The standard model (SM) is the present theoretical framework that describes the elementary particles and their interactions [
7]. Despite its tremendous success in explaining many phenomena in nature, several mysteries remain unsolved, such as matter antimatter asymmetry, the nature of dark matter (DM), the neutrino mass and the hierarchy problem and many other open questions [
8]. Furthermore, it is worth noting that besides its deep investigation about the Universe puzzles, HEP has demonstrated significant practical utility when used with advanced technologies [
9]. As a matter of fact, the development of many techniques and technologies in this sector has driven notable progress in medical imaging [
10,
11], radiation therapy [
12,
13], and materials research [
14,
15].
The data acquisition system of large hadron collider (LHC) stores the data on tape using grid computing facilities, it can be disseminated for offline analysis aimed at extracting information concerning particle trajectories formed within the detectors. These trajectories contain concealed details about numerous particle characteristics. Jets are reconstructed by combining information from multiple detector subsystems, primarily calorimeters and trackers. The calorimeters (electromagnetic and hadronic) play a central role by capturing the energy deposits from both neutral and charged particles. These deposits are clustered using algorithms such as anti-
, which group the energy into Jets based on angular proximity in
-space. While tracking systems provide detailed momentum and charge information for individual charged particles, they cannot detect neutral particles, such as photons or neutrons. Therefore, the calorimeter serves as the primary tool for measuring the total energy of the Jet. This reconstruction process ensures that Jets are defined as comprehensive objects representing the full range of particle constituents, crucial for subsequent analyses in HEP experiments [
16].
Computer vision techniques become relevant and play a crucial role during the analysis of offline data. Specifically, in the realm of HEP data analysis, machine learning (ML) algorithms have found success, leading to significant enhancements in event classification performance when contrasted with traditional methods rooted in expert understanding. Techniques like boosted decision trees (BDT), shallow neural networks, and similar approaches have been employed in HEP data analysis. More recently, deep neural network (DNN) or deep learning (DL) has gained widespread adoption due to its applicability to intricate data structures such as images, videos, natural language, or sensor data. There are ongoing investigations into applying DNNs for analyzing granular details like particle positions and momentum as they traverse the detector. This has shown increased effectiveness in selecting signal events compared to ML algorithms employing conventional feature variables rooted in physics knowledge [
17].
1.1 Motivation
In HEP, a track typically refers to the trajectory or path followed by a charged particle as it moves through a particle detector. HEP experiments often involve the collision of high-energy particles, such as those produced in particle accelerators like LHC. When these particles collide, they produce various other particles as a result of the collisions. These newly created particles then pass through several sub-detectors where each designed to measure their corresponding properties. Each charged particle leaves behind a trace or track as it interacts with the detector’s various components, such as tracking chambers or silicon detectors. These tracks provide information about the particle’s momentum, charge, and the path it took through the detector. Analyzing these tracks is very crucial for understanding the physics of the collisions and for identifying the types of particles produced.
The reconstruction of particle tracks involves sophisticated algorithms and software that piece together the recorded data from various detector components to reconstruct the paths of the particles accurately. Then, the reconstructed tracks are essential for a wide range of analyses in HEP, including the discovery of new particles, the measurement of particle properties, and the investigation of fundamental forces and interactions in the universe.
However, in HEP experiments, there are always chances for high background contributions or events that are not of primary interest and can eventually mimic the physics signal and moreover can interfere along the physics collision. The background sources could be the electronic components in the different detector systems, when high-energetic particles pass through the material budget of the detector, they can also generate secondary tracks through different interactions, and possible decay modes.
In the light of the aforementioned phenomena and challenges, treating tracks/Jets in HEP as image or point cloud (PC)-like data for processing and analysis is a useful approach, especially when dealing with the output from particle detectors. Hence, ML and DL play vital roles in HEP experiments. They serve the following purposes: i) Identifying and classifying particles by analyzing their tracks and energy deposits in detectors, thereby enhancing precision and identification speed, ii) assisting in the accurate reconstruction of particle tracks from detector data, particularly in complex environments with numerous particles and interactions, iii) enabling efficient data analysis schemes, one can sift through extensive datasets to pinpoint rare or noteworthy events or particles, iv) detecting anomalies or unexpected patterns in the recorded data, which could potentially signify the existence of new particles and physics beyond the SM, among other applications. These contributions underscore the significance of ML and DL in advancing HEP research topics.
1.2 Related work
In recent years, there has been a surge in reviews addressing various aspects of HEP [
18–
21]. The review presented in [
18] delved into the realm of supervised DL applied to high-energy phenomenology, discussing specific use cases such as employing ML to explore new physics parameter spaces and utilizing graph neural networks for particle production and energy measurements at the LHC. Meanwhile, Ref. [
19] provided an overview of the initial forays into quantum ML in the context of HEP and offered insights into potential future applications. In Ref. [
20], an array of novel tools relevant to HEP were introduced, complete with assessments of their performance, though there was limited discussion about future prospects. Lastly, the review [
21] comprehensively examined both theoretical and experimental aspects of Jets such as triggering, data acquisition systems, propagation, interactions, and related phenomena in HEP.
Tab.1 assesses how the proposed review aligns with previous research in the field of HEP. Based on the assessment, it appears that our proposed review aims to comprehensively cover a wide range of topics related to the ML- and DL-based in HEP, including Jet preliminaries, taxonomy of HEP, available Jet datasets, Jet tagging preprocessing, quantum ML, DL models for Jet tagging, classification techniques, Jet tagging DL applications, and research gaps/future directions. This suggests that the proposed review aims to provide a comprehensive overview of the current state of research in HEP and potential avenues for future work.
Tab.1 Assessing how the proposed review aligns with previous research in the field of HEP. The ( ) indicates that those specific areas have been addressed, whereas () and ( ) signify instances where certain areas have not been addressed, or partially addressed, respectively. |
| Ref. | Paper type | Publication year | Jet prelimanaries | Taxonomy of HEP Jet | Available Jet datasets and tools | Jet tagging pre-process | Quantium ML for HEP Jet classification | ML and DL models for Jet classification | Transformers for Jet classification | ML and DL-based Jet classif. techniques | AI-based Jet apps | Research gaps and future direction |
|
| [ 18] | Mini-review | 2019 |  |  |  |  |  |  |  |  |  |  |
| [ 22] | Review | 2019 |  |  |  |  |  |  |  |  |  |  |
| [ 19] | Review | 2021 |  |  |  |  |  |  |  |  |  |  |
| [ 20] | Review | 2021 |  |  |  |  |  |  |  |  |  |  |
| [ 23] | Review | 2022 |  |  |  |  |  |  |  |  |  |  |
| [ 21] | Review | 2023 |  |  |  |  |  |  |  |  |  |  |
| This work | Review | 2024 |  |  |  |  |  |  |  |  |  |  |
1.3 Contribution and survey structure
The objective of this survey is to provide a robust foundation for both HEP researchers aiming to grasp the principles of DL and its applications within the HEP domain, and computer science researchers familiar with artificial intelligence (AI) seeking insights into the fundamental features and prerequisites essential for constructing a robust AI model tailored specifically for HEP, employing Jet images and PC. To achieve this goal, our contribution is encapsulated in the following key points:
– The survey offers preliminary insights into the various types of particles and performance metrics associated with both AI-based and non-AI-based Jet particle physics methodologies.
– The taxonomy of ML and DL-based techniques in HEP for analyzing Jet images and PC, along with their respective preprocessing and feature extraction methodologies, is thoroughly explored.
– The widely adopted AI models designed for analyzing HEP Jet tagging, along with their descriptive layered architectures, are extensively elaborated upon. Furthermore, their performance metrics are summarized and compared.
– Different state-of-the art (SOTA) methods are clustered based on the AI techniques employed and comprehensively reviewed accordingly. Additionally, the exploration of AI-based applications in HEP Jet classification is thoroughly detailed.
– Future directions and outlooks are explored, which aims to offer researchers insights into existing research gaps and areas within AI concepts and fields that remain unexplored in AI-based Jet images and PC.
The structure of this paper is as follows: Section 2 presents the preliminaries necessary for understanding Jet images and PC. In Section 3, the representation of Jet in DL-based HEP is discussed. Section 4 provides a summary of the most available ML or DL models for analyzing HEP Jet tagging. Section 5 showcases various AI-based applications of Jet tagging. Section 6 highlights the gaps and areas that remain unexplored in AI-based Jet analysis, encompassing both techniques and applications. Finally, Section 7 concludes the survey.
2 Preliminaries
2.1 Types of particles
W and Z bosons are important closely related particles described by the SM of particle physics. They are together known as the weak bosons or more generally as the intermediate vector bosons and plays a significant role in the weak nuclear force, which is responsible for certain types of specific interactions and radioactive decay. The existence and properties of the boson, along with the bosons, provided strong support for the electroweak theory and the SM as a whole. However, as with the boson, the SM has limitations and does not explain all aspects of particle physics, such as gravity, dark matter, and the hierarchy of particle masses. Here are some key points about the and bosons:
– Charge and variants: The boson comes in two varieties: the and the , which carry a positive and negative electric charge, respectively. These particles are antiparticles of each other. The boson is a neutral elementary particle.
– Mass and spin: The bosons masses are around 80.4 GeV/ (gigaelectronvolts per speed of light squared). The boson has a relatively large mass. Its mass is around 91.2 GeV/. Both and bosons have a spin of 1, which is a measure of their intrinsic angular momentum.
– Decay: The and bosons are unstable and have a very short lifetime. They quickly decay into other particles. For example, a boson can decay into a positron (an antielectron) and a neutrino, while a boson can decay into an electron and an antineutrino. The can decay into various combinations of charged leptons (such as electrons and muons) and their corresponding antiparticles, as well as neutrinos and antineutrinos.
The Higgs boson is crucial to our understanding of how other particles acquire mass and, by extension, how the universe’s structure and behavior arise. The key points about the Higgs boson are [
24]
Fig.1 Mind-map of the proposed review. |
Full size|PPT slide
– Origin of mass is associated with the Higgs field, a theoretical field that permeates all of space. In the SM, particles acquire mass by interacting with the Higgs field. The more a particle interacts with this field, the greater its mass will be. This mechanism explains why some particles are heavier than others.
– Mass and spin the Higgs boson itself has a mass of around 125.1 GeV/. It has a spin of 0, which means it has no intrinsic angular momentum.
– Decay is unstable and quickly decays into other particles after its creation in high-energy collisions. The specific decay modes and products depend on the energy at which it is produced.
– Higgs field interaction is a carrier of the interaction associated with the Higgs field. When particles move through space, they interact with this field, which gives them mass. The Higgs boson itself is the quantized excitation of this field.
The top quark is one of the heavy fundamental particles described by the SM. It holds a special place in particle physics due to its extremely large mass and its role in various processes involving high-energy collisions. Here are some key points about the top quark [
25]:
Fig.2 Visualization of decay involving a reconstructed Jet and a secondary vertex, showcasing various noteworthy features [27]. |
Full size|PPT slide
– Mass. The top quark is the heaviest known elementary particle. Its mass is approximately 173.2 GeV/, which is even heavier than an entire atom of gold.
– Quarks and the strong force. Quarks are the building blocks of protons and neutrons, which are the constituents of atomic nuclei. The top quark, like all quarks, experiences a strong nuclear force, which is responsible for holding quarks together within hadrons (particles composed of quarks).
– Weak decays. Due to its high mass, the top quark is relatively short-lived and decays before it can form bound states with other quarks to create hadrons. It decays primarily through weak interaction, one of the fundamental forces described by the SM.
– Production and detection. The top quark is typically produced in high-energy particle collisions, such as those that occur in experiments at particle accelerators like the LHC. Due to its high mass, the top quark is often produced along with its corresponding antiquark. Researchers detect its presence indirectly by observing its decay products, which can include other quarks, leptons (such as electrons and muons), and neutrinos.
– Role in electroweak symmetry breaking. The top quark is of particular interest in theories related to electroweak symmetry breaking, a phenomenon that explains why certain particles acquire mass. Its large mass plays a significant role in the behavior of the Higgs boson and its interactions.
The and Jets. Jets composed of
and
pairs are identified by mandating a minimum transverse momentum (
) of
for each Jet and restricting their pseudorapidity (
) to the interval
. This criterion ensures the Jets are well contained within the detector’s instrumented region. Following initial selection, 16 distinct Jet substructure features are utilized as inputs for the classification algorithms. Within a Jet, the highest
pT muon, kaon, pion, electron, and proton are chosen. For each of these particles, three physical parameters are evaluated: the relative transverse momentum to the Jet’s axis (
), the electric charge (
), and the separation in the
space from the Jet axis (
). Should any particle type be absent, its corresponding features are assigned a value of 0. An additional characteristic, the weighted Jet charge
, is computed as the sum of the particles’ charges inside the Jet, each multiplied by its respective
[
26].
2.2 Key concepts of ML-based HEP
When discussing ML and its subset DL in HEP, maintaining uniform and precise terminology is crucial for clear communication. Supervised learning, for instance, refers to training models using labeled datasets, where the model learns to map input features to known outputs, such as identifying particles or classifying Jets based on their physical properties. In contrast, unsupervised learning involves identifying patterns or structures in data without predefined labels, often used in anomaly detection or clustering in particle physics. Feature selection is an essential process that focuses on choosing the most informative input features — such as track momentum, calorimeter energy deposits, and hit patterns in detectors — thereby improving the performance and efficiency of ML models by reducing dimensionality and computational load.
The growing adoption of DL techniques, such as convolutional neural networks (CNNs) and graph neural networks (GNNs), has revolutionized analyses in HEP. These methods rely on different types of layers and architectures designed to handle the complexity and scale of particle physics data.
Convolutional layers in CNNs, for instance, are particularly effective at detecting patterns in images or PCs, by learning local features. These layers operate by applying convolutional filters to input data, extracting hierarchical patterns, which are then pooled to reduce dimensionality. Pooling layers, such as
max-pooling, downsample the spatial dimensions of the data, retaining the most important features while reducing computational cost. This structure allows CNNs to efficiently process large-scale data and is widely used in Jet classification and particle identification tasks. Further advancements include the use of
EdgeConv layers in GNNs [
28], where the network learns the relationships between particles represented as nodes in a graph. In these models, the
EdgeConv block aggregates local particle information, capturing spatial relationships and interactions based on particle kinematics and connectivity, which are essential for Jet tagging. The use of
global average pooling in these models helps aggregate information from individual particles, producing a global representation of the Jet that can then be used for classification or regression tasks.
Dense layers (also known as fully connected layers) play a critical role in transforming high-level features learned by convolutional and graph-based layers into a final prediction. Dense layers are used in DNNs, CNNs, GNNs, and others, after the feature extraction phase, where the output of the convolutional or graph layers is flattened into a one-dimensional vector and passed through one or more fully connected layers. These layers allow the network to combine the learned features in a non-linear way, making complex decisions such as event classification, particle identification, or regression for Jet properties. The dense layer’s ability to connect all input neurons to all output neurons allows the model to capture intricate relationships between features, making it highly effective for tasks like anomaly detection, signal classification, and event reconstruction in HEP.
An essential innovation in modern DL is the
Attention layer [
29], a core layer in building Transformers, enables the model to focus on the most relevant parts of the input data. Attention mechanisms are particularly useful in scenarios where certain elements in a sequence (or graph) are more important for the task than others. In particle physics, this could involve focusing on particular particle interactions or energy deposits in Jets. The
scaled dot-product Attention mechanism, used in Transformer models, computes attention scores for each pair of input elements [
30]. The attention output
is calculated as follows:
where , , and represent the query, key, and value matrices, respectively, and is the dimension of the key vectors. The softmax function normalizes the attention scores, allowing the model to weigh the importance of different elements in the input sequence. This mechanism enables the model to prioritize relevant information, improving the accuracy of particle event classification, Jet tagging, and anomaly detection, particularly when the input data has complex dependencies or long-range interactions between particles.
2.3 Performance measures
In the realm of HEP, performance assessment is divided into two main categories. The first encompasses classical metrics like energy loss, path length, and axis distance. The second involves metrics related to DL-based HEP techniques, such as accuracy, true positive rate (TPR), false-positive rate (FPR), receiver operating characteristic (ROC), area under curve (AUC), mean squared error (MSE), Fubini-study tensor (FST), among others. Tab.2 outlines these metrics, including mathematical formulations and descriptions.
Tab.2 An overview of the metrics employed to evaluate performance in ML and DL-based HEP. |
| Metric | Formula | C/R | Description |
|
| FPR and TPR | | C | The FPR, is the ratio (or percentage) of the background signal that are incorrectly identified as containing Jet. The TPR. is the ratio (or percentage) of the Jet signal that is correctly identified as Jet (particle). |
| AUC | | C | The area beneath the ROC curve is represented. It delivers a singular numeric score reflecting the cumulative effectiveness of the classification technique. An elevated AUC score signifies superior performance, with the ideal score being 1. |
| Accuracy | | C | The accuracy is the ratio (or percentage) of correctly detected instances of Jet in the signal. A high accuracy indicates that the classification algorithm is more effective in detecting Jet than background. |
| MSE | | R | The training procedure seeks to discover the model parameter values denoted as , which minimize the loss function known as MSE. Where is the number of training Jets, and is the predicted and target probabilities, respectively, for the -th Jet. |
| F1-score | | C | Represents the harmonic mean between precision and recall metrics. This measure is applied to assess the comprehensive efficacy of the classification algorithm in identifying or tagging Jets. |
3 HEP Jet representation
This section provides an overview of the Jet datasets comprising various forms of Jet data obtained and generated through different methods. Additionally, the current section delves into diverse pre-processing and feature extraction techniques employed in this context.
3.1 Available datasets and simulation tools
The conseil Européen pour la recherche nucléaire (CERN) open data portal provides access to a variety of datasets from experiments conducted at the Large LHC. These datasets include information about collisions, particles, and Jet images and PCs. The portal offers a great starting point for those interested in HEP datasets. Fig.3 illustrates samples of Jet images, featuring the average of pT-normalized quark and gluon Jet images across 5 distinct bins. The Jet images or PC may undergo different preprocessing techniques, discussed later, prior to input into ML/DL models for classification or prediction tasks. Tab.3 presents the datasets, along with several simulation tools, most commonly used in the research reviewed in this paper.
Fig.3 Jet images summed online and categorized into different channels employed in the analysis within the 100−200 GeV pT range. |
Full size|PPT slide
Tab.3 A summary of available datasets, and simulation tools for Jet HEP analysis |
| Name | Description | DLA? |
|
| Datasets | ATLAS open data | Is one of the largest particle physics experiments at the LHC. They offer an “Open Data” initiative with datasets that include collision data and simulated samples. These datasets can be used to study Jet images and other particle physics phenomena. | Yes† URL: opendata.cern.ch/search?page=1&size=20&experiment=ATLAS |
| CMS open data | Compact muon solenoid (CMS) is another major experiment at the LHC. Similar to ATLAS, CMS provides open data for educational and research purposes. The datasets include information about collisions, particles, and Jets. | Yes† URL: opendata.cern.ch/search?page=1&size=20&q=jet%20images&experiment=CMS |
| Complete | It belongs to CERN and contains muon, kaon, pion, electron, and proton. In the complete dataset training, 400000 Jets are used for training, and the remaining 290000 are used for testing and assessing performance [26]. | No |
| Top tagging | This dataset comprises 1.2 million training samples, 400000 for validation, and another 400000 for testing. Each entry in this dataset corresponds to an individual Jet, with its source being either an energetic top quark, a light quark, or a gluon. These events were generated using the PYTHIA8 Monte Carlo event generator, and the response of the ATLAS detector is simulated using the DELPHES software package. | Yes† URL: zenodo.org/record/2603256 |
| Quark-gluon tagging | The dataset is created by generating signal (quark) and background (gluon) Jets through PYTHIA8. For the signal Jets, the process involves , and for the background Jets, it uses . Notably, there is no simulation of the detector. The particles that are not neutrinos in the final state are grouped into Jets using the anti-kT algorithm with a radius parameter of . In total, this dataset contains 2 million Jets, evenly split between signal and background categories [31]. | No |
| Higgs dataset | The dataset originates from Monte Carlo simulations. The initial 21 attributes (found in columns 2−22) represent particle detector-derived kinematic properties within the accelerator. The remaining seven attributes are transformations of the initial 21, constituting high-level features engineered by physicists to aid in distinguishing between the two categories. | Yes† URL: archive.ics.uci.edu/dataset/280/higgs |
| QCD multi-Jet | Samples are generated across different ranges of scalar sum of , namely 1000−1500 GeV, 1500−2000 GeV, and 2000-Inf GeV. After excluding samples with values less than 1000 GeV, the dataset consists of around 450 × 103 training images, 150 × 103 validation images, and 150 × 103 testing images [17]. | No |
| Simulation tools | Delphes | Is a particle physics event generator designed to produce simulated collision events that are similar to those observed in real experiments. It includes tools to generate Jet based on the data produced in simulations. | Yes† URL: cp3.irmp.ucl.ac.be/projects/delphes |
| MadGraph | Is a popular event generator used in particle physics simulations. It can generate events involving Jets and other particles, which can then be turned into Jet PC or images. | Yes† URL: madgraph.phys.ucl.ac.be/ |
| FASTSim | Is a tool for simulating high-energy particle collisions. It can generate Jets from simulated collision events and is often used for studying ML techniques in HEP. | Yes† URL: twiki.cern.ch/twiki/bin/view/CMSPublic/SWGuideFastSimulation |
| Monte Carlo | It is generated through a dependable framework, created by integrating various tools like Pythia 8 for generating HEP events, Delphes for emulating the detector’s response, and RAVE for reconstructing secondary vertices [32]. | No |
3.2 Pre-processing for ML-based Jet analysis
The objective of preprocessing input data is to support the model in addressing an optimization challenge. Usually, these preprocessing actions are not mandatory, but they are employed to enhance the numerical convergence of the model, considering the real-world constraints imposed by limited datasets and model dimensions, along with the specific parameter initialization choices. In HEP, (i) represents pseudorapidity, which is a measure related to the polar angle of a particle’s trajectory. It is commonly used because it is less affected by relativistic effects and is approximately invariant under boosts along the beamline, (ii) represents the azimuthal angle, which is the angle around the beamline, (iii) together, and provide a way to specify the direction and position of particles or energy deposits within the detector. These coordinates are particularly useful for representing and analyzing the distribution of particles produced in high-energy collisions, (iv) the combination of and can be thought of as a way to navigate and map the detector’s components in a way that is sensitive to the underlying physics processes, (v) space is a coordinate system used to describe the properties and positions of particles or objects within particle detectors, particularly in experiments at large colliders like the LHC.
The subsequent sequence of data-driven preprocessing procedures was employed on the Jet images and can also be adapted for PCs:
– Center (translation and rotation). Center the Jet image by translating it in coordinates, such that the pixel with the centroid weighted by total pT is located at . This procedure involves rotating and boosting the Jet along the beam direction to position it at the center.
– Crop. Trim to a region of pixels centered around , encompassing the area where fall within the range .
– Normalize. adjust the pixel intensities to ensure that the sum of all pixel values, , equals 1 across the image, with and serving as the pixel indices.
– Zero-center. Remove the average value, represented by , from the normalized training set images from every image, thereby altering each pixel’s intensity to .
– Standardize. Normalize each pixel by dividing it by (the standard deviation) of the corresponding pixel value in the training dataset. This process is represented as: . A value of was employed to reduce the influence of noise.
–
Clustering and trimming. Reconstruct Jets by applying the anti-
algorithm [
33] to all calorimeter towers, utilizing a specific Jet size parameter, such as
, and then choose the primary (leading) Jet. Subsequently, refine the Jet by employing the
algorithm with a subjet size parameter of
, such as
[
34].
– Pixelisation. Create a Jet image by discretizing the transverse energy of the Jet into pixels with dimensions (0.1, 0.1) in the space.
– Zooming. It is the option to magnify the Jet image by a factor that diminishes its reliance on the Jet’s momentum.
3.3 Feature extraction and selection
Feature extraction and selection are important techniques in HEP for analyzing and interpreting data from experiments conducted at particle accelerators like the LHC. HEP experiments produce vast amounts of data, and the goal is to extract relevant characteristics from this data to make: (i) particles identifications, (ii) extract kinematic variables, such as pT, energy (E), rapidity (y), and azimuthal angle () for each detected particle, (iii) calculating the invariant mass of particle can reveal the presence of new particles, (iv) extract topological features related to the spatial distribution of particles or their interactions such as angular separations, impact parameters, and vertex finding. The benefit of feature selection is to make: (i) dimensionality reduction techniques like principal component analysis (PCA) or t-distributed stochastic neighbor embedding (t-SNE) may be employed to reduce the number of features while retaining as much information as possible, (ii) identify the most discriminating features that separate signal from background, (iii) identify the most relevant features for ML classification and model building.
Di Luca
et al. [
32] presents an automated feature selection procedure for particle Jet classification in HEP experiments. The authors use ML boosted tree algorithms to rank the importance of observables and select the most important features associated with a particle Jet. They apply this method to the specific case of boosted Higgs boson decaying to two b-quarks (
) tagging and demonstrate the impact of feature selection on the performance of the classifier to distinguish these events amidst the substantial and unalterable background originating from quantum chromodynamics (QCD) multi-Jet production. They also train a fully connected neural network to tag the Jets and compare the results obtained using all the features or only those selected from the procedure which consists of two main steps: data preparation and feature ranking extraction. The authors discover that the
azimuthal angles of the large-R Jet and the
variable radius (VR)-track Jets appear towards the end of the feature ranking. At the top of the ranking, they find the
pT of the two VR-track Jets, along with certain details regarding the secondary vertex, such as its
mass, energy, and
displacement. The study shows that selecting the highest-ranked features achieves performance nearly as effective as that of the full model, with only a slight deviation of a few percent. This approach can be expanded to accommodate the increased number of observable variables that upcoming collider experiments will gather from high
pT particle Jets. The data for this research comes from proton−proton collision events featuring a boosted Higgs boson that decays into two
quarks. In Ref. [
35], solutions have been proposed for classifying events extracted from the 2014 Higgs ML Kaggle dataset
†8) URL: www.kaggle.com/c/higgs-boson
. The dataset includes a mix of low-level and high-level attributes: it contains 18 low-level features that include three-dimensional momenta (
,
,
), missing transverse momentum, and the total transverse momentum from all Jets; additionally, there are 13 high-level features motivated by physics, covering invariant masses and angular separations among objects in the final state. Tab.4 summarizes the features utilized, which hold potential for future application within the context of HEP. The authors aim to ensure that the suggested networks make effective use of low-level information; otherwise, there’s a risk of losing these features during selection. Their focus lies in determining the necessity of high-level features. The proposed DNN model effectively utilize the low-level information in the data and autonomously learn their own high-level representations. Boost-invariant polynomial (BIP) features are a type of mathematical representation used in HEP for analyzing particle collision data. They are constructed to be invariant under boosts, meaning they remain unchanged under transformations to different reference frames with different velocities. These features are designed to capture important characteristics of particle Jets, such as their energy distribution and substructure, while ensuring consistency across various experimental conditions. BIP features are particularly useful for tasks like Jet tagging and classification in HEP experiments, as employed in Ref. [
36].
Tab.4 Possible combinations of Jet features to generate new high- and low-level features that could potentially improve ML classification for Jet HEP. The performance of employing these features are presented in Ref. [35]. |
| Level | Suggested feature name | Description | Grouping |
|
| High-level features | DER_mass_MMC | The Higgs boson’s mass was estimated using a hypothesis-driven fitting method | Higgs, Mass |
| DER_mass_transverse_met_lep | Transverse mass associated with the lepton and | Higgs, Mass |
| DER_mass_vis | The mass invariant to both the lepton and the tau | Higgs, Mass |
| DER_pt_h | Transverse momenta of the combined vector of the lepton, tau, and | Higgs, 3-momenta |
| DER_deltaeta_jet_jet | Absolute disparity in pseudorapidity between the leading and subleading Jets (undefined for less than two Jets) | Jet with angular properties |
| DER_mass_jet_jet | The invariant mass of the primary and secondary Jets (not applicable when there are fewer than two jets) | Jet, Mass |
| DER_prodeta_jet_jet | The multiplication of the pseudo rapidities for the foremost and next-to-foremost Jets (inapplicable if fewer than two Jets are present) | Jet, 3-momenta |
| DER_deltar_tau_lep | Distance between the lepton and the tau in the − plane | Final state, Angular |
| DER_pt_tot | The resulting from the vector addition of the of the lepton, tau, the primary and secondary Jets (when applicable), and | Final-state, Sum |
| DER_sum_pt | Total transverse momentum of the lepton, tau, and all Jets | global event, Sum |
| DER_pt_ratio_lep_tau | Ratio of the transverse momenta of the lepton to that of the tau | Final state, 3-momenta |
| DER_met_phi_centrality | Centrality of the azimuthal angle of relative to the lepton and the tau | Final state, Angular |
| DER_lep_eta_centrality | The centrality measure of the lepton’s pseud-orapidity in comparison to the primary and secondary Jets (not applicable for fewer than two Jets) | Jet, Angular |
| Low-level features | PRI_tau_[px/py/pz] | The 3-momenta of the tau expressed in Cartesian coordinates | Final state, 3-momenta |
| PRI_lep_[px/py/pz] | The lepton’s 3-momenta represented in Cartesian coordinates | Final state, 3-momenta |
| PRI_met_[px/py] | The constituent parts of the missing transverse momentum vector expressed in Cartesian coordinates | Final state, 3-momenta |
| PRI_met | The magnitude of the missing transverse momentum vector represented in Cartesian coordinates | Final state, 3-momenta |
| PRI_met_sumet | Total sum of transverse energy | Final-state, Energy |
| PRI_jet_num | Count of Jets present in the event | Jet, Multiplicity |
| PRI_jet_leading_[px/py/pz] | The three-dimensional momenta of the primary Jet expressed in Cartesian coordinates (not applicable if there are no Jets present) | Jet, 3-momenta |
| PRI_jet_subleading_[px/py/pz] | The 3-momenta of the secondary Jet represented in Cartesian coordinates (not defined if fewer than two Jets are present) | Jet, 3-momenta |
| PRI_jet_all_pt | Total sum of the transverse momenta of all Jets in Cartesian coordinates | Jet, 3-momenta |
4 Available AI models for HEP Jet classification
Many DL architectures have been proposed in the SOTA of HEP domain to identify particles. Some of these architectures require input data in the form of images, while others utilize PC representations [
37]. Tab.5 summarizes and compares the most efficient ML and DL models, used in HEP, based on their architectures and performances.
Tab.5 A summary of available ML and DL architectures for Jet HEP classification, including columns for biases, generalizability, and recommended use cases. Bias levels range from moderate (limited datasets) to high (overfitting, dataset reliance), while generalizability is categorized as high (broad applicability), moderate (adequate performance with some limitations), and low (poor performance or untested on other tasks). |
| Ref. | Year | Model | IN | Acc. TT | AUC TT | Acc. QG | AUC QG | Acc. Other | AUC Other | Link | Biases | General. | Recommended scenarios |
|
| [45] | 2017 | TopoDNN | Image | 0.916 | 0.972 | – | – | – | – | No | M | L | Top quark identification |
| [46] | 2018 | CNN tagger | Image | – | – | – | – | 0.87 (DTJ) | 0.943 (DTJ) | No | H | H | Jet substructure |
| [47] | 2019 | PFN-ID | PC | 0.932 | 0.981 | 0.900 | – | – | – | No | L | L | Energy flow studies |
| [48] | 2020 | LGN | PC | 0.929 | 0.964 | 0.803 | 0.832 | – | – | Yes† URL: github.com/fizisist/LorentzGroupNetwork | L | M | Lorentz invariance studies |
| [49] | 2020 | ParticleNet | PC | 0.940 | 0.985 | 0.840 | 0.911 | – | – | No | M | H | Point cloud analysis |
| [50] | 2021 | EGNN | PC | 0.922 | 0.976 | 0.803 | 0.880 | – | – | Yes† URL: github.com/vgsatorras/egnn | L | M | Graph neural networks |
| [51] | 2021 | PCT | PC | 0.940 | 0.985 | 0.841 | 0.914 | – | – | No | L | H | Point cloud processing |
| [31] | 2022 | LorentzNet | PC | 0.942 | 0.986 | 0.844 | 0.915 | – | – | No | L | M | Lorentz group studies |
| [52] | 2022 | PartT | PC | 0.944 | 0.987 | 0.852 | 0.923 | – | – | Yes† URL: github.com/jet-universe/particle_transformer | L | H | Analysis of long-range feature dependencies in particles |
| [38] | 2022 | PELICAN | PC | 0.942 | 0.986 | – | – | – | – | Yes† URL: github.com/abogatskiy/PELICAN | M | L | Particle cloud matching |
| [53] | 2024 | CGENNs | PC | 0.942 | 0.986 | – | – | – | – | Yes† URL: github.com/DavidRuhe/clifford-group-equivariant-neural-networks | L | H | Clifford group analysis |
| [54] | 2024 | L-GATr | PC | 0.942 | 0.987 | – | – | – | – | Yes† URL: github.com/Qualcomm-AI-research/geometric-algebra-transformer | M | H | Geometric algebra studies |
| [55] | 2024 | MIParT-L | PC | 0.944 | 0.987 | 0.853 | 0.923 | – | – | Yes† URL: github.com/jet-universe/particle_transformer | L | H | Analysis of long-range feature dependencies in particles |
ML, especially DL, has a rich historical presence in the field of particle physics. The concept of applying neural networks for tasks like distinguishing quarks and gluons, tagging Higgs particles, and identifying particle tracks has been around for more than two and a half decades. Nevertheless, the recent advancements in DL and the increased computational capabilities offered by graphics processing units (GPUs) have led to a significant enhancement in image recognition technology. As a result, there has been a renewed and heightened interest in utilizing these techniques. In the subsequent sections, we provide an overview of SOTA methods in both ML and DL. Fig.4 depicts a taxonomy of existing ML and DL techniques, summarizes the reviewed AI-based Jet classification models (discussed in Section 4), preprocessing and datasets (discussed in Section 3), and metrics (discussed in Section 2).
Fig.4 Taxonomy of ML and DL-based HEP techniques for Jet classification, with associated preprocessing, metrics, simulation tools and datasets. |
Full size|PPT slide
4.1 ML-based methods
ML-based analysis of HEP Jet tagging has become an important technique in recent years. Jets are collimated sprays of particles, i.e., emitted from a source in a way that they are parallel or nearly parallel to each other, produced in high-energy particle collisions. Analyzing their properties is crucial for understanding the underlying physics processes. Jet images and PC are essentially 2D and 3D representations of the energy distribution within a Jet, where each pixel corresponds to a small region of the Jet. For example, Bogatskiy
et al. in Ref. [
38] introduced PELICAN, an ML architecture for particle physics that leveraged permutation-equivariant and Lorentz-invariant techniques, along with elementary equivariant aggregators and dense message-passing blocks. It processed 4-vector inputs representing particle jets as point clouds and employed a classifier to reduce rank-2 input arrays (pairwise dot products of 4-momentum vectors of particles in a jet) to permutation-invariant scalars using trace and total sum aggregation functions. Dense layers and a cross-entropy loss function were then used for optimization. Additionally, the PELICAN regressor predicted 4-momentum of particles using a permutation- and Lorentz-equivariant architecture with rank-preserving transformations and loss functions based on relative momentum and mass resolutions. Evaluation metrics included accuracy, AUC, background rejection rate, and relative resolutions. PELICAN achieved state-of-the-art performance in Jet classification, outperforming methods like LorentzNet while using approximately five times fewer parameters (45k only). Its low complexity, enhanced by equivariant aggregation, message-passing mechanisms, and its ability to handle regression tasks, made it suitable for real-time applications. However, its limitations included evaluation on limited datasets and reliance on hyperparameter tuning.
ML technique have been used in Ref. [
39] by applying the shapley additive explanations (SHAP) method to explain the output of two HEP events ML classifiers (XGBoost and DNN) using the Higgs dataset. It demonstrates SHAP’s utility in understanding complex ML systems, particularly in the context of HEP event classifiers. The TreeExplainer and DeepExplainer methods from the Python SHAP library were used to compute SHAP values, revealing that features like
,
, and
were crucial in both models, although their distribution of SHAP values differed, indicating distinct learning processes. The process of extracting SHAP values are depicted in Fig.5.
Fig.5 (a) Diagram illustrating the localized explanation of an event classifier with the SHAP method. (b) Localized SHAP explanation represented using a waterfall plot. It can be observed that the SHAP values are associated with individual event features. The classifier’s prediction (XGBoost) is , while the base value is . In this context, the feature “m_wwbb” contributes positively with a SHAP value of +0.77, increasing the prediction, whereas the feature “m_wbb” has a SHAP value of −0.6, reducing the prediction. |
Full size|PPT slide
In addition, quantum machine learning (QML) methods have recently found applications in addressing challenges within HEP, including separating signal from background [
40], detecting anomalies [
41], and reconstructing particle tracks [
42].
Blance and Spannowsky [
40] proposed a hybrid variational quantum classifier that combines quantum computing methods with classical neural network techniques to improve classification performance in particle physics research. The algorithm is applied to a resonance search in di-top final states, and it outperforms both classical neural networks and QML methods trained with non-quantum optimization methods. The classifier’s ability to be trained on small amounts of data indicates its potential benefits in data-driven classification problems. The proposed methodology was applied to the generated dataset, and the hybrid approach using the FST metric outperformed both classical neural networks and QML methods trained with non-quantum optimization methods in terms of maximizing learning outcomes; its accuracy can reach 72.6%. The hybrid approach also learned faster than an equivalent classical neural network or the classically trained variational quantum classifier. The paper [
43] discusses the potential applications of quantum computation and QML in HEP, rather than focusing on deep mathematical structures. The authors claim that statistical ML methods are used for track and vertex reconstruction. These methods vary depending on the detector geometry and magnetic field used in the experiment. ML can help address these challenges by providing efficient and accurate methods for pattern recognition and particle identification. They suggest that quantum algorithms could potentially improve upon existing methods by offering faster and more efficient solutions to challenging problems in experimental HEP, such as particle identification and track reconstruction. This can be realized by creating a dataset recorded on tape through grid computing, which can be distributed for offline analysis using QML to extract information about particle trajectories developed inside the detectors. The work [
44] investigates the potential of QML in HEP analysis at the LHC. The authors compare the performance of the quantum kernel algorithm to classical ML algorithms using 15 input variables and up to 50 000 events. They used 60 statistically independent datasets of 20 000 events each for their analysis. The AUC is used as the metric, and the results show that the performance of all methods improves with increasing dataset size. For 15 qubits, the quantum SVM-Kernel algorithm performs similarly to the classical support vector machine (SVM) and classical BDT algorithms. The quantum SVM-Kernel performances from the three different quantum computer simulators (Google, IBM, and Amazon) are comparable. The authors also claim that when a selection is implemented, permitting a signal acceptance rate of 70%, it results in the rejection of approximately 92% of background events, as indicated by the AUC. Consequently, the
ratio will experience an enhancement of approximately 150% compared to a scenario without any selection. Similarly, the researchers in Ref. [
26] present a new approach to Jet classification using QML. The method involves embedding data into a quantum state, passing it through a variational quantum circuit, and performing a training procedure by minimizing a classical loss function. Probability measurements of the final state are then used to perform the classification. By exploiting the intrinsic properties of quantum computation, such as superposition and entanglement, the team aims to identify if a Jet contains a hadron formed by a
or
quark at the moment of production. The approach could lead to new insights and enhance the classification performance in particle physics experiments. Two datasets have been used in this research: the complete dataset and the muon dataset, both of which belong to CERN. In the muon dataset analysis, 60 000 Jets are used for training and 40 000 Jets are used for testing. The muon dataset is a subset of the complete dataset, and it is used to evaluate the dependence of the quantum algorithms’ performance on the number of training events and the circuit complexity. The researchers compare the performance of their QML approach with that of DNN, long short-term memory (LSTM), and LSTM with convolutional layer models. They show that the results for tagging power as a function of the Jet
pT and
are comparable within the MSE error, and therefore, they consider only the DNN model for comparison with QML algorithms.
4.2 MLP and DNN-based methods
Multi-layer perceptron (MLP) is an artificial neural network composed of multiple layers of nodes, including an input layer, one or more hidden layers, and an output layer. Each node in one layer is connected to every node in the subsequent layer. MLP can handle complex nonlinear relationships between input and output data, making them suitable for various tasks. MLPs are versatile, scalable, and can be trained using back-propagation, enabling them to learn from large datasets effectively and generalize well to unseen data. Kinematic parameters describe the motion of particles, including velocity, momentum (
) and trimmed Jet momentum (
), energy, Jet mass
and Jet mass trimmed
, and angles of emission, commonly used in physics and engineering analyses. Chakraborty
et al. in Ref. [
56] employed both kinematics and spectral function, which typically refers to a function that describes the distribution of energy or momentum states of particles in a particular physical system, to feed MLP classifier as described in Fig.6. The authors aim is to trim/discard Jet that are unlikely to have originated from the process of interest (effects of background noise). This selective removal helps to improve the accuracy of measurements and analyses by focusing only on the most relevant particles within a jet.
Fig.6 An example of classifier utilizing MLP trained using kinematic and spectrum variables for Jet classification [56]. and correspond to hard and soft substructure information. |
Full size|PPT slide
The paper [
48] introduces the Lorentz group network (LGN) neural network model designed for particle physics identification. This model is characterized by its full equivariance to transformations under the Lorentz group, which represents a crucial symmetry of space-time in physics and allows for equivariant nonlinearity. The LGN architecture has been successfully applied to a classification task in particle physics called top tagging, whose objective is to distinguish top quark “Jets” from a backdrop of lighter quarks. The LGN model consists of several layers, including the linear input layer (
), iterated Clebsch−Gordan (CG) layers (
), and the perceptrons
layer. This design reduces the number of learnable parameters and provides a deeper understanding of the physical interpretation of the results (Fig.7). The initial linear layer processes the 4-momenta of
particles originating from a collision event, and it can also handle associated scalar quantities like label, charge, spin, and more. The iterated
layers are defined by a CG decomposition of the tensor product of representations of the Lorentz group, which allows for equivariant non-linearity. The CG layers are alternated with perceptrons
layer, which act only on Lorentz invariants. At the end of each CG layer, a MLP is applied to the isotypic component of the tensor product. The MLP accepts
scalar inputs and generates an equivalent number of outputs, with its parameters uniformly applied across all
nodes within the CG layer. The output layer computes the arithmetic sum of the activations from
and extracts the invariant isotypic aspect of this sum. It subsequently employs a final fully connected linear layer, denoted as
, on the
scalars, generating two scalar weights for binary classification. In the LGN model’s output layer,
conducts the projection onto invariants, combines contributions from particles to ensure permutation invariance and subsequently applies a linear transformation.
operates independently on each individual particle but maintains consistent parameter values across all particles. The LGN model has demonstrated competitive performance while using between 10 and 1000 times fewer parameters than other SOTA models.
Fig.7 The architecture of LGN model suggested in Ref. [48]. |
Full size|PPT slide
The DNNs are a type of artificial neural network that are composed of multiple layers of nodes (i.e., MLP with multiple hidden layers), with each node connected to every node in the previous and next layers. They are particularly well-suited for processing high-dimensional data, such as images or collections of features, and can learn complex non-linear relationships between inputs and outputs. In the context of HEP, the DNN was used in to classify hadronic Jets based on their input features. DNNs typically require a fixed-size input, which can be a limitation when working with variable-length inputs such as particle lists.
In Ref. [
57], DNNs are used in HEP to classify Jets produced in particle collisions. DNNs can automatically extract features from Jet tagging, allowing for more accurate classification than traditional methods that rely on expert-designed features. Parton shower in HEP refers to the process where high-energy particles, such as quarks and gluons, emit further particles as they evolve, simulating the fragmentation and radiation patterns observed in particle collisions within particle accelerators, which is crucial for understanding particle interactions. Barnard
et al. [
34] advocate for DNNs as hadronic resonance taggers, trained on Jet tagging generated from different generators. The DNN showed improved performance on test events generated by the default PYTHIA shower instead of using HERWIG and SHERPA generators, suggesting acquisition of PYTHIA-specific features. However, they noticed that biases may arise from generator approximations. They examine parton shower variations’ impact on tagger performance using LHC data. Results show up to 50% differences in background rejection. They introduced the “zooming” method, enhancing performance between 10% and 20% across Jet transverse momenta. The TopoDNN model proposed in Ref. [
45] is a DNN-based architecture (Fig.8). The network’s input layer is designed to process vectors containing the Jet constituents’
pT,
, and
values. Manual tuning of the network’s architecture involved adjusting the depth and node count per layer, within a range of 4−6 layers and 40−1000 nodes per layer, respectively. rectified linear unit (ReLU) activation function was implemented in the hidden layers, whereas a sigmoid function was applied to the output node. The training process utilized the Adam optimizer, with training sessions capped at a maximum of 40 epochs. An early stopping mechanism was employed, utilizing a patience parameter set to 5 epochs based on the validation set loss. The final architecture selected features 4 hidden layers, comprising 300, 102, 12, and 6 nodes in each layer respectively. TopoDNN achieved a significant background rejection of 45 at a 50% efficiency operating point for reconstruction-level Jets, yielding to correctly identify top quark Jets with a high level of accuracy while rejecting a large portion of background events.
Fig.8 The architecture of the TopoDNN model, consists of 4 layers with 300, 102, 12, and 6 nodes, respectively [45]. |
Full size|PPT slide
The researchers in Ref. [
58] discusses the application of DNNs to a wide range of physics problems, particularly in HEP. Specifically, DNNs have been successfully applied to tasks such as Jet tagging and event classification. The authors explore the use of a simple but effective preprocessing step that transforms observational quantities into a binary number with a fixed number of digits, representing the quantity or magnitude in different scales. This approach has been shown to significantly improve the performance of DNNs for specific tasks without complicating feature engineering, particularly in b-Jet tagging using daughter particles’ momenta and vertex information. However, the authors in Ref. [
47] used DNNs to process collections of ordered inputs, which can be thought of as a fixed-size representation of variable-length inputs. This allows the DNN to learn features sensitive to particle ordering, which can be important for discriminating between different types of Jets. Particle flow network with ID (PFN-ID) model [
47] is another proposed type of DL architecture that takes particles as input and processes them in a way that is dependent on the order the particles were fed into the network. The PFN-ID architecture is based on the Deep Sets framework and includes full particle ID information (Fig.9). The Deep Sets framework is a ML approach that allows for learning directly from sets of features or “point clouds”. The following are the main steps of the framework: (i) Map each element of the set to a latent space using a shared function. (ii) Aggregate the latent representations of the elements using a symmetric function. (iii) Map the aggregated latent representation back to the output space using a shared function. An additive latent space can be used to express a general symmetric function, as provided by the framework. Within the scope of particle-level collider observables, the process involves mapping each particle to a latent representation, which is subsequently collected. Subsequently, the observables are expressed as functions on this latent space. This decomposition includes a diverse range of current collider observables and representations at the event and Jet levels, including as image-based and moment-based techniques. The PFN-ID improves the classification performance of the particle flow network (PFN) model for discriminating quark and gluon Jets. Results show that PFN-ID slightly outperforms recurrent neural network (RNN)-ID, whereas the PFN and RNN are comparable.
Fig.9 The architecture of PFN-ID model suggested in Ref. [47]. (a) Per-particle mapping . (b) The binary output signal or background can be identified. |
Full size|PPT slide
The authors in Ref. [
59] introduce a novel DNN model, called sparse autoregressive model (SARM), that learns data sparsity explicitly, yielding stable and interpretable results compared to generative adversarial networks (GANs). In two case studies, the first, referred to as
, employs a discrete mixture model by discretizing pixel values using predetermined grid points, while the second,
, utilizes a discrete mixture model constructed with a truncated logistic distribution for pixel modeling. In two case studies, SARM outperforms GANs by 24%−52% and 66%−68% on images with high sparsity.
In the study conducted by Ref. [
60], the identification of
Jets was investigated utilizing QCD inspired observables. The process entails the utilization of Jet substructure observables, including one-dimensional Jet angularities and the two-dimensional primary lund plane (PLP). DNNs are employed to identify
Jets using these QCD-inspired observables. The DNNs are trained on a set of input features, which include Jet angularities and the PLP, in order to efficiently distinguish
Jets from light ones. The performance of the DNNs is evaluated by comparing their results with those of conventional track-based taggers, such as JetFitter, IP3D, and DL1 taggers. In this study, the results indicate that the DNN discriminants exhibit better performance than the IP3D tagger.
4.3 CNN-based methods
CNNs have revolutionized Jet image classification and prediction in particle physics. CNNs excel in image recognition by leveraging convolutional layers, weight sharing, and pooling to capture hierarchical features, enabling effective pattern recognition and classification [
61,
62]. This enables precise particle identification using Jet images, improved event classification, and deeper insights into HEP experiments, advancing researchers’ understanding of fundamental particles and interactions. For example, the authors in Ref. [
63] investigate the capability of CNNs in discriminating quark and gluon Jets, comparing their performance to traditionally designed physics observables. In the realm of Jet image classification, researchers proposed combining CNN with various other DL techniques. For instance, Farrell’s paper [
64], hybrid DLs revolutionize particle tracking. LSTMs excel in sequential data analysis, replacing Kalman filtering for hit assignment, while CNNs construct valuable detector data representations. Their fusion unveils a potent end-to-end model, with GPU training addressing traditional tracking algorithm scaling challenges. The CNN tagger architecture proposed in the paper [
46] consists of a CNN with four identical convolutional layers, each with 8 feature maps and a
kernel. These layers are separated in half by one
max-pooling layer. The CNN also includes three fully connected layers of 64 neurons each and an output layer of two softmax neurons. Zero-padding is included before each convolutional layer to prevent spurious boundary effects. The architecture ends with a flatten layer and three fully connected layers with sizes 64, 256, 256, and 2, respectively (Fig.10). The CNN is trained on a total of 150 k + 150 k top and QCD Jet images, by minimizing a MSE loss function using the stochastic gradient descent algorithm in mini-batches of 1000 Jet images and a learning rate of 0.003.
Fig.10 The architecture of CNN tagger model suggested in Ref. [46]. |
Full size|PPT slide
Oliveira
et al. [
65] applied a CNN directly to Jet tagging, showcasing its effectiveness as a powerful tool for identifying boosted hadronically decaying
bosons amid QCD multi-Jet processes. Similarly, in order to discriminate Quark-Gluon Jet, Lee
et al. in their research [
66], employed various pretrained CNN models, including VGG, ResNet, Inception-ResNet, DenseNet, Xception, Vanilla ConvNet, and Inception-ResNet, to classify Jet images for distinguishing quark and gluon hadron Jets. The study reveals that DenseNet outperforming larger, higher-structured networks. Despite marginal improvements over a traditional BDT classifier, stability in training can be enhanced using the RMSProp optimizer, an adaptive learning rate optimization algorithm. Similarly, significant progress resulted from integrating 1D CNN and LSTM, resulting in DeepJet NN model [
27] for Jet identification. The architecture extract abstract features from three input collections — secondary vertices, charged particles (tracks), and neutral particles. The final Jet flavor probabilities are determined by combining outputs with global Jet features in dense layers. This architecture was also applied to heavy flavour classification, with the model further adapted for quark-gluon tagging tasks [
67]. In Ref. [
67], the model architecture consists of several components: (i) Automatic feature extraction is conducted for each constituent through convolutional branches that include
convolutional layers. Distinct convolutional branches are allocated for vertices, charged particle flow candidates, and neutral particle flow candidates, (ii) the output of the convolutional branches is used to construct a graph representation of the Jet, where each constituent is represented as a node in the graph. The edges between the nodes are determined by a distance metric that takes into account the kinematic properties of the constituents, (iii) the graph representation of the Jet is then processed by several graph convolutional layers, which are designed to capture the correlations between the constituents. The graph convolutional layers use a learnable filter that is applied to the graph representation of the Jet, and (iv) the output of the graph convolutional layers is then fed into several dense layers, which are designed to perform the final classification task. The dense layers use a combination of fully connected and batch normalization layers. In the context of the DeepJet model, the RNN layer is an important component of the DeepJet model (Fig.11), as it allows the model to capture the sequential information in the charged particle tracks and to use this information to improve the classification performance. The DeepJet model has been shown to achieve SOTA performance in Jet flavour classification and quark/gluon discrimination tasks. The model was tested using CMS simulation and was found to outperform previous classifiers, including the IP3D algorithm. The DeepJet model underwent a comparative analysis against a binary quark/gluon classifier from the CMS reconstruction framework. An improvement in performance was noted with the use of the DeepJet model on a dataset comprised exclusively of light quark and gluon Jets. Moreover, the DeepJet model was found to be more robust to variations in the Jet constituents and kinematics, which makes it more suitable for use in real-world scenarios. In terms of DeepJet’s performance, using the function of reconstructed vertices, b-Jet efficiency can reach 92%, and when the function of Jet
pT, b-Jet efficiency is around 95%.
Fig.11 The architecture of DeepJet model suggested in Ref. [67]. |
Full size|PPT slide
Du
et al. in their paper [
68] addressed challenges in assessing Jet distribution modification in a hot QCD medium during heavy-ion collisions. It utilizes a CNN trained on a hybrid strong/weak coupling model, achieving good performance and emphasizing result interpretability. The study reveals discriminating power in the angular distribution of soft particles and explores the potential of DL for tomographic studies of Jet quenching.
The study [
69] demonstrates CNN’s efficacy in predicting energy loss for quark and gluon Jets, yielding comparable results. It highlights distinctions post-quenching and employs DL for classification, emphasizing energy loss’s impact on classification difficulty. In Fig.12, a CNN architecture is presented specifically designed for identifying quark and gluon Jets. The researchers [
17] employed CNN to analyze LHC proton-proton collision simulation data. Their CNN model, utilizing detector responses as images, distinguishes r-parity violating super-symmetry (RPV SUSY) signal events from QCD multi-Jet background events. Achieving 1.85 times efficiency and 1.2 times expected significance over traditional methods. the authors showcased the model’s scalability on HPC resources, reaching 1024 nodes.
Fig.12 Example of CNN architecture with input Jet image, three convolutional layers, dense layer, and output layer are involved. In this context, red represents the transverse momenta of charged particles, green corresponds to the pT of neutral particles, and blue signifies the charged particle multiplicity [63]. |
Full size|PPT slide
4.4 Adversarial training-based methods
GANs in image processing enhance creativity and realism by generating new images through a dynamic interplay. The generator creates images, while the discriminator evaluates and refines them, enabling tasks like image-to-image translation, style transfer, and data augmentation with unparalleled versatility [
62,
70]. GANs are powerful tools for Jet image classification in particle physics. They create realistic Jet images, enabling robust testing of classification algorithms. GANs enhance the accuracy of identifying particles and contribute to breakthroughs in HEP research. However, the authors in Ref. [
71] employed another technique for adversarial training for physics object identification and decreased the effect of simulation-specific artifacts. They systematically distorted inputs that have been generated with fast gradient sign method (FGSM) adversarial attack technique, this latter altering model predictions using gradient information. The method showed how model performance and robustness are related. They explored the trade-off between performance on unperturbed and on distorted test samples, investigating ROC curves and AUC scores for the used discriminators. Similarly, in Ref. [
72], the paper investigates the loss manifold of a Jet tagging algorithm concerning input features on nominal and adversarial samples. Discrepancies in flatness reveal differences in robustness and generalization. The study suggests refined training approaches through macro-scale loss manifold exploration for two features and devising attacks that maintain the gradient’s directionality. This leverages acquired insights for enhanced object identification in particle physics.
4.5 RNN-based methods
Various types of RNNs such as bidirectional RNNs (BRNNs), LSTM, and gated recurrent units (GRUs) differ in architecture at the cell level within the RNN layer. BRNNs propagate information in both forward and backward directions, influencing predictions by surrounding words. LSTM tackles vanishing gradients with inner cells containing input, output, and forget gates, regulating information flow. GRUs-based networks address short-term memory issues with reset and update gates controlling information utilization akin to LSTM gates [
61,
73]. Recursive neural networks (RecNNs), are designed to operate on hierarchical or tree-structured data, where the relationships between elements are defined by a recursive structure. Instead of processing sequences sequentially with temporal dependencies, like RNNs, RecNNs recursively apply the same neural network operation to combine representations of child nodes to produce a representation of their parent node, traversing the hierarchical structure. In light of this, the authors in Ref. [
74] investigate RecNNs for quark/gluon discrimination. Results indicate RecNNs outperform baseline, boosted decision tree, in gluon rejection rate by a few percent. Even with minimal input features such as
, RecNNs yield promising results, suggesting tree structure contains essential discrimination information. Additionally, rough up or down quark Jet discrimination is explored. In Ref. [
73], a neural network was created specifically for Jet binary classifying. The network comprises two hidden layers employing recurrent cells, with a structure consisting of 25 LSTM cells and utilizing a tanh activation function at its core.
4.6 GNN-based methods
GNNs are neural networks designed for graph-structured data, learning node and edge representations while capturing complex relationships and dependencies within graphs for tasks such as classification and prediction. In the HEP context, the authors in Ref. [
49] proposed the ParticleNet model (Fig.13). The architecture is a customized neural network that operates directly on particle clouds for Jet tagging. It uses dynamic graph CNNs to process the unordered set of constituent particles that make up a Jet. The architecture consists of three EdgeConv blocks, each with a different number of channels and nearest neighbors. EdgeConv block starts by representing a point cloud as a graph, whose vertices are the points themselves, and the edges are constructed as connections between each point to its K-nearest neighbors (KNN) points. The EdgeConv block then finds the KNN particles for each particle, using the “coordinates” input of the EdgeConv block to compute the distances. Inputs to the EdgeConv operation, the “edge features”, are constructed from the “features” input using the indices of KNN particles. The EdgeConv procedure is executed using a three-layer MLP. Each layer is structured to include a linear transformation, succeeded by batch normalization, and subsequently a ReLU activation. Additionally, a shortcut connection is integrated into every block parallel to the EdgeConv operation, facilitating the direct passage of input features. An EdgeConv block is defined by two key hyper-parameters: the neighbor count
and the channel count
, which respectively denote the number of neighbors to consider and the number of units within each layer of linear transformation. The EdgeConv blocks play a crucial role in learning the local features of the particle cloud and aggregating them into a global feature vector for the Jet. Following EdgeConv blocks, global average pooling aggregates particle features, leading to a 256-unit fully connected layer, ReLU activation, dropout, and a 2-unit softmax output for binary classification. The ParticleNet architecture achieves SOTA performance on two representative Jet tagging benchmarks and is improved significantly over existing methods.
Fig.13 The architecture of ParticleNet model suggested in Ref. [49]. |
Full size|PPT slide
Similarly, Ref. [
50] proposed the equivariant graph neural networks (EGNN) model, which is a GNN architecture that is translation, rotation, and reflection equivariant [
E(
n)], and permutation equivariant with respect to an input set of points. It uses a set of filters that are equivariant to the action of the symmetry group, which are constructed using a combination of radial basis functions and Chebyshev polynomials. The EGNN algorithm possesses the same flexibility as the GNN technique, while also maintaining
E(
n) equivariance similar to the radial field algorithm. Additionally, it eliminates the requirement for computationally intensive procedures, such as spherical harmonics. The EGNN exceeds other equivariant and non-equivariant options while maintaining efficiency in terms of running time. Moreover, the EGNN approach demonstrates a 32% reduction in error compared to the SOTA method.
Another architecture called the LorentzNet is proposed in Ref. [
31], which is based on the Lorentz group equivariant block (LGEB) block. The structure of LGEB consists of several layers, including Minkowski norm and inner product, sum pooling, a MLP, and a Clebsch−Gordan tensor product. The input of LGEB is a set of 4-momentum vectors, which are transformed by the Minkowski norm and inner product layer to obtain Lorentz-invariant geometric quantities. The sum pooling layer aggregates the geometric quantities to obtain a scalar representation of the input. The MLP layer is used to learn a nonlinear mapping from the scalar representation to a new feature space. Finally, the Clebsch−Gordan tensor product layer is used to combine the new feature space with the original input to obtain the output of LGEB. It is designed as a Lorentz group-equivariant mapping to preserve the symmetries of the Lorentz group, ensuring the model’s equivariance and universality.
Fig.14 The architecture of EGNN model suggested in Ref. [50]. |
Full size|PPT slide
Fig.15 (a) The architecture of LorentzNet model. (b) LGEB block [31]. |
Full size|PPT slide
The paper [
53] introduced Clifford group equivariant neural networkss (CGENNs), a novel GNN framework designed to construct
- and
-equivariant models using Clifford algebra. CGENNs leveraged the geometric properties of Clifford algebras, such as the geometric product, to parameterize equivariant neural network layers. These layers operated on multivectors — structures encompassing scalars, vectors, and higher-dimensional geometric features — enabling symmetry-aware computations. Input point cloud included scalars (e.g., mass) and vectors (e.g., positions), embedded into multivector subspaces. CGENNs achieved SOTA performance across domains, including 3D
-body simulations and 4D Lorentz-equivariant tasks, and Jet tagging in HEP, outperforming models like LorentzNet and EGNN. However, their computational costs, due to complex geometric products, remained a challenge for scalability and real-time applications.
4.7 Transformer-based methods
Transformers are AI models using self-attention mechanisms to process sequential data, excelling in natural language processing [
81], computer vision [
82], and time-series tasks by capturing long-range dependencies and contextual relationships efficiently. Researchers in HEP have investigated transformers for the Jet tagging task. For example, Ref. [
51] introduced a modified point cloud Transformer (PCT) for Jet-tagging tasks in collider physics. The PCT leveraged self-attention layers and EdgeConv blocks to handle the unordered nature of particle data, ensuring permutation invariance. Jets were represented as point clouds with up to 100 particles, described by kinematic features such as momentum and particle types. The suggested PCT achieved SOTA performance, with an high AUC for both top tagging and quark-gluon classification, showing up to a 20% improvement in background rejection over models like ParticleNet. Despite its superior performance, the computational cost was significant, with 266M FLOPs, making real-time applications challenging.
In addition, the work in Ref. [
52] proposed PartT, which is a new Transformer-based architecture for Jet tagging. Its main task is to identify the origin of a Jet of particles produced in HEP experiments. ParT makes use of two sets of inputs: (i) the particle input, which includes a list of features for every particle and forms an array, and (ii) the interaction input, which is a matrix of features for every pair of particles. ParT employs a novel pairwise multi-head attention (P-MHA) mechanism, which allows the model to attend to pairs of particles and learn their interactions. The P-MHA is more effective than standard plain multi-head attention. This assertion is substantiated when the pre-trained ParT models are fine-tuned on two widely adopted Jet tagging benchmarks, the quark-gluon tagging dataset and the binary classification dataset for identifying boosted
bosons decaying to two quarks. The fine-tuning process involves training the ParT models on a smaller labeled dataset specific to each benchmark, which allows the models to learn the specific features and patterns relevant to each task. The fine-tuned ParT models achieve significantly higher tagging performance than the models trained from scratch and outperform the previous SOTA models, including ParticleNet and other Transformer-based models.
Moving on, Ref. [
54] introduced the Lorentz geometric algebra Transformer (L-GATr), a versatile architecture designed for high-energy physics. L-GATr combined Lorentz-equivariant geometric algebra with attention mechanisms, enabling robust handling of particle physics data in four-dimensional spacetime. The architecture accommodated variable-length inputs, exploited Lorentz symmetry, and extended to generative modeling via continuous normalizing flows trained with Riemannian flow matching. It used Transformer-based layers with Lorentz-equivariant attention and normalization tailored to Minkowski space, processing particle data parameterized by type and four-momentum vectors. The evaluation employed metrics such as accuracy, AUC, background rejection rates, MSE, likelihood, and two-sample tests. L-GATr demonstrated competitive or superior performance compared to Lorentz-equivariant graph networks. However, it had computational overhead relative to standard transformers and left its potential for pretraining in HEPs unexplored. Similarly, more-interaction particle Transformer (MIParT) scheme [
55] introduced the more-interaction attention (MIA) mechanism to enhance Jet tagging by embedding detailed particle interactions. Based on the Transformer architecture, MIParT-L doubled the dimensions of interaction embeddings for large datasets while reducing model complexity, with 30% fewer parameters and 53% lower computational demands than its predecessor, ParT. Tested on top tagging and quark-gluon datasets, MIParT-L achieved nearly identical accuracy and AUC to leading models while improving background rejection by 25% and 3%, respectively. Fine-tuning on large pre-trained datasets further improved performance by 39% and 6%. Despite its efficiency, the interpretability of MIParT-L remained a challenge, limiting insights into its decision-making process. This trade-off underscored the computational of model efficiency and robust performance across diverse Jet tagging tasks.
5 Applications of AI-based Jet classification
Jet images and PC processed through ML and DL techniques hold vast potential across various applications within the HEP domain, some of theme are already described in Ref. [
18]. This section presents a comprehensive overview of cutting-edge work in this area, categorized into several key domains: Jet parameter scanning, event classification, Jet tagging, multi-Jet classification, energy estimation, and beyond [
83]. The taxonomy of AI-based Jet image and PC applications is visualized in Fig.17, illustrating their scope and relationships. The section thoroughly reviews some applications conducted by researchers, while suggesting future directions for those not yet explored. Additionally, Tab.6 provides a concise summary of performance metrics, limitations, online project availability, and results obtained across these applications, offering valuable insights into their efficacy and applicability.
Tab.6 Summary of the performance of certain ML and DL frameworks proposed for HEP. Only the best performance is reported in the case of multiple tests. |
| Ref. | DLM | Dataset | Description | BP (%) | Limitations | PLA |
|
| [17] | CNN | QCD multi-Jet | Classification of multi-Jet events using CNN at high energies of 13 TeV | AUC = 99.03 | The proposed CNN model needs validation with additional datasets to ensure its generalizability. | No |
| [36] | SVM | Simulated | BIP features invariant under boosts for improved Jet tagging | Acc = 92.7 | Performance could be enhanced through comprehensive hyperparameter tuning. | Yes† URL: zenodo.org/records/7271316 |
| [45] | DNN | Simulated | Sequence of Jet components arranged in a specific order for training inputs. | Acc = 50 | Could be enhanced by employing the LSTM method to efficiently classify Jet from background. | No |
| [57] | DNN | Simulated† URL: www.igb.uci.edu/~pfbaldi/physics/ | DNNs for categorizing Jet substructure in HEP | AUC = 95.3 | The accuracy of the DNN models is limited by the accuracy of the simulation models used to generate the training data. | No |
| [39] | DNN | Higgs | Clarifying HEP event classification with SHAP | Acc = 66 | SHAP may not comprehensively capture feature interactions or explain model behavior in all cases. It could demand substantial computational resources for large datasets or intricate models. | Yes† URL: github.com/rpezoa/hep_shap/ |
| [60] | DNN | ATLAS | Detection of b Jets utilizing QCD-inspired measurements | AUC = 67 | The DNN performed slightly less effectively than the JetFitter algorithm. | No |
| [59] | DNN | Pythia Jet images | Creating images with low pixel density in particle physics for two cased and | AUC = 86.9, AUC = 84.1 | Slower than the non-autoregressive model LAGAN. performed better than for both Pythia and Monte Carlo images. | Yes† URL: mlphysics.ics.uci.edu/ |
| [69] | CNN | Simulated | CNN for predicting quark and gluon Jets | Acc = 75.9 | The higher the energy loss, the more challenging the task of classifying the Jets becomes. | No |
| [74] | RecNN | Simulated | Enhance Quark/gluon classification | AUC = 86.37 | Event-level analysis is not performed. | Yes† URL: github.com/glouppe/recnn |
| [75] | CNN-AE | Daya Bay | Classification for different event types, including IBD prompt, IBD delay, Muon, Flasher, and other | Acc = 99.9 (Muon) | SVM and KNN exhibit inferior performance compared to CNN in identifying event types. Moreover, semi-supervised techniques have not been examined. | No |
| [76] | CNN | Simulated | Employing a quantum CNN to categorize events in HEP | Acc = 97.5 | Quantum CNN showed a lower performance than CNN when it comes to a binary classification of Muon and Electron. Besides, CNN showed low performance when classifying Muon and Pion compared to quantum CNN. | No |
| [77] | ML | ATLAS | Predict if the LHC trials have dismissed a new physics model | Acc = 93.8 | Enhancing reliability can be achieved by requiring a minimum confidence level for the prediction. | Yes† |
| [78] | ANN | Simulated | Identifying boosted top quarks using pattern recognition through an artificial neural network (ANN) in HEP experiments | Eff = 60 | It has 4% mis-tag rate. It exclusively utilizes hadronic calorimete (HCAL) data, though additional data, like sub-Jet b-tags, are crucial for top tagging. | No |
| [79] | DNN | Real data | Enhancing Jet reconstruction at CMS through DL | FPR = 65 | The computational costs, wnen employing the proposed model, have not been verified. | No |
| [80] | CNN | Simulated | Detection of Jet quenching effects caused by the presence of the quarkgluon plasma (QGP) | AUC = 75 | The computational costs, when employing the proposed model, have not been verified. When data normalized, AUC reached only 67% (when ). | No |
Fig.16 The architecture of PartT model suggested in Ref. [52]. (a) Particle transformer. (b) Particle attention block. |
Full size|PPT slide
Fig.17 Taxonomy of AI-based HEP applications using Jet images or PC. |
Full size|PPT slide
5.1 Jet parameters scan
A parameter scan in HEP involves systematically exploring a wide range of values for the theoretical parameters that define a given model. These parameters often characterize the masses of new particles, coupling strengths, or other fundamental quantities hypothesized in extensions of the SM. By examining different combinations of these parameters, researchers aim to identify which sets are compatible with current experimental data or make predictions that can be tested in future experiments. This process helps narrow down the vast theoretical landscape to more plausible scenarios, guiding ongoing investigations and informing the design of new searches [
84].
The utilization of ML and DL models enables the comprehension and estimation of the correlation between the parameter space of new physics models and the experimental physical observables, including signatures characterized by Jets, leptons, and missing transverse energy. This facilitates the efficient constraint of the parameter space of the new physics model [
18]. Given the sensitivity of the ATLAS experiment to exploring parameters, event counts, and Jet distributions in new physics scenarios, significant computing power is required to deduce the surviving regions of the parameter space of constrained minimal super-symmetric standard model (CMSSM) using Bayesian posterior probability and likelihood function ratio tests.
To mitigate computational demands, the study [
85] utilizes an MLP as a regressor to learn the mapping from CMSSM model parameters
to weak-scale supersymmetric particle masses
. The output of the SoftSusy physical package serves as the target output value of the neural network. Approximately 4000 sample points in the parameter space form the training set. With a given set of CMSSM parameters, this MLP model rapidly predicts the corresponding supersymmetric particle mass spectrum, which can then be used to forecast observable distributions at the LHC, including Jet multiplicities and kinematic features. This approach significantly accelerates the process compared to traditional methods. To identify the parameters of a new physics model, [
86] trained an MLP using 84 physical observables from the 14 TeV LHC as inputs, many of which involve Jets and their kinematic properties, with the parameters of a supersymmetric model as the desired outputs. The study revealed that with a collider luminosity of 10
, the CMSSM model’s parameters
and
could be reliably determined with just a 1% margin of error. With a collider luminosity of 500
, additional model parameters such as
and
could also be accurately estimated. In contrast, the conventional approach of minimizing
yielded comparatively inferior results.
Generating collider event samples at the LHC through Monte Carlo simulation can be time-intensive, especially when analyzing detailed Jet structures. While a rapid detector simulation requires only a few minutes, a comprehensive simulation using the GEANT4 framework, as employed by ATLAS and CMS, may necessitate several days. To address this, Ref. [
87] applied parallel full detector simulations using four parameters—common scalar mass (
), universal gaugino mass (
), the trilinear coupling (
), and the ratio of vacuum expectation values (
)— to produce events including Jets and other final-state objects more efficiently. Two ML models, the MLP and SVM, were employed to learn the correlation between the number of signal events and the CMSSM parameters. The results showed that predicting the likelihood function, which strongly depends on Jet signatures and other observables, could achieve several percent accuracy with just 2000 training samples. Moving on, the paper [
88] proposed a machine learning scan (MLS) framework for efficient exploration of multi-parameter supersymmetric models, surpassing traditional methods like MCMC and MultiNest. Utilizing deep neural networks, the MLS incrementally learns parameter space, reducing computational costs while improving target discovery. It integrates HEP packages for precise calculations, including tools like GAMBIT and micrOMEGAs, demonstrating efficiency on toy and CMSSM datasets. Achieving up to 80% sampling efficiency in constrained parameter spaces, MLS outperforms MultiNest under 68% and 95% confidence levels, offering scalability and adaptability for physics model analysis.
5.2 Jet classification and tagging
Despite treating Jets as images or PC in the calorimeter and exploiting the benefits of DNNs in classification for improved Jet substructure detection, these approaches encounter hurdles. Challenges such as Jet image sparsity and potential precision loss arise from constructing Jet images through pixelation or creating advanced Jet features. In this study [
45], a sequential method is employed, utilizing an ordered sequence of Jet constituents as inputs for training. Unlike many prior methods, this approach avoids information loss during pixelization or high-level feature computation. The Jet classification technique achieves a considerable background rejection efficiency operating point for reconstructed Jets with transverse momentum ranging from 600 to 2500 GeV. Moreover, it remains unaffected by multiple proton-proton interactions at levels anticipated during Run 2 of the LHC.
Particles generated in a collider with significant center-of-mass energy typically exhibit high velocity. As a result, their decay products tend to align closely, leading to overlapping Jets. It is crucial in collider data analysis to discern whether a Jet originates from a solitary light particle or from the decay of a heavier particle. Traditional approaches rely on manually crafted distribution features based on energy deposition in calorimeter cells. However, due to the intricate nature of the data, ML techniques have proven more efficient than human efforts for this task [
89]. In Ref. [
90], the Jet image concept treats the detector as a camera, capturing Jet energy distribution in calorimeters as a digital image. This enables Jet tagging as a pattern recognition task, utilizing ML, like Fisher classification, to differentiate between hadronic
W boson decay and Jets from quarks or gluons. Monte Carlo simulation shows superior discrimination compared to traditional methods, offering insights into Jet structure. In Ref. [
63], CNNs improve tagging by treating Jet energy distribution as an image, using channels for features like particle momentum and count. Results show CNNs can surpass traditional methods, providing reliable insights from collider simulation data despite variations in event generators. However, CNNs demonstrate a lack of sensitivity to quark/gluon Jets from different generators, akin to conventional Jet measurements. Moving on, in Ref. [
91], Jet tagging is performed using RNN, leveraging the similarity between Jet clustering and natural language structure. Final-state particle four-momenta are treated as language words, and Jet clustering as grammatical analysis. RNN efficiently processes the tree-like Jet structures, enabling direct use of particle data regardless of count. This method yields higher data utilization efficiency and prediction accuracy than Jet image-based ML, extending to event classification. In Ref. [
74], RNNs distinguish quark and gluon Jets, showing higher gluon suppression. Factors affecting RNN performance are explored, with preliminary quark tagging results. Numerous explorations for phenomena beyond the SM at the LHC depend on top tagging techniques that distinguish between boosted hadronic top quarks and the more prevalent Jets that originate from light quarks and gluons. The HCAL essentially captures a “digital image” of each Jet, where the pixel brightness represents the energy deposited in HCAL cells. Therefore, top tagging is essentially a matter of recognizing patterns. The work in Ref. [
78] propose a novel top tagging algorithm based on an ANN, a popular pattern recognition approach. The ANN is developed using a substantial dataset of boosted tops along with light quark/gluon Jets and is subsequently evaluated on separate datasets. In Monte Carlo simulations, particularly within the 1100−1200 GeV range, the ANN-based tagger demonstrates outstanding efficacy.
Efficient HEP data analysis is imperative with the surge in data from modern particle detectors. However, detectors have limited access to the substructure of Jets, especially those distant from the center-of-mass frame. To address this, the authors [
36] integrate BIP features with standard classification methods, significantly improving Jet tagging efficiency. Notably, supervised methods like MLP, XGBoost, LogReg, SVM, and unsupervised approaches like Gaussian mixture model (GMM) and KNN achieve exceptional performance with uniform manifold approximation and projection (UMAP) dimensionality reduction technique, surpassing contemporary DL systems while reducing training and evaluation times significantly. In Ref. [
79], the authors introduce a novel network architecture designed for Jet tagging in experiments conducted at the LHC. DeepCSV, currently endorsed by CMS and employing a DNN, has significantly improved tagging performance, as validated using real collision data. It surpasses other tagging methods, particularly at high transverse momenta, with nearly an order of magnitude reduction in FPRs using standard threshold definitions.
Multi-Jet classification is a a key task in particle physics aimed at distinguishing between events with varying numbers of Jets. Using ML techniques, such as DNNs, researchers develop classification models to accurately identify these events. Achieving high classification accuracy is crucial for understanding fundamental particle interactions and discovering new physics phenomena in experiments like those conducted at the LHC. The work in Ref. [
17] presents an application of scalable DL to analyze simulation data from proton-proton collisions at 13 TeV in the LHC. The researchers developed a CNN model which utilizes detector responses as two-dimensional images reflecting the geometry of the CMS detector. The model discriminates between signal events of R-parity violating super-symmetry and background events with multiple Jets resulting from inelastic QCD scattering (QCD multi-Jets). With the CNN model, they achieved 1.85 times higher efficiency and 1.2 times higher expected significance compared to the traditional cut-based method. They demonstrated the scalability of the model at a large scale using high-performance computing (HPC) resources with up to 1024 nodes. The authors in Ref. [
56] proposing an interpretable network for multi-Jet classification using the Jet spectrum, termed S2(R), derived from a Taylor series of an arbitrary Jet MLP classifier function. The network’s intermediate feature is an infrared and collinear safe variables, named C-correlator, estimating the importance of S2(R) deposits at angular scales. It offers comparable performance to CNNs with simpler architecture and fewer inputs. The paper [
92] proposes a jet origin identification method for the electron−positron Higgs factory, classifying Jets into 11 categories: 5 quark species, 5 anti-quarks, and gluons. It achieves jet tagging efficiencies ranging from 67% to 92% and charge flip rates between 7% and 24%, utilizing the ParticleNet model. The method benefits jet physics and HEP by enhancing rare Higgs decay measurements. It reduces QCD backgrounds and improves flavor tagging, crucial for Higgs boson property studies. The dataset consists of simulated
events at 240 GeV, generated with a Geant4-based detector simulation. The best reported performance includes a 92% efficiency for b-Jets and a 7% charge flip rate for charm quarks.
5.3 Jet tracking
Jet tracking involves reconstructing the trajectories and properties of particles within Jets, formed when quarks and gluons fragment. Accurate tracking is vital for particle physics analyses, aiding in discoveries, SM measurements, and searches for new phenomena. Advanced algorithms, including pattern recognition and ML, are employed for precise tracking in modern detectors. In this research paper [
64], the authors present early attempts at applying ML techniques to address particle tracking challenges. This area remains largely unexplored, and they have just scratched the surface. Nonetheless, certain DL methods show promise. LSTMs were found to be effective in solving the hit assignment problem in both 2D and 3D scenarios using a sequence of detector layer measurements, potentially offering an alternative to the combinatorial Kalman Filter. CNNs demonstrated the ability to construct representations of detector data from the ground up, aiding in hit assignment and parameter/uncertainty estimation. Through the combination of LSTM and CNN, the authors showcased a potentially powerful end-to-end model capable of identifying a variable number of tracks within detector images. Fig.18 displays sample 2D data generated with various types of tracks, including single-track, multi-track, and single-track with uniform noise.
Fig.18 A toy dataset with adjustable dimensions, straight line representations for tracks, and the option to include uniform noise hits, all on a smaller scale. |
Full size|PPT slide
5.4 Jet generation
In order to study new physics phenomena at the LHC, it is necessary to simulate Monte Carlo events for both new physics signals and backgrounds. This simulation helps predict the experimental data expected from collider experiments. However, generating the large number of simulated events required for data analysis is time-consuming and computationally intensive using existing algorithms. Additionally, accurately simulating how energetic particles interact with detector materials can be a time-consuming process. In Ref. [
93], researchers proposed using GANs to build LAGAN framework, that is trained to generate authentic radiation distributions from simulated collisions involving high-energy particles. The authors found that the generated Jet images exhibited a wide range of pixel brightness levels and accurately reproduced low-dimensional physical observables such as reconstructed Jet mass and n-subJettiness. However, the study also acknowledges the limitations of this method and presents an empirical validation of the image quality. With further improvement, this approach could lead to faster simulation of HEPs events. Physicists at the LHC use complex simulations to predict experimental outcomes. Generating vast amounts of simulated data is costly, but crucial for technique development. Challenges include accurately modeling detectors and particle interactions. In Ref. [
94], researchers proposed a GAN-nased model for fast, accurate simulation of electromagnetic calorimeters. Despite ongoing precision challenges, this solution offers significant speed-ups, up to 100 000×, promising savings in computing resources and advancing physics research at the LHC and beyond.
5.5 Case studies in Jet tagging and classification
To provide a deeper insight into the applications of ML and DL techniques in jet classification for HEP, this section explores three critical case studies: top quark tagging, Higgs boson tagging, and photon Jet classification.
–
Top quark tagging. This process is essential for distinguishing boosted top quarks from background events involving light quarks and gluons. Boosted top quarks often decay into a collimated spray of particles, which requires advanced tagging techniques to identify effectively. The ATLAS open data provides a comprehensive dataset for top quark tagging studies. Additionally, simulation tools like Delphes and MadGraph are frequently used to generate top quark events. Recent methods, including ParticleNet [
49] and LorentzNet [
31], have achieved significant improvements in classification accuracy by leveraging point-cloud representations of jets. These models employ graph-based architectures and permutation-invariant structures to enhance the discrimination power. Metrics such as classification accuracy and AUC have demonstrated significant improvements for top quark tagging using LorentzNet, achieving values exceeding 94% and 98.6%, respectively.
–
Higgs boson tagging. It is crucial for validating the SM and investigating potential new physics phenomena. Higgs bosons decaying into b-quarks generate jet structures with distinctive substructure features, making them a key focus for tagging studies. Datasets such as the CMS open data and the Higgs dataset from the University of California, Irvine ML repository serve as valuable resources for developing tagging algorithms. Traditional methods like BDTs and modern approaches such as CNNs have been employed extensively. Furthermore, advanced architectures like LGN [
48] and ParticleNet [
49] have demonstrated superior classification capabilities. By utilizing high-level kinematic features and DL techniques, classification accuracies exceeding 92% and AUC values surpassing 96% have been achieved, along with notable background suppression.
–
Photon Jet classification. Photon jet classification is a critical task for studying the quark-gluon plasma and distinguishing between direct photons and those originating from fragmentation processes. Quark-gluon datasets generated using PYTHIA8 simulations form the basis for training and evaluating classification models, with additional opportunities provided by CMS open data for analyzing real collision events. Advanced models such as EGNN [
50] and PCT [
51] have demonstrated effectiveness in capturing the energy deposits and angular distributions of particles within jets. Notably, state-of-the-art methods, such as EGNN, have demonstrated exceptional performance in photon jet classification tasks, achieving accuracies above 92% and AUC values exceeding 97%.
6 Future direction and outlook
The future of ML and DL in HEP, particularly in Jet analysis, is poised for transformative advancements. As researchers delve deeper into the petabyte-scale datasets generated by experiments like those at the LHC and QCD, the role of DL becomes increasingly vital. The potential implications of QML-baset Jet research for future particle physics experiments are significant. By demonstrating the effectiveness of QML for Jet classification in section 4.1, this opens up new possibilities for improving the performance of particle physics experiments. Researchers could apply the suggested QML-based approaches to Jet images and PCs to other HEP problems, such as signal versus background separation, anomaly detection, and particle track reconstruction. Furthermore, QML-based research on Jet tagging could pave the way for the development of new quantum algorithms and hardware that could be used to solve complex problems in particle physics and other fields.
There are multiple other compelling aspects and potential extensions that warrant further exploration, which are outlined here. For examples, for
event-level analysis, a Jet, in essence, cannot be entirely separated from an event’s remaining parts, yet “pure” Jets can be achieved through grooming techniques. The utility of color connections is notable in various scenarios. The exploration into how to effectively demonstrate these effects is important, as there is potential in enhancing event-level analysis. The RNN approach, particularly RecNN, is easily adaptable for event-level analysis due to its natural fit into larger hierarchical structures. Previous studies have examined event analysis focusing solely on Jets, utilizing simple RNN chains to reconstruct events from Jets. When considering event-level implementation, structuring the entire event poses a significant challenge. Viewing each event as a structured data tree, where the entire event’s information is encapsulated in the nodes’ properties and their interconnections, is vital. Therefore, accurately representing each element and its connections within the event is crucial for developing neural network architectures. For
Jet unsupervised learning, within the DNN framework, adjusting Jet clustering could potentially enhance performance. Treating Jet finding as a minimization problem presents an intriguing perspective, making it appealing to incorporate Jet finding processes directly into event-level analysis. Another example, for
new physics phenomena often display distinctive patterns related to their particle spectrum and decay modes. For instance, supersymmetry (SUSY) events typically generate a high number of final states, presenting a more complex hierarchical structure, and may include several soft leptons in electroweakino searches. Investigating whether DNNs can more effectively accommodate such topologies is also a worthwhile endeavor [
74]. Moreover, distinguishing between quark-initiated and gluon-initiated Jets is crucial in collider experiments like the LHC. Discriminating between these Jets is challenging due to complex correlations in radiation patterns and non-perturbative effects like hadronization. AI methods, such as deep generative models, offer promising solutions to address this challenge [
63]. Moving forward, there is a notable scarcity of published research on the application of auto-encoder (AE) for Jet image processing, highlighting an opportunity for researchers to explore this field further. The potential for AE to significantly improve the separation of Jet images and PC from background noise presents a promising area of study. By focusing on this niche, researchers can contribute to advancing our understanding and methodologies in particle physics, potentially leading to more accurate and efficient analysis techniques.
The complexity and volume of the data necessitate sophisticated analytical techniques that DL models, especially those based on CNNs and GNNs, are well-equipped to handle. These models excel in identifying intricate patterns and correlations within the data, making them invaluable for tasks such as Jet tagging, particle tracking, and event classification. Furthermore, the scalability of DL models needs to be addressed to handle the increasing data rates from next-generation detectors and accelerators. Efficient training algorithms and model compression techniques will be essential for deploying these models in real-time analysis frameworks, enabling faster decision-making processes for data acquisition and retention. The future of DL in Jet energy progression and estimation promises enhanced precision and efficiency. Innovations will likely focus on developing more sophisticated neural network models that can accurately predict Jet energies in complex environments. Emphasis on real-time data analysis capabilities and integration with experimental workflows will be crucial, driving advancements in detecting and interpreting high-energy particle collisions more effectively and swiftly. The future of DL-based Jet anomaly detection in HEP lies in advancing unsupervised learning techniques to uncover new physics signals hidden in complex data. Innovations in model interpretability and real-time processing will enhance detection capabilities. Cross-disciplinary collaboration will drive these advancements, leading to breakthroughs in identifying rare phenomena and expanding our understanding of the fundamental constituents of the universe. Others applications such as flavor tagging, pileup mitigation, and the reconstruction of decay chains. These DL-based Jet classification can help in distinguishing between different types of particles based on their energy deposition patterns, aiding in the precise determination of particle origins and decay pathways. Additionally, they can be used for enhancing signal-to-noise ratios in complex collision environments, improving the accuracy of particle trajectory tracking, and in the analysis of Jet substructure to identify specific decay processes, contributing to a deeper understanding of the underlying physics in high-energy collisions. The application of DL-based HEP Jet for tomography is promising. This approach has the potential to revolutionize how we visualize and analyze subatomic particles, offering unprecedented precision and insight. By leveraging DL techniques, researchers can improve the accuracy of tomographic reconstructions, enhancing our understanding of particle interactions and the fundamental structure of matter.
Transfer learning (TL), encompassing all its forms, including techniques like fine-tuning and domain adaptation [
95,
96], is poised to revolutionize Jet HEP applications by leveraging pre-trained models from vast datasets to enhance performance on specific tasks with limited data. This approach can significantly reduce computational costs and training times, making it ideal for adapting models to new experiments or rare phenomena. As HEP experiments generate increasingly complex data, the ability to apply knowledge from one context to another will be invaluable for improving event classification, anomaly detection, and signal processing. Looking ahead, TL will be crucial for efficiently extracting insights from new particle interactions and advancing our understanding of fundamental physics. Exploring advanced architectures as sources of prior knowledge, such as EfficientNet, vision Transformers (ViT), Swin Transformers, ConvNeXt, GNNs, neural ordinary differential equations (NODEs), physics-informed neural networks (PINNs), and and AutoML for architecture optimization, could offer substantial improvements to target models conducting AI-based Jet tasks [
46]. These SOTA methods are better suited to handling the complexities of particle physics data compared to older architectures like AlexNet or VGG. Generalizing the top tagger to classify other boosted objects, such as W/Z bosons, Higgs bosons, and other particles, remains straightforward, and extending it to partially-merged and fully resolved tops could enhance background rejection.
Systematic errors are a significant concern in HEP experiments, particularly in image classification tasks involving jet analysis. These errors can arise from various sources, including detector calibration inaccuracies, biases in data reconstruction, and environmental factors during data acquisition. Addressing these uncertainties is crucial for the reliability and accuracy of ML models applied in HEP. One approach to mitigating systematic errors is through systematics-aware learning, which involves developing models that account for potential biases in the data. For instance, Estrade
et al. [
97] discussed the importance of creating benchmarks that capture realistic cases of systematic errors in HEP analysis to facilitate experimental comparisons of different techniques. Another strategy involves adversarial learning to eliminate systematic errors [
98]. This paper discusses the application of adversarial domain adaptation in an unsupervised setting to reduce sample bias in supervised HEP event classifier training. The authors utilize a neural network with a gradient reversal layer to simultaneously enable signal versus background event classification while minimizing differences in the network’s response to background samples from different Monte Carlo models. Ghosh
et al. [
99] proposed classifiers that are fully aware of uncertainties and their corresponding nuisance parameters, demonstrating that this approach can enhance sensitivity to parameters of interest. By incorporating uncertainty directly into the learning process, models can achieve better performance compared to traditional strategies that do not account for such uncertainties.
To further enhance the mitigation of systematic errors, future research should focus on integrating uncertainty quantification and robust optimization directly into the design of ML architectures. This includes the development of hybrid models that combine traditional statistical techniques with modern ML approaches to explicitly model and correct for systematic effects. Additionally, employing advanced simulation techniques that better mimic real-world data will help reduce discrepancies between training datasets and experimental observations. Efforts should also be directed toward leveraging transfer learning to adapt models trained on simulated data to real-world experimental conditions more effectively. Another promising avenue is the application of federated learning in HEP, which enables collaborative training across multiple experimental datasets while preserving data privacy. This approach could be particularly effective in creating more generalized models that are less sensitive to dataset-specific biases. Finally, incorporating interpretability and explainability methods into systematic error analysis will help researchers better understand how models respond to uncertainties and biases, providing actionable insights to refine both experiments and ML methodologies. Such advancements will ultimately ensure that ML models in HEP are robust, transparent, and ready for real-world applications.
Reinforcement learning (RL), with all its variants [
100,
101], in HEP Jet applications is set to open novel pathways for optimizing experimental setups and data analysis strategies. By leveraging RL’s ability to learn optimal policies through interaction with an environment, future HEP experiments could see enhanced automation in event selection, detector alignment, and real-time data processing. The adaptability of RL models to dynamic systems makes them particularly suited for managing the complexities of particle collision events. As the technology matures, integrating RL into HEP could lead to significant advancements in experiment efficiency, discovery potential, and the ability to navigate vast datasets to uncover new physics phenomena. Additionally, federated learning (FL)-based computer vision [
102] presents a promising frontier for Jet images applications, offering a pathway to harness collaborative model training while preserving data privacy and security. By distributing the learning process across multiple nodes, each holding its own subset of data, FL enables a collective improvement of models without direct data sharing. This approach is particularly suited for HEP collaborations spread across global institutions, where data locality and privacy concerns can limit traditional centralized training methods. Advancements in FL could lead to more robust, accurate models, enhancing our understanding of complex particle physics phenomena through cooperative, privacy-preserving analysis between different LHCs.
The integration of large language models (LLMs) and generative AI [
103] into HEP has the potential to enhance the precision of particle detection and characterization. By leveraging these advanced AI models, researchers can identify subtle patterns and anomalies in Jet tagging that might be missed by conventional methods. This improved accuracy is crucial for discovering new particles or interactions that could lead to breakthroughs in our understanding of the universe. For example, in the search for dark matter or other exotic particles, detecting faint signals amid a noisy background is a significant challenge. Generative AI can help by producing simulations that highlight these weak signals, allowing physicists to fine-tune their detection algorithms. Similarly, LLMs can assist by providing context and insight into these findings, suggesting potential theoretical implications and further areas of exploration. The application of LLMs and generative AI in HEP also promotes a more collaborative and interdisciplinary approach to research. By integrating AI experts with physicists, new methodologies and tools can be developed that leverage the strengths of both fields. This collaboration can lead to the creation of more sophisticated models that are specifically tailored to the needs of HEP. Furthermore, the insights gained from HEP research using AI can be applied to other fields, such as astrophysics, medical imaging, and materials science. This cross-pollination of ideas and techniques can drive innovation across multiple disciplines, leading to advancements that benefit a wide range of scientific endeavors.
7 Conclusion
Given the comprehensive assessment of ML and DL applications within the realm of HEP presented in this survey, it is evident that these techniques have significantly impacted various aspects of HEP experimentation and phenomenological studies. Through a detailed exploration of diverse DL approaches, including their application to HEP classification, Jet particle analysis, and other pertinent areas, this paper has highlighted the potential of ML and DL techniques to enhance our understanding of particle physics phenomena. The analysis undertaken throughout this survey underscores the importance of leveraging AI models tailored to HEP images and PCs, as well as the significance of SOTA ML and DL techniques in advancing HEP inquiries. Specifically, the review has elucidated the implications of these techniques for tasks such as Jet tagging, Jet tracking, and particle classification, shedding light on their capabilities and limitations in addressing key challenges within the field. As we reflect on the current status of HEP grounded in DL methodologies, it becomes evident that while significant progress has been made, and there remain inherent challenges that must be addressed to fully harness the potential of these approaches. These challenges include issues related to data quality, model interpretability, and generalization to diverse experimental conditions. Nonetheless, the survey also identifies promising avenues for future research endeavors, such as the development of novel DL architectures tailored to HEP data and the integration of domain-specific knowledge to enhance the performance of learning models. By addressing the challenges and leveraging the opportunities highlighted in this survey, researchers can continue to push the boundaries of HEP experimentation and pave the way for groundbreaking discoveries in particle physics using AI techniques.
{{custom_sec.title}}
{{custom_sec.title}}
{{custom_sec.content}}
 PDF(4030 KB)
PDF(4030 KB)


 PDF(4030 KB)
PDF(4030 KB)
 PDF(4030 KB)
PDF(4030 KB)







































































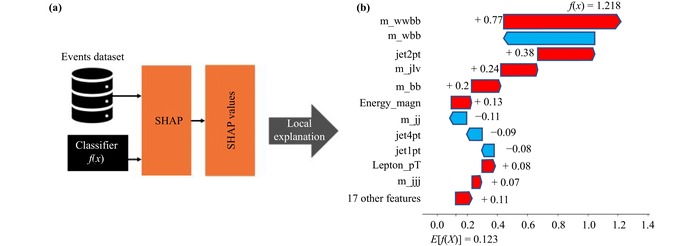

 PDF(4030 KB)
PDF(4030 KB)
 Tab.1 Assessing how the proposed review aligns with previous research in the field of HEP. The ( ) indicates that those specific areas have been addressed, whereas () and ( ) signify instances where certain areas have not been addressed, or partially addressed, respectively.
Tab.1 Assessing how the proposed review aligns with previous research in the field of HEP. The ( ) indicates that those specific areas have been addressed, whereas () and ( ) signify instances where certain areas have not been addressed, or partially addressed, respectively. Fig.1 Mind-map of the proposed review.
Fig.1 Mind-map of the proposed review. Fig.2 Visualization of decay involving a reconstructed Jet and a secondary vertex, showcasing various noteworthy features [27].
Fig.2 Visualization of decay involving a reconstructed Jet and a secondary vertex, showcasing various noteworthy features [27]. Tab.2 An overview of the metrics employed to evaluate performance in ML and DL-based HEP.
Tab.2 An overview of the metrics employed to evaluate performance in ML and DL-based HEP. Fig.3 Jet images summed online and categorized into different channels employed in the analysis within the 100−200 GeV pT range.
Fig.3 Jet images summed online and categorized into different channels employed in the analysis within the 100−200 GeV pT range. Tab.3 A summary of available datasets, and simulation tools for Jet HEP analysis
Tab.3 A summary of available datasets, and simulation tools for Jet HEP analysis Tab.4 Possible combinations of Jet features to generate new high- and low-level features that could potentially improve ML classification for Jet HEP. The performance of employing these features are presented in Ref. [35].
Tab.4 Possible combinations of Jet features to generate new high- and low-level features that could potentially improve ML classification for Jet HEP. The performance of employing these features are presented in Ref. [35]. Tab.5 A summary of available ML and DL architectures for Jet HEP classification, including columns for biases, generalizability, and recommended use cases. Bias levels range from moderate (limited datasets) to high (overfitting, dataset reliance), while generalizability is categorized as high (broad applicability), moderate (adequate performance with some limitations), and low (poor performance or untested on other tasks).
Tab.5 A summary of available ML and DL architectures for Jet HEP classification, including columns for biases, generalizability, and recommended use cases. Bias levels range from moderate (limited datasets) to high (overfitting, dataset reliance), while generalizability is categorized as high (broad applicability), moderate (adequate performance with some limitations), and low (poor performance or untested on other tasks). Fig.4 Taxonomy of ML and DL-based HEP techniques for Jet classification, with associated preprocessing, metrics, simulation tools and datasets.
Fig.4 Taxonomy of ML and DL-based HEP techniques for Jet classification, with associated preprocessing, metrics, simulation tools and datasets. Fig.5 (a) Diagram illustrating the localized explanation of an event classifier with the SHAP method. (b) Localized SHAP explanation represented using a waterfall plot. It can be observed that the SHAP values are associated with individual event features. The classifier’s prediction (XGBoost) is f(x)=1.218, while the base value is E[f(x) ]=0.123. In this context, the feature “m_wwbb” contributes positively with a SHAP value of +0.77, increasing the prediction, whereas the feature “m_wbb” has a SHAP value of −0.6, reducing the prediction.
Fig.5 (a) Diagram illustrating the localized explanation of an event classifier with the SHAP method. (b) Localized SHAP explanation represented using a waterfall plot. It can be observed that the SHAP values are associated with individual event features. The classifier’s prediction (XGBoost) is f(x)=1.218, while the base value is E[f(x) ]=0.123. In this context, the feature “m_wwbb” contributes positively with a SHAP value of +0.77, increasing the prediction, whereas the feature “m_wbb” has a SHAP value of −0.6, reducing the prediction. Fig.6 An example of classifier utilizing MLP trained using kinematic and spectrum variables for Jet classification [56]. S2 ,trim and S2 ,soft correspond to hard and soft substructure information.
Fig.6 An example of classifier utilizing MLP trained using kinematic and spectrum variables for Jet classification [56]. S2 ,trim and S2 ,soft correspond to hard and soft substructure information. Fig.7 The architecture of LGN model suggested in Ref. [48].
Fig.7 The architecture of LGN model suggested in Ref. [48]. Fig.8 The architecture of the TopoDNN model, consists of 4 layers with 300, 102, 12, and 6 nodes, respectively [45].
Fig.8 The architecture of the TopoDNN model, consists of 4 layers with 300, 102, 12, and 6 nodes, respectively [45]. Fig.9 The architecture of PFN-ID model suggested in Ref. [47]. (a) Per-particle mapping Φ. (b) The binary output signal or background can be identified.
Fig.9 The architecture of PFN-ID model suggested in Ref. [47]. (a) Per-particle mapping Φ. (b) The binary output signal or background can be identified. Fig.10 The architecture of CNN tagger model suggested in Ref. [46].
Fig.10 The architecture of CNN tagger model suggested in Ref. [46]. Fig.11 The architecture of DeepJet model suggested in Ref. [67].
Fig.11 The architecture of DeepJet model suggested in Ref. [67]. Fig.12 Example of CNN architecture with input Jet image, three convolutional layers, dense layer, and output layer are involved. In this context, red represents the transverse momenta of charged particles, green corresponds to the pT of neutral particles, and blue signifies the charged particle multiplicity [63].
Fig.12 Example of CNN architecture with input Jet image, three convolutional layers, dense layer, and output layer are involved. In this context, red represents the transverse momenta of charged particles, green corresponds to the pT of neutral particles, and blue signifies the charged particle multiplicity [63]. Fig.13 The architecture of ParticleNet model suggested in Ref. [49].
Fig.13 The architecture of ParticleNet model suggested in Ref. [49]. Fig.14 The architecture of EGNN model suggested in Ref. [50].
Fig.14 The architecture of EGNN model suggested in Ref. [50]. Fig.15 (a) The architecture of LorentzNet model. (b) LGEB block [31].
Fig.15 (a) The architecture of LorentzNet model. (b) LGEB block [31]. Tab.6 Summary of the performance of certain ML and DL frameworks proposed for HEP. Only the best performance is reported in the case of multiple tests.
Tab.6 Summary of the performance of certain ML and DL frameworks proposed for HEP. Only the best performance is reported in the case of multiple tests. Fig.16 The architecture of PartT model suggested in Ref. [52]. (a) Particle transformer. (b) Particle attention block.
Fig.16 The architecture of PartT model suggested in Ref. [52]. (a) Particle transformer. (b) Particle attention block. Fig.17 Taxonomy of AI-based HEP applications using Jet images or PC.
Fig.17 Taxonomy of AI-based HEP applications using Jet images or PC. Fig.18 A toy dataset with adjustable dimensions, straight line representations for tracks, and the option to include uniform noise hits, all on a smaller scale.
Fig.18 A toy dataset with adjustable dimensions, straight line representations for tracks, and the option to include uniform noise hits, all on a smaller scale.