High-flux and stable MgF molecular beam for one-dimensional Doppler cooling applications

Abstract

A novel cryogenic MgF molecular beam, characterized by high flux and exceptional stability, has been successfully generated within a helium buffer gas environment. This achievement is facilitated by the innovative use of an in-cell stepper motor, which continuously rotates the sample rod during laser ablation. Through meticulous optimization of the ablation laser energy, the position of the ablation spot, and the gas flow rate, among other critical parameters, the resulting MgF beam exhibits a remarkable forward velocity of 209 m/s and an impressive brightness of approximately 1.36 × 10¹² molecules per pulse per steradian per internal state. Subsequent attempts at one-dimensional Doppler cooling of the MgF beam have been made, with theoretical calculations closely aligning with experimental outcomes. These findings demonstrate a significant compression in the transverse spatial distribution of the molecular beam, from 7.8 to 6.5 mm, and a substantial cooling of the transverse temperature, from 8.1 to 5.6 mK. This work lays a crucial foundation for the advancement of molecular slowing and magneto-optical trapping techniques for MgF molecules.

Graphical abstract

Keywords

cold molecules / buffer gas cooling / laser cooling of molecules / Doppler cooling

1 Introduction

Ultracold molecular physics has garnered significant attention from researchers due to its critical applications in areas such as quantum computing and simulation [1−7], precision metrology, and the investigation of fundamental physical laws and constants [8−12], as well as ultracold chemical reactions and collisions [13−17]. However, in contrast to atoms, the internal degrees of freedom inherent in molecules introduce additional complexities in their cooling and trapping processes [18, 19]. Cryogenic buffer gas cooling is a widely utilized technique that facilitates the generation of intense beams of atoms and molecules with low forward velocities. Notably, this method enables the straightforward and efficient cooling of both vibrational−rotational and translational degrees of freedom in molecules [20−23]. Consequently, buffer gas cooling techniques are now commonly employed for laser cooling and magneto-optical trapping (MOT) of molecules [24−30].

Currently, tremendous progress has been made in direct laser cooling and the MOT of diatomic molecules, i.e., SrF [24], YO [27], CaF [25, 26], BaF [30], and triatomic molecule CaOH [29]. And some groups have proposed to achieve Bose−Einstein condensation of molecules [31, 32]. Such results often stem from cryogenic buffer gas beam sources. However, molecular laser cooling is currently limited by the low final trapped molecule density, which is partly due to the limited number of molecules from the buffer gas beam sources, requiring continuous optimization of the parameters associated with the buffer gas beam sources. The first issue is obviously the stability of the beam. Currently, almost all buffer gas cooling experiments rely on direct laser ablation (SrF [33], YO [34], BaF [35, 36]) or laser ablation of metal species plus chemical reactions (CaF [37, 38], AlF [39], MgF [40−43], YbF [44]). During laser ablation process, different ablation target locations, varying gas flow rates and the energy of the ablation laser all affect the stability of the beam. Another problem is the repeatability of the beam sources. As the species is ablated at a fixed location relative to the ablation laser beam, the focused laser will dig deeper and deeper into the species surface over time, possibly forming small craters that substantially affect the persistence of the molecular beam. To overcome the second issue, some groups have designed the manually rotatable targets outside the chamber [22]. However, the manual target rotation is non-uniform.

In this paper, we designed a beam source system using an in-cell stepper motor to automatically drive the rotation of the ablation rod. We further optimized the MgF beam source conditions to produce a high brightness and stable MgF beam. To quantitatively analyze the number of MgF molecules generated per laser pulse in the beam source system, herein we adopt the method based on the photomultiplier tube (PMT) measurement according to Ref. [45]. This method considers the parameters including the divergence angle of the molecules, the fluorescence collection angle, the PMT quantum efficiency, and the signal sampling impedance. From theories fitting well with the experimental results, the MgF beam brightness is derived to reveal the success of the cryogenic cooling experiments. Initial Doppler laser cooling of MgF molecules also shows encouraging results.

2 Experimental setup

2.1 Molecular beam source

The buffer gas cell is built based on previous publication [41]. In brief, it is cooled by the pulsed tube helium cryocooler (CRYOMECH, PT 415). The PT 415 includes two stage heat exchangers. The base temperatures of the first and second stage heat exchangers are 40.0 K and 4.0 K, respectively. The sketch of the buffer gas cell is shown in Fig.1. The cell is consisted of a copper cube of a 30.0 mm length with a bore of 10 mm diameter. The cell is in close contact with the second stage cold plate. In order to increase the cooling efficiency, an indium sheet (a thickness of 0.5 mm) is placed between the second stage cold plate and the cell. The exit aperture of the cell has a diameter of 4.5 mm. The Nd:YAG 532 nm laser with a pulse of 7 ns (Beamtech, Dawa-200) enters the cell through a small window perpendicular to the molecular beam. The buffer gas and the fluorine donor gas we used are helium (He) and nitrogen trifluoride (NF₃). The main chemical reaction pathway is Mg + NF₃ → MgF + NF₂. Since the freezing point and boiling point of NF₃ are 66 K and 144 K, respectively, we monitor the temperatures of the He and NF₃ lines and the corresponding temperatures are 4.5 K and 130.0 K, respectively. The extension piece is added between the cell and the exit, allowing us to install a different number of extensions to change the structure of the cell. The produced MgF molecular beam then exits, as shown in Fig.1(b).

Fig.1 Assembly diagram: (a) Drawings of the main assembly parts of the motor. (b) Assembly drawing of the cell.

Full size|PPT slide

2.2 Stepper motor drive system

The molecular signal will decrease gradually if the metal target/rod is bombarded by the YAG laser over hundreds of times at the same location. To address this issue, we can change the ablation spot by rotating either the ablation target or translating the YAG laser beam. In general, rotating the ablation target is superior to translating the ablation laser beam [22]. However, manual operation of the ablation target is neither uniform, nor stable. Therefore, we designed an in-cell stepper motor system to rotate the ablation target instead. The stepper motor and the cell are shown in Fig.1(a) and (b), respectively. As shown in Fig.1(b), the motor is connected to the cell by the connecting piece. To avoid heat conduction generated by the motor, the connecting piece is made of polyimide. Fig.1(a) illustrates the details of the motor drive. The Mg sample is affixed to the top of the motor shaft, allowing the Mg sample to reciprocate up and down as the motor shaft rotates.

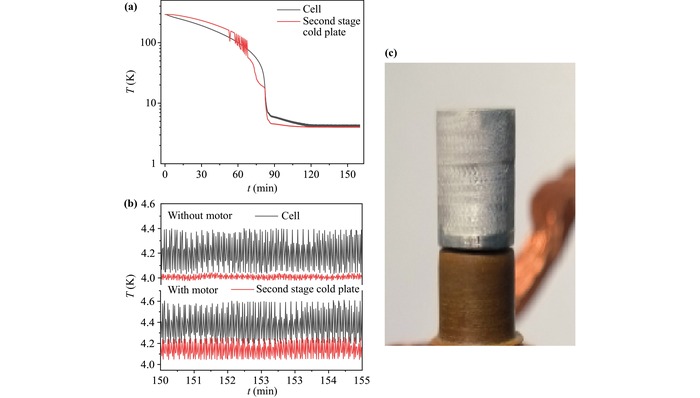
One critical aspect is that the lowest stable temperature the cell can reach is associated with all thermal loads, such as those from the stepper motors. The temperature sensor used is the DT 670. We employ LakeShore to measure the temperature. In Fig.2(a), when the cell experiences heat loads from the motor, the temperatures in the second stage cold plate and the cell reach the lowest stable temperature limit after 120 minutes. In Fig.2(a), the oscillation of the red temperature curve between 200 K and 50 K is attributed to the influence of the temperature sensor itself. The temperature over the 150−155 minutes is depicted in Fig.2(b). The mean temperature of the cell without the motor and the cold plate during this period is 4.2 K and 4.0 K, respectively. When the cell is loaded with the motor, the mean temperatures are 4.4 K and 4.2 K, respectively. The actual ablation marks on the surface of the Mg target, as it is driven by the motor, are shown in Fig.2(c). When the motor operates for 2−3 hours, the cell temperatures are maintained at approximately 4.5 K, indicating good consistency.

Fig.2 Temperature variation and ablation marks of the Mg target. (a) The temperatures of the cell and the second stage cold plate during the cooling process with heat loads from the motor. (b) Between 150 to 155 minutes after cooling, the temperatures of the cell and the second stage cold plate with and without heat loads from the motor. (c) The actual laser ablation marks on the surface of the Mg target as driven by the motor.

Full size|PPT slide

3 Characteristics of MgF beam

To detect the MgF signal, we mainly use two detection methods − direct absorption and laser-induced fluorescence (LIF) [46]. The molecular beam system consists of three main regions. The absorption signal is used to measure the MgF in the cell (region 1). After exiting from the cell, the MgF beam enters regions 2 and 3. Region 2 is 33.00 cm downstream from the exit port of the cell, which is the location of PMT1. The distance between region 2 and 3 is D = 25.00 cm. Region 3 is the location of PMT2. The time-of-flight (ToF) signal can be obtained by collecting the LIF signals in regions 2 and 3. According to the ToF signals collected in regions 2 and 3, the forward velocity of MgF beam is then measured and optimized [41].

The stability and consistency of MgF signals are critical. In Fig.3, we show that for the first time in our laboratory, we achieve the stable MgF beam incorporating this new stepper motor system. In this study, the 532 nm laser fires at a rate of 2 Hz and the pulse energy is 20 mJ. When the motor is not turned on, the YAG laser bombards the target in the same spot and the measured MgF signal is declining over time or laser pulses, as shown in Fig.3 (the red curve). After 4000 laser pulses, signal is almost gone. When the motor is turned on, the MgF signal is stable and persistent, also shown in Fig.3 (the black curve). Even after 10 000 laser pulses, the MgF signal does not change much.

Fig.3 MgF signal in region 2 with the stepper motor on and off. The red dots show the molecular signal measured when the motor is not operating. The black dots show the measured signal as the motor rotates.

Full size|PPT slide

We study the relationship between the yield of MgF and YAG energy. In this experiment, the focused laser diameter on the rotating rod is estimated to be 1.0 mm. In Fig.4, it is found that the energy threshold for generating MgF molecules is 5−10 mJ. From 10 mJ to 30 mJ, the yield of MgF increases rapidly with the YAG energy. It can be considered that 10−30 mJ is a suitable range. However, when the YAG energy exceeds 30 mJ, the MgF signal shows a continuous decreasing trend. Therefore, excessively high YAG energy should be avoided in the experiment, and 10−20 mJ is generally used.

Fig.4 Relationship between the yield of MgF and YAG energy (532 nm pulse).

Full size|PPT slide

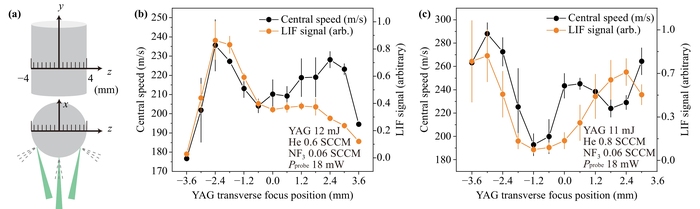
In the laboratory reference frame, we established the coordinate system, as shown in Fig.5(a). The gray cylinder represents the Mg sample rod. The center of the Mg rod is the coordinate origin. The diameter of the Mg rod is 8.0 mm. The green arrow represents the focusing position of the YAG laser. When the YAG laser hits different positions of the Mg rod, the directions of the sputtered Mg atoms are different as shown by the dashed line in Fig.5(a), which will affect the chemistry of MgF synthesis and gas dynamics process in the cell, thereby affecting the yield and velocity of the molecules. In the z direction, the MgF rod is divided into 13 regions spanning −4.0 mm to +4.0 mm. The left side is close to the He tube, and the right side is close to the cell exit port. When the 532 nm laser hits the 13 regions and the corresponding LIF signals are recorded by PMT1 and PMT2. According to the ToF signal, the intensity and velocity of the MgF beam are plotted in Fig.5(b, c).

Fig.5 The relationship between the transverse position of the YAG ablation points and the forward velocity and LIF signals under different cell structures. (a) Schematics of ablation points at different positions on the Mg rod. (b) The relationship between the forward velocity, LIF signal and YAG transverse position with one extension. (c) The relationship between the forward velocity, LIF signal and YAG transverse position with two extensions.

Full size|PPT slide

In Fig.5(b), with an extension piece attached to the cell, the relative beam brightness and central velocity of the molecular beam increase synchronously when the lateral ablation position moves from −3.6 to −2.4 mm. When the ablation point in the cell moves from −2.4 mm to the center, the sputtering direction of Mg atoms gradually changes from the cell axis to the cell radius. Some molecules are lost on the inner wall of the cell and only a fraction of the molecules will form a beam under the thermalization of the carrier gas, resulting in a decrease in signal. When the ablation point in the cell moves from the center to the outlet, the sputtering direction of Mg atoms gradually returns to the cell axis. Once MgF molecules are formed, there is almost no thermalization distance before leaving the cell, causing the signal to rise and the velocity to increase.

For comparison, similar experiments are performed using two extension pieces. In Fig.5(c), when the ablation point position in the cell is on the left, the beam brightness and the central velocity increase synchronously, as shown in Fig.5(b). However, when the position is in the range of 1.8−2.4 mm, due to the longer thermalization distance provided by the two extensions, the velocity decreases while the signal increases. Therefore, in the cell structure with two extensions, the ablation point position of 1.8−2.4 mm in the cell is a good choice.

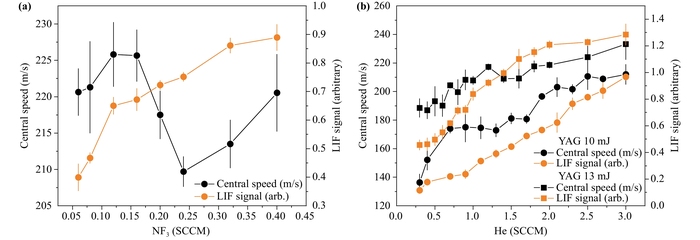
With two extensions in the cell, we optimized other parameters. NF₃ acts as a fluorine donor because it is directly related to the generation of MgF molecules. The flow rate of NF₃ ($n_{{\mathrm{N}\mathrm{F}}_3}$) directly determines the density of generated MgF molecules. In Fig.6(a), with the experimental parameters fixed as shown in the figure annotation, the central forward velocity and LIF signal are recorded by changing the flow rate of NF₃. When $F_{{\mathrm{N}\mathrm{F}}_3}$ increases, the overall trend of the beam brightness of molecules also increases because more MgF molecules are generated. With 0.04 < $F_{{\mathrm{N}\mathrm{F}}_3}$ < 0.12 standard cubic centimeters per minute (SCCM), the beam brightness increases rapidly with $F_{{\mathrm{N}\mathrm{F}}_3}$. With 0.12 < $F_{{\mathrm{N}\mathrm{F}}_3}$ < 0.4 SCCM, the beam brightness increases slowly with $F_{{\mathrm{N}\mathrm{F}}_3}$. With 0.16 < $F_{{\mathrm{N}\mathrm{F}}_3}$ < 0.25 SCCM, the velocity and beam brightness show a good negative correlation. When $F_{{\mathrm{N}\mathrm{F}}_3}$ increases further, the velocity of the molecules increases again. Therefore, based on the experimental results shown in Fig.6(a), we typically set the NF₃ flow rate at 0.24 SCCM, which results in a smaller forward velocity for the molecular beam and a considerable brightness of the molecular beam.

Fig.6 The relationship between molecular longitudinal central velocity and LIF signals with NF3 flow rate and He flow rate. (a) Relationship between the forward velocity, beam brightness and NF3 flow rate. Experimental conditions: YAG energy 13 mJ, $F_{\mathrm{H}\mathrm{e}}$ = 0.7 SCCM, probe laser power $P_{\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{e}}$ = 20 mW. (b) Relationship between the forward velocity, beam brightness and He flow rate. Experimental conditions: $F_{{\mathrm{N}\mathrm{F}}_3}$ = 0.24 SCCM, $P_{\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{e}}$= 20 mW.

Full size|PPT slide

The carrier gas He acts as a buffer gas, and the flow rate of He will affect the buffer gas cooling process in the cell. In Fig.6(b), with the experimental parameters fixed as shown in the figure annotation, the forward velocity and LIF signal are recorded by changing the flow rate of He. The circular data represents the test results under the YAG laser energy of 10 mJ; the square data represents the test results under the YAG laser energy of 13 mJ. At 10 mJ, as $F_{\mathrm{H}\mathrm{e}}$ increases, the beam signal increases almost linearly, indicating that the increase in flow rate allows the carrier gas to carry more molecules out of the cell during the thermalization process. At 13 mJ, more Mg atoms are excited due to the high YAG energy, so more MgF molecules are produced. In Fig.6(b), with 1.2 SCCM < $F_{\mathrm{H}\mathrm{e}}$ < 1.7 SCCM is observed to be the optimal flow range, because the molecular beam velocity increases slowly, while the signal intensity increases rapidly.

After optimizing the ablation point position within the cell, the flow rates of NF₃ and He, the parameters are as follows: the energy of the YAG is set at 13 mJ; the ablation point position is adjusted to be at +2.4 mm; and the flow rates for NF₃ and He are 0.24 SCCM and 1.4 SCCM, respectively.

4 Brightness measurement of MgF beams

4.1 MgF signal collection

The fluorescence wavelength collected and detected by the PMT is 359 nm. The PMT model is R9880U-210 (Hamamatsu). It has a very high quantum efficiency of about 42.8% at this wavelength band, corresponding to a cathode sensitivity $\eta$ of around 120 mA/W. In the experiment, the PMT is applied with a high voltage of −800 V, at which the gain G is about 149470. Therefore, the relationship between the internal response current of the PMT and the incident optical power on the cathode is 17816 A/W. The PMT is a constant current source, and its current signal passes through a commercial transimpedance matching resistor Z (1.1 MΩ) to achieve current-to-voltage signal conversion. Finally, the voltage signal is fed into the analog-to-digital converter card via BNC transmission line to acquire the signal Sig. According to the card’s voltage reading Sig, the transimpedance matching value Z, and the current-optical power relationship $\eta$, the optical power received by the cathode can be obtained,

(1)$P_{\mathrm{e}\mathrm{x}\mathrm{p}}={\displaystyle \frac{Sig}{\eta GZ}}.$

However, due to the limitations of the PMT collection system, only a portion of the fluorescence is collected by the PMT. After the molecular beam passes through the skimmer at a distance of L1 from the outlet, it flies along z to L2. The LIF signal passes through two lenses with a diameter of 50.8 mm and a bandpass filter (Thorlabs, FGUV11-UV) and is focused on the cathode of the PMT. Combining the cavity window, the overall transmittance T is 54%. Len 1 is about 93 mm away from the center of the molecular beam, so the collection solid angle is approximately $\mathrm{\Omega }=0.222Sr$. Combining the transmittance T, collection angle $\mathrm{\Omega }$, and Eq. (1), the total optical power $P_{\mathrm{t}\mathrm{o}\mathrm{t}}$ can be obtained,

(2)$P_{\mathrm{t}\mathrm{o}\mathrm{t}}={\displaystyle \frac{P_{\mathrm{e}\mathrm{x}\mathrm{p}}}{T\left[\mathrm{\Omega }/(4\pi )\right]}}={\displaystyle \frac{Sig}{\eta GZT\left[\mathrm{\Omega }/(4\pi )\right]}}.$

4.2 Calculating the single molecule optical power

The energy of a single photon is $E=hc/\lambda$, where h is the Planck constant, c is the speed of light, and $\lambda$ is the wavelength. If the average photon scattering rate of a molecule under the action of probe light with a beam waist w is known ${\mathrm{\Gamma }}_{sc}$, then the single molecule optical power $P_m$ can be obtained as $P_m={\mathrm{\Gamma }}_{sc}\cdot E$. By comparing theory and experiment, ${\mathrm{\Gamma }}_{sc}$ under a certain probe light intensity can be confirmed. According to Eq. (3), an Optical Bloch Equation model for the MgF $X^2{\mathrm{\Sigma }}_{1/2}^{+}(v=0,N=1)\to A^2{\mathrm{\Pi }}_{1/2}(v^{\prime }=0,J^{\prime }=1/2)$ transition is established, with the ground state including 12 magnetic sublevels under N = 1 and 1 leak channel; the excited state includes 4 magnetic sublevels under $J^{\prime }=1/2$. The model considers the effect of a 0.5 G geomagnetic field on the system, and sets the pump light covering the $|F=1^{-}⟩\to |F^{\prime }=1,0⟩$ transitions, as shown in Fig.7(a). By varying the intensity of the pump light, and then calculating the corresponding scattering rate using Eq. (5), the scattering rate under different pump light intensities can be obtained [48]:

Fig.7 Single molecule scattering rate. (a) Pumping scheme. (b) The relationship between the LIF signal and the probe light intensity. (c) The response of the PMT under different light intensities.

Full size|PPT slide

(3)${\displaystyle \frac{\mathrm{d}\sigma }{\mathrm{d}t}}={\displaystyle \frac{1}{\mathrm{i}\hslash }}\left[\hat{H},\sigma \right]+L\left(\sigma \right),$

(4)$\hat{H}={\hat{H}}_0+{\hat{H}}_B+{\hat{H}}_{int},$

(5)${\overline{R}}_{sc}={\displaystyle \sum _i{\displaystyle \frac{1}{T}}{{\displaystyle \int }}_0^T{\sigma }_{e_i{e}_i}\left(\tau \right)\mathrm{\Gamma }\mathrm{d}\tau .}$

In the experiment, the probe light is locked to the $|F=1^{-}⟩\to |F^{\prime }=1,0⟩$ transition frequency. By varying the intensity of the probe light, the relationship between the LIF signal recorded by the PMT and the probe light intensity recorded by the power meter is obtained, resulting in the experimental data. As shown in Fig.7(b), the normalized experimental and theoretical curves match each other. As the probe light intensifies, the curve slope becomes smaller and gradually saturates. The horizontal axis gives the saturation parameter S, which is the ratio of the laser intensity I to the saturation intensity $I_s$. The saturation intensity of MgF is $I_s=62.5\mathrm{m}\mathrm{W}/{\mathrm{c}\mathrm{m}}^2$. By comparing theory and experiment, the average scattering rate of a single molecule under a certain probe light intensity can be determined, which gives the $P_m$ (e.g., for a probe light of 30 mW, beam waist of 2.8 mm, the saturation parameter is 7.8, corresponding to a scattering rate of 0.1139 MHz and single molecule optical power $P_m=6.29\times {10}^{-14}\mathrm{W}$). Combining with Eq. (2), the number of detected molecules is

(6)$N={\displaystyle \frac{P_{\mathrm{t}\mathrm{o}\mathrm{t}}}{P_m}}={\displaystyle \frac{Sig}{\eta GZT\left[\mathrm{\Omega }/\left(4\pi \right)\right]P_m}}.$

In addition, after recording the baseline of the PMT at different light intensities, it is confirmed that the PMT current responds linearly within the range of probe light intensities, as shown in Fig.7(c). As the probe light intensifies, the baseline maintains a linear response within the range of 0−3.25 V. Therefore, the experimental curve in Fig.7(b) is reliable without needing additional corrections.

4.3 Calculating the brightness of MgF molecules

After obtaining the number of molecules, combining with the detection solid angle of the molecular beam, the brightness of the beam can be obtained. After passing through the skimmer, the divergence angle of the molecular beam is constrained. By combining L1, L2 and the skimmer diameter ($D_{ski}$) of 4.0 mm, the lateral width of the molecular beam at the PMT position is $d=(L_2\times D_{ski})/L_1$. Since the probe light passes through the molecular beam transversely and the beam waist is smaller than $d$, only molecules within the approximate rectangular area with width $w$ and height $d$ are induced to fluoresce, with a corresponding solid angle of $(w\times d)/{L_2}^2$. Dividing the number of molecules [Eq. (6)] by this solid angle finally gives the beam brightness

(7)$\mathcal{B}=Sig\times {\displaystyle \frac{L_1\cdot L_2}{\eta GZT\left[\mathrm{\Omega }/(4\pi )\right]P_{m}w{D}_{ski}}}.$

4.4 The measurement of molecular beam brightness

The parameters used in subsequent experiments are the same in Section 3. In experiments, the longitudinal center velocity and beam brightness are typically measured using LIF signals after allowing the system to stabilize for 10 minutes. When measuring the beam brightness, based on the single molecule optical power $P_m$ under different probe powers, and combining with Eq. (7), the brightness of the molecular beam can be obtained. The probe system parameters are given in Tab.1. The results are shown in Fig.8. The orange line is the average value, $1.36\times {10}^{12}$/pulse/solid angle/quantum state. The brightness of the beam under different probe powers are around the average line, with the maximum deviation from the average line not exceeding 2.7%. This means our method is reliable.

Tab.1 Parameters used in beam density measurement.

Parameter	Unit	Value
The sensitivity of PMT	A/W	0.12
Amplification gain	−	144596.35
Impedance	Ω	1.1M
Collected solid angle	Sr	0.222
Transmittance	%	54
Beam waist	mm	2.8
The diameter of skimmer	mm	4.0
L1	mm	10.0
L2	mm	30.0

Fig.8 Molecular beam brightness of MgF at different detection powers.

Full size|PPT slide

The current brightness of the molecular beam sources produced by buffer gas cooling are summarized in Tab.2. The Yb atoms can reach ${10}^{13}$/pulse/solid angle/quantum state, indicating that the low-temperature beam apparatus has outstanding capabilities for generating cold atoms. Moreover, since atomic beams are generated without chemical reactions, their buffer gas cooling yield is higher than that of molecules by two orders of magnitude. The brightness of AlF is up to ${10}^{12}$/pulse/solid angle/quantum state. For other diatomic free radicals such as SrF, CaF, BaF, YbF and MgF, their brightness is in the range of ${10}^9$−${10}^{11}$/pulse/solid angle/quantum state, and the central longitudinal velocities are between 140−200 m/s. In addition, the reaction between laser ablated Ca atoms and atmospheric H₂O can generate the triatomic molecule CaOH, with a brightness up to ${10}^{10}$/pulse/solid angle/quantum state. In contrast, the brightness of our MgF molecular beam is quite good, $1.36\times {10}^{12}$/pulse/solid angle/quantum state, as reported in this study.

Tab.2 Brightness of the buffer gas cooled molecules. Note: Yb is an atom produced by laser ablation. YO is directly generated by laser ablation of Y2O3 solids without chemical reactions.

Molecule	Beam brightness	Longitudinal velocity	Ref.
Unit	Per pulse per solid Angle per quantum state	m/s
Yb	${10}^{12}$−${10}^{13}$	150	[20, 22]
AlF	$2.5\times {10}^{12}$	180	[22]
SrF	$1.2\times {10}^{11}$	140	[21]
CaF	$1.9\times {10}^{11}$/$1.4\times {10}^{11}$	178/180	[47]
YO	1010	120	[49]
CaOH	$5\times {10}^{10}$	140	[50]
MgF	$1.1\times {10}^{11}$	180	[22]
BaF	${10}^9$−${10}^{10}$	180/200	[35, 36]
YbF	${10}^9$−${10}^{10}$	190	[22, 44]
MgF	$1.36\times {10}^{12}$	209	This work

5 1D Doppler cooling of MgF

After optimizing the molecular beam, we carry out one-dimensional Doppler cooling of MgF molecules. In this experiment, the conditions of the molecular beam source are set according to Section 3.

In the transverse cooling experiment as shown in Fig.9, the beam parameters are as follows: The powers of the cooling and repumping lasers λ₀₀, λ₁₀ and λ₂₁ in region 1 are 400 mW, 400 mW and 40 mW, respectively, with a beam waist of about 5.0 mm. The powers of the clear up lasers λ₁₀ and λ₂₁ in region 2 are 100 mW and 10 mW, respectively, with a beam waist of about 6.0 mm. The magnetic field is aligned along the y-axis with a strength of 10 Gauss. It forms a 65° angle with the polarization of the cooling light, which is used to eliminate the dark states. The EOM (Electro-Optic Modulator) modulation frequency is set at 115 MHz to cover the hyperfine energy levels. The power of the λ₀₀ probe beam in region 3 is 15 mW, with a beam waist of about 3 mm. Finally, the fluorescence image is recorded by a camera.

Fig.9 Schematics of the 1D Doppler cooling experiment system.

Full size|PPT slide

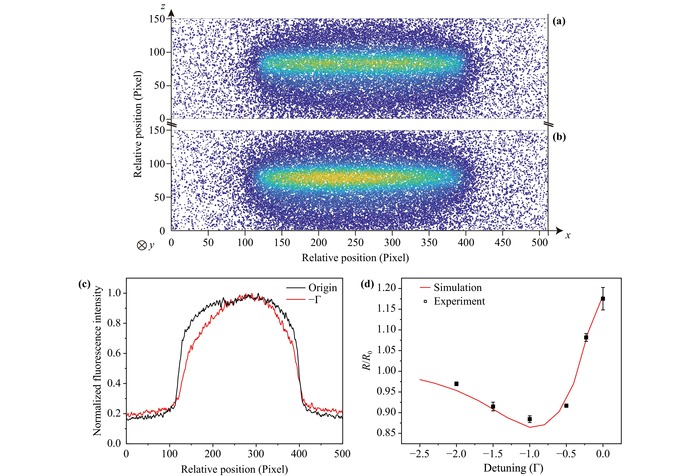
The final results of the transverse cooling experiment are shown in Fig.10. Firstly, the initial two-dimensional spatial distribution of the molecular beam is shown in Fig.10(a). Subsequently, a standing wave light field with a red detuning of −Γ is turned on in region 1, resulting in the transverse compression of the molecular beam distribution as shown in Fig.10(b). The one-dimensional transverse distributions from Fig.10(a) and (b) are shown in Fig.10(c). The black curve represents the normalized origin signal, while the red curve shows the normalized cooled signal under the influence of a standing wave light field with a detuning of −Γ. To extract the transverse temperature information, the image is integrated along the y direction and we measure the full width at half maximum (FWHM) along the x direction. The transverse temperature is given by Eq. (8), where $\delta v$ is the transverse velocity, and $k_{\mathrm{B}}$ is the Boltzmann constant,

Fig.10 Transverse cooling of an MgF molecular beam. Signal is accumulated for 300 shots. Probe laser power is at 10 mW. (a) Original 2D spatial profile of the molecular beam. (b) 2D spatial profile of the transversely cooled molecular beam with a detuning Δ = −Γ of the standing wave light field. (c) 1D transverse spatial distribution of the molecular beam after transverse cooling (red curve) and without cooling (black curve). (d) The relationship between R/R0 and the detuning; the red curve is from Monte Carlo simulation.

Full size|PPT slide

(8)$T=m{\left(\delta v\right)}^2/\left(8k_{\mathrm{B}}\ln 2\right).$

The FWHM of two molecular beams has been measured: one without the cooling laser (labeled as R₀) and another with the cooling laser activated (labeled as R). The ratio R/R₀ indicates whether cooling (R/R₀ < 1) or heating (R/R₀ > 1) occurred. By varying the detuning of the standing wave field while keeping other parameters constant, the corresponding ratio R/R₀ is recorded. The relationship between R/R₀ and the detuning is plotted, as shown in Fig.10(d). According to the results obtained from Monte Carlo simulations (represented by the red curve) and the experimental data (depicted by the black dots and error bars), a decent agreement can be observed between the experimental and theoretical results. As shown in Fig.10, the detection region is situated 531.0 mm downstream from the cell’s exit. Given the molecular beam’s initial forward velocity of 209 m/s, coupled with a skimmer diameter of 4.0 mm and a transverse FWHM of 7.8 mm, the initial transverse velocity of the molecular beam is estimated to be ~2.9 m/s. This velocity corresponds to an initial transverse temperature of 8.1 mK according to Eq. (8). Upon exposure to transverse cooling lasers with a detuning of Δ = −Γ, the molecular beam’s FWHM narrows to 6.5 mm. This reduction indicates a temperature decrease to 5.6 mK.

6 Conclusion

We have successfully demonstrated the implementation of an in-cell stepper motor to facilitate the rotation of the sample rod, thereby generating a high flux and stable MgF beam source through buffer gas cooling. We meticulously optimize parameters including YAG ablation energy, the positioning of the ablation point within the cell, as well as the flow rates of He and NF₃, to establish a set of conditions that yield a high-brightness and stable MgF beam. The resultant MgF beam source exhibits a brightness of 1.36×10¹²/pulse/solid angle/quantum state and a forward velocity of 209 m/s. Utilizing this optimized beam source, we conduct one-dimensional Doppler laser cooling experiments on MgF molecules, where theoretical predictions align well with experimental results. At a detuning of −Γ, the transverse spatial distribution of the MgF molecular beam is compressed from 7.8 to 6.5 mm, while the transverse temperature is reduced from 8.1 to 5.6 mK.

According to our previous work [43], when a MgF beam has a forward velocity of 200 m/s and FWHM of 100 m/s and the brightness of ~10¹¹−10¹²/pulse/solid angle/quantum state, the beam can be slowed down to ~10 m/s to reach a number of ~10⁶−10⁷ at MOT. Thus, our molecular beam source provides a solid basis for further slowing, loading and MOT of MgF molecules.

References

[1] D. DeMille, Quantum computation with trapped polar molecules, Phys. Rev. Lett. 88(6), 067901 (2002)

[2] Y. C. Bao, S. S. Yu, L. Anderegg, E. Chae, W. Ketterle, K. K. Ni, and J. M. Doyle, Dipolar spin-exchange and entanglement between molecules in an optical tweezer array, Science 382(6675), 1138 (2023)

[3] C. M. Holland, Y. Lu, and L. W. Cheuk, On-demand entanglement of molecules in a reconfigurable optical tweezer array, Science 382(6675), 1143 (2023)

[4] S. F. Yelin, K. Kirby, and R. Côté, Schemes for robust quantum computation with polar molecules, Phys. Rev. A 74(5), 050301 (2006)

[5] G. Pupillo, A. Griessner, A. Micheli, M. Ortner, D. W. Wang, and P. Zoller, Cold atoms and molecules in self-assembled dipolar lattices, Phys. Rev. Lett. 100(5), 050402 (2008)

[6] M. Karra, K. Sharma, B. Friedrich, S. Kais, and D. Herschbach, Prospects for quantum computing with an array of ultracold polar paramagnetic molecules, J. Chem. Phys. 144(9), 094301 (2016)

[7] K. K. Ni, T. Rosenband, and D. D. Grimes, Dipolar exchange quantum logic gate with polar molecules, Chem. Sci. (Camb.) 9(33), 6830 (2018)

[8] D. DeMille, J. M. Doyle, and A. O. Sushkov, Probing the frontiers of particle physics with tabletop-scale experiments, Science 357(6355), 990 (2017)

[9] J. Baron, W. C. Campbell, D. DeMille, J. M. Doyle, G. Gabrielse, Y. V. Gurevich, P. W. Hess, N. R. Hutzler, E. Kirilov, I. Kozyryev, B. R. O’Leary, C. D. Panda, M. F. Parsons, E. S. Petrik, B. Spaun, A. C. Vutha, and A. D. West, Order of magnitude smaller limit on the electric dipole moment of the electron, Science 343(6168), 269 (2014)

[10] L. Anderegg, N. B. Vilas, C. Hallas, P. Robichaud, A. Jadbabaie, J. M. Doyle, and N. R. Hutzler, Quantum control of trapped polyatomic molecules for eEDM searches, Science 382(6671), 665 (2023)

[11] C. Chin, V. V. Flambaum, and M. G. Kozlov, Ultracold molecules: New probes on the variation of fundamental constants, New J. Phys. 11(5), 055048 (2009)

[12] J. J. Hudson, D. M. Kara, I. J. Smallman, B. E. Sauer, M. R. Tarbutt, and E. A. Hinds, Improved measurement of the shape of the electron, Nature 473(7348), 493 (2011)

[13] T. Langen, G. Valtolina, D. Wang, and J. Ye, Quantum state manipulation and cooling of ultracold molecules, Nat. Phys. 20(5), 702 (2024)

[14] J. L. Bohn, A. M. Rey, and J. Ye, Cold molecules: Progress in quantum engineering of chemistry and quantum matter, Science 357(6355), 1002 (2017)

[15] M. T. Hummon,T. V. Tscherbul,J. Kłos,H. I. Lu, E. Tsikata,W. C. Campbell,A. Dalgarno,J. M. Doyle,N. Cold, NH⁺ collisions in a magnetic trap, Phys. Rev. Lett. 106(5), 053201 (2011)

[16] K. Jachymski, M. Gronowski, and M. Tomza, Collisional losses of ultracold molecules due to intermediate complex formation, Phys. Rev. A 106(4), L041301 (2022)

[17] S. Ospelkaus, K. K. Ni, D. Wang, M. H. G. De Miranda, B. Neyenhuis, G. Quéméner, P. S. Julienne, J. L. Bohn, D. S. Jin, and J. Ye, Quantum-state controlled chemical reactions of ultracold potassium-rubidium molecules, Science 327(5967), 853 (2010)

[18] M. D. Rosa, Laser-cooling molecules: Concept, candidates, and supporting hyperfine-resolved measurements of rotational lines in the A−X(0, 0) band of CaH, Eur. Phys. J. D 31(2), 395 (2004)

[19] B. K. Stuhl, B. C. Sawyer, D. Wang, and J. Ye, Magneto-optical trap for polar molecules, Phys. Rev. Lett. 101(24), 243002 (2008)

[20] N. R. Hutzler, H. I. Lu, and J. M. Doyle, The buffer gas beam: An intense, cold, and slow source for atoms and molecules, Chem. Rev. 112(9), 4803 (2012)

[21] J. F. Barry, E. S. Shuman, D. DeMille, and A. Bright, Slow cryogenic molecular beam source for free radicals, Phys. Chem. Chem. Phys. 13(42), 18936 (2011)

[22] S. C. Wright, M. Doppelbauer, S. Hofsäss, H. Christian Schewe, B. Sartakov, G. Meijer, S. Truppe, C ryogenic buffer gas beams of AlF, CaF , MgF , YbF , Al , and Ca , Yb and NO – a comparison, Mol. Phys. 121(17−18), e2146541 (2023)

[23] S. E. Maxwell, N. Brahms, R. deCarvalho, D. R. Glenn, J. S. Helton, S. V. Nguyen, D. Patterson, J. Petricka, D. DeMille, and J. M. Doyle, High-flux beam source for cold, slow atoms or molecules, Phys. Rev. Lett. 95(17), 173201 (2005)

[24] J. F. Barry, D. J. McCarron, E. B. Norrgard, M. H. Steinecker, and D. DeMille, Magneto-optical trapping of a diatomic molecule, Nature 512(7514), 286 (2014)

[25] S. Truppe, H. J. Williams, M. Hambach, L. Caldwell, N. J. Fitch, E. A. Hinds, B. E. Sauer, and M. R. Tarbutt, Molecules cooled below the Doppler limit, Nat. Phys. 13(12), 1173 (2017)

[26] L. Anderegg, B. L. Augenbraun, E. Chae, B. Hemmerling, N. R. Hutzler, A. Ravi, A. Collopy, J. Ye, W. Ketterle, and J. M. Doyle, Radio frequency magneto-optical trapping of CaF with high density, Phys. Rev. Lett. 119(10), 103201 (2017)

[27] A. L. Collopy,S. Ding,Y. Wu, I. A. Finneran,L. Anderegg,B. L. Augenbraun,J. M. Doyle,J. Ye, 3D magneto-optical trap of yttrium monoxide, Phys. Rev. Lett. 121(21), 213201 (2018)

[28] J. C. Shaw and D. J. McCarron, Bright, continuous beams of cold free radicals, Phys. Rev. A 102(4), 041302 (2020)

[29] N. B. Vilas, C. Hallas, L. Anderegg, P. Robichaud, A. Winnicki, D. Mitra, and J. M. Doyle, Magneto-optical trapping and sub-Doppler cooling of a polyatomic molecule, Nature 606(7912), 70 (2022)

[30] Z. X. Zeng, S. Deng, S. Yang, and B. Yan, Three-dimensional magneto-optical trapping of barium monofluoride, Phys. Rev. Lett. 133(14), 143404 (2024)

[31] J. J. Burau, P. Aggarwal, K. Mehling, and J. Ye, Blue-detuned magneto-optical trap of molecules, Phys. Rev. Lett. 130(19), 193401 (2023)

[32] T. K. Langin and D. DeMille, Toward improved loading, cooling, and trapping of molecules in magneto-optical traps, New J. Phys. 25(4), 043005 (2023)

[33] E. S. Shuman, J. F. Barry, D. R. Glenn, and D. DeMille, Radiative force from optical cycling on a diatomic molecule, Phys. Rev. Lett. 103(22), 223001 (2009)

[34] M. T. Hummon,M. Yeo,B. K. Stuhl, A. L. Collopy,Y. Xia,J. Ye, 2D magneto-optical trapping of diatomic molecules, Phys. Rev. Lett. 110(14), 143001 (2013)

[35] W. H. Bu, Y. H. Zhang, Q. Liang, T. Chen, and B. Yan, Saturated absorption spectroscopy of buffer-gas-cooled Barium monofluoride molecules, Front. Phys. 17(6), 62502 (2022)

[36] P. Aggarwal, H. L. Bethlem, A. Borschevsky, M. Denis, K. Esajas, P. A. B. Haase, Y. Hao, S. Hoekstra, K. Jungmann, T. B. Meijknecht, M. C. Mooij, R. G. E. Timmermans, W. Ubachs, L. Willmann, and A. Zapara, Measuring the electric dipole moment of the electron in BaF, Eur. Phys. J. D 72(11), 197 (2018)

[37] E. Chae, L. Anderegg, B. L. Augenbraun, A. Ravi, B. Hemmerling, N. R. Hutzler, A. L. Collopy, J. Ye, W. Ketterle, and J. M. Doyle, One-dimensional magneto-optical compression of a cold CaF molecular beam, New J. Phys. 19(3), 033035 (2017)

[38] L. Caldwell, J. A. Devlin, H. J. Williams, N. J. Fitch, E. A. Hinds, B. E. Sauer, and M. R. Tarbutt, Deep laser cooling and efficient magnetic compression of molecules, Phys. Rev. Lett. 123(3), 033202 (2019)

[39] S. Hofsäss, M. Doppelbauer, S. C. Wright, S. Kray, B. G. Sartakov, J. Pérez-Ríos, G. Meijer, and S. Truppe, Optical cycling of AlF molecules, New J. Phys. 23(7), 075001 (2021)

[40] M. Xia, R. X. Gu, K. Yan, D. Wu, L. Xu, Y. Xia, and J. P. Yin, Destabilization of dark states in MgF molecules, Phys. Rev. A 103(1), 013321 (2021)

[41] R. X. Gu, K. Yan, D. Wu, J. Wei, Y. Xia, and J. P. Yin, Radiative force from optical cycling on magnesium monofluoride, Phys. Rev. A 105(4), 042806 (2022)

[42] M. Doppelbauer, S. C. Wright, S. Hofsäss, B. G. Sartakov, G. Meijer, and S. Truppe, Hyperfine-resolved optical spectroscopy of the A²Π ← X²Σ₊ transition in MgF, J. Chem. Phys. 156(13), 134301 (2022)

[43] K. Yan, R. X. Gu, D. Wu, J. Wei, Y. Xia, and J. P. Yin, Simulation of EOM-based frequency-chirped laser slowing of MgF radicals, Front. Phys. 17(4), 42502 (2022)

[44] X. Alauze, J. Lim, M. A. Trigatzis, S. Swarbrick, F. J. Collings, N. J. Fitch, B. E. Sauer, and M. R. Tarbutt, An ultracold molecular beam for testing fundamental physics, Quantum Sci. Technol. 6(4), 044005 (2021)

[45] P. Aggarwal,H. L. Bethlem,A. Boeschoten,A. Borschevsky,K. Esajas,Y. Hao, S. Hoekstra,K. Jungmann,V. R. Marshall,T. B. Meijknecht,M. C. Mooij,R. G. E. Timmermans,A. Touwen,W. Ubachs,L. Willmann,Y. Yin,A. Zapara, A supersonic laser ablation beam source with narrow velocity spreads, Rev. Sci. Instrum. 92(3), 033202 (2021)

[46] R. X. Gu, M. Xia, K. Yan, D. Wu, J. Wei, L. Xu, Y. Xia, and J. P. Yin, Rotational analysis and hyperfine structures of A²Π_1/2 → X²Σ_1/2 transition in ^{25, 26}MgF isotope molecules, J Quant. Spectrosc. Ra. 278, 108015 (2022)

[47] S. Truppe, H. J. Williams, N. J. Fitch, M. Hambach, T. E. Wall, E. A. Hinds, B. E. Sauer, and M. R. Tarbutt, An intense, cold, velocity-controlled molecular beam by frequency-chirped laser slowing, New J. Phys. 19(2), 022001 (2017)

[48] J. A. Devlin and M. R. Tarbutt, Laser cooling and magneto-optical trapping of molecules analyzed using optical bloch equations and the Fokker−Planck−Kramers equation, Phys. Rev. A 98(6), 063415 (2018)

[49] M. T. Hummon,M. Yeo,B. K. Stuhl, A. L. Collopy,Y. Xia,J. Ye, 2D magneto-optical trapping of diatomic molecules, Phys. Rev. Lett. 110(14), 143001 (2013)

[50] N. B. Vilas, C. Hallas, L. Anderegg, P. Robichaud, A. Winnicki, D. Mitra, and J. M. Doyle, Magneto-optical trapping and sub-Doppler cooling of a polyatomic molecule, Nature 606(7912), 70 (2022)

Declarations

The authors declare that they have no competing interests and there are no conflicts.

Acknowledgements

Financial supports are from the National Natural Science Foundation of China under Nos. 12174115, 91836103, and 11834003.

RIGHTS & PERMISSIONS

2025 Higher Education Press