Buckling optimization of curvilinear fiber-reinforced composite structures using a parametric level set method

Abstract

Owing to their excellent performance and large design space, curvilinear fiber-reinforced composite structures have gained considerable attention in engineering fields such as aerospace and automobile. In addition to the stiffness and strength of such structures, their stability also needs to be taken into account in the design. This study proposes a level-set-based optimization framework for maximizing the buckling load of curvilinear fiber-reinforced composite structures. In the proposed method, the contours of the level set function are used to represent fiber paths. For a composite laminate with a certain number of layers, one level set function is defined by radial basis functions and expansion coefficients for each layer. Furthermore, the fiber angle at an arbitrary point is the tangent orientation of the contour through this point. In the finite element of buckling, the stiffness and geometry matrices of an element are related to the fiber angle at the element centroid. This study considers the parallelism constraint for fiber paths. With the sensitivity calculation of the objective and constraint functions, the method of moving asymptotes is utilized to iteratively update all the expansion coefficients regarded as design variables. Two numerical examples under different boundary conditions are given to validate the proposed approach. Results show that the optimized curved fiber paths tend to be parallel and equidistant regardless of whether the composite laminates contain holes or not. Meanwhile, the buckling resistance of the final design is significantly improved.

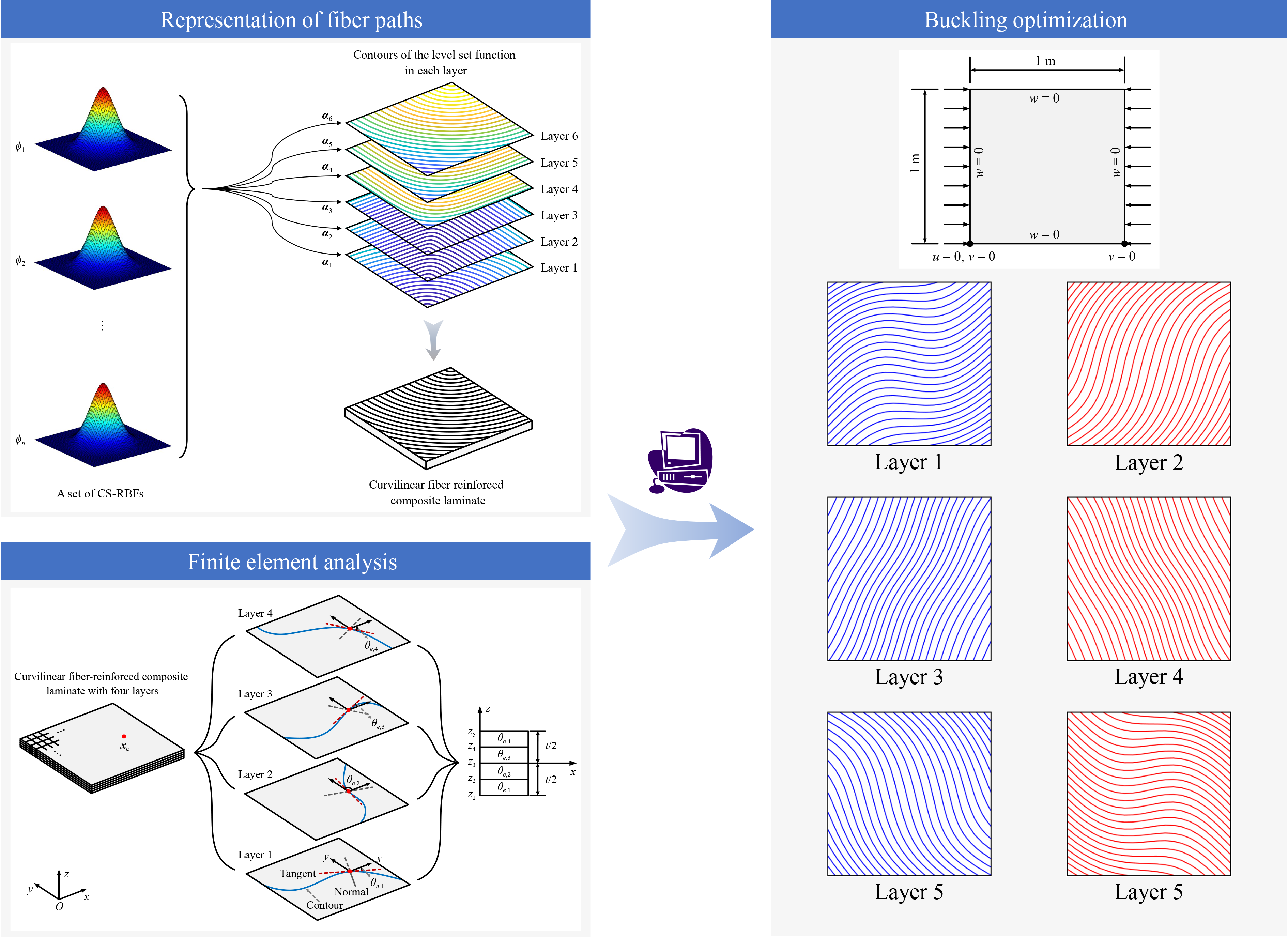
Key words： buckling optimization; curvilinear fiber; composite structure; level set method; manufacturing constraint

Nomenclature

Abbreviations
CS-RBF	Compactly supported radial basis function
FEA	Finite element analysis
FRC	Fiber-reinforced composite
MMA	Method of moving asymptotes
RBF	Radial basis function
VSCL	Variable stiffness composite laminate
Variables
A	Matrix of expansion coefficients
b	Current number of iterations
Bb, Bm	Strain‒displacement matrics for bending and membrane, respectively
de,i	Gradient constraint for the ith layer of the eth element
di	Gradient constraint for the ith level set function
dpn,i	Gradient p-norm constraint for the ith layer
Di	Elastic matrix related to the fiber angle θe,i for membrane and bending
E1	Elasticity modulus along the fiber orientation
E2	Elasticity modulus perpendicular to the fiber orientation
F	Force vector
G12, G13, G23	Shear moduli in the 12-, 13-, and 23-plane, respectively
g	Matrix consisting of the partial derivatives of the shape function
G	Global geometric stiffness matrix
Ge	Geometric stiffness matrix of the eth element
hs	Support size for CS-RBFs
J	Objective function
Jerr	Error of the objective function value
K	Global stiffness matrix
Ke	Stiffness matrix of the eth element
{\mathit{K}}_e^{\mathrm{b}\mathrm{b}}	Bending component
{\mathit{K}}_e^{\mathrm{m}\mathrm{b}}, {\mathit{K}}_e^{\mathrm{b}\mathrm{m}}	Coupling components
{\mathit{K}}_e^{\mathrm{m}\mathrm{m}}	In-plane component
{\mathit{K}}_e^{\mathrm{s}\mathrm{s}}	Shearing component
l	Total number of layers
n	Total number of RBFs
N	Shape function
m	Total number of elements
M	Total number of eigenvalues
p	Power parameter of p-norm function
pj	Coordinate vector of the jth RBF knot
r	Support radius of CS-RBF
t	Total thickness of composite laminate
ue	Displacement vector of the eth element
U	Global displacement vector
ν12	Poisson’s ratio in the 12-plane
x	x-directional coordinate of an arbitrary point
xe	x-directional coordinate of the center of the eth element
x	Coordinate vector of an arbitrary point
xe	Coordinate vector of the center of the eth element
y	y-directional coordinate of an arbitrary point
ye	y-directional coordinate of the center of the eth element
zi	z-directional coordinate of the ith layer
αi,j	Coefficient of the jth RBF in the ith layer
αmax	Upper bound of the design variables
αmin	Lower bound of the design variables
αi	Set of coefficients in the ith layer
δ	Maximum permissible error
ε	Control parameter for constraints
θe,i	Fiber angle of the ith layer at the center of the eth element
λk	kth eigenvalue
ξ	Tiny positive number to avoid the division by 0
σx	x-directional stress
σy	y-directional stress
σi	Stress matrix in the ith layer of one element
τxy	Shear stress in the xy-plane
φk	kth eigenvector
ϕj	jth radial basis function
ϕ	Vector of RBFs
Φi	ith level set function
Φ	Vector of level set functions
Ω	Area of region
Ωe	Occupied area by the eth element

Acknowledgements

This research work was supported by the National Natural Science Foundation of China (Grant Nos. 51975227 and 12272144). The authors are grateful to Krister Svanberg for providing the MMA codes.

Conflict of Interest

Tielin SHI and Qi XIA are members of the Editorial Board of Frontiers of Mechanical Engineering, who were excluded from the peer-review process and all editorial decisions related to the acceptance and publication of this article. Peer-review was handled independently by the other editors to minimise bias.

References

1 Rajak D K , Pagar D , Menezes P L , Linul E . Fiber-reinforced polymer composites: manufacturing, properties, and applications. Polymers, 2019, 11(10): 1667

2 Zhang J , Lin G , Vaidya U , Wang H . Past, present and future prospective of global carbon fibre composite developments and applications. Composites Part B: Engineering, 2023, 250: 110463

3 Wong J , Altassan A , Rosen D W . Additive manufacturing of fiber-reinforced polymer composites: a technical review and status of design methodologies. Composites Part B: Engineering, 2023, 255: 110603

4 Lozano G G , Tiwari A , Turner C , Astwood S . A review on design for manufacture of variable stiffness composite laminates. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2016, 230(6): 981–992

5 Xu Y J , Zhu J H , Wu Z , Cao Y F , Zhao Y B , Zhang W H . A review on the design of laminated composite structures: constant and variable stiffness design and topology optimization. Advanced Composites and Hybrid Materials, 2018, 1(3): 460–477

6 Marques F E C , Mota A F S d , Loja M A R . Variable stiffness composites: optimal design studies. Journal of Composite Science, 2020, 4(2): 80

7 Punera D , Mukherjee P . Recent developments in manufacturing, mechanics, and design optimization of variable stiffness composites. Journal of Reinforced Plastics and Composites, 2022, 41(23–24): 917–945

8 Sobhani Aragh B , Borzabadi Farahani E , Xu B X , Ghasemnejad H , Mansur W J . Manufacturable insight into modelling and design considerations in fibre-steered composite laminates: state of the art and perspective. Computer Methods in Applied Mechanics and Engineering, 2021, 379: 113752

9 Rousseau G , Wehbe R , Halbritter J , Harik R . Automated fiber placement path planning: a state-of-the-art review. Computer-Aided Design & Applications, 2019, 16(2): 172–203

10 Oromiehie E , Prusty B G , Compston P , Rajan G . Automated fibre placement based composite structures: review on the defects, impacts and inspections techniques. Composite Structures, 2019, 224: 110987

11 Bakhshi N , Hojjati M . Time-dependent wrinkle formation during tow steering in automated fiber placement. Composites Part B: Engineering, 2019, 165: 586–593

12 Bakhshi N , Hojjati M . An experimental and simulative study on the defects appeared during tow steering in automated fiber placement. Composites Part A: Applied Science and Manufacturing, 2018, 113: 122–131

13 Peeters D M J , Lozano G , Abdalla M . Effect of steering limit constraints on the performance of variable stiffness laminates. Computers & Structures, 2018, 196: 94–111

14 Brasington A , Sacco C , Halbritter J , Wehbe R , Harik R . Automated fiber placement: a review of history, current technologies, and future paths forward. Composites Part C: Open Access, 2021, 6: 100182

15 Plocher J , Panesar A . Review on design and structural optimisation in additive manufacturing: towards next-generation lightweight structures. Materials & Design, 2019, 183: 108164

16 Stegmann J , Lund E . Discrete material optimization of general composite shell structures. International Journal for Numerical Methods in Engineering, 2005, 62(14): 2009–2027

17 Xia Q , Shi T L . Optimization of composite structures with continuous spatial variation of fiber angle through Shepard interpolation. Composite Structures, 2017, 182: 273–282

18 Kiyono C Y , Silva E C N , Reddy J N . A novel fiber optimization method based on normal distribution function with continuously varying fiber path. Composite Structures, 2017, 160: 503–515

19 Ding H Q , Xu B , Li W B , Huang X D . A novel CS-RBFs-based parameterization scheme for the optimization design of curvilinear variable-stiffness composites with manufacturing constraints. Composite Structures, 2022, 299: 116067

20 Hao P , Yuan X J , Liu C , Wang B , Liu H L , Li G , Niu F . An integrated framework of exact modeling, isogeometric analysis and optimization for variable-stiffness composite panels. Computer Methods in Applied Mechanics and Engineering, 2018, 339: 205–238

21 Alhajahmad A , Abdalla M , Gürdal Z . Design tailoring for pressure pillowing using tow-placed steered fibers. Journal of Aircraft, 2008, 45(2): 630–640

22 Wu Z M , Weaver P M , Raju G , Kim B C . Buckling analysis and optimisation of variable angle tow composite plates. Thin-Walled Structures, 2012, 60: 163–172

23 van Campen J M J F , Kassapoglou C , Gürdal Z . Generating realistic laminate fiber angle distributions for optimal variable stiffness laminates. Composites Part B: Engineering, 2012, 43(2): 354–360

24 Hao P , Liu D C , Wang Y , Liu X , Wang B , Li G , Feng S W . Design of manufacturable fiber path for variable-stiffness panels based on lamination parameters. Composite Structures, 2019, 219: 158–169

25 Guo Y , Serhat G , Pérez M G , Knippers J . Maximizing buckling load of elliptical composite cylinders using lamination parameters. Engineering Structures, 2022, 262: 114342

26 Alhajahmad A , Mittelstedt C . Buckling capacity of composite panels with cutouts using continuous curvilinear fibres and stiffeners based on streamlines. Composite Structures, 2022, 281: 114974

27 Fernandez F , Compel W S , Lewicki J P , Tortorelli D A . Optimal design of fiber reinforced composite structures and their direct ink write fabrication. Computer Methods in Applied Mechanics and Engineering, 2019, 353: 277–307

28 Zhou X Y , Ruan X , Gosling P D . Thermal buckling optimization of variable angle tow fibre composite plates with gap/overlap free design. Composite Structures, 2019, 223: 110932

29 Kim D H , Choi D H , Kim H S . Design optimization of a carbon fiber reinforced composite automotive lower arm. Composites Part B: Engineering, 2014, 58: 400–407

30 Rouhi M , Ghayoor H , Hoa S V , Hojjati M . Multi-objective design optimization of variable stiffness composite cylinders. Composites Part B: Engineering, 2015, 69: 249–255

31 Wang Z X , Wan Z Q , Groh R M J , Wang X Z . Aeroelastic and local buckling optimisation of a variable-angle-tow composite wing-box structure. Composite Structures, 2021, 258: 113201

32 Rouhi M , Ghayoor H , Hoa S V , Hojjati M , Weaver P M . Stiffness tailoring of elliptical composite cylinders for axial buckling performance. Composite Structures, 2016, 150: 115–123

33 Ding H Q , Xu B , Song L , Li W B , Huang X D . Buckling optimization of variable-stiffness composites with multiple cutouts considering manufacturing constraints. Advances in Engineering Software, 2022, 174: 103303

34 Chu S , Featherston C , Kim H A . Design of stiffened panels for stress and buckling via topology optimization. Structural and Multidisciplinary Optimization, 2021, 64(5): 3123–3146

35 Townsend S , Kim H A . A level set topology optimization method for the buckling of shell structures. Structural and Multidisciplinary Optimization, 2019, 60(5): 1783–1800

36 Ishida N , Kondoh T , Furuta K , Li H , Izui K , Nishiwaki S . Topology optimization for maximizing linear buckling load based on level set method. Mechanical Engineering Journal, 2022, 9(4): 21-00425

37 Tian Y , Pu S M , Shi T L , Xia Q . A parametric divergence-free vector field method for the optimization of composite structures with curvilinear fibers. Computer Methods in Applied Mechanics and Engineering, 2021, 373: 113574

38 Tian Y , Shi T L , Xia Q . A parametric level set method for the optimization of composite structures with curvilinear fibers. Computer Methods in Applied Mechanics and Engineering, 2022, 388: 114236

39 Tian Y , Shi T L , Xia Q . Optimization with manufacturing constraints for composite laminates reinforced by curvilinear fibers through a parametric level set method. Composite Structures, 2023, 321: 117310

40 Wei P , Li Z Y , Li X P , Wang M Y . An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions. Structural and Multidisciplinary Optimization, 2018, 58(2): 831–849

41 Yang K , Tian Y , Shi T L , Xia Q . A level set based density method for optimizing structures with curved grid stiffeners. Computer-Aided Design, 2022, 153: 103407

42 Huang Z , Tian Y , Yang K , Shi T L , Xia Q . Shape and generalized topology optimization of curved grid stiffeners through the level set-based density method. Journal of Mechanical Design, 2023, 145(11): 111704

43 Dash P , Singh B N . Buckling and post-buckling of laminated composite plates. Mechanics Research Communications, 2012, 46: 1–7

44 FerreiraA J MFantuzziN. MATLAB Codes for Finite Element Analysis: Solids and Structures. 2nd ed. Cham: Springer, 2020

45 Svanberg K . The method of moving asymptotes—a new method for structural optimization. International Journal for Numerical Methods in Engineering, 1987, 24(2): 359–373

46 SvanbergK. MMA and GCMMA—Two Methods for Nonlinear Optimization. 2007

47 BarberoE J. Finite Element Analysis of Composite Materials Using ABAQUS. Boca Raton: CRC Press, 2013

48 Wang X , Meng Z , Yang B , Cheng C Z , Long K , Li J C . Reliability-based design optimization of material orientation and structural topology of fiber-reinforced composite structures under load uncertainty. Composite Structures, 2022, 291: 115537

49 Zhang L T , Guo L F , Sun P W , Yan J S , Long K . A generalized discrete fiber angle optimization method for composite structures: bipartite interpolation optimization. International Journal for Numerical Methods in Engineering, 2023, 124(5): 1211–1229

50 Yan J S , Sun P W , Zhang L T , Hu W F , Long K . SGC—a novel optimization method for the discrete fiber orientation of composites. Structural and Multidisciplinary Optimization, 2022, 65(4): 124