

A new modeling approach for stress–strain relationship taking into account strain hardening and stored energy by compacted graphite iron evolution
Received date: 06 Jan 2023
Accepted date: 05 Jun 2023
Copyright
Compacted graphite iron (CGI) is considered to be an ideal diesel engine material with excellent physical and mechanical properties, which meet the requirements of energy conservation and emission reduction. However, knowledge of the microstructure evolution of CGI and its impact on flow stress remains limited. In this study, a new modeling approach for the stress–strain relationship is proposed by considering the strain hardening effect and stored energy caused by the microstructure evolution of CGI. The effects of strain, strain rate, and deformation temperature on the microstructure of CGI during compression deformation are examined, including the evolution of graphite morphology and the microstructure of the pearlite matrix. The roundness and fractal dimension of graphite particles under different deformation conditions are measured. Combined with finite element simulation models, the influence of graphite particles on the flow stress of CGI is determined. The distributions of grain boundary and geometrically necessary dislocations (GNDs) density in the pearlite matrix of CGI under different strains, strain rates, and deformation temperatures are analyzed by electron backscatter diffraction technology, and the stored energy under each deformation condition is calculated. Results show that the proportion and amount of low-angle grain boundaries and the average GNDs density increase with the increase of strain and strain rate and decreased first and then increased with an increase in deformation temperature. The increase in strain and strain rate and the decrease in deformation temperature contribute to the accumulation of stored energy, which show similar variation trends to those of GNDs density. The parameters in the stress–strain relationship model are solved according to the stored energy under different deformation conditions. The consistency between the predicted results from the proposed stress–strain relationship and the experimental results shows that the evolution of stored energy can accurately predict the stress–strain relationship of CGI.
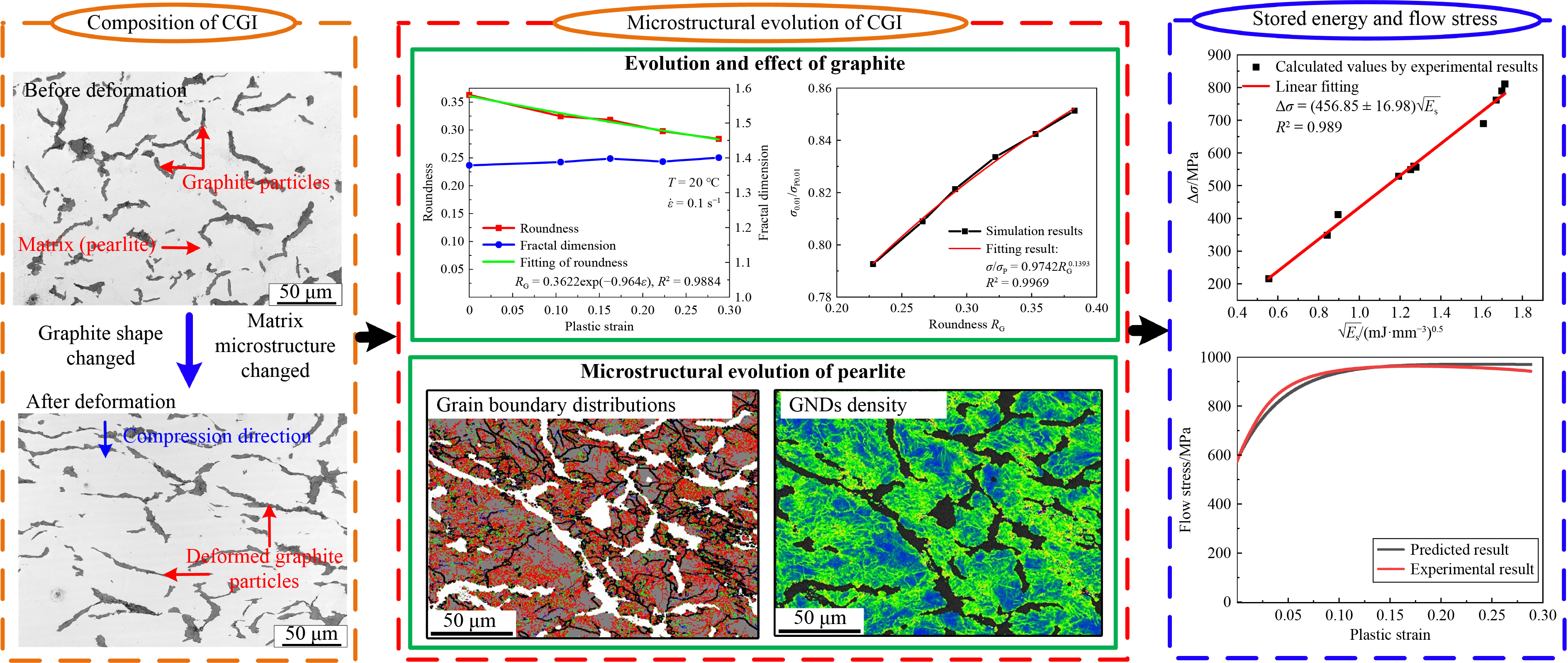
Jiahui NIU , Chuanzhen HUANG , Zhenyu SHI , Hanlian LIU , Zhengyi TANG , Binghao LI , Zhen CHEN , Guoyan JIANG . A new modeling approach for stress–strain relationship taking into account strain hardening and stored energy by compacted graphite iron evolution[J]. Frontiers of Mechanical Engineering, 2023 , 18(4) : 45 . DOI: 10.1007/s11465-023-0761-3
| Abbreviations | |
| CGI | Compacted graphite iron |
| EBSD | Electron backscatter diffraction |
| GND | Geometrically necessary dislocation |
| HAGB | High-angle grain boundary |
| JC | Johnson−Cook |
| KAM | Kernel average misorientation |
| LAGB | Low-angle grain boundary |
| Variables | |
| a, kHP | Correlation coefficients between λ and σ(λ) |
| A, B, n | Parameters in JC constitutive equation |
| b | Magnitude of the Burgers vector |
| C | Constant reflecting the relationship between Es and Ess |
| Ed | Constant depends on the material properties and the interaction forms of dislocations |
| Es | Stored energy |
| Ess | Saturation value of stored energy |
| f(G)/f(RG) | Effect function of graphite particles on the flow stress of CGI |
| k | Parameter related to the type of grain boundary |
| k1 | Energy accumulation coefficient |
| k2 | Energy release coefficient |
| K | Correlation coefficient between Es and σ |
| m | Number of selected nearest neighbors to calculate ρGNDs |
| M | Taylor factor |
| RG | Roundness of graphite particles |
| T | Celsius temperature |
| u | Step size of the EBSD test |
| α | Numerical factor characterizing dislocation−dislocation interaction |
| ρ | Dislocation density |
| ρGNDs | GNDs density |
| σ | Flow stress |
| σ0 | Friction stress of pure ferrite |
| σ00 | Lattice friction of ferrite |
| σJC | Flow stress defined by the JC constitutive equation |
| σP | Flow stress of pearlite |
| σRuT450 | True stress obtained from compression test of RuT450 |
| σ(λ) | Boundary strengthening term |
| σ(ρ) | Dislocation strengthening term |
| σP(ε) | Stress‒strain relationship of pearlite |
| Δθ | KAM value at one point in EBSD test |
| μ | Shear module |
| ε | Plastic strain |
| Plastic strain rate | |
| λ | Interlamellar spacing of pearlite matrix |
| λ0 | Interlamellar spacing in the as-received samples |
| 1 |
Dawson S , Hollinger I , Robbins M , Daeth J , Reuter U , Schulz H . The effect of metallurgical variables on the machinability of compacted graphite iron. SAE International, 2001, 110(5): 334–352
|
| 2 |
Dawson S . Compacted graphite iron—a material solution for modern diesel engine cylinder block and heads. China Foundry, 2009, 6(3): 241–246
|
| 3 |
Su R , Huang C Z , Xu L H , Zou B , Liu H L , Liu Y , Li C W . Research on the serrated chip in the milling of compacted graphite iron by cemented carbide tool. The International Journal of Advanced Manufacturing Technology, 2018, 99(5–8): 1687–1698
|
| 4 |
Kuzu A T , Berenji K R , Bakkal M . Thermal and force modeling of CGI drilling. The International Journal of Advanced Manufacturing Technology, 2016, 82(9–12): 1649–1662
|
| 5 |
Meng F N , Zhang Z Y , Wu B , Hu W , Ai X N , Meng X D , Ding Z , Zhang L Z . Turning processes and mechanism of compacted graphite iron used for high performance engine. Journal of Manufacturing Processes, 2021, 68: 951–960
|
| 6 |
Niu J H , Huang C Z , Su R , Zou B , Wang J , Liu Z Q , Li C W . Study on surface integrity of compacted graphite iron milled by cemented carbide tools and ceramic tools. The International Journal of Advanced Manufacturing Technology, 2019, 103(9–12): 4123–4134
|
| 7 |
TooptongSNguyenDParkK HKwonP. Crater wear on multi-layered coated carbide inserts when turning three distinct cast irons. Wear, 2021, 484–485: 203982
|
| 8 |
Souza T A , De Paula M A , Konatu R T , Ribeiro M V , De Campos E , Souza J V C . Investigation of the performance of ceramic tools of alumina doped with magnesium oxide in the dry machining of compacted graphite iron. Materials Research Express, 2019, 6(4): 046546
|
| 9 |
Nguyen D , Tooptong S , Park K H , Kwon P . Formation mechanism of alumina layer in protecting cubic boron nitride inserts in turning cast irons. International Journal of Machine Tools and Manufacture, 2020, 153: 103539
|
| 10 |
Elwazri A M , Wanjara P , Yue S . The effect of microstructural characteristics of pearlite on the mechanical properties of hypereutectoid steel. Materials Science and Engineering: A, 2005, 404(1–2): 91–98
|
| 11 |
Hyzak J M , Bernstein I M . The role of microstructure on the strength and toughness of fully pearlitic steels. Metallurgical Transactions A, 1976, 7(8): 1217–1224
|
| 12 |
O’Donnelly B E , Baker T N . Strengthening in low carbon pearlitic steels. Materials Science and Engineering, 1986, 84(1–2): 131–135
|
| 13 |
Zhang X D , Godfrey A , Huang X X , Hansen N , Liu Q . Microstructure and strengthening mechanisms in cold-drawn pearlitic steel wire. Acta Materialia, 2011, 59(9): 3422–3430
|
| 14 |
Dollar M , Bernstein I M , Thompson A W . Influence of deformation substructure on flow and fracture of fully pearlitic steel. Acta Metallurgica, 1988, 36(2): 311–320
|
| 15 |
Rodríguez R , Gutierrez I . Correlation between nanoindentation and tensile properties: influence of the indentation size effect. Materials Science & Engineering: A, 2003, 361(1–2): 377–384
|
| 16 |
Tang Z Y , Huang C Z , Niu J H , Jiang G Y , Li B H , Chen Z , Liu H L . The relation among the stored energy, microstructure and hardening effect of SA508-III steel under different deformation conditions. Materials Science and Engineering: A, 2022, 847: 147333
|
| 17 |
Bever M B , Holt D L , Titchener A L . The stored energy of cold work. Progress in Materials Science, 1973, 17: 5–177
|
| 18 |
Rusinek A , Klepaczko J R . Experiments on heat generated during plastic deformation and stored energy for TRIP steels. Materials & Design, 2009, 30(1): 35–48
|
| 19 |
Kapoor G , Péter L , Fekete É , Lábár J L , Gubicza J . Stored energy in nanocrystalline Ni-Mo films processed by electrodeposition. Journal of Alloys and Compounds, 2019, 796: 307–313
|
| 20 |
Ateba Betanda Y , Helbert A L , Brisset F , Mathon M H , Waeckerlé T , Baudin T . Measurement of stored energy in Fe–48%Ni alloys strongly cold-rolled using three approaches: neutron diffraction, Dillamore and KAM approaches. Materials Science and Engineering: A, 2014, 614: 193–198
|
| 21 |
Iza-Mendia A , Gutiérrez I . Generalization of the existing relations between microstructure and yield stress from ferrite–pearlite to high strength steels. Materials Science and Engineering: A, 2013, 561: 40–51
|
| 22 |
Embury J D , Fisher R M . The structure and properties of drawn pearlite. Acta Metallurgica, 1966, 14(2): 147–159
|
| 23 |
Liu Y , Yang C D , Liu M , Wang C H , Dai Y C , Li X , Russell A M , Zhang C X , Zhang Z H , Cao G H . Effects of microstructure and crystallography on mechanical properties of cold-rolled SAE1078 pearlitic steel. Materials Science and Engineering: A, 2018, 709: 115–124
|
| 24 |
BouazizOLe CorreC. Flow stress and microstructure modelling of ferrite–pearlite steels during cold rolling. Materials Science Forum, 2003, 426–432: 1399–1404
|
| 25 |
Saez-de-Buruaga M , Aristimuño P , Soler D , D’Eramo E , Roth A , Arrazola P J . Microstructure based flow stress model to predict machinability in ferrite–pearlite steels. CIRP Annals, 2019, 68(1): 49–52
|
| 26 |
TottenG EHowesMInoueT. Handbook of Residual Stress and Deformation of Steel. Ohio: ASM International, 2002, 3–10
|
| 27 |
Hansen N . Boundary strengthening in undeformed and deformed polycrystals. Materials Science and Engineering: A, 2005, 409(1–2): 39–45
|
| 28 |
Kuhlmann-wilsdorf D . A critical test on theories of work-hardening for the case of drawn iron wire. Metallurgical Transactions, 1970, 1(11): 3173–3179
|
| 29 |
Kocks U F . Laws for work-hardening and low-temperature creep. Journal of Engineering Materials and Technology, 1976, 98(1): 76–85
|
| 30 |
Hu Q S , Zhao F , Fu H , Li K W , Liu F S . Dislocation density and mechanical threshold stress in OFHC copper subjected to SHPB loading and plate impact. Materials Science and Engineering: A, 2017, 695: 230–238
|
| 31 |
Jing J T , Feng P F , Wei S L , Zhao H , Liu Y F . Investigation on the surface morphology of Si3N4 ceramics by a new fractal dimension calculation method. Applied Surface Science, 2016, 387: 812–821
|
| 32 |
Korolev A , Isaac G . Roundness and aspect ratio of particles in ice clouds. Journal of the Atmospheric Sciences, 2003, 60(15): 1795–1808
|
| 33 |
Mandelbrot B B , Passoja D E , Paullay A J . Fractal character of fracture surfaces of metals. Nature, 1984, 308(5961): 721–722
|
| 34 |
Gagnepain J J , Roques-Carmes C . Fractal approach to two-dimensional and three-dimensional surface roughness. Wear, 1986, 109(1–4): 119–126
|
| 35 |
Wang Q Y , Liang Z Q , Wang X B , Zhou T F , Zhao W X , Wu Y B , Jiao L . Investigation on surface formation mechanism in elliptical ultrasonic assisted grinding (EUAG) of monocrystal sapphire based on fractal analysis method. The International Journal of Advanced Manufacturing Technology, 2016, 87(9–12): 2933–2942
|
| 36 |
Zhang X , Zheng G M , Cheng X , Li Y , Li L , Liu H B . 2D fractal analysis of the cutting force and surface profile in turning of iron-based superalloy. Measurement, 2020, 151: 107125
|
| 37 |
Chuzhoy L , DeVor R E , Kapoor S G , Bammann D J . Microstructure-level modeling of ductile iron machining. Journal of Manufacturing Science and Engineering, 2002, 124(2): 162–169
|
| 38 |
Jaspers S P F C , Dautzenberg J H . Material behaviour in conditions similar to metal cutting: flow stress in the primary shear zone. Journal of Materials Processing Technology, 2002, 122(2–3): 322–330
|
| 39 |
Ljustina G , Larsson R , Fagerström M . A FE based machining simulation methodology accounting for cast iron microstructure. Finite Elements in Analysis and Design, 2014, 80: 1–10
|
| 40 |
Johnson G R , Cook W H . A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. Engineering Fracture Mechanics, 1983, 21: 541–548
|
| 41 |
de Campos M F , Rolim Lopes L C , Magina P , Lee Tavares F C , Kunioshi C T , Goldenstein H . Texture and microtexture studies in different types of cast irons. Materials Science and Engineering: A, 2005, 398(1–2): 164–170
|
| 42 |
De Koning M , Miller R , Bulatov V V , Abraham F F . Modelling grain-boundary resistance in intergranular dislocation slip transmission. Philosophical Magazine A, 2002, 82(13): 2511–2527
|
| 43 |
Wu X Y , Suo H L , Ji Y T , Li J Z , Ma L , Liu M , Zhang Z L , Wang Q L . Systematical analysis on the grain orientation evolution of pure nickel under plastic deformation by using in-situ EBSD. Materials Science and Engineering: A, 2020, 792: 139722
|
| 44 |
Liu M M , Liu Y L , Li H . Deformation mechanism of ferrite in a low carbon Al-killed steel: slip behavior, grain boundary evolution and GND development. Materials Science and Engineering: A, 2022, 842: 143093
|
| 45 |
Calcagnotto M , Ponge D , Demir E , Raabe D . Orientation gradients and geometrically necessary dislocations in ultrafine grained dual-phase steels studied by 2D and 3D EBSD. Materials Science and Engineering: A, 2010, 527(10–11): 2738–2746
|
| 46 |
Gao H , Huang Y , Nix W D , Hutchinson J W . Mechanism-based strain gradient plasticity—I. Theory. Journal of the Mechanics and Physics of Solids, 1999, 47(6): 1239–1263
|
| 47 |
Azzeddine H , Tirsatine K , Baudin T , Mathon M H , Helbert A L , Brisset F , Bradai D . On the stored energy evolution after accumulative roll-bonding of invar alloy. Materials Chemistry and Physics, 2017, 201: 408–415
|
| 48 |
Zheng H , Fu L M , Ji X B , Ding Y , Wang W , Wen M , Shan A D . Microstructural evolution and mechanical property of ultrafine-grained pearlitic steel by cold rolling: the influence of cementite morphology. Materials Science and Engineering: A, 2021, 824: 141860
|
| 49 |
Azzeddine H , Brisset T , Helbert A L , Brisset F , Huang Y , Kawasaki M , Bradai D , Langdon T G . A stored energy analysis of grains with shear texture orientations in Cu-Ni-Si and Fe-Ni alloys processed by high-pressure torsion. Journal of Alloys and Compounds, 2021, 864: 158142
|
/
| 〈 |
|
〉 |