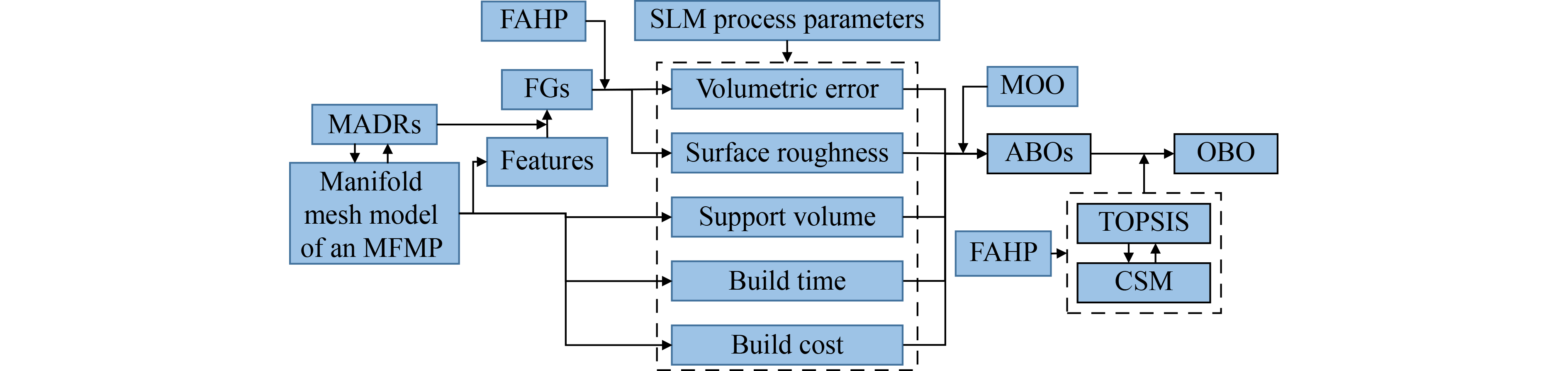
| Abbreviations |
| ABO | Alternative build orientation |
| AM | Additive manufacturing |
| CSM | Cosine similarity measure |
| FAHP | Fuzzy analytical hierarchy process |
| FDM | Fused deposition modeling |
| FG | Feature group |
| GA | Genetic algorithm |
| MADR | Machining accuracy design requirement |
| MFMP | Multi-feature mechanical part |
| MODM | Multi-objective decision making |
| MOO | Many-objective optimization |
| NSGA-II | Non-dominated sorting genetic algorithm II |
| OBO | Optimal build orientation |
| SLA | Stereolithography |
| SLM | Selective laser melting |
| SLS | Selective laser sintering |
| STL | Standard tessellation language |
| TFN | Triangular fuzzy number |
| TOPSIS | Technique for order of preference by similarity to ideal solution |
| WSM | Weighted sum model |
| Variables |
| | Triangular fuzzy number |
| | Positive ideal solution |
| | Negative ideal solution |
| | Area of the grid generated in the projection of the bounding box on the platform |
| | Area of the ith facet |
| Aplatform | Area of the fabrication platform |
| Blength | Length of the part’s bounding box along the x-axis |
| Bwidth | Width of the part’s bounding box along the y-axis |
| Cbuild | Build cost of an SLM part |
| Cenergy | Energy cost for building an SLM part |
| Ci | Relative closeness to the ideal solution of the ith alternative |
| | Normalized relative closeness to the ideal solution of the ith alternative |
| | Indirect build cost of an SLM part |
| | Material cost used for the part, support structure, and wasted material |
| d | Ordinate of the highest intersection point D between and |
| | Normalized weight of the ith object |
| | Weight of the ith object obtained by the FAHP |
| | Distance of the ith alternative to the positive ideal solution |
| | Distance of the ith alternative to the negative ideal solution |
| d | Build direction vector |
| DM | Decision matrix of an MODM problem |
| | Energy consumption rate |
| | Estimation model function of the ith objective |
| | ith facet |
| | WSM evaluation value of one solution |
| | ith object |
| | Height of the jth segment of the ith supported ray |
| | Hatch distance for filling the part |
| | Hatch distance of the lattice support structure |
| | Part’s height |
| | Height between the part and the platform |
| | Integrated MODM evaluation value |
| | Integrated MODM evaluation value of the ith alternative |
| | Number of convex fuzzy numbers |
| l | Lower bound of a TFN |
| | Edge length of the grid |
| | Lower bound of the TFN |
| | Layer thickness |
| | Lower bound of the TFN Si |
| m | Most promising value of a TFN |
| | Most promising value of the TFN |
| | Most promising value of the TFN Si |
| | Density of the material |
| | Extent analysis value of the jth factor to the ith object |
| | CSM value between the ith alternative and the positive ideal solution |
| | Normalized CSM value between the ith alternative and the positive ideal solution |
| | Porosity of the material |
| | Fuzzy judgment matrix used in the FAHP |
| n | Number of the objects |
| nf | Number of facets of the manifold mesh model |
| nfg | Number of the feature groups |
| | Number of the facets without supports |
| | Number of the facets with supports |
| ng | Number of the grids |
| | Number of the grids along the x-axis |
| | Number of the grids along the y-axis |
| no | Number of the considered objectives |
| nr | Number of the rays intersected with the overhang facets |
| | Unit normal vector of the ith facet |
| | Value of the ith objective |
| | Maximum value of the ith objective |
| | Minimum value of the ith objective |
| | Energy price |
| | Material price |
| | Number of the factors of one object |
| | Pairwise fuzzy comparison matrix of the feature groups of the ith part |
| | Pairwise fuzzy comparison matrix of the optimization objectives |
| | Normalized value of the jth objective for the ith alternative |
| | Build rate of the part |
| | Build rate of the support |
| | Indirect cost rate |
| | Material waste rate |
| | Average surface roughness of an SLM part |
| | Average surface roughness of the ith feature group |
| | Surface roughness of the ith facet |
| | Surface roughness of the ith supported facet |
| | Weighted average surface roughness of an SLM part |
| | Volume fraction of the lattice support structure |
| | Fuzzy synthetic extent concerning the ith object |
| | Build time of an SLM part |
| | Recoating time of each layer |
| u | Upper bound of a TFN |
| | Upper bound of the TFN |
| | Upper bound of the TFN Si |
| | Weighted normalized value of the jth objective for the ith alternative |
| | Positive ideal weighted normalized value of the jth objective among all alternatives |
| | Negative ideal weighted normalized value of the jth objective among all alternatives |
| | Laser scanning speed |
| | Support volume of the ith grid |
| | Part volume |
| | Support volume of an SLM part |
| Vwve | Weighted volumetric error of an SLM part |
| VE | Volumetric error of an AM part |
| | Volumetric error of the ith feature group |
| | Degree of possibility of a TFN greater than a TFN |
| | Degree of possibility for a convex fuzzy number to be greater than k convex fuzzy numbers |
| | Weight of the ith feature group |
| | Weight of the ith objective |
| W | Normalized non-fuzzy weight vector |
| | Weight vector of the feature groups of the ith part |
| | Weight vector of the considered objectives |
| x | Real value |
| | Value of the jth objective for the ith ABO |
| | Angle between the build direction and normal vector of the ith facet |
| | Rotation angle of the part around x-axis |
| | Rotation angle of the part around y-axis |
| ρ | Coefficient to adjust the relative importance of the TOPSIS and CSM |
| σ | Weight for the surface roughness calculation of a supported facet |
| | Membership function of the TFN |
| | Membership function of the TFN |