

Mechanical behavior and semiempirical force model of aerospace aluminum alloy milling using nano biological lubricant
Received date: 13 Mar 2022
Accepted date: 29 Jun 2022
Copyright
Aerospace aluminum alloy is the most used structural material for rockets, aircraft, spacecraft, and space stations. The deterioration of surface integrity of dry machining and the insufficient heat transfer capacity of minimal quantity lubrication have become the bottleneck of lubrication and heat dissipation of aerospace aluminum alloy. However, the excellent thermal conductivity and tribological properties of nanofluids are expected to fill this gap. The traditional milling force models are mainly based on empirical models and finite element simulations, which are insufficient to guide industrial manufacturing. In this study, the milling force of the integral end milling cutter is deduced by force analysis of the milling cutter element and numerical simulation. The instantaneous milling force model of the integral end milling cutter is established under the condition of dry and nanofluid minimal quantity lubrication (NMQL) based on the dual mechanism of the shear effect on the rake face of the milling cutter and the plow cutting effect on the flank surface. A single factor experiment is designed to introduce NMQL and the milling feed factor into the instantaneous milling force coefficient. The average absolute errors in the prediction of milling forces for the NMQL are 13.3%, 2.3%, and 7.6% in the x-, y-, and z-direction, respectively. Compared with the milling forces obtained by dry milling, those by NMQL decrease by 21.4%, 17.7%, and 18.5% in the x-, y-, and z-direction, respectively.
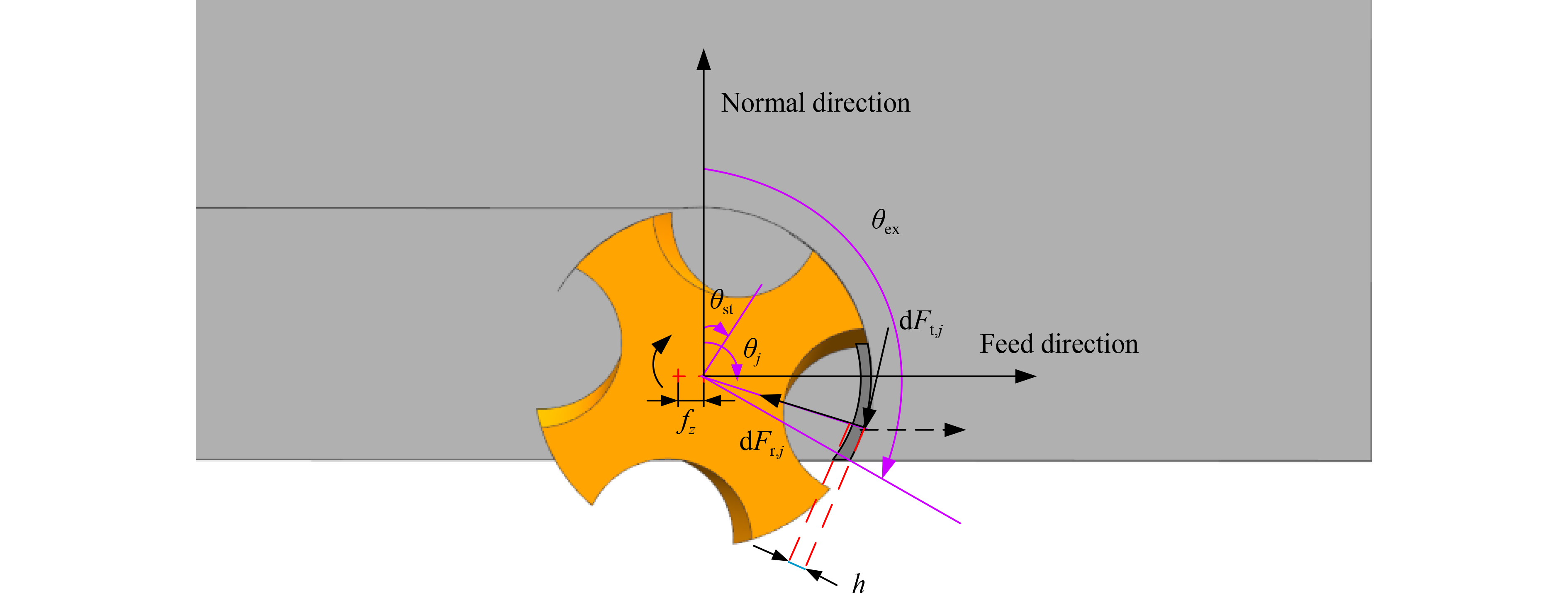
Zhenjing DUAN, Changhe LI, Yanbin ZHANG, Min YANG, Teng GAO, Xin LIU, Runze LI, Zafar SAID, Sujan DEBNATH, Shubham SHARMA. Mechanical behavior and semiempirical force model of aerospace aluminum alloy milling using nano biological lubricant[J]. Frontiers of Mechanical Engineering, 2023, 18(1): 4. DOI: 10.1007/s11465-022-0720-4
| ap | Axial cutting depth |
| A(θ) | Determining whether the tool is involved in cutting |
| fz | Feed speed |
| | Periodic average milling force per tooth |
| | Coefficient component of cutting edge force |
| | Component of cutting edge force |
| dFa | Axial force |
| dFr | Radial force |
| dFt | Tangential force |
| dFx,j(θ, z), dFy,j(θ, z), dFz,j(θ, z) | x-, y-, and z-direction forces applied to the jth micro element cutting edge, respectively |
| h | Instantaneous cutting thickness |
| j | jth cutting tooth |
| Kac | Axial shearing force coefficient |
| Kae | Axial edge force coefficient |
| Krc | Radial shearing force coefficient |
| Kre | Radial edge force coefficient |
| Ktc | Tangential shearing force coefficient |
| Kte | Tangential edge force coefficient |
| n | Spindle speed |
| N | Number of milling cutter teeth |
| R | Diameter of the tool |
| t | Milling time |
| zj,1 | Lower axial meshing limit of the cutting part of the cutter tooth j |
| zj,2 | Upper axial meshing limit of the cutting part of the cutter tooth j |
| dz | Axial cutting height element |
| θ | Angular position of the tooth in the cutting |
| θex | Cutter exit angle |
| θj | Instantaneous tooth position angle of the jth slot |
| θj(z) | Instantaneous tooth position angle |
| θp | Angle between teeth of milling cutter |
| θst | Cutter entry angle |
| ρ | Spiral angle of the milling cutter |
| ψa | Lag angle at the maximum cutting axial depth |
| 1 |
WahabM A, Park J H, AlamM S, PangS S. Effect of corrosion prevention compounds on fatigue life in 2024-T3 aluminum alloy. Journal of Materials Processing Technology, 2006, 174(1‒3): 211–217
|
| 2 |
Oguri K. Fatigue life enhancement of aluminum alloy for aircraft by fine particle shot peening (FPSP). Journal of Materials Processing Technology, 2011, 211(8): 1395–1399
|
| 3 |
Yang Y Y, Gong Y D, Li C H, Wen X L, Sun J Y. Mechanical performance of 316 L stainless steel by hybrid directed energy deposition and thermal milling process. Journal of Materials Processing Technology, 2020, 291: 117023
|
| 4 |
Yuan J L, Lyu B H, Hang W, Deng Q F. Review on the progress of ultra-precision machining technologies. Frontiers of Mechanical Engineering, 2017, 12(2): 158–180
|
| 5 |
Qi H, Qin S K, Cheng Z C, Zou Y L, Cai D H, Wen D H. DEM and experimental study on the ultrasonic vibration-assisted abrasive finishing of WC-8Co cemented carbide cutting edge. Powder Technology, 2021, 378: 716–723
|
| 6 |
Qu S S, Yao P, Gong Y D, Yang Y Y, Chu D K, Zhu Q S. Modelling and grinding characteristics of unidirectional C–SiCs. Ceramics International, 2022, 48(6): 8314–8324
|
| 7 |
Chen X Z, Li C B, Tang Y, Li L, Li H C. Energy efficient cutting parameter optimization. Frontiers of Mechanical Engineering, 2021, 16(2): 221–248
|
| 8 |
Qin C J, Tao J F, Shi H T, Xiao D G, Li B C, Liu C L. A novel Chebyshev-wavelet-based approach for accurate and fast prediction of milling stability. Precision Engineering, 2020, 62: 244–255
|
| 9 |
Huang Z W, Zhu J N, Lei J T, Li X R, Tian F Q. Tool wear predicting based on multi-domain feature fusion by deep convolutional neural network in milling operations. Journal of Intelligent Manufacturing, 2020, 31(4): 953–966
|
| 10 |
Li X, Zhao W, Li L, He N, Chi S W. Modeling and application of process damping in milling of thin-walled workpiece made of titanium alloy. Shock and Vibration, 2015,
|
| 11 |
Jiang X H, Kong X J, He S R, Wu K. Modeling the superposition of residual stresses induced by cutting force and heat during the milling of thin-walled parts. Journal of Manufacturing Processes, 2021, 68: 356–370
|
| 12 |
Niccolò G, Lorenzo M, Antonio S, Gianni C. A frequency-based analysis of cutting force for depths of cut identification in peripheral end-milling. Mechanical Systems and Signal Processing, 2022, 171: 108943
|
| 13 |
Song Y, Qu D, Wu B, Cao H J. Composite light ropes model-based dynamics force prediction model of high speed dry milling UD-CF/PEEK considering size effect. Journal of Manufacturing Processes, 2022, 76: 210–222
|
| 14 |
Liao Z R, Axinte D, Gao D. On modelling of cutting force and temperature in bone milling. Journal of Materials Processing Technology, 2019, 266: 627–638
|
| 15 |
Farhadmanesh M, Ahmadi K. Online identification of mechanistic milling force models. Mechanical Systems and Signal Processing, 2021, 149: 107318
|
| 16 |
Zheng L, Chiou Y S, Liang S Y. Three dimensional cutting force analysis in end milling. International Journal of Mechanical Sciences, 1996, 38(3): 259–269
|
| 17 |
Yun W S, Cho D W. Accurate 3-D cutting force prediction using cutting condition independent coefficients in end milling. International Journal of Machine Tools and Manufacture, 2001, 41(4): 463–478
|
| 18 |
DesaiK A, Agarwal P K, RaoP V M. Process geometry modeling with cutter runout for milling of curved surfaces. International Journal of Machine Tools and Manufacture, 2009, 49(12–13): 1015–1028
|
| 19 |
Montgomery D, Altintas Y. Mechanism of cutting force and surface generation in dynamic milling. Journal of Engineering for Industry, 1991, 113(2): 160–168
|
| 20 |
Rao V S, Rao P V M. Effect of workpiece curvature on cutting forces and surface error in peripheral milling. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2006, 220(9): 1399–1407
|
| 21 |
KoenigsbergerF, SabberwalA J P. An investigation into the cutting force pulsations during milling operations. International Journal of Machine Tool Design and Research, 1961, 1(1–2): 15–33
|
| 22 |
Sutherland J W, DeVor R E. An improved method for cutting force and surface error prediction in flexible end milling systems. Journal of Engineering for Industry, 1986, 108(4): 269–279
|
| 23 |
Budak E, Altintas Y. Peripheral milling conditions for improved dimensional accuracy. International Journal of Machine Tools and Manufacture, 1994, 34(7): 907–918
|
| 24 |
Armarego E J A, Whitfield R. C. Computer based modelling of popular machining operations for force and power prediction. CIRP Annals, 1985, 34(1): 65–69
|
| 25 |
Davoudinejad A, Parenti P, Annoni M. 3D finite element prediction of chip flow, burr formation, and cutting forces in micro end-milling of aluminum 6061-T6. Frontiers of Mechanical Engineering, 2017, 12(2): 203–214
|
| 26 |
AltintasY. Manufacturing Automation: Metal Cutting Mechanics, Machine Tool Vibrations, and CNC Design. 2nd ed. Cambridge: Cambridge University Press, 2012
|
| 27 |
Chen Y H, Lu J, Deng Q L, Ma J Y, Liao X P. Modeling study of milling force considering tool runout at different types of radial cutting depth. Journal of Manufacturing Processes, 2022, 76: 486–503
|
| 28 |
Wang C X, Zhang X W, Zhai Z, Chen X F. Parametric prediction model and periodic fluctuation interpretation of unidirectional CFRP edge milling force. Composite Structures, 2022, 287: 115387
|
| 29 |
Wang F J, Li Y, Zhang B Y, Deng J, Lin Y Q, Yang L L, Fu R. Theoretical model of instantaneous milling force for CFRP milling with a ball-end milling cutter: considering spatial dimension and temporal dimension discontinuity effects. Journal of Manufacturing Processes, 2022, 75: 346–362
|
| 30 |
Arnaud L, Gonzalo O, Seguy S, Jauregi H, Peigné G. Simulation of low rigidity part machining applied to thin-walled structures. The International Journal of Advanced Manufacturing Technology, 2011, 54(5): 479–488
|
| 31 |
Zaghbani I, Songmene V. A force-temperature model including a constitutive law for dry High speed milling of aluminium alloys. Journal of Materials Processing Technology, 2009, 209(5): 2532–2544
|
| 32 |
MerdolS D. Mechanics and dynamics of serrated end mills. Thesis for the Master’s Degree. Vancouver: University of British Columbia, 2003
|
| 33 |
Gradišek J, Kalveram M, Weinert K. Mechanistic identification of specific force coefficients for a general end mill. International Journal of Machine Tools and Manufacture, 2004, 44(4): 401–414
|
| 34 |
Wan M, Pan W J, Zhang W H, Ma Y C, Yang Y. A unified instantaneous cutting force model for flat end mills with variable geometries. Journal of Materials Processing Technology, 2014, 214(3): 641–650
|
| 35 |
Sun T, Qin L F, Fu Y C, Liu C Q, Shi R L. Mathematical modeling of cutting layer geometry and cutting force in orthogonal turn-milling. Journal of Materials Processing Technology, 2021, 290: 116992
|
| 36 |
Cai S J, Cai Z Q, Yao B, Shen Z H, Ma X F. Identifying the transient milling force coefficient of a slender end-milling cutter with vibrations. Journal of Manufacturing Processes, 2021, 67: 262–274
|
| 37 |
Coz G L, Marinescu M, Devillez A, Dudzinski D, Velnom L. Measuring temperature of rotating cutting tools: application to MQL drilling and dry milling of aerospace alloys. Applied Thermal Engineering, 2012, 36: 434–441
|
| 38 |
BruniC, Forcellese A, GabrielliF, SimonciniM. Effect of the lubrication-cooling technique, insert technology and machine bed material on the workpart surface finish and tool wear in finish turning of AISI 420B. International Journal of Machine Tools and Manufacture, 2006, 46(12–13): 1547–1554
|
| 39 |
Yang M, Li C H, Luo L, Li R Z, Long Y Z. Predictive model of convective heat transfer coefficient in bone micro-grinding using nanofluid aerosol cooling. International Communications in Heat and Mass Transfer, 2021, 125: 105317
|
| 40 |
Yang M, Li C H, Zhang Y B, Jia D Z, Li R Z, Hou Y L, Cao H J, Wang J. Predictive model for minimum chip thickness and size effect in single diamond grain grinding of zirconia ceramics under different lubricating conditions. Ceramics International, 2019, 45(12): 14908–14920
|
| 41 |
Zhang X P, Li C H, Zhang Y B, Wang Y G, Li B K, Yang M, Guo S M, Liu G T, Zhang N Q. Lubricating property of MQL grinding of Al2O3/SiC mixed nanofluid with different particle sizes and microtopography analysis by cross-correlation. Precision Engineering, 2017, 47: 532–545
|
| 42 |
Wang X M, Li C H, Zhang Y B, Ding W F, Yang M, Gao T, Cao H J, Xu X F, Wang D Z, Zafar S, Debnath S, Jamil M, Ali H M. Vegetable oil-based nanofluid minimum quantity lubrication turning: academic review and perspectives. Journal of Manufacturing Processes, 2020, 59: 76–97
|
| 43 |
Wang X M, Li C H, Zhang Y B, Zafar S, Debnath S, Sharma S, Yang M, Gao T. Influence of texture shape and arrangement on nanofluid minimum quantity lubrication turning. The International Journal of Advanced Manufacturing Technology, 2022, 119(1): 631–646
|
| 44 |
Iyappan S K, Ghosh A. Small quantity lubrication assisted end milling of aluminium using sunflower oil. International Journal of Precision Engineering and Manufacturing—Green Technology, 2020, 7(2): 337–345
|
| 45 |
Haq M A U, Hussain S, Ali M A, Farooq M U, Mufti N A, Pruncu C I, Wasim A. Evaluating the effects of nano-fluids based MQL milling of IN718 associated to sustainable productions. Journal of Cleaner Production, 2021, 310: 127463
|
| 46 |
Li H N, Wang J P, Wu C Q, Zhao Y J, Xu X L, J W Q. Damage behaviors of unidirectional CFRP in orthogonal cutting: a comparison between single- and multiple-pass strategies. Composites Part B: Engineering, 2020, 185: 107774
|
| 47 |
Ni C B, Zhu L D. Investigation on machining characteristics of TC4 alloy by simultaneous application of ultrasonic vibration assisted milling (UVAM) and economical-environmental MQL technology. Journal of Materials Processing Technology, 2020, 278: 116518
|
| 48 |
Jang D Y, Jung J, Seok J. Modeling and parameter optimization for cutting energy reduction in MQL milling process. International Journal of Precision Engineering and Manufacturing—Green Technology, 2016, 3(1): 5–12
|
| 49 |
Zhang Y B, Li C H, Jia D Z, Li B K, Wang Y G, Yang M, Hou Y L, Zhang X W. Experimental study on the effect of nanoparticle concentration on the lubricating property of nanofluids for MQL grinding of Ni-based alloy. Journal of Materials Processing Technology, 2016, 232: 100–115
|
| 50 |
Said Z, Arora S, Farooq S, Sundar L S, Li C H, Allouhi A. Recent advances on improved optical, thermal, and radiative characteristics of plasmonic nanofluids: academic insights and perspectives. Solar Energy Materials and Solar Cells, 2022, 236: 111504
|
| 51 |
Said Z, Jamei M, Sundar L S, Pandey A K, Allouhi A, Li C H. Thermophysical properties of water, water and ethylene glycol mixture-based nanodiamond + Fe3O4 hybrid nanofluids: an experimental assessment and application of data-driven approaches. Journal of Molecular Liquids, 2022, 347: 117944
|
| 52 |
Gaurav G, Sharma A, Dangayach G S, Meena M L. Assessment of jojoba as a pure and nano-fluid base oil in minimum quantity lubrication (MQL) hard-turning of Ti–6Al–4V: a step towards sustainable machining. Journal of Cleaner Production, 2020, 272: 122553
|
| 53 |
Yang M, Li C H, Said Z, Zhang Y B, Li R Z, Debnath S, Ali H M, Gao T, Long Y Z. Semiempirical heat flux model of hard-brittle bone material in ductile microgrinding. Journal of Manufacturing Processes, 2021, 71: 501–514
|
| 54 |
Qu S S, Gong Y D, Yang Y Y, Wang W W, Liang C Y, Han B. An investigation of carbon nanofluid minimum quantity lubrication for grinding unidirectional carbon fibre-reinforced ceramic matrix composites. Journal of Cleaner Production, 2020, 249: 119353
|
| 55 |
Gao T, Li C H, Yang M, Zhang Y B, Jia D Z, Ding W F, Debnath S, Yu T B, Said Z, Wang J. Mechanics analysis and predictive force models for the single-diamond grain grinding of carbon fiber reinforced polymers using CNT nano-lubricant. Journal of Materials Processing Technology, 2021, 290: 116976
|
| 56 |
Gao T, Li C H, Zhang Y B, Yang M, Jia D Z, Jin T, Hou Y L, Li R Z. Dispersing mechanism and tribological performance of vegetable oil-based CNT nanofluids with different surfactants. Tribology International, 2018, 131: 51–63
|
| 57 |
Wojciechowski S, Matuszak M, Powałka B, Madajewski M, Maruda R W, Królczyk G M. Prediction of cutting forces during micro end milling considering chip thickness accumulation. International Journal of Machine Tools and Manufacture, 2019, 147: 103466
|
| 58 |
Kline W A, DeVor R E, Lindberg J R. The prediction of cutting forces in end milling with application to cornering cuts. International Journal of Machine Tool Design and Research, 1982, 22(1): 7–22
|
| 59 |
Martellotti M E. An analysis of the milling process. Transaction of ASME, 1941, 63: 677–695
|
| 60 |
Duan Z J, Yin Q A, Li C H, Dong L, Bai X F, Zhang Y B, Yang M, Jia D Z, Li R Z, Liu Z Q. Milling force and surface morphology of 45 steel under different Al2O3 nanofluid concentrations. The International Journal of Advanced Manufacturing Technology, 2020, 107(3): 1277–1296
|
| 61 |
Zhao Y J, Xu W H, Xi C Z, Liang D T, Li H N. Automatic and accurate measurement of microhardness profile based on image processing. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1–9
|
| 62 |
Yang M, Li C H, Zhang Y B, Jia D Z, Zhang X P, Hou Y L, Li R Z, Wang J. Maximum undeformed equivalent chip thickness for ductile-brittle transition of zirconia ceramics under different lubrication conditions. International Journal of Machine Tools and Manufacture, 2017, 122: 55–65
|
| 63 |
HuangB T, Zhang Y B, WangX M, ChenY, CaoH J, LiuB, NiuX L, LiC H. Experimental evaluation of wear mechanism and grinding performance of SG wheel in machining nickel-based alloy GH4169. Surface Technology, 2021, 50(12): 62–70 (in Chinese)
|
| 64 |
Said Z, Ghodbane M, Boumeddane B, Tiwari A K, Sundar S, Li C H, Aslfattahi N, Bellos E. Energy, exergy, economic and environmental (4E) analysis of a parabolic trough solar collector using MXene based silicone oil nanofluids. Solar Energy Materials and Solar Cells, 2022, 239: 111633
|
| 65 |
Duan Z J, Li C H, Zhang Y B, Dong L, Bai X F, Yang M, Jia D Z, Li R Z, Cao H J, Xu X F. Milling surface roughness for 7050 aluminum alloy cavity influenced by nozzle position of nanofluid minimum quantity lubrication. Chinese Journal of Aeronautics, 2021, 34(6): 33–53
|
| 66 |
Zhang Y R, Guo K, Sun J. Investigation on the milling performance of amputating clamping supports for machining with industrial robot. The International Journal of Advanced Manufacturing Technology, 2019, 102: 3573–3586
|
| 67 |
Shi Y B, Li H L, Li J C, Zhi D J, Zhang X Y, Liu H, Wang H Q, Li H Y. Development, optimization and evaluation of emodin loaded nanoemulsion prepared by ultrasonic emulsification. Journal of Drug Delivery Science and Technology, 2015, 27: 46–55
|
| 68 |
JiaD Z, Zhang N Q, LiuB, ZhouZ M, WangX P, ZhangY B, Mao C, LiC H. Particle size distribution characteristics of electrostatic minimum quantity lubrication and grinding surface quality evaluation. Diamond & Abrasives Engineering, 2021, 41(3): 89–95 (in Chinese)
|
| 69 |
Liu M Z, Li C H, Zhang Y B, An Q L, Yang M, Gao T, Mao C, Liu B, Cao H J, Xu X F, Said Z, Debnath S J, Jamil M, Ali H M, Sharma S. Cryogenic minimum quantity lubrication machining: from mechanism to application. Frontiers of Mechanical Engineering, 2021, 16(4): 649–697
|
| 70 |
JiaD Z, Li C H, ZhangY B, YangM, CaoH J, LiuB, ZhouZ M. Evaluation of electro traction grinding performance and surface morphology of titanium alloy biological lubricant. Chinese Journal of Mechanical Engineering, 2022, 58(5): 198–211 (in Chinese)
|
| 71 |
LiuM Z, Li C H, CaoH J, ZhangS, ChenY, LiuB, ZhangN Q, ZhouZ M. Research progresses and applications of CMQL machining technology. China Mechanical Engineering, 2022, 33(5): 529–550 (in Chinese)
|
| 72 |
ShiZ, GuoS M, LiuH J, Li C H, ZhangY B, YangM, ChenY, LiuB, ZhouZ M, NiuX L. Experimental evaluation of minimum quantity lubrication of biological lubricant on grinding properties of GH4169 nickel-base alloy. Surface Technology, 2021, 50(12): 71–84 (in Chinese)
|
| 73 |
WangX M, Li C H, ZhangY B, YangM, ZhouZ M, ChenY, Liu B, WangD Z. Research progress on enabled atomization and supply system of minimum quantity lubrication. Surface Technology, 2022, 51(9): 1–14 (in Chinese)
|
/
| 〈 |
|
〉 |