1 Introduction

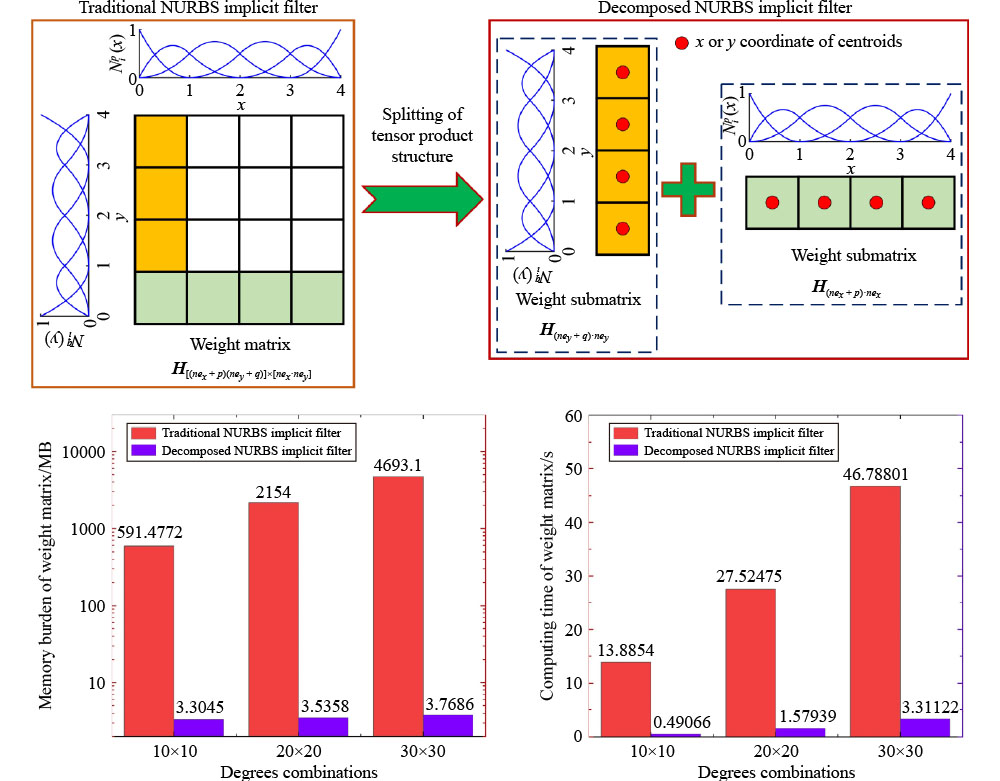
Fig.1 Illustration of the decomposition of the weight matrix into two weight submatrices for B-splines implicit filter, with and representing the number of elements along with the x and y directions, respectively, and p and q denoting the degrees of B-splines in the x and y directions, respectively. |
2 TO based on the splitting of implicit B-splines filter
2.1 TO using non-uniform B-spline parametrization
2.2 Sensitivity analysis by the splitting of B-splines tensor product structure
2.3 Computing and storing of the decomposed weight matrices of implicit filter
3 TO based on explicit tensor product filter
3.1 TO using variable density method
3.2 Construction of explicit filter based on tensor product structure
3.3 Sensitivity analysis by the splitting of explicit filter
3.4 Computing and storing of the weight matrices of explicit filter
4 Numerical examples with IGA-based TO method
4.1 Quarter annulus cantilever

Fig.11 Illustration of the optimized structures for the quarter annulus cantilever design problem: the results obtained by isogeometric analysis-based topology optimization method with traditional non-uniform rational B-splines filter under three different degree combinations (on the top row); the results obtained by isogeometric analysis-based topology optimization method with the proposed decomposed non-uniform rational B-splines filter by the splitting technique under three different degree combinations (on the bottom row). |

Fig.12 Comparisons in convergence histories of isogeometric analysis-based topology optimization method between the traditional and the proposed decomposed NURBS implicit filters under three different degree combinations: (a) 10 × 10-degree combination, (b) 20 × 20-degree combination, and (c) 30 × 30-degree combination. NURBS: non-uniform rational B-spline. |

Fig.14 Comparisons in storage and computational efficiencies between the traditional and the proposed decomposed NURBS implicit filters under three different degree combinations: (a) comparisons in memory burden and (b) comparisons in pre-computing time of weight matrix. NURBS: non-uniform rational B-spline. |
4.2 Three-dimensional cantilever

Fig.16 Illustrations of the optimized structures for the 3D cantilever beam: (a) result obtained by traditional B-spline implicit filter, (b) result obtained by decomposed B-spline implicit filter using slice splitting technique, and (c) result obtained by decomposed B-spline implicit filter using directional splitting technique. Iterations = 301, c = 4.8034. |
5 Numerical examples with FEM-based TO method
5.1 Short beam problem

Fig.21 Illustration of the optimized structures for the short beam problem by finite element method-based topology optimization methods using different filters: traditional explicit sensitivity filter (on the left column); decomposed explicit sensitivity filter (on the right column). |
5.2 3D cantilever

Fig.26 Illustration of some intermediate and the final designs of three examples for 3D cantilever beam: traditional explicit sensitivity filter (on the top row); decomposed explicit sensitivity filter using the slice splitting technique of tensor product structure (on the middle row); and decomposed explicit sensitivity filter using the directional splitting technique of tensor product structure (on the bottom row). |
6 Conclusions
7 Nomenclature
| Abbreviations | |
| ESO | Evolutionary structural optimization |
| FEM | Finite element method |
| IGA | Isogeometric analysis |
| MTOP | Multi-resolution topology optimization |
| NURBS | Non-uniform rational B-spline |
| PDE | Partial differential equation |
| SIMP | Solid isotropic material with penalization |
| TO | Topology optimization |
| Variables | |
| c | Compliance |
| Modified sensitivity of the (i,j)th design element | |
| Sensitivities of the objective function with respect to the centroid densities for all design elements | |
| Sensitivities of the volume fraction with respect to the centroid densities for all elements | |
| Young’s modulus of solid elements | |
| Young’s modulus of void elements | |
| Interpreted Young’s modulus by the modified SIMP model of the (ex,ey)th IGA element | |
| Interpreted Young’s modulus by the modified SIMP model of the (i,j)th finite element | |
| f | External load |
| Sum of the weights over the influence region of the (i,j)th design element | |
| Univariate B-spline basis functions at the centroids of all design elements along with the x direction | |
| , | Weight matrices along with the x and y directions in FEM, respectively |
| Univariate B-spline basis functions at the centroids of all design elements along with the y direction | |
| k0 | Standard elemental stiffness matrix for the finite element mesh |
| Solid elemental structural stiffness for the (ex,ey)th IGA element | |
| K(ρ) | Global structural stiffness matrix in IGA |
| Global stiffness of the FEM mesh | |
| m, n | Number of control points along with the horizontal and vertical directions, respectively |
| , , | Number of elements along with the x, y, and z directions, respectively |
| ith B-spline basis function along with the x direction with degree equals to p | |
| jth B-spline basis function along with the y direction with degree equals to q | |
| Bivariate B-spline basis function with (p × q)-degree combination | |
| Neighborhood region of the (i,j)th element defined by the filter radius | |
| p | Degree of B-splines in the x direction |
| penal | Penalty factor to steer black and white design |
| q | Degree of B-splines in the y direction |
| S | Overall storing burden of the B-spline weights |
| Sx | Storing burden of the B-spline weights along with the x direction |
| Sy | Storing burden of the B-spline weights along with the y direction |
| Filter radius | |
| Local displacement vector for the (i,j)th finite element | |
| Local displacement vector of control points for the (ex,ey)th IGA element | |
| u(ρ) | Global displacement vector of control points |
| Global displacement vector of the FEM mesh | |
| volfrac | Volume fraction of solid material |
| V | Volume of solid material |
| V0 | Volume of the whole design domain |
| Weight of the th design element along with the x direction contributed to the modified sensitivity | |
| Weight of the th design element along with the y direction contributed to the modified sensitivity | |
| Weight of the sensitivity of the (i1,j1)th design element contributed to the modified sensitivity | |
| Centroid coordinate of the (ex,ey)th IGA element | |
| Density of an arbitrary point (x,y) in the design domain | |
| Nodal density of the (i,j)th control points | |
| Centroid density values for the (ex,ey)th IGA element | |
| ρ | Union of nodal design variables |
| Union of discrete design variables in FEM | |
| γ | Parameter to avoid division by zero |
| Ξ | Knot vector |
| ψ | Admissible space for the union of nodal design variables ρ |
| Admissible space for | |
| θIterative_step | Maximum derivation of design variables on consecutive iterative steps |