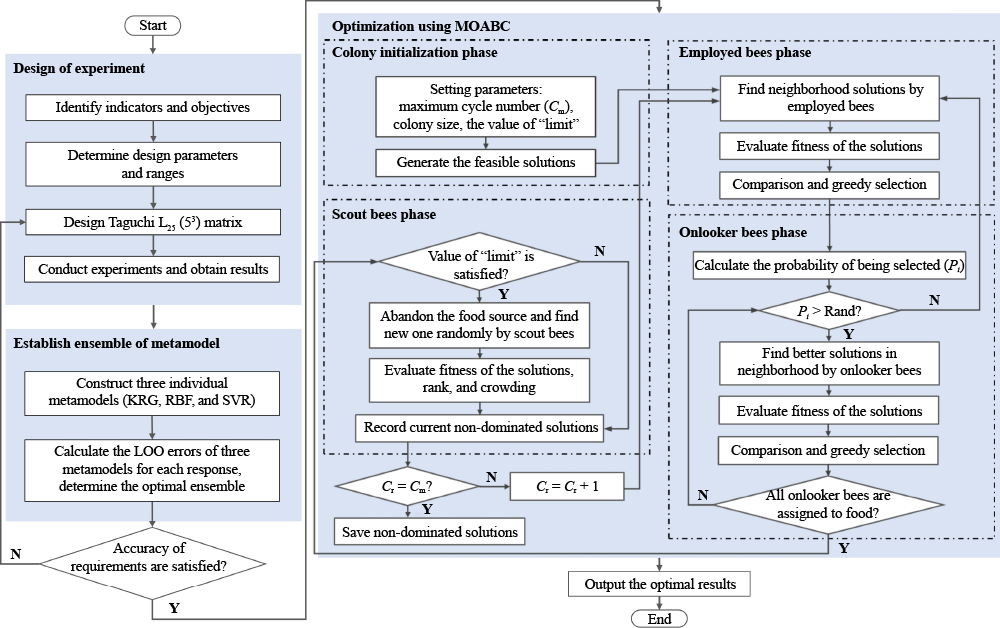
Processing parameter optimization of fiber laser beam welding using an ensemble of metamodels and MOABC

Abstract

In fiber laser beam welding (LBW), the selection of optimal processing parameters is challenging and plays a key role in improving the bead geometry and welding quality. This study proposes a multi-objective optimization framework by combining an ensemble of metamodels (EMs) with the multi-objective artificial bee colony algorithm (MOABC) to identify the optimal welding parameters. An inverse proportional weighting method that considers the leave-one-out prediction error is presented to construct EM, which incorporates the competitive strengths of three metamodels. EM constructs the correlation between processing parameters (laser power, welding speed, and distance defocus) and bead geometries (bead width, depth of penetration, neck width, and neck depth) with average errors of 10.95%, 7.04%, 7.63%, and 8.62%, respectively. On the basis of EM, MOABC is employed to approximate the Pareto front, and verification experiments show that the relative errors are less than 14.67%. Furthermore, the main effect and the interaction effect of processing parameters on bead geometries are studied. Results demonstrate that the proposed EM-MOABC is effective in guiding actual fiber LBW applications.

Key words： laser beam welding; parameter optimization; metamodel; multi-objective

1 Introduction

Fiber laser beam welding (LBW) is an advanced joining technology that is widely used to manufacture large equipment (including those in aerospace, automotive, and shipbuilding industries) [1–3], electronic instruments, and medical devices [4–6] where stainless steel is a commonly used weldment [7–9]. Given the high laser electro-optical efficiency [10] and high energy density [11] of the fiber LBW process, high welding speed and deep penetration can be obtained [12]. However, the performance of fiber LBW in certain areas could still be improved further, and parameter optimization is one of such areas. Studies have shown that many processing parameters (e.g., laser power, welding speed, defocus distance, and type and flow rate of shielding gas) can considerably influence the LBW bead profile, thus affecting the final welding quality [3,13,14]. Therefore, bead geometry should be adopted as an indicator to guide the selection of processing parameters for good welding quality.

Processing parameter optimization for LBW involves establishing the nonlinear relation between the studied parameters and the welding results, which is a challenging task that is typically carried out through trial and error [15]. Given the intrinsic complexity of LBW processes, extensive human effort and high financial costs are needed to conduct the required experiments, and oftentimes, the insights gained are not proportionate to the effort spent [3,7]. To address this issue, some studies have used various modeling methods to optimize processing parameters [16–19]. Among these methods, metamodeling is considered a promising technique to reveal the relationships between processing parameters and welding results [20–24]. In this vein, Srivastava and Garg [22] used the response surface method (RSM) in arc welding to investigate the effects of process parameters on bead geometries. Rong et al. [23] employed the back-propagation neural network and genetic algorithm to optimize the seam shape in laser brazing processes with welding crimping butt and conducted experiments to demonstrate the feasibility of this method. Wang et al. [24] combined the Gaussian process regression model with the simulation results of laser direct energy deposition to predict the geometrical characteristics of cladding tracks by using various process parameters. However, every metamodel has its own characteristic [25], and no individual metamodel has been proven to be the most effective for all applications [26]. Specifically, RSM is suitable for the overall trend of data and excels in fitting convex problems [27,28], whereas kriging (KRG), radial basis function (RBF), and support vector regression (SVR) are appropriate for multimodal and nonlinear problems [28,29]. RBF is recommended for high-order nonlinear problems, and KRG is recommended for low-order nonlinear problems in high-dimension spaces [26,30]. Thus, randomly selecting a metamodel may increase the possibility of obtaining suboptimal results [31,32]. The accuracy of an individual metamodel relies mostly on the specific training sample set used and the characteristics of the problems faced; therefore, the selected metamodels may be inaccurate when new sample points are employed [25,31].

Recognizing the drawbacks associated with relying on an individual metamodel, this study presents an inverse proportional weighting method that considers the leave-one-out (LOO) prediction error to construct an ensemble of metamodels (EMs) that incorporates the competitive strengths of three individual metamodels and reduces the risk of adopting an inappropriate individual metamodel to guarantee accuracy for different output responses. The constructed EM is combined with the multi-objective artificial bee colony algorithm (MOABC) to develop the proposed data-driven framework for optimizing the processing parameters.

In the following sections, the experimental design of Taguchi L₂₅ (5³) for LBW on 316L is described. KRG, RBF, and SVR are then integrated into the constructed EM to build the relationships between processing parameters and bead geometries. Next, MOABC is employed based on EM to optimize the solutions in the design space. The main effect and the interaction effect of processing parameters on the experimental results are investigated. Afterward, the reliability of the identified processing parameters is validated through experiments. The proposed data-driven approach, EM-MOABC, can identify ideal processing parameters and serve as a guide for fiber LBW in engineering applications.

The remainder of this article is organized as follows. Section 2 presents the experiment details and the employed equipment. Section 3 explains the proposed methodology, including the data-driven models and the algorithm used. Section 4 presents the results and discussion. The conclusions and future studies are provided in Section 5.

2 Experiments

2.1 Materials

AISI 316L austenite stainless steel with workpiece dimensions of 150 mm × 100 mm × 3 mm was used in the fiber LBW process, and Tab.1 shows its chemical components. Before the LBW process, the specimen surface was pretreated and degreased with acetone to prevent the effects of oil or oxide films.

Tab.1 Chemical composition of AISI 316L stainless steel

Elements	Mass proportion/wt.%
C	≤0.030
Si	≤1.000
Mn	≤2.000
P	≤0.045
S	≤0.030
Cr	16.000‒18.000
Mo	2.000‒3.000
Ni	10.000‒14.000
N	≤0.100
Fe	Balance

2.2 Equipment

The fiber LBW equipment shown in Fig.1 was applied in this study. The equipment included an IPG YLR-4000 fiber laser device, a shielding gas system, an ABB IRB4400 robot, and a workbench. The maximum power of this continuous fiber laser was 4000 W. The beam parameter product of optical quality was 6.5 mm·mrad. The inclination angle of the fiber laser beam with respect to the vertical direction was set to 8° [33]. The diameter of the laser light spot on the workpiece surface was about 0.6 mm, and the flow rate of the shielding gas (argon) was set to 0.8 m³/h.

Fig.1 Fiber laser beam welding platform.

Full size|PPT slide

2.3 Design of experiments

Related studies have shown that the bead profile geometries of LBW are mainly influenced by three parameters, namely, laser power (P), welding speed (S), and defocus distance (D) [3,16,34]. Bead width (W_b), depth of penetration (D_p), neck width (W_n), and neck depth (D_n) are four prominent features of the bead profile that significantly influence welding quality. Fig.2 shows a schematic of fiber LBW processing and the bead profile.

Fig.2 Processing schematic and welding bead profile.

Full size|PPT slide

Five candidate levels were determined for each parameter to investigate the effects of P, S, and D on the profile geometries of the welding bead. The design of experiments (DOEs) was constructed using MINITAB19 software. Taguchi is an effective method that can investigate the parameter space via a few experiments [35]. Taguchi L₂₅ (5³), the design of 25 groups of experiments with three factors and five levels, was used to perform the current experiments. Tab.2 lists the factor levels and values of DOE. The values of P, S, and D were inputted into the LBW platform before the experiments. Additional experiments were performed to verify the effectiveness of EM-MOABC.

Tab.2 LBW experimental factors and levels

Factor level	P/kW	S/(m·min−1)	D/mm
1	2.000	2.50	0.0
2	2.375	2.75	−0.5
3	2.750	3.00	−1.0
4	3.125	3.25	−1.5
5	3.500	3.50	−2.0

2.4 Experimental results

The experiments were conducted using parameters from the DOE table. Table A1 in the Appendix shows the experimental results. The bead profile samples were sectioned, molded, sanded, and wet polished finely to obtain the results. Then, HCl:HNO₃:H₂O (3:1:20 vol.%) mixtures were used to reveal the fusion zone. The geometrical characteristic of the bead profile was measured with a microscope.

3 Proposed approach

3.1 Construct an EM

Metamodels are efficient multivariate statistical analysis methods that can build the underlying relationships between input variables and output responses [25,36], which can be defined as

(1)Y=\hat{f}(x,\alpha )+\epsilon ,

where x is the input value of the metamodel, Y is the output response of the metamodel, α is the coefficient vector of the metamodel, ε is the stochastic factor of the metamodel, and \hat{f}(\cdot ) is the approximation approach using the metamodel. In this study, three metamodels (KRG, RBF, and SVR) were selected and integrated to construct the data-driven EM. The supplementary file describes the details of the three individual metamodels.

For one output response, the most accurate metamodel among the three was selected, and the other metamodels with less accuracy were discarded. In this way, the advantages of the individual metamodels could be inherited by EM when facing data of different output responses. Specifically, the LOO cross-validation method was used here. The generalized root mean square error under the LOO method (E_sl) and the generalized relative maximum absolute error under the LOO method (E_al) were calculated to measure the prediction accuracy of the three individual metamodels for each output response. E_sl and E_al are defined respectively as

(2)E_{\text{sl}}=\sqrt{\frac{{\displaystyle \sum _{i=1}^m{\left(f(x_i)-\hat{f}(x_{-i})\right)}^2}}{m}},

(3)E_{\text{al}}=max\left|\frac{f(x_i)-\hat{f}(x_{-i})}{f(x_i)}\right|,i=1,2,...,m,

where m is the number of sample points, \hat{f}(x_{-i}) is the predictive response from the metamodel trained using full data sets with the ith sample point excluded out, and f(x_i) is the actual experimental value of the ith sample point. The lower the value of E_sl and/or E_al is, the more accurate the metamodel is. Afterward, the most accurate one among the three metamodels is selected for the corresponding output response. Therefore, for various output responses, different metamodels can be employed to make accurate predictions.

In this study, an inverse proportional weighting method that considers the LOO error size of the metamodel was presented. The essential idea of this integrating method is that the smaller the prediction error of a metamodel is, the larger the weight that should be assigned to it. For an output response, if two or more metamodels in the candidates perform well and have a similar LOO error size (E_sl and/or E_al), to avoid the risk of randomly choosing one, these metamodels can be integrated with suitable weights. With the case of two metamodels as an example, the weights can be defined as follows:

(4){\omega }_1^k=E_2^k{\left(E_1^k+E_2^k\right)}^{-1},

(5){\omega }_2^k=E_1^k{\left(E_1^k+E_2^k\right)}^{-1},

where k is the output response variable, {\omega }_1^k and {\omega }_2^k are weights of the first and the second metamodel for the variable k, and E_1^k and E_2^k denote the LOO errors (E_sl or E_al) of the two selected metamodels for output variable k. The relation can be formulated as follows:

(6){\hat{f}}_{\mathrm{E}}^k(x)={\omega }_1^k{\hat{f}}_1^k(x)+{\omega }_2^k{\hat{f}}_2^k(x),

where {\hat{f}}_{\mathrm{E}}^k(x) is the prediction value of the integrated EM for output variable k, and {\hat{f}}_1^k(x) and {\hat{f}}_2^k(x) denote the first and the second metamodel selected for the variable k.

3.2 Background of MOABC

The artificial bee colony (ABC) algorithm is derived from the foraging behavior of honey bee colonies [37] and is popular for solving single- and multi-objective optimization problems [38,39] because of its simplicity, ease of implementation, and few control parameters [40,41]. MOABC extends the capability of the traditional ABC to solve optimization problems involving multiple objectives. Tab.3 lists the correspondence between the observed foraging behaviors of honey bees and various components of the optimization process. Fig.3 shows the workflow of MOABC.

Tab.3 Corresponding relationship between foraging and function optimization

Foraging of bees	Function optimization
Positions of food sources	Feasible solutions
Nectar amount	Fitness of solutions
Foraging	Search for solutions
Gathering of nectar	Calculation of fitness

Fig.3 Workflow of multi-objective artificial bee colony algorithm.

Full size|PPT slide

MOABC involves three kinds of artificial bees, namely, employed, onlooker, and scout bees. The four phases in the workflow of MOABC are initialization, employed bee, onlooker bee, and scout bee phases. The following part describes each phase in detail.

a) Colony initialization phase

The initial solution population is composed of u randomly generated v-dimensional vectors, and v is the dimension (number) of optimization parameters. u is the number of the initial solution population in colony initialization phase, which can be expressed as Q = {X₁, X₂, ..., X_u}. X_i = {x_i,1, x_i,2, ..., x_i,v} is the ith solution. The initial positions of food sources are generated based on the following equation:

(7)x_{i,j}=x_{min,j}+\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}(0,1)\times \left(x_{max,j}-x_{min,j}\right),

where x_i,j is the jth dimension of the ith food source in MOABC, i\in \{1,2,...,u\} and j\in \{1,2,...,v\} are the selected parameters, rand(0,1) is a random number between 0 and 1, and x_max,j and x_min,j are the upper and lower bounds of the jth dimension, respectively. The solutions go through a repeated cycle C_{\text{r}}\in \{1,2,...,C_{\text{m}}\}. C_m can be predetermined as the maximum cycle number of the searching processes for the bees.

b) Employed bee phase

The number of employed bees is similar to that of food sources because only one employed bee is assigned per food source. On the basis of the initial location x_i,j of a feasible solution (food source), its neighborhood is searched to identify an improved food source θ_i,j, which is achieved using the equation

(8){\theta }_{i,j}=x_{i,j}+{\varphi }_{i,j}\left(x_{i,j}-x_{p,j}\right),

where p\in \{1,2,...,u\} (p\ne i) and x_p,j is one of the u food sources other than x_i,j. {\varphi }_{i,j}=\text{rand}(-1,1), and the value of {\varphi }_{i,j} is the change rate of food sources during the employed bees phase, which affects the convergence rate of the algorithm. Two multi-objective optimization operators, rank and crowding, are applied to find the Pareto solutions, similar to the non-dominated sorting genetic algorithm II [19]. Pareto dominance states that two solutions are non-dominated with respect to each other if neither solution is worse than the other and both are strictly better than other solutions in at least one objective. Then, the neighboring food source with a better fitness value is used to replace the current one.

c) Onlooker bee phase

After the employed bees finish the search process, they come back to the hive and share information about food sources to the onlooker bees by dancing. The onlooker bees select the food sources according to the probability value calculated using the fitness value. The food source with more nectar indicates better solution quality and therefore has a higher probability to be selected. Equation (9) defines the probability value for onlooker bees to select the ith food source P_i, X_i is the ith feasible solution (food source) in MOABC, and fitness(X_i) is quality (fitness value) of the food source of X_i:

(9)P_i=\frac{fitness\left(X_i\right)}{{\displaystyle \sum _{i=1}^{u}fitness\left(X_i\right)}},i=1,2,\dots ,u.

Then, the neighborhoods of the food sources are searched for new solutions with better fitness by using Eq. (8), and a greedy selection mechanism is employed to retain the better solutions.

d) Scout bee phase

In MOABC, the parameter called “limit” is preseted. If a food source cannot be improved after the preset number of iterations, the corresponding employed or onlooker bees will abandon the food source and become scouts. Then, the scouts will begin to search for new food sources stochastically in accordance with Eq. (7). This process can help prevent the algorithm from falling into local optima and continue to search for the global optimal solution.

3.3 Workflow of the proposed optimization method

The data-driven EM-MOABC proposed in this study aims to solve the processing parameter optimization in fiber LBW. The nonlinear correlation between the processing parameters and bead geometry is constructed using EM. Next, MOABC is applied to solve the optimal processing parameters by taking the predicted responses from EM as the fitness values. Fig.4 shows a flowchart of the entire procedure, and six corresponding steps are described as follows:

Fig.4 Proposed data-driven framework combining the ensemble of metamodels with multi-objective artificial bee colony algorithm. MOABC: multi-objective artificial bee colony algorithm, KRG: kriging, RBF: radial basis function, SVR: support vector regression.

Full size|PPT slide

Step 1. Identify optimization objectives. The output responses (W_b, D_p, W_n, and D_n) of the bead geometries that influence the welding quality are selected, and the corresponding optimization objectives are determined.

Step 2. DOE. The experiments aim to produce a set of data for EM to uncover the relationship between processing parameters and bead geometries. The ranges and parameter levels are determined, and Taguchi L₂₅ (5³) is employed as a design matrix to conduct the actual experiments for the result data.

Step 3. Construct an EM. Three individual metamodels (KRG, RBF, and SVR) are implemented and evaluated using E_sl and E_al. The optimal metamodels of each response are selected, and the inverse proportional weighting method that considers the LOO error is used to create an EM.

Step 4. Check the accuracy. If the accuracy of the constructed EM meets requirements, then proceed to Step 5; otherwise, return to Step 2 and adjust DOE.

Step 5. Determine the optimal parameters. On the basis of the predicted response by EM, MOABC is implemented to find the Pareto optimal solution sets of the processing parameters.

Step 6. Experimental verifications. Optimal solutions from the Pareto fronts are selected, and corresponding experiments are performed to confirm the actual reliability of EM-MOABC.

4 Results and discussion

4.1 Ensemble of metamodels

4.1.1 Construction of EM

MATLAB R2018b was used to run the programs in this study. The function “dacefit” of the DACE toolbox was employed to predict the responses. In consideration of prediction accuracy, the zero-order regression polynomial function and the Gaussian correlation function were used. The optimizing range of the theta parameter was set from 0.001 to 20.

Equations (2) and (3) were used to calculate the values of E_sl and E_al for the four output responses (W_b, D_p, W_n, and D_n). As illustrated in Fig.5, the KRG metamodel performed well in D_p and W_n, but SVR is more accurate than KRG in terms of W_b. For D_n, the three metamodels showed different performance. In this study, the optimal metamodel was selected from the ensemble by using Eq. (10):

Fig.5 Error evaluations of the three metamodels for different responses: (a) W_b, (b) D_p, (c) W_n, and (d) D_n.

Full size|PPT slide

(10)\{\begin{array}{c}\text{Find:}{\hat{f}}_i(x),\\ \text{Minimize:}{E}_{\text{sl}}\left\{{\hat{f}}_i(x)\right\},\end{array}

where {\hat{f}}_i(x) is the predictive response of the ith individual metamodel at sample point x. The E_sl values of KRG and SVR for output response D_n were close, so Eqs. (4) and (5) were employed to determine the weights in consideration of the LOO error sizes of KRG and SVR for variable D_n. Equation (6) was applied to form {\hat{f}}_{\mathrm{E}}^{D_{\text{n}}}(x), which is the EM for D_n.

Colored diagrams of the four bead geometries based on EM are presented in Fig.6 to intuitively represent the relationships between the input and output variables. Fig.6 shows that the different output results varied with the processing parameters.

Fig.6 EMs for the four output responses: (a) W_b, (b) D_p, (c) W_n, and (d) D_n.

Full size|PPT slide

4.1.2 EM validation

Five additional experiments with processing parameters randomly chosen in the design space were conducted to verify the accuracy of the constructed EM. Fig.7 presents the experimental values (V_e), the predicted values (V_p), and the relative error (E_r) of the four outputs. E_r was calculated using Eq. (11) to indicate the accuracy of EM:

Fig.7 Comparison of experimental and predicted results for (a) W_b, (b) D_p, (c) W_n, and (d) D_n.

Full size|PPT slide

(11)E_{\text{r}}=\frac{|V_{\text{e}}-V_{\text{p}}|\times 100\mathrm{\%}}{V_{\text{e}}}.

The maximal E_r is 17.953%, which is shown in the No. 5 experiment for D_n in Fig.7(d). The average E_r of the four output responses (W_b, D_p, W_n, and D_n) for the five validations were calculated to be 10.945%, 7.038%, 7.630%, and 8.621%, respectively. The errors could have originated from the measurements, process parameter fluctuations, environmental effects, and other factors. For the same welding bead, the bead geometries changed slightly in different positions. The geometries at the half-length of the bead were more stable than the geometries at the two ends of the bead. Although the geometries in the middle of the welding length were extracted as experimental results, some measurement errors still existed.

Compared with the maximum errors of 29.13% and 60.35% in the prediction results for bead geometries of different welding types in other studies [23,42], the prediction error of EM of this work is more satisfactory for actual fiber LBW. Overall, most of the experimental results were consistent with the output predictions of EM. Therefore, the constructed EM can be used reliably in engineering applications.

4.1.3 Effects of processing parameters on bead geometries

According to the experimental results, the laser processing parameters exerted significant effects on the four welding bead geometries. In this subsection, the influences of processing parameters on W_b, D_p, W_n, and D_n are analyzed through the main effects and the first-order interactions of P, S, and D.

The main effect graph is employed to show the differences in the average responses of the input parameters at different levels. Fig.8 plots the main effect graphs of the input parameters on the output responses. For each output response, δ is listed in Fig.8 to evaluate the difference between the maximum and minimum values. As illustrated in Fig.8, P had the most influence on output responses W_b, D_p, and W_n, and S took the second place. For the response D_n, processing parameters S and P were the first and second most significant factors, respectively. Increasing P and decreasing S could increase the energy input, causing abundant metal of the welding zone to melt, which affected the bead geometries.

Fig.8 Main effects of processing parameters on bead geometries: (a) W_b, (b) D_p, (c) W_n, and (d) D_n.

Full size|PPT slide

The first-order interaction indicates the difference in the amount of responses between the various levels of one factor as it changes with the different levels of other factors. Fig.9 shows the first-order interactions of the input variables P, S, and D. The crossing lines imply that the three welding parameters exert complex interactive effects on bead geometries in the design space.

Fig.9 First-order interaction diagrams of the processing parameters on (a) W_b, (b) D_p, (c) W_n, and (d) D_n.

Full size|PPT slide

For W_b, P*S: Strong fluctuations occurred at 2.0 and 3.5 kW levels of P, and W_b increased with the increase in P. P*D: P had a greater influence on W_b at the 0 mm levels of D than at the other levels. S*D: Significant changes occurred at the level of 0 mm of D, whereas D of −0.5 mm had a limited impact. For D_p, P*S: D_p showed an upward trend with the increase in P. Additionally, when P varied from 2.00 to 2.75 kW, the two lines of S at 3.00 and 3.25 m/min were almost parallel, indicating that the interaction was not considerable. P*D: P at 3.125 and 3.500 kW had notable effects on D_p compared with the other levels. S*D: The strong fluctuations showed that the interactions were obvious. For W_n, P*S: The two lines of P at 2.375 and 2.750 kW exhibited locally insignificant interactions when S varied from 2.75 to 3.50 m/min. P*D: P at 2.0 and 3.5 kW had great impacts on W_n, whereas P at the other levels had weak effects. S*D: S at the level of 2.75 m/min had a more substantial effect on W_n than that at other levels. For D_n, P*S: As S increased, D_n exhibited a general downward trend, although some fluctuations were observed. P*D: D at 0 mm had a greater impact on D_n compared with that at other levels. S*D: Noticeable variations occurred at 0 and −0.5 mm of D.

4.2 Multi-objective optimization using MOABC

4.2.1 MOABC parameter settings

The residual stress and distortion induced by welding are influenced significantly by the weld metal volume. With the same level of penetration depth, a wide bead usually leads to abundant weld metal, which increases the residual stress and distortion [43]. In this study, W_b, D_p, W_n, and D_n were selected as the bead profile geometries, and H was the thickness of the workpiece. Equation (12) lists the optimization objectives that significantly affected the welding integrity and reduced the stress concentrations in the weldments:

(12)Objectives\{\begin{array}{c}\text{Minimize:}|D_{\text{p}}-H|,\\ \text{Minimize:}{W}_{\text{b}},\\ \text{Minimize:}{W}_{\text{n}},\\ \text{Minimize:}{D}_{\text{n}}.\end{array}

Moreover, the LBW processing parameters were set within the ranges given in Tab.2. Multi-objective optimization was conducted in MATLAB R2018b by using MOABC. Tab.4 shows the parameter settings of MOABC. The values of the profile geometries used in MOABC were derived from the responses predicted using the established EM. The optimal solution sets (Pareto fronts) of the processing parameters were then obtained.

Tab.4 Parameter settings of MOABC in the optimization

Parameter	Value
Food number	60
Maximum number of preserved food	40
Limit for scout	20
Limit for external archive	20
Deep mining times	15
Iteration numbers	300

4.2.2 Optimization results and verifications

Fig.10 illustrates the Pareto front produced by MOABC for the LBW processing parameters. Each point in the Pareto front represents an independent solution, which is a set of processing parameters. For each sample point, when the represented parameters were employed, the corresponding results (|D_p − H|, W_b, W_n, and D_n) were available as expected. The four response results were conflicting, so trade-offs were required. Generally, optimal solutions of processing parameters are provided by the Pareto front, so the desired bead geometries can be selected efficiently in fiber LBW.

Fig.10 Pareto front for the bead geometries.

Full size|PPT slide

To confirm the effectiveness of the proposed data-driven optimization methodology, two solutions were selected in the Pareto front, and LBW experiments using the corresponding welding parameters were conducted. For the multi-objective Pareto fronts, the selection of the compromise solution generally needs to comprehensively consider the optimization results of multiple objectives. Commonly used methods for evaluating and ranking Pareto optimal solutions have been presented in extant Refs. [20,21,33,44,45]. This study employed the sum of normalized bead geometries (S_n) as the evaluation indicator, which is expressed as follows:

(13)\begin{array}{rl}{S}_{\text{n}}=& w_1\cdot \frac{W_{\text{b}}-{W_{\text{b}}}^{-}}{{W_{\text{b}}}^{+}-{W_{\text{b}}}^{-}}+w_2\cdot \frac{W_{\text{n}}-{W_{\text{n}}}^{-}}{{W_{\text{n}}}^{+}-{W_{\text{n}}}^{-}}+w_3\cdot \frac{D_{\text{n}}-{D_{\text{n}}}^{-}}{{D_{\text{n}}}^{+}-{D_{\text{n}}}^{-}}\\ & +w_4\cdot \frac{\left|D_{\text{p}}-H\right|-{\left|D_{\text{p}}-H\right|}^{-}}{{\left|D_{\text{p}}-H\right|}^{+}-{\left|D_{\text{p}}-H\right|}^{-}},\end{array}

where w₁, w₂, w₃, and w₄ indicate the weighting values of the four optimization objectives. W_{\text{b}}^{+}, W_{\text{n}}^{+}, D_{\text{n}}^{+}, and |D_p − H|⁺ are the maximum values of the four objectives in the Pareto optimal solutions shown in Fig.10, and W_{\text{b}}^{-}, W_{\text{n}}^{-}, D_{\text{n}}^{-}, and |D_p − H|⁻ are the corresponding minimum values. Additionally, D_p is a key factor that influences welding integrity. Incomplete penetration and root humping can be regarded as obvious defects. Therefore, the minimization of \left|D_{\text{p}}-H\right| is given priority among the four optimization objectives. In this study, w₄ was set to 0.55, and w₁, w₂, and w₃ were set to 0.15. The Pareto solutions can be ranked by the S_n value, and a low S_n value means a good solution. Afterward, for an accurate and easy adjustment of defocus distance, two solutions with D of the integer or half-integer were chosen as validations from the Pareto solutions with low S_n values. The profile geometries of welding beads obtained from the two optimal solutions are displayed in Fig.11.

Fig.11 Bead geometry of the two optimal solutions selected.

Full size|PPT slide

Tab.5 and Tab.6 show the validation results of the profile geometries of the two optimal solutions selected (labeled No. 1 and No. 2). The processing parameters (P, S, and D) of the No. 1 optimal solution were 3.41 kW, 2.82 m/min, and −1.5 mm; those of the No. 2 optimal solution were 3.5 kW, 2.74 m/min, and −2 mm. The average relative errors for W_b, D_p, W_n, and D_n of the two validations were calculated to be 9.27%, 5.97%, 2.95%, and 7.39%, respectively. The errors may have resulted from the parameter deviation and measurement error. In one bead cross-section, sometimes the D_n values of the left and right neck points are inconsistent, which leads to certain measurement errors for the variable D_n. Generally, relative errors are acceptable, so the proposed EM-MOABC is suitable for the multi-objective optimization of process parameters in fiber LBW. Notably, the proposed data-driven framework is limited to optimizing only four cross-sectional features and does not consider other performance indicators (e.g., tensile strength). In addition, the pore defect is considered. According to the statistics on the welding beads in the Taguchi L₂₅ experiments conducted in this study, the maximum area proportion of the pores in the welding bead was less than 3.1%. Thus, the pore defect had a limited impact on the geometries of the welding bead.

Tab.5 Validation results of the No. 1 optimal solution

Bead geometry	Experimental value/mm	Optimized value/mm	Relative error/%
Wb	1.846	1.720	6.83
Dp	3.119	2.927	6.16
Wn	0.766	0.805	5.09
Dn	0.827	0.826	0.12

Tab.6 Validation results of the No. 2 optimal solution

Bead geometry	Experimental value/mm	Optimized value/mm	Relative error/%
Wb	1.998	1.764	11.71
Dp	3.097	2.918	5.78
Wn	0.877	0.884	0.80
Dn	0.859	0.733	14.67

As shown in Fig.11, the welding bead profiles that used the optimized parameters were satisfactory. Experiments with two sets of stochastically selected parameters were performed for comparison, and Fig.12 demonstrates the cross-sections. Some defects, such as incomplete penetration, obvious collapse, and root humping, were observed, and they considerably damaged the welding quality. The primary reason for these defects was that the laser energy corresponding to the employed processing parameters did not match the required welding conditions. The two random solutions are also presented in Fig.10 to show their undesirable values of \left|D_{\text{p}}-H\right|. Notably, \left|D_{\text{p}}-H\right| is considered the priority optimization objective. Therefore, the proposed EM-MOABC can help avoid the above-mentioned defects through suitable processing parameter decision-making.

Fig.12 Cross-sections using random process parameters.

Full size|PPT slide

4.3 Microstructures

The ultra-depth 3D microscope VHX-1000C (KEYENCE) was used to observe the microstructure of the fiber LBW bead profile. With the No. 1 optimal solution of Fig.11 as an example, the welding, fusion, and substrate zones were observed, as shown in Fig.13. The fusion zone was narrow, which contributed to the welding quality. Fig.14 presents the bead geometries of the No. 3 experiment of Taguchi L₂₅ in Table A1. To further study the microstructures of the different laser process parameters, the welding bead profile beside the centerline in Fig.14 and that of the No. 2 optimal solution in Fig.11 were compared, as shown in Fig.15. The results showed that the columnar grains in the welding zone had different directions.

Fig.13 Microstructures of the welding bead for the No. 1 optimal solution.

Full size|PPT slide

Fig.14 Bead geometries in the No. 3 Taguchi L₂₅ experiment.

Full size|PPT slide

Fig.15 Microstructures of the welding bead profiles beside the centerline: (a) No. 2 optimal solution and (b) No. 3 Taguchi L₂₅ experiment.

Full size|PPT slide

For the fiber LBW process, changes in laser process parameters result in different heat inputs, and the heat input can be expressed by the formula [46]:

(14)\text{Heat input}=\frac{P}{S}.

A small heat input results in a high cooling rate and vice versa [47,48]. Specifically, the cooling rate can be calculated as [46,49]

(15)\frac{\mathrm{\partial }T}{\mathrm{\partial }t}=\frac{2\text{π}K\rho C_0{(SH)}^2}{P^2}{\left(T-T_0\right)}^3,

where K is the thermal conductivity (15 W∙m⁻¹∙K⁻¹), ρ is the material density (8000 kg/m³), C₀ is the specific heat at constant pressure (500 J∙kg⁻¹∙K⁻¹), H is the thickness of the workpiece (0.003 m), T is the reference temperature (1523.2 K), t is the duration of temperature variation, and T₀ is room temperature (300.15 K). The values of P and S are based on Table A1. Thus, decreasing the laser power or increasing the welding speed can increase the cooling rate. In accordance with Eq. (15), the cooling rates of the two sets of processing parameters corresponding to Fig.15(a) and Fig.15(b) were calculated as 1056.73 and 3879.48 K/s, respectively. As the cooling rate increases, the obtained microstructures of the welding zone become finer than before [46,47,50]. The microstructure in Fig.15(b) is finer than that in Fig.15(a), which is consistent with the calculated cooling rates. Additionally, a low heat input generally leads to a high volume fraction of ferrite in weldments because the high cooling rate represses the transformation from ferrite to austenite [51–53].

Several analytical models have been developed to predict the primary dendrite arm spacing (PDAS), and these models assume that PDAS decreases as the cooling rate increases [50,54,55]. To further quantify and compare the microstructures of the welding bead beside the centerline, this study adopted the PDAS measurement method based on actual microstructure figures [51,56]. The PDAS for Fig.15(a) was (4.7 ± 0.4) μm, and the PDAS for Fig.15(b) was (2.9 ± 0.3) μm. Furthermore, microhardness tests were performed within the welding zone at a distance of 300 μm from the upper surface of the workpiece. The average microhardness of the No. 2 optimal solution was 163.2 HV and that of the No. 3 Taguchi L₂₅ experiment was 176.1 HV. The microhardness tests were in agreement with the cooling rate calculations and PDAS measurements.

5 Conclusions

In this study, the relationship between fiber LBW processing parameters and multiple output results was constructed via EM using three metamodels. A data-driven methodology, EM-MOABC, was developed to optimize the processing parameters of fiber LBW with 316L in consideration of the bead geometry. The reliability of the proposed optimization methodology was validated. Additionally, the effects of processing parameters on four welding bead geometries were studied. The developed EM-MOABC combined with Taguchi is expected to provide a robust empirical foundation for fiber LBW applications to facilitate the identification of ideal processing parameters. The following conclusions were obtained:

1) An inverse proportional weighting method that considers the LOO error was presented to construct an EM that inherited the prediction strengths of KRG, RBF, and SVR. Thus, the EM could reduce the risk of selecting an inappropriate individual metamodel.

2) The main effect analysis suggested that parameter P had the most influence on bead geometries W_b, D_p, and W_n. For D_n, parameter S was the most significant factor. Moreover, the first-order interaction of the processing parameters exerted significant impacts on the bead geometries.

3) Experimental verifications of the optimal solutions from the Pareto fronts showed that the relative errors (less than 14.67%) were acceptable.

4) Changes in the processing parameters led to different cooling rates, which could affect the microstructure and microhardness of the welding zone.

The proposed optimization framework can also be applied to other criteria of welding quality and other laser processes (laser additive manufacturing, laser quenching, etc.). In the future, additional studies could be conducted to improve the constructed data-driven EM and achieve enhanced optimization. First, mechanisms could be constructed to fine-tune the metamodels by changing some constants to conveniently adapt to similar processing conditions. Second, prior knowledge on fiber LBW could be combined into the metamodels for a highly accurate prediction.

Nomenclature

Abbreviations
ABC	Artificial bee colony
DOE	Design of experiment
EM	Ensemble of metamodel
KRG	Kriging
LBW	Laser beam welding
LOO	Leave-one-out
MOABC	Multi-objective artificial bee colony algorithm
PDAS	Primary dendrite arm spacing
RBF	Radial basis function
RSM	Response surface method
SVR	Support vector regression
Variables
C0	Specific heat at constant pressure of the workpiece
Cm	Predetermined maximum cycle number of the searching processes for the bees
Cr	Repeated cycle number of the searching processes for the bees
D	Defocus distance
Dn	Neck depth
D_{\text{n}}^{+}, D_{\text{n}}^{-}	Maximum and minimum values of Dn in the Pareto optimal solutions, respectively
Dp	Depth of penetration
{\left|D_{\text{p}}-H\right|}^{+}, {\left|D_{\text{p}}-H\right|}^{-}	Maximum and minimum values of \left|D_{\text{p}}-H\right| in the Pareto optimal solutions, respectively
E_1^k, E_2^k	LOO errors of the first and second metamodels selected for the variable k, respectively
Eal	Generalized relative maximum absolute error under the leave-one-out method
Er	Relative error of the four outputs
Esl	Generalized root mean square error under the leave-one-out method
\hat{f}(\cdot )	Approximation approach using the metamodel
{\hat{f}}_i(x)	Predictive response of the ith individual metamodel at sample point x
f(x_i)	Actual experimental value of the ith sample point
\hat{f}(x_{-i})	Predictive response from the metamodel trained using the full data sets with the ith sample point excluded out
{\hat{f}}_1^k(x), {\hat{f}}_2^k(x)	First and second metamodel selected for the variable k, respectively
{\hat{f}}_{\mathrm{E}}^k(x)	Prediction value of the integrated EM for the variable k
{\hat{f}}_{\mathrm{E}}^{D_{\text{n}}}(x)	Integrated EM for the variable Dn
fitness(Xi)	Quality (fitness value) of the food source of Xi
H	Thickness of the workpiece
k	Output response variable
K	Thermal conductivity of the workpiece
m	Number of sample points
P	Laser power
Pi	Probability value for onlooker bees to select the ith food source
Q	u feasible solutions (food sources)
rand(0, 1)	A random number between 0 and 1
S	Welding speed
Sn	Sum of normalized bead geometries
t	Duration of temperature variation
T	Reference temperature
T0	Room temperature
u	Number of the initial solution population in colony initialization phase
v	Dimension of each initial solution in colony initialization phase
Ve	Experimental values of the four outputs
Vp	Predicted values of the four outputs
w1, w2, w3, w4	Weighting values of the four optimization objectives
Wb	Bead width
W_{\text{b}}^{+}, W_{\text{b}}^{-}	Maximum and minimum values of Wb in the Pareto optimal solutions, respectively
Wn	Neck width
W_{\text{n}}^{+}, W_{\text{n}}^{-}	Maximum and minimum values of Wn in the Pareto optimal solutions, respectively
x	Input value of the metamodel
xi,j	jth dimension of the ith feasible solution
xp,j	One of the u food sources other than xi,j
xmax,j, xmin,j	Upper and lower bounds of the jth dimension, respectively
Xi	ith feasible solution (food source) in MOABC
Y	Output response of the metamodel
α	Coefficient vector of the metamodel
δ	Difference between the maximum and minimum mean bead geometries
ε	Stochastic factor of the metamodel
θi,j	Neighborhood of xi,j for searching a better food source
ρ	Material density of the workpiece
{\varphi }_{i,j}	Change rate of food sources during the employed bees phase
{\omega }_1^k, {\omega }_2^k	Weights of first and second metamodel for the variable k, respectively

Acknowledgements

This research was partially supported by the Project of International Cooperation and Exchanges NSFC (Grant No. 51861165202), the National Natural Science Foundation of China (Grant Nos. 51575211, 51705263, and 51805330), and the 111 Project of China (Grant No. B16019). The authors thank the technical support from the Experiment Center for Advanced Manufacturing and Technology in the School of Mechanical Science & Engineering of HUST.

Appendix

Table A1 Fiber LBW processing parameters and experimental results

No.	Processing parameters				Experimental results
	P/kW	S/(m·min−1)	D/mm		Wb/mm	Dp/mm	Wn/mm	Dn/mm
1	2.000	3.50	0.0		1.055	1.686	0.679	0.410
2	2.000	3.25	−0.5		1.204	1.823	0.583	0.601
3	2.000	3.00	−1.0		1.266	1.702	0.569	0.625
4	2.000	2.75	−1.5		1.195	1.950	0.512	0.806
5	2.000	2.50	−2.0		1.546	2.241	0.655	0.624
6	2.375	3.25	0.0		1.266	2.123	0.628	0.700
7	2.375	3.00	−0.5		1.323	2.059	0.608	0.691
8	2.375	2.75	−1.0		1.301	2.168	0.631	0.724
9	2.375	2.50	−1.5		1.538	2.225	0.651	0.699
10	2.375	3.50	−2.0		1.306	2.152	0.629	0.470
11	2.750	3.00	0.0		1.567	2.289	0.670	0.780
12	2.750	2.75	−0.5		1.497	2.339	0.717	0.684
13	2.750	2.50	−1.0		1.777	2.265	0.601	0.847
14	2.750	3.50	−1.5		1.510	2.534	0.712	0.561
15	2.750	3.25	−2.0		1.576	2.340	0.672	0.628
16	3.125	2.75	0.0		1.579	2.720	0.668	0.965
17	3.125	2.50	−0.5		1.587	2.921	0.669	1.046
18	3.125	3.50	−1.0		1.518	2.228	0.671	0.631
19	3.125	3.25	−1.5		1.637	2.804	0.724	0.668
20	3.125	3.00	−2.0		1.599	2.863	0.599	0.914
21	3.500	2.50	0.0		1.927	2.820	0.789	0.792
22	3.500	3.50	−0.5		1.418	2.447	0.825	0.576
23	3.500	3.25	−1.0		1.875	2.759	0.696	0.812
24	3.500	3.00	−1.5		1.719	2.966	0.738	0.871
25	3.500	2.75	−2.0		1.798	2.917	0.884	0.718

References

1 Huang L J , Hua X M , Wu D S , Ye Y X . Role of welding speed on keyhole-induced porosity formation based on experimental and numerical study in fiber laser welding of Al alloy. The International Journal of Advanced Manufacturing Technology, 2019, 103(1): 913–925

2 Hong K M , Shin Y C . Prospects of laser welding technology in the automotive industry: a review. Journal of Materials Processing Technology, 2017, 245: 46–69

3 Stavridis J , Papacharalampopoulos A , Stavropoulos P . Quality assessment in laser welding: a critical review. The International Journal of Advanced Manufacturing Technology, 2018, 94(5): 1825–1847

4 Zeng Z , Panton B , Oliveira J P , Han A , Zhou Y N . Dissimilar laser welding of NiTi shape memory alloy and copper. Smart Materials and Structures, 2015, 24(12): 125036

5 Oliveira J P , Braz Fernandes F M , Miranda R M , Schell N , Ocana J L . Effect of laser welding parameters on the austenite and martensite phase fractions of NiTi. Materials Characterization, 2016, 119: 148–151

6 Oliveira J P , Shen J J , Escobar J D , Salvador C A F , Schell N , Zhou N , Benafan O . Laser welding of H-phase strengthened Ni-rich NiTi-20Zr high temperature shape memory alloy. Materials & Design, 2021, 202: 109533

7 Ruggiero A , Tricarico L , Olabi A G , Benyounis K Y . Weld-bead profile and costs optimisation of the CO₂ dissimilar laser welding process of low carbon steel and austenitic steel AISI316. Optics & Laser Technology, 2011, 43(1): 82–90

8 Oliveira J P , Shen J J , Zeng Z , Park J M , Choi Y T , Schell N , Maawad E , Zhou N , Kim H S . Dissimilar laser welding of a CoCrFeMnNi high entropy alloy to 316 stainless steel. Scripta Materialia, 2022, 206: 114219

9 Jiang P , Wang C C , Zhou Q , Shao X Y , Shu L S , Li X B . Optimization of laser welding process parameters of stainless steel 316L using FEM, Kriging and NSGA-II. Advances in Engineering Software, 2016, 99: 147–160

10 Assunção E , Quintino L , Miranda R . Comparative study of laser welding in tailor blanks for the automotive industry. The International Journal of Advanced Manufacturing Technology, 2010, 49(1): 123–131

11 Kumar C , Das M , Paul C P , Bindra K S . Comparison of bead shape, microstructure and mechanical properties of fiber laser beam welding of 2 mm thick plates of Ti−6Al−4V alloy. Optics & Laser Technology, 2018, 105: 306–321

12 Sokolov M , Salminen A . Improving laser beam welding efficiency. Engineering, 2014, 6(09): 559–571

13 Abioye T E , Mustar N , Zuhailawati H , Suhaina I . Prediction of the tensile strength of aluminium alloy 5052-H32 fibre laser weldments using regression analysis. The International Journal of Advanced Manufacturing Technology, 2019, 102(5): 1951–1962

14 Zhang M J , Liu T T , Hu R Z , Mu Z Y , Chen S , Chen G Y . Understanding root humping in high-power laser welding of stainless steels: a combination approach. The International Journal of Advanced Manufacturing Technology, 2020, 106(11): 5353–5364

15 Shanthos Kumar G , Raghukandan K , Saravanan S , Sivagurumanikandan N . Optimization of parameters to attain higher tensile strength in pulsed Nd: YAG laser welded Hastelloy C-276–Monel 400 sheets. Infrared Physics & Technology, 2019, 100: 1–10

16 Du Y , Mukherjee T , DebRoy T . Physics-informed machine learning and mechanistic modeling of additive manufacturing to reduce defects. Applied Materials Today, 2021, 24: 101123

17 Huang Z , Cao H J , Zeng D , Ge W W , Duan C M . A carbon efficiency approach for laser welding environmental performance assessment and the process parameters decision-making. The International Journal of Advanced Manufacturing Technology, 2021, 114(7): 2433–2446

18 Mackwood A P , Crafer R C . Thermal modelling of laser welding and related processes: a literature review. Optics & Laser Technology, 2005, 37(2): 99–115

19 Peng S T , Li T , Zhao J L , Lv S P , Tan G Z , Dong M M , Zhang H C . Towards energy and material efficient laser cladding process: modeling and optimization using a hybrid TS-GEP algorithm and the NSGA-II. Journal of Cleaner Production, 2019, 227: 58–69

20 Akbari M , Shojaeefard M H , Asadi P , Khalkhali A . Hybrid multi-objective optimization of microstructural and mechanical properties of B4C/A356 composites fabricated by FSP using TOPSIS and modified NSGA-II. Transactions of Nonferrous Metals Society of China, 2017, 27(11): 2317–2333

21 Akbari M , Asadi P , Zolghadr P , Khalkhali A . Multicriteria optimization of mechanical properties of aluminum composites reinforced with different reinforcing particles type. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 2018, 232(3): 323–337

22 Srivastava S , Garg R K . Process parameter optimization of gas metal arc welding on IS:2062 mild steel using response surface methodology. Journal of Manufacturing Processes, 2017, 25: 296–305

23 Rong Y M , Zhang Z , Zhang G J , Yue C , Gu Y F , Huang Y , Wang C M , Shao X Y . Parameters optimization of laser brazing in crimping butt using Taguchi and BPNN-GA. Optics and Lasers in Engineering, 2015, 67: 94–104

24 Wang S H , Zhu L D , Fuh J Y H , Zhang H Q , Yan W T . Multi-physics modeling and Gaussian process regression analysis of cladding track geometry for direct energy deposition. Optics and Lasers in Engineering, 2020, 127: 105950

25 Wang G G , Shan S . Review of metamodeling techniques in support of engineering design optimization. Journal of Mechanical Design, 2007, 129(4): 370–380

26 Goel T , Haftka R T , Shyy W , Queipo N V . Ensemble of surrogates. Structural and Multidisciplinary Optimization, 2007, 33(3): 199–216

27 Younis A , Dong Z M . Trends, features, and tests of common and recently introduced global optimization methods. Engineering Optimization, 2010, 42(8): 691–718

28 Dong H C , Li C S , Song B W , Wang P . Multi-surrogate-based Differential Evolution with multi-start exploration (MDEME) for computationally expensive optimization. Advances in Engineering Software, 2018, 123: 62–76

29 Díaz-Manríquez A , Toscano G , Coello Coello C A . Comparison of metamodeling techniques in evolutionary algorithms. Soft Computing, 2017, 21(19): 5647–5663

30 Jin R , Chen W , Simpson T W . Comparative studies of metamodelling techniques under multiple modelling criteria. Structural and Multidisciplinary Optimization, 2001, 23(1): 1–13

31 Acar E . Effect of error metrics on optimum weight factor selection for ensemble of metamodels. Expert Systems with Applications, 2015, 42(5): 2703–2709

32 Song X G , Sun G Y , Li G Y , Gao W Z , Li Q . Crashworthiness optimization of foam-filled tapered thin-walled structure using multiple surrogate models. Structural and Multidisciplinary Optimization, 2013, 47(2): 221–231

33 Gao Z M , Shao X Y , Jiang P , Cao L C , Zhou Q , Yue C , Liu Y , Wang C M . Parameters optimization of hybrid fiber laser-arc butt welding on 316L stainless steel using kriging model and GA. Optics & Laser Technology, 2016, 83: 153–162

34 Ayoola W A , Suder W J , Williams S W . Parameters controlling weld bead profile in conduction laser welding. Journal of Materials Processing Technology, 2017, 249: 522–530

35 Huang Y J , Gao X D , Ma B , Liu G Q , Zhang N F , Zhang Y X , You D Y . Optimization of weld strength for laser welding of steel to PMMA using Taguchi design method. Optics & Laser Technology, 2021, 136: 106726

36 Cai X W , Qiu H B , Gao L , Li X K , Shao X Y . A hybrid global optimization method based on multiple metamodels. Engineering Computations, 2018, 35(1): 71–90

37 Karaboga D , Basturk B . A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm. Journal of Global Optimization, 2007, 39(3): 459–471

38 Jia H F , Miao H Z , Tian G D , Zhou M C , Feng Y X , Li Z W , Li J C . Multiobjective bike repositioning in bike-sharing systems via a modified artificial bee colony algorithm. IEEE Transactions on Automation Science and Engineering, 2020, 17(2): 909–920

39 Wang W J , Tian G D , Chen M N , Tao F , Zhao C Y , AI-Ahmari A , Li Z W , Jiang Z G . Dual-objective program and improved artificial bee colony for the optimization of energy-conscious milling parameters subject to multiple constraints. Journal of Cleaner Production, 2020, 245: 118714

40 Verma B K , Kumar D . A review on artificial bee colony algorithm. International Journal of Engineering and Technology, 2013, 2(3): 175–186

41 Ren Y P , Jin H Y , Zhao F , Qu T , Meng L L , Zhang C Y , Zhang B , Wang G , Sutherland J W . A multiobjective disassembly planning for value recovery and energy conservation from end-of-life products. IEEE Transactions on Automation Science and Engineering, 2021, 18(2): 791–803

42 Manikya Kanti K , Srinivasa Rao P . Prediction of bead geometry in pulsed GMA welding using back propagation neural network. Journal of Materials Processing Technology, 2008, 200(1–3): 300–305

43 Ragavendran M , Chandrasekhar N , Ravikumar R , Saxena R , Vasudevan M , Bhaduri A K . Optimization of hybrid laser—TIG welding of 316LN steel using response surface methodology (RSM). Optics and Lasers in Engineering, 2017, 94: 27–36

44 Zhang F , Zhou T T . Process parameter optimization for laser-magnetic welding based on a sample-sorted support vector regression. Journal of Intelligent Manufacturing, 2019, 30(5): 2217–2230

45 Jiang P , Cao L C , Zhou Q , Gao Z M , Rong Y M , Shao X Y . Optimization of welding process parameters by combining kriging surrogate with particle swarm optimization algorithm. The International Journal of Advanced Manufacturing Technology, 2016, 86(9): 2473–2483

46 Soltani H M , Tayebi M . Comparative study of AISI 304L to AISI 316L stainless steels joints by TIG and Nd:YAG laser welding. Journal of Alloys and Compounds, 2018, 767: 112–121

47 Shao J Y , Yu G , He X L , Li S X , Chen R , Zhao Y . Grain size evolution under different cooling rate in laser additive manufacturing of superalloy. Optics & Laser Technology, 2019, 119: 105662

48 Yang Z Y , Jin K N , Fang H , He J S . Multi-scale simulation of solidification behavior and microstructure evolution during vacuum electron beam welding of Al-Cu alloy. International Journal of Heat and Mass Transfer, 2021, 172: 121156

49 Kumar N , Mukherjee M , Bandyopadhyay A . Comparative study of pulsed Nd:YAG laser welding of AISI 304 and AISI 316 stainless steels. Optics & Laser Technology, 2017, 88: 24–39

50 Lenart R , Eshraghi M . Modeling columnar to equiaxed transition in directional solidification of Inconel 718 alloy. Computational Materials Science, 2020, 172: 109374

51 de Souza Silva E M F , da Fonseca G S , Ferreira E A . Microstructural and selective dissolution analysis of 316L austenitic stainless steel. Journal of Materials Research and Technology, 2021, 15: 4317–4329

52 Ragavendran M , Vasudevan M . Laser and hybrid laser welding of type 316L(N) austenitic stainless steel plates. Materials and Manufacturing Processes, 2020, 35(8): 922–934

53 Mohammed G R , Ishak M , Aqida S N , Abdulhadi H A . Effects of heat input on microstructure, corrosion and mechanical characteristics of welded austenitic and duplex stainless steels: a review. Metals, 2017, 7(2): 39

54 Huang W D , Geng X G , Zhou Y H . Primary spacing selection of constrained dendritic growth. Journal of Crystal Growth, 1993, 134(1–2): 105–115

55 Kurz W , Fisher D J . Dendrite growth at the limit of stability: tip radius and spacing. Acta Metallurgica, 1981, 29(1): 11–20

56 McCartney D G , Hunt J D . Measurements of cell and primary dendrite arm spacings in directionally solidified aluminium alloys. Acta Metallurgica, 1981, 29(11): 1851–1863