Toward autonomous mining: design and development of an unmanned electric shovel via point cloud-based optimal trajectory planning

Abstract

With the proposal of intelligent mines, unmanned mining has become a research hotspot in recent years. In the field of autonomous excavation, environmental perception and excavation trajectory planning are two key issues because they have considerable influences on operation performance. In this study, an unmanned electric shovel (UES) is developed, and key robotization processes consisting of environment modeling and optimal excavation trajectory planning are presented. Initially, the point cloud of the material surface is collected and reconstructed by polynomial response surface (PRS) method. Then, by establishing the dynamical model of the UES, a point to point (PTP) excavation trajectory planning method is developed to improve both the mining efficiency and fill factor and to reduce the energy consumption. Based on optimal trajectory command, the UES performs autonomous excavation. The experimental results show that the proposed surface reconstruction method can accurately represent the material surface. On the basis of reconstructed surface, the PTP trajectory planning method rapidly obtains a reasonable mining trajectory with high fill factor and mining efficiency. Compared with the common excavation trajectory planning approaches, the proposed method tends to be more capable in terms of mining time and energy consumption, ensuring high-performance excavation of the UES in practical mining environment.

Key words： autonomous excavation; unmanned electric shovel; point cloud; excavation trajectory planning

1 Introduction

As an important type of engineering equipment in open-pit mining industry, electric shovels are widely used in mining and loading operations [1–7]. From the viewpoint of design, electric shovels are generally believed to be of high efficiency, wide operating range, and strong environmental adaptability. However, this finding is usually not true during the practical mining because the large size, complex ore pile condition, and inappropriate excavation of the operator often lead to inefficient production, high energy consumption, and frequent failures [8–13]. To address these challenges, electric shovels are developed and upgraded at the roboticized and unmanned direction for more efficient and intelligent excavation.

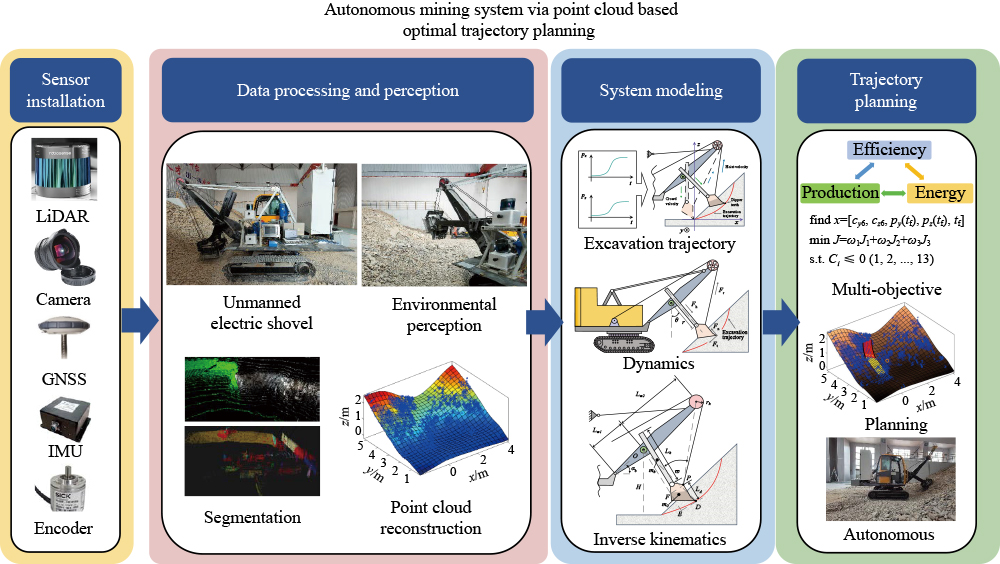
In the field of autonomous excavation, environmental perception and excavation trajectory planning serve as the foundations for the development of autonomous excavation because they directly influence the operation performance [14–18]. Currently, some works have been carried out and made some strides. For environmental perception, the primary objective is imaging terrain and objects in the work space, including trucks, bulldozers, and ancillary equipment. Nowadays, the range-scanning sensors, such as LiDAR, are used for terrain mapping and surface mining automation applications. Phillips et al. [19] introduced four types of LiDAR and summarized their advantages and limitations in the application of automatic mining. Phillips et al. [20] further analyzed four types of LiDAR behavior in the presence of dusts when mining. Green et al. [21] proposed a Bayesian method for verifying the accuracy of estimated truck poses based on a pair of planar LiDAR sensors. D’Adamo et al. [22] proposed a maximum sum of evidence (MSoE) method for registering LiDAR sensors to moving platforms; it yields more accurate registration solutions than the classical methods. Dunbabin and Corke [23] used LiDAR to generate terrain maps of the environment surrounding the shovel, thereby assisting in shovel planning and collision detection. In terms of excavation trajectory planning, Awuah-Offei and Frimpong [24] established an optimization model of the electric shovel to minimize the energy per unit loading rate in excavation process based on kinematics and dynamics, and the optimal speeds of the crowd arm and hoist rope are obtained by using steepest descent method. Bi et al. [25] proposed a multiobjective optimization model, which considers digging time and energy consumption per payload as objects, and then a two-phase optimization method to apply to reduce the mining time and energy consumption. Jud et al. [26] developed a mapping approach for excavation trajectory planning based on an improved state machine. Son et al. [27] proposed a novel excavation trajectory planning method for autonomous excavators based on human expert knowledge. Lee et al. [28] proposed a two-phase motion planning framework for excavators. Wang et al. [29] analyzed corresponding forces in excavation and proposed a polynomial-based trajectory planning method to minimize the energy consumption. Wang et al. [30] further improved the approximation method about mining trajectory by using radial basis functions (RBF) model, which yielded a better performance than other conventional methods. Although some studies have been conducted to improve excavation performance, most studies are only carried out under simulation conditions rather than practical equipment, and the internal connection between environmental perception and autonomous excavation are not yet established. More importantly, most works neglect the real-time requirements of the excavation trajectory planning, thereby hindering its application in practical autonomous excavation.

To address these challenges, an unmanned electric shovel (UES) based on a scaled shovel prototype is designed for autonomous excavation, and the key robotization processes consisting of environment modeling and excavation trajectory planning are discussed. An analytical point cloud reconstruction model based on polynomial response surface (PRS) method is established, and a concise environment model of the material pile is obtained to assist subsequent real-time trajectory planning. Then, the dynamics of the UES is modeled, and a point to point (PTP) excavation trajectory planning method based on higher-degree polynomial is proposed for real-time calculation and autonomous excavation. To the best of our knowledge, this study is the first to combine point cloud modeling with excavation trajectory planning to guide autonomous decision-making and excavation of the UES. The proposed autonomous excavation framework for UES has salient features: (1) The material surface is reconstructed in an analytic form to ensure real-time trajectory planning; (2) a PTP-based multiobjective trajectory planning model is established to ensure the fill factor, mining efficiency, and energy consumption; (3) the calculation time of the proposed autonomous excavation framework satisfies real-time requirements in practical unmanned excavation scenarios.

The remainder of this paper is organized as follows. Section 2 introduces the framework of the designed UES. Section 3 proposes a PRS-based surface reconstruction method for environmental point cloud. In Section 4, a PTP trajectory planning method based on surface model is proposed for autonomous excavation. Section 5 presents the experimental results. Finally, the conclusions are drawn in Section 6.

2 Framework of the UES

Fig.1 illustrates the framework of our designed UES. It is developed based on a 1:7 scale prototype of a WK-55-type electric shovel. For the mechanical structure, the UES is identical to that of the traditional manual shovel and includes three parts: a lower body, an upper body, and an attachment. The lower body mainly consists of the propel drive and crawler system, the upper body mainly provides a platform for the boom attachment, electronic control cabinet, and transmission machinery. The attachment assembly consists of the boom, hoist rope, dipper handle, and dipper. The working device of the UES is a mechanism with two degrees of freedom, which is driven by the hoist and crowd mechineries synergistically to excavate the material from the bottom up.

Fig.1 Framework of the unmanned electric shovel. GNSS: global navigation satellite system, IMU: inertial measurement unit.

Full size|PPT slide

On the basis of the prototype, an unmanned excavation system is developed for autonomous decision-making and excavation. In unmanned excavation system, some sensors consisting of LiDAR, global navigation satellite system (GNSS), inertial measurement unit (IMU), and absolute encoders are used for information perception, and an industrial control computer is used for autonomous decision-making, as shown in Fig.1. In summary, one cycle autonomous excavation procedure includes the following: Two LiDARs are used for material environmental perception by collecting point cloud data of the material surface. The GNSS, IMU, and encoders are used for pinpointing the location and attitude of the robot. Based on the obtained point cloud of the material surface, as well as the position and attitude pose information of the robot itself, the industrial control computer (upper computer) performs trajectory planning operation to determine a reasonable excavation trajectory and feeds the excavation command back to the Programmable Logic Controller (PLC), which is used as the lower computer to control the inverter and related actuators. Finally, the hoist machinery and crowd machinery synergistically drive the dipper to excavate materials based on excavation command. When excavation is completed, the UES performs rotation and unloading, and the above-mentioned procedure is repeated. The flowchart of the autonomous excavation is shown in Fig.2.

Fig.2 Flowchart of the autonomous excavation.

Full size|PPT slide

3 Surface reconstruction for environmental point cloud

3.1 Environmental point cloud acquisition

The 3D point cloud acquisition device is shown in Fig.3, it is composed of two RS-Ruby Lite 80 laser-beam LiDARs. The sampling frequency is 10, and the vertical and horizontal angle resolutions are 0.1° and 0.2°, respectively. The two LiDARs are installed at a certain angle for scanning the upper part and the lower part of the material surface. We set up the space coordinate system at the center of the bottom of the rotation spindle, where the x-axis is parallel to the lower body of the UES.

Fig.3 3D point cloud acquisition device composed of two RS-Ruby Lite 80 laser-beam LiDARs.

Full size|PPT slide

Fig.4(a) illustrates the actual material surface, and Fig.4(b) shows the corresponding environmental point cloud acquired after filtering [31], registration [32], and segmentation [33]. Fig.4(b) shows that the outline of the material pile can be clearly depicted on high-resolution point cloud. However, an important issue is that massive environmental point cloud is not conducive to real-time decision-making and trajectory planning of the UES. Therefore, a reasonable mathematical model should be established and approximated by utilizing geometric information from collected point cloud data.

Fig.4 (a) Actual material surface and (b) corresponding environmental point cloud.

Full size|PPT slide

3.2 Surface reconstruction definition

Nowadays, surface reconstruction can be conducted using several approaches, such as support vector regression [34], deep neural networks [35], and RBF [36]. The above methods have high reconstruction accuracy, but they are unsuitable for real-time material surface reconstruction and trajectory planning due to the substantial runtime cost. To achieve an ideal trade-off between the reconstruction accuracy and computational efficiency, a PRS method [37] is applied to the material surface reconstruction to find an analytic function to approximate the given point cloud.

The acquired cloud point is organized as three column vectors, where the elements of three vectors represent the positions along x, y, and z axes in the Cartesian coordinate system. The cloud point is denoted as \mathit{P}=[\mathit{x},\mathit{y},\mathit{z}]\in {\mathbb{R}}^{N\times 3} where N denotes the number of points, \mathit{x}={\left[x_1,x_2,...,x_N\right]}^{\text{T}} represents the coordinate vector of the point cloud in the x direction, \mathit{y}={\left[y_1,y_2,...,y_N\right]}^{\text{T}} represents the coordinate vector of the point cloud in the y direction, and \mathit{z}={\left[{\mathit{\text{z}}}_1,{\mathit{\text{z}}}_2,...,{\mathit{\text{z}}}_N\right]}^{\text{T}} represents the coordinate vector of the point cloud in the z direction. Formally, the material surface reconstruction is represented as a function f_{\text{s}}, as follows:

(1)\hat{\mathit{z}}=f_{\text{s}}(\mathit{x},\mathit{y}),

where \hat{\mathit{z}} is the prediction value of z. The main purpose of modeling is to find a suitable polynomial function f_{\text{s}} that minimizes the expected loss between the actual outputs and predictions so that \hat{\mathit{z}} are consistent with z. Once the model is established, it can assist the subsequent trajectory planning to ensure the real-time and rationality of autonomous excavation.

3.3 PRS-based surface reconstruction

The polynomial function f_{\text{s}} for z-direction response variable \widehat{\mathit{\text{z}}} with k order is written as follows:

(2)\widehat{\mathit{\text{z}}}=f_{\text{s}}(x,y)=\sum _{i=0}^{k-1}\sum _{j=0}^{k-1}{\beta }_{ij}{x}^i{y}^j,

where {\beta }_{ij} is the coefficient of the polynomial function, x and y represent the coordinates of the point in the x and y directions, respectively. The polynomial order k is a hyperparameter, which can be determined by the fitting accuracy. Considering N samples, Eq. (2) can be written as follows:

(3)\begin{array}{rl}& \left[\begin{array}{cccccccc}1& x_1& y_1& x_1{y}_1& x_1^2{y}_1& x_1{y}_1^2& \cdots & x_1^{k-1}{y}_1^{k-1}\\ 1& x_2& y_2& x_2{y}_2& x_2^2{y}_2& x_2{y}_2^2& \cdots & x_2^{k-1}{y}_2^{k-1}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& x_N& y_N& x_N{y}_N& x_N^2{y}_N& x_N{y}_N^2& \cdots & x_N^{k-1}{y}_N^{k-1}\end{array}\right]\\ & \cdot \left[\begin{array}{c}{\beta }_{00}\\ {\beta }_{10}\\ ⋮\\ {\beta }_{k-1,k-1}\end{array}\right]\text{=}\left[\begin{array}{c}{\mathit{\text{z}}}_1\\ {\mathit{\text{z}}}_2\\ ⋮\\ {\mathit{\text{z}}}_N\end{array}\right]\Rightarrow \mathit{D}\times \mathit{\beta }=\mathit{z},\end{array}

where D represents the Vandermonde matrix composed of x and y, β is coefficient column vector. The purpose for PRS modeling is to find the coefficient β to minimize loss function L_{\text{s}} as follows:

(4)L_{\text{s}}=(\mathit{z}-\mathit{D}\mathit{\beta }{)}^{\text{T}}(\mathit{z}-\mathit{D}\mathit{\beta }).

The coefficient β can be solved using the method of least squares, as follows:

(5)\mathit{\beta }=({\mathit{D}}^{\text{T}}\mathit{D}{)}^{-1}{\mathit{D}}^{\text{T}}\mathit{z}.

Note that only one-step calculation is carried out in the model solving. As a result, the real-time performance for point cloud modeling can be satisfied.

4 PTP trajectory planning method

4.1 Higher degree polynomial based PTP method

A typical excavation trajectory of the UES is illustrated in Fig.5; it is directly determined by the velocity of the crowd and hoist motors, as mentioned in Section 2. To facilitate the subsequent calculation, a PTP trajectory planning method based on higher-degree polynomial is proposed for autonomous decision making of the UES. In this study, two different polynomials are defined to synergistically describe the excavation trajectory, as follows:

Fig.5 Excavation trajectory of the unmanned electric shovel.

Full size|PPT slide

(6)\{\begin{array}{c}{p}_y(t)=c_{y_n}{t}^n+c_{y_{n-1}}{t}^{n-1}+\cdots +c_{y_2}{t}^2+c_{y_1}t+c_{y_0},\\ p_{\mathit{\text{z}}}(t)=c_{{\mathit{\text{z}}}_n}{t}^n+c_{{\mathit{\text{z}}}_{n-1}}{t}^{n-1}+\cdots +c_{{\mathit{\text{z}}}_2}{t}^2+c_{{\mathit{\text{z}}}_1}t+c_{{\mathit{\text{z}}}_0},\end{array}

where t is time, p_y and p_z represent the positions of the excavation trajectory in the y and z directions, respectively, n represents the degree of the polynomial, and c represents polynomial trajectory coefficient.

To ensure the mining stability, the initial/final excavation velocities and the initial/final excavation accelerations in two directions are set to 0, as follows:

(7)\{\begin{array}{c}{v}_y(t_{\text{0}})=p_y^{\prime }(t_0)=0,a_y(t_0)=p_y^{″}(t_0)=0,\\ v_{\mathit{\text{z}}}(t_{\text{f}})=p_{\mathit{\text{z}}}^{\prime }(t_{\text{f}})=0,a_{\mathit{\text{z}}}(t_0)=p_{\mathit{\text{z}}}^{″}(t_{\text{f}})=0,\end{array}

where v_y and v_{\mathit{\text{z}}} are the excavation velocities in the y and z directions, respectively, a_y and a_{\mathit{\text{z}}} are excavation accelerations in the y and z directions, respectively, t_0 is the initial time in excavation, and t_{\text{f}} is final time in excavation. The polynomial trajectory coefficients in y or z direction can be calculated as follows:

(8)\{\begin{array}{c}{c}_0=0,c_1=0,c_2=0,\\ c_3=\frac{10p\left(t_{\text{f}}\right)}{t_{\text{f}}^3}-t_{\text{f}}^3{c}_6-3t_{\text{f}}^4{c}_7-6t_{\text{f}}^5{c}_8-10t_{\text{f}}^6{c}_9-\cdots ,\\ c_4=-\frac{15p\left(t_{\text{f}}\right)}{t_{\text{f}}^4}+3t_{\text{f}}^2{c}_6+8t_{\text{f}}^3{c}_7+15t_{\text{f}}^4{c}_8+24t_{\text{f}}^5{c}_9+\cdots ,\\ c_5=\frac{6p\left(t_{\text{f}}\right)}{t_{\text{f}}^5}-3t_{\text{f}}{c}_6-6t_{\text{f}}^2{c}_7-10t_{\text{f}}^3{c}_8-15t_{\text{f}}^4{c}_9-\cdots .\end{array}

Once the polynomial function is established, by combining with the point cloud model, objective function, and constraints, the optimal excavation trajectory as well as the control signal can be obtained.

4.2 Dynamics of the unmanned electric shovel

To obtain the high-performance excavation trajectory, a dynamics model of the UES should be established. Considering that UES is a complex electromechanical coupling system, the Lagrange method is applied to establish the theoretical model of the working device [38], as follows:

(9)\frac{\text{d}}{\text{d}t}\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_i}\right)-\frac{\mathrm{\partial }L}{\mathrm{\partial }{q}_i}=F_i\text{,}i=1,2,...,s,

where L is the Lagrange function, q_i is the generalized coordinate, F_i is the generalized force, and s is the degree of freedom. The hoist machinery and crowd machinery synergistically drive the dipper in excavation; thus, the stretching length of the dipper handle r and the angle between the vertical direction and the axis of the dipper handle θ are considered the generalized coordinates, as shown in Fig.6. The final dynamics equation of the UES is denoted by Eq. (10), as follows:

Fig.6 Generalized coordinates and force analysis in excavation.

Full size|PPT slide

(10)\{\begin{array}{rl}& \left[m_{\mathrm{h}}\left(r^2-L_{\mathrm{h}}r+\frac{1}{3}{L}_{\mathrm{h}}^2\right)+m_{\mathrm{d}}\left(r^2+L_{\mathrm{d}}r+\frac{1}{3}{L}_{\mathrm{d}}^2\right)\right]\ddot{\theta }\\ & +\left[2\left(m_{\mathrm{h}}+m_{\mathrm{d}}\right)r-\left(m_{\mathrm{h}}{L}_{\mathrm{h}}-m_{\mathrm{d}}{L}_{\mathrm{d}}\right)\right]\dot{\theta }\dot{r}\\ & +\left[m_{\mathrm{h}}g\sin \theta \left(r-\frac{L_{\mathrm{h}}}{2}\right)+m_{\mathrm{d}}g\sin \theta \left(r+\frac{L_{\mathrm{d}}}{2}\right)\right]=\\ & F_{\mathrm{h}}r\sin \varpi -F_{\mathrm{t}}(L_{\mathrm{d}}+r),\\ & \left(m_{\mathrm{h}}+m_{\mathrm{d}}\right)\ddot{r}-\left[\left(m_{\mathrm{h}}+m_{\mathrm{d}}\right)\cdot r-\frac{1}{2}\left(m_{\mathrm{h}}{L}_{\mathrm{h}}-m_{\mathrm{d}}{L}_{\mathrm{d}}\right)\right]{\dot{\theta }}^2\\ & -\left(m_{\mathrm{h}}+m_{\mathrm{d}}\right)g\cos \theta =F_{\mathrm{c}}-F_{\mathrm{n}}-F_{\mathrm{h}}\cos \varpi ,\end{array}

where L_{\text{h}} is the length of the dipper handle, L_{\text{d}} is the length of the dipper, F_{\text{h}} is the hoist force, F_{\text{c}} is the crowd force, F_{\text{n}} is the normal excavation resistance, F_{\text{t}} is the tangential excavation resistance, g is acceleration of gravity, \varpi is the angle between the hoist rope and the dipper handle, m_{\text{h}} is the mass of the dipper handle, and m_{\text{d}} is the total mass of the dipper including the mass of the empty dipper m_{\text{0}} and the mass of the loaded material m_{\text{m}} ( m_{\text{d}}=m_{\text{0}}+m_{\text{m}}). Based on Eq. (10), the dynamical characteristics of the UES can be guaranteed by adding related constraints in the optimization model. The structural parameters of the UES are listed in Tab.1, and a corresponding explanation is illustrated in Fig.7.

Tab.1 Values of relevant structural parameters of the UES

Parameters	Value
L_{\text{m1}}	1.04 m
L_{\text{m2}}	2.13 m
r_{\text{h}}	0.18 m
L_{\text{h}}	2.36 m
L_{\text{d}}	0.47 m
H	1.45 m
m_{\text{h}}	129.38 kg
m_0	364.12 kg
{\alpha }_{\text{b}}	45.00°
EF	0.45 m
ED	0.36 m
PF	0.38 m

Fig.7 Explanatory diagram of unmanned electric shovel’s key structural parameters.

Full size|PPT slide

In addition, the loaded material m_{\text{m}} is updated continuously as the dipper excavates the ore, and it can be calculated by surface integral operation, as follows:

(11)m_{\text{m}}=\rho \cdot V=\rho \cdot \underset{D_{xy}}{\iint }\left(f_{\text{s}}(x,y)-f_{\text{tr}}(x,y)\right)\text{d}x\text{d}y,

where \rho is the material density, V is the loaded volume, D_{xy} is the projection area in the horizontal direction when the dipper teeth cut the material surface, f_{\text{tr}}(x,y) is the excavation trajectory.

4.3 Objective function

As shown in Section 4.1, the essence of excavation trajectory planning is to calculate the optimal velocity command of the hoist and crowd motors to improve mining efficiency and dipper fill factor and to reduce the energy consumption. Thus, the objective function consists of three items, as follows:

(I) The mining efficiency ( J_1) can be quantitatively described by the final time in excavation, as follows:

(12)J_1=t_{\text{f}}.

(II) The mining production ( J_2) can be quantitatively described by the dipper fill factor which is the ratio of the excavation volume and nominal load capacity. The fill factor should be close to 100% as far as possible. Thus, the sub-objective J_2 can be written as follows:

(13)J_2=\left|1-\frac{V}{V_{\text{n}}}\right|\times 100\mathrm{\%},

where V_{\text{n}} is nominal load capacity.

(III) The energy consumption ( J_3) is quantitatively described by unit energy consumption per payload, as follows:

(14)J_3=\frac{E_{\text{h}}+E_{\text{c}}}{V},

where E_{\text{h}} and E_{\text{c}} are the energy consumption of the hoist and crowd machineries, respectively. The energy consumption for each machinery can be denoted by the following integral operations:

(15)E_{\text{h}}={\int }_0^{t_{\text{f}}}{F}_{\text{h}}(t)v_{\text{r}}(t)\text{d}t,

(16)E_{\text{c}}={\int }_0^{t_{\text{f}}}{F}_{\text{c}}(t)\dot{r}(t)\text{d}t,

where v_{\text{r}}(t) is the rope velocity, and \dot{r}(t) is the velocity of the dipper handle. Accordingly, the objective function J is expressed as the weighted sum of three sub-objectives, as follows:

(17)J={\omega }_1{J}_1+{\omega }_2{J}_2+{\omega }_3{J}_3,

where {\omega }_1, {\omega }_2, and {\omega }_3 are the corresponding weight coefficients with respect to each item.

Based on dynamics model, constraints, and objective function, the excavation trajectory planning of the UES is transformed into a nonlinear programming problem with multiple constraints. To ensure the simplicity of optimization variables, the six-degree polynomial is selected to describe the excavation trajectory. Therefore, the six-degree polynomial coefficient in the y direction c_{y6} and the six-degree polynomial coefficient in the z direction c_{\mathit{\text{z}}6} are selected as optimization variables. In addition, to obtain a planned trajectory with certain adaptability, the final time in excavation t_{\text{f}}, the final position of the excavation trajectory in the y and z directions p_y(t_{\text{f}}) and p_{\mathit{\text{z}}}(t_{\text{f}}) are selected as optimization variables. Therefore, the trajectory planning model can be formed as follows:

(18)\begin{array}{c}\text{find}\mathit{x}=[c_{y6},c_{\mathit{\text{z}}6},p_y(t_{\text{f}}),p_{\mathit{\text{z}}}(t_{\text{f}}),t_{\text{f}}],\\ minJ={\omega }_1{J}_1+{\omega }_2{J}_2+{\omega }_3{J}_3\text{,}\\ \text{s}\text{.t}\text{.:}{C}_i⩽0(i=1,2,...,13),\end{array}

where C_i denotes the constraint in trajectory planning, and detailed definition is shown in the next section.

4.4 Constraints

To ensure that the obtained trajectory satisfies practical engineering, some constraints should be considered in excavation. Generally, the constraints can be classified into two categories: geometrical constraints and performance constraints.

For geometrical constraints, the following items should be considered:

(I) The minimum vertical height of the dipper bottom in excavation should be limited to not less than 0 to ensure no interference with the ground:

(19)C_1=-h_{\text{b}min}⩽0,

where h_{\text{b}min} is the minimum vertical height of the dipper bottom.

(II) The final position of the excavation trajectory in vertical direction should be above the material surface, computed as follows:

(20)C_2=h_{\text{mf}}-p_{\mathit{\text{z}}}(t_{\text{f}})+h_{\epsilon }⩽0,

where h_{\text{mf}} is the material height corresponding to the final position of the excavation trajectory, and h_{\epsilon } is the set margin height to ensure that the dipper is separated from the material.

(III) The maximum stretching length of the dipper handle r_{max} should be limited to a certain range, as follows:

(21)C_3=r_{max}-r_{\text{a}}⩽0,

where r_{\text{a}} is the maximum allowable value of the stretching length of the dipper handle.

For performance constraints, the following constraints should be satisfied:

(I) The loaded materials for the UES at final time should be limited in a reasonable range. Here, the range is set from 80% to 110% of the nominal loading capacity, as follows:

(22)\{\begin{array}{c}{C}_4=0.8V_{\text{n}}-V⩽0,\\ C_5=V-1.1V_{\text{n}}⩽0.\end{array}

(II) Considering the actual characteristics of the hoist and crowd motors, the maximum rope velocity and the stretching velocity of the dipper handle in excavation should not be greater than the design values, computed as follows:

(23)\{\begin{array}{c}{C}_6=v_{\text{r max}}-v_{\text{ra}}⩽0,\\ C_7={\dot{r}}_{max}-v_{\text{ha}}⩽0,\end{array}

where v_{\text{r}max} is the maximum velocity of the hoist rope, v_{\text{ra}} is the maximum allowable value of the rope velocity, {\dot{r}}_{max} is the maximum velocity of the dipper, and v_{\text{ha}} is the maximum allowable velocity of the dipper handle in excavation.

(III) To stabilize the control process, the minimum rope velocity v_{\text{r}min} and the minimum dipper handle velocity {\dot{r}}_{min} in excavation are limited and should not be less than 0, computed as follows:

(24)\{\begin{array}{c}{C}_8=-v_{\text{r}min}⩽0,\\ C_9=-{\dot{r}}_{min}⩽0.\end{array}

(IV) To ensure the accessibility in excavation, the maximum values with respect to the hoist force, the crowd force, the hoist machinery power, and the crowd power should not exceed the rated capacity of the corresponding motor, as follows:

(25)\{\begin{array}{c}{C}_{10}=F_{\text{h}max}-F_{\text{ha}}⩽0,\\ \begin{array}{c}{C}_{11}=F_{\text{c}max}-F_{\text{ca}}⩽0,\\ C_{12}=P_{\text{h}max}-P_{\text{ha}}⩽0,\\ C_{13}=P_{\text{c}max}-P_{\text{ca}}⩽0,\end{array}\end{array}

where F_{\text{h}max} is maximum hoist force, F_{\text{c}max} is maximum crowd force, P_{\text{h}max} is maximum hoist power, P_{\text{c}max} is maximum crowd power, and F_{\text{ha}}, F_{\text{ca}}, P_{\text{ha}}, and P_{\text{ca}} are maximum allowable values with respect to the hoist force, crowd force, hoist power, and crowd power, respectively. The maximum allowable values are calculated by the rated torque and power of the corresponding motors.

The values of the relevant constraints are shown in Tab.2.

Tab.2 Values of the constraints in trajectory planning

Constraints	Value
h_{\epsilon }	0.10 m
V_{\text{n}}	0.16 m3
v_{\text{ha}}	0.11 m/s
F_{\text{ca}}	19.25 kN
P_{\text{ca}}	3.50 kN
r_{\text{a}}	2.12 m
v_{\text{ra}}	0.25 m/s
F_{\text{ha}}	38.76 kN
P_{\text{ha}}	8.20 kW

4.5 Optimization algorithm

To ensure the real-time solution and stability, COBYLA [39] algorithm is applied to solve the optimization model. COBYLA is an implementation of Powell’s nonlinear derivative–free constrained optimization that uses a linear approximation approach. On the basis of Nelder–Mead simplex search method, the linear polynomial approximation of the objective function and the constraints is constructed by interpolating at the vertex of the simplex, and the optimal solution of the problem is found iteratively in the trust region. More detailed description of the algorithm architecture is shown in Ref. [39].

Through iterative optimization, the optimal variables [c_{y6},c_{z6},p_y(t_{\text{f}}),p_{\mathit{\text{z}}}(t_{\text{f}}),t_{\text{f}}] can be obtained, and the optimal excavation trajectory can be determined. By converting the trajectory velocity into the motor speeds, the UES performs autonomous excavation.

5 Experimental results

This section presents the experimental results of the point cloud modeling and PTP trajectory planning method for autonomous excavation of the UES. All the algorithms are implemented in Visual Studio 2019 and written with C++ at an industrial control computer (CPU: Intel Core i7-10700; RAM: 32 GB). For visualization, the results are plotted by calling MATLAB Engine.

5.1 Surface reconstruction

The scope of the point cloud is further segmented in the range of [‒2, 4] in the x direction, as shown in Fig.8, to improve the modeling accuracy and reduce the computational burden because the excavation scope of the UES only accounts for a small part of the material pile.

Fig.8 Point cloud of material surface to be reconstructed.

Full size|PPT slide

As shown in Section 3.3, the polynomial order k is a hyperparameter, which greatly influences the modeling accuracy and efficiency. A grid search method is carried out in which the polynomial order k is selected from {2, 4, 6, 8, 10} to determine a relatively optimal polynomial order, and the visualized modeling results with different k are shown in Fig.9. The subfigures on the left show the established material surface by PRS. By observing the modeling results with different k, we can find that the modeling accuracy is relatively poor when k is small because a small value of k limits the degree of freedom of the polynomial, and the potential forms of the PRS are restrained. When k is large, the surface exhibits flexibility but is no longer smooth, thereby leading to over fitting and loss of generalization. The right subfigures illustrate the absolute residual between the actual value and the predicted value of PRS at the corresponding point. The results indicate that when k = 6 and 8, the PRS shows relatively satisfactory modeling performance.

Fig.9 Modeling accuracy and error comparison with different k: (a) polynomial model with k = 2, (b) model absolute residual with k = 2, (c) polynomial model with k = 4, (d) model absolute residual with k = 4, (e) polynomial model with k = 6, (f) model absolute residual with k = 6, (g) polynomial model with k = 8, (h) model absolute residual with k = 8, (i) polynomial model with k = 10, and (j) model absolute residual with k = 10.

Full size|PPT slide

To quantitatively calculate the modeling accuracy, the coefficient of determination (R²) [40] is used as metric, as follows:

(26){\text{R}}^{\text{2}}=1-\frac{{\displaystyle \sum _{i=1}^N{({\mathit{\text{z}}}_i-{\widehat{\mathit{\text{z}}}}_i)}^2}}{{\displaystyle \sum _{i=1}^N{({\mathit{\text{z}}}_i-\overline{\mathit{\text{z}}})}^2}},

where {\mathit{\text{z}}}_i is the true value of the sample i, {\widehat{\mathit{\text{z}}}}_i is the prediction value of the sample i, and \overline{\mathit{\text{z}}} is the mean value for all samples. {\text{R}}^{\text{2}} value closer to 1 indicates a better performance.

The relationship between the polynomial order k and computational performance is shown in Fig.10. Clearly, the modeling time increases gradually with the increase k, and when {\text{R}}^{\text{2}} reaches 0.99, it does not increase even if k continues to increase. Based on these results, we can conclude that when k = 6, the PRS provides a relatively balanced modeling performance between the computational efficiency and accuracy.

Fig.10 Relationship between different k and computational performance.

Full size|PPT slide

5.2 Trajectory planning and autonomous excavation

When the PRS modeling is completed, the autonomous trajectory planning is carried out based on established surface model. In trajectory optimization, the maximum permission iterative number of times is set to 300, and the tolerance on constraint violation is set to 0.01. The lower and upper boundary values of optimization variables are shown in Tab.3.

Tab.3 Upper and lower bounds of optimization variables

Constrained boundary	c_{y6}	c_{\mathit{\text{z}}6}	p_y(t_{\text{f}})/m	p_{\mathit{\text{z}}}(t_{\text{f}})/m	t_{\text{f}}/s
Lower bound	−5.00	0.00	1.20	1.60	8.00
Upper bound	0.00	5.00	2.25	1.90	16.00

In addition, the weight of each sub-objective {\omega }_1, {\omega }_2, and {\omega }_3 is set to 0.4, 0.3, and 0.3, respectively, which represents the proportion of each sub-objective in the objective function. Considering the different dimensions of each sub-objective, the maximum–minimum normalization is used to obtain dimensionless sub-objective, as follows:

(27)J_{\text{norm}}=\frac{J-J_{min}}{J_{max}-J_{min}},

where J_{max} and J_{min} are the upper and lower bounds, respectively, and the values are listed in Tab.4.

Tab.4 Upper and lower bounds of sub-objective

Constrained boundary	J_1/s	J_2	J_3/(kW∙h∙m‒3)
Lower bound	8.00	0.00	0.00
Upper bound	16.00	2.00	0.03

The convergence curve in the iteration optimization process is shown in Fig.11. Fig.11 shows that the convergence curve converges rapidly and approaches the optimal solutions at the 247th iteration. The whole optimization process takes 2.14 s, and the final objective value is 0.5065.

Fig.11 Convergence curve of the objective value.

Full size|PPT slide

The obtained excavation trajectory is shown in Fig.12(a), where the orange dot denotes the axis of the crowd gear, the red line represents the excavation trajectory of the dipper teeth, and the yellow line represents the projection of the excavation trajectory on the material surface. The figure shows that the planned excavation trajectory is relatively smooth. Fig.12(b) shows the changing process of the rope length and stretching length of the dipper handle, indicating that the states are stable in the early and late stages. Thus, the stability of the subsequent excavation is ensured. Fig.12(c) shows that the hoist and crowd velocities are 0 at the initial and final moments, and the crowd velocity is greater than the hoist velocity at the early stage, ensuring the fill factor of the dipper. Fig.12(d) and Fig.12(e) show the digging force and output power provided by the hoist motor and crowd motor. The figures indicate that the results satisfy the constraints.

Fig.12 Excavation trajectory and related states: (a) planned excavation trajectory, (b) rope and dipper hand lengths, (c) hoist and crowd velocities, (d) digging forces, and (e) motor powers.

Full size|PPT slide

In practical mining, the speed control mode is adopted for the motor control. Therefore, the planned hoist and crowd velocities should be further converted to the speeds of the corresponding motors in the upper computer (industrial control computer). The lower computer (PLC) receives the speed instructions from the upper computer via PROFINET communication and further transmits it to the frequency converter by converting into 0–20 mA current signal. Finally, the frequency converter regulates the motor speed by internal proportional integral derivative (PID) algorithm to perform the excavation. The whole autonomous excavation process is illustrated in Fig.13, where Fig.13(a) shows the LiDAR scanning the material surface, Fig.13(b) depicts the initial condition of the UES, Fig.13(c) shows the excavation process, Fig.13(d) shows the final state when the mining is completed, Fig.13(e) shows the rotation process, and Fig.13(f) shows the unloading process.

Fig.13 Autonomous excavation process: (a) material scanning, (b) mining initialization, (c) mining process, (d) mining accomplished, (e) rotation process, and (f) unloading process.

Full size|PPT slide

When the excavation is completed, we estimate the volume of material in the dipper and calculate the fill factor at about 90%. Compared with the planned result 96.8%, the error is within 10%, indicating the effectiveness of our method. Notably, the major cause of lower fill factor is that some materials cannot enter the dipper in the excavation because the material in the dipper hinders the incoming material.

Fig.14 illustrates the comparison of the planned motor speed and actual motor speed. The figure shows that the actual execution speed almost completely follows the planned motor speed. In 2–6 s, the speed of the crowd motor has a certain fluctuation, given that the dipper suffered with considerable resistance with the increase in the cutting depth of the dipper. Moreover, at the beginning and end moment, only a certain error is obtained due to the threshold protection in the program. When the speed command is less than 50, the motor does not perform the corresponding action. The comparison of the theoretical digging forces obtained by Lagrange equation and actual digging forces is shown in Fig.15. Fig.15 shows that the trend and magnitude of the actual signal are basically consistent with the theoretical value, verifying the accuracy of our dynamic modeling for the UES. In the first 4.5 s, the actual value is greater than the theoretical value due to the complexity and non-uniformity of the material, neglected dynamics, and external torque disturbance when the dipper goes deep into the material.

Fig.14 Comparison of actual and planned motor speeds: (a) comparison of actual and planned hoist motor speeds, and (b) comparison of actual and planned crowd motor speeds.

Full size|PPT slide

Fig.15 Comparison of planned and actual digging forces: (a) comparison of actual and planned hoist forces, and (b) comparison of actual and planned crowd forces.

Full size|PPT slide

5.3 Performance comparison of the different trajectory planning methods

In this section, the proposed method is compared with the two typical approaches to demonstrate the superiority of the six-degree polynomial based PTP method, as follows:

1) Trapezoidal velocity profile (TVP): a typical motion description method used to trajectory planning in velocity space [41], where the motion process is divided into uniform acceleration, uniform speed, and uniform deceleration. It is mathematically described as follows:

(28)

where v_0 is the initial velocity, and it is set to 0, v_{\text{u}} is the velocity in uniform stage, t_1 is the switching time between uniform acceleration and uniform stage, t_2 is the switching time between uniform stage and uniform deceleration stage, a_1 and a_2 are the accelerations in uniform acceleration stage and uniform deceleration stage, respectively. The hoist machinery and crowd machinery synergistically drive the dipper to generate the mining trajectory. Thus, the velocities of the dipper teeth in the y and z directions are considered, and the optimization variable is set to [t_{y1},t_{y2},a_{y1},t_{\mathit{\text{z}}1},t_{\mathit{\text{z}}2},a_{\mathit{\text{z}}1},t_{\text{f}}], where t_{y1} and t_{\mathit{\text{z}}1} are switching time between uniform acceleration and uniform stage in the y and z directions, respectively, t_{y2} and t_{\mathit{\text{z}}2} are switching time between uniform stage and uniform deceleration stage in the y and z directions, respectively, and a_{y1} and a_{\mathit{\text{z}}1} are accelerations in uniform acceleration stage and uniform deceleration stage in the y and z directions, respectively.

2) Logarithmic spiral (LS): a commonly used method to describe the mining trajectory of the electric shovel [25]. It is characterized as a constant cutting angle and denoted as follows:

(29)\rho (t)={\rho }_0{\mathrm{e}}^{{\theta }_{\text{p}}(t)\cot \delta },

where {\rho }_0 is the initial polar diameter, {\theta }_{\text{p}} is the polar angle, and δ is the cutting angle. The optimization variables are selected as [{\rho }_0,{\theta }_{\text{p}},\delta ].

In comparison, the experimental parameters are still consistent with the previous section. The performance of three different methods, consisting of actual objective function J, loaded material volume V, time t_f, and energy consumption per volume E_per, is listed in Tab.5. Tab.5 shows that the six-degree polynomial obtains a minimal value of the objective function J. In terms of loaded material volume, the six-degree polynomial and LS are comparable, and they are superior to that of TVP. Moreover, the six-degree polynomial yields a slightly better performance in terms of mining time and energy consumption per volume than that of the TVP and LS. Therefore, we can conclude that the mining trajectory planned by the six-degree polynomial yields a better mining performance than TVP and LS under the same working conditions.

Tab.5 Performance comparison with three different trajectory planning methods

Method	J	V/m3	tf/s	Eper/ \text{(kW}\cdot \text{h}\cdot {\text{m}}^{-3})
6-D poly	0.6114	0.1452	13.20	0.1061
TVP	0.6581	0.1245	13.70	0.1124
LS	0.6455	0.1441	12.06	0.1058

Note: 6-D poly presents the abbreviation of six-degree polynomial.

Fig.16 compares the actual motor speed and force information monitored by corresponding sensors during excavation process. Fig.16 and Fig.16 show that the hoist motor speed generated by the six-degree polynomial is lower than the two other methods in the early stage of excavation. On the contrary, the crowd motor speed is higher than TVP and LS in the early stage, ensuring that the dipper is pushed forward as far as possible and excavates more materials. Fig.16 and Fig.16 show the output forces provided by the hoist and crowd motors. Clearly, the hoist force and crowd force generated by the six-degree polynomial are slightly lower than TVP and LS in general, resulting in less energy consumption in the excavation process.

Fig.16 Comparison of the motor speeds and digging forces: (a) hoist motor speed, (b) crowd motor speed, (c) hoist force provided by hoist motor, (d) crowd force provided by crowd motor. 6-D poly: six-degree polynomial.

Full size|PPT slide

6 Conclusions

In this study, a UES is designed for autonomous excavation, and the key robotization methodologies consisting of the material surface reconstruction based on environmental point cloud and optimal excavation trajectory planning are presented. The material surface can be quickly and accurately modeled by the introduction of PRS method in surface reconstruction, in which the modeling accuracy R² can be guaranteed above 0.98. To quickly obtain the optimal excavation trajectory under the current material surface, a PTP excavation trajectory planning method based on six-degree polynomial is developed to improve the mining efficiency and fill factor and to reduce the energy consumption. Experimental results show that the proposed trajectory planning method can calculate the optimal excavation trajectory in real-time. The UES completes the autonomous excavation based on the obtained trajectory. The experiments demonstrate the accuracy of the dynamics modeling and trajectory tracking by comparison of theoretical and practical sensor information. Compared with the existing excavation trajectory planning methods consisting of TVP and LS, the proposed framework tends to be more capable in terms of mining time, fill factor, and energy consumption, indicating considerable potential in autonomous excavation scenarios of the UES.

As a bold attempt to autonomous mining, this study combines point cloud reconstruction with excavation trajectory planning to guide autonomous decision-making and excavation of the UES. However, margins are still available for further improvement. Due to the harsh environment in practical open-pit mining, relying only on point cloud may lead to information loss under extreme conditions, which requires more types of sensors consisting of LiDAR and camera to improve the robustness of environmental perception.

In the future, we will further investigate the performance of UES in more complex practical mining conditions and expand the proposed method to the direction of multisource information fusion. Moreover, we plan to study the cooperation between UES and unmanned mining trucks.

Nomenclature

Abbreviations
GNSS	Global navigation satellite system
IMU	Inertial measurement unit
LS	Logarithmic spiral
MSoE	Maximum sum of evidence
PID	Proportional integral derivative
PLC	Programmable Logic Controller
PRS	Polynomial response surface
PTP	Point to point
RBF	Radial basis functions
TVP	Trapezoidal velocity profile
UES	Unmanned electric shovel
Variables
a1, a2	Acceleration in uniform acceleration and deceleration stages, respectively
ay	Excavation acceleration in the y direction
ay1	Acceleration in uniform acceleration stage and uniform deceleration stage in the y direction
az	Excavation acceleration in the z direction
az1	Acceleration in uniform acceleration stage and uniform deceleration stage in the z direction
c	Polynomial trajectory coefficient
cy6, cz6	Six-degree polynomial coefficients in the y andz directions, respectively
Ci	Constraint in trajectory planning
D	Vandermond matrix
Dxy	Projection area in the horizontal direction when the dipper teeth cut the material surface
Ec	Energy consumption of the crowd machinery
Eh	Energy consumption of the hoist machinery
Eper	Energy consumption per volume
fs	Polynomial function
Fc	Crowd force
Fca	Maximum allowable value of the crowd force
ftr(x, y)	Excavation trajectory
F_{\text{c}max}	Maximum crowd force
F_{\text{h}}	Hoist force
F_{\text{ha}}	Maximum allowable value of the hoist force
F_{\text{h}max}	Maximum hoist force
F_i	Generalized force
F_{\text{n}}	Normal excavation resistance
F_{\text{t}}	Tangential excavation resistance
g	Acceleration of gravity
h_{\text{b}min}	Minimum vertical height of the dipper bottom
h_{\text{mf}}	Material height corresponding to the final position of the excavation trajectory
h_{\epsilon }	Margin height
J	Objective function
J_1	Mining efficiency
J_2	Mining production
J_3	Energy consumption
J_{max}	Upper bound
J_{min}	Lower bound
k	Polynomial order
L	Lagrange function
L_{\text{d}}	Length of the dipper
L_{\text{h}}	Length of the dipper handle
L_{\text{s}}	Loss function
m_0	Mass of the empty dipper
m_{\text{d}}	Total mass of the dipper
m_{\text{h}}	Mass of the dipper handle
m_{\text{m}}	Mass of the loaded material
n	Degree of the polynomial
N	Number of points
p_y	Position of the excavation trajectory in the y direction
p_y(t_{\text{f}})	Final position of the excavation trajectory in the y direction
p_{\mathit{\text{z}}}	Position of the excavation trajectory in the z direction
p_{\mathit{\text{z}}}(t_{\text{f}})	Final position of the excavation trajectory in the z direction
\mathit{P}	Point cloud
P_{\text{ca}}	Maximum allowable value of the crowd power
P_{\text{c}max}	Maximum crowd power
P_{\text{ha}}	Maximum allowable value of the hoist power
P_{\text{h}max}	Maximum hoist power
q_i	Generalized coordinate
r	Stretching length of the dipper handle
r_{\text{a}}	Maximum allowable value of the stretching length of the dipper handle
r_{max}	Maximum stretching length of the dipper handle
\dot{r}(t)	Velocity of the dipper handle
{\dot{r}}_{max}	Maximum velocity of the dipper
{\dot{r}}_{min}	Minimum dipper handle velocity
s	Degree of freedom
t	Time
t_0	Initial time in excavation
t_1	Switching time between uniform acceleration and uniform stage
t_2	Switching time between uniform stage and uniform deceleration stage
t_{\text{f}}	Final time in excavation
t_{y1}	Switching time between uniform acceleration and uniform stage in the y direction
t_{y2}	Switching time between uniform stage and uniform deceleration stage in the y direction
t_{\mathit{\text{z}}1}	Switching time between uniform acceleration and uniform stage in the z direction
t_{\mathit{\text{z}}2}	Switching time between uniform stage and uniform deceleration stage in the z direction
v_0	Initial velocity
v_{\text{ha}}	Maximum allowable velocity of the dipper handle
v_{\text{ra}}	Maximum allowable value of the rope velocity
v_{\text{r}max}	Maximum velocity of the hoist rope
v_{\text{r}min}	Minimum rope velocity
v_{\text{u}}	Velocity in uniform stage
v_y	Excavation velocity in the y direction
v_{\mathit{\text{z}}}	Excavation velocity in the z direction
v_{\text{r}}(t)	Rope velocity
V	Loaded volume
V_{\text{n}}	Nominal load capacity
x	Coordinate of the point in the x direction
x	Coordinate vector of the point cloud in the x direction
y	Coordinate of the point in the y direction
y	Coordinate vector of the point cloud in the y direction
{\mathit{\text{z}}}_i	True value of the sample i
\overline{\mathit{\text{z}}}	Mean value for all samples
\widehat{\mathit{\text{z}}}	Z-direction response variable
{\widehat{\mathit{\text{z}}}}_i	Prediction value of the sample i
\mathit{z}	Coordinate vector of the point cloud in the z direction
\hat{\mathit{z}}	Prediction value of z
\mathit{\beta }	Coefficient column vector
{\beta }_{ij}	Coefficient of the polynomial function
\delta	Cutting angle
\theta	Angle between the vertical direction and the axis of the dipper handle
{\theta }_{\text{p}}	Polar angle
\rho	Material density
{\rho }_0	Initial polar diameter
{\omega }_1, {\omega }_2, {\omega }_3	Weight coefficients
\varpi	Angle between the hoist rope and the dipper handle

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 52075068) and the Science and Technology Major Project of Shanxi Province, China (Grant No. 20191101014).

References

1 Wei B C , Gao F . A method to calculate working capacity space of multi-DOF manipulator and the application in excavating mechanism. Frontiers of Mechanical Engineering, 2012, 7( 2): 109– 119

2 Wei B , Gao F , Chen J , He J , Zhao X . A method for selecting driving system parameters of a new electric shovel’s excavating mechanism with three-DOF. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2011, 225( 11): 2661– 2672

3 Wu J Q , Wang G Q , Bi Q S , Hall R . Digging force and power consumption during robotic excavation of cable shovel: experimental study and DEM simulation. International Journal of Mining, Reclamation and Environment, 2021, 35( 1): 12– 33

4 Awuah-Offei K , Frimpong S . Numerical simulation of cable shovel resistive forces in oil sands excavation. International Journal of Mining, Reclamation and Environment, 2006, 20( 3): 223– 238

5 Stavropoulou M , Xiroudakis G , Exadaktylos G . Analytical model for estimation of digging forces and specific energy of cable shovel. Coupled Systems Mechanics, 2013, 2( 1): 23– 51

6 Rasuli A , Tafazoli S , Dunford W G . Dynamic modeling, parameter identification, and payload estimation of mining cable shovels. In: Proceedings of 2014 IEEE Industry Application Society Annual Meeting. Vancouver: IEEE, 2014, 1– 9

7 Shekhar R C , Maciejowski J M . Surface excavation with model predictive control. In: Proceedings of the 49th IEEE Conference on Decision and Control (CDC). Atlanta: IEEE, 2010, 5239– 5244

8 Awuah-Offei K , Frimpong S . Efficient cable shovel excavation in surface mines. Geotechnical and Geological Engineering, 2011, 29( 1): 19– 26

9 Patnayak S , Tannant D D . Performance monitoring of electric cable shovels. International Journal of Surface Mining, Reclamation and Environment, 2005, 19( 4): 276– 294

10 Frimpong S , Li Y . Stress loading of the cable shovel boom under in-situ digging conditions. Engineering Failure Analysis, 2007, 14( 4): 702– 715

11 Li Y , Frimpong S . Hybrid virtual prototype for analyzing cable shovel component stress. The International Journal of Advanced Manufacturing Technology, 2008, 37( 5–6): 423– 430

12 Frimpong S , Hu Y F . Intelligent cable shovel excavation modeling and simulation. International Journal of Geomechanics, 2008, 8( 1): 2– 10

13 Song X G , Zhang T C , Yuan Y L , Wang X B , Sun W . Multidisciplinary co-design optimization of the structure and control systems for large cable shovel considering cross-disciplinary interaction. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2020, 234( 22): 4353– 4365

14 Osa T , Aizawa M . Deep reinforcement learning with adversarial training for automated excavation using depth images. IEEE Access: Practical Innovations, Open Solutions, 2022, 10 : 4523– 4535

15 Yoshida H , Yoshimoto T , Umino D , Mori N . Practical full automation of excavation and loading for hydraulic excavators in indoor environments. In: Proceedings of 2021 IEEE the 17th International Conference on Automation Science and Engineering (CASE). Lyon: IEEE, 2021, 2153– 2160

16 Zhang L J , Zhao J X , Long P X , Wang L Y , Qian L F , Lu F X , Song X B , Manocha D . An autonomous excavator system for material loading tasks. Science Robotics, 2021, 6( 55): eabc3164

17 Phillips T G Green M E McAree P R. Is it what I think it is? Is it where I think it is? Using point-clouds for diagnostic testing of a digging assembly’s form and pose for an autonomous mining shovel. Journal of Field Robotics, 2016, 33(7): 1013– 1033

18 Zhang T C , Fu T , Song X G , Qu F Z . Multi-objective excavation trajectory optimization for unmanned electric shovels based on pseudospectral method. Automation in Construction, 2022, 136 : 104176

19 Phillips T , Hahn M , McAree R . An evaluation of ranging sensor performance for mining automation applications. In: Proceedings of 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Wollongong: IEEE, 2013, 1284– 1289

20 Phillips T G , Guenther N , McAree P R . When the dust settles: the four behaviors of LiDAR in the presence of fine airborne particulates. Journal of Field Robotics, 2017, 34( 5): 985– 1009

21 Green M E , Ridley A N , McAree P R . Pose verification for autonomous equipment interaction in surface mining. In: Proceedings of 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Wollongong: IEEE, 2013, 1199– 1204

22 D’Adamo T A , Phillips T G , McAree P R . Registration of three-dimensional scanning LiDAR sensors: an evaluation of model-based and model-free methods. Journal of Field Robotics, 2018, 35( 7): 1182– 1200

23 Dunbabin M , Corke P . Autonomous excavation using a rope shovel. Journal of Field Robotics, 2006, 23( 6–7): 379– 394

24 Awuah-Offei K , Frimpong S . Cable shovel digging optimization for energy efficiency. Mechanism and Machine Theory, 2007, 42( 8): 995– 1006

25 Bi Q S , Wang G Q , Wang Y P , Yao Z W , Hall R . Digging trajectory optimization for cable shovel robotic excavation based on a multi-objective genetic algorithm. Energies, 2020, 13( 12): 3118

26 Jud D , Leemann P , Kerscher S , Hutter M . Autonomous free-form trenching using a walking excavator. IEEE Robotics and Automation Letters, 2019, 4( 4): 3208– 3215

27 Son B , Kim C U , Kim C , Lee D . Expert-emulating excavation trajectory planning for autonomous robotic industrial excavator. In: Proceedings of 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Las Vegas: IEEE, 2020, 2656– 2662

28 Lee D , Jang I , Byun J , Seo H , Kim H J . Real-time motion planning of a hydraulic excavator using trajectory optimization and model predictive control. In: Proceedings of 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Prague: IEEE, 2021, 2135– 2142

29 Wang X B , Sun W , Li E , Song X G . Energy-minimum optimization of the intelligent excavating process for large cable shovel through trajectory planning. Structural and Multidisciplinary Optimization, 2018, 58( 5): 2219– 2237

30 Wang X B , Song X G , Sun W . Surrogate based trajectory planning method for an unmanned electric shovel. Mechanism and Machine Theory, 2021, 158 : 104230

31 Nurunnabi A , West G , Belton D . Robust locally weighted regression techniques for ground surface points filtering in mobile laser scanning three dimensional point cloud data. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54( 4): 2181– 2193

32 Holz D , Ichim A E , Tombari F , Rusu R B , Behnke S . Registration with the point cloud library: a modular framework for aligning in 3-D. IEEE Robotics & Automation Magazine, 2015, 22( 4): 110– 124

33 Durovsky F . Point cloud based bin picking: object recognition and pose estimation using region growing segmentation algorithm. Applied Mechanics and Materials, 2015, 791 : 189– 194

34 Jain K , Pannu H S . Autonomic point cloud-based surface reconstruction using SVR. The Imaging Science Journal, 2018, 66( 1): 59– 67

35 Slabanja J , Meden B , Peer P , Jaklič A , Solina F . Segmentation and reconstruction of 3D models from a point cloud with deep neural networks. In: Proceedings of 2018 International Conference on Information and Communication Technology Convergence (ICTC). Jeju: IEEE, 2018, 118– 123

36 Pan R J , Skala V . A two-level approach to implicit surface modeling with compactly supported radial basis functions. Engineering with Computers, 2011, 27( 3): 299– 307

37 Zhao S , Lu T F , Koch B , Hurdsman A . Dynamic modelling of 3D stockpile for life-cycle management through sparse range point clouds. International Journal of Mineral Processing, 2013, 125 : 61– 77

38 Nazemizadeh M , Rahimi H N , Amini Khoiy K . Trajectory planning of mobile robots using indirect solution of optimal control method in generalized point-to-point task. Frontiers of Mechanical Engineering, 2012, 7( 1): 23– 28

39 Powell M J D. A direct search optimization method that models the objective and constraint functions by linear interpolation. In: Gomez S, Hennart J P, eds. Advances in Optimization and Numerical Analysis. Mathematics and Its Applications, vol 275. Dordrecht: Springer, 1994

40 Panda B , Garg A , Jian Z , Heidarzadeh A , Gao L . Characterization of the tensile properties of friction stir welded aluminum alloy joints based on axial force, traverse speed, and rotational speed. Frontiers of Mechanical Engineering, 2016, 11( 3): 289– 298

41 Rossi C , Savino S . Robot trajectory planning by assigning positions and tangential velocities. Robotics and Computer-Integrated Manufacturing, 2013, 29( 1): 139– 156