Fault diagnosis of axial piston pumps with multi-sensor data and convolutional neural network

Abstract

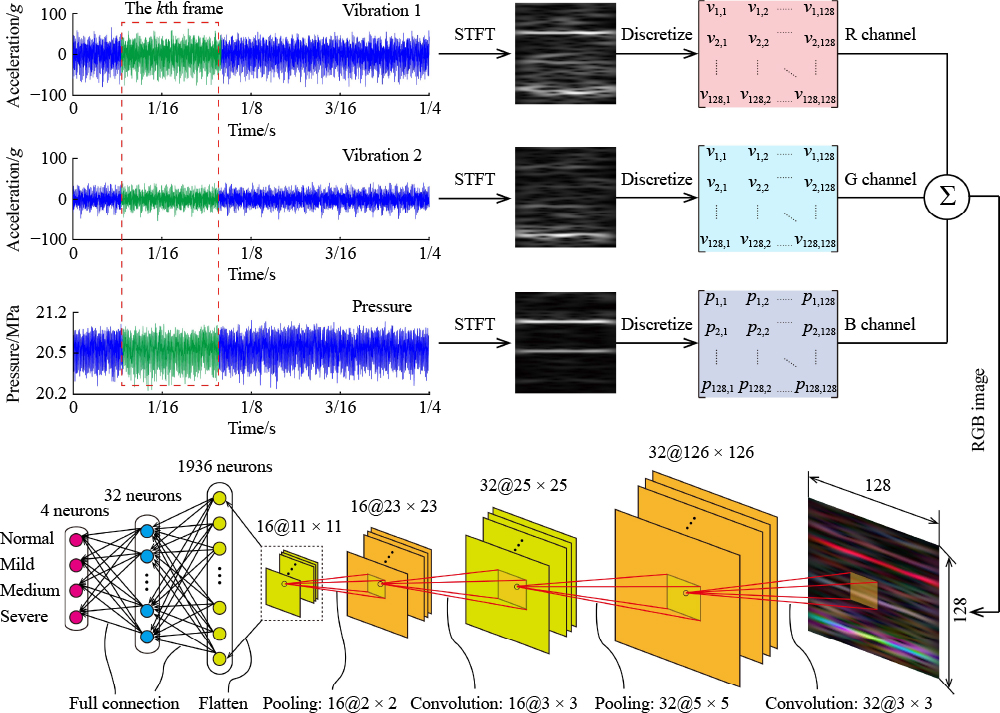
Axial piston pumps have wide applications in hydraulic systems for power transmission. Their condition monitoring and fault diagnosis are essential in ensuring the safety and reliability of the entire hydraulic system. Vibration and discharge pressure signals are two common signals used for the fault diagnosis of axial piston pumps because of their sensitivity to pump health conditions. However, most of the previous fault diagnosis methods only used vibration or pressure signal, and literatures related to multi-sensor data fusion for the pump fault diagnosis are limited. This paper presents an end-to-end multi-sensor data fusion method for the fault diagnosis of axial piston pumps. The vibration and pressure signals under different pump health conditions are fused into RGB images and then recognized by a convolutional neural network. Experiments were performed on an axial piston pump to confirm the effectiveness of the proposed method. Results show that the proposed multi-sensor data fusion method greatly improves the fault diagnosis of axial piston pumps in terms of accuracy and robustness and has better diagnostic performance than other existing diagnosis methods.

Key words： axial piston pump; fault diagnosis; convolutional neural network; multi-sensor data fusion

Nomenclature

Abbreviations
1D	One-dimensional
2D	Two-dimensional
CNN	Convolutional neural network
SNR	Signal-to-noise ratio
STFT	Short-time Fourier transform
Variables
ahw	Feature map element at pixel (h, w) in the pooling window
$A_k^l$	The kth feature map at layer l
${\mathit{B}}_k^l$	Bias of the kth group filter at layer l
c	Index of channels for input feature maps or the group filters
C	Total number of filter channels
f(·)	Activation function
H	Pooling window height
$i^{\prime }$	Height index of element pixels
j	Imaginary unit
$j^{\prime }$	Width index of element pixels
J	Loss function
k	Index of group filters or output feature maps
l	Index of network layers
L	Total layer number
m, n	Indices of discrete sampling points
N	Size of Hanning window
$p_k^{l+1}$	Maximum element in the pooling window
q	The qth class
Q	Total classification number
s	Index of samples
S	Total number of samples
t	Time
x(τ)	Vibration signal
x(s)	The sth sample
${\mathit{X}}_c^{l-1}$	The cth-channel component of the input feature map at layer (l – 1)
${\mathit{X}}_k^l$	The kth output feature map at layer l
y(s)	Predicted label
w(τ), w*(τ)	Window function and its conjugated form
W	Pooling window width
${\mathit{W}}_{c,k}^l$	The cth-channel component of the kth group filter weight at layer l
η	Learning rate
${\mathit{\theta }}^L$	Trainable parameters at the last layer L
θnew, θold	Trainable parameters after and before update, respectively
$\tau$	Time variable of integration
$\omega$	Angular frequency

Acknowledgements

This study was supported by the National Key R&D Program of China (Grant No. 2018YFB1702503), the Open Foundation of the State Key Laboratory of Fluid Power and Mechatronic Systems, China (Grant No. GZKF-202108), the National Postdoctoral Program for Innovative Talents, China (Grant No. BX20200210), the China Postdoctoral Science Foundation (Grant No. 2019M660086), and Shanghai Municipal Science and Technology Major Project, China (Grant No. 2021SHZDZX0102).

References

1 ChaoQ, ZhangJ H, XuB, WangQ N, LyuF, LiK. Integrated slipper retainer mechanism to eliminate slipper wear in high-speed axial piston pumps. Frontiers of Mechanical Engineering, 2022, 17( 1): 1– 13

2 ChaoQ, XuZ, TaoJ F, LiuC L, ZhaiJ. Cavitation in a high-speed aviation axial piston pump over a wide range of fluid temperatures. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2022, 236( 4): 727– 737

3 MaradeyLázaro J G, BorrásPinilla C. Detection and classification of wear fault in axial piston pumps: using ANNs and pressure signals. In: Burgos D A T, Vejar M A, Pozo F, eds. Pattern Recognition Applications in Engineering. Hershey: IGI Global, 2020, 286– 316

4 XiaS Q, ZhangJ H, YeS G, XuB, HuangW D, XiangJ W. A spare support vector machine based fault detection strategy on key lubricating interfaces of axial piston pumps. IEEE Access, 2019, 7 : 178177– 178186

5 LanY, HuJ W, HuangJ H, NiuL K, ZengX H, XiongX Y, WuB. Fault diagnosis on slipper abrasion of axial piston pump based on extreme learning machine. Measurement, 2018, 124 : 378– 385

6 GuoR, ZhaoZ Q, WangT, LiuG H, ZhaoJ Y, GaoD R. Degradation state recognition of piston pump based on ICEEMDAN and XGBoost. Applied Sciences, 2020, 10( 18): 6593

7 KellerN, SciancaleporeA, VaccaA. Demonstrating a condition monitoring process for axial piston pumps with damaged valve plates. International Journal of Fluid Power, 2022, 23( 2): 205– 236

8 WangS H, XiangJ W, ZhongY T, TangH S. A data indicator-based deep belief networks to detect multiple faults in axial piston pumps. Mechanical Systems and Signal Processing, 2018, 112 : 154– 170

9 ChaoQ, TaoJ F, WeiX L, WangY H, MengL H, LiuC L. Cavitation intensity recognition for high-speed axial piston pumps using 1-D convolutional neural networks with multi-channel inputs of vibration signals. Alexandria Engineering Journal, 2020, 59( 6): 4463– 4473

10 ChaoQ, TaoJ F, WeiX L, LiuC L. Identification of cavitation intensity for high-speed aviation hydraulic pumps using 2D convolutional neural networks with an input of RGB-based vibration data. Measurement Science and Technology, 2020, 31( 10): 105102

11 WangS H, XiangJ W. A minimum entropy deconvolution-enhanced convolutional neural networks for fault diagnosis of axial piston pumps. Soft Computing, 2020, 24( 4): 2983– 2997

12 TangS N, YuanS Q, ZhuY, LiG P. An integrated deep learning method towards fault diagnosis of hydraulic axial piston pump. Sensors, 2020, 20( 22): 6576

13 ChaoQ, GaoH H, TaoJ F, WangY H, ZhouJ, LiuC L. Adaptive decision-level fusion strategy for the fault diagnosis of axial piston pumps using multiple channels of vibration signals. Science China Technological Sciences, 2022, 65( 2): 470– 480

14 TangS N, ZhuY, Yuan S Q. Intelligent fault diagnosis of hydraulic piston pump based on deep learning and Bayesian optimization. ISA Transactions, 2022 (in press)

15 TangS N, ZhuY, YuanS Q. A novel adaptive convolutional neural network for fault diagnosis of hydraulic piston pump with acoustic images. Advanced Engineering Informatics, 2022, 52 : 101554

16 LuC Q, WangS P, MakisV. Fault severity recognition of aviation piston pump based on feature extraction of EEMD paving and optimized support vector regression model. Aerospace Science and Technology, 2017, 67 : 105– 117

17 WangY D, ZhuY, WangQ L, YuanS Q, TangS N, ZhengZ J. Effective component extraction for hydraulic pump pressure signal based on fast empirical mode decomposition and relative entropy. AIP Advances, 2020, 10( 7): 075103

18 LuC Q, WangS P, ZhangC. Fault diagnosis of hydraulic piston pumps based on a two-step EMD method and fuzzy C-means clustering. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2016, 230( 16): 2913– 2928

19 YuH, LiH R, LiY L. Vibration signal fusion using improved empirical wavelet transform and variance contribution rate for weak fault detection of hydraulic pumps. ISA Transactions, 2020, 107 : 385– 401

20 YuH, LiH R, LiY L, LiY F. A novel improved full vector spectrum algorithm and its application in multi-sensor data fusion for hydraulic pumps. Measurement, 2019, 133 : 145– 161

21 SafizadehM S, LatifiS K. Using multi-sensor data fusion for vibration fault diagnosis of rolling element bearings by accelerometer and load cell. Information Fusion, 2014, 18 : 1– 8

22 XiaM, LiT, XuL, LiuL Z, de SilvaC W. Fault diagnosis for rotating machinery using multiple sensors and convolutional neural networks. IEEE/ASME Transactions on Mechatronics, 2018, 23( 1): 101– 110

23 WangH Q, LiS, SongL Y, CuiL L. A novel convolutional neural network based fault recognition method via image fusion of multi-vibration-signals. Computers in Industry, 2019, 105 : 182– 190

24 GongW F, ChenH, ZhangZ H, ZhangM L, WangR H, GuanC, WangQ. A novel deep learning method for intelligent fault diagnosis of rotating machinery based on improved CNN-SVM and multichannel data fusion. Sensors, 2019, 19( 7): 1693

25 WangJ J, FuP L, ZhangL B, GaoR X, ZhaoR. Multilevel information fusion for induction motor fault diagnosis. IEEE/ASME Transactions on Mechatronics, 2019, 24( 5): 2139– 2150

26 ChenH P, HuN Q, ChengZ, ZhangL, ZhangY. A deep convolutional neural network based fusion method of two-direction vibration signal data for health state identification of planetary gearboxes. Measurement, 2019, 146 : 268– 278

27 AzamfarM, SinghJ, Bravo-ImazI, LeeJ. Multisensor data fusion for gearbox fault diagnosis using 2-D convolutional neural network and motor current signature analysis. Mechanical Systems and Signal Processing, 2020, 144 : 106861

28 KolarD, LisjakD, PająkM, PavkovićD. Fault diagnosis of rotary machines using deep convolutional neural network with wide three axis vibration signal input. Sensors, 2020, 20( 14): 4017

29 YanX S, SunZ, ZhaoJ J, ShiZ G, ZhangC A. Fault diagnosis of rotating machinery equipped with multiple sensors using space-time fragments. Journal of Sound and Vibration, 2019, 456 : 49– 64

30 ChaoQ, ZhangJ H, XuB, HuangH P, PanM. A review of high-speed electro-hydrostatic actuator pumps in aerospace applications: challenges and solutions. Journal of Mechanical Design, 2019, 141( 5): 050801

31 MaJ M, ChenJ, LiJ, LiQ L, RenC Y. Wear analysis of swash plate/slipper pair of axis piston hydraulic pump. Tribology International, 2015, 90 : 467– 472

32 HuangJ H, YanZ, QuanL, LanY, GaoY S. Characteristics of delivery pressure in the axial piston pump with combination of variable displacement and variable speed. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2015, 229( 7): 599– 613

33 ChaoQ, TaoJ F, LeiJ B, WeiX L, LiuC L, WangY H, MengL H. Fast scaling approach based on cavitation conditions to estimate the speed limitation for axial piston pump design. Frontiers of Mechanical Engineering, 2021, 16( 1): 176– 185

34 ChaconR, IvantysynovaM. Virtual prototyping of axial piston machines: numerical method and experimental validation. Energies, 2019, 12( 9): 1674

35 DahlG E, SainathT N, HintonG E. Improving deep neural networks for LVCSR using rectified linear units and dropout. In: Proceedings of 2013 IEEE International Conference on Acoustics, Speech and Signal Processing. Vancouver: IEEE, 2013, 8609– 8613

36 StankovicL, DakovićM, ThayaparanT. Time–Frequency Signal Analysis with Applications. Boston: Artech House, 2013

37 LeCunY, BottouL, BengioY, HaffnerP. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 1998, 86( 11): 2278– 2324

38 ZhangW, LiC H, PengG L, ChenY H, ZhangZ J. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load. Mechanical Systems and Signal Processing, 2018, 100 : 439– 453

39 LiuX C, ZhouQ C, ZhaoJ, ShenH H, XiongX L. Fault diagnosis of rotating machinery under noisy environment conditions based on a 1-D convolutional autoencoder and 1-D convolutional neural network. Sensors, 2019, 19( 4): 972

40 TangS N, ZhuY, YuanS Q, LiG P. Intelligent diagnosis towards hydraulic axial piston pump using a novel integrated CNN model. Sensors, 2020, 20( 24): 7152

41 JiangW L, WangC Y, ZouJ Y, ZhangS Q. Application of deep learning in fault diagnosis of rotating machinery. Processes, 2021, 9( 6): 919