A zone-layered trimming method for ceramic core of aero-engine blade based on an advanced reconfigurable laser processing system

Abstract

Ceramic structural parts are one of the most widely utilized structural parts in the industry. However, they usually contain defects following the pressing process, such as burrs. Therefore, additional trimming is usually required, despite the deformation challenges and difficulty in positioning. This paper proposes an ultrafast laser processing system for trimming complex ceramic structural parts. Opto-electromechanical cooperative control software is developed to control the laser processing system. The trimming problem of the ceramic cores used in aero engines is studied. The regional registration method is introduced based on the iterative closest point algorithm to register the path extracted from the computer-aided design model with the deformed ceramic core. A zonal and layering processing method for three-dimensional contours on complex surfaces is proposed to generate the working data of high-speed scanning galvanometer and the computer numerical control machine tool, respectively. The results show that the laser system and the method proposed in this paper are suitable for trimming complex non-datum parts such as ceramic cores. Compared with the results of manual trimming, the method proposed in this paper has higher accuracy, efficiency, and yield. The method mentioned above has been used in practical application with satisfactory results.

Key words： ceramic parts trimming; computer-aided laser manufacturing; 3D vision; reconfigurable laser processing system

1 Introduction

Ceramic cores, which are employed to form cavities in the turbine blade, are one of the main components for casting hollow high-performance aircraft engine turbine blades. The surface quality of the ceramic core directly affects the forming process as well as the casting quality of the monocrystalline silicon blade [1]. Ceramic cores are manufactured via pressing and sintering processes. Thus, they usually contain manufacture-related defects such as burrs and blocked holes, as presented in Fig.1. These defects have to be trimmed to meet the requirements of blade casting.

Fig.1 Defects such as burrs and blockage of the ceramic core: (a) turbine blade and ceramic core and (b) burrs and blockage on the ceramic core.

Full size|PPT slide

However, the ceramic material is brittle, the surface is rough, and the contact pressure between the tool and the workpiece is relatively high. Thus, it is often difficult to position and process the ceramic core on the traditional machining systems. Currently, ceramic core trimming relies on manual hand-held diamond abrasive tools or small electric drills, resulting in low efficiency, poor product consistency, and low yield. Laser processing, one of the non-contact processing methods, can be employed to process hard and brittle materials such as glass or single-crystal silicon [2–4]. In recent years, laser processing technology has been rapidly expanding to many industrial application fields, such as laser drilling [5–7], laser-assisted milling [8–10], laser polishing [11–14], and laser surface texturing [15–18]. Although lasers can be used to trim ceramic cores, there are still some key issues that need to be resolved, which are summarized as follows:

1) The surface is rough, and the core is deformed compared to the CAD model, making it impossible to effectively locate by using a fixture and trimming the burrs according to the path generated by the CAD.

2) The trimming profile is a set of complex 3D spatial curves, so an advanced laser processing system with five-axis processing functions and unique processing methods is needed to achieve trimming.

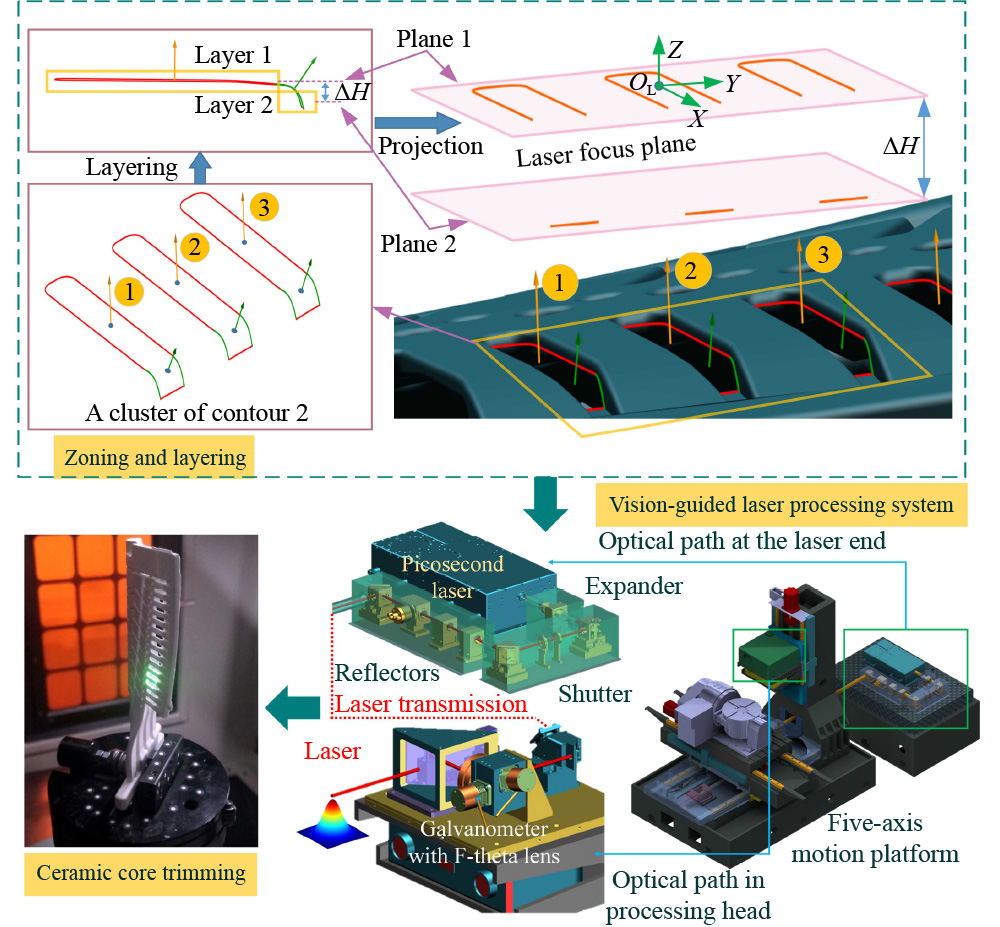
The trimming problem of the ceramic core can be summarized as the laser trimming problem for complex non-datum components. Researches on this problem are rare at present, and similar research mainly focuses on the repair of damaged areas of aero-engine blades [19–23]. Yilmaz et al. [19] investigated the repair methodology of thin-curved blades. In this methodology, non-contact optical measurement equipment is used to obtain 3D data on the surface of the damaged blades. Furthermore, a three-axis machining strategy is employed to remove the excess weld material. Both smoothness and error requirements of the repair path are investigated in depth. Bremer [21] described the importance of automatic blade repair and provided a complete set of blade automatic repair processes, including inspection, weld preparation, welding and reprofiling. In another study [20], the authors detailed reverse engineering technology application in blade repair. Liu et al. [22] investigated in detail the application of additive manufacturing technology for repairing military aircraft components. Gao et al. [23] described 3D non-contact measurement technology in blade repair and equipment integration. Chen et al. [24] proposed a repair method based on non-damaged blades in service at the same time instead of the original design model so that the reconstructed target repairing surface will more accord with the deformation state of damaged blades. However, the research above mainly focuses on the repair of metal components. Compared with ceramic cores, the repair of metal components such as blades focuses on the reconstruction of the damaged part of the blade, and rarely considers the deformation of blades, and there is no positioning problem. At the same time, most of the utilized processing systems are traditional cutting machine tools.

For the problem that the trimming path extracted by the computer-aided design (CAD) model cannot be used due to the core’s deformation, the laboratory researchers have proposed a corresponding solution. Based on the iterative closest point (ICP) registration algorithm and the sub-regional operation of the CAD model and the scanned point cloud model, Hou et al. [25] realized the registration of CAD extracted path and deformed ceramic core. There are many similar kinds of research [26–31] on estimating the spatial pose of objects or matching edges based on the point cloud registration algorithm. Fan et al. [26] pointed out that edges are more common than feature points or feature planes, so edges can be used to register point clouds with CAD models. Vock et al. [27] proposed a sampling strategy with hypothesis validation to drastically reduce runtime. They demonstrated that the point cloud-based pose estimation was helpful for fast matching. Xie et al. [30] proposed an iterative variance-minimization matching method to address measured points that have measuring defects. Furthermore, a distance based on point to tangent distance and first-order point-to-point distance is presented to construct the objective function to speed up convergence. The results show that the method has excellent stability in dealing with measured points with measuring defects. Li et al. [31] proposed a new partial shape matching method via constructing an objective function considering the requirements associated with different grinding allowances. In addition to the matching method, Xiao et al. [32] proposed a tool path generation method directly with point clouds without surface fitting. Machining areas could be recognized from the entire blade model by splitting the point cloud and analyzing geometric parameters of points. The cutter location point is generated by extending on the normal vector direction of the corresponding point.

In addition to pose measurement and path generation problems, advanced laser processing systems are also essential for the laser trimming of complex components. Nowadays, there are many studies on the function expansion of the laser processing system. Such investigations aim to achieve higher equipment functions utilized in special material processing, composite processing, and complex component processing. Many researchers [33–35] have conducted investigations in this field. Erkorkmaz et al. [33] introduced an advanced five-axis laser drilling system to achieve flying drilling of groups of holes on curved surfaces. Jiang et al. [34] introduced a laser lithography system for surface texturing. In addition, the authors achieved texture marking on large-scale surfaces and proposed a new laser layered lithography method for large-scale surface texturing. Cuccolini et al. [35] introduced a five-axis laser milling system composed of a two-dimensional (2D) high-speed galvanometer and a five-axis computer numerical control (CNC) machine tool. This milling system can achieve pattern-like laser milling on complex surfaces.

Aiming at the trimming problem of the ceramic core, an advanced ultrafast laser processing system is developed in this paper. A laser processing head with a high-speed scanning galvanometer inside is installed on a conventional five-axis CNC machine tool. In order to scan the clamped deformed ceramic core to obtain the point cloud model and achieve registration of CAD extracted path and deformed ceramic core, a stereo vision measuring device is integrated within the system. An opto-electromechanical cooperative control (OEMCC) software is developed to realize the collaborative work of the CNC machine tool, laser, galvanometer and stereo vision measuring device. A zonal and layering processing algorithm for contour clusters on freeform surfaces is proposed to deal with the complex spatial path. The algorithm generates the processing data of both the high-speed scanning galvanometer and the CNC machine tool.

The content of this paper is arranged as follows. In Section 2, the zonal and layering processing algorithm is introduced in detail. In Section 3, the hardware and software of the laser system are introduced, and the trimming process of the ceramic core is given. In Section 4, the experiments and the results of the ceramic core trimming are presented. Finally, the conclusions are made in Section 5.

2 Laser zone-layered trimming method for surface contour cluster

2.1 Principle of the laser layering process

Due to the 3D processing capability of the laser focal depth, the 3D contours can be layer-processed by a 2D laser galvanometer [34]. According to the energy distribution characteristics in the proximity of the laser beam focus, the principle of 3D contour layering processing is provided. Following the focus of the laser beam via field lens, the energy distribution near the focus can be expressed as Eq. (1) [36]:

(1)I(r ,\mathit{\text{z}})=I_0\cdot \frac{w_0}{w(\mathit{\text{z}})}\cdot \exp \left(\frac{-2r^2}{w{(\mathit{\text{z}})}^2}\right),

where r is the laser spot radius, I_0 is the energy density at the center of the spot, which can be expressed by the laser power and the spot radius at the focal, w_0 is the radius of the laser beam at the waist and w(\mathit{\text{z}}) is the radius at various positions along the optical axis, and z represents the distance to the center of the focus along the optical axis. Parameters I_0 and w(\mathit{\text{z}}) can be expressed as Eqs. (2)‒(6) [36]:

(2)I_0=\frac{2E}{\text{π}{w}_0^2},

(3)w(\mathit{\text{z}})=w_0\cdot {\left(1+{\left(\frac{\mathit{\text{z}}}{{\mathit{\text{z}}}_{\text{R}}}\right)}^2\right)}^{1/2},

(4)E=P/\phantom{Ph}h,

(5){\mathit{\text{z}}}_{\text{R}} =\frac{\text{π}{w}_0^2}{\lambda },

(6)w_0=\frac{4M_{}^2\lambda f}{\text{π}D},

where parameter P represents the laser power, h is the repetition frequency, E is the single pulse energy, \lambda is the laser wavelength, f is the focal length of the field lens, M² is the mode parameter that characterizes the beam quality and the value is 1.1, D is the diameter of the laser beam, and {\mathit{\text{z}}}_{\text{R}} is the Rayleigh length. In this research, a picosecond laser with a power of 53.59 W, a repetition frequency of 250 kHz, and a wavelength of 532 nm is used for ceramic core trimming, an f-theta lens with an effective focal length of 259.4 mm is used for laser focus. The spot radius w_0 at the focal plane can be obtained from Eq. (6) after the experimentally measured beam diameter D. The measurement results of the beam quality at the entrance of the field lens are shown in Fig.2. The ellipticity of the spot is 89.5%. The minor ellipse diameter is 4.468 mm, and the major ellipse diameter is 4.994 mm. The beam diameter D takes the average of the minor and the major ellipse diameters, the value is 4.7313 mm. Then the relevant laser parameters can be calculated by Eqs. (1)‒(6). The single pulse energy E = 214.36 μJ, the Rayleigh length {\mathit{\text{z}}}_{\text{R}}=4.994 mm, the spot radius w_0= 20.4 μm, and the energy density I_0=32.724\text{J/c}{\text{m}}^{\text{2}}.

Fig.2 Laser beam quality measurement: (a) measuring device and (b) beam quality.

Full size|PPT slide

The focus energy distribution is depicted in Fig.3, where the energy density I_0 at the focal (z = 0) is 32.7248 J/cm². The distribution of laser energy on the focal plane at various positions near the focus is shown in Fig.3(a). The variation of the maximum energy density near the focus is presented in Fig.3(b). It can be observed that the attenuation of the maximum energy density increases with the increase in distance from the focus.

Fig.3 Laser energy distribution near the laser focus (a) for different radii on the focal plane near the focus and (b) maximum energy density at different locations.

Full size|PPT slide

According to Fig.3, the variety of laser energy density can be ignored within a specific range near the focus. The laser energy density within this range can meet the processing requirements, so the range is defined as laser focus processing length (LPL) [34]. The size of LPL is related to the energy density that meets the processing requirements. For example, if an energy density higher than 97% of the maximum energy density I_0 can meet the processing requirements, the value z can reach 0.4 mm. Therefore, even if a scanning galvanometer is often employed as a 2D galvanometer in practical applications, the laser has 3D processing ability, which is the basis of layered processing.

2.2 Theoretical basis for laser zone trimming of ceramic core contour clusters

It is challenging to ensure that the incident direction of the laser is consistent with the ideal direction during the actual processing when processing the contours of the curved surface. Generally, there is an angle between the direction of the optical axis and the ideal processing direction of the contour. As shown in Fig.4, this angle is defined as the incident angle of the laser, and the tilt of the optical axis will affect the shape and size of the spot near the laser focus, which in turn affects the line width of laser engraving. Therefore, to ensure that the size of the laser engraving is within the allowable range of the design requirements, the range of the laser incident angle needs to be limited.

Fig.4 Effect of laser incident angle on the shape and size of the spot.

Full size|PPT slide

Generally, the energy distribution of the laser beam can be described by Gaussian distribution. In the case of unbiased incidence, the laser spot radius r can be expressed as Eq. (7) [37]:

(7)r_{}^2=\frac{w_0^2}{2}\cdot \ln \frac{I_0}{I_{\text{th}}},

where the parameter I_{\text{th}} represents the ablation threshold of the material. When the incident angle of the laser is \theta, the changes of the laser spot size is as shown in Fig.5. The laser spot on the curved surface is approximately an ellipse, and the spot size can be further expressed as Eq. (8) [38]:

Fig.5 Change of the laser spot size with the angle of incidence: (a) r_{min}/r and (b) r_{max}/r.

Full size|PPT slide

(8)\{\begin{array}{c}{I}_{\text{θ}}=\frac{\text{2}E\cos \theta }{\text{π}{w}_0^2},\\ r_{min}^2=\frac{w_0^2}{2}\cdot \ln \frac{I_{\text{θ}}}{I_{\text{th}}},\\ r_{max}^2=\frac{w_0^2}{2{\cos }_{}^2\theta }\cdot \ln \frac{I_{\text{θ}}}{I_{\text{th}}},\end{array}

where r_{min} and r_{max} respectively represent the radius size along the ellipse’s minor axis and major axis. When the material and laser parameters are fixed, the change rate of the laser spot size with the angle of incidence is shown in Fig.5.

It can be observed in Fig.5 that when the laser incident angle is less than a certain angle, the change rate of the laser spot size is close to 1, that is, the laser spot size is approximately unchanged. For example, when the value I_0/\phantom{I_0{I}_{\text{th}}}{I}_{\text{th}} is 2, and the incident angle is 5°, the change rates of the minor and major semi-axes of the spot are 99.72% and 100.11%, respectively. With the laser incidence angle increasing, the change rate will change drastically, so in actual processing, the incident angle of the laser should be limited to a specific range.

In order to explain the influence of the incidence angle on the line width, the laser grooving experiment under different incidence angles is designed. The experimental device is shown in Fig.6. The laser processing head is configured on a five-axis motion platform, and the silicon wafer is clamped by the plane fixture. The rotation of the five-axis motion platform is used to realize the laser grooving with different incident angles.

Fig.6 Grooving experiment device under different laser incident angles: (a) experimental equipment and (b) experimental material.

Full size|PPT slide

It is necessary to find the position of the laser focus before grooving. For this purpose, an experiment of finding the focus is carried out. First, the five-axis motion platform moves along the Y-axis and scans a groove on the silicon wafer with a galvanometer at a certain distance. The change of the groove width near the focus is shown in Fig.7. When the coordinate of the Y-axis is ‒155.16, the width of the groove is the smallest, which is 47 μm. Take this position as the focus position under the current clamping condition.

Fig.7 Width of the groove near the focus.

Full size|PPT slide

Engrave the first groove with the focus position, then rotate the turntable, and use the laser with different incident angles to engrave the groove. The groove width is shown in Fig.8. It can be seen from the measurement data that when the incident angle is less than 5°, the groove width of the main ablation zone changes little, which is consistent with the results given in Fig.5. Therefore, a specific incident angle can be allowed in actual processing, which is also the basis of the zonal laser processing of the surface contours.

Fig.8 Width of the groove at different incidence angles under the microscope 1000 times magnification: (a) \theta = 0^{\circ }, (b) \theta =1^{\circ }, (c) \theta =2^{\circ }, (d) \theta =3^{\circ }, (e) \theta =4^{\circ }, and (f) \theta =5^{\circ }.

Full size|PPT slide

2.3 Laser zone-layered trimming process for ceramic core trimming

Typically, the position coordinates and the normal vectors of the contours can be extracted by computer-aided manufacturing (CAM) software and the corresponding CAD models. This information enables the pre-processing of the ceramic core trimming path. The geometric information of the surface contours is shown in Fig.9, including the contour position data and the contour feature vectors. These contours can be divided into three types: The first type is a cluster of circular contours on the curved surface, while the second and the third type are two parts of the same strip contour. The reason for dividing a complete strip contour into two smaller parts with corresponding feature vectors is that the direction of the feature vectors should be more conducive to the layering operation.

Fig.9 Edges of the ceramic core designated for trimming.

Full size|PPT slide

In Fig.10, the extracted contour clusters of the ceramic core designated for trimming and the corresponding feature vectors are presented. There are a total of 60 feature vectors corresponding to 60 contours. The corresponding data is provided in detail in Electronic Supplementary Materials. The maximum angle between the feature vectors can be calculated for each type of contour. The maximum included angle of the feature vectors in area 1 is 13.9697°. The maximum included angle of the feature vectors in area 2 is 15.82°. And the maximum included angle of the feature vectors in area 3 is 13.03°. Section 2.2 shows that when the laser incident angle is relatively small, the line width of laser engraving is basically the same. For a higher trimming quality, the maximum incident angle is limited to 5°, and the contours in areas 1‒3 are partitioned. The maximum incident angle between the feature vectors of each cluster after the partition is less than 5°.

Fig.10 Contour clusters extracted by CAM software of the ceramic core designated for trimming.

Full size|PPT slide

2.4 Partitioning method of surface contour clusters based on k-means clustering

In order to improve the processing efficiency of surface contours with similar features, a partition method based on the k-means clustering algorithm is presented. This method groups the contours with similar machining characteristics. First, the position data and feature vectors of the trimming contours are extracted via CAM software. The feature vector is defined as the ideal direction of the laser axis when the contours are trimmed, which is manually specified according to the contour characteristics. Then, the k-means clustering algorithm is used to cluster these contours.

The k-means clustering algorithm is an iterative clustering algorithm that uses distance as a similarity measure. The algorithm sets the number of clusters k in advance, and the clustering center is obtained based on the sample average within the cluster. The algorithm takes the error square sum function as the objective function, and the objective function minimization criterion as the basis for evaluating whether the clustering converges. In this paper, the contour feature vectors are used as the clustering data, and the objective function (J) can be written as Eq. (9):

(9)J=\sum _{j=1}^k\sum _{i=1}^n{\Vert {\mathit{x}}_i^{(j)}-{\mathit{c}}_j\Vert }^2,

where n is the number of feature vectors, k is the preset number of categories, and {\mathit{x}}_i^{(j)}(x_i,y_i,z_i,u_i,v_i,w_i) is the six-dimensional data representing the feature vector, {\mathit{c}}_j is the coordinate of the cluster center. For the ceramic core used in this paper, n is 60. Since the data representing the geometric positions and the feature vectors have different scales, position data is normalized to obtain a more accurate clustering result. The essence of normalization is to assign data weights in different dimensions and to improve the clustering effects by adjusting those weights. Thus, the clustering effects under various weights can be further studied. In this paper, the clustering result via normalization operations is achieved. The formula for normalization is shown in Eq. (10):

(10)\{\begin{array}{c}{\hat{x}}_i=x_i/\phantom{x_i{x}_{max}}{x}_{max},\\ {\hat{y}}_i=y_i/\phantom{y_i{y}_{max}}{y}_{max},\\ {\widehat{\mathit{\text{z}}}}_i={\mathit{\text{z}}}_i/\phantom{{\mathit{\text{z}}}_i{\mathit{\text{z}}}_{max}}{\mathit{\text{z}}}_{max},\end{array}

where x_{max}, y_{max}, and {\mathit{\text{z}}}_{max} represent the maximum values of the feature vector data in the X-, Y-, and Z-axis directions, respectively, and {\hat{x}}_i, {\hat{y}}_i, and {\widehat{\mathit{\text{z}}}}_i represent normalized data. The normalized feature vector data is expressed as {\hat{\mathit{x}}}_i({\hat{x}}_i,{\hat{y}}_i,{\widehat{\mathit{\text{z}}}}_i, u_i,v_i,w_i).

For the k-means clustering, the desired result is that contours with close distances and similar feature vectors are grouped into one category, and the contours in the same category meet the requirement that the maximum included angle between feature vectors is less than 5°. Since areas 1‒3 have their characteristics, and the maximum angles are all greater than 5°, each area must be divided into at least two regions, that is, the value k must be greater than 6. Through verification, when k is equal to 10, the ideal clustering result can be obtained. The normalized clustering result is shown in Fig.11(a), and the non-normalized clustering effect is shown in Fig.11(b).

Fig.11 k-means clustering results: (a) normalized processing; (b) non-normalized processing.

Full size|PPT slide

According to Fig.11, when the clustering data is not normalized, the clustering results tend to be based on the position data. It is due to the weight of the feature vector data being relatively insignificant compared to the weight of the position data in the objective function. As a result, the partition effect of the contour cluster is incorrect. However, the contour cluster can be correctly classified following the normalization process. In Tab.1, the clustering centers and the maximum included angles between the feature vectors in each category are shown. All included angles are less than 5°.

Tab.1 Clustering centers after k-means clustering

Cluster number	Feature vector of cluster (x, y, z, u, v, w)	Included angles/(° )
1	(18.900, 13.328, 91.963, 0.980, 0.002, 0.187)	0.7926
2	(20.407, 9.027, 55.203, 0.752, ‒0.644, 0.136)	2.1245
3	(14.876, 4.870, 62.983, 0.607, ‒0.788, 0.092)	2.6773
4	(13.510, 6.862, 90.157, 0.665, ‒0.742, 0.082)	3.1366
5	(15.849, 3.973, 49.748, 0.559, ‒0.822, 0.104)	0.8989
6	(16.909, 10.216, 90.34, 0.780, ‒0.617, 0.100)	0.5320
7	(22.774, 12.273, 56.966, 0.994, ‒0.044, 0.098)	1.4632
8	(14.129, 5.896, 76.977, 0.647, ‒0.756, 0.088)	3.0762
9	(18.472, 9.572, 72.676, 0.770, ‒0.626, 0.116)	1.3031
10	(20.952, 13.396, 76.144, 0.991, ‒0.010, 0.127)	2.8984

2.5 3D contour layering algorithm and processing path generation

The clustering results of the ceramic core contours designated for trimming are provided in Section 2.4. In this paper, the 5 + 2 axis processing method is employed to trim the ceramic core. In other words, positioning is done via the five-axis machine tool, while simultaneously scanning with 2D high-speed galvanometer. Thus, it is necessary to further process the clustered 3D contours to meet the processing requirements of the 2D galvanometer. The specific steps are: (1) transformation of the contour data corresponding to the same cluster from the workpiece coordinate system (WCS) to the local coordinate system (LCS), (2) the layering operation of the contour data, and (3) the projection transformation from 3D data to 2D data. After clustering, the vector direction of the clustering center corresponds to the positioning direction of the five-axis machine tool during processing. In other words, it corresponds to the direction of the laser beam, i.e., the Z-axis direction in LCS, as demonstrated in Fig.12. The contour data is transformed from the WCS to the LCS. The contours in the LCS can be obtained for further layering and projection operations.

Fig.12 Schematic diagram of WCS and LCS.

Full size|PPT slide

The coordinate transformation relationship between WCS and LCS can be expressed as Eq. (11):

(11){\mathit{x}}_{\text{L}}^{(i)}={\mathit{H}}^{(i)}\cdot {\mathit{x}}_{\text{W}}^{(i)},

where parameter {\mathit{x}}_{\text{W}}^{(i)} represents the data of the ith cluster in WCS, {\mathit{x}}_{\text{L}}^{(i)} represents the data in LCS after the coordinate transformation of {\mathit{x}}_{\text{W}}^{(i)}, and {\mathit{H}}^{(i)} represents the transformation matrix from WCS O_{\text{W}} to LCS O_{\text{L}}^{(i)}. Here, i represents the index of the contour cluster.

The contour point data in the LCS can be determined by Eq. (11). {\mathit{X}}_{\text{L}}^{(i)}, {\mathit{Y}}_{\text{L}}^{(i)}, and {\mathit{Z}}_{\text{L}}^{(i)} represent the unit vector along the coordinate axis in the ith LCS. Then {\mathit{X}}_{\text{L}}^{(i)}, {\mathit{Y}}_{\text{L}}^{(i)}, and {\mathit{Z}}_{\text{L}}^{(i)} are defined as follows: {\mathit{Z}}_{\text{L}}^{(i)} is the feature vector of the cluster after contour clustering; {\mathit{Y}}_{\text{L}}^{(i)} is determined as the difference between the unit vector {\mathit{V}}_{\text{WZ}} in the Z-axis direction in WCS and the projection {\mathit{V}}_{\text{WZ}} in the Z-axis direction in LCS, as shown in Fig.12. The parameter {\mathit{X}}_{\text{L}}^{(i)} can be determined by the cross product of {\mathit{Y}}_{\text{L}}^{(i)} and {\mathit{Z}}_{\text{L}}^{(i)}, as shown in Eq. (12):

(12)\begin{array}{rl}& {\mathit{Y}}_{\text{L}}^{(i)}={\mathit{V}}_{\text{WZ}}-{\mathit{V}}_{\text{WZ}}\cdot {\mathit{Z}}_{\text{L}}^{(i)}\cdot {\mathit{Z}}_{\text{L}}^{(i)},\\ & {\mathit{Y}}_{\text{L}}^{(i)}={\mathit{Y}}_{\text{L}}^{(i)}/\phantom{{\mathit{Y}}_{\text{L}}^{(i)}{\Vert ({\mathit{Y}}_{\text{L}}^{(i)})\Vert }_2}{\Vert ({\mathit{Y}}_{\text{L}}^{(i)})\Vert }_2,\\ & {\mathit{X}}_{\text{L}}^{(i)}={\mathit{Z}}_{\text{L}}^{(i)}\times {\mathit{Y}}_{\text{L}}^{(i)},\\ & i=1,2,...,10.\end{array}

The LCS calculation results of some contour clusters are shown in Fig.13, such as contour cluster 2, contour cluster 8, and contour cluster 10. The results of the LCS defined in the above manner are satisfactory.

Fig.13 LCS results of the contour cluster.

Full size|PPT slide

The value of the unit vectors {\mathit{X}}_{\text{L}}^{(i)}, {\mathit{Y}}_{\text{L}}^{(i)}, and {\mathit{Z}}_{\text{L}}^{(i)} can be obtained via Eq. (12). Then, the transformation matrix {\mathit{H}}^{(i)}(i=1 ,2,... ,k) can be obtained via Eq. (13). The contour data in the WCS can be converted to the LCS by applying Eq. (11).

(13){\mathit{I}}_{4\times 4}= {\mathit{H}}^{(i)}\cdot \left[\begin{array}{cccc}\begin{array}{c}{\mathit{X}}_{\text{L}}^{(i)}\\ 0\end{array}& \begin{array}{c}{\mathit{Y}}_{\text{L}}^{(i)}\\ 0\end{array}& \begin{array}{c}{\mathit{Z}}_{\text{L}}^{(i)}\\ 0\end{array}& \begin{array}{c}{\mathit{O}}_{\text{WL}}^{(i)}\\ 1\end{array}\end{array}\right],

where {\mathit{O}}_{\text{WL}}^{(i)} represents the coordinate of the coordinate origin O_{\text{L}}^{(i)} of LCS in WCS O_{\text{W}}. After the contour data is transformed to LCS, layering and projection operations are required, as shown in Fig.14. With {\mathit{Z}}_{\text{L}}^{(i)} being the direction of the Z-axis for LCS O_{\text{L}}^{(i)} and simultaneously the direction of the contour layering, the layering operation can be executed based on the Z-axis coordinates of the data.

Fig.14 Schematic representation of layering and projection of the contour cluster: (a) Contour 2, (b) Contour 3, and (c) Contour 1.

Full size|PPT slide

First, the maximum and minimum coordinates {\mathit{\text{z}}}_{\text{max}} and {\mathit{\text{z}}}_{\text{min}} of the points in the current layering are obtained. Then, the contour data is divided into several layers along the {\mathit{Z}}_{\text{L}}^{(i)} direction with \mathrm{\Delta }H interval. When finished, the contours of each layer are still represented as 3D data. Since the galvanometer is 2D, it is necessary to project the 3D data in each layer along the {\mathit{Z}}_{\text{L}}^{(i)} direction. The 2D projected contour data required for the galvanometer can be obtained by this means. As previously mentioned, {\mathit{Z}}_{\text{L}}^{(i)} is the direction of Z-axis for LCS. Thus, the coordinates x and y in each layer can be extracted to obtain the projection data. The layering and projection results of clusters 2, 8, and 10 are shown in Fig.15, where the 3D data after layering processing are shown in Fig.15(a), 15(c) and 15(e), and the 2D contour data obtained after projection operation on the layered data in LCS are shown in Fig.15(b), 15(d) and 15(f), which can be used as input data of 2D galvanometer.

Fig.15 Layering and projection results of the contour clusters in LCS: (a) 3D data after layering of cluster 2, (b) 2D projection data in LCS of cluster 2, (c) 3D data after layering of cluster 10, (d) 2D projection data in LCS of cluster 10, (e) 3D data after layering of cluster 8, and (f) 2D projection data in LCS of cluster 8.

Full size|PPT slide

The positioning data of the five-axis machine tool corresponding to each layer can be obtained in the following way. Assuming that the clustering center of the ith cluster is expressed as {\mathit{C}}^{(i)}({\mathit{O}}_{\text{WL}}^{(i)}, {\mathit{Z}}_{\text{L}}^{(i)}), i=1,2,\dots ,k, then the position data of the five-axis machine tool corresponding to each layer can be calculated by Eq. (14):

(14)\begin{array}{rl}& N_{\text{layer}}=\text{floor}\left(\left({\mathit{\text{z}}}_{\text{max}}-{\mathit{\text{z}}}_{\text{min}}\right)/\phantom{\left({\mathit{\text{z}}}_{\text{max}}-{\mathit{\text{z}}}_{\text{min}}\right)\mathrm{\Delta }H}\mathrm{\Delta }H\right)+1,\\ & {\mathit{P}}_1^{(i)}={\mathit{O}}_{\text{WL}}^{(i)}+\left({\mathit{\text{z}}}_{\text{max}}-\mathrm{\Delta }H/\phantom{\mathrm{\Delta }H2}2\right)\cdot {\mathit{Z}}_{\text{L}}^{(i)},\\ & {\mathit{P}}_m^{(i)}={\mathit{P}}_1^{(i)}-\left(m-1\right)\cdot \mathrm{\Delta }H\cdot {\mathit{Z}}_{\text{L}}^{(i)}\text{,}\\ & m=2,3,...,N_{\text{layer}},\end{array}

where the function \text{floor}(x) represents the downward rounding of the variable x, N_{\text{layer}} is the layer number of the current cluster, {\mathit{P}}_m^{(i)} represents the positioning coordinates of the mth layer of the ith contour cluster, and \mathrm{\Delta } H is the layering distance, the value is 0.3 mm.

3 Process and control of ceramic core trimming

Galvanometer scanning and machine tool positioning data can be obtained by layering and projecting the 3D contours. The five-axis ultra-fast laser processing system employed within this paper is shown in Fig.16. The system is integrated with a high-precision five-axis motion platform, a 2D scanning galvanometer, an ultra-fast picosecond laser and a 3D structured light vision measurement module. The five-axis motion platform, the scanning galvanometer and the 3D visual scanner are high-precision equipment and instruments. The positioning accuracy and repeat positioning accuracy of the linear axes of the five-axis motion platform are higher than 5 μm, and the rotating axes are higher than 3″. The repeatability accuracy of the scanning galvanometer is higher than 1 μrad. The measurement accuracy of the 3D scanner is 15‒8 μm.

Fig.16 Five-axis ultrafast laser processing system.

Full size|PPT slide

In Fig.17, the hardware integration scheme of the system is shown. The industrial computer, visual measurement computer, five-axis numerical control system and scanning galvanometer are connected through an Ethernet switch, and communication and data transmission between them is realized based on socket communication technology. The laser is connected with industrial control computer and numerical control system through RS232 serial communication technology. The components above are mutually combined through the OEMCC software. The software is developed via C# language, using WinForm interface library, OpenTK graphics display library, and point cloud processing library. During ceramic core trimming, the point cloud model of the ceramic core is first obtained via a 3D vision measurement device. Then, the standard template trajectory exported by CAM is registered with the actual point cloud model through the registration algorithm to obtain the registered 3D trajectory. According to the contour feature vectors, the contours are clustered, layered and projected to machine tool positioning data as well as the galvanometer scanning data. The ceramic core trimming process is completed by the OEMCC software. The specifics of the process are shown in Fig.18.

Fig.17 Hardware integration scheme of the five-axis ultra-fast laser processing system.

Full size|PPT slide

Fig.18 Ceramic core trimming process.

Full size|PPT slide

The direction of the optical axis for machine tool positioning is the direction of the feature vector at the center of the ith cluster. In actual processing, when the machine tool locates the corresponding position {\mathit{P}}_m^{(i)} of a specific layer of data, the high-speed galvanometer is used to scan the contours of the layer. Then the machine tool is located to the position of the next layer, and the galvanometer completes the scanning of the contours in the current layer again. After the contours of all layers in the current region have been scanned, the contour processing of the following area is performed.

4 Experimental validation

In this paper, online trimming of the ceramic core is achieved. Following the clamping of the ceramic core, the point cloud model is obtained via a stereo vision measuring device. The trimming trajectory following the position correction is obtained via the ICP registration algorithm, which registers the template trajectory and the point cloud model. The registration process between CAD extracted trajectory and the edges to be trimmed of the measured point cloud is shown in Fig.19. Firstly, the template trajectory is extracted from the CAD model. Then, taking the points of the CAD model as the source point cloud and the measured point cloud of the ceramic core as the target point cloud, the coarse registration is carried out based on the ICP registration algorithm. The template trajectory is transformed with the obtained transformation matrix to realize the rough registration between the template trajectory and the edges of the measured point cloud. Then, taking the template trajectory points as the reference points, the point cloud data is clipped within a specific range of the reference points to obtain the sub-point clouds near the reference points in the source point cloud and the target point cloud, respectively. These sub-point clouds represent the feature contour on the ceramic core. The ceramic core is deformed compared with the standard CAD model, the coarse registration cannot achieve the complete alignment between the template trajectory and the edges to be trimmed, so it is necessary to further fine registration based on sub-point clouds. The registration in this step is based on the scale ICP registration algorithm, that is, the point cloud registration algorithm with scale scaling. The accurate registration of template trajectory and trimming edges can be realized through the fine registration. Finally, the fine registration operation is carried out for all sub-point clouds to obtain the modified trajectory that can be used for practical ceramic core trimming.

Fig.19 Registration process between CAD extracted trajectory and the edges of the measured point cloud.

Full size|PPT slide

The detailed process is shown in Ref. [25]. The visual ceramic core measurement is shown in Fig.20(a). The visual measurement system is installed on the five-axis motion platform to measure the ceramic core from various angles, thus generating the point cloud model as shown in Fig.20(b). Template trajectory results before and after the registration are depicted in Fig.21. It can be observed that the post-registration modified trajectory is well aligned with the ceramic core edges. After obtaining the registered trajectory, the trajectory is partitioned and layered according to the method proposed in this paper. Both scanning data of the high-speed scanning galvanometer and the movement path data of the five-axis motion platform are obtained.

Fig.20 Online measurement of the ceramic core via stereo vision: (a) online measurement and (b) point cloud model.

Full size|PPT slide

Fig.21 Template trajectory registration: (a) before registration and (b) after registration.

Full size|PPT slide

In the experiment, the picosecond laser is used. The output laser wavelength is 532 nm, the repetition frequency is 1 Hz‒2 MHz, the maximum output power is 60 W, the maximum single pulse energy is 30 μJ, the pulse width is 10 ps, and the beam quality is equal to M² = 1.1. After a triple beam expander expands the laser beam, it is transmitted through a series of reflectors, a galvanometer and a field lens to focus on the edge of the ceramic core designated for trimming. The optical system is shown in Fig.22.

Fig.22 Optical system: (a) laser side and (b) laser processing head side.

Full size|PPT slide

Laser trajectory during ceramic core trimming is shown in Fig.23. The laser scanning trajectory after layered processing of the contour cluster 2 is shown in Fig.23(a). The laser scanning trajectory of the contour cluster 8 is shown in Fig.23(c), and the laser scanning trajectory of the contour cluster 10 is shown in Fig.23(b). The results before and after ceramic core trimming are shown in Fig.24. There are defects such as burrs and hole blockages in the characteristic structure of the ceramic core before trimming, as shown in Fig.24(a)‒24(c). The effect of the trimming using the method proposed in this paper is shown in Fig.24(d)‒24(f), which show that the burrs and hole blockages have been trimmed. The results of manual trimming are shown in Fig.24(g)‒24(i). To guarantee the quality of trimming for manual trimming is challenging, and there are often phenomena such as uneven burr trimming and burr residue. Although the manual trimming method has been used in the ceramic core of aero-engine blades, in contrast, the effect of using the laser processing equipment and the methods proposed in this paper has been significantly improved, not only has a higher trimming accuracy and efficiency but also dramatically improves the yield.

Fig.23 Laser scanning trajectory: (a) contour cluster 2, (b) cluster 10, and (c) cluster 8.

Full size|PPT slide

Fig.24 Trimming results of the ceramic core: (a) ceramic core before trimming, (b) burr and hole blockage of long groove, (c) burr and hole blockage of hole, (d) ceramic core after laser trimming, (e) long groove after laser trimming, (f) hole after laser trimming, (g) ceramic core after manual trimming, (h) long groove after manual trimming, and (i) hole after manual trimming.

Full size|PPT slide

The experimental results show that the method proposed in this paper can effectively realize the trimming of ceramic cores. The method makes full use of the characteristics of the galvanometer and the machine tool, that is, it avoids the vibration caused by the frequent start and stop in pure machine tool processing and makes full use of the high speed and high dynamic response characteristics of the galvanometer.

5 Conclusions

This paper proposes a zonal and layering laser processing method of 3D surface contour clusters, and the experimental validation is carried out via ceramic core trimming. The overall benefits of the proposed method can be summarized as follows:

(1) Based on the feature vector and the position data of the contours, the k-means clustering algorithm is utilized to partition the contour cluster. By normalizing the position data and the feature vector data, the problem of contour misclassification caused by using only position data is solved.

(2) To construct the LCS, the clustering center is employed as the origin point, and the vector direction of the clustering center is taken as the Z-axis direction. To obtain the scanning data of the galvanometer, the contour cluster data in the WCS is transformed into the LCS by the coordinate transformation algorithm. The definition method of the LCS greatly facilitates the subsequent layering and projection operations.

(3) In order to achieve the online ceramic core trimming, a laser processing system with the reconfiguration of the multi-axis motion platform and the galvanometer is implemented. A laser processing software OEMCC is employed. This software can realize functions such as vision measurement, motion control, trajectory registration and generation, and laser scanning. The software is suitable for laser processing systems with similar configurations.

The processing technology and equipment proposed within this paper are suitable for online laser trimming of workpieces with curved contour clusters, especially for non-metallic, difficult-to-process materials such as ceramic cores. In the future, further optimization of process parameters will be implemented to achieve better trimming quality.

Nomenclature

Abbreviations
2D	Two-dimensional
CAD	Computer-aided design
CAM	Computer-aided manufacturing
CNC	Computer numerical control
ICP	Iterative closest point
LCS	Local coordinate system
LPL	Laser focus processing length
OEMCC	Opto-electromechanical cooperative control
WCS	Workpiece coordinate system
Variables
cj	Coordinate of the cluster center
{\mathit{C}}^{(i)}({\mathit{O}}_{\text{WL}}^{(i)},{\mathit{Z}}_{\text{L}}^{(i)})	Center of the ith cluster
D	Diameter of the laser beam
E	Single pulse energy
f	Focal length of the field lens
floor(x)	Downward rounding of the variable x
h	Repetition frequency
H(i)	Transformation matrix from WCS OW to LCS O_{\text{L}}^{(i)}
\mathrm{\Delta }H	Layering distance
I_0	Energy density at the center of the spot
I_{\text{th}}	Ablation threshold of the material
J	Objective function
k	Preset number of categories
M^2	Mode parameter that characterizes the beam quality
n	Number of feature vectors
N_{\text{layer}}	Layer number of the current cluster
O_{\text{L}}^{(i)}	ith LCS
O_{\text{W}}	Workpiece coordinate system
{\mathit{O}}_{\text{WL}}^{(i)}	Coordinate of the coordinate origin O_{\text{L}}^{(i)} of LCS in WCS O_{\text{W}}
P	Laser power
{\mathit{P}}_m^{(i)}	Positioning coordinates of the mth layer of the ith contour cluster
r	Laser spot radius
r_{max}	Radius size along the ellipse’s major axis
r_{min}	Radius size along the ellipse’s minor axis
{\mathit{V}}_{\text{WZ}}	Unit vector along the Z-axis in WCS
w_0	Radius of the laser beam at the waist
w(\mathit{\text{z}})	Radius at various positions along the optical axis
{\hat{x}}_i	Normalization of x_i
{\mathit{x}}_i^{(j)}(x_i,y_i,z_i,u_i,v_i,w_i)	Six-dimensional data representing the feature vector
{\hat{\mathit{x}}}_i({\hat{x}}_i,{\hat{y}}_i,{\hat{z}}_i,u_i,v_i,w_i)	Normalization data
x_{max}	Maximum values of x_i
{\mathit{x}}_{\text{W}}^{(i)}	Data of the ith cluster in WCS
{\mathit{x}}_{\text{L}}^{(i)}	Data in LCS after the coordinate transformation of {\mathit{x}}_{\text{W}}^{(i)}
{\mathit{X}}_{\text{L}}^{(i)}	Unit vector along the X-axis in the ith LCS
{\hat{y}}_i	Normalization of y_i
y_{max}	Maximum values of y_i
{\mathit{Y}}_{\text{L}}^{(i)}	Unit vector along the Y-axis in the ith LCS
z	Distance to the center of the focus along the optical axis
{\widehat{\mathit{\text{z}}}}_i	Normalization of {\mathit{\text{z}}}_i
{\mathit{\text{z}}}_{max}, {\mathit{\text{z}}}_{\text{min}}	Maximum and minimum values of {\mathit{\text{z}}}_i, respectively
{\mathit{\text{z}}}_{\text{R}}	Rayleigh length
{\mathit{Z}}_{\text{L}}^{(i)}	Unit vector along the Z-axis in the ith LCS
\lambda	Laser wavelength
\theta	Incident angle of the laser

Acknowledgements

The authors gratefully acknowledge the financial support extended by the National Key R&D Program of China (Grant No. 2016YFB1102500), the Key R&D Project in Shaanxi Province (Grant No. 2019ZDLGY01-07), and the Science and Technology Program of Jiangsu Province, China (Grant No. SBK2019041271). Xiaodong WANG, Dongxiang HOU, Bin LIU, Xuesong MEI, Xintian WANG, and Renhan LIAN declare that they have no conflict of interest or financial conflicts to disclose.

Electronic Supplementary Materials

The supplementary materials can be found in the online version of this article at https://doi.org/10.1007/s11465-022-0675-5 and are accessible to authorized users.

Open Access

This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution, and reproduction in any medium or format as long as appropriate credit is given to the original author(s) and source, a link to the Creative Commons license is provided, and the changes made are indicated.

The images or other third-party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.

Visit http://creativecommons.org/licenses/by/4.0/ to view a copy of this license.

References

1 WangF, MaD X, Bührig-PolaczekA. Effect of ceramic cores on the freckle formation during casting Ni-based single crystal superalloys. Metallurgical and Materials Transactions A, Physical Metallurgy and Materials Science, 2019, 50( 2): 804– 815

2 LiW Y, ZhangG J, ChenL, HuangY, RongY M, GaoZ R. Dimethicone-aided laser cutting of solar rolled glass. Frontiers of Mechanical Engineering, 2021, 16( 1): 111– 121

3 LiW Y, HuangY, RongY M, ChenL, ZhangG J, GaoZ R. Analysis and comparison of laser cutting performance of solar float glass with different scanning modes. Frontiers of Mechanical Engineering, 2021, 16( 1): 97– 110

4 WuY Q, MuD K, HuangH. Deformation and removal of semiconductor and laser single crystals at extremely small scales. International Journal of Extreme Manufacturing, 2020, 2( 1): 012006

5 YuZ, HuJ, LiK M. Investigating the multiple-pulse drilling on titanium alloy in picosecond laser. Journal of Materials Processing Technology, 2019, 268 : 10– 17

6 WlodarczykK L, BruntonA, RumsbyP, HandD P. Picosecond laser cutting and drilling of thin flex glass. Optics and Lasers in Engineering, 2016, 78 : 64– 74

7 LiuY Z. Coaxial waterjet-assisted laser drilling of film cooling holes in turbine blades. International Journal of Machine Tools and Manufacture, 2020, 150 : 103510

8 BrecherC, EmontsM, RosenC J, HermaniJ P. Laser-assisted milling of advanced materials. Physics Procedia, 2011, 12 : 599– 606

9 ItoY, KizakiT, ShinomotoR, UekiM, SugitaN, MitsuishiM. High-efficiency and precision cutting of glass by selective laser-assisted milling. Precision Engineering, 2017, 47 : 498– 507

10 WooW S, LeeC M. A study of the machining characteristics of AISI 1045 steel and Inconel 718 with a cylindrical shape in laser-assisted milling. Applied Thermal Engineering, 2015, 91 : 32– 42

11 MaC P, GuanY C, ZhouW. Laser polishing of additive manufactured Ti alloys. Optics and Lasers in Engineering, 2017, 93 : 171– 177

12 SchanzJ, HofeleM, HitzlerL, MerkelM, RiegelH. Laser polishing of additive manufactured AlSi₁₀Mg parts with an oscillating laser beam. In: Öchsner A, Altenbach H, eds. Machining, Joining and Modifications of Advanced Materials. Advanced Structured Materials, vol 61. Singapore: Springer, 2016, 61 : 159– 169

13 WeingartenC, SchmicklerA, WillenborgE, WissenbachK, PopraweR. Laser polishing and laser shape correction of optical glass. Journal of Laser Applications, 2017, 29( 1): 011702

14 KrishnanA, FangF Z. Review on mechanism and process of surface polishing using lasers. Frontiers of Mechanical Engineering, 2019, 14( 3): 299– 319

15 RuzankinaJ S, VasilievO S. Study on possibility for the improvement of corrosion resistance of metals using laser-formed oxide surface structure. Journal of Physics: Conference Series, 2016, 735( 1): 012050

16 PengE, TsubakiA, ZuhlkeC A, WangM Y, BellR, LucisM J, AndersonT P, AlexanderD R, GogosG, ShieldJ E. Micro/nanostructures formation by femtosecond laser surface processing on amorphous and polycrystalline Ni60Nb40. Applied Surface Science, 2017, 396 : 1170– 1176

17 Rico SierraD, EdwardsonS P, DeardenG. Laser surface texturing of titanium with thermal post-processing for improved wettability properties. Procedia CIRP, 2018, 74 : 362– 366

18 ZhangC, ZhuJ K, ZhengH, LiH, LiuS, ChengG J. A review on microstructures and properties of high entropy alloys manufactured by selective laser melting. International Journal of Extreme Manufacturing, 2020, 2( 3): 032003

19 YilmazO, GindyN, GaoJ. A repair and overhaul methodology for aeroengine components. Robotics and Computer-Integrated Manufacturing, 2010, 26( 2): 190– 201

20 BremerC. Adaptive strategies for manufacturing and repair of blades and blisks. In: Proceedings of the ASME Turbo Expo 2000: Power for Land, Sea, and Air. Volume 4: Manufacturing Materials and Metallurgy; Ceramics; Structures and Dynamics; Controls, Diagnostics and Instrumentation; Education. Munich: ASME, 2000, V004T01A010

21 BremerC. Automated repair and overhaul of aero-engine and industrial gas turbine components. In: Proceedings of the ASME Turbo Expo 2005: Power for Land, Sea, and Air. Volume 2: Turbo Expo 2005. Reno: ASME, 2005, 841– 846

22 LiuQ C, DjugumR, SunS D, WalkerK, ChoiY R, BrandtM. Repair and manufacturing of military aircraft components by additive manufacturing technology. In: Proceedings of the 17th Australian International Aerospace Congress (AIAC 2017). Melbourne: Engineers Australia, Royal Aeronautical Society, 2017, 363– 368

23 GaoJ, FolkesJ, YilmazO, GindyN. Investigation of a 3D non-contact measurement based blade repair integration system. Aircraft Engineering and Aerospace Technology, 2005, 77( 1): 34– 41

24 ChenZ L ChenZ T ZhuZ Q ZhangY. Research on remanufacturing and repairing method of aero-engine blade based on reverse engineering. Aeronautical Manufacturing Technology, 2020, 63(23): 80– 86, 93 (in Chinese)

25 HouD X, MeiX S, WangG C, LiJ, WangC J, HuangW, ChenC, LiuR. An accurate 3D edge measurement method for guided precise modification. Measurement Science and Technology, 2021, 32( 2): 025006

26 FanJ J, MaL Q, ZouZ. A registration method of point cloud to CAD model based on edge matching. Optik, 2020, 219 : 165223

27 VockR, DieckmannA, OchmannS, KleinR. Fast template matching and pose estimation in 3D point clouds. Computers & Graphics, 2019, 79 : 36– 45

28 OpromollaR, FasanoG, RufinoG, GrassiM. A model-based 3D template matching technique for pose acquisition of an uncooperative space object. Sensors, 2015, 15( 3): 6360– 6382

29 GuoW L, HuW D, LiuC, LuT T. Pose initialization of uncooperative spacecraft by template matching with sparse point cloud. Journal of Guidance, Control, and Dynamics, 2021, 44( 9): 1707– 1720

30 XieH, LiW L, YinZ P, DingH. Variance-minimization iterative matching method for free-form surfaces—part I: theory and method. IEEE Transactions on Automation Science and Engineering, 2019, 16( 3): 1181– 1191

31 LiW L, XieH, ZhangG, YanS J, YinZ P. 3-D shape matching of a blade surface in robotic grinding applications. IEEE/ASME Transactions on Mechatronics, 2016, 21( 5): 2294– 2306

32 XiaoW L, LiuG Y, ZhaoG. Generating the tool path directly with point cloud for aero-engine blades repair. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2021, 235( 5): 877– 886

33 ErkorkmazK, AlzaydiA, ElfizyA, EnginS. Time-optimal trajectory generation for 5-axis on-the-fly laser drilling. CIRP Annals, 2011, 60( 1): 411– 414

34 JiangM, WangX Z, KeS H, ZhangF, ZengX Y. Large scale layering laser surface texturing system based on high speed optical scanners and gantry machine tool. Robotics and Computer-Integrated Manufacturing, 2017, 48 : 113– 120

35 CuccoliniG, OraziL, FortunatoA. 5 axes computer aided laser milling. Optics and Lasers in Engineering, 2013, 51( 6): 749– 760

36 DuesingJ F, SuttmannO, KochJ, StuteU, OvermeyerL. Ultrafast laser patterning of thin films on 3-D shaped surfaces for strain sensor applications. Journal of Laser Micro/Nanoengineering, 2012, 7( 3): 311– 315

37 KoS H, ChoiY, HwangD J, GrigoropoulosC P, ChungJ, PoulikakosD. Nanosecond laser ablation of gold nanoparticle films. Applied Physics Letters, 2006, 89( 14): 141126

38 OvermeyerL, DuesingJ F, SuttmannO, StuteU. Laser patterning of thin film sensors on 3-D surfaces. CIRP Annals, 2012, 61( 1): 215– 218