Modeling and simulation of normal and hemiparetic gait

Abstract

Gait is the collective term for the two types of bipedal locomotion, walking and running. This paper is focused on walking. The analysis of human gait is of interest to many different disciplines, including biomechanics, human-movement science, rehabilitation and medicine in general. Here we present a new model that is capable of reproducing the properties of walking, normal and pathological. The aim of this paper is to establish the biomechanical principles that underlie human walking by using Lagrange method. The constraint forces of Rayleigh dissipation function, through which to consider the effect on the tissues in the gait, are included. Depending on the value of the factor present in the Rayleigh dissipation function, both normal and pathological gait can be simulated. First of all, we apply it in the normal gait and then in the permanent hemiparetic gait. Anthropometric data of adult person are used by simulation, and it is possible to use anthropometric data for children but is necessary to consider existing table of anthropometric data. Validation of these models includes simulations of passive dynamic gait that walk on level ground. The dynamic walking approach provides a new perspective of gait analysis, focusing on the kinematics and kinetics of gait. There have been studies and simulations to show normal human gait, but few of them have focused on abnormal, especially hemiparetic gait. Quantitative comparisons of the model predictions with gait measurements show that the model can reproduce the significant characteristics of normal gait.

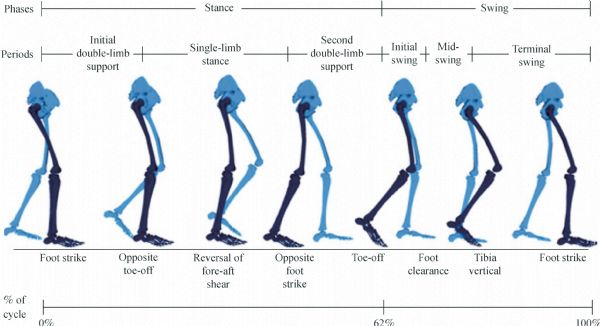
Key words： bipedal gait; biomechanics; dynamic walking; gait model; human gait; hemiparetic human gait

1 Introduction

The analysis of bipedal gait has been of interest from many years ago because studies have shown objective and efficient parameters of gait. These studies have helped us to appreciate the factors that allow us to modify the gait, diagnose alterations in the gait pattern of distinct pathologies and traumatic injuries, monitor the evolution of the patient recovery [1], and also generate mathematical models that allow us to reproduce the gait when it is used in a physical model.

This paper proposes a model that will allow us to model, simulate, and analyze the normal human gait as a complex system. We use a parameter that have not been included in other models, the constraint force, through which to consider the effect on the tissues in the gait. From it, the model will be able to simulate the right side hemiplegia pathology. Section 2 introduces the kinetics and kinematics aspects of human gait. Section 3 describes the hemiparetic human gait. Section 4 presents the kinematic parameters of the hemiparetic gait. Section 5 explains the proposed normal human gait model and the hemiparetic human gait, and Section 6 shows the results. Finally, Section 7 draws conclusions that analyze the advantages and disadvantages of the model presented throughout the paper in terms of their potential to describe natural normal and abnormal patterns, and their relevancy in the medical field.

2 Human gait

Walking is a cyclical activity that consists of a sequence of steps divided into two major phases: A stance phase and a swing phase. The stance phase is initiated when a foot strikes the ground and ends when the foot is lifted. The swing phase is initiated when the foot is in the air and advances to the next-heel contact position. Each stance phase has a period of time at the beginning and at the end, referred to as double stance. In this period both legs are on the ground. In normal walking, the stance phase extends over 60% of the gait cycle, while the swing phase occupies the remaining 40%. The duration of each double stance is approximately 10% of the whole cycle. The stance phase is further sub-divided into: Initial contact, loading response, mid-stance, push-off and pre-swing. Likewise the swing phase is sub-divided into: Initial swing, mid-swing and terminal swing. A graphical description of gait cycle is shown in Fig. 1 [2]. The position of the limbs at each phase represents a general instantaneous position, since each joint is moving continually throughout each phase. Each cycle is completed in a stride interval. The gait cycle is most frequently defined as a period from heel contact of one leg until the next heel contact of the same leg [1−6].

Fig.1 Representation of a patient’s gait cycle [2]

Full size|PPT slide

The analysis of the gait involves some measurements, such as walking speed, step length, and cadence. The walking speed refers to the speed at which humans choose to walk. Step length is the distance covered during the step time, from the time of the initial contact of one limb to the time of initial contact of the contralateral limb. The cadence of gait can be expressed in steps per minute. Also, it requires detailed measurements of the relative motion of the body segments and joints, the patterns of the forces applied to the ground, and the sequence and timing of muscular activity. The movements of joints and segments, including body position, velocity and acceleration, regardless of the forces that caused the movement, are termed kinematics [7]. Kinetics describes the mechanisms that cause movement, namely ground-reaction forces, joint moments, and joint powers. Analysis of the gait cycle is possible for all of the joint levels (foot, ankle, knee and hip) [6−8]. Figure 2 shows the angles for these joints [9].

Fig.2 Sagittal plane kinematics for the hip, knee, and ankle (values in degrees) during a single gait cycle of right hip (flexion positive), knee (flexion positive) and ankle (dorsiflexion positive) [9]

Full size|PPT slide

The forces that are involved in walking apart from friction are gravity and inertia. The motion is characterized by forward propulsion of center of gravity of the human body, momentarily reaching a position beyond the front edge of the support base. This causes a temporary loss of balance, so the action of gravity tends to fall forward and downward towards the body, increasing the speed and turning potential energy into kinetic energy. At this point, the ranging foot reaches the ground, regaining its balance to provide a much larger base of support and to avoid falling over. The reaction force is exerted by the ground on a person through the foot and it is equal in magnitude and opposite direction to the downward momentum of the foot during gait. Gait also requires adequate friction between the foot and the floor to keep from slipping. The friction force or material friction depends on the type of contact and pressure forces exerted between surfaces. Inertia, defined as the inability of the body to change its state of rest or motion unless a force intervenes, must be defeated at every step, thus the heavier the body is, the greater inertia to be overcome will be [4−8].

3 Hemiparetic human gait

Patients with total or partial hemiplegia suffer from paralysis of one side of the body, which results from a disease or injury to the central motor of the brain. This will lead to losing muscle control during the voluntary movement that is produced in the normal gait and will be replaced by repetitive movements and hemiparetic gait, as shown in Fig. 3. Where, the right side of the body is affected [10].

Fig.3 Subject with spastic hemiplegia [10]

Full size|PPT slide

Muscle weakness influences gait deviations. Previous studies have reported the contribution of muscle weakness to an impaired gait pattern. Mulroy et al. [11] found that torque change depends on gait pattern. Hsu et al. [12] showed that gait velocity after stroke was mainly affected by muscle weakness. Jonkers et al. [13] investigated the relationship between muscle weakness and resulting deviations in gait kinematics.

This type of gait is very variable, but has distinctive characteristics in postural attitude and movement of the limbs [14]. The abnormal gait in the hemiplegic subject is due to defective control of balance during one leg on the affected limb and during the progression of the center of gravity in the swing phase [15]. The gait patterns of permanent hemiplegic subjects have been described as asymmetric, slow, and rigid. They present a decrease in stride length, step frequency and time on the full cycle of the gait. The affected lower leg acts as if it was longer than the other one. It keeps the knee in extension and the foot pointing downward and inward, almost touching the floor with the ankle and foot, in an equinovarus attitude [16]. Therefore, all the propulsion motion is concentrated at the hips. The described movements present high energy consumption and low efficiency due to the extra work forced on the healthy leg; the translation mechanism of the body and the position of the center of gravity of the patient have also been affected [17,18].

The alterations on the hemiparetic gait are observed in the loss of the smooth sinusoidal oscillations describing in normal conditions and resulting in claudication and additional energy expenditure [19−21]. Winter [22] and Knutsson [23] found that all muscle groups had increased tonic activity. When the body weight is being supported by the paretic limb, the synergy extender is activated. Therefore, an extension of hip, knee, and ankle occurs with a minor hip adduction than in a normal individual. This will cause a reduction to the lateral displacement toward the paretic side.

During the swing phase, the hip flexion, knee flexion, and the dorsiflexion of the foot are reduced, due to weakness of distal muscles (foot drop) and extensor hypertonia in lower limb. This will imply a circumduction of the hip, and the patient drags the affected leg in a semicircle and leans towards the unaffected side to create sufficient hip height on the affected side to accommodate adapted leg [17,18].

4 Kinematic parameters of the hemiparetic gait

The variations of the joints movement patterns are more noticeable in the hemiplegic gait due to a loss of movement and the extra work needed. Following patterns of a hemiplegic leg are described:

1) Swing phase: Low hip flexion, low knee extension, inwards foot flexion and leg circumduction.

2) Stance phase: Low hip flexion, knee extension blockage, inwards foot flexion with support on the outside of the foot, knee hyperextension in the mid-support phase and the wrong takeoff of the tip of the foot [17,18].

Figure 4 shows the comparisons of the deviation in degrees of the joint movements of a subject who has hemiplegia at the left side versus a subject who has normal gait. The gray shadow shows the normal gait.

Fig.4 Lower limb kinematic of a patient with brain damage, left spastic hemiplegia [24]

Full size|PPT slide

5 Normal human gait model

A double inverted pendulum model like biped model was used for investigating the control of balance and posture during human walking, because the displacement of the center of gravity in gait shows a similar motion as described in the cyclic movement of this pendulum [5,23,25,26]. The model assumes that the reaction force from the ground is generated from the point and reaches the center of gravity of the pendulum. The double pendulum consists of two solid rods attached to an oscillating pivot, about which the rods are free to rotate, as shown in Fig. 5. In Fig. 5, the pendulum is depicted as a two massless rods of length l₁ and l₂ attached to a two particles mass m₁ and m₂.

Fig.5 Double inverted pendulum

Full size|PPT slide

For analysis, Lagrange method is used because it allows to include constraint forces as Rayleigh dissipation function, through which to consider the effect on the tissues in the gait. Movement equation of Lagrange depends on Lagrange function (L), equation of Rayleigh (D) and generalized forces (Q), which is shown as

(1){\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial L}{\partial {\dot{q}}_j}}\right)-{\displaystyle \frac{\partial L}{\partial q_j}}+\left({\displaystyle \frac{\partial D}{\partial {\dot{q}}_j}}\right)=Q,

where the value of Rayleigh (D) depends on the segment length and mass, the gravity force and the gait cycle period, these parameters are included in the variable b, the overall system stiffness measure, t represents time.

Lagrange function for the system is given by

(2)$$\begin{gathered} L={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(m_{\mathrm{1}}+m_{\mathrm{2}})l_{\mathrm{1}}^{\mathrm{2}}{\dot{\theta }}_{\mathrm{1}}^{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{m}_{\mathrm{2}}{l}_{\mathrm{2}}^{\mathrm{2}}\left({\dot{\theta }}_{\mathrm{1}}^{\mathrm{2}}+{\dot{\theta }}_{\mathrm{2}}^{\mathrm{2}}+\mathrm{2}{\dot{\theta }}_{\mathrm{1}}{\dot{\theta }}_{\mathrm{2}}\right)+m_{\mathrm{2}}{l}_{\mathrm{1}}{l}_{\mathrm{2}}\left({\dot{\theta }}_{\mathrm{1}}^{\mathrm{2}}+{\dot{\theta }}_{\mathrm{1}}{\dot{\theta }}_{\mathrm{2}}\right)\cos {\theta }_{\mathrm{2}} \\ +(m_{\mathrm{1}}+m_{\mathrm{2}})g{l}_{\mathrm{1}}\cos {\theta }_{\mathrm{1}}+m_{\mathrm{2}}g{l}_{\mathrm{2}}\cos ({\theta }_{\mathrm{1}}+{\theta }_{\mathrm{2}}), \end{gathered}$$

where g is the acceleration of gravity, {\theta }_{\mathrm{1}} and {\theta }_{\mathrm{2}} describe the angle between the upward vertical in the counterclockwise direction and the pendulum arm of Rods 1 and 2, respectively, {\dot{\theta }}_{\mathrm{1}} and {\dot{\theta }}_{\mathrm{2}} describe the derivative of {\theta }_{\mathrm{1}} and {\theta }_{\mathrm{2}} with respect to time, respectively, m_{\mathrm{1}} and m_{\mathrm{2}} are the masses of Pendulums 1 and 2, respectively, and l₁ and l₂ are the lengths of the Pendulums 1 and 2, respectively.

The movement equation of Lagrange for Rod 1 is

(3)$$\begin{gathered} \begin{array}{l}{\displaystyle \frac{\partial L}{\partial {\dot{\theta }}_{\mathrm{1}}}}=(m_{\mathrm{1}}+m_{\mathrm{2}})l_{\mathrm{1}}^{\mathrm{2}}{\dot{\theta }}_{\mathrm{1}}+m_{\mathrm{2}}{l}_{\mathrm{2}}^{\mathrm{2}}\left({\dot{\theta }}_{\mathrm{1}}+{\dot{\theta }}_{\mathrm{2}}\right)+\mathrm{2}{m}_{\mathrm{2}}{l}_{\mathrm{1}}{l}_{\mathrm{2}}\cos {\theta }_{\mathrm{2}}{\dot{\theta }}_{\mathrm{1}}+m_{\mathrm{2}}{l}_{\mathrm{1}}{l}_{\mathrm{2}}\cos {\theta }_{\mathrm{2}}{\theta }_{\mathrm{2}},\hfill \\ {\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial L}{\partial {\dot{\theta }}_{\mathrm{1}}}}\right)=[(m_{\mathrm{1}}+m_{\mathrm{2}})l_{\mathrm{1}}^{\mathrm{2}}+m_{\mathrm{2}}{l}_{\mathrm{2}}^{\mathrm{2}}+\mathrm{2}{m}_{\mathrm{2}}{l}_{\mathrm{1}}{l}_{\mathrm{2}}\cos {\theta }_{\mathrm{2}}]{\ddot{\theta }}_{\mathrm{1}}+(m_{\mathrm{2}}{l}_{\mathrm{2}}^{\mathrm{2}}+m_{\mathrm{2}}{l}_{\mathrm{1}}{l}_{\mathrm{2}}\cos {\theta }_{\mathrm{2}}){\ddot{\theta }}_{\mathrm{2}} \\ -\mathrm{2}{m}_{\mathrm{2}}{l}_{\mathrm{1}}{l}_{\mathrm{2}}{\dot{\theta }}_{\mathrm{1}}{\dot{\theta }}_{\mathrm{2}}\sin {\theta }_{\mathrm{2}}-m_{\mathrm{2}}{l}_{\mathrm{1}}{l}_{\mathrm{2}}{\dot{\theta }}_{\mathrm{2}}^{\mathrm{2}}\sin {\theta }_{\mathrm{2}},\hfill \\ {\displaystyle \frac{\partial L}{\partial {\theta }_{\mathrm{1}}}}=-(m_{\mathrm{1}}+m_{\mathrm{2}})g{l}_{\mathrm{1}}\sin {\theta }_{\mathrm{1}}-m_{\mathrm{2}}g{l}_{\mathrm{2}}\sin ({\theta }_{\mathrm{1}}+{\theta }_{\mathrm{2}}),\hfill \\ {\displaystyle \frac{\partial D}{\partial {\dot{\theta }}_{\mathrm{1}}}}=b_{\mathrm{1}}{\dot{\theta }}_{\mathrm{1}},\hfill \end{array} \end{gathered}$$

where b₁ is the overall system stiffness measure of Rod 1. The b₁ factor can be obtained with Eq. (4):

(4)b^{\mathrm{2}}={\displaystyle \frac{m{l}^{\mathrm{2}}}{{\left({\displaystyle \frac{{\tau }_{\mathrm{0}}}{\mathrm{2}\pi }}\right)}^{\mathrm{2}}}}+mgl,

where m is the mass of the pendulum, l is the length of the pendulum, and {\tau }_{\mathrm{0}} is the gait cycle period.

The movement equation of Lagrange for Rod 2 is

(5)\begin{array}{l}{\displaystyle \frac{\partial L}{\partial {\dot{\theta }}_{\mathrm{2}}}}=m_{\mathrm{2}}{l}_{\mathrm{2}}^{\mathrm{2}}\left({\dot{\theta }}_{\mathrm{1}}+{\dot{\theta }}_{\mathrm{2}}\right)+m_{\mathrm{2}}{l}_{\mathrm{1}}{l}_{\mathrm{2}}\cos {\theta }_{\mathrm{2}}{\dot{\theta }}_{\mathrm{1}},\hfill \\ {\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial L}{\partial {\dot{\theta }}_{\mathrm{2}}}}\right)=m_{\mathrm{2}}{l}_{\mathrm{2}}^{\mathrm{2}}\left({\ddot{\theta }}_{\mathrm{1}}+{\ddot{\theta }}_{\mathrm{2}}\right)+m_{\mathrm{2}}{l}_{\mathrm{1}}{l}_{\mathrm{2}}{\ddot{\theta }}_{\mathrm{1}}\cos {\theta }_{\mathrm{2}}-m_{\mathrm{2}}{l}_{\mathrm{1}}{l}_{\mathrm{2}}{\dot{\theta }}_{\mathrm{1}}{\dot{\theta }}_{\mathrm{2}}\sin {\theta }_{\mathrm{2}},\hfill \\ {\displaystyle \frac{\partial L}{\partial {\theta }_{\mathrm{2}}}}=-m_{\mathrm{2}}{l}_{\mathrm{1}}{l}_{\mathrm{2}}\sin {\theta }_{\mathrm{2}}\left({\dot{\theta }}_{\mathrm{1}}^{\mathrm{2}}+{\dot{\theta }}_{\mathrm{1}}{\dot{\theta }}_{\mathrm{2}}\right)-m_{\mathrm{2}}g{l}_{\mathrm{2}}\sin ({\theta }_{\mathrm{1}}+{\theta }_{\mathrm{2}}),\hfill \\ {\displaystyle \frac{\partial D}{\partial {\dot{\theta }}_{\mathrm{2}}}}=b_{\mathrm{2}}{\dot{\theta }}_{\mathrm{2}},\hfill \end{array}

where b₂ is the overall system stiffness measure of Rod 2.

The double inverted pendulum is inherently unstable. By oscillating the base at high enough excitation amplitudes, the system can be stabilized. The trajectory of the end mass can be irregular and may not display periodicity or symmetry about the vertical axis and will often exhibit chaotic behavior. For this reason, it needs a system that provides a control in the joint. The system selected is a proportional-derivate (PD) controller.

5.1 Joint model

Joints are modeled as servomotors. The servomotors are characterized by a position control, that is, the motors are immediately placed in a given angular position. Equation (6) is the transfer function of a servomotor.

(6){\displaystyle \frac{\mathrm{\Theta }(s)}{E(s)}}={\displaystyle \frac{K_m}{s(T_{m}s+\mathrm{1})}}.

Each joint requires a transition of control to the phase leg in the contralateral pendulum support leg, for this reason, a PD controller is used for controlled trajectory of the mechanisms. The PD controller should be stable, with a time of low delay and must be given to represent excellent progress since the model repositions the system response. The initial conditions of the positions must be fed with external information.

5.2 Simulation

In order to observe the operation of the model obtained for gait, it is necessary to apply forces to musculoskeletal model and the simulation. The model is done with both lower limbs of the human body and joint, given the above mathematical models obtained. Figure 6 shows both models of the leg (Fig. 6(a)) and controlled articulation (Fig. 6(b)). Table 1 shows the size and mass of each body segment for an adult. For b value, we consider a normal gait with velocity as 1.2 m/s and gait cycle period {\tau }_{\mathrm{0}}=1.0 s [27] and a hemiplegia with gait velocity as 0.7 m/s and {\tau }_{\mathrm{0}}=0.6 s. Each rod is simulated with a cylinder body part, the revolute part is used for connection between different parts, and the inertial system part gives a position reference.

Fig.6 Model of (a) the leg without control, where the leg is modeled as a double pendulum, and (b) servomotor for the control of the leg joint

Full size|PPT slide

Tab.1 Size and mass of each body segment

Segment	Mass/g	Length/cm	Radius/cm	Density/(g·cm-3)
Hip	4000	35	14	0.866
Thing	7004	40	7	1.542
Leg	2924	40	5	0.646

6 Results

A muscle-skeletal model describing the human gait is obtained. Each lower segment is a double inverted pendulum, and joints are servomotors. The model in this study has five segments to be represented, namely the hip, right-and-left legs, and four degrees of freedom to represent articulations at the hip and knee joints.

In general, the results do not reveal any significant difference with the literature data, agreeing with the findings by Gage et al. [4], Kuo [5], Whittle [6], and McGeer [8]. Such references’ data are important in all gait analysis.

6.1 Normal gait

The results of the simulation of the model are displayed in Fig. 7. Angles for the hip, knee, and ankle respectively in the sagittal plane are showed respectively. From the figure, it can be concluded that the results are satisfactory since waveforms are closely related to those previously reported in the Refs. [4,18]. In the simulation, the gait cycle period is 1.1 s, and the step length is 0.71 m. The maximum hip flexion and extension are 35° and 11°, respectively. In terms of knee, the maximum flexion and extension are 60° and 5°, respectively.

Fig.7 Angles of joint obtained through simulation. (a) Hip angle; (b) knee angle

Full size|PPT slide

All results presented are captured for an entire gait cycle which starts with heel contact and ends with the next heel contact. The gait periods found in the simulation are compatible with those in Refs. [2,4,5,17].

6.2 Hemiparetic human gait

Due to the characteristics of hemiplegic march described above, an increase occurs in reflex activity, with mechanical changes in the muscles and a high stiffness in the affected limb, influencing the walking speed, the cycle period, cadence, and stride length [28]. Besides, it presents alteration in the angles of the joints of the lower extremities.

Figure 8 is obtained from the simulation, which shows the weakness in the flexion and extension of hip and knee. The cycle period is 0.6 s with a step length of 0.33 m. The results are very similar to those observed in Fig. 4 which presents the waveforms of a hemiplegic person. Consistent with speed decrease, both stride length and cadence of a hemiplegic person are lower than that of able-bodied subjects.

Fig.8 Hip and knee angle in subject with hemiparesis in left side. (a) Hip angle; (b) knee angle

Full size|PPT slide

As for the joint ranges, the hip flexion angle of the hemiplegic side in the initial contact sub-phase increases comparing with the able-bodied subject and this is the maximum value in flexion 44°, in stance phase is the minimum of hip flexion 5°. There are lower flexion angles on the healthy side, while minimum values are close in both legs. No angles are presented in hip extension. The presence of high values of the angles of the hip can show the existence of a compensation mechanism for hip displacement during the gait. The knee flexion increases at initial contact, the minimum of knee flexion is presented in mid-stance, the peak of knee flexion (maximum value of angle) appears in swing phase. Low variation flexion along cycle gait is observed, demonstrating that the knee tends to be hyperextended.

Subjects’ major kinematic differences from the able-bodied are:

1) Decreased knee flexion during swing phase;

2) Increased hip flexion at initial contact, increased hip flexion at toe off, and decreased hip flexion during mid-swing;

3) Knee flexion increases at initial contact and reduced knee flexion at toe off and mid-swing;

4) Serious reduction in maximum hip extension.

7 Conclusions

We have introduced an application of the inverted pendulum where we include a factor to consider the effect on the tissues in the gait. This model is able to mimic the complexity of sequences stride interval of human gait. We have also performed the abnormal gait model, such as hemiplegic gait.

The presented model allows easier analysis of gait movements and provides a useful insight. The proposed gait system discloses angles of the lower limbs through time. The spatial-temporal parameters and joint angles defined during the gait cycle in literature data are similar to that found in the simulation. The wave and data show close resemblance. The maximum and minimum value of each angle are close to those found in previous studies of this type of gait.

The presented model is compared with natural human responses. Knee and hip angles are found to exhibit a curved shape similar to those described in literatures. The PD controller produces an optimal control of gait. Thus, the PD controller scheme, in conjunction with body dynamics, is sufficient to reproduce the major characteristics of human responses in gait.

The model is only able to simulate the hemiparetic gait and not all kinds of pathological gait. It decisively uses the stiffness parameter, because it helps to simulate the action of tissue in the gait. Through this parameter, we can simulate the effect on muscles and therefore hemiparesis. The results show that the modeling and simulation of the musculoskeletal system can recognize gait disturbances. The model of hemiparetic gait allows to observe deviations from the kinematic values in this type of gait for a person with certain anthropometric characteristics.

Considering the literature data, it is not unlikely that curves described by each joint vary by changing the type of floor, because the type of surface affects joint range of motion, the instantaneous values of joint angles and change in dynamics of these values.

Future work should address changes to the model in order to observe abnormal gait in amputees, which may provide an abnormal-gait model intending to design assistive mechanical devices for the disabled. Modeling and simulation of the muscle-skeletal system can provide insights into gait abnormalities and the functional consequences of treatment. The muscle-skeletal model used in simulations is thoroughly tested. However, this modeling and simulations have not considered the effects of muscle-tendon modeling. Further (continued) work is also needed to ensure that the results generated by muscle-skeletal simulations are accurate and clinically relevant.

Acknowledgements

This research was supported by Universidad Distrital Francisco Jose de Caldas.

References

1 Collado S. Analysis of human walking with load platforms. Influence of freight. Dissertation for the Doctoral Degree. Madrid: Universidad Complutense de Madrid, 2002

2 Routson R L, Kautz S A, Neptune R R. Modular organization across changing task demands in healthy and poststroke gait. Physiological Reports, 2014, 2(6): e12055

3 Lim M R, Huang R C, Wu A, Evaluation of the elderly patient with an abnormal gait. Journal of the American Academy of Orthopaedic Surgeons, 2007, 15(2): 107–117

PMID

4 Gage J, Deluca P, Renshaw T. Gait analysis: Principles and applications. Journal of Bone and Joint Surgery—American Volume, 1995, 77: 1607–1623

5 Kuo A D. The six determinants of gait and the inverted pendulum analogy: A dynamic walking perspective. Human Movement Science, 2007, 26(4): 617–656

PMID

6 Whittle M. Gait Analysis: An Introduction. 4th ed. Elsevier, 2007

7 Luengas L, Camargo E, Sanchez G. Patellar tendon behavior during the sub-phase loading response. In: Proceedings of 2011 International Symposium on IT in Medicine and Education (ITME). Guangzhou: IEEE, 2011, 1, 694–698

8 McGeer T. Dynamics and control of bipedal locomotion. Journal of Theoretical Biology, 1993, 163(3): 277–314

PMID

9 Chai H. The gait during ambulation

10 Dupilka A. Pediatric patient resources.

11 Mulroy S, Gronley J, Weiss W, Use of cluster analysis for gait pattern classification of patients in the early and late recovery phases following stroke. Gait & Posture, 2003, 18(1): 114–125

12 Hsu A L, Tang P F, Jan M H. Analysis of impairments influencing gait velocity and asymmetry of hemiplegic patients after mild to moderate stroke. Archives of Physical Medicine and Rehabilitation, 2003, 84(8): 1185–1193

PMID

13 Jonkers I, Stewart C, Spaepen A. The study of muscle action during single support and swing phase of gait: clinical relevance of forward simulation techniques. Gait & Posture, 2003, 17(2): 97–105

PMID

14 Giuliani C A. Adult hemiplegic gait. In: Smitd G L, ed. Gait in Rehabilitation: Clinics Physical Therapy. New York: Churchill Livingstone, 1990, 253–266

15 Pai Y C, Rogers M W, Hedman L D, Alterations in weight-transfer capabilities in adults with hemiparesis. Physical Therapy, 1994, 74: 647–659

PMID

16 Palencia R. Trastornos de la marcha. Protocolo diagnóstico. Boletín Pediatrico, 2000, 40: 97–99 (in Spanish)

17 Beséler M. Estudio de los parámetros cináticos de la marcha del paciente hemipléjico mediante plataformas dinamométricas.

18 Perry J. Gait Analysis: Normal and Pathological Function. Thorofare: Slack, Inc., 1992

19 Tesio L, Civaschi P, Tessari L. Motion of the center of gravity of the body in clinical evaluation of gait. American Journal of Physical Medicine, 1985, 64(2): 57–70

PMID

20 Olney S J, Colborne G R, Martin C S. Joint angle feedback and biomechanical gait analysis in stroke patients: A case report. Physical Therapy, 1989, 69(10): 863–870

PMID

21 Olney S J, Griffin M P, McBride I D. Temporal, kinematic, and kinetic variables related to gait speed in subjects with hemiplegia: a regression approach. Physical Therapy, 1994, 74(9): 872–885

PMID

22 Winter D A. Energy generation and absorption at the ankle and knee during fast, natural, and slow cadences. Clinical Orthopaedics and Related Research, 1983, (175): 147–154

PMID

23 Knutsson E. Can gait analysis improve gait training in stroke patients. Scandinavian Journal of Rehabilitation Medicine, 1994, 30(Suppl): 73–80

PMID

24 Peterson D, Bronzino J. Biomechanics Principles and Applications. Boca Raton: CRC Press, 2008

25 Tang Z, Meng Joo Er, Chien C J. Analysis of human gait using an inverted pendulum model. In: Proceedings of IEEE International Conference on Fuzzy Systems. Hong Kong: IEEE, 2008

26 Kuo A D, Donelan J M. Dynamic principles of gait and their clinical implications. Physical Therapy, 2010, 90(2): 157–174

PMID

27 Oberg T, Karsznia A, Oberg K. Basic gait parameters: reference data for normal subjects, 10−79 years of age. Journal of Rehabilitation Research and Development, 1993, 30(2): 210–223

28 Onyshko S, Winter D A. A mathematical model for the dynamics of human locomotion. Journal of Biomechanics, 1980, 13(4): 361–368

PMID