1 Introduction
Edge detection is an important image processing technology that has special application potential in the fields of modern artificial intelligence, machine vision, and medical image recognition [1–3]. The realization of edge detection is conventionally based on digital operations with computers, which generally consumes considerable energy and time. Recently, the development of optical analog computing has provided new opportunities for the ultrafast and efficient acquisition of image edge information with the advantages of parallel processing capability, excellent computing speed, and low or even nearly zero energy consumption [4–6]. Optical analog computing can be constructed in traditional optical systems composed of lenses and spatial filters. However, the bulky optical elements are harmful to the on-chip integration of devices. The use of dielectric metasurfaces for optical analog computing can pave the way to the realization of small-footprint integrated spatial operation devices.
Two-dimensional (2D) dielectric metamaterials or metasurfaces as a representative device prototype are composed of artificial subwavelength structures over planar dielectric material surfaces, which can facilitate flexible manipulation of the amplitude, phase, and polarization of electromagnetic waves [7–32]. By designing the geometries of dielectric metasurfaces, optical analog computing devices with different functionalities can be obtained, such as spatial differentiators [33–35], integrators [36], and equation solvers [37,38]. The introduction of 2D dielectric metasurfaces simplifies the fabrication flow and increases the design flexibility of optical analog computing devices in comparison with conventional multilayer film structures [6,35]. As important devices in optical analog computing, spatial differentiators have been extensively studied to improve the availability of devices, such as first- and second-order spatial differentiators.
In 2017, by exploiting the critical coupling condition of a surface plasmon polariton, a first-order spatial differentiator was experimentally demonstrated at the interface between a metal film and a dielectric substrate [39]. However, the angle sensitive excitation property of the surface plasmon polariton limits the range of incident angles and the frequency bandwidth of devices to some extent. In addition, spatial differentiators based on plasmonic metal metasurfaces commonly operate in the reflection mode and at near-infrared wavelengths owing to the strong visible light absorption [40–44], which compromises the compatibility of devices in commercial optical imaging systems. All-dielectric metasurfaces are preferred to explore their functionalities in mathematical operation and edge detection. With the mechanism of spin-orbit interaction, first-order spatial differentiation and broadband edge detection with high working efficiency based on a Pancharatnam–Berry phase metasurfaces were proposed by Zhou et al. [45]. Circularly polarized beams further expanded the capabilities of the Pancharatnam–Berry phase gradient metasurfaces, which were employed in polarization-dependent high-contrast microscopy operating in transmission mode.
In 2019, a metasurface composed of silicon square nanopatches sitting on a reflective backplate was developed to achieve first-order spatial differentiation of an incident Gaussian beam and edge detection of letters [46]. However, polarization-dependent optical features reduce the visibility of edge information along some directions. To accelerate the development of monolithic 2D-metasurfaces-based spatial differentiators, a compound flat image differentiator was reported by integrating the differentiator with a metalens [47]. By combining the image differentiator and traditional imaging system, such as a commercial optical microscope and camera sensor, the advantages of the monolithic 2D-metasurfaces-based spatial differentiator used for edge detection of biological cells were further revealed. Similarly, polarization-sensitive edge detection of a device consisting of an array of cylindrical silicon nanorods and supported quasi-guided modes affects the durability and effectiveness of the spatial differentiator. To overcome the problem of polarization, we recently presented a different design of second-order spatial differentiator by engineering the spatial dispersion of electric dipole resonances, which were supported by silicon nanodisks in a 2D metasurface [48]. For the unpolarized beam, a similar edge profile was obtained as the case of linearly polarized light. The study of monolithic 2D dielectric metasurfaces simplifies the design and fabrication of optical spatial differentiators and meanwhile increases the practicability and flexibility of edge detection in realistic image processing applications.
In this work, typical examples of 2D-metasurfaces-based optical spatial differentiators for edge detection are reviewed. The working principle, design of optical transfer function (OTF), and characteristic analysis of devices are discussed in detail. In addition to comparing different 2D dielectric metasurface geometries, the characteristics of on-chip optical spatial differentiators are also estimated, including working mode, spatial bandwidth, efficiency, and polarization dependence. To describe the operational capabilities of 2D spatial differentiators in image processing, applications of edge detection are introduced to illustrate the advantages of 2D-metasurfaces-based spatial differentiators in high-speed parallel image information acquisition.
2 Working principles
Spatial differentiation and edge detection of an image can be achieved by examining the intensity variations of signals at different positions. Traditionally, this requires intensive digital operations performed by an electronic computer using sophisticated algorithms. For example, the image is first carefully pixelated. Then, proper values are assigned according to the intensity of brightness and even different colors. Finally, proper mathematical operations are adopted to correctly extract the edge information. In contrast, Fourier optics provides another fascinating approach to conduct the functionality of edge detection [5]. The working mechanism is simple and entirely different from the electronic way mentioned above. It takes the advantage of diffraction of a light beam carrying the necessary information of an image. The image can be directly obtained from the scattered light by the given object or by modulating the light beam with a device, such as a spatial light modulator. Generally, the modulated light beam is orientated to an optical lens, which can perform the Fourier transform (FT); thus, the Fourier spectrum can be obtained at the back focal plane. Since the edge information is presented by high-order Fourier components, which are usually at the outside area of the Fourier pattern, carefully selecting these high-order components can consequently extract the edge information. Finally, real images containing the edge profile can be obtained via the inverse Fourier transform (IFT) by another optical lens. As all operations are performed as light propagates, the processes of optical analog computing are much faster and have lower energy consumption than the electronic method.
Although the above-mentioned optical analog computing of spatial differentiation and edge detection is simple and straightforward, the bulky size of the lens is a critical problem for device integration. To overcome this challenge, the concepts of metamaterials and metasurfaces have been employed [49,50]. They are consisting of arrays of nanoscale light scatters, which can locally modify the intensity and phase of the incident light. Based on these flexible platforms for light manipulation, traditional lenses and systems mentioned above can be replaced by metamaterials and metasurfaces [6]. The basic configuration is presented in Fig. 1. In this process, a 2D graded-index (GRIN) dielectric slab was used to carry out the FT and output the Fourier information. The required Fourier information was selected by a suitably designed metasurface as a spatial filter, and the IFT was realized with another graded-index metamaterial. With this configuration, the first- and second-order derivatives, integration, and convolution of spatial signals had been numerically demonstrated. In particular, this concept had been extended to a more realistic platform of dielectric metamaterials with only holes, providing practical ways to solve differential equations [37].
As the sizes of metamaterials and metasurfaces are of wavelength scale, the complex designs still limit practical applications. A simplified scheme based on the gap-surface plasmon (GSP) in a plasmonic metasurface was proposed and experimentally demonstrated [33]. It operates in the reflection mode, and the FT can consequently be realized with only one block. To filter the required information in the Fourier domain, different sizes of plasmonic bricks were selected to achieve the proper amplitude and phase for reflection. By applying the same concept to a dielectric metasurface, absorption loss of the plasmonic metasurface can be reduced. Meanwhile, it is beneficial to increase the working efficiency and integration of device [38,52].
Fig.1 Basic principle of spatial differentiation and edge detection with metamaterials and metasurfaces. (a) Fourier information of the input signal can be obtained by a block with the Fourier transform (FT) function. After passing through the metasurface, the output signal can be obtained with the inverse Fourier transform (IFT) operation. (b) Graded index (GRIN) metamaterials can be employed to realize the FT and IFT. Reprinted with permission from Ref. [51]. Copyright 2013, The Optical Society of America. (c) Practical realization of the configuration. Reprinted with permission from Ref. [6]. Copyright 2014, American Association for the Advancement of Science |
Another method for performing spatial differentiation and edge detection is the Green’s function (GF) method [6]. With this method, no FT is required, thus further minimizing the size of the whole system. The critical point when utilizing the GF method is to achieve a specific OTF with properly designed metasurfaces. In this way, the input light field can be processed after passing through the metasurfaces, and the desired light field determined by the OTF can be obtained. This process can be described as follows. Considering a 2D light field as the input signal, we can achieve it by impinging a monochromatic plane wave to a target object; therefore, the input-modulated light field can be expressed as as it propagates along the z direction. While this modulated light field results from diffraction by the target object, it contains the wavevector components in the x-y plane. Consequently, the modulated light field can also be expressed in the momentum domain, i.e., , where kx and ky are the in-plane wave numbers. After the modulated light field passes through the metasurfaces, the output light field, , can be expressed as [53]
where is the corresponding OTF of the metasurface. Generally, when an incident modulated light field is impinged to a planar structure, both the reflection and transmission show polarization dependence. Therefore, the OTF of a metasurface can be expressed with a 2-by-2 matrix that relates the input and output fields as follows:
in which two polarizations of s and p waves are considered, and polarization conversion is also taken into account with the off-diagonal terms of the OTF matrix. Consequently, by judiciously tailoring the metasurfaces, we can obtain proper OTF that can realize the desired processing or operation to the input information for specific applications. In fact, the diffraction of light is more significant at the edges of the target, leading to larger in-plane wave numbers. This means that if we can achieve an OTF to transmit these components of larger wave number while blocking those of smaller wave number, we can then have only the edge information at the output, resulting in the realization of spatial differentiation and edge detection.
The key of the GF method is to design specific OTFs with metasurfaces so that the input light field can be processed in a suitable manner. As a specific case, we briefly explain how spatial differentiation can be realized with specific OTFs. For first-order spatial differentiation, we consider that the incident light field includes an in-plane wavevector along the x direction. The relationship between the output and input fields can be expressed as [39]
where the incident light field is assumed as . Therefore, the OTF should be a linear function of the in-plane wave number. For second-order spatial differentiation, we can obtain the OTF in a similar way:
This indicates that the OTF should behave as a parabola. We notice that in both cases, the intensity of the output light field is closely related to the wave number. Both OTFs should allow incident light fields with larger wave numbers while suppressing those with smaller wave numbers, thereby achieving image edge detection.
To design proper OTF for the spatial differentiation and edge detection of images, tailoring the nonlocal effects of metasurfaces is a promising way. In the nonlocal effect, the responses of metasurfaces to the incident light field are not only related to the normal component of the incident wave, but are also affected by the in-plane components. This means that the transmission, reflection, and OTF of metasurface depend on the incident angle of the light field. Such incidence-angle dependence of OTF is usually engineered by tailoring the resonances of metasurfaces, which usually include guided-mode resonance (GMR), Fano resonance, multipolar resonance (electric or magnetic dipole), and so on. GMR is a unique kind of resonance that can be strongly confined in structures but still has weak coupling with external radiation [54]. Compared with the traditional guided wave in a waveguide, GMR is usually accompanied by a limited but high quality factor. Moreover, its resonance frequency and quality factor present significant dependence on the in-plane wavevector. As another important kind of resonance, Fano resonances have been demonstrated in various platforms [55]. Fano resonances originate from the interference between two wave channels, which usually have a narrow and broad bandwidth or even continued radiation. In particular, the resonance with narrow bandwidth that tailored by structures provides a versatile tuning degree of freedom for Fano resonances.
In addition to the two kinds of resonances discussed above, the multipolar resonances of dielectric nanoparticles also provide a promising route to tailor the OTF of metasurfaces [48,56]. Compared with plasmonic structures, dielectric nanostructures can not only address the loss problem and improve the working efficiency of metasurfaces, but also facilitate the manipulation of light scattering and propagation. The electric and magnetic dipole resonances of nanostructures offer many degrees of freedom to tailor the OTF of metasurfaces. Such kinds of dielectric metasurfaces are featured with large spatial bandwidths, and 2D edge detection of images for arbitrary polarizations have also been successfully demonstrated. With these advantages, we envision that dielectric metasurfaces can play an important role in other mathematical operations and optical analog computing. In addition to the resonant schemes mentioned above for realizing spatial differentiation and edge detection of images, non-resonant schemes, such as spin-to-orbit interaction in Pancharatnam–Berry phase metasurfaces, have also been explored to achieve edge detection of images [45,57]. In this review, we mainly discuss the development of dielectric metasurfaces in spatial differentiation and edge detection based on resonance mechanisms with the GF approach.
3 Results and discussion
As discussed above, based on the GF approach, different kinds of dielectric metasurface device prototypes used for spatial differentiation and edge detection have been subsequently proposed and demonstrated recently. In this section, we mainly focus on the characteristic analysis and comparison of on-chip spatial differentiators realized with GMR, Fano resonance, and multipolar resonance. Meanwhile, as a typical application, the results of edge detection are also illustrated combined with the characteristics of small-footprint spatial differentiators.
With a 2D array of holes in a dielectric slab, photonic crystals can provide nearly isotropic second-order differentiation, or the Laplace mathematical operation [53,58]. Figure 2(a) presents the device structure of a photonic crystal slab-based optical spatial differentiator, which consists of a photonic crystal slab and a separate dielectric slab. A Fano resonance can be constructed by interfering with the GMR of the structured slab with an incident wave, enabling the establishment of proper OTF for Laplace calculation in the transmission mode. In fact, the reflection and transmission properties of a metasurface are polarization-dependent. It is therefore necessary to consider the effects of polarization on the optical analog computing. For a linearly polarized wave, the OTFs of dielectric metasurfaces-based spatial differentiator are usually different between the s and p waves. As illustrated in Figs. 2(b) and 2(c), the transmission of the p wave is much lower than that of the s wave. Lower transmission in the p wave limits the practicability of a device. Therefore, spatial differentiation and edge detection can only work for certain polarization. For unpolarized light, similar isotropic OTF can be obtained owing to the reality of vector composition between the s and p waves, as presented in Fig. 2(d). Consequently, the edges of an image can be successfully detected, as demonstrated by the edge images of the incident Stanford emblem and slot patterns in Fig. 2(f).
As a key parameter of the spatial differentiator, a large spatial bandwidth reflects the ability of a device to extract light waves with large incident angles. In particular, for the case of the GF method, the input spatial signals and images can be constructed by the incident light beam. The edges of targets diffract the beam, leading the edge information to be incorporated in the light components with additional wavevectors. In other words, the variation and edge information are carried by the diffracted light components with large propagation angles with respect to the incident beam. In this way, metasurfaces can be designed to allow oblique light to pass through while blocking normal light, thereby filtering the desired information. However, the photonic crystal slab-based spatial differentiator supporting GMR has a small spatial bandwidth (less than 1°, as indicated in Fig. 2(e)). This is because GMR usually features a large quality factor [53,58,59]. Different from the above-mentioned two-layer structure, single-layer dielectric metasurface was also introduced by Cordaro et al. to construct first- and second-order spatial differentiators in 2019, which was designed by a similar Fano resonance in the transmission spectrum [60,61]. The metasurface was composed of an appropriately engineered array of silicon nanobeams. Changing the angles of incident light, the transmission variations of asymmetric metasurfaces achieved the corresponding mathematical operations within the range of 17°. Clear edge detection experimentally demonstrated the optical processing capability of the metasurface. Therefore, metasurfaces should support a larger spatial bandwidth to filter the finer features of spatial signals or images.
Fig.2 (a) Schematic of an isotropic second-order spatial differentiator realized by a photonic crystal slab and a separate dielectric slab. (b) Optical transfer functions (OTFs) of the device for the s wave, (c) p wave, and (d) unpolarized light. (e) One-dimensional (1D) OTF as a function of the wavevector and the corresponding quadratic fitting. (f) Morphologies of the incident Stanford emblem and slot patterns (left column) and the corresponding edge images (right column). Reproduced with permission from Ref. [53]. Copyright 2018, The Optical Society of America |
The spatial bandwidth can be extended by engineering the nonlocal response of metasurfaces. In 2018, Kwon et al. reported a second-order spatial differentiator with a large spatial bandwidth of approximately 40° based on a nonlocal metasurface [36]. The metasurface was composed of an array of split-ring resonators, as illustrated in Fig. 3(a). The transmission properties of the metasurfaces were influenced by the scattering between unit cells, leading to different transmission curves at different incident angles, which are depicted in Fig. 3(b). As seen in the figure, the realization of a second-order differentiation operation was facilitated by the Fano resonance of the metasurfaces. When a one-dimensional (1D) sinusoidal function wave as an input signal was incident onto the device, a reverse sinusoidal function was obtained as the output result, similar to the calculated results of the ideal mathematical operation (Fig. 3(c)). Figure 3(d) presents the 2D OTF of a second-order spatial differentiator, demonstrating the characteristics of a device with large spatial bandwidth along both x and y directions. By engineering the nonlocal response of the metasurfaces, both first- and second-order differentiation could be achieved with a permittivity-modulated split-ring resonator array.
Given the polarization dependence of the OTF, edge detection images were calculated by exploiting x-polarized and y-polarized wave illumination, as displayed in Figs. 3(e) and 3(f), respectively. However, the missing edge information along some directions further illustrates the anisotropic optical transmission properties of the spatial differentiator. For the recognition of finer edge profiles, a greatly increased spatial bandwidth is helpful to realize a resolution on the wavelength scale. Concerning the morphology of the devices, three-dimensional symmetric or antisymmetric split-ring resonator arrays increased the fabrication difficulties. Although the proposed nonlocal metasurfaces based on the split-ring resonator array significantly improved the performance of the spatial differentiator, the realization of the device configuration should be carefully considered in practical applications.
Fig.3 (a) Schematic of the second-order spatial differentiator based on nonlocal metasurfaces consisting of split-ring resonators. (b) Evolution of transmission curves of the metasurface-based spatial differentiator with an increasing incident angle from 0° to 45°. (c) Output results of an ideal second-order differentiation operation and of the nonlocal metasurface corresponding to a sinusoidal function input. (d) Two-dimensional (2D) OTF of the differentiator as a function of incident angle q. (e) Results of edge detection corresponding to x-polarized wave illumination and (f) y-polarized wave illumination. Reproduced with permission from Ref. [36]. Copyright 2018, The Physical Society of America |
Apart from the transmission mode, the dielectric metasurface-based spatial differentiator can also operate in the reflection mode. In 2020, Zhou et al. [46] proposed a first-order spatial differentiator employing a dielectric metasurface, which consisted of an array of silicon square patches over a gold backplate, as illustrated in Fig. 4(a). This device was designed to operate in the reflection mode owing to the existence of a gold backplate. A sharp reflection change was achieved accompanied by a π phase variation near an incident angle of 25.4° at a wavelength of 1565 nm, leading to the OTF for the first-order spatial differentiation. In principle, the realization of the first-order differentiation operation benefited from the hybridization of the localized magnetic resonance mode with the classical grating-modulated bounded surface mode. Figure 4(b) presents the corresponding magnetic field distributions at planes x = 0 and y = 0 under the excitation of transverse-magnetic (TM) polarized light. Compared with the ideal OTF of the first-order differentiator, the linear reflection evolution of the designed metasurface matched well with the theoretical calculation result around q = 25.4°, as depicted in Fig. 4(c). To demonstrate the operation effect of the first-order spatial differentiator, a Gaussian beam as the input signal was incident onto the metasurface to observe the output intensity distribution (Fig. 4(d)). Good operational capability was further experimentally verified by inspecting the effect of edge detection, in which “ZJU” letters as test chart were used, as presented in Figs. 4(e) and 4(f). However, the lost information along the horizontal direction influenced edge detection owing to the polarization dependence.
Fig.4 (a) Schematic of the first-order spatial differentiator based on the reflective dielectric metasurface. (b) Magnetic field profiles at the x-z and x-y planes, respectively. (c) 1D OTF of the first-order spatial differentiator corresponding to changes of reflection amplitude and phase for the transverse-magnetic (TM) polarization light incidence. (d) Output intensity curve of the metasurface and the theoretically calculated results corresponding to the input Gaussian signal. (e) Incident image consisting of “ZJU” letters. (f) Reflected edge detection image corresponding to (e). Reproduced with permission from Ref. [46]. Copyright 2020, John Wiley & Sons Inc |
To further break the limitations of polarization dependence, Kwon et al. presented a design of polarization-independent metasurfaces on the basis of Fano resonances in 2020 [62]. As illustrated in Fig. 5(a), the metasurfaces were formed by a triangular lattice of holes in a suspended silicon membrane. The generation of a Fano resonance originated from the coupling between the leaky-wave and longitudinal Fabry–Perot resonance in the lossless metasurface structure. By optimizing the geometries of the unit cell in the dielectric metasurfaces, 2D OTFs approaching to isotropic transmission were achieved for the s- and p-polarized beam incidence within 8° (Figs. 5(c) and 5(d)). To verify the operational capability of the isotropic metasurfaces in second-order spatial differentiation, a 2D input image (Fig. 5(e)) was projected to the metasurface, and the output results were calculated corresponding to the x-polarized and unpolarized light, respectively. As seen in the images (Figs. 5(e) and 5(d)), the edge profile for the x-polarized beam illumination presents the morphology of the 2D input image. Meanwhile, it could be found that the effect of edge detection was similar to that of unpolarized beam illumination. In addition to the implementation of even-order differentiation, the isotropic odd-order response was also obtained by modifying the unit cell of the metasurface to break both transverse and longitudinal mirror symmetries. The engineering of 2D nonlocal dielectric metasurfaces thus provides an extensive and realistic platform for different types of mathematical operations.
Fig.5 (a) Unit cell of the second-order spatial differentiator based on the hole dielectric metasurface. (b) Fano transmission curves of the spatial differentiator as functions of an incident angle from 0° to 25°. 2D OTFs of device corresponding to (c) s-polarized and (d) p-polarized wave incidence. The output result of edge detection of (e) a 2D input image based on the second-order spatial differentiator for x-polarized light illumination. Reproduced with permission from Ref. [62]. Copyright 2020, The Chemical Society of America |
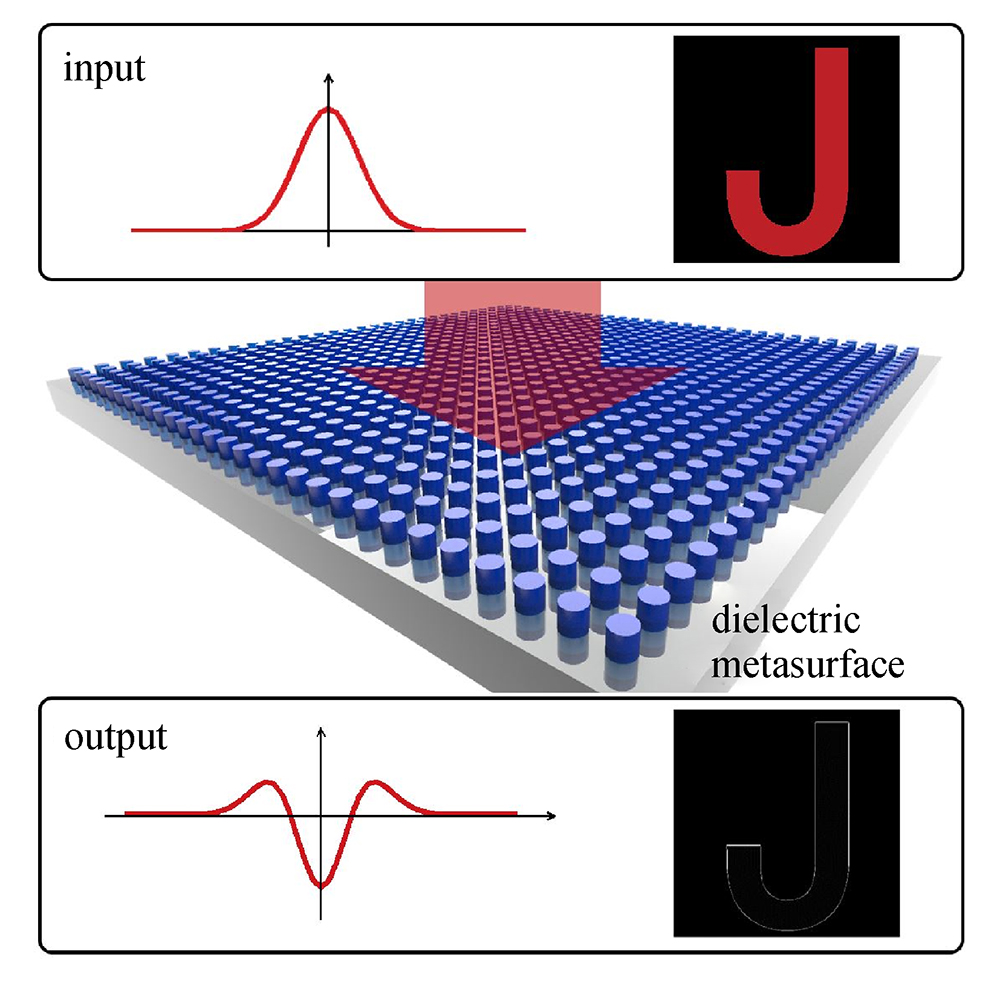
Recently, we proposed a single-layer metasurface of silicon nanodisks to realize spatial differentiation and edge detection with high efficiency and large bandwidth for both polarizations. The proposed metasurface supports electric dipole resonance, and its spatial dispersion can be effectively tailored for specific OTF [48]. Figure 6(a) presents the basic morphology of the device, which allowed the direct transmission of diffracted light with large wave numbers from the edges of the character U, and blocked those with small incident angles from the uniform area, leading to the realization of spatial differentiation and edge detection. By tailoring the spatial dispersion of the electric dipole resonance, the scattered power of the plane wave could be dramatically reduced when the incident angle was increased at the wavelength of 630 nm. In contrast, the scattering behavior of the magnetic dipole exhibited an approximately constant trend, as displayed in Fig. 6(b). Benefiting from the mechanism of electric dipole resonance, high transmission at the incident angle of 15° was obtained, which enabled the achievement of second-order derivation with large spatial bandwidth in the transmission mode. In fact, the working efficiency is important. For the reflection mode, the metal sheet behind the metasurface could guarantee a reflection larger than 60% at the critical spatial frequency of the device bandwidth [33,46,52]. However, for the transmission mode, the absorption of metal could greatly reduce the maximum transmission down to about 36% [63,64]. In contrast, dielectric metasurface can increase the maximum transmission. In the case of neglecting material absorption, the transmission can theoretically approach to one. When silicon material with loss was considered, it could still maintain about 80% [38,47,48,64]. As seen in Figs. 6(c) and 6(d), the dielectric metasurfaces displayed excellent transmission properties along the two orthogonal directions of the 2D OTF images corresponding to s- and p-polarized waves. Complementary OTF characteristics at both polarizations confirmed the realization of second-order spatial differentiation and edge detection for an arbitrary polarization. To demonstrate the effectiveness, the logo of Jinan University as the input image was chosen to observe the output results of the designed metasurfaces for x-polarized and unpolarized light illumination, as illustrated in Figs. 6(e) and 6(f), respectively. Given that the nanodisk was isotropic, the results of edge detection corresponding to both polarizations exhibited similar features. The large spatial bandwidth and polarization-independent characteristics demonstrated the capability of the designed second-order spatial differentiator in high-performance edge detection.
Fig.6 (a) Schematic of the second-order spatial differentiator consisting of a silicon nanodisk metasurface. (b) Scattered power of the electric and magnetic dipole resonances as functions of wavelength for different incident angles from 0° to 25°. 2D OTFs of the device corresponding to the (c) s-polarized wave and (d) p-polarized wave incidence. The output images for edge detection for (e) x-polarized and (f) unpolarized light illumination. Reproduced with permission from Ref. [48]. Copyright 2020, The Optical Society of America |
As mentioned before, spatial differentiation and edge detection can work in both transmission and reflection modes. In fact, the transmission mode is preferred in traditional optical systems because the setup is usually more convenient than that in the reflection mode. Therefore, it is desirable to transfer conventional optical configurations to the metamaterials and metasurfaces platform working in the transmission mode. Furthermore, the module of transmission type is more conveniently to be integrated with other modules, especially in optical imaging systems.
To demonstrate the applicability of dielectric metasurfaces-based spatial differentiators in realistic optical imaging system, a 2D silicon photonic crystal slab embedded in polymethyl methacrylate (PMMA) on a silicon dioxide (SiO2) substrate was fabricated by e-beam lithography and etching processes as a Laplacian operator realizing the second-order derivative of input image Ein [47]. Figure 7(a) presents a schematic of the 2D metasurfaces and the corresponding scanning electron microscope (SEM) image of the cylindrical silicon nanorods. The height of the nanorod was 440 nm, whereas the diameter and period were 280 and 600 nm, respectively. In this structure, the transmission coefficient amplitude as a function of the incident angle along the G-X direction (ϕ = 0°) was theoretically calculated to be 0 at 268 THz (l0 = 1120 nm) for the s-polarized light incidencedue to the presence of Mie resonance with low quality factor. Given the mirror symmetry and reciprocity of the 2D photonic crystal slab along the direction perpendicular to the metasurfaces, there was no output signal for s-polarized light illumination. However, a Fano resonance formed by the quasi-guided mode resulted in a sharp transmission change with an increase in the incident angle for p-polarized light illumination.
The 1D OTF (H(kx)) was measured along the ϕ = 0° azimuthal plane and fitted using a parabolic curve well within the range of numerical aperture (NA) (nkx) = 0.3, as depicted in Fig. 7(b). Here, n means refractive index of dielectric. As an on-chip second-order spatial differentiator, the operational capabilities of the device were experimentally verified using a resolution test chart under the illumination of unpolarized and collimated light at a wavelength of 1120 nm. The results shown in Fig. 7(c) presents the images of edge detection when the modulated light passed through the silicon nanorods metasurfaces, which illustrates that the spatial detection resolution was less than 4 mm over the fabricated 2D differentiator. Combined with the 2D metasurfaces-based spatial differentiator and practical optical imaging system, three types of optical pathway configurations based on a commercial microscope and charge-coupled device (CCD) elements were built to acquire the shapes and boundaries of different biological cells and a plastic flower mold, as illustrated in Figs. 7(d), 7(e), and 7(f). By integrating the differentiator on the surfaces of the objective lens and CCD camera, the target edge images were clearly observed to demonstrate the possibility of achieving a compact optical image processing system based on all-dielectric metasurfaces (Figs. 7(g), 7(h), and 7(i)). The realization of monolithic optical spatial differentiator based on 2D silicon metasurfaces and its integration applications in image processing systems can pave the way to the development of on-chip optical analog computing devices in biological imaging.
Thus far, diverse on-chip optical spatial differentiators have been demonstrated using different artificial metasurfaces [65–67]. Compared with the configurations of metal metasurface-based spatial differentiators, all-dielectric metasurfaces-based operation devices have recently become a popular research topic owing to their excellent compatibility and integration with realistic imaging systems. To further satisfy the requirements of edge detection in practical applications, high-performance spatial differentiators with high efficiency and resolution will be preferred due to the continually increasing demands in imaging visibility and contrast [68,69]. Achieving spatial differentiators with high energy transmission, large spatial bandwidth, and polarization independence are dominating challenges currently. Combining with commercial silicon photonic platform and advanced nanofabrication technologies, experimental demonstrations of the mathematical operation and edge detection in numerous optical image processing scenes will be significantly pursued to excavate much more application potentials [70,71]. Moreover, the integration of on-chip operation devices with other planar optical elements based on dielectric metasurface platforms, such as metalens, metathin diffraction element, will also be a valuable direction in the future.
Fig.7 (a) Schematic of a second-order spatial differentiator consisting of a silicon nanorod array, and the corresponding scanning electron microscope (SEM) image. (b) Measurement results and fitted parabolic curve of the 1D OTF as a function of numerical aperture (NA). (c) Edge detection images using a resolution test chart with the differentiator under unpolarized light illumination of 1120 nm. Optical pathway configurations corresponding to the differentiators integrated in the front of (d) an objective lens, in the front of (e) a commercial charge-coupled device camera, and in the back of (f) a metalens. Target edge images of (g), (h) a biological cell and (i) a plastic flower mold with a 2D spatial differentiator corresponding to the three types of optical pathway configurations. Reproduced with permission from Ref. [47]. Copyright 2020, The Nature Publishing Group |
4 Conclusions
In this review, we summarized the basic working principles of on-chip spatial differentiators based on 2D dielectric metasurfaces. As a widely adopted mechanism, the GF approach with different resonances was discussed by engineering the spatial dispersion of subwavelength structures in metasurfaces, aiming to control the transmission or reflection of light waves with different incident angles. With the help of nonlocal metasurfaces, first- and second-order spatial differentiators with different unit cell geometries, such as the photonic crystal hole, split ring, triangular hole lattice, and nanodisk, were subsequently proposed to design appropriate OTFs. To estimate the performance of 2D-metasurface-based spatial differentiators, optical characteristics, including the spatial bandwidth, polarization dependence, working mode, and efficiency were systematically analyzed and compared for different 2D dielectric metasurface prototypes. Given the important application of spatial differentiators in edge detection, high-efficiency monolithic spatial differentiators with large spatial bandwidth and polarization independence are expected to successfully perform high-resolution edge information acquisition in image processing technology. Combined the realistic optical microscope system with the compact spatial differentiator, the operational capabilities and advantages of 2D devices for edge detection were experimentally demonstrated at three different optical pathway configurations. Clear edge profiles sufficiently verified the practicability and effectiveness of 2D dielectric metasurfaces-based spatial differentiators in the edge detection. The realization of spatial differentiation and edge detection with dielectric metasurfaces paves the way toward the study of complex optical analog computing devices in the future.