Dual non-diffractive terahertz beam generators based on all-dielectric metasurface

Abstract

The applications of terahertz (THz) technology can be greatly extended using non-diffractive beams with unique field distributions and non-diffractive transmission characteristics. Here, we design and experimentally demonstrate a set of dual non-diffractive THz beam generators based on an all-dielectric metasurface. Two kinds of non-diffractive beams with dramatically opposite focusing properties, Bessel beam and abruptly autofocusing (AAF) beam, are considered. A Bessel beam with long-distance non-diffractive characteristics and an AAF beam with low energy during transmission and abruptly increased energy near the focus are generated for x- and y-polarized incident waves, respectively. These two kinds of beams are characterized and the results agree well with simulations. In addition, we show numerically that these two kinds of beams can also carry orbital angular momentum by further imposing proper angular phases in the design. We believe that these metasurface-based beam generators have great potential use in THz imaging, communications, non-destructive evaluation, and many other fields.

Key words： terahertz (THz) wave; all-dielectric metasurface; Bessel beam; abruptly autofocusing (AAF) beam; vortex beam

1 Introduction

Terahertz (1 THz= 10¹² Hz) waves usually refer to the electromagnetic waves with a frequency in the range of 0.1–10 THz, which is a band between far-infrared light and microwaves. With the development of generation [1–3] and detection techniques [4], more research now focuses on the applications of THz waves [5,6] and the development of THz functional devices [7–9]. THz waves have a low photon energy and are transparent to non-polar and non-metallic materials, and many molecules have rotational and low-vibrational lines in the THz band, so that THz waves can be used in spectroscopy and imaging [5,6,10], non-destructive testing [11], chemical analysis [12], communications [13], and many other fields.

Gaussian beams are subject to diffraction, which limits their applications in fields like optical tweezers, optical imaging, laser fabrication. The emergence of diffraction-free beams like Bessel beams [14] and Airy beams [15–17], have greatly overcome this limitation. Bessel beams are characterized by a propagation-invariant intensity distribution over a long distance, and the electric field distribution of such beams is described by a zeroth-order Bessel function of the first kind, which consists of a central lobe with high intensity and several side lobes. Thanks to their properties of non-diffraction and self-reconstruction, Bessel beams are especially useful in laser material processing [18], optical microscopy [19], and optical micromanipulation [20]. In the THz domain, Bessel beams also find important applications in long depth-of-focus imaging [21], detection [22], and tomography [23]. In these applications, Bessel THz beams can alleviate the problem of quick beam-spreading caused by the diffraction of tightly-focused Gaussian beams. Airy beams are also diffraction-free beams, but unlike Bessel beams, they propagate along a curved patch. The main characteristics of Airy beams are diffraction-free propagation, self-bending, and self-recovery, making such beams valuable tools in a wide range of fields such as optical tweezers [24], light-sheet microscopy [25], and laser micromachining [26]. Abruptly autofocusing (AAF) beams, also termed circular Airy beams, have a unique feature of maintaining a low intensity during propagation and this intensity suddenly rises by several orders of magnitude at the focal point, which is just opposite to the long depth-of-focus property of Bessel beams. AAF beams have a great intensity contrast along the transmission path, so they are widely used in laser ablation [27], microparticle trapping [28], and multiscale photo-polymerization [29]. As the power or intensity of THz sources rises, the AAF THz beams are also expected to have important applications in similar areas, such as in biomedical inspection to avoid tissue damage and in imaging to elude obstacles, etc.

Metasurfaces are two-dimensional metamaterials consisting of an array of subwavelength elements, which can modulate the phase, amplitude, and polarization of the incident electromagnetic wave [30–34]. They have been widely used as metalenses [35], polarization controllers [36], beam splitters [37], holographic plates [38], and other functional devices. In addition, the flexible design of metasurfaces allows them to be widely used to generate non-diffractive beams, including Bessel beams [39–41], Airy beams [42–44], and vector vortex beams [45,46]. They have also become an important method to fabricate functional devices in the THz frequency range [47–50]. This is especially true for the case of generation of diffraction-free beams and structured beams due to the lack of devices like spatial light modulators which are often used in the optical and infrared frequency ranges. Compared with plasmonic metasurfaces with metallic elements, metasurfaces based on dielectric materials (such as the widely used silicon) as the building block suffer no ohmic loss introduced by the metallic elements, so their transmission efficiency is usually much higher [51,52]. In addition, a great advantage of metasurfaces is that the meta-atoms have many degrees of freedom such that the metasurfaces can be designed to be multifunctional planar devices.

In this work, we report a set of polarization-dependent transmission-type all-silicon dielectric metasurfaces for the generation of two different types of non-diffractive THz beams, i.e., Bessel beams and AAF beams. These dual non-diffractive THz beam generators are designed to generate Bessel beams and AAF beams under x- and y-polarized incidences, respectively. The focusing characteristics of these two beams are opposite, so the metasurfaces can control the transmitted THz waves depending on the needs, and these metasurface-based beam generators will contribute to a wider application of THz technology.

2 Design strategy

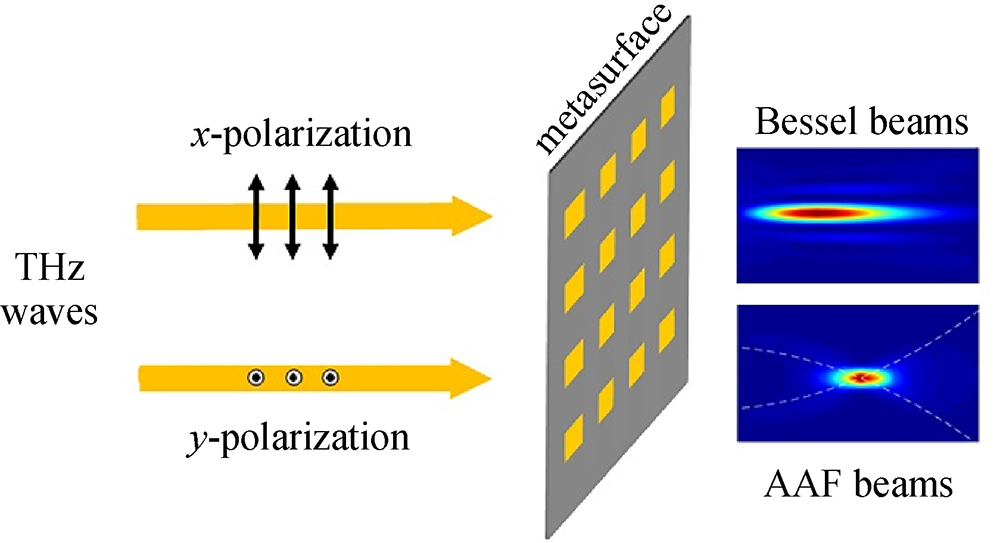
To realize the desired dual non-diffractive THz beam generators, the meta-atoms of the designed metasurface are polarization-dependent rectangular-shaped silicon pillars on a silicon substrate, as schematically shown in Fig. 1(a). These anisotropic meta-atoms act as rectangular waveguides, allow the phases of the incident x- and y-polarized waves to be modulated separately [53]. The commercial software CST MICROWAVE STUDIO is used to simulate the response of the lossless silicon meta-atoms (n_Si = 3.4496) for x- and y-polarized incident THz waves at 1 THz. The side lengths of the pillars l_x and l_y are from 30 to 135 mm, the height of the pillars is h = 200 mm, and the period of the square unit cell is p = 150 mm. From the simulation results, 64 meta-atoms in total are selected to achieve the phase modulation within the 0 to 2π range at an interval of π/4 for incident THz waves with x- and y-polarized incidences, that is, 8 side lengths are used for each polarization. To illustrate the design procedure, we can consider putting the 64 meta-atoms in an 8 × 8 table, where the row of the table corresponds to the phase delay for x-polarized incident light (0, π/4, π/2, 3π/4, π, 5π/4, 3π/2, 7π/4) and the column corresponds to the phase delay for y-polarized incident light (0, π/4, π/2, 3π/4, π, 5π/4, 3π/2, 7π/4). The phase delays ϕ_x and ϕ_y required at point (x, y) can be calculated as described later, and by matching this set of data to the closest position in the table, the meta-atom that should be selected at point (x, y) can be determined. Figure 1(b) shows a scanning electron microcopy (SEM) image of the fabricated metasurface.

Fig.1 (a) Schematic of the rectangular-shaped pillar unit cell of the metasurface-based dual beam generator, which is made of silicon. The period of the square unit cell is p, the height is h, and the sides are l_x and l_y, respectively. (b) Scanning electron microcopy (SEM) image of the fabricated metasurface. The inset shows a zoomed portion

Full size|PPT slide

First, we consider the case of x-polarized incidence, which will generate a Bessel beam in our design. The phase profile for the Bessel beam is described by [54]

(1){\varphi }_x(x,y)=\mathrm{2}\mathrm{\pi }-{\displaystyle \frac{\mathrm{2}\mathrm{\pi }}{\lambda }}\sqrt{x^{\mathrm{2}}+y^{\mathrm{2}}}\mathrm{NA},

where \sqrt{x^{\mathrm{2}}+y^{\mathrm{2}}}=r is the radius in polar coordinates, l = 300 mm is the wavelength of the incident THz wave, and NA is the numerical aperture of the equivalent axicon for the metasurface beam generator, related to the base angle α of the axicon by

(2)\mathrm{NA}=\sin \left({\sin }^{-\mathrm{1}}\right(n_{\mathrm{mat}}\sin \alpha )-\alpha ).

Here n_mat is the refractive index of the constituent material, chosen as n_Si = 3.4496 in this work.

According to Eq. (1), ϕ_x(0, 0) = 2π, which is equivalent to ϕ_x(0, 0) = 0, the period of the pillars is p = 150 mm, and the phase value of the silicon pillar closest to the center is ϕ_x(150, 0) = –π/4 (r = 150 mm in this case). By substituting the above data into Eq. (1), we can get NA= 0.25. Then substituting this NA value into Eq. (2) yields α = 5.75°. Thus, it can be seen that the metasurface designed with the above parameters can be equivalent to an axicon with a base angle α = 5.75° for the x-polarized incident beam.

The diffraction-free transmission distance Z_max of the zeroth-order Bessel beam can be derived as [21]

(3)Z_{\max }={\displaystyle \frac{{\omega }_{\mathrm{0}}}{\tan \left(\left(n_{\mathrm{mat}}-\mathrm{1}\right)\alpha \right)}},

where ω₀ is the radius of the incident Gaussian beam waist. When ω₀ = 1.5 mm is assumed, Z_max = 6 mm will be obtained.

The full width at half maximum (FWHM) of the zeroth-order Bessel beam can be derived as [54]

(4)\mathrm{FWHM}={\displaystyle \frac{\mathrm{0.358}\lambda }{\mathrm{NA}}}.

Here l = 300 mm, NA= 0.25, so we can get FWHM= 429.6 mm.

Figures 2(a) and 2(b) show the simulation results of a generated Bessel beam, where Z_max is very close to 6 mm, and the FWHM is 447.7 mm, and they conform well to the theoretical values.

Fig.2 Simulated performance of the dual non-diffractive THz beam generator. (a) and (b) Simulated intensity profiles for a Bessel beam with Z_max = 6 mm in the x-z (y = 0) and x-y cross-sections (z = 4 mm), respectively, under x-polarized incidence. (c) and (d) Simulated intensity profiles for a Bessel beam with Z_max = 10 mm in the x-z (y = 0) and x-y cross-sections (z = 7 mm), respectively, under x-polarized incidence. (e) and (f) Simulated intensity profiles for the AAF beam in the x-z (y = 0) and x-y cross-sections (z = 2.5 mm), respectively, under y-polarized incidence

Full size|PPT slide

In the above simulation, ω₀ = 1.5 mm, that is, the diameter of the beam waist is 3 mm, so the corresponding number of working meta-atoms is 21 × 21. According to Eq. (3), the non-diffraction distance Z_max of the Bessel beam generated is directly proportional to the radius of the incident Gaussian beam. Thus, the size of the incident beam allows for easy tuning of Z_max. In Figs. 2(c) and 2(d), the simulation of another Bessel beam with Z_max = 10 mm is shown. In this case, the incident Gaussian beam radius is 2.5 mm and the number of required meta-atoms would be 35 × 35. In the fabricated devices, the samples are large enough to take this tuning possibility into account. It should also be pointed out that the focus of the AAF beam is not affected by the incident beam size.

Then we consider the case of y-polarized incidence, where an AAF beam will be generated. The AAF beam can be generated by an airy beam whose trajectory is c(z) = r₀− az^m rotated around the transmission z axis [55]. Here r₀ is the radius of the initial annulus-type spot of the AAF beam, a is a parameter which determines the trajectory of the beam and is far less than 1, and m is the order of the trajectory of the Airy beam.

The phase profile required for the AAF beam is [56]

(5)

AAF beams with different trajectories can be realized with the choice of the parameters a, m, and r₀. According to the trajectory equation, when c(z) = 0, all the Airy beams that form the AAF beam focus on one point. This value of z represents the focal length of the AAF beam and can be derived as

(6)z_c={\left({\displaystyle \frac{r_{\mathrm{0}}}{a}}\right)}^{\frac{\mathrm{1}}{m}}.

According to Eq. (6), the focal position of the AAF beams can be adjusted by r₀ and a. As an example, the case of c(z) = 350 – 5.6 × 10⁻⁵z² is considered, and the focal length is determined to be z_c = 2.5 mm. Figures 2(e) and 2(f) show the simulation results, where it can be seen that the focal position is consistent with the theoretical calculation. Note that the focal length determined above is from the output surface of the device, while the distance z in the figure is measured from the bottom of the pillars and hence the focus will be around 2.7 mm in the simulation considering the height of the pillars (h = 200 mm).

Fig.3 Illustration of experimental setup. 3-D TSH: three-dimensional translational sample holder; 2-D TD: two-dimensional translational detector

Full size|PPT slide

3 Experimental results and discussion

To experimentally demonstrate the feasibility of the dual non-diffractive THz beam generator, all-dielectric metasurface samples based on silicon are fabricated by optical lithography followed by deep reactive ion etching [57]. The metasurface samples are composed of 41 × 41 silicon pillars to allow for a wide tuning the propagation-invariant distance of the Bessel beam, the thickness of the substrate is 800 mm, the size of the metasurface samples is 6.15 mm × 6.15 mm, and the working frequency in the whole work is 1 THz. To characterize the fabricated dual non-diffractive THz beam generators, a near-field scanning THz microscopy system is used, which can also measure the far-field distributions, as illustrated in Fig. 3 [58]. We use a 1550 nm femtosecond fiber laser as the light source and a beam splitter to divide its output into two beams. One beam passes through a piece of fiber and is back-coupled into free space, then this beam is focused on a probe which is based on low-temperature-grown GaAs. This part of the optical path is used to detect the THz signals. The frequency doubling module is used to convert the light to 780 nm to excite the carriers in GaAs. The other beam passes through an optical fiber delay line and then is incident on the photoconductive antenna fabricated on an InGaAs/InAlAs substrate. This part of the optical path is used to generate the THz radiation. In the measurement, the THz radiation is incident onto the substrate side of the metasurface, and the metasurface is placed on a three-dimensional translational sample holder that can be translated in the x, y, and z directions. On the other side of the metasurface, a THz probe with a two-dimensional translational detector that can be translated in the x and y directions is used to scan point by point the electric field of the transmitted THz waves. The beam waist radius of the incident THz waves is 1.5 mm, and the waves are linearly polarized, and the x and y polarization states of the incident radiation can be switched by rotating the metasurface device by 90°. The current dumping amplifier and lock-in amplifier enable the probe to collect the electrical signal, and then send the collected time-domain data to the computer for processing, after which the measured electric field distribution can be obtained.

Fig.4 Experimental results of the dual non-diffractive THz beam generator. (a) and (b) Measured normalized intensity distributions for the Bessel beam in the x-z (y = 0) and x-y cross-sections (z = 4 mm), respectively, under x-polarized incidence. (c) and (d) Measured normalized intensity distributions for the AAF beam in the x-z (y = 0) and x-y cross-sections (z = 2.5 mm), respectively, under y-polarized incidence

Full size|PPT slide

Figure 4(a) shows the x-z plane intensity distribution of the Bessel beam generated by the metasurface for x-polarized incidence, and Fig. 4(b) shows the x-y cross-section distribution of the Bessel beam at a transmission distance of 4 mm. It can be observed that the diffraction-free propagation distance (Z_max) and the FWHM of the Bessel beam generated in the experiment are consistent with the theoretical prediction and simulation results: Z_max is approximately 6 mm, and the FWHM is 414.5 mm. When the polarization state of the incident radiation is changed to y-polarization, an AAF beam is generated instead by the metasurface, and Fig. 4(c) shows its intensity distribution in the x-z plane. As can be seen, the focal position of the AAF beam coincides with the theoretical prediction and simulation results. Figure 4(d) shows the x-y cross-section distribution of the AAF beam at a transmission distance 2.5 mm. Again, good agreement with Fig. 2(d) is observed.

Fig.5 (a) and (b) Simulated intensity profiles for AAF beams with two different focal lengths (z_c = 3.5 mm and z_c = 4.5 mm, respectively) in the x-z cross-section (y = 0). (c) and (d) Corresponding experimental results

Full size|PPT slide

The parameters of the Bessel beams and AAF beams can be easily tuned. As a further illustration, we show how the focal length of the AAF beams can be adjusted by changing the parameters of the trajectory c(z). As shown in Fig. 5(a), when the trajectory is c(z) = 500 − 4.08163 × 10⁻⁵z², an AAF beam with a focal length of 3.5 mm is generated. Figure 5(b) shows the x-z plane intensity distribution of an AAF beam with c(z) = 600 − 2.96296 × 10⁻⁵z², and the focal length of the AAF beam is changed to 4.5 mm. Figures 5(c) and 5(d) show the corresponding experimental results of the above two designs.

Additionally, an angular phase term nϕ for an nth-order vortex beam can be added to the above radial phase distribution for the Bessel and AAF beams, and then the nth-order Bessel beam and the nth-order AAF vortex beam carrying orbital angular momentum can be generated [54,59]. Here, we design a non-diffractive beam generator that can respectively generate a 1st-order Bessel beam under x-polarized incidence and a 2nd-order AAF vortex beam under y-polarized incidence. Under x-polarized incidence, Figs. 6(a) and 6(b) show the x-z and x-y cross-sections (z = 7 mm) intensity profile of the 1st-order Bessel beam with a diffraction-free distance of 10 mm, where we can see that the center of the higher-order Bessel beam is a dark spot. The diffraction-free distance can be adjusted by changing the waist radius of the incident beam, and in the case of Fig. 6(a) the waist of the incident beam is ω₀ = 2.5 mm. Under y-polarized incidence, Figs. 6(c) and 6(d) show the x-z and x-y cross-sections (z = 3.85 mm) intensity profile of the 2nd-order AAF vortex beam, whose focal length is 3.5 mm. In Fig. 6(c), the maximum intensity of the AAF vortex beam is located at 3.85 mm. Considering the height of the pillars being 0.2 mm that is included in the z distance, the corresponding theoretical focal position by Eq. (6) would be 3.7 mm, resulting in an error of 0.15 mm, which is within an acceptable range. The focal spot of the AAF vortex beam is an annulus in this case.

To characterize the efficiency of the proposed beam generators, we calculate the intensity of the wave transmitted through the silicon substrate as the reference I_ref. The efficiency of the Bessel beam generator is then calculated as E_BB = I_BB/I_ref = 93.3%, and the efficiency of the AAF beam generator E_AAF = I_AAF/I_ref = 90.4%, where I_BB and I_AAF represent the intensity distributions of the Bessel and AAF beams after the devices, respectively.

The designed metasurface beam generator is based on the propagation phase, which is supposed to control linearly polarized waves. The metasurface designed by this design method is a narrowband device. The designed working frequency in this work is 1 THz, and the device can work within the range of about 0.95–1.05 THz. Geometric phase, also known as called Pancharatnam-Berry phase, can be used (even in combination with propagation phase) to control circularly polarized waves [44,60,61], and the device is often broadband.

Fig.6 (a) and (b) Intensity profile of the 1st-order Bessel beam (Z_max = 10 mm) in the x-z and x-y cross-sections (z = 7 mm), respectively, under x-polarized incidence. (c) and (d) Intensity profile of the 2nd-order AAF vortex beam (z_c = 3.5 mm) in the x-z and x-y cross-sections (z = 3.85 mm), respectively, under y-polarized incidence

Full size|PPT slide

4 Conclusions

All-silicon dielectric metasurfaces that can produce two different types of non-diffractive THz beams are proposed and demonstrated. By changing the polarization state of the incident waves, the transmission can be switched between two non-diffractive THz beams with dramatically different focusing characteristics, that is, a Bessel beam with a long-distance non-diffractive propagation feature and an AAF beam with low energy during transmission but abruptly increased energy near the focus will be generated for x- and y-polarized incident waves, respectively. These two kinds of beams are characterized and the results agree well with simulations. Such multifunctional metadevices are compatible with current standard fabrication technology and suited in different application scenarios. We believe that these metasurface-based dual non-diffractive THz beam generators have great potential use in THz imaging, non-destructive testing, biomedical science, and many other fields.

Acknowledgements

This work was funded by the National Key Research and Development Program of China (No. 2017YFA0701004), the National Natural Science Foundation of China (Grant Nos. 61935015, 61875150, 61605143, 61735012, 61722509, and 61871212), Tianjin Municipal Fund for Distinguished Young Scholars (No. 18JCJQJC45600), and King Abdullah University of Science and Technology (KAUST) Office of Sponsored Research (OSR) (No. OSR-2016-CRG5-2950).

References

1 Stepanov A G, Henin S, Petit Y, Bonacina L, Kasparian J, Wolf J P. Mobile source of high-energy single-cycle terahertz pulses. Applied Physics B, Lasers and Optics, 2010, 101(1–2): 11–14

2 Hebling J, Almási G, Kozma I, Kuhl J. Velocity matching by pulse front tilting for large area THz-pulse generation. Optics Express, 2002, 10(21): 1161–1166

PMID

3 Polyushkin D K, Hendry E, Stone E K, Barnes W L. THz generation from plasmonic nanoparticle arrays. Nano Letters, 2011, 11(11): 4718–4724

PMID

4 Lu X, Zhang X C. Balanced terahertz wave air-biased-coherent-detection. Applied Physics Letters, 2011, 98(15): 151111

5 Tonouchi M. Cutting-edge terahertz technology. Nature Photonics, 2007, 1(2): 97–105

6 Ferguson B, Zhang X C. Materials for terahertz science and technology. Nature Materials, 2002, 1(1): 26–33

PMID

7 Liu X, Fan K, Shadrivov I V, Padilla W J. Experimental realization of a terahertz all-dielectric metasurface absorber. Optics Express, 2017, 25(1): 191–201

PMID

8 Chen H T, Padilla W J, Zide J M, Gossard A C, Taylor A J, Averitt R D. Active terahertz metamaterial devices. Nature, 2006, 444(7119): 597–600

PMID

9 Liu X, Parrott E P J, Ung B S Y, Pickwell-MacPherson E. Exploiting total internal reflection geometry for efficient optical modulation of terahertz light. APL Photonics, 2016, 1(7): 076103

10 Löffler T, Bauer T, Siebert K, Roskos H, Fitzgerald A, Czasch S. Terahertz dark-field imaging of biomedical tissue. Optics Express, 2001, 9(12): 616–621

PMID

11 Amenabar I, Lopez F, Mendikute A. In introductory review to THz non-destructive testing of composite mater. Journal of Infrared, Millimeter and Terahertz Waves, 2013, 34(2): 152–169

12 Liu J, Mao L, Ku J, Peng H, Lao Z, Chen D, Yang B. Using terahertz spectroscopy to identify transgenic cottonseed oil according to physicochemical quality parameters. Optik (Stuttgart), 2017, 142: 483–488

13 Federici J F, Moeller L. Review of terahertz and subterahertz wireless communications. Journal of Applied Physics, 2010, 107(11): 111101

14 Durnin J, Miceli J Jr, Eberly J H. Diffraction-free beams. Physical Review Letters, 1987, 58(15): 1499–1501

PMID

15 Siviloglou G A, Christodoulides D N. Accelerating finite energy Airy beams. Optics Letters, 2007, 32(8): 979–981

PMID

16 Efremidis N K, Christodoulides D N. Abruptly autofocusing waves. Optics Letters, 2010, 35(23): 4045–4047

PMID

17 Cottrell D M, Davis J A, Hazard T M. Direct generation of accelerating Airy beams using a 3/2 phase-only pattern. Optics Letters, 2009, 34(17): 2634–2636

PMID

18 Bhuyan M K, Courvoisier F, Lacourt P A, Jacquot M, Salut R, Furfaro L, Dudley J M. High aspect ratio nanochannel machining using single shot femtosecond Bessel beams. Applied Physics Letters, 2010, 97(8): 081102

19 Dufour P, Piché M, De Koninck Y, McCarthy N. Two-photon excitation fluorescence microscopy with a high depth of field using an axicon. Applied Optics, 2006, 45(36): 9246–9252

PMID

20 Arlt J, Garceschavez V, Sibbett W, Dholakia K. Optical micromanipulation using a Bessel light beam. Optics Communications, 2001, 197(4–6): 239–245

21 Bitman A, Moshe I, Zalevsky Z. Improving depth-of field in broadband THz beams using nondiffractive Bessel beams. Optics Letters, 2012, 37(19): 4164–4166

PMID

22 Ok G, Choi S W, Park K H, Chun H S. Foreign object detection by sub-terahertz quasi-Bessel beam imaging. Sensors (Basel), 2013, 13(1): 71–85

PMID

23 Busch S F, Town G, Scheller M A, Koch M. Focus free terahertz reflection imaging and tomography with Bessel beams. Journal of Infrared, Millimeter and Terahertz Waves, 2015, 36(3): 318–326

24 Baumgartl J, Mazilu M, Dholakia K. Optically mediated particle clearing using Airy wavepackets. Nature Photonics, 2008, 2(11): 675–678

25 Vettenburg T, Dalgarno H I, Nylk J, Coll-Lladó C, Ferrier D E K, Čižmár T, Gunn-Moore F J, Dholakia K. Light-sheet microscopy using an Airy beam. Nature Methods, 2014, 11(5): 541–544

PMID

26 Mathis A, Courvoisier F, Froehly L, Furfaro L, Jacquot M, Lacourt P A, Dudley J M. Micromachining along a curve: femtosecond laser micromachining of curved profiles in diamond and silicon using accelerating beams. Applied Physics Letters, 2012, 101(7): 071110

27 Papazoglou D G, Efremidis N K, Christodoulides D N, Tzortzakis S. Observation of abruptly autofocusing waves. Optics Letters, 2011, 36(10): 1842–1844

PMID

28 Zhang P, Prakash J, Zhang Z, Mills M S, Efremidis N K, Christodoulides D N, Chen Z. Trapping and guiding microparticles with morphing autofocusing Airy beams. Optics Letters, 2011, 36(15): 2883–2885

PMID

29 Manousidaki M, Papazoglou D, Farsari M, Tzortzakis S. Abruptly autofocusing beams enable advanced multiscale photo-polymerization. Optica, 2016, 3(5): 525–530

30 Yu N, Genevet P, Kats M A, Aieta F, Tetienne J P, Capasso F, Gaburro Z. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science, 2011, 334(6054): 333–337

PMID

31 Pors A, Bozhevolnyi S I. Plasmonic metasurfaces for efficient phase control in reflection. Optics Express, 2013, 21(22): 27438–27451

PMID

32 Ni X, Emani N K, Kildishev A V, Boltasseva A, Shalaev V M. Broadband light bending with plasmonic nanoantennas. Science, 2012, 335(6067): 427

PMID

33 Hu Y, Luo X, Chen Y, Liu Q, Li X, Wang Y, Liu N, Duan H. 3D-Integrated metasurfaces for full-colour holography. Light, Science & Applications, 2019, 8(1): 86

PMID

34 Zhang C, Divitt S, Fan Q, Zhu W, Agrawal A, Lu Y, Xu T, Lezec H J. Low-loss metasurface optics down to the deep ultraviolet region. Light, Science & Applications, 2020, 9(1): 55

PMID

35 Wen D, Yue F, Ardron M, Chen X. Multifunctional metasurface lens for imaging and Fourier transform. Scientific Reports, 2016, 6(1): 27628

PMID

36 Liu Z, Li Z, Liu Z, Cheng H, Liu W, Tang C, Gu C, Li J, Chen H, Chen S, Tian J. Single-layer plasmonic metasurface half-wave plates with wavelength-independent polarization conversion angle. ACS Photonics, 2017, 4(8): 2061–2069

37 Wang B, Dong F, Feng H, Yang D, Song Z, Xu L, Chu W, Gong Q, Li Y. Rochon-prism-like planar circularly polarized beam splitters based on dielectric metasurfaces. ACS Photonics, 2018, 5(5): 1660–1664

38 Zhang C, Yue F, Wen D, Chen M, Zhang Z, Wang W, Chen X. Multichannel metasurface for simultaneous control of holograms and twisted light beams. ACS Photonics, 2017, 4(8): 1906–1912

39 Dharmavarapu R, Hock Ng S, Eftekhari F, Juodkazis S, Bhattacharya S. MetaOptics: opensource software for designing metasurface optical element GDSII layouts. Optics Express, 2020, 28(3): 3505–3516

PMID

40 Mahmood N, Jeong H, Kim I, Mehmood M Q, Zubair M, Akbar A, Saleem M, Anwar M S, Tahir F A, Rho J. Twisted non-diffracting beams through all dielectric meta-axicons. Nanoscale, 2019, 11(43): 20571–20578

PMID

41 Akram M R, Mehmood M Q, Tauqeer T, Rana A S, Rukhlenko I D, Zhu W. Highly efficient generation of Bessel beams with polarization insensitive metasurfaces. Optics Express, 2019, 27(7): 9467–9480

PMID

42 Hao W, Deng M, Chen S, Chen L. High-efficiency generation of Airy beams with Huygens’ metasurface. Physical Review Applied, 2019, 11(5): 054012

43 Yu B, Wen J, Chen L, Zhang L, Fan Y, Dai B, Kanwal S, Lei D, Zhang D. Polarization-independent highly efficient generation of Airy optical beams with dielectric metasurfaces. Photonics Research, 2020, 8(7): 1148–1154

44 Fan Q, Zhu W, Liang Y, Huo P, Zhang C, Agrawal A, Huang K, Luo X, Lu Y, Qiu C, Lezec H J, Xu T. Broadband generation of photonic spin-controlled arbitrary accelerating light beams in the visible. Nano Letters, 2019, 19(2): 1158–1165

PMID

45 Yue F, Wen D, Xin J, Gerardot B D, Li J, Chen X. Vector vortex beam generation with a single plasmonic metasurface. ACS Photonics, 2016, 3(9): 1558–1563

46 Dharmavarapu R, Izumi K, Katayama I, Ng S H, Vongsvivut J, Tobin M J, Kuchmizhak A, Nishijima Y, Bhattacharya S, Juodkazis S. Dielectric cross-shaped-resonator-based metasurface for vortex beam generation at mid-IR and THz wavelengths. Nanophotonics, 2019, 8(7): 1263–1270

47 He J, Dong T, Chi B, Zhang Y. Metasurfaces for terahertz wavefront modulation: a review. Journal of Infrared, Millimeter and Terahertz Waves, 2020, 41(6): 607–631

48 Guo J, Wang T, Zhao H, Wang X, Feng S, Han P, Sun W, Ye J, Situ G, Chen H, Zhang Y. Reconfigurable terahertz metasurface pure phase holograms. Advanced Optical Materials, 2019, 7(10): 1801696

49 Liu W, Hu B, Huang Z, Guan H, Li H, Wang X, Zhang Y, Yin H, Xiong X, Liu J, Wang Y. Graphene-enabled electrically controlled terahertz meta-lens. Photonics Research, 2018, 6(7): 703–708

50 Zhao H, Quan B, Wang X, Gu C, Li J, Zhang Y. Demonstration of orbital angular momentum multiplexing and demultiplexing based on a metasurface in the terahertz band. ACS Photonics, 2018, 5(5): 1726–1732

51 Genevet P, Capasso F, Aieta F, Khorasaninejad M, Devlin R. Recent advances in planar optics: from plasmonic to dielectric metasurfaces. Optica, 2017, 4(1): 139–152

52 Staude I, Schilling J. Metamaterial-inspired silicon nanophotonics. Nature Photonics, 2017, 11(5): 274–284

53 Arbabi A, Horie Y, Bagheri M, Faraon A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nature Nanotechnology, 2015, 10(11): 937–943

PMID

54 Chen W T, Khorasaninejad M, Zhu A Y, Oh J, Devlin R C, Zaidi A, Capasso F. Generation of wavelength-independent subwavelength Bessel beams using metasurfaces. Light, Science & Applications, 2017, 6(5): e16259

PMID

55 Chremmos I, Efremidis N K, Christodoulides D N. Pre-engineered abruptly autofocusing beams. Optics Letters, 2011, 36(10): 1890–1892

PMID

56 Zhao Z, Xie C, Ni D, Zhang Y, Li Y, Courvoisier F, Hu M. Scaling the abruptly autofocusing beams in the direct-space. Optics Express, 2017, 25(24): 30598–30605

PMID

57 Wang Q, Xu Q, Zhang X, Tian C, Xu Y, Gu J, Tian Z, Ouyang C, Zhang X, Han J, Zhang W. All-dielectric meta-holograms with holographic images transforming longitudinally. ACS Photonics, 2018, 5(2): 599–606

58 Xu Y, Zhang X, Tian Z, Gu J, Ouyang C, Li Y, Han J, Zhang W. Mapping the near-field propagation of surface plasmons on terahertz metasurfaces. Applied Physics Letters, 2015, 107(2): 021105

59 Ou K, Li G, Li T, Yang H, Yu F, Chen J, Zhao Z, Cao G, Chen X, Lu W. High efficiency focusing vortex generation and detection with polarization-insensitive dielectric metasurfaces. Nanoscale, 2018, 10(40): 19154–19161

PMID

60 Yang Q, Chen X, Xu Q, Tian C, Xu Y, Cong L, Zhang X, Li Y, Zhang C, Zhang X, Han J, Zhang W. Broadband terahertz rotator with an all-dielectric metasurface. Photonics Research, 2018, 6(11): 1056–1061

61 Zhang D, Lin Z, Liu J, Zhang J, Zhang Z, Hao Z, Wang X. Broadband high-efficiency multiple vortex beams generated by an interleaved geometric-phase multifunctional metasurface. Optical Materials Express, 2020, 10(7): 1531–1544