Intense terahertz radiation: generation and application

Abstract

Strong terahertz (THz) radiation provides a powerful tool to manipulate and control complex condensed matter systems. This review provides an overview of progress in the generation, detection, and applications of intense THz radiation. The tabletop intense THz sources based on Ti:sapphire laser are reviewed, including photoconductive antennas (PCAs), optical rectification sources, plasma-based THz sources, and some novel techniques for THz generations, such as topological insulators, spintronic materials, and metasurfaces. The coherent THz detection methods are summarized, and their limitations for intense THz detection are analyzed. Applications of intense THz radiation are introduced, including applications in spectroscopy detection, nonlinear effects, and switching of coherent magnons. The review is concluded with a short perspective on the generation and applications of intense THz radiation.

Key words： terahertz (THz) radiation; THz generation; THz detection; light–matter interaction

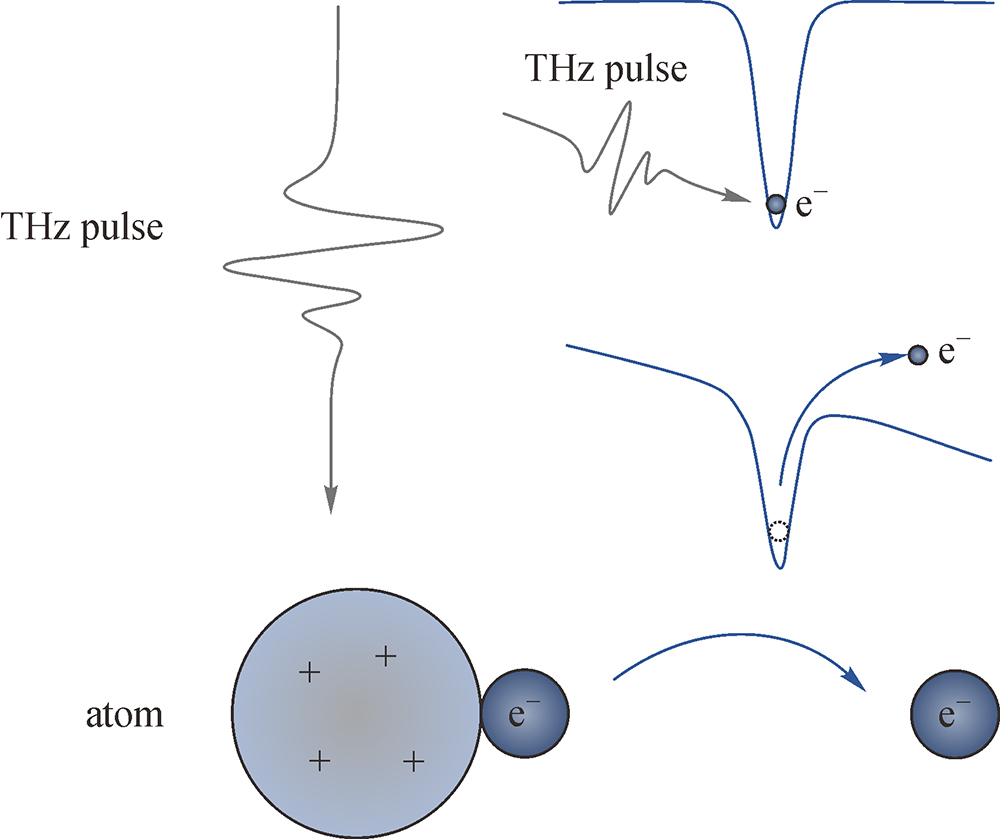
Introduction

Terahertz (THz) radiation comprises electromagnetic waves whose frequency range (0.1–30 THz) lies between the microwave and infrared bands. It is a spectral window that is rich with scientific opportunities [¹–⁴]. THz waves allow direct access to numerous low-energy excitations such as lattice vibrations, molecular rotations, spin waves, internal excitations of bound electron–hole pairs, phonons in crystalline solids, and hydration states of biological systems [⁵]. In particular, time-domain spectroscopy can measure the THz transient in the time domain and after Fourier transformation; both the amplitude and phase information of the THz radiation at each frequency can be obtained, such that the complex dielectric function of a sample can be extracted without having to rely on the Kramers–Kronig relation. Owing to the rapid development of THz sources and detectors, the understanding of the physics of elementary excitations has grown significantly.

Beyond spectroscopy, recent developments in intense THz sources with electric fields up to 100 MV/cm [⁶] make it possible to investigate dynamical nonlinear transport phenomena and nonlinear interactions of excitation modes [⁷]. In a single-cycle THz electric field, an electron will be accelerated and has an average kinetic energy U_k [⁸].

(1)U_{\mathrm{k}}={\displaystyle \frac{e^{\mathrm{2}}{E}_{\mathrm{THz}}^{\mathrm{2}}}{\mathrm{4}m{\omega }_{\mathrm{THz}}^2}},

where E_THz and ω_THz are the electric-field amplitude and frequency of the THz transient, e is the elementary charge, and m the mass of electron. Because U_k increases quadrat-ically with the inverse square of the frequency, the THz electric field can provide a kinetic energy four orders of magnitude larger than that of a visible light source. For an electron in a THz field of 10 MV/cm amplitude, U_k can reach 100 eV, which is much larger than the escape energy of an electron from a hydrogen atom and large enough to induce nonlinear transport phenomena.

Intense THz transients also provide an alternative to study magnetic excitation. The magnetic field can exceed 33 T for a THz transient with an electric field of 100 MV/cm while the duration is less than 1 ps. This magnetic field can directly excite antiferromagnetic resonances irrespective of the magneto-optical susceptibility without excessive thermal effects [⁹,¹⁰]. It can also exert a significant torque on the electron spin magnetic-dipole moment.

In this review, we summarize methods for generation of intense THz transients based on tabletop Ti:sapphire femtosecond laser systems. The advantages and disadvantages of each approach are analyzed. Next techniques for intense THz detection are introduced and difficulties to be solved are discussed. Some applications of strong THz field are reviewed and an outlook is given.

Generation of intense terahertz transients

In this section, we summarize approaches for generation of strong-field THz radiation. Although free-electron lasers can radiate intense THz radiation with peak field amplitudes of several tens of MV/cm [¹¹,¹²], they are large, costly, and complex. Therefore, we focus our attention on tabletop THz generation systems. Tabletop THz systems can be divided into the three major categories of photoconductive antenna (PCA), optical rectification, and laser–plasma interaction systems. Recently, new methods for THz generation, including topological insulators, spintronic materials, and metasurfaces, have also been reported, and these new technologies that are expected to be applied to intense THz generation are also summarized.

Photoconductive antenna

PCA is a kind of electron switch commonly used for THz generation. It is composed of an antenna and a semiconductor or dielectric substrate. The conductivity of semiconductor or insulator substrate will be enhanced under light illumination. To emit THz radiation, the photoconductive switch should operate on the sub-picosecond time scale. The time of the photoconductive switch is determined by the lifetime of photo-excited carriers in the substrate. The carrier mobility and breakdown voltage threshold are two factors that affect the THz radiation generated by the PCA. Materials which can effectively produce THz radiation are low temperature grown gallium arsenide (LT-GaAs) [¹³–¹⁵], radiation-damaged silicon-on-sapphire (RD-SOS) [¹⁶], chromium-doped gallium arsenide (Cr-GaAs) [¹⁷], indium phosphide (InP) [¹⁸], and amorphous silicon [¹⁹].

To meet the demand for the rapid development of high-power THz sources, the large aperture photoconductive antenna (LA-PCA) was proposed in 1993 [²⁰], which can radiate THz radiation up to µJ. For the PCA, the radiated THz electric field is proportional to the time derivative of the transient current and to the bias voltage. The maximum efficiency of a PCA, η_max, is obtained when the LA-PCA is irradiated with an excitation fluence equal to the saturation fluence F_sat [²¹]:

(2){\eta }_{\max }={\displaystyle \frac{\tau E_{\mathrm{b}}^2}{\mathrm{8}{F}_{\mathrm{sat}}{Z}_{\mathrm{0}}}},

where τ is the duration of the excitation pulse, E_b is the bias field applied to the antenna, and Z₀ is the impedance of free space. Thus, the maximum conversion efficiency is inversely roportional to the saturation fluence F_sat, which in turn is inversely proportional to the carrier mobility. Therefore, selection of the semiconductor substrate is quite important. Materials with high carrier mobility and the ability to withstand high bias voltage are commonly used as substrates. The often-used substrate material LT-GaAs, has a high breakdown field and its carrier lifetime is as high as picoseconds. Annealing can further improve the performance of semiconductor substrates. It is found that the intensity of the THz wave radiated from the annealed antenna is 1.4 times higher than that of the unannealed one [²²], as shown in Fig. 1.

Fig.1 Terahertz signals generated from annealed and unannealed LT-GaAs PCAs [²²]. (a) Time-domain terahertz waveforms. (b) Fourier spectra of the waveforms. The Fourier spectra were both normalized by the peak values of the respective terahertz waveforms. A 700°C annealed PCA (bow-tie type) and an unannealed one were used in these measurements. Another unannealed PCA (bow-tie type) was used as a common detector

Full size|PPT slide

However, GaAs is not a suitable substrate for LA-PCA due to its relatively low threshold of breakdown which limits the maximum bias field that can be applied to the antenna. As LA-PCAs have a large gap size, carriers are accelerated by the bias field to high energies which may damage the substrate. To overcome this limitation, wide band gap semiconductor materials, such as diamond [²³], ZnO [²⁴], and GaN [²⁵], have been evaluated. However, the band gaps of these materials exceed 3.1 eV, necessitating the use of at least the third harmonic of the conventional Ti:sapphire laser to excite the carriers. With a band gap of 2.7 eV, ZnSe is another candidate substrate, which requires the second harmonic or two-photon absorption of a Ti:sapphire laser pulse. The breakdown electric field of ZnSe can attain 70 kV/cm [²⁶] and the carrier mobility is about 140 cm²/(V·s) [²⁷]. However, ZnSe has the same drawback as GaAs: the temperature increases due to Joule heating, which causes the performance of the LA-PCA to decrease rapidly. Recently, 6H and 4H-SiC semiconductor crystals have also been employed as substrates for LA-PCA. The bandgap is 3.03 eV for 6H-SiC and 3.26 eV for 4H-SiC. These two crystals can overcome the thermal effects well. Compared with ZnSe crystals, 6H-SiC has a 2.3 times higher THz field under optimal conditions [²⁸].

Many efforts have been made to improve the performance of LA-PCA as a strong-field THz source, including increasing generation efficiency and electric-field strength. The LA-PCA can be optimized by adjusting the following parameters: substrate [²⁹,³⁰], defect concentration [³¹], and electrodes. Another means to improve the performance of LA-PCA is the use of interdigitated electrodes [³²]. The interdigitated PCA is an effective way to reduce the bias voltage while maintaining a large lighting aperture. Figure 2 presents the classic structure of an interdigital LA-PCA [³³], in which the interdigitated structure reduces the gap size between the electrodes while a large photoexcitation area is maintained. The main advantage of the interdigitated PCA is that a specific electric field can be achieved with a lower bias voltage eliminating damage to the substrate [³⁴]. Therefore, a higher bias electric field can be applied, the effect of Joule heating is limited, and THz generation efficiency can be improved due to the enhancement of trap fields near multiple anodes [²¹]. A pump laser at a repetition rate of 250 kHz and a bias voltage of 70 kV/cm can produce THz radiation with an electric field of 36 kV/cm [³⁵].

Fig.2 Schematic diagram of terahertz emitting metal-semiconductor-metal structure [³²]. (1) Interdigitated finger electrodes. (2) Semi-insulating GaAs substrate. (3) Opaque metallization shadowing one electric-field direction. The electric-field direction is indicated by arrows

Full size|PPT slide

Yardimci et al. implemented a GaAs based interdigitated LA-PCA with a plasma electrode. It is shown that the LA-PCA is more powerful and can achieve an optical-THz conversion efficiency of 1.6%, which is an order of magnitude higher than that of the GaAs LA-PCA with a traditional structure [³⁶]. Figure 3(a) presents a schematic diagram of the transmitter used in the experiment and Fig. 3(b) shows the transmission power of the polarized beam incident on the GaAs substrate as a function of light wavelength. The inset shows light absorption in the GaAs substrate for a TM-polarized beam at 800 nm. Madéo et al. investigated the effect of gap size on THz radiation of an interdigitated GaAs substrate LA-PCA [³⁷], it was shown that the peak frequency of the THz spectrum shifts to higher frequencies when the interstitial PCA gap size is reduced from 20 to 2μm . Due to the space charge shielding effect, the THz spectrum becomes wider. Similarly, the interdigitated LA-PCA also has certain limitations. If the gap size is too small, as a result of the space charge shielding mechanism, the LA-PCA will cause the radiation field to saturate.

Fig.3 (a) Schematic diagram and operating principle of a large-area plasmonic photoconductive emitter fabricated on a GaAs substrate [³⁶]. (b) Power transmission of a TM-polarized optical beam incident on the GaAs substrate as a function of optical wavelength. The inset shows color plot of optical absorption in the GaAs substrate in response to a TM-polarized optical beam at 800 nm

Full size|PPT slide

An interdigital GaAs LA-PCA using a binary phase mask is demonstrated for improved optical-THz conversion efficiency and THz pulse shape [³⁸]. As shown in Fig. 4, a binary phase mask is attached to the device, which causes a π phase delay between the excitation pulses of the interdigitated antennas, thus all positive half cycles (or negative half cycles) can be coherently enhanced. The interdigitated GaAs LA-PCA can achieve an enhanced THz field with an offset field of 1.2 kV/cm and an excitation flux of 14 μJ/cm².

Fig.4 (a) Principle of a binary phase mask for single-cycle terahertz pulse generation from an interdigitated photoconductive antenna (PCA). (b) Terahertz pulse shape from an interdigitated GaAs antenna at a bias field of 1.2 kV/cm and a fluence of 14 mJ/cm² with a standard shadow mask, a 510-mm-thick binary phase mask, and no mask (offset introduced for improved clarity). The inset shows the power spectra for a shadow mask and 510 mm glass phase mask [³⁸]

Full size|PPT slide

A ZnSe interdigitated LA-PCA with a gap size of 700 mm excited by a 400 nm laser has been demonstrated to generate THz energy up to 8.3 mJ with an electric field of 331 kV/cm [³⁹]. The gap size is chosen to limit saturation of the THz field through space charge screening. To investigate the effect of gap size, three different ZnSe interdigitated LA-PCAs (gap sizes of 460, 700, and 932 mm, respectively, with equal photoconductive areas) were characterized [⁴⁰]. The experimental results show that the size of the slot has a small effect on the THz waveform and spectrum, but the saturation of the THz field appears faster and more strongly for antennas with smaller slots. The saturation of the THz field can be offset by applying a larger bias field. This phenomenon can be attributed to the relatively large capacitance of the interdigitated LA-PCA, which can be related to the space charge screening. The performance and fabrication techniques of AuGeNi alloy electrodes and Ti/Au electrodes are also investigated, it is found that the THz intensity from the antenna with ohmic contact electrodes is 3–8 times higher than that from the antenna with Schottky contact electrodes, and the larger gap antennas with ohmic contact electrodes have higher optical and electrical energy to THz intensity conversion efficiency [⁴¹].

Optical rectification

Optical rectification (OR) in nonlinear crystals is the preferred technique for strong single-cycle THz radiation generation. The process of OR (or photo-induced DC electric field) is a second-order nonlinear process. When the light field interacts with a medium with second-order nonlinear properties, a direct current electric field proportional to the intensity of the light is obtained from the difference between two photons with the same frequency. This process can be expressed by

(3)P\left(\mathrm{0}\right)={\chi }^{\left(\mathrm{2}\right)}\left(\omega ,-\omega ,\mathrm{0}\right)E\left(\omega \right)E^{*}\left(-\omega \right),

where P is the electric polarization, χ is the second-order nonlinear polarizability, and E and ω are the field amplitude and frequency of the fundamental wave, respectively. If the light field exists in the form of pulses, this will generate an alternating electric field in the medium and radiate electromagnetic waves. The electric field of the radiated electromagnetic wave is proportional to the second-order differential of the alternating electromagnetic field with time t:

(4)E\left(t\right)\propto {\displaystyle \frac{{\partial }^{\mathrm{2}}P\left({{\displaystyle \omega }}_{\mathrm{T}\mathrm{H}\mathrm{z}},t\right)}{\partial t^{\mathrm{2}}}}={\chi }^{\left(\mathrm{2}\right)}{\displaystyle \frac{{\partial }^{\mathrm{2}}I\left(t\right)}{\partial t^{\mathrm{2}}}},

where ω_THz is the frequency of the THz radiation, ω_THz = ω₁−ω₂ , and ω₁ and ω₂ are two frequency components of the fundamental pulse. To produce high-energy THz radiation, the crystal should have a high electro-optic coefficient and be transparent for all the frequencies involved. Another important factor is phase matching which requires that the group velocity of the light pulse is equal to the phase velocity of the THz wave. The phase matching condition is expressed as

(5)k\left({{\displaystyle \omega }}_{\mathrm{1}}\right)-k\left({{\displaystyle \omega }}_{\mathrm{2}}\right)=k\left({{\displaystyle \omega }}_{\mathrm{T}\mathrm{H}\mathrm{z}}\right),

where k is the wave vector of the corresponding electromagnetic wave. When the phase matching condition is met, the nonlinear process will have a higher efficiency. The commonly used crystals are ZnTe, GaP, GaSe, LiNbO₃, and some organic crystals such as DAST and BNA [²¹,⁴²,⁴³]. The properties of some common crystals for OR are presented in Table 1.

Tab.1 Optical properties of common materials for optical rectification [²¹,⁴²,⁴³]

crystal	effective nonlinear coefficient/(pm·V−1)	index of refraction	THz index of refraction	THz absorption coefficient/cm−1
ZnTe	68.5	2.85 (800 nm)	~3.17	1.3
GaP	24.8	3.67 (800 nm)	~3.34	0.2
GaSe	28.0	2.85 (800 nm)	~3.72	0.5
GaAs	65.6	3.61 (800 nm)	~3.4	0.5
LiNbO3	168.0	2.25 (800 nm)	no~6.8, ne~4.98	18.2
LiTaO3	170.0	2.18 (800 nm)	no~6.5, ne~6.4	46.0
DAST	615.0	2.25 (1550 nm)	~2.4	41.5

ZnTe is the crystal most used in OR for THz pulse generation. It has a relatively high quality-factor compared to other crystals and the Ti:sapphire laser phase matching condition can easily be realized. It can generate THz pulses with a spectrum of 0.1–3.0 THz. However, it has been observed in the experiment that ZnTe has strong two-photon absorption when it is pumped with 800 nm light. The generation of free carriers results in enhanced absorption of THz radiation and this limits the generation of strong-field THz radiation. Large aperture monocrystalline ZnTe can be used to enhance THz generation [⁴⁴,⁴⁵]. Employing 48 mJ, 800 nm, 30 fs excitation pulses at a repetition rate of 100 Hz, single-cycle THz pulses with energies as high as 1.5 mJ per pulse and with a spectral range extending to 3 THz are observed with an energy conversion efficiency of 3.1 × 10⁻⁵ [⁴⁴].

As shown in Table 1, lithium niobate (LiNbO₃) has a higher effective nonlinear coefficient, however, the large difference between the index of refraction for the pump beam and THz radiation brings the difficulty for phase matching. The tilted-pulse-front technique was proposed to generate intense THz pulses from LiNbO₃. The basic idea is shown in Fig. 5. The pulse of the optical pump light is titled using a diffraction grating and a lens is used to project the titled-pulse at the cystal position. The phase matching condition, thus, becomes

(6){{\displaystyle \upsilon }}_{\mathbf{T}\mathrm{H}\mathrm{z}}^{\mathrm{p}\mathrm{h}}={{\displaystyle \upsilon }}_{\mathrm{p}\mathrm{u}\mathrm{m}\mathrm{p}}^{\mathrm{g}\mathrm{r}}\cos \beta ,

where {{\displaystyle \upsilon }}_{\mathrm{T}\mathrm{H}\mathrm{z}}^{\mathrm{p}\mathrm{h}} is the phase velocity of the THz wave, {{\displaystyle \upsilon }}_{\mathrm{p}\mathrm{u}\mathrm{m}\mathrm{p}}^{\mathrm{g}\mathrm{r}} is the group velocity of the pump light, and b is the tilt angle between the pulse front and phase front. Typical tilted-pulse-front LiNbO₃ can generate THz radiation with peak electric fields of >200 kV/cm, and the spectral range is from 0.1 to 2.5 THz [²¹].

Fig.5 Phase matching in a LiNbO₃ crystal

Full size|PPT slide

Several methods have been proposed to improve the energy conversion efficiency in LiNbO₃. The duration of Fourier-transform-limited pump pulses can enhance the conversion efficiency. The theoretical calculation predicts an order-of-magnitude increase in the efficiency of THz pulse generation when 500 fs pump pulses are used, rather than the commonly used ~100 fs pulses [⁴⁶,⁴⁷]. Doping 1 mol% Mg in LiNbO₃ crystal can effectively avoid the photorefractive effect and reduce the THz absorption [⁴⁸]. Another way to reduce THz absorption in LiNbO₃ is cooling. It was demonstrated that near-optimal pump pulses centered at 1.03 μm in low-temperature cooled LiNbO₃ can produce highly efficient THz radiation by OR [⁴⁹]. Using a near-optimal 680 fs pulse duration and a pump energy of 1.2 mJ, the light-THz conversion efficiency is higher than 3.8%, an order of magnitude higher than the no cooling case. Figure 6(a) presents the experimental setup where the LiNbO₃ crystal is cooled. The dependence of efficiency on temperature at a fixed pump energy is shown in Fig. 6(b). It can be seen that the highest efficiency is achieved at 150 K.

Fig.6 (a) Experimental setup for terahertz generation from a cooled LiNiO₃ crystal. L1: best-form lens with f= 20 cm; L2: cylindrical lens with f= 15 cm; HWP: half-wave plate at 1030 nm. (b) Efficiency enhancement versus temperature at a fixed pump energy of 1.2 mJ [⁴⁹]

Full size|PPT slide

Recently, demonstration of 0.2 mJ THz pulses in LiNbO₃ at room temperature was presented. Adopting the tilted-pulse-front configuration and chirping the pump laser pulse below 50 fs, an energy conversion efficiency from 800 nm to THz of 0.3% was achieved [⁵⁰]. The corresponding experimental setup is shown in Fig. 7(a), where an acousto-optic programmable dispersive filter is introduced to generate the second-order dispersion. The duration of the pump pulses is about 30 fs, as shown in Fig. 7(b). The calculated chirped pulse duration as a function of the group velocity dispersion is shown in Fig. 7(c). The measured spectra for different group velocity dispersions are shown in Fig. 7(d). The position of the incident pump beam on the LiNiO₃ crystal is shown in Fig. 7(e).

Fig.7 (a) Schematic of a high energy terahertz source with tilted pulse wave front technique and electro-optic sampling (EOS) setup [⁵⁰]. HWP: half-wave plate; LN: lithium niobate; OAP: 90° off-axis parabolic mirror; IS: integrating sphere; BPD: balanced photodiode. (b) Autocorrelation measurement of the pump laser pulse at its shortest duration of 30 fs. (c) Calculated chirped pulse duration as a function of the group velocity dispersion. (d) Input spectra for different group velocity dispersion measured before the laser beam enters the tilted pulse wave front setup. (e) Pump beam position relative to the edge of the LiNbO₃ prism

Full size|PPT slide

However, although the LiNbO₃ light source with a tilted pulse wave front produced high-THz energy with an electric field exceeding 1 MV/cm, the LiNbO₃ crystal has its limitations. The spectrum of LiNbO₃ THz sources is usually limited due to its absorption at high frequencies. It is difficult to attain very high-THz electric fields. The maximum THz electric field is determined by the three factors of THz energy, spot size, and pulse duration [⁵¹]:

(7)\mathcal{E}={{\displaystyle \epsilon }}_{\mathrm{0}}c{\displaystyle \int \mathrm{d}A{\displaystyle {\int }_{-\infty }^{\infty }{E}^{\mathrm{2}}\left(t,A\right)}}\mathrm{d}t,

where\mathcal{E} is the measured THz energy, ε₀ the permittivity of vacuum, c the speed of light in vacuum, E\left(t,A\right)\approx {{\displaystyle E}}_{\max }{{\displaystyle \widehat{E}}}_{\mathrm{t}}\left(t\right){{\displaystyle \widehat{E}}}_{\mathrm{s}}\left(A\right) is the spatio-temporal THz waveform at the detection plane, and A is the area of THz beam. {{\displaystyle \widehat{E}}}_{\mathrm{t}}\left(t\right) is the normalized waveform in the time domain and {{\displaystyle \widehat{E}}}_{\mathrm{s}}^{\mathrm{\hspace{0.17em}}}\left(A\right) is the normalized spatial profile at the detection plane. An increased maximum electric field E_max can be achieved with higher THz energy, smaller spot size, and shorter pulse duration. High-THz energy requires high optical-to-THz conversion efficiency, small spot size requires a short wavelength and high numerical aperture focusing lens, and short pulse duration results in a broader spectrum of the generated THz radiation.

Organic crystals that have larger nonlinear coefficient are widely used in ultra-wideband tunable THz generation [⁵²]. DAST, DSTMS, OH1, HMQ-TMS, and BNA are commonly used. Using an optical parametric amplifier (OPA) pumped by a Ti:sapphire laser to generate a pump beam with a center wavelength of 1500 nm, the room temperature pump-THz conversion efficiency is 2.1%, and the peak electric field can attain a value of 1.35 MV/cm [⁵³]. The central frequency is 2.1 THz with a bandwidth of approximately 2 THz. The corresponding experimental setup is shown in Fig. 8(a). The spectrum of the pump laser and measured autocorrelation signal of the THz pulse are presented in Figs. 8(b) and 8(c), respectively.

Fig.8 Terahertz generation with a DAST crystal [⁵³]. (a) Schematic setup for terahertz generation and electro-optic detection. 50 fs probe pulses centered at 810 nm (inset) are used for sampling the terahertz pulse with a 95-mm-thick GaP crystal. QWP: quarter wave plate; WP: Wollaston prism; BPD: balanced photodiode detector. (b) Spectrum of pump pulse. (c) Measured autocorrelation signal of terahertz pulse

Full size|PPT slide

Adopting wave front correctors, low-frequency THz (<5 THz) radiation generated from DSTM1 and OH1 are well focused to a diffraction-limited spot size and the peak fields can reach 83 MV/cm [⁵⁴]. Using a DSTM1 crystal and two linearly chirped near-infrared pulses, high-energy THz pulses tunable between 4 and 18 THz have been generated. The bandwidth is less than 1 THz and the maximum pulse energy is 1.9 mJ, resulting in a peak electric field of 3.7 MV/cm [⁵⁵]. Pumped with 1150–1550 nm infrared pules, the BNA crystal can generate THz pules with a spectrum extending up to 7 THz and a peak electric field of 10 MV/cm [⁵⁶].

GaSe is another crystal used for intense THz generation by difference frequency mixing [⁵⁷]. It is very easy to achieve the phase matching condition due to the small difference in refractive index between the THz and infrared pump waves. The nonlinear coefficient of GaSe is nearly the same as that of ZnTe, but the frequency of the generated THz pulse is higher than 10 THz, thus, the generated THz pulse can be focused into a smaller point, thus the peak electric field can be greatly enhanced. Using two parametrically amplified pulse trains from a single white-light seed, THz transients with peak electric fields of 108 MV/cm and center frequencies continuously tunable from 10–72 THz are generated [⁶]. When the wavelength of one OPA is fixed at 1.1 mm and the signal wavelength of the other OPA is changed from 1.1 to 1.5 mm, the center frequency of the THz transients can be tuned from 10 to 72 THz, as shown in Fig. 9. Matching the group velocities of the signal and idler components, phase-locked single-cycle transients with frequency widths from 1 to 60 THz are generated and the peak field can reach 12 MV/cm [⁵⁸].

Fig.9 (a) Time-domain transients and (b) corresponding normalized amplitude spectra for widely tuned center frequencies. Emitter: GaSe (thickness: 140 mm, solid curves) or AgGaS₂ (thickness: 800 mm, broken curve) [⁶]

Full size|PPT slide

Terahertz sources based on plasma

Plasmas created by high-intensity femtosecond laser pulses can emit coherent radiation from X-ray to THz wavelengths [⁵⁹]. Laser-induced air plasma has a higher damage threshold than PCAs and nonlinear crystals, and therefore stronger THz radiation generation is expected. By applying a direct current (DC) bias voltage along the direction of the electric field of incident beam, enhanced THz pulses have been measured and the peak field enhanced 32 times of that without external electric field [⁶⁰]. The efficiency can also be enhanced when a static magnetic field is applied to the plasma parallel or perpendicular to the electric field [⁶¹]. Inserting a second harmonic generation crystal before the focal point, the THz radiation generated can be enhanced 40 times [⁶²] and this method is referred to as the two-color filamentation approach. The maximum fields can approach 100 MV/cm using two-color filamentation of femtosecond mid-infrared laser pulses at 3.9 mm [⁶³] and the spectrum can be extended to 75 THz [⁶⁴].

The mechanism of generating THz by air plasma can be explained as four-wave mixing between the fundamental frequency and second harmonic in the plasma. When the fundamental frequency ω and its second harmonic 2ω are focused in the air, the THz radiation observed is [⁶²,⁶⁵]

(8){{\displaystyle E}}_{\mathrm{T}\mathrm{H}\mathrm{z}}\propto {\chi }^{\left(\mathrm{3}\right)}{{\displaystyle E}}_{\mathrm{2}\omega }\left(t\right){{\displaystyle E}}_{\omega }^{*}\left(t\right){{\displaystyle E}}_{\omega }^{*}\left(t\right)\cos \phi ,

where E_ω(t) and E_2ω(t) are the amplitudes of the fundamental frequency and second harmonic, φ is the relative phase between them, and χ⁽³⁾ is the third-order nonlinear coefficient. It was shown that the relative phase between the fundamental frequency and its second harmonic is critical to efficient THz generation. If the relative phase is precisely controlled, THz radiation from the gas plasma can be generated more efficiently. As shown in Fig. 10, a phase compensator is used to control the phase shift between the ω and 2ω pulses propagating in the dispersion medium, resulting in strong THz emission at a distance exceeding 100 m [⁶⁶]. By precisely controlling the relative phase between the ω and 2ω pulses and the polarization of the 2ω beam, a peak THz electric field exceeding 60 kV/cm can be routinely obtained in ambient air with a total excitation energy of approximately 500 µJ. However, this theory cannot explain THz radiation obtained via two-color filamentation with uncommon frequency ratios [⁶⁷]. Furthermore, the generated THz radiation strongly saturates with increasing pump laser energy. Using an aperture to limit the pump laser beam, the amplitude of THz radiation can be enhanced more than eight times of that in aperture-free cases [⁶⁸].

Fig.10 Schematic of the phase compensator incorporating a wedge pair. DM: dichroic mirror used to separate or recombine ω and 2ω beams; HWP: half-wave plate used to control the polarization of the 2ω beam [⁶⁶]

Full size|PPT slide

To better explain THz generation from two-color filamentation, the transient photocurrent model was established [⁶⁹]. The intense laser field causes free electrons and positively charged ions from the plasma to form a transverse current. This current surge will emit THz radiation which is proportional to the derivative of the current density:

(9){{\displaystyle E}}_{\mathrm{T}\mathrm{H}\mathrm{z}}\propto {\displaystyle \frac{\mathrm{d}J\left(t\right)}{\mathrm{d}t}}={\displaystyle \frac{{{\displaystyle N}}_{\mathrm{e}}{\mathit{e}}^{\mathrm{2}}}{{{\displaystyle m}}_{\mathrm{e}}}}{{\displaystyle E}}_{\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{r}},

where J(t) is the electron current density, N_e is the electron density, m_e is the electron rest mass, e is the electron charge, and E_laser is the laser electric field. For the two-color case:

(10){{\displaystyle E}}_{\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{r}}={{\displaystyle E}}_{\omega }\cos \left(\omega t\right)+{{\displaystyle E}}_{\mathrm{2}\omega }\cos \left(\mathrm{2}\omega t+\phi \right).

Good agreement is obtained between this model and the experimental results [⁶⁴].

THz radiation can also be emitted from plasma generated on a solids’ surface. When the laser-produced electron beam passes through the rear solid-vacuum interface, THz radiation can be emitted via coherent transition radiation [⁷⁰]. The total THz energy from the rear side of the metal foils is approximately 400 mJ/pulse and the energy conversion efficiency from the laser-to-THz radiation is approximately 2.0×10⁻⁴. By irradiating a metallic wire with an intense femtosecond laser pulse to produce both guided energetic electrons and a gyrotron-like undulator, intense THz pulses with narrow band can be generated [⁷¹]. The central frequency can be tuned over the range 0.1–0.4 THz and the conversion efficiency can reach 1%.

Liquid water is usually considered a strong absorber in the THz range. Recent experiments have shown that THz radiation can be excited from liquid water by femtosecond laser pulses [⁷²,⁷³]. Figure 11 presents the experimental setup for THz generation from liquid water. The water is formed into a film with the thickness of approximately 177 mm, and the laser is incident on the water film at an angle of 25° [⁷²]. Using single-color filamentation in liquids, ultra-broadband THz radiation can reach approximately 100 THz, and energy up to 76 mJ/pulse [⁷³]; an order of magnitude higher than that of two-color filamentation in air. Using a water line of approximately 200 mm in diameter as the source, a field strength of 0.2 MV/cm has been achieved [⁷⁴]. Due to the large nonlinear coefficient of liquid water, higher THz radiation is expected to be generated from its optimal situation.

Fig.11 Experimental setup for terahertz generation from a water film [⁷²]. OAPM: off-axis parabolic mirror; HWP: half-wave plate

Full size|PPT slide

Novel approaches for intense terahertz generation

In recent years, new materials, including topological insulators, spintronic materials, and metasurfaces, have been used as THz sources. The topological insulator has an energy band structure with a narrow band gap bulk state and a zero-band gap surface state. Furthermore, such materials have high carrier mobility and a linear dispersion relation. Therefore, topological insulator materials can have good application prospects in the field of THz [⁷⁵,⁷⁶].

Fig.12 (a) Band structure of n-doped Bi₂Se₃ [⁷⁵]. Surface electrons are directly excited by optical transitions from the conduction band (CB) to the second surface state (SS). Bulk electrons are directly excited by optical transitions from the valence band (VB) to the CB. (b) Schematic diagram of the experimental setup. WP: wave plate; WGP: wire grid polarizer

Full size|PPT slide

Bi₂Se₃ is a kind of three-dimensional topological insulators that has an insulator inside but a metallic material on the surface with a Dirac surface state, which is protected by the topological properties of the bulk wave function. Using a Ti:sapphire femtosecond laser to directly excite the second surface state at 1.5 eV above the conduction band of n-doped Bi₂Se₃, effective THz generation was observed [⁷⁵]. The generation of THz is explained by the transient photocurrent emission under the influence of surface depletion field and nonlinear OR. The nonlinear OR may contribute to the broad spectrum. As shown in Fig. 12(a), when the Bi₂Se₃ is pumped by femtosecond laser pulses, the surface electrons are directly excited from the conduction band to the second surface state and the bulk electrons are directly excited from the valence band to the conduction band. The experimental setup is shown in Fig. 12(b). The center wavelength of the optical pulse used was 800 nm, the pulse duration 50 fs, and the repetition frequency 1 kHz. The excitation pulse was incident on the sample surface at an angle of 45°, and the emitted THz pulse was detected by a ZnTe crystal. The spectrum of the generated THz radiation can expand from 0.1 to 3 THz. It was found that the intensity of THz emission is largely determined by the carrier concentration and ratio of doping. Strong pump energy will produce more free carriers, which in turn will cause a greater change in the transient current, resulting in stronger THz radiation [⁷⁶].

Metals are also good materials for THz generation. The optical characteristics of metals are as follows: 1) The pump absorption rate is not dependent on wavelength; 2) The electronic lifetime in metals are as short as 10–50 fs; 3) They have featureless THz refractive indices and large thermal conductivities, and 4) Metal thin film stacks (heterostructures) are simple and cheap to fabricate. With the recent rapid development of spintronics and femtomagnetism, electron spins which can generate transient currents in metals are used to produce THz radiation. An efficient metallic spintronic emitter was proposed recently for ultra-broadband THz generation [⁷⁷]. As shown in Fig. 13(a), the emitter has a bilayer structure consisting of ferromagnetic (FM) and nonferromagnetic (NM) metal thin films [⁷⁸]. A femtosecond laser pulse excites electrons in the metal stack, thereby changing their band velocity and launching a current along the z direction. In the FM layer, the mobility of spin-up (majority) electrons is significantly higher than that of spin-down (minority) electrons, thus the z current is spin-polarized. The spin–orbit interaction deflects spin-up and spin-down electrons in opposite directions and transforms the spin current j_s into an ultrafast transverse charge current j_c = gj_s, which leads to the emission of a THz pulse. A time-domain transient obtained from photoexcited Ta- and Ir-capped Co₂₀Fe₆₀B₂₀ thin films and detected by a 50-µm-thick GaP crystal is shown in Fig. 13(b) and the corresponding Fourier spectrum is shown in Fig. 13(c). The spectrum of the THz transient can reach 30 THz when the emitter is excited by femtosecond pulses from a Ti:sapphire laser oscillator (10 fs, 2.5 nJ). By optimally selecting the materials and thickness of a multi-layer structure, the generated THz radiation can be greatly enhanced. A peak THz pulse field of 300 kV/cm has been generated by using a large-area metallic spintronic emitter [⁷⁹].

Fig.13 Metallic spintronic terahertz emitter [⁷⁸]. (a) Principle of operation. (b) Time-domain transient obtained from photoexcited Ta- and Ir- capped Co₂₀Fe₆₀B₂₀ thin films (3-nm-thick) and detected by a 50-µm-thick GaP crystal. Inset: Terahertz signal amplitude as a function of incident pump power. (c) Fourier spectra of terahertz signal and the extracted transient terahertz electric-field incident on the electro-optic detector

Full size|PPT slide

A metasurface composed of gold split ring resonators (SRR) fabricated on glass coated with indium tin oxide can also be used to generate THz radiation [⁸⁰]. The metasurface structure and experimental schematic diagram are shown in Fig. 14. The spectrum of the generated THz radiation can cover 0–4 THz. The THz emission is caused by the resonance of the magnetic dipole that excites the open-loop resonator, and it rapidly decreases under non-resonant pumping. The optical-THz conversion efficiency can exceed that of conventional sub-millimeter crystals (ZnTe and GaP) through OR. By judicious engineering of the single-emitters that comprise the metasurface, unprecedented control of the spatio-temporal properties of the emitted THz wavepackets can be achieved [⁸¹]. Generally speaking, due to their negligible thickness, strong plasticity, and other advantages, metasurfaces have significant prospects for strong-field THz generation.

Fig.14 Experimental setup and results of a metasurface terahertz source [⁸⁰]. (a) Schematic of terahertz generation and detection. The insert shows an electron micrograph of the SRR array. PM: parabolic mirror; WP: Wollaston prism. (b) Measured terahertz time-domain transient obtained by pumping the SRR electric-dipole resonance (red line) at 800 nm, magnetic-dipole resonance (black dots) at 1500 nm, and substrate only (green line) at 1500 nm, respectively. The inset shows the linear optical transmission including the electric (red curve) and magnetic (black curve) dipole resonances of the SRRs measured with the polarization of the incident light perpendicular and parallel to the gap of SRRs, respectively

Full size|PPT slide

To conclude this section, the various tabletop techniques for intense THz generation based on the Ti:sapphire laser are summarized in Table 2.

Tab.2 Comparison of terahertz generation techniques

Ref.		peak electric field	Bandwidth/THz	advantage	disadvantage
LAPCA [39]		few hundreds kV/cm	20	high stability	relatively low peak electric field
OR	DAST [38]	about 7 MV/cm	0.3–20	low dielectric constant	low damage threshold
	ZnTe [44]	about 70 kV/cm	0.2–4	better phase matching conditions	strong two-photon absorption
	LiNbO3 [40]	up to 1.2 MV/cm	0.1–2.5	high damage threshold	low frequency
	BNA [56]	10 MV/cm	7	highly nonlinear organic crystal	low damage threshold
air plasma [64]		several MV/cm	0.1–75	no concerns for damage with air	phase matching sensitivity
spintronic [80]		about 300 kV/cm	0–4	high potential	difficulty of artificial structure design and fabrication

Detection of intense terahertz radiation

The rapid onset of strong-field THz sources pushes the peak THz electric field from a level below MV/cm to several MV/cm [⁸²,⁸³], enabling the study of fascinating nonlinear phenomena of materials in the THz frequency range on picosecond or even sub-picosecond time scales. High-intensity THz sources and their detection methods are the main tools driving the development of such science and technologies. Therefore, the development of high-field THz detectors is very important, as traditional PCA detection techniques [⁸⁴] and electro-optical sampling [⁸⁵] have presented several challenges.

Detection by PCA

The emission and detection of pulsed broadband THz radiation of optically pumped PCA was completed in the late 1980s [⁸⁴]. Unlike the THz PCA transmitter, the receiver PCA has no external DC bias. When photo-carriers are injected through a detection light pulse, the THz electric field induces a current between the gaps of the PCA [⁸⁶]. The photocurrent lasts the entire carrier life cycle, but is much shorter than the THz pulse duration. The induced current I(t) is proportional to the field amplitude of the THz radiation collected between the photoconductive gaps:

(11)I\left(t\right)={\displaystyle {\int }_{-\infty }^t{{\displaystyle \sigma }}_{\mathrm{s}}}\left(t-t^{\prime }\right){{\displaystyle E}}_{\mathrm{T}\mathrm{H}\mathrm{z}}\left(t^{\prime }\right)\mathrm{d}{t}^{\prime },

here {{\displaystyle \sigma }}_{\mathrm{s}}\left(t\right) is the transient surface conductivity. By measuring the variation of the current with the time delay between the THz pulse and detection light pulse, the shape of the time-domain THz pulse can be mapped. The coherent nature of this detection method provides a high signal-to-noise ratio (SNR) because it greatly reduces the effects of blackbody radiation and other THz radiation sources on the receiver [⁸⁷]. To obtain a higher SNR, the signal is measured by using a lock-in amplifier after being passed through an optical chopper.

Equation (11) indicates that the detection bandwidth of the PCA detector is limited by the carrier dynamics of the PCA material. The photocurrent signal is not a complete copy of the THz waveform, but presents a frequency filtering characteristic through conductivity [⁸⁸]. Thus, materials with shorter carrier lifetimes (such as LT-GaAs and doped GaAs) are usually chosen to reduce the effect of conductivity on the results [⁸⁹]. The carrier lifetime of LT-GaAs is shorter than 0.5 ps. By combining a substrate with a short carrier lifetime and a short duration light pulse, the maximum detected bandwidth can be increased. For example, using a 15-fs laser pulse detection probe, THz pulses with frequencies up to 30 THz can be detected from doped GaAs PCA [⁹⁰]. Recently, THz pulses with a bandwidth extended to 100 THz have been proven with LT-GaAs PCA and a 10-fs optical probe light [⁹¹].

The geometry of the PCA detector is also a factor affecting the detected THz pulse bandwidth. There are four main types of geometry: strip line, bow tie, butterfly, and logarithmic antenna. These PCAs have different characteristics. The butterfly PCA is effective for detecting low frequencies, while the strip line PCA is sensitive to high frequencies. The size of the PCA has a significant impact on the detection signal. A smaller gap size will allow detection of higher frequencies and larger amplitude signals, while a longer electrode will increase the amplitude of the detected signal, but will have a greater effect on low frequencies [⁹²].

However, since the PCA detector is very sensitive to ambient electromagnetic noise, the noise may be relatively high when using a high-energy amplification laser system. Strong THz fields may cause nonlinear effects in semiconductor substrates [⁹³], thus, it is difficult to obtain correct detection signals. Therefore, although PCA detectors are high quality, they are not commonly used for the detection of strong-field THz pulses.

Detection by electro-optic sampling

Free-space EOS technology uses the linear Pockels effect in EO crystals and femtosecond optical strobe pulses to detect the electric field of THz pulses [⁸⁵]. The Pockels effect causes birefringence in a nonlinear crystal that is proportional to the applied THz electric field. By measuring the birefringence via detection of changes in the polarization state of the beam, the THz electric-field strength can be determined.

Ideally, the group velocity of light in the EO crystal should match the phase velocity of the THz well. Thus, during the transmission process, the light pulse experiences a constant THz electric field. The THz field-induced birefringence causes the detection pulse to have a slight elliptical polarization. A Wollaston prism divides the detection beam into two mutually orthogonal components which are then incident on an equalized photo-detector. The detector measures the intensity difference between the two orthogonal components of the detected pulse I=I_y−I_x, which is proportional to the applied THz amplitude,

(12)\begin{array}{l}{{\displaystyle I}}_x={\displaystyle \frac{{{\displaystyle I}}_{\mathrm{0}}}{\mathrm{2}}}\left[\mathrm{1}-\sin \left(\mathrm{\Delta }\varphi \right)\right]\approx {\displaystyle \frac{{{\displaystyle I}}_{\mathrm{0}}}{\mathrm{2}}}\left[\mathrm{1}-\mathrm{\Delta }\varphi \right],\hfill \\ {{\displaystyle I}}_y={\displaystyle \frac{{{\displaystyle I}}_{\mathrm{0}}}{\mathrm{2}}}\left[\mathrm{1}+\sin \left(\mathrm{\Delta }\varphi \right)\right]\approx {\displaystyle \frac{{{\displaystyle I}}_{\mathrm{0}}}{\mathrm{2}}}\left[\mathrm{1}+\mathrm{\Delta }\varphi \right],\hfill \end{array}

where \mathrm{\Delta }\varphi is the rotation angle of refraction index ellipsoid caused by the THz field. The approximation requires that .

For detection of quasi-DC THz electric fields, the use of femtosecond optical probe pulses is practical. However, for ultra-short THz pulses with a wide spectrum, the time offset caused by the velocity mismatch between the detection pulse and the THz pulse is a key factor in detection. The sensitivity increases as the crystal thickness increases, but the corresponding detection bandwidth decreases. Therefore, the thickness of the EO crystal should be appropriately selected. The use of thinner crystals for broadband detection allows velocity matching. Additionally, phonon absorption is a key factor limiting detection bandwidth. For example, in ZnTe crystals, phonon absorptions at 1.6, 3.7, and 5.31 THz usually limit the detection spectrum to low frequency [⁹⁴]. Therefore, other EO crystals (such as GaP and GaSe) are often a better choice for broadband detection [⁹⁵,⁹⁶]. Selecting the detection crystal and optimizing the detection scheme require a full understanding of the THz/optical characteristics of crystal, such as its linear dispersion and absorption in the THz frequency range [⁹⁷].

However, EOS technology is not useful in a strong THz field. If the rotation angle exceeds π/2, inversion of the detection pulse intensity will occur [⁹⁸]. This limitation is called over-rotation. For example, higher spectral resolution in THz time-domain spectroscopy requires longer scanning durations that can be achieved using thicker EO detection crystals, with the added benefit that thicker EO crystals can provide a higher SNR. However, the use of thicker crystals increases the chance of excessive rotation because the birefringence induced in the detection crystal is proportional to both the THz electric field and thickness of the crystal. High-intensity THz measurement requires a high dynamic range detection technology.

Detection by air plasma

To coherently measure the THz field with air plasma, a local oscillator of frequency 2ω is introduced to interfere with the second harmonic induced by the THz field, thus the intensity of the 2ω frequency is [⁹⁹]

(13){{\displaystyle I}}_{\mathrm{2}\omega }\propto {\left|{{\displaystyle E}}_{\mathrm{2}\omega }\right|}^{\mathrm{2}}={\left({{\displaystyle E}}_{\mathrm{2}\omega }^{\mathrm{T}\mathrm{H}\mathrm{z}}+{{\displaystyle E}}_{\mathrm{2}\omega }^{\mathrm{L}\mathrm{O}}\right)}^{\mathrm{2}}={{\displaystyle E}}_{\mathrm{2}\omega }^{{\mathrm{T}\mathrm{H}\mathrm{z}}^{\mathrm{2}}}+\mathrm{2}{{\displaystyle E}}_{\mathrm{2}\omega }^{\mathrm{T}\mathrm{H}\mathrm{z}}{{\displaystyle E}}_{\mathrm{2}\omega }^{\mathrm{L}\mathrm{O}}+{{\displaystyle E}}_{\mathrm{2}\omega }^{{\mathrm{L}\mathrm{O}}^{\mathrm{2}}}.

Here, {{\displaystyle E}}_{\mathrm{2}\omega }^{\mathrm{T}\mathrm{H}\mathrm{z}} and {{\displaystyle E}}_{\mathrm{2}\omega }^{\mathrm{L}\mathrm{O}} are the amplitudes of the second harmonic induced by the THz field and local oscillator, respectively. When the probe intensity is higher than the air ionization threshold and the local oscillation becomes sufficiently large, the second term of the equation becomes the dominant term, {{\displaystyle I}}_{\mathrm{T}\mathrm{H}\mathrm{z}}^{\mathrm{2}}\propto {{\displaystyle E}}_{\mathrm{T}\mathrm{H}\mathrm{z}}, which is coherent detection.

By further introducing an alternating current (AC) bias voltage which is synchronized with the laser repetition rate, the symmetry of the plasma is broken [¹⁰⁰]; thus, the detection power required for the THz pulses can be reduced and the SNR can be effectively improved by an order of magnitude. An important feature of the air-biased coherent detection method is that the THz bandwidth is limited only by the duration of the light pulses [¹⁰¹].

The fluorescence emission of the plasma is also used to detect the strong-field THz radiation in the air [¹⁰²,¹⁰³]. The interaction between the THz pulse and laser plasma can enhance the fluorescence emission of the plasma. Accordingly, coherent detection of a strong-field THz wave can be achieved by applying an external bias field parallel to the THz field on the plasma as a local oscillator or by applying an AC bias voltage at the common focal point of the THz pulse and the laser pulse [¹⁰⁴]. A two-color laser-induced air-plasma system is used for all-optical THz wave remote sensing. Compared with previous technologies, the signal detected is enhanced by an order of magnitude. Another technique that uses air plasma to detect strong THz fields is called THz enhanced acoustics [¹⁰⁵].

Applications of intense terahertz radiation

The rapid progress of intense THz sources and detectors has motivated researchers to use intense THz radiation for various applications. Since intense THz pulses can provide higher energy for photoexcited carriers, many studies use intense THz radiation for THz time-domain spectroscopy (TDS) to characterize the carrier dynamic properties of semiconductors and other condensed matter systems [¹⁰⁶–¹¹⁹]. Additionally, intense THz radiation has a relatively high peak electric-field strength that allows various traditional optical nonlinear effects such as high-order harmonic generation [¹¹⁰,¹¹¹], saturation and anti-saturation absorption [¹¹²–¹¹⁶], and four-wave mixing. Moreover, it can also serve as an intense magnetic field source for magnon switching [¹⁰,¹¹⁷–¹²¹]. In this section, we will review the majority of intense THz pulse applications and related novel phenomena.

Applications of intense terahertz radiation in spectroscopy

With the rapid development of THz science, THz-TDS has become a mature method to study the properties of materials. In particular, the optical pump THz-TDS technique is useful for characterization of ultrafast carrier dynamic properties. Moreover, using an intense THz pulse in such a system can provide new interesting effects. Nowadays, there are four techniques mainly used in intense THz pulse involved spectroscopy detection, including intense THz-TDS, optical-pump/intense-THz-probe (OPITP), intense-THz-pump/THz-probe (ITPTP), and intense-THz-pump/other radiation-probe (ITPOP) techniques. In this section, we will mainly review the applications and new effects when intense THz pulses are used in these four techniques.

Intense terahertz time-domain spectroscopy technique

The THz-TDS technique is a well-known characterization method in the THz field. Along with the development of intense THz pulses, some studies have used the THz-TDS technique for investigation of nonlinear effects by the conventional Z-scan technique. In 2009, nonlinear absorption bleaching in an n-doped semiconductor was demonstrated in the THz band [¹²²]. By using a large aperture ZnTe crystal, THz pulses with a peak field strength of 200 kV/cm were generated in a THz-TDS system and the tested sample was a sample of 500-nm-thick n-type indium gallium arsenide (InGaAs) on InP substrate. By moving the sample close to the focus of the THz wave along the z-axis, transmission was obtained at different z positions, as shown in Fig. 15. One can see that a significant enhancement in the transmission is observed near the focus of the THz wave (i.e., at z = 0), in both the pyroelectric detector (Fig. 15(a)) and THz-TDS results (Fig. 15(b)). This is called the absorption bleaching effect [⁷³]. The well-known electric-field-driven intervalley scattering model is used to explain this effect. When the sample is irradiated by the THz pulse, the free carriers in the G valley are accelerated and scattered into an upper energy level, i.e., the L valley. The carrier mobility is lower in the satellite valleys, thus, reducing the conductivity of the sample. Since the transmission of the THz pulse is higher when the conductivity of the sample is lower, the transmission is enhanced when carriers are scattered to the upper satellite valleys. By using this model, a fit which agrees with the experimental results is derived. A similar THz field strength dependent transmission enhancement of intense THz pulses in doped silicon was demonstrated in 2010, by Z-scan measurement [¹²³]. The THz-TDS Z-scan experimental setup is shown in Fig. 16(a). By adjusting the THz peak field strength from 16 to 135 kV/cm, an 18% enhancement in the transmission is observed in the frequency domain, as shown in Fig. 16(b). Accompanying the rapid development of graphene in recent years, an increasing number of THz-TDS studies have been performed revealing the linear carrier dynamics of this material [¹²⁴–¹²⁸]. Several works have predicted that it has a strong nonlinear electromagnetic response at THz frequencies due to the linear energy dispersion relation of graphene [¹²⁹–¹³¹]. Intense THz transmission enhancement of monolayer graphene has been demonstrated experimentally [¹³²] for monolayer graphene grown on a SiC substrate by a conventional CVD method. Using the titled-pulse-front technique with a LiNbO₃ crystal, a THz field with a peak electric-field strength of up to 63 kV/cm is generated and used to excite the graphene sample in the THz-TDS system shown in Fig. 17(a). The experimental time-domain signal and the transmission spectrum results are shown in Figs. 17(b) and 17(c), respectively. By increasing the peak THz field from 13 to 63 kV/cm, the THz transmission increases by ~5%, as shown. The transmission enhancement is attributed to the photoconductivity reduction of the graphene sample due to current saturation effects as well as increased scattering rates when carriers are excited by the THz field. Further, a numerical model of carrier dynamics, in which the graphene conduction band is calculated by using the tight binding approximation, is proposed to explain the nonlinear effect. We review these works in Section 4.2.

Fig.15 Terahertz Z-scan experimental results for InGaAs [¹²²]. (a) Z-scan normalized transmission of the total terahertz pulse energy measured with a pyroelectric detector after the sample (black curve: InGaAs epilayer on an InP substrate; red curve: InP substrate only). (b) Transmitted terahertz pulse electric field at different positions of the Z-scan. (c) Normalized transmission of the time integral of the modulus squared for the transmitted electric field as a function of z position along the scan. (d) Normalized electric field differential transmission as a function of time for different z positions along the scan. Note that the initial positive slope is related to the terahertz pulse duration and the population rate, while the negative slope is indicative of the carrier decay time

Full size|PPT slide

Fig.16 Terahertz Z-scan experimental results for n-doped silicon [¹²³]. (a) Experimental setup. The terahertz pulses are generated by tilted-pulse-front excitation in LiNbO₃ and electro-optically detected by a ZnTe crystal. (b) Open-aperture Z-scan: change in transmitted terahertz amplitude through the doped silicon sample as a function of distance from the terahertz beam focus. Also, see Ref. [⁷³]

Full size|PPT slide

Fig.17 Terahertz Z-scan experimental results for graphene [¹³²]. (a) Schematic of the experimental setup based on the titled-pulse-front technique and a LiNbO₃ crystal. (b) Time-domain signal of terahertz pulses transmitted through the bare SiC substrate and the graphene sample for two terahertz electric-field strength levels, normalized to the response of the bare SiC (the inset shows a detail of the peaks of the three pulses), and (c) the transmission spectra for four different terahertz electric-field strength levels

Full size|PPT slide

Optical-pump/intense-terahertz-probe technique

In the optical pump THz-TDS technique, the THz signal is detected under an extra optical pump beam which impinges on the sample. Usually, the optical pump beam is a pulsed beam with a wavelength between the visible and infrared. By tuning the delay between the pump and probe pulses, one can study the carrier dynamics. The optical-pump/intense-THz-probe (OPITP) technique uses the intense THz pulses as the probe beam in the experiment so that one can observe nonlinear carrier behavior. The nonlinear absorption bleaching effect of the intense THz pulse in photoexcited GaAs has been observed by the OPITP technique [¹³³]. An optical pump pulse whose wavelength is 800 nm is incident on the sample, and a THz pulse generated by a large-area ZnTe crystal is used to probe the absorption of a 0.5-mm-thick GaAs sample. THz fields of 173 and 4 kV/cm are generated and defined as the high-field and low-field, respectively. The transmission of the main THz peak under the optical pump at different pump-probe time delays is shown in Fig. 18. The red and black lines represent the high- and low-THz electric-field probes, respectively. One can see that the transmission of the high-THz electric field in the GaAs sample is approximately 60% higher than that of the low-THz probe. This phenomenon is attributed to THz-pulse-induced intervalley scattering of electrons between the G and L valleys, as shown in Fig. 18(b). First, the 800 nm pump pulse excites the electrons and holes in the normally insulating GaAs sample and the electrons are injected into the higher mobility central G valley of the conduction band. The high-THz electric field later induces intervalley scattering, injecting electrons into the higher energy state L valley. Since the mobility of electrons in the L valley is much less than that of the central G valley, the conductivity of the GaAs sample decreases. Thus, the high-THz electric probe has higher transmission than the low-THz electric-field probe. The dynamic intervalley-electron-transfer model based on intervalley scattering is introduced and the results based on the model are derived. Figure 19 shows the experimental and calculated conductivities of GaAs and indicates good agreement. The conductivity of the GaAs sample in the low- and high-THz electric fields are different. Moreover, without consideration of the intervalley scattering effect, the calculated results do not match the experimental data.

Fig.18 Experimental results and theoretical explanation of transmission of pumped GaAs [¹³³]. (a) Transmission of the GaAs sample of the terahertz peak under the 800 nm pump. (b) Schematic of the electronic band structure of GaAs and related excitation mechanisms

Full size|PPT slide

Fig.19 Calculated and experimental complex conductivity of pumped GaAs [¹³³]. The experimental complex conductivity is extracted at a pump-probe delay time of 10 ps measured at low (a) and high (b) terahertz-probe fields. The solid blue lines in (a) and (b) are corresponding fits using the dynamic intervalley-electron-transfer model. The effect of neglecting intervalley scattering in the model is shown in (c)

Full size|PPT slide

Intense THz induced transmission enhancement is observed in monolayer graphene by the OPITP technique [¹³⁴]. It is found that the transmission enhancement increases with increasing optical pump fluence. After the photoexcitation, the transmission enhancement decreases as the THz field strength is increased. This can be attributed to an increased photoconductivity in the graphene sample induced by the optical pump. The photoexcitation of graphene results in hot electron–hole pairs generated by exciting electrons from the valence band into the conduction band, increasing the carrier density. In addition to the optical pump increasing the carrier density, it also raises the temperature of carriers through exchange of heat between the photoexcited carriers and cold carriers below the Fermi level via carrier-carrier scattering and optical phonon emission. The increase in the electron–hole density along with the heating of carriers leads to a higher carrier scattering rate and results in a net suppression in the photoconductivity of the graphene sample that leads to the observed pump-induced transmission enhancement. The measured sample is epitaxial monolayer graphene developed by thermal decomposition on a 4H-SiC substrate. The intense THz pulse is generated by a LiNbO₃ crystal using the titled-pulse-front technique. The sample is placed at the focus of the THz pulse, having a peak electric-field strength between 9 and 63 kV/cm on the sample. The transmitted THz field is detected by a 0.5-mm-thick ZnTe crystal using EOS. The pump beam is emitted by an 800 nm, 40 fs, 2.5 kHz amplified Ti:sapphire laser system. The optical pump fluence is varied from 29 to 137 mJ/cm². Figure 20(a) is the time-domain signal under the low-THz peak electric-field probe (9 kV/cm) showing an obvious THz transmission enhancement. All signals are normalized to the peak THz field transmitted through the bare SiC substrate. Figure 20(b) shows the differential transmission DT/T₀ of the THz pulse peak as a function of the delay time between the optical pump and THz probe under different pump fluences. T₀ is the THz transmission of the unpumped sample and DT is the difference between the THz transmission of the pumped and unpumped sample. After photoexcitation, a rapid increase and subsequent decrease in the THz transmission of the graphene sample was measured. As the optical pump fluence increases, DT/T₀ also increases. With the optical pump fluence fixed at 137 mJ/cm², the time-domain signals for different THz electric-field probes (9 and 63 kV/cm) are shown in Fig. 20(c). A clear decrease in the differential signal is observed. Figure 20(d) shows the pump-probe response of the graphene sample at different THz probe field levels. The peak of the differential THz signal decreases when the THz probe field strength is increased.

Fig.20 Intense terahertz-induced transmission enhancement in monolayer graphene [¹³⁴]. (a) Time-domain signals of transmitted terahertz pulses without and with the pump beam probed by 9 kV/cm peak terahertz field. (b) Differential transmission DT/T₀ of the peak terahertz field as a function of the pump-probe delay time, for various optical pump fluences. (c) Differential terahertz field DE/E₀ of terahertz pulses at low (9 kV/cm) and high (63 kV/cm) terahertz peak electric fields. (d) Transient differential transmission DT/T₀ of the terahertz peak field as a function of the pump-probe delay time at a fixed pump fluence of 137 mJ/cm² while the terahertz field is varied from 9 to 63 kV/cm

Full size|PPT slide

Terahertz-pump/terahertz-probe technique

TPTP spectroscopy uses a THz pulse as the pump beam and another THz pulse as a probe. This technique is widely used nowadays for characterizing materials [¹³⁵,¹³⁶]. Hoffmann et al. used the TPTP technique to investigate the impact ionization effect in InSb semiconductor material [¹³⁷] on picosecond time scales. The experimental setup is shown in Fig. 21(a). Two optical beams, split from a Ti:sapphire laser, are incident on a LiNiO₃ crystal and generate THz pulses by the tilted-pulse-front method. The 10% energy beam is used to generate the probe THz pulse and the 90% energy beam is used to generate the pump THz pulse. The single-cycle THz pump pulses are focused to a 1 mm diameter spot at the sample and a 1.1-mm-thick ZnTe crystal is used for EOS of the THz field using a balanced detector and a lock-in amplifier. The samples are n-type Te doped and nominally undoped InSb wafers. Figures 21(a) and 21(b) show the time-resolved absorption traces of the doped sample under different pump-probe time delays at temperatures of 80 and 200 K, respectively. For both temperatures, the absorption increases after THz excitation (after 0 ps) and reaches a peak at 30 ps, the total increase in absorption being 80–90 cm⁻¹. This effect is attributed to the generation of new carriers through impact ionization. In the measurement at 200 K, there is an initial dip in the absorption after THz excitation, attributed to the decrease in the mobility of hot electrons as a result of both strong nonparabolicity of the G valley in the conduction band of InSb and scattering of these hot electrons into side valleys. Moreover, the intrinsic carrier concentration at 200 K is much higher than that at 80 K due to the small band gap of InSb, thus, the effect of absorption saturation is much stronger at 200 K than at 80 K. After 4 ps, the additional absorption caused by the newly generated carriers exceeds the saturation effect, thereby leading to the observed overall absorption increase for the 200 K case. The absorption spectra for the doped and undoped samples obtained with different pump intensities at a probe delay of 35 ps and a temperature of 80 K are shown in Figs. 21(c) and 21(d). One can easily observe that the expected Drude-type contribution from free-carrier absorption is more pronounced at higher pump fluences.

Fig.21 Terahertz-pump/terahertz-probe time-resolved measurement of InSb [¹³⁷]. Terahertz absorption data of the doped InSb sample at (a) 80 K and (b) 200 K. Terahertz absorption spectra at various pump intensities measured at a probe delay time of 35 ps at 80 K for (c) doped and (d) undoped InSb samples

Full size|PPT slide

A strong THz induced transparency in CVD-grown graphene is also observed using the TPTP technique [¹³⁸]. This THz induced transparency is attributed to the nonlinear pumping of carriers in graphene that suppresses the conductivity. The high-field THz pulses are generated by OR based on the tilted-pulse-front method in a LiNiO₃ crystal, as shown in Fig. 22. The generated THz pulse is focused onto the sample with a pair of off-axis parabolic mirrors, the pulse energy of the THz pulse at the sample is estimated to be 1.5 mJ and the spot size was 1 mm, giving a maximum fluence of 190 mJ/cm². The transmitted THz pulse was focused onto a ZnTe crystal for detection by EOS. Figure 23(a) shows the THz field transmissions defined as t= |E_sam(ω)|/|E_ref(ω)|, for various THz pump field strengths in the frequency domain. The insets are the TDS signals of the sample and substrate, and corresponding spectra. One can see that the transmission increases with increasing THz pump strength, indicating strong THz field-induced transparency. To understand THz saturable absorption in graphene, a Drude-like treatment is used to calculate the conductivity of graphene and to fit the data in Fig. 23(b). The large induced transparency can be explained as a THz pump pulse induced creation of electron-hole pairs and carrier redistribution that suppresses the carrier mobility through enhanced scattering processes at higher carrier densities and lattice energies.

Fig.22 Experimental TPTP setup [¹³⁸]. RM: recombination mirror; EO/EOS: electro-optic sampling; LN: lithium niobate; l/2: half-waveplate; l/4: quarter waveplate; WP: Wollaston prism; PD: photodiode; LIA: lock-in amplifier

Full size|PPT slide

Fig.23 Terahertz-induced transparency of graphene [¹³⁹]. (a) Transmission spectra of CVD graphene on fused silica at different fluences. The insets are the time-domain signals and spectra of the sample and bare substrate. The transmission increases with increasing terahertz field strength. (b) Terahertz power transmission integrated over the entire terahertz pulse as a function of the terahertz fluence

Full size|PPT slide

Intense terahertz-pump/other radiation-probe technique

Because the THz pulse has a duration of several ps, it is a good candidate for short excitation to explore carrier dynamics [¹³⁹]. A large THz derived transparency is observed by the intense THz pump infrared probe (ITPOP) technique [¹⁴⁰]. In this work, the high peak THz electric field is used as the excitation field in the graphene sample and the excited carriers are monitored by the near-infrared pulse. The sample is a commercial CVD graphene grown on Cu foil that is transferred onto a SiO₂ substrate. The experimental setup is shown in Fig. 24(a), an 800 nm laser pulse (Ti:sapphire amplifier that delivers pulse of 3 mJ and 35 fs pulse width) is split into two pulses for (a) THz generation (2.4 mJ) based on the air-plasma method and (b) the time-resolved transmission probe (<1 nJ). The generated intense THz pulse and the optical probe pulse are focused on the graphene sample and the time delay between these two pulses is controlled by translating a stage to adjust a delay line. By replacing the sample with a GaP crystal, the THz time delay can be obtained by EOS detection, as shown in Fig. 24(b). The THz pulse is estimated to have a peak electric field of 300 kV/cm and a pulse width of 100 fs. Figure 25(c) shows a typical THz induced differential optical density (OD) measurement as a function of time with a peak pump THz electric field of 300 kV/cm. The normalized differential OD is defined as DT/OD_ref, where OD_ref is the OD of graphene at 800 nm without THz pulse excitation. The maximum value of DT is 10³ for the highest THz electric field. This large THz induced transparency is caused by electron filling or hole depletion of the corresponding energy levels. Figure 25 shows the experimental results of intense THz induced infrared transparency at 170 and 300 kV/cm. The transparency increases for higher THz electric fields because the carrier relaxation time tends to increase with field strength. The maximum of induced transparency as a function of the peak THz electric field is shown in Fig. 25(e). A fit with an exponent of 2.5 is found experimentally, suggesting that increasing the THz field strength causes nonlinear transmission attributed to the rapid increase in the number of carriers.

Fig.24 Terahertz derived transparency in graphene [¹⁴⁰]. (a) Schematic of ITPOP experimental setup. An 800 nm laser pulse is frequency doubled using a β-barium borate crystal. (b) Time-domain signal of the incident terahertz electric field and its spectrum. (c) Terahertz-induced normalized differential optical density of graphene at 800 nm as a function of delay time

Full size|PPT slide

Fig.25 Time-resolved ITPOP results [¹⁴⁰]. Normalized differential optical density as a function of time delay with peak electric fields of (a) 170 kV/cm and (b) 300 kV/cm (experiment: circle, simulation: solid line). (c) and (d) Corresponding calculated carrier densities as a function of time delay. Dashed lines represent initial carrier density. (e) Terahertz-induced transparency of graphene as a function of a peak electric field (experiment: filled circle, simulation: solid and dashed lines). Experimental results follow a power law with an exponent of 2.5 (dotted line)

Full size|PPT slide

In a summary, many spectroscopy detection techniques have employed intense THz waves to reveal the carrier dynamics of semiconductors and other condensed matter systems.

Applications of intense terahertz radiation to traditional nonlinear effects

Nonlinear effects require strong electric-field excitation. Due to the lack of intense sources, THz nonlinear effects have not been fully explored historically. Benefiting from recent developments of intense THz sources, there are increasing studies on nonlinear effects, such as high-order harmonic generation (HHG), saturation/non-saturation of absorption, and four-wave mixing. In this section, we will review the traditional optical nonlinear effects with intense THz pulses.

High-order harmonic generation

HHG is a fascinating and very useful nonlinear effect, that is relatively easy to realize in the optical region. In the THz region, there are two main obstacles to realizing HHG. The first is that the THz electric field may not be strong enough to excite nonlinearity. The second is that the efficiency of HHG is relatively low. With THz fields as high as several hundred MV/cm, HHG is beginning to be explored. THz HHG in semiconducting GaSe based on dynamical Bloch oscillations has been demonstrated experimentally [¹¹⁰]. The intense THz field drives the interband polarization in a bulk semiconductor and accelerates the excited electron–hole pairs to perform dynamical Bloch oscillations, which generate carrier-envelope phase stable radiation whose frequency range is between 0.1 and 675 THz. The intense THz pulse is generated by the difference frequency mixing effect in the GaSe crystal and HHG is detected with different sensors. The central frequency of the generated THz wave is 30 THz and the peak electric-field strength is 72 MV/cm. The time-domain waveform of the generated THz source is shown in Fig. 26(a). The waveform is detected with a 40-mm-thick GaSe crystal and the full width at half-maximum (FWHM) of the THz pulse is 109 fs. The inset shows the corresponding spectrum with a central frequency of 30 THz. The generated intense THz pulse is focused on another bulk GaSe crystal to generate HHG, which is detected by an AgGaS₂ sensor based on the EOS method. The results are shown in Fig. 26(b). From the inset one can observe the fundamental wave, second harmonic wave, and a low-frequency offset wave located between 0.1 and 10 THz that is generated by OR in the sample.

Fig.26 Time-domain transients of pump terahertz and HHG [¹¹⁰]. (a) Waveform of the intense terahertz source (blue, solid curve) features a Gaussian envelope (black dashed curve) with an intensity full width at half-maximum of 109 fs. Inset: corresponding spectrum. (b) Electro-optic trace of the waveform generated by the intense terahertz pulse in a GaSe single crystal (220-μm-thick). The data are recorded by an AgGaS₂ detector (100-μm-thick). Insets: corresponding amplitude spectrum and experimental geometry, indicating the incident angle of 70°

Full size|PPT slide

Moreover, HHG waves as high as the 22nd order are detected by different detection methods, as shown in Fig. 27. In this figure, the 6th to 9th order waves are detected by a grating spectrometer with an InGaAs array detector, while the 10th to 22nd order waves are detected by a cooled silicon charge-coupled device. HHG intensity decreases with order as expected. Figure 27(b) presents a trace of HHG intensity as a function of the THz amplitude for the 13th order wave. The intensity initially scales asymptotically as I¹³ is proportional to E_a²⁶, as shown by the dashed line. While at the higher incident electric field, the increase is slower, as shown by the dotted line. This confirms the non-perturbative nature of HHG. Note that all generated HHG waves are phase locked, therefore spectral interference may occur in the full spectrum regime. Figure 27(c) shows an interferogram of the 12th and the frequency-doubled sixth harmonic waves. A theory accounting for both off-resonance excitation of interband polarization and intraband acceleration of electronic wavepackets throughout the Brillouin zone is used for the explanation of HHG waves. The HHG wave spectrum is calculated using this method and indicated in Fig. 27(a) as a dashed line. Moreover, a THz-induced dynamical band mixing is obtained by including three valence and two conduction bands as shown in Fig. 27(d), which identifies dynamical Bloch oscillations combined with coherent interband excitation as the physical origin of the HHG process.

Fig.27 Terahertz HHG waves in bulk GaSe [¹¹⁰]. (a) High-order harmonic (HH) intensity spectrum (solid line and shaded area) emitted from a GaSe single crystal. The blue dashed curve shows the computed HH intensity spectrum, obtained from a five-band model. (b) Dependence of the intensity I¹³ of the 13th harmonic on the incident terahertz amplitude E_a. Dashed line, scaling law of I¹³\propto {{\displaystyle E}}_{\mathrm{a}}^{\mathrm{26}}; dotted line, scaling law of I¹³\propto {{\displaystyle E}}_{\mathrm{a}}. (c) Spectral interference between the frequency-doubled sixth harmonic and the 12th harmonic confirms the CEP stability of the HH radiation. (d) Model electronic band structure of GaSe between the G- and K-points, underlying the subsequent computations. Two conduction bands (CB1 and CB2) and three valence bands (VB1, VB2, and VB3) are considered. Coherent excitation of electrons (symbols), for example, from the second valence to the lowest conduction band, can proceed via interfering pathways with different scaling in powers of the terahertz field

Full size|PPT slide

THz HHG in single-layer graphene has also been performed experimentally [¹¹¹]. HHG up to the 7th order in single-layer graphene at room temperature and under ambient conditions was driven by a THz field of only tens kV/cm. The extremely efficient generation of THz high-order harmonics in graphene is attributed to the collective thermal response of its background Dirac electrons to the driving THz field. The sample is a typical monolayer graphene grown by the CVD method, deposited on a fused SiO₂ substrate. The THz source used is a new superconducting radiofrequency accelerator-based superradiant THz source: TELBE facility, which can generate narrow-band, multi-cycle quasi-monochromatic THz radiation. The peak electric-field strength can be tuned over the range 12–85 kV/cm, and the central frequency varied over the range 0.3–0.68 THz. The generated narrow-band THz wave is focused on the graphene sample, driving a nonlinear current in the graphene and leading to re-emission at higher odd-order harmonics. The experimental results are shown in Fig. 28(a), the frequency of the fundamental wave was 0.3 THz and the peak electric-field strength was E_f = 85 kV/cm. The blue line is the transmitted spectrum of the graphene sample and the red line is the spectrum of the bare SiO₂ substrate. One can see that in the graphene sample the odd-order HHG up to the seventh order is observed with a pump-to-harmonic field conversion efficiencies of 10⁻³, 10⁻⁴, and 10⁻⁵ for the 3rd, 5th, and 7th harmonics, respectively. This exceeds the respective nonlinear coefficients of typical solids by 7–18 orders of magnitude [¹⁴¹,¹⁴²]. The underlying physical mechanism of THz harmonic generation in graphene is the creation of nonlinear electrical currents resulting from the strongly nonlinear intraband THz conductivity of graphene background electrons. The processes of heating and cooling of background Dirac electron populations, leading to the reduction and recovery of the intraband THz conductivity in graphene, are schematically shown in Fig. 28(b). Here N(E) = D(E)f_FD(E,T) is the energy-dependent population density function for graphene background electrons, a product of the density of states D(E) and the Fermi–Dirac distribution f_FD(E,T). The energy relaxation (cooling) of the hot electron population in graphene occurs through phonon emission on a timescale of a few picoseconds and is in the THz region. This phonon emission completes the energy conversion process in the THz excitation of graphene, in which the background population of Dirac electrons serves as a nonlinear intermediary in the transfer of energy from the absorbed THz field to the lattice of graphene.

Fig.28 Experimental results and schematic diagram for explanation of HHG in graphene [¹¹¹]. (a) Spectrum of the graphene sample (red line) and bare SiO₂ substrate (blue line), the odd-order HHG waves are clearly observed. (b) Illustration of the mechanism of terahertz harmonic generation in graphene, based on calculations with the thermodynamic model of intraband nonlinear terahertz conductivity of graphene

Full size|PPT slide

Saturation of absorption

Saturation of absorption is a nonlinear effect in which the absorption of a material will saturate when the incident optical intensity exceeds the materials threshold. The THz nonlinear absorption in graphene nanoribbons has been demonstrated by using the ITPTP technique [¹¹³]. A strong saturation of plasmon absorption followed by a 10 ps relaxation time is observed experimentally. The observed nonlinearity is enhanced by two orders of magnitude compared to unpatterned graphene without plasmon resonance. The observed strong linearity is contributed to by an unexpected redshift of plasmon resonance together with a broadened and weakened resonance caused by the increase in electron temperature. The sample is a CVD-grown monolayer graphene which is transferred to the silicon substrate later. Graphene ribbons of width w = 730 nm and period L = 1.5 mm are fabricated by electron-beam lithography and a lift-off process. The fabricated graphene grating covers a region of 1.5 mm × 1.5 mm. The false color scanning electron micrograph of the sample is shown in Fig. 29(a) and a schematic of the structure is shown in Fig. 29(b). The transmission spectrum, shown as a blue line in Fig. 29(c), exhibits an absorption peak at the plasmon frequency of 9.4 THz. The ITPTP setup used is shown in Fig. 29(d), in which the intense THz radiation is generated by a free-electron laser (FEL) tuned to produce 5.5 ps pulses at a repetition rate of 13 MHz. The THz beam is split into two beams that comprise the pump and probe beams, and the time delay is controlled by a motion stage. The state of polarization of copolarized pump and probe beams can be set to be either perpendicular or parallel to the graphene ribbons in order to control plasmon excitation. Figure 30(a) shows the transmission of the sample as a function of the time delay between the pump and probe THz waves for different pump fluences. One can see that the pump causes a decrease in absorption in all cases. The observed nonlinear response decay for the wake pump pulse has a time constant of ~10 ps, which is close to the electron-phonon relaxation time in the graphene. A nonlinear thermal model for plasmonic absorption that includes supercollision cooling and longitudinal acoustic phonon scattering is introduced to explain this nonlinear absorption effect. The calculated transmission results are shown in Fig. 30(b), and are in close agreement with the experimental results. Moreover, the nonlinearity of the sample can be enhanced by the plasmonic structure, as shown in Fig. 30(c). The plasmons are excited when the THz wave is polarized perpendicular to the ribbons.

Fig.29 Terahertz nonlinear absorption in graphene nanoribbons [¹¹³]. (a) False color scanning electron micrograph of fabricated graphene ribbons. (b) Cross sectional diagram of device. (c) Measured (blue) and best fit (green) linear transmission spectrum of device. (d) Sketch of the experimental setup for the pump-probe measurements

Full size|PPT slide

Fig.30 Experimental results of nonlinear absorption in graphene nanoribbons [¹¹³]. (a) Measured relative change in transmission of the probe signal as a function of pump-probe time delay Dt for different pump fluences. The positive signal indicates a decrease in absorption that becomes stronger at higher pump fluences. (b) Calculated relative change in transmission based on a nonlinear thermal model for plasmonic absorption in graphene nanoribbons that includes supercollision cooling and longitudinal acoustic phonon scattering. (c) Comparison of normalized change in transmission for two different polarizations

Full size|PPT slide

Four-wave mixing

THz fields reaching 100 MV/cm [¹¹⁷] have enabled exploration of light–matter interaction in a regime where the Rabi frequency becomes comparable to the oscillation frequency of the driving THz field and the nonlinear response reaches the limit of non-perturbative optics. The coherent nonlinear THz response of the interband polarization in the semiconductor InSb has been revealed by the ITPTP technique. The most interesting result is the observation of four-wave mixing signal separated from the other THz signals [¹¹⁷]. The experimental results show that when the peak electric fields of the THz pulses are in excess of 3 MV/cm, the four-wave mixing signal shows a clear signature of a non-perturbative response caused by coherent Rabi flopping. The schematic of the experimental setup is shown in Fig. 31, in which pulses A and B are two intense THz pulses which are generated by difference frequency mixing in a GaSe emitter. Pulse A is fixed and pulse B is delayed by a time t. The transmitted pump-probe signal is detected as a function of t. The interference of these two THz pulses generates a four-wave mixing signal which is emitted in a different direction, as the red dashed line shown in Fig. 31. The sample is a bulk InSb, which has a small energy gap that results in a relatively large density of intrinsic charge carriers.

Fig.31 Schematic representation of a non-collinear four-wave mixing experiment [¹¹⁷]. Two high-field terahertz pulses are focused into an InSb sample. The dashed lines illustrate the generated nonlinear signal. The pump-probe signals PP-BA (pump B/probe A) and PP-AB (pump A/probe B) propagate in the same direction as the probe pulses A and B, respectively. The coherent four-wave mixing signal depends on the relative phase of the interacting pulses and propagates in a different direction

Full size|PPT slide

Fig.32 Experimental results of terahertz four-wave mixing [¹¹⁷]. (a) Transmitted terahertz signal through InSb as a function of the electro-optic sampling delay time t and relative pulse delay t. (b) Nonlinear four-wave mixing signal. (c) Two-dimensional Fourier spectrum of pump-probe and four-wave mixing contributions located at different points of the frequency plane. (d) and (e) Time-domain pump-probe signals PP-BA and PP-AB obtained by inverse Fourier transform of the signals at k_A and k_B, respectively. (f) Time-domain four-wave mixing signal obtained by inverse Fourier transform of the signal at 2k_A− k_B

Full size|PPT slide

Figure 32(a) shows the transmitted THz field as a function of the EOS delay time t and the relative pulse delay t. The nonlinear contribution is obtained by subtracting the transmitted fields of the individual pulses A and B from the total electric field. The resulting two time-dependent nonlinear response is shown in Fig. 32(b). Since the four-wave mixing process relies on the interference of two excitation fields, the phase of the signal varies periodically with the relative pulse delay t. Fourier transformation in two-dimensional frequency space allows us to separate the four-wave mixing signal from the pump-probe signals, as shown in Fig. 32(c). Different contributions to the nonlinear signal are manifested as distinct pairs of maxima conjugated by the inversion operation with respect to the origin. Figure 32(d) shows the temporal evolution the signal obtained by the selective inverse Fourier transform of the signal at k_A that represents pump and probe beams of B and A pulses, respectively. Figure 32(e) shows the inverse Fourier transform of the signal at k_B that represents pump and probe beams of A and B pulses, respectively. Figure 32(f) is the inverse Fourier transform of the signal at 2k_A−k_B, and is a clear four-wave mixing signal.

Application of intense terahertz magnetic field

Along with the development of intense THz sources, intense THz magnetic fields have also been explored. The intense THz magnetic field can strongly couple to a spin subsystem and be used to coherently control the precession of macroscopic magnetization [¹¹⁸,¹⁴³]. Ultrafast control of collective spin precession in antiferromagnetic NiO at frequencies of 1 THz was demonstrated [¹⁰,¹¹⁷]. Using intense THz magnetic fields, the coherent magnon can be switched on and off with sub-cycle precision. The experiment is schematically shown in Fig. 33(a). An intense THz magnetic field transient with a strength of ~0.5 T excites the sample and perturbs the electron spins via the direct Zeeman interaction. The induced magnetization M(t) is probed by a near-infrared laser pulse as a function of the delay time t. The quasi-cubic crystal structure of the sample is shown in Fig. 33(b). Figure 33(c) shows the time trace B(t) of the incident magnetic pulse recorded by EOS. It indicates that the incident THz pulse has a 0.13 T magnetic field and a frequency range of 0.1–3 THz in the spectrum that fully covers the magnon resonance frequency of the NiO sample. An 8-fs ultrafast pulse with a central photon energy of 1 eV serves as the probe beam to obtain the pump-induced Faraday rotation q_F as a function of the EOS time t. The experimental results are shown in Fig. 33(d). A harmonic oscillation with a period of 1 ps that reaches its maximum amplitude at t = 3 ps is clearly shown, and decays exponentially with a time constant of 39 ps. The resulting spectrum that is obtained as the Fourier transform of the time-domain Faraday transient is shown in Fig. 33(e). A narrow peak is evident at 1.0 THz, clearly identifying the signal as the magnetization signature of a coherent oscillation of a long-wavelength antiferromagnetic magnon in the NiO sample. Because the magnon has a long lifetime of 39 ps, coherent control can be demonstrated by using two THz pulses. When the second THz pulse is applied precisely six precession cycles (6 ps) after the first pulse, the amplitude of the induced magnetization is doubled as shown in Fig. 33(f). This amplification arises from that the torque of the second pulse being in phase with the spin precession induced by the first pulse. The amplification effect is reversed if the second pulse is delayed 6.5 precession cycles after the first, as shown in Fig. 33(g). In this case, the torque of the second pulse is in antiphase with the spin precession and switches the dynamics off. All simulation results agree with the experimental data.

Fig.33 Switching of coherent magnon [¹⁰]. (a) Schematic of terahertz-pump magneto optic-probe system. (b) Lattice geometry of NiO with the incident of terahertz magnetic field pulse. (c) Magnetic field of an incident single terahertz pulse B(t). (d) Induced Faraday rotation q_F(t) as a function of pump-probe delay t. (e) Fourier amplitude spectrum of B and q_F. (f) Double-pulse excitations with the second pulse in and (g) out of phase with the spin precession triggered by the first pulse. The red lines are the trace of the terahertz pulses, green lines are the experimental results for q_F(t), and black lines are the simulation results

Full size|PPT slide

Perspectives

This article provides an overview of the current status of the generation and applications of intense THz radiation. Intense THz sources are becoming increasingly accessible. The intensity of THz generated from LiNbO₃ can be increased by using a large crystal and liquid nitrogen cooling. The potential of organic crystals is yet to be fully realized. With the improvement in high-intensity femtosecond lasers, THz from laser plasma will provide a novel avenue for intense THz sources, especially from metal surfaces, water films, and bulk liquids. Spintronic materials and metasurfaces are two emerging systems. By optimally designing these artificial structures, the generated THz radiation can be greatly enhanced. Furthermore, metasurfaces provide an approach to control the polarization and phase of the generated THz field, which is useful for precise control of THz–matter interaction. With the development of intense THz sources, it is possible to access the nonlinear properties of materials in the THz range, such as HHG from two-dimensional materials and their heterostructures, Kerr effects, and saturation of absorptions. Therefore, the strong THz magnetic field opens an avenue for switching magnons on the ps time scale, and we expect more exciting contributions to appear in this promising field.

Acknowledgements

This work was supported by the National Key R&D Program of China (No. 2019YFC1711905), the National Natural Science Foundation of China (Grant Nos. 11774243, 11774246, and 6167513), the Youth Innovative Research Team of Capital Normal University (No. 19530050146), the Capacity Building for Science & Technology Innovation Fundamental Scientific Research Funds (Nos. 19530050170 and 19530050180), and the Scientific Research Base Development Program of the Beijing Municipal Commission of Education.

References

1 Tonouchi M. Cutting-edge terahertz technology. Nature Photonics, 2007, 1(2): 97–105

2 Beard M C, Turner G M, Schmuttenmaer C A. Terahertz spectroscopy. Journal of Physical Chemistry B, 2002, 106(29): 7146–7159

3 Ulbricht R, Hendry E, Shan J, Heinz T F, Bonn M. Carrier dynamics in semiconductors studied with time-resolved terahertz spectroscopy. Reviews of Modern Physics, 2011, 83(2): 543–586

4 Jepsen P U, Cooke D G, Koch M. Terahertz spectroscopy and imaging-modern techniques and applications. Laser & Photonics Reviews, 2011, 5(1): 124–166

5 Kampfrath T, Tanaka K, Nelson K A. Resonant and nonresonant control over matter and light by intense terahertz transients. Nature Photonics, 2013, 7(9): 680–690

6 Sell A, Leitenstorfer A, Huber R. Phase-locked generation and field-resolved detection of widely tunable terahertz pulses with amplitudes exceeding 100 MV/cm. Optics Letters, 2008, 33(23): 2767–2769

PMID

7 Zhang X C, Shkurinov A, Zhang Y. Extreme terahertz science. Nature Photonics, 2017, 11(1): 16–18

8 Hirori H, Tanaka K. Dynamical nonlinear interaction of solids with strong terahertz pulses. Journal of the Physical Society of Japan, 2016, 85(8): 082001

9 Yamaguchi K, Nakajima M, Suemoto T. Coherent control of spin precession motion with impulsive magnetic fields of half-cycle terahertz radiation. Physical Review Letters, 2010, 105(23): 237201

PMID

10 Kampfrath T, Sell A, Klatt G, Pashkin A, Mährlein S, Dekorsy T, Wolf M, Fiebig M, Leitenstorfer A, Huber R. Coherent terahertz control of antiferromagnetic spin waves. Nature Photonics, 2011, 5(1): 31–34

11 Daranciang D, Goodfellow J, Fuchs M, Wen H, Ghimire S, Reis D A, Loos H, Fisher A S, Lindenberg A M. Single-cycle terahertz pulses with >0.2 V/Å field amplitudes via coherent transition radiation. Applied Physics Letters, 2011, 99(14): 141117

12 Li H T, Lu Y L, He Z G, Jia Q K, Wang L. Generation of intense narrow-band tunable terahertz radiation from highly bunched electron pulse train. Journal of Infrared, Millimeter and Terahertz Waves, 2016, 37(7): 649–657

13 Hou L, Shi W. An LT-GaAs terahertz photoconductive antenna with high emission power, low noise, and good stability. IEEE Transactions on Electron Devices, 2013, 60(5): 1619–1624

14 Beard M C, Turner G M, Schmuttenmaer C A. Subpicosecond carrier dynamics in low-temperature grown GaAs as measured by time resolved terahertz spectroscopy. Journal of Applied Physics, 2001, 90(12): 5915–5923

15 Buryakov A M, Ivanov M S, Nomoev S A, Khusyainov D I, Mishina E D, Khomchenko V A, Vasilevskii I S, Vinichenko A N, Kozlovskii K I, Chistyakov A A, Paixão J A. An advanced approach to control the electro-optical properties of LT-GaAs based terahertz photoconductive antenna. Materials Research Bulletin, 2020, 122: 110688

16 Doany F E, Grischkowsky D, Chi C C. Carrier lifetime versus ion-implantation dose in silicon on sapphire. Applied Physics Letters, 1987, 50(8): 460–462

17 Sarkisov S Y, Safiullin F D, Skakunov M S, Tolbanov O P, Tyazhev A V, Nazarov M M, Shkurinov A P. Dipole antennas based on SI-GaAs:Cr for generation and detection of terahertz radiation. Russian Physics Journal, 2013, 55(8): 890–898

18 Rode J C, Chiang H W, Choudhary P, Jain V, Thibeault B J, Mitchell W J, Rodwell M J W, Urteaga M, Loubychev D, Snyder A, Wu Y, Fastenau J M, Liu A W K. Indium phosphide heterobipolar transistor technology beyond 1-THz bandwidth. IEEE Journal of Transactions on Electron Devices, 2015, 62(9): 2779–2785

19 Simoens F, Meilhan J, Delplanque B, Gidon S, Lasfargues G, Dera J L, Nguyen D T, Ouvrier-Buffet J L, Pocas S, Maillou T, Cathabard O, Barbieri S. Real-time imaging with THz fully-customized uncooled amorphous-silicon microbolometer focal plane arrays. Proceedings of the Society for Photo-Instrumentation Engineers, 2012, 8363: 83630D, 83630D-12

20 You D, Jones R R, Bucksbaum P H, Dykaar D R. Generation of high-power sub-single-cycle 500-fs electromagnetic pulses. Optics Letters, 1993, 18(4): 290–292

PMID

21 Hafez H A, Chai X, Ibrahim A, Mondal S, Férachou D, Ropagnol X, Ozaki T. Intense terahertz radiation and their applications. Journal of Optics, 2016, 18(9): 093004

22 Kasai S, Watanabe M, Ouchi T. Improved terahertz wave intensity in photoconductive antennas formed of annealed low-temperature grown GaAs. Japanese Journal of Applied Physics, 2007, 46(7A): 4163–4165

23 Yoneda H, Tokuyama K, Nagata H. Generation of high-peak-power THz radiation by using diamond photoconductive antenna array. In: Proceedings of the 14th Annual Meeting of the IEEE Lasers and Electro-Optics Society (LEOS). San Diego: IEEE, 2001, 644–645

24 Ono S, Murakami H, Quema A, Diwa G, Sarukura N, Nagasaka R, Ichikawa Y, Ogino H, Ohshima E, Yoshikawa A, Fukuda T. Generation of terahertz radiation using zinc oxide as photoconductive material excited by ultraviolet pulses. Applied Physics Letters, 2005, 87(26): 261112

25 Ahi K. Review of GaN-based devices for terahertz operation. Optical Engineering (Redondo Beach, Calif.), 2017, 56(09): 090901

26 Cho P S, Ho P T, Goldhar J, Lee C H. Photoconductivity in ZnSe under high electric fields. IEEE Journal of Quantum Electronics, 1994, 30(6): 1489–1497

27 Kikuma I, Matsuo M, Komuro T. In situ annealing of melt-Grown ZnSe crystals under Zn partial pressure. Japanese Journal of Applied Physics, 1992, 31(Part 2, No. 5A): L531–L534

28 Ropagnol X, Bouvier M, Reid M, Ozaki T. Improvement in thermal barriers to intense terahertz generation from photoconductive antennas. Journal of Applied Physics, 2014, 116(4): 043107

29 Imafuji O, Singh B P, Hirose Y, Fukushima Y, Takigawa S. High power subterahertz electromagnetic wave radiation from GaN photoconductive switch. Applied Physics Letters, 2007, 91(7): 071112

30 Xu M, Mittendorff M, Dietz R J B, Künzel H, Sartorius B, Göbel T, Schneider H, Helm M, Winnerl S. Terahertz generation and detection with InGaAs-based large-area photoconductive devices excited at 1.55 µm. Applied Physics Letters, 2013, 103(25): 251114

31 Salem B, Morris D, Aimez V, Beerens J, Beauvais J, Houde D. Pulsed photoconductive antenna terahertz sources made on ion-implanted GaAs substrates. Journal of Physics Condensed Matter, 2005, 17(46): 7327–7333

32 Dreyhaupt A, Winnerl S, Dekorsy T, Helm M. High-intensity terahertz radiation from a microstructured large-area photoconductor. Applied Physics Letters, 2005, 86(12): 121114

33 Ropagnol X, Morandotti R, Ozaki T, Reid M. Toward high-power terahertz emitters using large aperture ZnSe photoconductive antennas. IEEE Journal of Photonics, 2011, 3(2): 174–186

34 Hattori T, Egawa K, Ookuma S I, Itatani T. Intense terahertz pulses from large-aperture antenna with interdigitated electrodes. Japanese Journal of Applied Physics, 2006, 45(15): L422–L424

35 Beck M, Schäfer H, Klatt G, Demsar J, Winnerl S, Helm M, Dekorsy T. Impulsive terahertz radiation with high electric fields from an amplifier-driven large-area photoconductive antenna. Optics Express, 2010, 18(9): 9251–9257

PMID

36 Yardimci N T, Yang S H, Berry C W, Jarrahi M. High-power terahertz generation using large-area plasmonic photoconductive emitters. IEEE Transactions on Terahertz Science and Technology, 2015, 5(2): 223–229

37 Madéo J, Jukam N, Oustinov D, Rosticher M, Rungsawang R, Tignon J, Dhillon S S. Frequency tunable terahertz interdigitated photoconductive antennas. Electronics Letters, 2010, 46(9): 611–613

38 Ropagnol X, Morandotti R, Ozaki T, Reid M. THz pulse shaping and improved optical-to-THz conversion efficiency using a binary phase mask. Optics Letters, 2011, 36(14): 2662–2664

PMID

39 Ropagnol X, Khorasaninejad M, Raeiszadeh M, Safavi-Naeini S, Bouvier M, Côté C Y, Laramée A, Reid M, Gauthier M A, Ozaki T. Intense THz Pulses with large ponderomotive potential generated from large aperture photoconductive antennas. Optics Express, 2016, 24(11): 11299–11311

PMID

40 Ropagnol X, Chai X, Raeis-Zadeh S M, Safavi-Naeini S, Kirouac-Turmel M, Bouvier M, Côté C Y, Reid M, Gauthier M A, Ozaki T. Influence of gap size on intense THz generation from ZnSe interdigitated large aperture photoconductive antennas. IEEE Journal of Selected Topics in Quantum Electronics, 2017, 23(4): 1–8

41 Shi W, Hou L, Wang X M. High effective terahertz radiation from semi-insulating-GaAs photoconductive antennas with ohmic contact electrodes. Journal of Applied Physics, 2011, 110(2): 023111

42 Hebling J, Yeh K L, Hoffmann M C, Bartal B, Nelson K A. Generation of high-power terahertz pules by tilted-pulse-front excitation and their application possibilities. Journal of the Optical Society of America B, Optical Physics, 2008, 25(7): B6–B19

43 Blanchard F, Sharma G, Razzari L, Ropagnol X, Bandulet H C, Vidal F, Morandotti R, Kieffer J C, Ozaki T, Tiedje H, Haugen H, Reid M, Hegmann F. Generation of intense terahertz radiation via optical methods. IEEE Journal of Selected Topics in Quantum Electronics, 2011, 17(1): 5–16

44 Blanchard F, Razzari L, Bandulet H C, Sharma G, Morandotti R, Kieffer J C, Ozaki T, Reid M, Tiedje H F, Haugen H K, Hegmann F A. Generation of 1.5 µJ single-cycle terahertz pulses by optical rectification from a large aperture ZnTe crystal. Optics Express, 2007, 15(20): 13212–13220

PMID

45 Löffler T, Hahn T, Thomson M, Jacob F, Roskos H. Large-area electro-optic ZnTe terahertz emitters. Optics Express, 2005, 13(14): 5353–5362

PMID

46 Fülöp J A, Pálfalvi L, Klingebiel S, Almási G, Krausz F, Karsch S, Hebling J. Generation of sub-mJ terahertz pulses by optical rectification. Optics Letters, 2012, 37(4): 557–559

PMID

47 Blanchard F, Ropagnol X, Hafez H, Razavipour H, Bolduc M, Morandotti R, Ozaki T, Cooke D G. Effect of extreme pump pulse reshaping on intense terahertz emission in lithium niobate at multimilliJoule pump energies. Optics Letters, 2014, 39(15): 4333–4336

PMID

48 Pálfalvi L, Hebling J, Almasi G, Peter A, Polgar K, Lengyel K, Szipocs R. Nonlinear refraction and absorption of Mg doped stoichiometric and congruent LiNbO₃. Journal of Applied Physics, 2004, 95(3): 902–908

49 Huang S W, Granados E, Huang W R, Hong K H, Zapata L E, Kärtner F X. High conversion efficiency, high energy terahertz pulses by optical rectification in cryogenically cooled lithium niobate. Optics Letters, 2013, 38(5): 796–798

PMID

50 Wu X J, Ma J L, Zhang B L, Chai S S, Fang Z J, Xia C Y, Kong D Y, Wang J G, Liu H, Zhu C Q, Wang X, Ruan C J, Li Y T. Highly efficient generation of 0.2 mJ terahertz pulses in lithium niobate at room temperature with sub-50 fs chirped Ti:sapphire laser pulses. Optics Express, 2018, 26(6): 7107–7116

PMID

51 Oh T I, Yoo Y J, You Y S, Kim K Y. Generation of strong terahertz fields exceeding 8 MV/cm at 1 kHz and real-time beam profiling. Applied Physics Letters, 2014, 105(4): 041103

52 Jazbinsek M, Puc U, Abina A, Zidansek A. Organic crystal for THz photonics. Applied Sciences (Basel, Switzerland), 2019, 9(5): 882

53 Hauri C P, Ruchert C, Vicario C, Ardana F. Strong-field single-cycle THz pulses generated in an organic crystal. Applied Physics Letters, 2011, 99(16): 161116

54 Shalaby M, Hauri C P. Demonstration of a low-frequency three-dimensional terahertz bullet with extreme brightness. Nature Communications, 2015, 6(1): 5976

PMID

55 Liu B, Bromberger H, Cartella A, Gebert T, Först M, Cavalleri A. Generation of narrowband, high-intensity, carrier-envelope phase-stable pulses tunable between 4 and 18 THz. Optics Letters, 2017, 42(1): 129–131

PMID

56 Zhao H, Tan Y, Wu T, Steinfeld G, Zhang Y, Zhang C L, Zhang L L, Shalaby M. Efficient broadband terahertz generation from organic crystal BNA using near infrared pump. Applied Physics Letters, 2019, 114(24): 241101

57 Kaindl R A, Eickemeyer F, Woerner M, Elsaesser T. Broadband phase-matched difference frequency mixing of femtosecond pulses in GaSe: experiment and theory. Applied Physics Letters, 1999, 75(8): 1060–1062

58 Junginger F, Sell A, Schubert O, Mayer B, Brida D, Marangoni M, Cerullo G, Leitenstorfer A, Huber R. Single-cycle multiterahertz transients with peak fields above 10 MV/cm. Optics Letters, 2010, 35(15): 2645–2647

PMID

59 Hamster H, Sullivan A, Gordon S, White W, Falcone R W. Subpicosecond, electromagnetic pulses from intense laser-plasma interaction. Physical Review Letters, 1993, 71(17): 2725–2728

PMID

60 Sun W F, Zhou Y S, Wang X K, Zhang Y. External electric field control of THz pulse generation in ambient air. Optics Express, 2008, 16(21): 16573–16580

PMID

61 Bakhtiari F, Esmaeilzadeh M, Ghafary B. Terahertz radiation with high power and high efficiency in a magnetized plasma. Physics of Plasmas, 2017, 24(7): 073112

62 Xie X, Dai J, Zhang X C. Coherent control of THz wave generation in ambient air. Physical Review Letters, 2006, 96(7): 075005

PMID

63 Koulouklidis A D, Gollner C, Shumakova V, Fedorov V Y, Pugžlys A, Baltuška A, Tzortzakis S. Observation of extremely efficient terahertz generation from mid-infrared two-color laser filaments. Nature Communications, 2020, 11(1): 292

PMID

64 Kim K Y, Taylor A J, Glownia J H, Rodriguez G. Coherent control of terahertz supercontinuum generation in ultrafast laser-gas interactions. Nature Photonics, 2008, 2(10): 605–609

65 Cook D J, Hochstrasser R M. Intense terahertz pulses by four-wave rectification in air. Optics Letters, 2000, 25(16): 1210–1212

PMID

66 Dai J M, Zhang X C. Terahertz wave generation from gas plasma using a phase compensator with attosecond phase-control accuracy. Applied Physics Letters, 2009, 94(2): 021117

67 Zhang L L, Wang W M, Wu T, Zhang R, Zhang S J, Zhang C L, Zhang Y, Sheng Z M, Zhang X C. Observation of terahertz radiation via the two-color laser scheme with uncommon frequency ratios. Physical Review Letters, 2017, 119(23): 235001

PMID

68 Peng X Y, Li C, Chen M, Toncian T, Jung R, Willi O, Li Y T, Wang W M, Wang S J, Liu F, Pukhov A, Sheng Z M, Zhang J. Strong terahertz radiation from air plasmas generated by an aperture-limited Gaussian pump laser beam. Applied Physics Letters, 2009, 94(10): 101502

69 Kim K Y, Glownia J H, Taylor A J, Rodriguez G. Terahertz emission from ultrafast ionizing air in symmetry-broken laser fields. Optics Express, 2007, 15(8): 4577–4584

PMID

70 Liao G Q, Li Y T, Zhang Y H, Liu H, Ge X L, Yang S, Wei W Q, Yuan X H, Deng Y Q, Zhu B J, Zhang Z, Wang W M, Sheng Z M, Chen L M, Lu X, Ma J L, Wang X, Zhang J. Demonstration of coherent terahertz transition radiation from relativistic laser-solid interactions. Physical Review Letters, 2016, 116(20): 205003

PMID

71 Tian Y, Liu J S, Bai Y F, Zhou S Y, Sun H Y, Liu W W, Zhao J Y, Li R X, Xu Z Z. Femtosecond-laser-driven wire-guided helical undulator for intense terahertz radiation. Nature Photonics, 2017, 11(4): 242–246

72 Jin Q, E Y, Williams K, Dai J, Zhang X C. Observation of broadband terahertz wave generation from liquid water. Applied Physics Letters, 2017, 111(7): 071103

73 Dey I, Jana K, Fedorov V Y, Koulouklidis A D, Mondal A, Shaikh M, Sarkar D, Lad A D, Tzortzakis S, Couairon A, Kumar G R. Highly efficient broadband terahertz generation from ultrashort laser filamentation in liquids. Nature Communications, 2017, 8(1): 1184

PMID

74 Zhang L L, Wang W M, Wu T, Feng S J, Kang K, Zhang C L, Zhang Y, Li Y T, Sheng Z M, Zhang X C. Strong terahertz radiation from a liquid-water line. Physical Review Applied, 2019, 12(1): 014005

75 Zhu L G, Kubera B, Fai Mak K, Shan J. Effect of surface states on terahertz emission from the Bi₂Se₃ surface. Scientific Reports, 2015, 5(1): 10308

PMID

76 Luo C W, Chen H J, Tu C M, Lee C C, Ku S A, Tzeng W Y, Yeh T T, Chiang M C, Wang H J, Chu W C, Lin J Y, Wu K H, Juang J Y, Kobayashi T, Cheng C M, Chen C H, Tsuei K D, Berger H, Sankar R, Chou F C, Yang H D. THz generation and detection on Dirac Fermions in topological insulators. Advanced Optical Materials, 2013, 1(11): 804–808

77 Seifert T, Jaiswal S, Martens U, Hannegan J, Braun L, Maldonado P, Freimuth F, Kronenberg A, Henrizi J, Radu I, Beaurepaire E, Mokrousov Y, Oppeneer P M, Jourdan M, Jakob G, Turchinovich D, Hayden L M, Wolf M, Münzenberg M, Kläui M, Kampfrath T. Efficient metallic spintronic emitters of ultrabroadband terahertz radiation. Nature Photonics, 2016, 10(7): 483–488

78 Yang D, Liang J, Zhou C, Sun L, Zheng R, Luo S N, Wu Y Z, Qi J B. Powerful and tunable THz emitters based on the Fe/Pt magnetic heterostructure. Advanced Optical Materials, 2016, 4(12): 1944–1949

79 Seifert T, Jaiswal S, Sajadi M, Jakob G, Winnerl S, Wolf M, Kläui M, Kampfrath T. Ultrabroadband single-cycle terahertz pulses with peak fields of 300 kV·cm⁻¹ from a metallic spintronic emitter. Applied Physics Letters, 2017, 110: 252402

80 Luo L, Chatzakis I, Wang J, Niesler F B P, Wegener M, Koschny T, Soukoulis C M. Broadband terahertz generation from metamaterials. Nature Communications, 2014, 5(1): 3055

PMID

81 Keren-Zur S, Tal M, Fleischer S, Mittleman D M, Ellenbogen T. Generation of spatiotemporally tailored terahertz wavepackets by nonlinear metasurfaces. Nature Communications, 2019, 10(1): 1778

PMID

82 Ropagnol X, Blanchard F, Ozaki T, Reid M. Intense terahertz generation at low frequencies using an interdigitated ZnSe large aperture photoconductive antenna. Applied Physics Letters, 2013, 103(16): 161108

83 Hirori H, Doi A A, Blanchard F, Tanaka K. Single cycle terahertz pulses with amplitudes exceeding 1 MV/cm generated by optical rectification in LiNbO₃. Applied Physics Letters, 2011, 98(9): 091106

84 Smith P R, Auston D H, Nuss M C. Subpicosecond photoconducting dipole antennas. IEEE Journal of Quantum Electronics, 1988, 24(2): 255–260

85 Wu Q, Zhang X C. Free-space electro-optic sampling of terahertz beams. Applied Physics Letters, 1995, 67(24): 3523–3525

86 Fattinger C, Grischkowsky D R. Terahertz beams. Applied Physics Letters, 1989, 54(6): 490–492

87 van Exter M, Grischkowsky D R. Characterization of an optoelectronic terahertz beam system. IEEE Transactions on Microwave Theory and Techniques, 1990, 38(11): 1684–1691

88 Lee Y S. Principles of Terahertz Science and Technology. Berlin: Springer, 2008

89 Singh A, Pal S, Surdi H, Prabhu S S, Mathimalar S, Nanal V, Pillay R G, Döhler G H. Carbon irradiated semi insulating GaAs for photoconductive terahertz pulse detection. Optics Express, 2015, 23(5): 6656–6661

PMID

90 Liu T A, Tani M, Nakajima M, Hangyo M, Pan C L. Ultrabroadband terahertz field detection by photoconductive antennas based on multi-energy arsenic-ion-implanted GaAs and semi-insulating GaAs. Applied Physics Letters, 2003, 83(7): 1322–1324

91 Hattori T, Tukamoto K, Nakatsuka H. Time-resolved study of intense terahertz pulses generated by a large aperture photoconductive antenna. Japanese Journal of Applied Physics, 2001, 40(Part 1, No. 8): 4907–4912

92 Jepsen P U, Jacobsen R H, Keiding S R. Generation and detection of terahertz pulses from biased semiconductor antennas. Journal of the Optical Society of America B, Optical Physics, 1996, 13(11): 2424–2436

93 Sharma G, Al-Naib I, Hafez H, Morandotti R, Cooke D G, Ozaki T. Carrier density dependence of the nonlinear absorption of intense THz radiation in GaAs. Optics Express, 2012, 20(16): 18016–18024

PMID

94 Gallot G, Zhang J, McGowan R, Jeon T, Grischkowsky D. Measurements of the THz absorption and dispersion of ZnTe and their relevance to the electro-optic detection of THz radiation. Applied Physics Letters, 1999, 74(23): 3450–3452

95 Kübler C, Huber R, Tübel S, Leitenstorfer A. Ultrabroadband detection of multi-terahertz field transients with GaSe electro-optic sensors: approaching the near infrared. Applied Physics Letters, 2004, 85(16): 3360–3362

96 Reimann K, Smith R P, Weiner A M, Elsaesser T, Woerner M. Direct field-resolved detection of terahertz transients with amplitudes of megavolts per centimeter. Optics Letters, 2003, 28(6): 471–473

PMID

97 Schall M, Helm H, Keiding S R. Far infrared properties of electro-optic crystals measured by THz time-domain spectroscopy. International Journal of Infrared and Millimeter Waves, 1999, 20(4): 595–604

98 Sharma G, Singh K, Al-Naib I, Morandotti R, Ozaki T. Terahertz detection using spectral domain interferometry. Optics Letters, 2012, 37(20): 4338–4340

PMID

99 Dai J, Xie X, Zhang X C. Detection of broadband terahertz waves with a laser-induced plasma in gases. Physical Review Letters, 2006, 97(10): 103903

PMID

100 Karpowicz N, Dai J, Lu X, Chen Y, Yamaguchi M, Zhao H, Zhang X C, Zhang L, Zhang C, Price-Gallagher M, Fletcher C, Mamer O, Lesimple A, Johnson K. Coherent heterodyne time-domain spectrometry covering the entire “terahertz gap”. Applied Physics Letters, 2008, 92(1): 011131

101 Ho I C, Guo X, Zhang X C. Design and performance of reflective terahertz air-biased-coherent-detection for time-domain spectroscopy. Optics Express, 2010, 18(3): 2872–2883

PMID

102 Liu J, Zhang X C. Terahertz-radiation-enhanced emission of fluorescence from gas plasma. Physical Review Letters, 2009, 103(23): 235002

PMID

103 Liu J L, Zhang X C. Plasma characterization using terahertz-wave-enhanced fluorescence. Applied Physics Letters, 2010, 96(4): 041505

104 Liu J L, Dai J M, Chin S L, Zhang X C. Broadband terahertz wave remote sensing using coherent manipulation of fluorescence from asymmetrically ionized gases. Nature Photonics, 2010, 4(9): 627–631

105 Clough B, Liu J, Zhang X C. Laser-induced photoacoustics influenced by single-cycle terahertz radiation. Optics Letters, 2010, 35(21): 3544–3546

PMID

106 Turchinovich D, Hvam J M, Hoffmann M C. Self-phase modulation of a single-cycle terahertz pulse by nonlinear free-carrier response in a semiconductor. Physical Review B, 2012, 85(20): 201304

107 Paul M, Chang Y, Thompson Z, Stickel A, Wardini J, Choi H, Minot E, Hou B, Nees J, Norris T, Lee Y. High-field terahertz response of graphene. New Journal of Physics, 2013, 15(8): 085019

108 Bowlan P, Martinez-Moreno E, Reimann K, Elsaesser T, Woerner M. Ultrafast terahertz response of multilayer graphene in the nonperturbative regime. Physical Review B, 2014, 89(4): 041408

109 Melnik M, Vorontsova I, Putilin S, Tcypkin A, Kozlov S. Methodical inaccuracy of the Z-scan method for few-cycle terahertz pulses. Scientific Reports, 2019, 9(1): 9146

PMID

110 Schubert O, Hohenleutner M, Langer F, Urbanek B, Lange C, Huttner U, Golde D, Meier T, Kira M, Koch S, Huber R. Sub-cycle control of terahertz high-harmonic generation by dynamical Bloch oscillations. Nature Photonics, 2014, 8(2): 119–123

111 Hafez H A, Kovalev S, Deinert J C, Mics Z, Green B, Awari N, Chen M, Germanskiy S, Lehnert U, Teichert J, Wang Z, Tielrooij K J, Liu Z, Chen Z, Narita A, Müllen K, Bonn M, Gensch M, Turchinovich D. Extremely efficient terahertz high-harmonic generation in graphene by hot Dirac fermions. Nature, 2018, 561(7724): 507–511

PMID

112 Bahk Y M, Kang B J, Kim Y S, Kim J Y, Kim W T, Kim T Y, Kang T, Rhie J, Han S, Park C H, Rotermund F, Kim D S. Electromagnetic saturation of angstrom-sized quantum barriers at terahertz frequencies. Physical Review Letters, 2015, 115(12): 125501

PMID

113 Jadidi M M, König-Otto J C, Winnerl S, Sushkov A B, Drew H D, Murphy T E, Mittendorff M. Nonlinear terahertz absorption of graphene plasmons. Nano Letters, 2016, 16(4): 2734–2738

PMID

114 Giorgianni F, Chiadroni E, Rovere A, Cestelli-Guidi M, Perucchi A, Bellaveglia M, Castellano M, Di Giovenale D, Di Pirro G, Ferrario M, Pompili R, Vaccarezza C, Villa F, Cianchi A, Mostacci A, Petrarca M, Brahlek M, Koirala N, Oh S, Lupi S. Strong nonlinear terahertz response induced by Dirac surface states in Bi₂Se₃ topological insulator. Nature Communications, 2016, 7(1): 11421

PMID

115 Vicario C, Shalaby M, Hauri C P. Subcycle extreme nonlinearities in GaP induced by an ultrastrong terahertz field. Physical Review Letters, 2017, 118(8): 083901

PMID

116 Chefonov O V, Ovchinnikov A V, Agranat M B, Fortov V E, Efimenko E S, Stepanov A N, Savel’ev A B. Nonlinear transfer of an intense few-cycle terahertz pulse through opaque n-doped Si. Physical Review B, 2018, 98(16): 165206

117 Pashkin A, Sell A, Kampfrath T, Huber R. Electric and magnetic terahertz nonlinearities resolved on the sub-cycle scale. New Journal of Physics, 2013, 15(6): 065003

118 Yamaguchi K, Nakajima M, Suemoto T. Coherent control of spin precession motion with impulsive magnetic fields of half-cycle terahertz radiation. Physical Review Letters, 2010, 105(23): 237201

PMID

119 Wang Z, Pietz M, Walowski J, Förster A, Lepsa M I, Münzenberg M. Spin dynamics triggered by subterahertz magnetic field pulses. Journal of Applied Physics, 2008, 103(12): 123905

120 Beaurepaire E, Merle J, Daunois A, Bigot J. Ultrafast spin dynamics in ferromagnetic nickel. Physical Review Letters, 1996, 76(22): 4250–4253

PMID

121 Li X, Qiu T, Zhang J, Baldini E, Lu J, Rappe A M, Nelson K A. Terahertz field-induced ferroelectricity in quantum paraelectric SrTiO₃. Science, 2019, 364(6445): 1079–1082

PMID

122 Razzari L, Su F, Sharma G, Blanchard F, Ayesheshim A, Bandulet H, Morandotti H, Kieffer J, Ozaki T, Reid M, Hegmann F. Nonlinear ultrafast modulation of the optical absorption of intense few-cycle terahertz pulses in n-doped semiconductors. Physical Review B, 2009, 79(19): 193204

123 Kaur G, Han P, Zhang X. Terahertz induced nonlinear effects in doped Silicon observed by open-aperture Z-scan. In: Proceedings of the 35th International Conference on Infrared, Millimeter, and Terahertz Waves. Rome: IEEE, 2010, 5613068

124 Strait J H, Wang H, Shivaraman S, Shields V, Spencer M, Rana F. Very slow cooling dynamics of photoexcited carriers in graphene observed by optical-pump terahertz-probe spectroscopy. Nano Letters, 2011, 11(11): 4902–4906

PMID

125 Boubanga-Tombet S, Chan S, Watanabe T, Satou A, Ryzhii V, Otsuji T. Ultrafast carrier dynamics and terahertz emission in optically pumped graphene at room temperature. Physical Review B, 2012, 85(3): 035443

126 Docherty C J, Lin C T, Joyce H J, Nicholas R J, Herz L M, Li L J, Johnston M B. Extreme sensitivity of graphene photoconductivity to environmental gases. Nature Communications, 2012, 3(1): 1228

PMID

127 Jnawali G, Rao Y, Yan H, Heinz T F. Observation of a transient decrease in terahertz conductivity of single-layer graphene induced by ultrafast optical excitation. Nano Letters, 2013, 13(2): 524–530

PMID

128 Tielrooij K J, Song J C W, Jensen S A, Centeno A, Pesquera A, Zurutuza Elorza A, Bonn M, Levitov L S, Koppens F H L. Photoexcitation cascade and multiple hot-carrier generation in graphene. Nature Physics, 2013, 9(4): 248–252

129 Wright A, Xu X, Cao J, Zhang C. Strong nonlinear optical response of graphene in the terahertz regime. Applied Physics Letters, 2009, 95(7): 072101

130 Ishikawa K. Nonlinear optical response of graphene in time domain. Physical Review B, 2012, 85: 035443

131 Shareef S, Ang Y, Zhang C. Room-temperature strong terahertz photon mixing in graphene. Journal of the Optical Society of America B, Optical Physics, 2012, 29(3): 274–279

132 Hafez H A, Al-Naib I, Oguri K, Sekine Y, Dignam M M, Ibrahim A, Cooke D G, Tanaka S, Komori F, Hibino H, Ozaki T. Nonlinear transmission of an intense terahertz field through monolayer graphene. AIP Advances, 2014, 4(11): 117118

133 Su F H, Blanchard F, Sharma G, Razzari L, Ayesheshim A, Cocker T L, Titova L V, Ozaki T, Kieffer J C, Morandotti R, Reid M, Hegmann F A. Terahertz pulse induced intervalley scattering in photoexcited GaAs. Optics Express, 2009, 17(12): 9620–9629

PMID

134 Hafez H, Al-Naib I, Dignam M, Sekine Y, Oguri K, Blanchard F, Cooke D, Tanaka S, Komori F, Hibino H, Ozaki T. Nonlinear terahertz field-induced carrier dynamics in photoexcited epitaxial monolayer graphene. Physical Review B, 2015, 91(3): 035422

135 Hoffmann M, Hebling J, Hwang H, Yeh K, Nelson K. THz-pump/THz-probe spectroscopy of semiconductors at high field strengths. Journal of the Optical Society of America B, Optical Physics, 2009, 26(9): A29–A34

136 Hebling J, Hoffmann M, Hwang H, Yeh K, Nelson K. Observation of nonequilibrium carrier distribution in Ge, Si, and GaAs by terahertz pump–terahertz probe measurements. Physical Review B, 2010, 81(3): 035201

137 Hoffmann M, Hebling J, Hwang H, Yeh K, Nelson K. Impact ionization in InSb probed by terahertz pump-terahertz probe spectroscopy. Physical Review B, 2009, 79(16): 161201

138 Hwang H Y, Brandt N C, Farhat H, Hsu A L, Kong J, Nelson K A. Nonlinear THz conductivity dynamics in P-type CVD-grown graphene. Journal of Physical Chemistry B, 2013, 117(49): 15819–15824

PMID

139 Sá J, Fernandes D L A, Pavliuk M V, Szlachetko J. Controlling dark catalysis with quasi half-cycle terahertz pulses. Catalysis Science & Technology, 2017, 7(5): 1050–1054

140 Tani S, Blanchard F, Tanaka K. Ultrafast carrier dynamics in graphene under a high electric field. Physical Review Letters, 2012, 109(16): 166603

PMID

141 Reyna A S, de Araújo C B. High-order optical nonlinearities in plasmonic nanocomposites—a review. Advances in Optics and Photonics, 2017, 9(4): 720–724

142 Reshef O, Giese E, Zahirul Alam M, De Leon I, Upham J, Boyd R W. Beyond the perturbative description of the nonlinear optical response of low-index materials. Optics Letters, 2017, 42(16): 3225–3228

PMID

143 Zhou R, Jin Z, Li G, Ma G, Cheng Z, Wang X. Terahertz magnetic field induced coherent spin precession in YFeO₃. Applied Physics Letters, 2012, 100(6): 061102