Nonlinear effects in topological materials

Abstract

Materials, where charge carriers have a linear energy dispersion, usually exhibit a strong nonlinear optical response in the absence of disorder scattering. This nonlinear response is particularly interesting in the terahertz frequency region. We present a theoretical and numerical investigation of charge transport and nonlinear effects, such as the high harmonic generation in topological materials including Weyl semimetals (WSMs) and a-T₃ systems. The nonlinear optical conductivity is calculated both semi-classically using the velocity operator and quantum mechanically using the density matrix. We show that the nonlinear response is strongly dependent on temperature and topological parameters, such as the Weyl point (WP) separation b and Berry phase {\phi }_{\mathrm{B}}. A finite spectral gap opening can further modify the nonlinear effects. Under certain parameters, universal behaviors of both the linear and nonlinear response can be observed. Coupled with experimentally accessible critical field values of 1{\mathrm{0}}^4-1{\mathrm{0}}^{\mathrm{5}}\mathrm{V/m}, our results provide useful information on developing nonlinear optoelectronic devices based on topological materials.

Key words： terahertz; nonlinear effects; topological materials; Weyl semimetals (WSMs); a-T₃ systems

Introduction

In recent years, materials with topological order [¹–⁷] have been intensively studied theoretically and experimentally. In particular, Dirac [⁸,⁹] and Weyl materials [¹⁰,¹¹] have attracted considerable interest owing to their exotic electronic properties and quantum transport related to their topological properties. Owing to the massless Fermion energy dispersion, these materials usually have high electronic mobility (≈ 3300 cm²/(V·s)) and a chemical potential that is tunable with gate voltage. It has been demonstrated that bulk Dirac materials, such as Cd₃As₂, can be applied in optoelectronics, e.g., in optical switching.

Weyl semimetals (WSMs) are a class of topological materials without time-reversal symmetry. This symmetry is broken by the separation of two three-dimensional (3D) Dirac (Weyl) cones in momentum space. The electrons near the Weyl points (WPs) behave like massless charge carriers, which are known as Weyl fermions. Although it is difficult to experimentally detect and manipulate Weyl fermions [¹²–¹⁵], the general thermal transport [¹⁶,¹⁷] and charge transport [¹³,¹⁸–²³] properties of WSMs have been investigated in depth both theoretically and experimentally [²⁴–²⁶]. The interaction of two Weyl cones of opposite chirality results in many interesting phenomena, such as the chiral magnetic effect (owing to interplay between bulk Weyl cones and surface Fermi arcs) [²⁷], Andreev–Bragg reflection, formation of Majorana modes via the connectivity of Fermi arcs, and the well-known chiral anomaly [²⁸,²⁹] (which results in negative magneto-optical resistance [³⁰,³¹] and ultra-high carrier mobility [³²]).

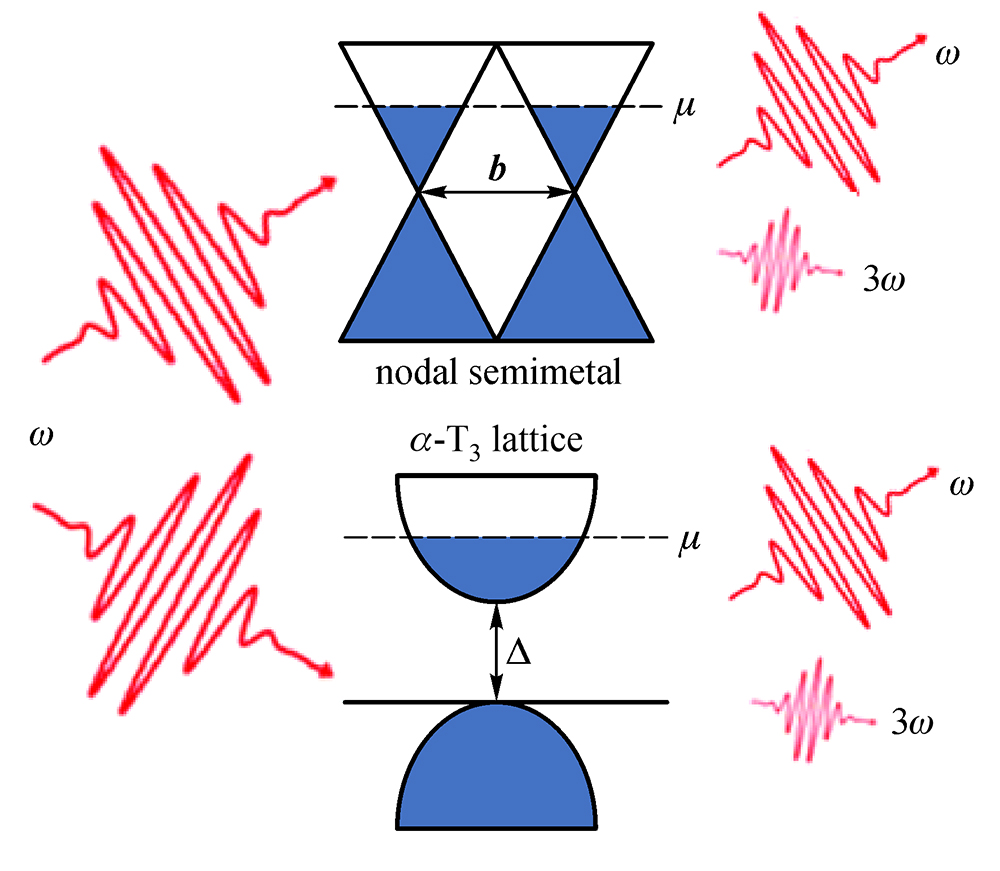
The a-T₃ model is best described as an interpolation model between graphene and dice (or T₃) lattice. The interpolation procedure is described by moveable atoms coupled to one of the two topologically inequivalent atomic sites of each hexagonal unit cell. The parameter a ∈ [0, 1] describes the distance of each moveable atom from the atomic site to which it is coupled so that if each moveable atom is in the center of the unit cell (a = 1), the lattice will resemble a dice lattice, and if the moveable atom is not present (a = 0), the lattice is a standard graphene honeycomb. This two-dimensional (2D) material has recently been fabricated in the (111) direction of SrTiO₃/SrIrO₃/SrTiO₃ [³³] or by confining cold atoms to an optical lattice [³⁴]. For the intermediate values of a, there is a significant influence of both the dispersionless flat band and valence band, which results in nontrivial topology [³⁵–³⁷], unusual interaction effects [³⁸–⁴¹], and electronic properties such as super-Klein tunneling [⁴²–⁴⁴], minimal conductivity [⁴⁵], orbital magnetic response [⁴⁶], and Weiss oscillations [⁴⁷].

It has been shown for both 2D and 3D materials, in both the classical description and full quantum mechanical approach, that the velocity of charge carriers following a linear energy dispersion is not directly proportional to the momentum of the carrier. This leads to the coupling of the particle with the electromagnetic fields to infinite orders in the absence of scattering by disorders [⁴⁸–⁵²]. Therefore, even in the single electron model, the Dirac system is a strong nonlinear material. For 2D Dirac systems, such as graphene, strong nonlinear effects (e.g., photomixing [⁴⁸], high harmonic generation (HHG), nonlinear surface plasmon polariton coupling to light [⁵³], and optical bistability [⁵⁴]) have been demonstrated. In 3D Dirac materials and WSMs, strong photomixing in the terahertz regime [⁵⁵] and ultrafast charge dynamics have been studied [⁵⁶,⁵⁷].

In this work, we review some specific theoretical and computation focus on the nonlinear optical response in 3D topological materials in the terahertz regime. We study WSMs and the α-T₃ system both with and without a spectral gap. This band gap is usually induced by impurity or structural asymmetry. On the basis of the quantum mechanical states and energy dispersion, the transport equation will be used to calculate current response using semi-classical and quantum mechanical approaches. The dependence of the nonlinear response on important parameters, such as Weyl cone separation and band gap, will be identified. In the semi-classical formalism, the Taylor expansion of the velocity operator allows one to calculate nonlinear conductivities. While in the quantum formalism, the order of both the matrix units and reduced density matrix must be taken into account when equating each order of the electric field. Both formalisms allow one to readily identify how the nonlinear effects dependent on the aforementioned intrinsic parameters.

The nonlinear optical properties are characterized by the required electric field strength so that the first order and lowest order nonlinear conductivities are equal in magnitude; this is known as the critical field. If the critical field is experimentally reachable for terahertz frequencies, there are a number of potential uses for this material, such as photo-mixing and tunable terahertz signal generation and receiving.

Theoretical methods

In this section, we characterize the two systems investigated by looking at their electronic structure and introduce the models used to determine their nonlinear properties.

Electronic structures

Weyl semimetals

Using the minimal coupling model, the Hamiltonian of a two-node semimetal is given by [¹⁹,⁵⁵]

(1)H_{\mathrm{W}\mathrm{S}\mathrm{M}}=\left(\begin{array}{ll}{v}_{\mathrm{F}}\mathit{\sigma }\cdot (\mathit{p}+\mathit{b})& \mathrm{\Delta }{\mathbb{I}}_2\\ \mathrm{\Delta }{\mathbb{I}}_2& v_{\mathrm{F}}\mathit{\sigma }\cdot (\mathit{b}-\mathit{p})\end{array}\right),

where {\mathbb{I}}_2 is the 2 × 2 identity matrix and v_F ≈ 10⁶ m/s is the Fermi velocity [⁵⁸], \sigma is the Pauli spin matrix, p is the linear momentum and b is Weyl points separation. This Hamiltonian is \mathcal{C}\mathcal{P}-invariant; however, time reversal invariance is broken by b≠ 0 [²⁰]. Equation (1) is explicitly diagonalizable.

(2)E_{\mathrm{W}\mathrm{S}\mathrm{M}}=s{v}_{\mathrm{F}}\sqrt{{\left({\displaystyle \frac{\mathrm{\Delta }}{v_{\mathrm{F}}}}\right)}^{\mathrm{2}}+|\mathit{b}{|}^{\mathrm{2}}+|\mathit{p}{|}^{\mathrm{2}}+r\sqrt{{(\mathit{b}+\mathit{p})}^{\mathrm{2}}+{\left({\displaystyle \frac{\mathrm{\Delta }\left|\mathit{b}\right|}{v_{\mathrm{F}}}}\right)}^{\mathrm{2}}}},

where s, r = ±1 denote the four bands. The dispersion in Eq. (2) is shown graphically in Fig. 1. For v_F|b|  >  D, the two nodes are separated into two WPs separated in momentum space by the vector \mathrm{2}\sqrt{\mathrm{1}-{\left({\displaystyle \frac{\mathrm{\Delta }}{v_F\left|\mathit{b}\right|}}\right)}^{\mathrm{2}}}\widehat{b}. We denote this as the WSM phase. If v_F|b| =  D, there is a single doubly degenerate WP, and the structure is in a 3D massive Dirac semimetal (MDSM) phase. The commonly studied massless DSM phase is a special case of the MDSM phase, where D = 0. The parameter D may be intrinsic or extrinsic and gaps out the spectrum by v_{\mathrm{F}}\left|{\displaystyle \frac{\mathrm{\Delta }}{v_{\mathrm{F}}}}-\left|\mathit{b}\right|\right| if \mathrm{\Delta }>v_{\mathrm{F}}\left|\mathit{b}\right|, in which case the structure is in a gapped semimetal phase (GSM).

Fig.1 Dispersion relation of Eq. (2) with: (a) v_F |b| >  D: WSM phase, (b) v_F |b| =  D: MDSM phase, and (c) v_F |b| <  D: GSM phase. The arrows in Fig. 1(a) show two types of intraband current contributions for an electric field parallel to b

Full size|PPT slide

a-T₃ model

The minimal coupling Hamiltonian for the a-T₃ lattice is given by [⁵⁹,⁶⁰]

(3)H_{\alpha -T_3}=\left(\begin{array}{lll}\mathrm{0}& {\tau }_1{f}_k^{}\cos \varphi & \mathrm{0}\\ {\tau }_1{f}_k^{\ast }\cos \varphi & \mathrm{\Delta }& {\tau }_2{f}_k^{}\sin \varphi \\ \mathrm{0}& {\tau }_{\mathrm{2}}{f}_k^{\ast }\sin \varphi & \mathrm{0}\end{array}\right),

where t₁ and t₂ are the hopping amplitudes between adjacent triangular lattice, k = (kx, ky), and ∗ denotes complex conjugation.

(4)f_k=-\left[\mathrm{1}+{\displaystyle \sum _{\mu }\exp (-i\mathit{k}\cdot {\mathit{a}}_{\mu })}\right],

is the structure factor formed by linear combinations of Bloch states from the three neighboring sublattices with µ = 1 and 2 for two Bravais lattice vectors, {\mathit{a}}_1=a(\sqrt{3}/2,3/\mathrm{2)} and {\mathit{a}}_2=a(-\sqrt{3}/2,3/\mathrm{2)}, where a is the inter-site distance, D arises from the real chemical potential of the movable atom gapping the spectrum, and finally the parameter \varphi is related to a by a = tan\varphi.

The three wave functions and associated eigen-energies are found as

(5){\xi }_{\mathrm{0}}={\displaystyle \frac{\mathrm{1}}{{\tau }^{\prime }}}\left(\begin{array}{l}-{\tau }_2\sin \varphi e^{\mathrm{i2}{\theta }_k}\\ \mathrm{0}\\ {\tau }_{\mathrm{1}}\cos \varphi \end{array}\right),

for E₀ = 0 and

(6){\xi }_{k,\lambda }={\displaystyle \frac{\mathrm{1}}{\sqrt{E_{\lambda }^{\mathrm{2}}+|f_k{|}^{\mathrm{2}}\tau {\prime }^2}}}\left(\begin{array}{l}{\tau }_1{f}_k\cos \varphi \\ E_{\lambda }\\ {\tau }_2{f}_k^{\ast }\sin \varphi \end{array}\right),

for E_{\lambda }=(\mathrm{\Delta }+\lambda \sqrt{{\mathrm{\Delta }}^2+4|f_k{|}^2\tau {\prime }^2})/2, respectively, where l = ±1 correspond to the conduction (+) and valence (-) bands, and \tau {\prime }^2={\tau }_{\mathrm{1}}^{\mathrm{2}}{\cos }^2\varphi +{\tau }_{\mathrm{2}}^{\mathrm{2}}{\sin }^2\varphi. The states {\xi }_{k,s}(s=\mathrm{0},\pm 1) satisfy the orthogonality condition \langle {\xi }_{\mathit{k},s}|{\xi }_{\mathit{k}\prime ,s\prime }\rangle ={\delta }_{s{s}^{\prime }}\delta （\mathit{k}-\mathit{k}\prime ）. The three-band dispersion relation is shown in Fig. 2.

Fig.2 Dispersion relation for the a-T₃ lattice. The lines on the right show two interband transitions, E_- →  E₀ →  E₊ and E₀ →  E₊ as well as one intraband transition E₊ →  E₊

Full size|PPT slide

The topology of the crystalline structure is manifested in the dispersion and wave functions by connecting

{\displaystyle \frac{{\varphi }_{\mathrm{B}}}{\mathrm{\pi }}}=\cos \left(2\phi \right)=\cos \left(\mathrm{2arctan}\alpha \right)

to the Berry phase {\phi }_{\mathrm{B}} [⁵⁹,⁶¹]. Then, it is readily observed that changing a continuously from 0 to 1 changes the Berry phase from p to 0. Hence, at the extremal value a = 0, there will be no conductivity contribution from the flat band with Chern number 0, and conversely for a = 1, there will be no conductivity contribution from the l =  -1 valence band with nonzero Chern number.

Nonlinear conductivity

We present two methods for calculating the nonlinear conductivities of the material, i.e., a semi-classical formalism based on the Taylor expansion of the velocity operator and a quantum formalism, which requires solving the equation of motion of the reduced density matrix. In both models, we truncate the nonlinear current after the third-order term

J_i={\sigma }_i^{(\mathrm{1})}{\mathit{ϵ}}_i+{\sigma }_{ii}^{(\mathrm{2})}{\mathit{ϵ}}_i^{\mathrm{2}}+{\sigma }_{iii}^{(\mathrm{3})}{\mathit{ϵ}}_i^{\mathrm{3}},

for an applied field {\mathit{ϵ}}_i directed along the ith direction. This is valid in the high-frequency/low applied field regime (w > 0.00355 THz for \mathit{ϵ} = 10²  - 10⁵ V/m [⁶⁰]), which aligns with the region of validity for the minimal coupling model: p\ggeA.

Semi-classical model

In the minimal coupling scheme, p →  p +  eA =  P, where e> 0 is the electron charge and \mathit{ϵ} =  -(1/c)∂tA determines the vector potential. To determine the nonlinear intraband conductivities in a semi-classical regime, we are free to use {\mathit{v}}_i(\Pi ) =  \nabla \mathit{p}{E}_i(\Pi ) for carriers in the i\mathrm{th} band:

(7)v_{\mathrm{W}\mathrm{S}\mathrm{M}}(\mathrm{\Pi })=v_{\mathrm{F}}{\displaystyle \frac{\mathrm{\Pi }-{\displaystyle \frac{\mathit{b}((\mathrm{\Pi })\cdot \mathit{b})}{\sqrt{{((\mathrm{\Pi })\cdot \mathit{b})}^2+{\left({\displaystyle \frac{\mathrm{\Delta |}\mathit{b}|}{v_{\mathrm{F}}}}\right)}^{\mathrm{2}}}}}}{\sqrt{|\mathrm{\Pi }{|}^{\mathrm{2}}+|\mathit{b}{|}^{\mathrm{2}}+{\left({\displaystyle \frac{\mathrm{\Delta }}{v_{\mathrm{F}}}}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{\Gamma }}}},

where \mathrm{\Gamma }=\sqrt{{(\mathrm{\Pi }\cdot \mathit{b})}^2+{(\mathrm{\Delta }|\mathit{b}|/v_{\mathrm{F}})}^2}. Note Eq. (7) does not include any anomalous terms related to the Berry curvature; \dot{k}\times \mathrm{\Omega }. This occurs because the \mathcal{P}-symmetry of Eq. (1) requires Ω(p) = Ω(-p) with the anomalous velocity contributions around each WP cancelled out, where the Chern numbers are±1.

Equation (7) includes all orders of the applied field. To isolate different order conductivities, we perform the Taylor expansion of v_WSM to isolate orders of A and hence the applied field, v(n) ∝  En. The nth order current response is calculated by the standard solid-state formula [⁵⁵].

(8){\mathit{J}}^{(n)}={\displaystyle \frac{\mathrm{e}}{{(\mathrm{2\pi }\hslash )}^3}}{\displaystyle {\int }_{{ℝ}^{\mathrm{3}}}}{\mathrm{d}}^{\mathrm{3}}\mathit{p}{\mathit{v}}^{(n)}{N}_{\mathrm{F}}.

The limits of integration for r =  -1 are chosen to avoid singular WPs, where the assumption that our model is based on p\gge|A| fails. Ns,r =  {\mathrm{(1}+\mathrm{exp\; [}(E_{s,r}-E_{\mathrm{F}}(\mathit{b},\mathrm{\Delta }))T^{-1}])}^{-\mathrm{1}} is the Fermi–Dirac distribution function, where the Fermi level EF is determined self-consistently by the condition of constant concentration [⁵⁵]. Finally, because we are interested in the intraband conductivity, we only consider the contribution from the s = 1, r =  -1 band because for typical parameters [²³,⁵⁸,⁶²] µ0 \llEs = 1, r = 1.

Quantum model

For a time-dependent radiation field, {\mathit{ϵ}}_{\mathrm{0}}{e}^{-i\omega t}{\widehat{e}}_x\mathit{ϵ}(t)={\mathit{ϵ}}_x{\widehat{e}}_x=, the vector potential in the velocity gauge isA=-i(c/\omega )e^{-i\omega t}{\mathit{ϵ}}_x{\widehat{e}}_x=A_{\omega }{e}^{-i\omega t}. Using the minimal coupling scheme, we Taylor expand the structure factor in Eq. (4) in powers of A (and hence applied field) to obtain

(9)f_{\Pi }=f_k-{\displaystyle \sum _{n=\mathrm{1}}}{\displaystyle \frac{\mathrm{1}}{n!}}{\left(-i{\displaystyle \frac{\mathrm{e}}{\hslash c}}\right)}^n{\mathcal{A}}^{(n)}(k),

where {\mathcal{A}}^{(n)}(\mathit{k}) =  {\displaystyle {\sum }_{\mu }{e}^{-i(\mathit{k}\cdot {\mathit{a}}_{\mu }+n\omega t)}{({\mathit{A}}_{\omega }\cdot {\mathit{a}}_{\mu })}^n}. The time-dependent Hamiltonian can now be written in the form

(10)H(\mathit{k},t)=H_{\alpha -T_3}(\mathit{k})+H_{\mathrm{e}\mathrm{m}}(\mathit{k},t),

where H_a-T3(k) is independent of A(t) and retains the eigenstates x₀ and x_k,l, and H_em(k, t) contains the interaction of electrons with the external field and is given by

(11)\begin{array}{l}{H}_{\mathrm{e}\mathrm{m}}(\mathrm{k},t)\\ \hspace{1em}=-{\displaystyle \sum _{n=\mathrm{1}}{\displaystyle \frac{\mathrm{1}}{n!}}{\left(-i{\displaystyle \frac{e}{\hslash c}}\right)}^n\left(\begin{array}{lll}\mathrm{0}& {\tau }_{\mathrm{1}}{\mathcal{A}}^{(n)}\cos \varphi & \mathrm{0}\\ {\tau }_{\mathrm{1}}{(-\mathrm{1})}^n{\mathcal{A}}^{(n)*}\cos \varphi & \mathrm{0}& {\tau }_{\mathrm{2}}{\mathcal{A}}^{(n)}\sin \varphi \\ \mathrm{0}& {\tau }_{\mathrm{2}}{(-\mathrm{1})}^n{\mathcal{A}}^{(n)*}\sin \varphi & \mathrm{0}\end{array}\right)}.\end{array}

We use the eigenstates of H_{\alpha -T_{\mathrm{3}}}(k) to write H(k, t) in a second quantized form. This is done via the standard procedure of writing the time-dependent wave function as \psi (t)={\displaystyle {\sum }_{\mathit{k}}{a}_{\mathit{k},\mathrm{0}}(t){\xi }_{\mathrm{0}}}+{\displaystyle {\sum }_{\mathit{k},\lambda }{a}_{\mathit{k},\lambda }(t){\xi }_{\mathit{k},\lambda }}, where a_{\mathit{k},s}^{†} and a_{\mathit{k},s} are the creation and annihilation operators of Bloch states, respectively. Then, the Hamiltonian in Eq. (10) becomes

(12)H={\displaystyle \sum _{\mathit{k},\lambda }[E_{\lambda }{a}_{\mathit{k},\lambda }^{†}{a}_{\mathit{k},\lambda }+(M_{\lambda ,\mathrm{0}}(\mathit{k})a_{\mathit{k},\lambda }^{†}{a}_{\mathit{k},\mathrm{0}}+h.c.)+M_{\lambda ,\lambda }(\mathit{k})a_{\mathit{k},\lambda }^{†}{a}_{\mathit{k},\lambda }+M_{\lambda ,-\lambda }(\mathit{k})a_{\mathit{k},\lambda }^{†}{a}_{\mathit{k},-\lambda }]},

where M_{i,j}={\displaystyle {\sum }_n{A}_x^n{M}_{i,j}^{(n)}} with i, j = 0, l and M_{i,j}^{(n)}(\mathit{k})={[M_{i,j}^{(n)}(\mathit{k})]}^{*} are the matrix units. For simplicity, we set t₁ =  t₂ =  t in our calculations so that t′ →  t. Mi,j is shown explicitly in Ref. [⁶⁰].

The reduced density matrix is given as {\rho }_{s,s\prime }(\mathit{k},t) =  \langle a_{k,s}^{†}(t)a_{k,s\prime }(t)\rangle. Using the equation of motion for a quantum operator, i\hslash [\mathrm{d}{\rho }_{s,s\prime }(\mathit{k})/\mathrm{d}t] =  \langle [a_{\mathit{k},s}^{†}{a}_{\mathit{k},s\prime }H(t)]\rangle, we obtain

(13)\begin{array}{l}\left(i\hslash {\displaystyle \frac{\partial }{\partial t}}+E_s-E_{s\prime }+M_{s,s}-M_{s\prime ,s\prime }\right){\rho }_{s,s\prime }\\ =-M_{\mathrm{0},s}{\rho }_{\mathrm{0},s\prime }+M_{s\prime ,\mathrm{0}}{\rho }_{s,\mathrm{0}}-M_{-s,s}{\rho }_{-s,s\prime }+M_{s\prime ,-s\prime }{\rho }_{s,-s\prime }\\ -{\displaystyle \sum _{\lambda }}({\delta }_{s,\mathrm{0}}{M}_{\lambda ,\mathrm{0}}{\rho }_{\lambda ,s\prime }-{\delta }_{s\prime ,\mathrm{0}}{M}_{\mathrm{0},\lambda }{\rho }_{s,\lambda }).\end{array}

This allows one to isolate different order optical response terms by expanding {\rho }_{s,s\prime }={\displaystyle {\sum }_m}{A}_x^m{\rho }_{s,s\prime }^{(m)} in powers of A. The Fourier transformed components {\rho }_{s,s\prime }^{(m)}(\mathit{k},\omega ) can be obtained from this recursion relation given that the zeroth-order reduced density matrix terms are defined {\rho }_{s,s\prime }^{(\mathrm{0})}(k)={\delta }_{s,s\prime }{N}_s(k), where Ns is the Fermi–Dirac distribution of band s at temperature T and chemical potential µ. Explicit expressions for the first-, second-, and third-order components can be found in Ref. [⁶⁰].

Finally, the current response in the x-direction is calculated using the standard electrodynamics formula

(14)\begin{array}{l}{J}_x(\omega )=c\langle {\nabla }_{A}H(\mathit{k},t)\rangle \\ =c{\displaystyle \sum _{k,\lambda ,n,m}n{\mathit{A}}_{\omega }^{n+m-\mathrm{1}}[{\mathit{M}}_{\lambda ,\mathrm{0}}^{(n)}(\mathit{k}){\rho }_{\lambda ,\mathrm{0}}^{(m)}+{\mathit{M}}_{\mathrm{0},\lambda }^{(n)}(\mathit{k}){\rho }_{\mathrm{0},\lambda }^{(m)}+{\mathit{M}}_{\lambda ,\lambda }^{(n)}(\mathit{k}){\rho }_{\lambda ,\lambda }^{(m)}+{\mathit{M}}_{\lambda ,-\lambda }^{(n)}(\mathit{k}){\rho }_{\lambda ,-\lambda }^{(m)}]},\end{array}

where the conditions n ≥ 1 ∈  \mathbb{Z} and m ≥ 0 ∈  \mathbb{Z} are used to determine the different order optical responses. For example, (n, m) = {(1, 1), (2, 0)} for the first order, and (n, m) = {(2, 1), (3, 0), (1, 2)} for the second order.

Results and discussion

Since the \mathcal{P}-symmetry in both Eqs. (1) and (3) is preserved, s(2) = 0 for both materials studied. Hence, s(3) is the lowest nonlinear term, and we approximate

J={\sigma }_i^{(1)}\mathit{ϵ}+{\sigma }^{(3)}{\mathit{ϵ}}^3

by dropping the tensor notation since J\left|\right|\mathit{ϵ}herein. The strength of the nonlinear term can be quantified by calculating the applied field strength at which the magnitude of the first-order current J^{(\mathrm{1})}={\sigma }^{(\mathrm{1})}\mathit{ϵ} is equal to the magnitude of the third-order current J^{(3)}={\sigma }^{(3)}{\mathit{ϵ}}^{\mathrm{3}}. This is known as the critical field and is given by

{\mathit{ϵ}}^c=\sqrt{{\displaystyle \frac{\left|{\sigma }^{(\mathrm{1})}\right|}{\left|{\sigma }^{(\mathrm{3})}\right|}}}.

Nonlinear conductivity in Weyl semimetals

In this section, we elucidate how the nonlinear response of the Hamiltonian in Eq. (1) depends on its topological phase (WSM, MDSM/DSM, or GSM) and further probe the intriguing anisotropic response caused by b\ne \mathrm{0}. For the discussion on how the nonlinear characteristics vary with intrinsic and extrinsic parameters, see Ref. [⁵⁵]. We begin by surveying how first- and third-order conductivities vary with (possibly) independent variables.

Fig.3 Band gap dependence of the first- and third-order conductivities of WSM with \mu = 80 meV, T = 300 K, and \omega = 1 THz for the field directed parallel to b

Full size|PPT slide

Figure 3 shows a discontinuous jump in s(3) as D\ne 0. Despite still being in the WSM phase, D\ne 0 destroys the linearity of the dispersion along the direction of b, which produces such discontinuity. Both third- and first-order conductivities decrease when approaching the MDSM phase, where a point of inflection occurs, and continue to decrease into the GSM phase. The decrease of both conductivities in the GSM phase is straightforwardly explained by the existence of a spectral gap, which more rapidly kills off third-order processes. Although in the region inter-cone transitions occur more readily, both conductivities are dominated by intra-cone processes, which die off as D → ∞ owing to the renormalization of the Fermi velocity.

Fig.4 Temperature dependence of the first- and third-order conductivities of WSM with µ = 80 meV, D = 53 meV, and w = 1 THz for the field directed parallel to b =  b_x\widehat{x} = 0.8 × 10⁸\hslash \widehat{x}

Full size|PPT slide

Contrary to the band gap dependence, Fig. 4 shows that the inter-cone current is essential in the temperature dependence of the third-order current. Although both MDSM and GSM phases see an exponential increase in both the first- and third-order conductivities with temperature, there is an initial decrease for the WSM phase. This decrease corresponds to inter-cone carriers coupling to a single photon more readily at lower temperatures. However, with an increase in temperature, the inter-cone current becomes a viable method of transport under three-photon absorption, and there is a “turn-on” temperature (≈275 K in Fig. 4) at which the third-order conductivity starts to increase.

Fig.5 Band gap dependence of the anisotropy of (a) first-order conductivities, (b) third-order conductivities, and (c) critical fields in WSM with µ = 80 meV, T = 300 K, and w = 1 THz for a field directed parallel to b =  b_x\widehat{x} = 0.8 × 10⁸  \hslash \widehat{x}

Full size|PPT slide

The conductivity for a field perpendicular to \mathit{b}({\sigma }_{\perp })can be simply obtained by changing \mathit{b}\to b_y\widehat{y}. This nonlinear anisotropy as a function of ∆ is investigated in Fig. 5. Each first-order curve in Fig. 5(a) reaches a minimum just prior to the MDSM/WSM phase boundary where the perpendicular conductivity reaches a maximum when the local maxima E_{\mathrm{W}\mathrm{S}\mathrm{M}}(\mathit{p}=\mathrm{0}) crosses the Fermi level. This minimum region is accentuated by the inflection of parallel conductivity at the WSM/MDSM boundary. Thereafter, in the GSM phase, the perpendicular conductivity approaches zero faster because there are no inter-cone transitions; thus, anisotropy increases. The three most prominent features in the third-order anisotropy diagram are the initial discontinuous spike, inflection at the MDSM phase boundary, and the minimum located in the GSM region. First, the initial spike is solely due to the parallel conductivity, as was previously shown in Fig. 3. The perpendicular component does not have such discontinuity because the carriers follow a conic dispersion for ∆ = 0. The point of inflection occurs when E_WSM(p = 0) =  E_F, and the ensuing minimum is at the WSM/MDSM boundary when the perpendicular conductivity is at the maximum. Because the ratio {\mathit{ϵ}}_{\mathrm{||}}^c/{\mathit{ϵ}}_{\perp }^c > 1, one can conclude that WSM is a better nonlinear material when the field is imposed perpendicular to b.

Fig.6 Temperature dependence of the anisotropy of (a) first-order conductivities, (b) third-order conductivities, and (c) critical fields in WSM with µ = 80 meV, D = 53 meV, and w = 1 THz

Full size|PPT slide

Though the temperature dependence of the first-order conductivity is similar in both parallel and perpendicular directions, the anisotropy is different, as shown in Fig. 6(a). The increase over this temperature range of the two lower b-valued curves is attributed to the increased gradient of the parallel component owing to the ease of inter-cone transitions. The negativity of the b=\mathrm{0.}5\times 1{\mathrm{0}}^8\hslash curve in Fig. 6(b) is because {\sigma }_{\perp }^{(\mathrm{3})}  < 0. Accounting for this conductivity parity in the GSM phase, all third-order curves behave similarly with temperature; i.e., they increase at the “turn on” temperature for inter-cone transitions. This increase is desirable in practice because it leads to the lower critical field at higher temperatures.

Nonlinear conductivity in \alpha -{\mathrm{T}}_3 model

From the quantum equation of motion (Eq. (13)), the first-order optical conductivity tensor is obtained as in Ref. [⁶⁰]. The first-order characteristics in frequency domain are shown in Fig. 7. The T = ∆ = 0 characteristics in Fig. 7 show that, as expected, the flat band plays no role in the a = 0 conductivity, whereas the E_- valence band plays no role in the a = 1 conductivity. However, for the intermediate values of a, both E₀ →  E₊ (at w =  µ) and E_- →  E₊ (at w = 2µ), interband processes are present. For each a-value, the parameters T, µ, and ∆ play the same role. An increase in T breaks the Hall quantization and smooths out the step function, whereas an increase in µ merely shifts the Hall effect frequency (or frequencies). The band gap parameter breaks quantization in a more topologically significant manner. First, the peaks become larger and are shifted in frequency by sgn(µ  - ∆)∆. Further, instead of exhibiting a Hall plateau, the conductivity decreases asymptotically toward the ∆ = 0 value at higher frequencies where \hslash \omega >  \epsilon.

Fig.7 First-order conductivity of the \alpha -T_3 lattice with (a) a = 0, (b) a = 0.5, and (c) a = 1. In each graph, a = 0.0142 nm, t = 3 eV, and µ = 1 meV are the original values. The µ → ∞ values are 100 meV (Fig. 7(a)) and 20 meV (Figs. 7(b) and 7(c)); the T> 0 value is 4 K in each graph, and the D> 0 values are 0.5 meV ((Fig. 7(a)), 1 meV (Fig. 7(b)), and 2 meV (Fig. 7(c))

Full size|PPT slide

For the third-order conductivity, we set D = 0 because we are interested in harmonics not quantization. The s(3) includes contributions from 3 intraband processes and 22 interband processes [⁶⁰]. Owing to the five unique harmonic processes embedded in the interband response, Fig. 8 shows a ridged response in the THz region.

Fig.8 Third-order conductivity in the \alpha -T_3 lattice for different Berry phases with a = 0.0142 nm, {\tau }_1 =  {\tau }_2 = 3 eV, and µ = 1 meV

Full size|PPT slide

The dice lattice ({\phi }_{\mathrm{B}}=\mathrm{0}) response is dominated by the three-photon flat-to-conduction band harmonic process located at \hslash \omega =  {\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}\mu, whereas the graphene lattice ({\phi }_{\mathrm{B}}=\pi) is dominated by the three-photon valence-to-conduction band harmonic process located at \hslash \omega =  {\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}\mu However, because the dice lattice peak is an order of magnitude larger, one can surmise that the dice lattice is a superior nonlinear conductor in the THz range. The most striking feature of Fig. 8 is that an intermediate Berry phase {\phi }_{\mathrm{B}}={\displaystyle \frac{\pi }{\mathrm{2}}} allows the coexistence of third-order flat-to-conduction and valence-to-conduction band processes, which highlight the underlying geometric nature of HHG. By tuning 0 < {\phi }_{\mathrm{B}} <  p, the dominant peak fluctuates by an order of magnitude and changes from \hslash \omega =  {\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}\mu near 0 to \hslash \omega =  {\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}\mu near p. This characteristic allows to construct tunable THz receivers.

Another promising application of the nonlinear response is to use the dominant peak to determine the Berry phase and characterize the crystalline structure. This phenomenon is best exhibited in the critical field characteristics shown in Figs. 9 and 10.

Fig.9 Frequency dependence of the critical field in the \alpha -T_3 lattice for different Berry phases with a = 0.0142 nm, {\tau }_1 =  {\tau }_2 = 3 eV, and µ = 1 meV

Full size|PPT slide

Figure 9 shows how the ideal operating THz bandwidths for nonlinear effects (lowest critical field region) change with the Berry phase. Although an intermediate Berry phase provides a more feature-rich nonlinear response, the ideal operating bandwidth is restricted by competing harmonic processes. Furthermore, although {\phi }_{\mathrm{B}}=\pi has a larger critical field, its ideal operating bandwidth of 1-3 THz is larger than that of {\phi }_{\mathrm{B}}=\mathrm{0}, where w ∈ [0.5, 1.5) THz provides the largest nonlinear effect.

Fig.10 Berry phase dependence of the critical field in the \alpha -T_3 lattice for different frequencies with a = 0.0142 nm, {\tau }_1 =  {\tau }_2 = 3 eV, and µ = 1 meV

Full size|PPT slide

Figure 10 shows that each frequency has a local maximum critical field that is unique to some Berry phases. In general, the maxima decrease with frequency for w ∈ (0.5, 3] THz. These maxima open characterization possibilities. If one were able to measure the critical field for this range of frequencies, the injective relationship between maxima in this domain and the Berry phase can be used to directly calculate the Berry phase of the material.

Conclusions

We analysed the nonlinear intraband conductivity of a two-node semimetal in WSM, MDSM, and GSM phases using a semi-classical model. It is shown that the topological phase, which is determined by the relative magnitudes of v_{\mathrm{F}}\mathit{b} and D, is responsible for most characteristics in a feature-rich and high magnitude nonlinear response. The third-order conductivity is greatly enhanced by a small but nonzero D if the applied field is parallel to b, whereas the temperature dependence is enhanced for E_{\mathrm{W}\mathrm{S}\mathrm{M}}(\mathit{p}=\mathrm{0})\ge E_{\mathrm{F}} when inter-cone transitions are guaranteed for any direction field. The nonlinear response is also shown to be highly anisotropic with conductivity parallel to b dominating at lower temperatures and affecting values of D for the WSM phase.

Using a quantum formalism, which is also valid for higher frequencies of w> 0.00355 THz, we compute the nonlinear optical response of the \alpha -T_3 lattice. The first-order conductivity shows Hall quantization at frequencies that are directly determined by the topological phase. This quantization is broken by both a nonzero temperature and a nonzero band gap. HHG in the nonlinear response is also determined by the topological phase. The flat band response is also negated in the nonlinear response for {\phi }_{\mathrm{B}}=\pi (graphene) and conversely for {\phi }_{\mathrm{B}}=\mathrm{0} (dice lattice) the E_- valence band response is negated. However, both contribute to the nonlinear response for intermediate values of the Berry phase. Although this dual contribution inhibits the bandwidth for observing nonlinear effects, an increase in the number of observable harmonics opens up the possibilities of tunable nonlinear materials or the characterization of topological materials based solely on their nonlinear response.

Owing to the large and tunable nonlinear response of all considered materials, we surmise that these topological materials would make ideal candidates for optoelectronics device applications such as optical mixers and THz receivers. The elucidation of how the topological phases directly relate to the discussed nonlinear properties could in practice lead to material characterization procedures that are based solely on optical responses. Similar calculations for other topological materials, such as nodal ring/line semimetals, may be informative and would allow to observe how symmetry breaking perturbations, such as spin orbit coupling, affect our results.

References

1 Ando Y. Topological insulator materials. Journal of the Physical Society of Japan, 2013, 82(10): 102001

2 Otsuji T, Popov V, Ryzhii V. Active graphene plasmonics for terahertz device applications. Journal of Physics D, Applied Physics, 2014, 47(9): 094006

3 Bansil A, Lin H, Das T. Topological band theory. Reviews of Modern Physics, 2016, 88(2): 021004

4 Qi X L, Zhang S C. Topological insulators and superconductors. Reviews of Modern Physics, 2011, 83(4): 1057–1110

5 Hasan M Z, Kane C L. Topological insulators. Reviews of Modern Physics, 2010, 82(4): 3045–3067

6 Reddy D, Register L F, Carpenter G D, Banerjee S K. Graphene field-effect transistors. Journal of Physics D, Applied Physics, 2011, 44(31): 313001

7 Sanderson M, Huang S, Bao Q, Zhang C. Optical conductivity of a commensurate graphene-topological insulator heterostructure. Journal of Physics D, Applied Physics, 2017, 50(38): 385301

8 Wehling T, Black-Schaffer A M, Balatsky A V. Dirac materials. Advances in Physics, 2014, 63(1): 1–76

9 Huang S C, Sanderson M, Zhang Y, Zhang C. High efficiency and non-Richardson thermionics in three dimensional Dirac materials. Applied Physics Letters, 2017, 111(18): 183902

10 Lundgren R, Fiete G A. Electronic cooling in Weyl and Dirac semimetals. Physical Review B: Condensed Matter and Materials Physics, 2015, 92(12): 125139

11 Burkov A A, Balents L. Weyl semimetal in a topological insulator multilayer. Physical Review Letters, 2011, 107(12): 127205

PMID

12 Xu S Y, Belopolski I, Alidoust N, Neupane M, Bian G, Zhang C, Sankar R, Chang G, Yuan Z, Lee C C, Huang S M, Zheng H, Ma J, Sanchez D S, Wang B, Bansil A, Chou F, Shibayev P P, Lin H, Jia S, Hasan M Z. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science, 2015, 349(6248): 613–617

PMID

13 Lv B Q, Weng H M, Fu B B, Wang X P, Miao H, Ma J, Richard P, Huang X C, Zhao L X, Chen G F, Fang Z, Dai X, Qian T, Ding H. Experimental discovery of Weyl semimetal TaAs. Physical Review X, 2015, 5(3): 031013

14 Lu L, Wang Z, Ye D, Ran L, Fu L, Joannopoulos J D, Soljačić M. Experimental observation of Weyl points. Science, 2015, 349(6248): 622–624

PMID

15 Xu S Y, Alidoust N, Belopolski I, Yuan Z, Bian G, Chang T R, Zheng H, Strocov V N, Sanchez D S, Chang G, Zhang C, Mou D, Wu Y, Huang L, Lee C C, Huang S M, Wang B K, Bansil A, Jeng H T, Neupert T, Kaminski A, Lin H, Jia S, Zahid Hasan M. Discovery of a Weyl fermion state with Fermi arcs in niobium arsenide. Nature Physics, 2015, 11(9): 748–754

16 Ouyang T, Xiao H, Tang C, Hu M, Zhong J. Anisotropic thermal transport in Weyl semimetal TaAs: a first principles calculation. Physical Chemistry Chemical Physics, 2016, 18(25): 16709

17 Meng T, Balents L. Weyl superconductors. Physical Review B: Condensed Matter and Materials Physics, 2012, 86(5): 054504

18 Hosur P, Parameswaran S A, Vishwanath A. Charge transport in Weyl semimetals. Physical Review Letters, 2012, 108(4): 046602

PMID

19 Goswami P, Tewari S. Axionic field theory of (3+1)-dimensional Weyl semimetals. Physical Review B: Condensed Matter and Materials Physics, 2013, 88(24): 245107

20 Vazifeh M M, Franz M. Electromagnetic response of Weyl semimetals. Physical Review Letters, 2013, 111(2): 027201

PMID

21 Armitage N P, Mele E J, Vishwanath A. Weyl and Dirac semimetals in three-dimensional solids. Reviews of Modern Physics, 2018, 90(1): 015001

22 Ashby P E, Carbotte J P. Magneto-optical conductivity of Weyl semimetals. Physical Review B: Condensed Matter and Materials Physics, 2013, 87(24): 245131

23 Fuchs J N. Dirac fermions in graphene and analogues: magnetic field and topological properties. 2013, arXiv:1306.0380

24 Castro Neto A H, Guinea F, Peres N M R, Novoselov K S, Geim A K. The electronic properties of graphene. Reviews of Modern Physics, 2009, 81(1): 109–162

25 Peres N M R. The transport properties of graphene: an introduction. Reviews of Modern Physics, 2010, 82(3): 2673–2700

26 Sarma S D, Adam S, Hwang E H, Rossi E. Electronic transport in two-dimensional graphene. Reviews of Modern Physics, 2011, 83(2): 407–470

27 Baireuther P S. Universiteit Leiden, (Doctoral dissertation). 2017

28 Bell J S, Jackiw R. A PCAC puzzle: π⁰→gg in the s-model. Il Nuovo Cimento, 1969, 60(1): 47–61

29 Adler S L. Axial-vector vertex in spinor electrodynamics. Physical Review, 1969, 177(5): 2426–2438

30 Son D T, Spivak B Z. Chiral anomaly and classical negative magnetoresistance of Weyl metals. Physical Review B: Condensed Matter and Materials Physics, 2013, 88(10): 104412

31 Landsteiner K. Anomalous transport of Weyl fermions in Weyl semimetals. Physical Review B: Condensed Matter and Materials Physics, 2014, 89(7): 075124

32 Shekhar C, Nayak A K, Sun Y, Schmidt M, Nicklas M, Leermakers I, Zeitler U, Skourski Y, Wosnitza J, Liu Z, Chen Y, Schnelle W, Borrmann H, Grin Y, Felser C, Yan B. Extremely large magnetoresistance and ultrahigh mobility in the topological Weyl semimetal candidate NbP. Nature Physics, 2015, 11(8): 645–649

33 Wang F, Ran Y. Nearly flat band with Chern number C = 2 on the dice lattice. Physical Review B: Condensed Matter and Materials Physics, 2011, 84(24): 241103

34 Bercioux D, Urban D F, Grabert H, Häusler H. Massless Dirac-Weyl fermions in a T₃ optical lattice. Physical Review A, 2009, 80(6): 063603

35 Liu Z, Wang Z F, Mei J W, Wu Y S, Liu F. Flat Chern band in a two-dimensional organometallic framework. Physical Review Letters, 2013, 110(10): 106804

PMID

36 Yamada M G, Soejima T, Tsuji N, Hirai D, Dincă M, Aoki H. First-principles design of a half-filled flat band of the kagome lattice in two-dimensional metal-organic frameworks. Physical Review B: Condensed Matter and Materials Physics, 2016, 94(8): 081102

37 Su N, Jiang W, Wang Z, Liu F. Prediction of large gap flat Chern band in a two-dimensional metal-organic framework. Applied Physics Letters, 2018, 112(3): 033301

38 Neupert T, Santos L, Chamon C, Mudry C. Fractional quantum Hall states at zero magnetic field. Physical Review Letters, 2011, 106(23): 236804

PMID

39 Malcolm J D, Nicol E J. Analytic evaluation of Kane fermion magneto-optics in two and three dimensions. Physical Review B: Condensed Matter and Materials Physics, 2016, 94(22): 224305

40 Häusler W. Flat-band conductivity properties at long-range Coulomb interactions. Physical Review B: Condensed Matter and Materials Physics, 2015, 91(4): 041102

41 Du L, Zhou X, Fiete G A. Quadratic band touching points and flat bands in two-dimensional topological Floquet systems. Physical Review B: Condensed Matter and Materials Physics, 2017, 95(3): 035136

42 Urban D F, Bercioux D, Wimmer W, Häusler W. Barrier transmission of Dirac-like pseudospin-one particles. Physical Review B: Condensed Matter and Materials Physics, 2011, 84(11): 115136

43 Shen R, Shao L B, Wang B, Xing D Y. Single Dirac cone with a flat band touching on line-centered-square optical lattices. Physical Review B: Condensed Matter and Materials Physics, 2010, 81(4): 041410

44 Illes E, Nicol E J. Klein tunneling in the α-T₃ model. Physical Review B: Condensed Matter and Materials Physics, 2017, 95(23): 235432

45 Louvet T, Delplace P, Fedorenko A A, Carpentier D. On the origin of minimal conductivity at a band crossing. Physical Review B: Condensed Matter and Materials Physics, 2015, 92(15): 155116

46 Illes E, Nicol E J. Magnetic properties of the α-T₃ model: magneto-optical conductivity and the Hofstadter butterfly. Physical Review B: Condensed Matter and Materials Physics, 2016, 94(12): 125435

47 Islam S K F, Dutta P. Valley-polarized magnetoconductivity and particle-hole symmetry breaking in a periodically modulated α-T₃ lattice. Physical Review B: Condensed Matter and Materials Physics, 2017, 96(4): 045418

48 Shareef S, Ang Y S, Zhang C. Room-temperature strong terahertz photon mixing in graphene. Journal of the Optical Society of America B, Optical Physics, 2012, 29(3): 274

49 Wright A R, Xu X G, Cao J C, Zhang C. Strong nonlinear optical response of graphene in the terahertz regime. Applied Physics Letters, 2009, 95(7): 072101

50 Ang Y S, Sultan S, Zhang C. Nonlinear optical spectrum of bilayer graphene in the terahertz regime. Applied Physics Letters, 2010, 97(24): 243110

51 Ang Y S, Zhang C. Enhanced optical conductance in graphene superlattice due to anisotropic band dispersion. Journal of Physics D, Applied Physics, 2012, 45(39): 395303

52 Mikhailov S A. Non-linear electromagnetic response of graphene. Europhysics Letters, 2007, 79(2): 27002

53 Gong S, Zhao T, Sanderson M, Hu M, Zhong R, Chen X, Zhang P, Zhang C, Liu S. Transformation of surface plasmon polaritons to radiation in graphene in terahertz regime. Applied Physics Letters, 2015, 106(22): 223107

54 Sanderson M, Ang Y S, Gong S, Zhao T, Hu M, Zhong R, Chen X, Zhang P, Zhang C, Liu S. Optical bistability induced by nonlinear surface plasmon polaritons in graphene in terahertz regime. Applied Physics Letters, 2015, 107(20): 203113

55 Zuber J W, Zhao T, Gong S, Hu M, Zhong R B, Zhang C, Liu S G. Tunable strong photo-mixing in Weyl semimetals. Physical Review B: Condensed Matter and Materials Physics, 2020, 101(8): 085307

56 Zhu C, Wang F, Meng Y, Yuan X, Xiu F, Luo H, Wang Y, Li J, Lv X, He L, Xu Y, Liu J, Zhang C, Shi Y, Zhang R, Zhu S. A robust and tuneable mid-infrared optical switch enabled by bulk Dirac fermions. Nature Communications, 2017, 8(1): 14111

PMID

57 Huang S, Sanderson M, Tian J, Chen Q, Wang F, Zhang C. Hot carrier relaxation in three dimensional gapped Dirac semi-metals. Journal of Physics D, Applied Physics, 2018, 51(1): 015101

58 Hwang C, Siegel D A, Mo S K, Regan W, Ismach A, Zhang Y, Zettl A, Lanzara A. Fermi velocity engineering in graphene by substrate modification. Scientific Reports, 2012, 2(1): 590

59 Illes E, Carbotte J P, Nicol E J. Hall quantization and optical conductivity evolution with variable Berry phase in the α-T₃ model. Physical Review B: Condensed Matter and Materials Physics, 2015, 92(24): 245410

60 Chen L, Zuber J W, Ma Z, Zhang C. Nonlinear optical response of the α-T₃ model due to the nontrivial topology of the band dispersion. Physical Review B: Condensed Matter and Materials Physics, 2019, 100(3): 035440

61 Dóra B, Kailasvuori J, Moessner R. Lattice generalization of the Dirac equation to general spin and the role of the flat band. Physical Review B: Condensed Matter and Materials Physics, 2011, 84(19): 195422

62 Tapasztó L, Dobrik G, Nemes-Incze P, Vertesy G, Lambin P, Biró L P. Tuning the electronic structure of graphene by ion irradiation. Physical Review B: Condensed Matter and Materials Physics, 2008, 78(23): 233407