Self-trapped excitons in two-dimensional perovskites

Abstract

With strong electron–phonon coupling, the self-trapped excitons are usually formed in materials, which leads to the local lattice distortion and localized excitons. The self-trapping strongly depends on the dimensionality of the materials. In the three-dimensional case, there is a potential barrier for self-trapping, whereas no such barrier is present for quasi-one-dimensional systems. Two-dimensional (2D) systems are marginal cases with a much lower potential barrier or nonexistent potential barrier for the self-trapping, leading to the easier formation of self-trapped states. Self-trapped excitons emission exhibits a broadband emission with a large Stokes shift below the bandgap. 2D perovskites are a class of layered structure material with unique optical properties and would find potential promising optoelectronic. In particular, self-trapped excitons are present in 2D perovskites and can significantly influence the optical and electrical properties of 2D perovskites due to the soft characteristic and strong electron–phonon interaction. Here, we summarized the luminescence characteristics, origins, and characterizations of self-trapped excitons in 2D perovskites and finally gave an introduction to their applications in optoelectronics.

Key words： self-trapped exciton (STE); two-dimensional (2D) perovskites; broadband emission; electron–phonon coupling; optoelectronic applications

Introduction

Since the rapid development in the field of solar cells, organic–inorganic hybrid perovskite has attracted tremendous interest [¹,²]. Recently, the power conversion efficiency of perovskite solar cells has overpassed to 25% [³]. Nevertheless, although great progress has been made in the perovskite-based solar cells, the stability of perovskites in ambient prevents perovskite solar cells from being commercialized [⁴]. One solution to address the stability issue is the insertion of organic chains between the inorganic octahedral sheets so that the inorganic layers are protected from being contacted by the moisture in the air. Under such a case, the so-called two-dimensional (2D) perovskites are formed with improved stability [⁵–⁷].

The 2D perovskites are one class of layered materials, and we can mechanically exfoliate thin flakes from their bulk crystals and further integrate with other layered materials to achieve the desired functionalities [⁷–¹⁰]. Furthermore, the bandgap and electronic band structure can be easily tuned by changing the organic cations or layer number, which provides great flexibility for the optoelectronic applications [¹¹–¹⁴]. Also, owing to the different dielectric constant between the organic chain and inorganic layers, 2D perovskites are naturally formed multi-quantum wells, and the exciton binding energy is over hundreds of meV in 2D perovskites [¹⁵,¹⁶]. Therefore, we could observe a pronounced exciton emission at room temperature, and 2D perovskites provide an ideal platform to investigate exciton emission and dynamics, and their related optoelectronic applications [¹⁷–²⁰].

In particular, 2D perovskites possess soft lattice and strong electron–phonon interaction [¹⁵,¹⁸,²¹]. As a result, the local lattice distortion can easily take place because of the strong electron–phonon interaction, leading to the self-trapped states within the bandgap [²²–²⁷]. Self-trapped excitons (STEs) are therefore formed with emission peak below free exciton emission peak. STEs are essentially localized excitons, and therefore, these emissions usually process a very broad full width at half maximum (FWHM) over 100 nm together with a large Stokes shift about hundreds of meV [²³,²⁸]. STEs are expected to play an important role in the electronic and optical properties of 2D perovskites [²⁹,³⁰]. To this end, it is essential to fully understand STEs in 2D perovskites to design the new device architecture and improve device performance rationally.

Here, we first introduced features of STEs in 2D perovskites and illustrated the possible reason for the formation of STEs. Subsequently, we analyzed the factors that influence the intensity of STEs, including dimension, temperature, and lattice distortion. Furthermore, we summarized the experimental route to characterize STEs and associated optoelectronic applications. Finally, we summed up the trends and challenges of STEs in 2D perovskites.

STEs in 2D perovskites

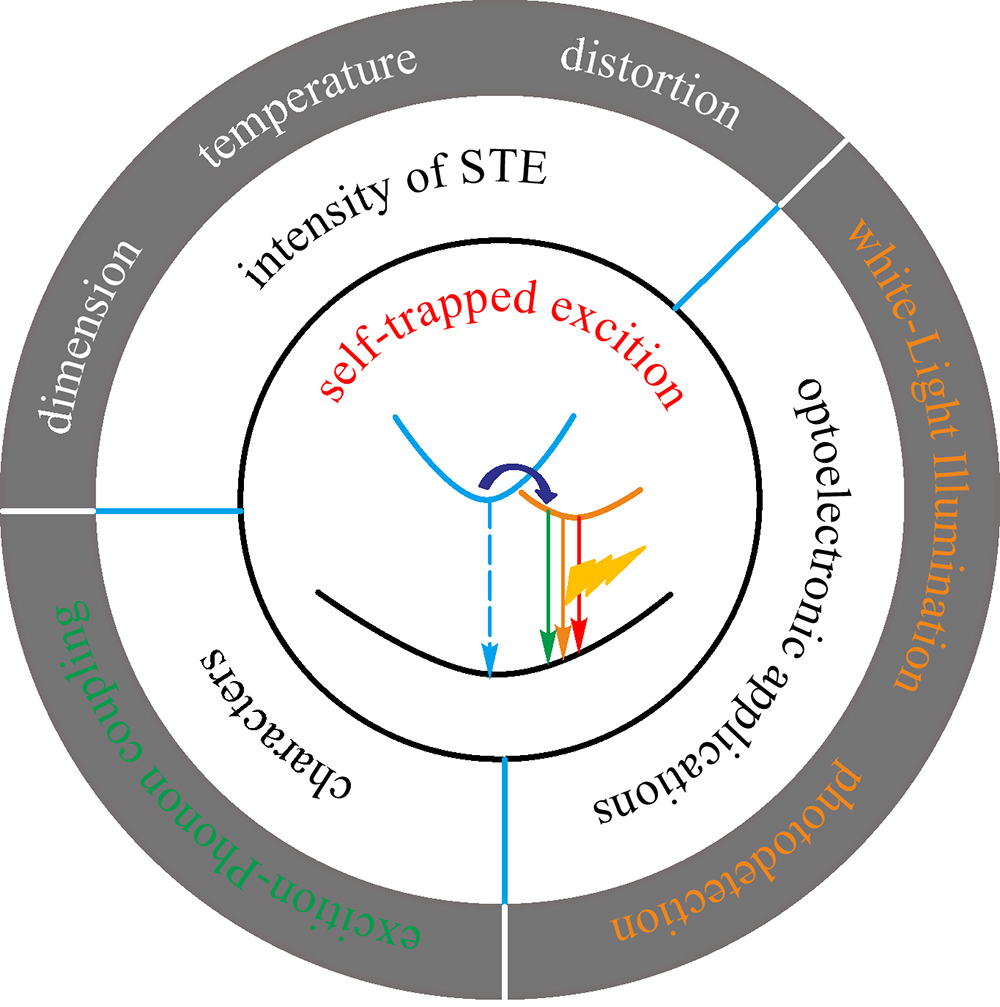
The general formula of 2D perovskites is R₂A_n−1M_nX_3n+1, where R is an organic spacer cation, A is an organic cation, M is a divalent metal, and X is a halide anion. The structure of 2D perovskites can be regarded as an organic chain inserting into three-dimensional (3D) perovskites to serve as a spacer layer (Fig. 1(a)) [⁷,³¹]. Thus, 2D perovskites process a natural quantum-well structure, and the width of the quantum well can be tuned by changing the inorganic layer number, n. With the increase of n, the bandgap of 2D perovskites shows a redshift, which is a result of reduced quantum confinement effect [¹⁵]. Taking (C₄H₉NH₃)₂(CH₃NH₃)_n−1Pb_nI_3n+1 emission spectra as an example (Fig. 1(b)), we can observe a clear redshift of peak position with increasing n [³²]. Only one emission peak is present at room temperature, whereas multiple emission peaks can be observed at low temperatures [³²,³³]. For n = 1 perovskite, we can observe additional broadband emission peaks below the free exciton emission peak, and the intensity of the broadband emission peaks becomes weaker for n > 2 perovskites; the reasons of which will be discussed in the following. The power-dependent emission intensity shows that the intensity of these broadband emission peaks linearly increases with the excitation intensity similar to that of free exciton emission (Fig. 1(d)), which indicates defects should not be the response to the broadband emission [³³,³⁴]. Thus, the broadband emission can be ascribed to the localized exciton states below the free excitons. Yu et al. [³⁵] measured the fluorescence lifetime of free excitons and localized excitons in 2D perovskite (PEA)₂PbI₄ and found a much longer lifetime for the broadband emissions (Fig. 1(e)). Besides, considering the large Stokes shift, these broadband emissions are similar to the STEs emission in alkali halides and organic molecular crystals, which are due to the strong electron–phonon interaction in the deformable lattice with distortion [²⁸,³⁵]. According to the different origination of lattice distortion, STEs can be divided into intrinsic and extrinsic. Intrinsic STEs exist in lattice without defects, and self-trapped states can be regarded as excited states. Once the excitation is removed, these excited states disappear. In terms of extrinsic STEs, permanent defects are required to nucleate the STEs. However, these defects do not induce any additional absorption onsets except the broadband emission with a large Stock shift [²⁹].

Fig.1 Luminescence characteristics of 2D perovskites. (a) Crystal structure schematics of 2D perovskites. (b) and (c) Photoluminescence (PL) spectra of (BA)₂(MA)_n−1Pb_nI_3n+1 2D perovskites at (b) room temperature (c) and low temperature. (d) Power-dependent emission intensity of free exciton (blue) and self-trapped exciton (black and red) in (BA)₂PbI₄ at low temperature. (e) Fluorescence lifetime spectra of the free exciton (green) and self-trapped excitons (red) in (PEA)₂PbI₄. (a) Reprinted with permission from Ref. [³¹]. Copyright (2016), American Chemical Society. (b) Adapted with permission from Ref. [¹⁶]. Copyright (2017), The American Association for the Advancement of Science. (c) and (d) Adapted with permission from Ref. [³³]. Copyright (2018), Nature Publishing. (e) Adapted with permission from Ref. [³⁵]. Copyright (2019), John Wiley & Sons

Full size|PPT slide

To describe the interaction of an electron or exciton with phonons, we introduced deformation potential [³⁶]. Figure 2 shows three pathways to form STEs: (1) direct relaxation, (2) thermal activation, and (3) tunneling. The potential barrier E_B is a critical factor that influences the transformation between free excitons and STEs. Usually, in 3D materials, a potential barrier is present to overcome and to initiate the self-trapping process. Nevertheless, in the low-dimensional materials, such a potential barrier for self-trapping is reduced or vanished, and thus, it is easier to observe STEs [²⁸]. Therefore, it is expected that STEs emission can be easily observed in 2D perovskites compared with 3D materials.

Fig.2 Band diagram of free exciton and self-trapped excitons. E_X is the free exciton. STE is the self-trapped exciton. E_B is the self-trapped energy. Three paths toward self-trapped excitons are represented: (1) direct relaxation, (2) thermal activation, and (3) tunneling

Full size|PPT slide

Factors affecting the intensity of STEs

The emission intensity of STEs is mainly affected by the potential barrier and the transformation between the free excitons and STEs. The dimension of the materials and electron–phonon coupling strength determines the height of the potential barrier, whereas the temperature limits the transformation between the free excitons and STEs. In this sense, the dimension of the materials, the electron–phonon coupling strength, and the temperature finally together decide the emission intensity of STEs [²⁸]. For 3D perovskites (Fig. 3(a)), only free exciton emission can be observed, and no STEs emission is present [²³]. Nevertheless, for (BA)₂PbI₄ 2D perovskite (Fig. 3(b)), the broadband STEs emission peak becomes obvious at low temperature [²³]. This is expected because the minimum electron–phonon coupling strength required to form STEs is related to the dimension of the crystals. The threshold value (g_c) to form STEs is given by the formula:

{{\displaystyle g}}_{\mathrm{c}}=\mathrm{1}-{(\mathrm{2}v)}^{-\mathrm{1}},

where v is a constant determined by the dimension of the system (v = 6 for 3D; v = 4 for 2D) [²⁸]. The threshold is smaller for 2D systems, and thus, STEs are prone to exist in 2D crystal. Wu et al. [²³] further synthesized 2D perovskites with different inorganic layer numbers, n, (Fig. 3(c)) and adopted a transient absorption technique to identify the intensity evolution of STEs against n. The intensity of STEs decreases as n increases, which is evidence that STEs are prone to exist in low-dimension materials. STEs emission in 1D and 0D perovskites reported with enhanced emission intensity compared with that in 3D perovskites, which further confirms that the dimension of the materials is an important factor in deciding the emission intensity of STEs [³⁷–³⁹].

Fig.3 Influence of dimension and temperature on self-trapped excitons in 2D perovskite. (a) Temperature-dependent fluorescence spectra of (MA)PbI₃ perovskite. (b) Temperature-dependent fluorescence spectra of (BA)₂PbI₄ 2D perovskite. (c) Absorption (dashed lines) and fluorescence spectra (solid lines) of (BA)₂(MA)_n−1Pb_nI_3n+1 (n = 1, 2, 3) perovskite. (d)–(f) Transition absorption spectra of (BA)₂(MA)_n−1Pb_nI_3n+1 (n = 1, 2, 3). (a)–(f) Adapted with permission from Ref. [²³]. Copyright (2015), American Chemical Society

Full size|PPT slide

There is a competition between free excitons and STEs, which can be modulated by thermal activation energy (E_T) [²⁸]. Therefore, the temperature is a critical factor that affects the thermal activation process. At low temperatures, free exciton emission and STEs emission can coexist, and their relative intensity varies with temperature, suggesting the presence of the competition between free excitons and STEs (Fig. 3(b)) [²³,³⁰,³⁴]. At low temperatures, E_T is smaller than E_B, and then STEs are trend to be localized in the deformable lattice. As the temperature increases, E_T becomes comparable with E_B, and free exciton emission intensity is accordingly comparable with that of STEs. At room temperature when E_T is larger than E_B, the free exciton becomes dominant, and STEs emission manifests itself as a long emission tail [²³]. Similar temperature-dependent emission evolution has been reported in other 2D perovskites with different compositions [⁴⁰].

The distortion degree of the lattice is another factor that influences the intensity of STEs in 2D perovskites [²⁶]. There is a clear relationship between the distortion degree of the lattice and the intensity of STEs emission. Usually, the relative bond distance of octahedral can be described via

\mathrm{\Delta }d={\displaystyle \frac{\mathrm{1}}{n}}{\displaystyle \sum {\displaystyle \frac{{{\displaystyle d}}_n-d^{\mathrm{2}}}{d}}},

where d is the mean of bond distance and d_n is individual bond distance. The average \mathrm{\Delta }d is the factor to describe the distortion degree of the structure. The crystal should process a large \mathrm{\Delta }d to achieve a noticeable STEs emission [²⁶]. In addition to the relative bond distance, bond angle (σ) is a parameter that reflects the deviation of the octahedron [²⁶], which can be expressed as

{\sigma }^{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{\mathrm{11}}}{\displaystyle \sum {({{\displaystyle \theta }}_i-\mathrm{90}°),}^{\mathrm{2}}}

where {{\displaystyle \theta }}_i is the X–M–X bond angle of the octahedron. By using \mathrm{\Delta }d and σ, we can describe the distortion levels of the individual octahedron and the degree of the lattice distortion. Mao et al. [⁴¹] used chloride ion to replace the bromide ion in 2D perovskites and to increase the lattice distortion (Fig. 4(a)) because of the smaller size of chloride ion that makes the lattice more deformable. On the other hand, halogen affects the self-trapping depth and the energy levels of free excitons, which impact the trapping and detrapping barriers of 2D perovskites [⁴²]. Hence, the intensity of STEs in the chloride perovskite is enhanced compared with that in the bromide counterpart (Fig. 4(b)) [⁴¹]. In addition to halogen, organic layers in 2D perovskites serve as a framework that influences the distortion degree of the inorganic layers (Fig. 4(c)). Thus, the intensity of STEs can be tuned by organic chains, which deserves further investigations. The PL spectra in Fig. 4(d) show that the larger the distortion is, the broader the emission peaks are. Yu et al. [³⁵] improved STEs emission in 2D perovskites by the tin doping process due to the increased lattice distortion (Fig. 4(e)). To sum up, the intensity of STEs can be tuned by halide ions, species of the organic layer, and a metal cation—all of which can affect the distortion degree of the lattice and further influence the potential barrier between the free excitons and STEs.

Fig.4 Effect of lattice distortion on the intensity of self-trapped excitons. (a) Schematic of the chloride-ion-enhanced lattice distortion. (b) Photoluminescence spectra of 2D perovskite with different ratios of chloride ion. (c) Structure diagram of 2D perovskite with the different organic layers. (d) Photoluminescence spectra of 2D perovskite in (c). (e) Photoluminescence spectra of (PEA)₂PbI₄ before and after incorporation of tin ions. (a) and (b) Adapted with permission from Ref. [⁴¹]. Copyright (2017), American Chemical Society. (c) and (d) Adapted with permission from Ref. [²⁷]. Copyright (2017), American Chemical Society. (e) Adapted with permission from Ref. [³⁵]. Copyright (2019), John Wiley & Sons

Full size|PPT slide

Characterizations of STEs

The STEs emission has a large Stocks shift and broad FWHM, which are the main characteristics to identify STEs emission. Nevertheless, additional experimental techniques are required to exclude further the possibility of localized excitons induced by defects. Time-resolved [³⁶], power-dependent PL [³³], and photoconductivity studies [²²] are feasible methods to distinguish STEs emission from defects emission.

Time-resolved PL spectroscopy provides a powerful way to investigate the details of STEs emissions (Fig. 5(a)) [³⁶]. We can distinguish two bands in the region of STEs emission and obtain the relative intensity of them against time by time-resolved PL spectra. These two small emission peaks can be indexed to different self-trapped centers in 2D perovskites predicted by calculations [⁴³]. Combined with time-resolved PL spectroscopy, the detail of the fine band structure, together with the decay process of these emission peaks, can be obtained.

Fig.5 Characterization of self-trapped excitons. (a) Time-resolved photoluminescence spectra of 2D perovskites at different temperatures. (b) Photocurrent spectra of (BA)₂(MA)Pb₂I₇. (c) Absorption spectra of (BA)₂(MA)Pb₂I₇ at different temperatures. The absorption coefficient is expressed in logarithmic form. Fitting lines indicate the slope of the Urbach tail. (a) Adapted with permission from Ref. [³⁶]. Copyright (2015), American Chemical Society. (b) and (c) Adapted with permission from Ref. [²²]. Copyright (2019), Nature Publishing

Full size|PPT slide

Photoconductivity measurement is another effective way to characterize STEs. Figure 5(b) exhibits the photocurrent of 2D perovskites [²²]. Three response peaks can be observed, which can be attributed to band-to-band transition (B), free excitons (X₀), and STEs (X_t) [²²]. The STEs peak with weak absorption intensity is observed in the photoresponse spectrum because the applied bias voltage magnifies the absorption.

In addition to these two methods mentioned above, the exciton–phonon coupling strength can be used to judge whether there are STEs existed or not. Usually, the empirical slope coefficient of Urbach Tail and Huang–Rhys factor are two parameters to describe the electron–phonon coupling strength. The absorption tail can be described by the formula:

\alpha ={{\displaystyle \alpha }}_{\mathrm{0}}\exp \left(-\sigma {\displaystyle \frac{{{\displaystyle E}}_{\mathrm{0}}-E}{kT}}\right),

where α is absorption coefficient, k is the Boltzmann constant, T is the temperature, σ is the empirical slope coefficient, and {{\displaystyle \alpha }}_{\mathrm{0}} and E₀ are fitting parameters [²⁸]. The slope coefficient can be extracted from the absorption spectra (Fig. 5(c)), from which the coupling strength (g) can be extracted by the following formula: g=s/\sigma (s=1.24 in 2D materials) [²⁸]. Once g is larger than the threshold value (g_c), STEs are prone to be formed. As we have already discussed, g_c is related to the dimension of the crystals, typically g_c =0.87 for 2D systems [²⁸]. In Fig. 5(c), the calculated g=1.817>g_c; therefore, STEs are expected to be present in 2D perovskites [²²].

The electron–phonon coupling strength can also be extracted from the FWHM of the emission spectra [⁴⁴]. The FWHM satisfies the following formula:

\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M}=\mathrm{2.36}\sqrt{s}{{\displaystyle \hslash \omega }}_{\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{n}\mathrm{o}\mathrm{n}}\sqrt{\coth {\displaystyle \frac{{{\displaystyle \hslash \omega }}_{\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{n}\mathrm{o}\mathrm{n}}}{\mathrm{2}kT}}},

where is the Planck constant, {{\displaystyle \omega }}_{\mathrm{phonon}} is the phonon frequency, k is the Boltzmann constant, and s is the Huang–Rhys factor. By extracting the FWHMs of emission peaks at a different temperature, we can estimate s [⁴⁴]. The bigger the s is, the stronger the exciton–phonon coupling is. Both s and g are factors that can be used to evaluate the intensity of exciton–phonon/electron–phonon coupling strength in semiconductors.

STEs-based optoelectronic applications in 2D perovskites

The large Stokes shift of STEs can greatly reduce the self-absorption effect in 2D perovskites [⁴⁵]. This merit makes 2D perovskites be a class of promising materials for luminescent solar concentrators, which can improve the efficiency of solar cells. The broadband emission of STEs in 2D perovskites would find promising applications in white-light illumination [²⁵]. Compared with traditional light-emitting diodes, 2D perovskites with STEs could achieve naturally white-light emission without requiring additional phosphors for color modulation (Fig. 6(a)) [²⁵]. Therefore, the device structure can be greatly simplified, and the cost can be reduced. Also, the bandgap of 2D perovskites can be easily tuned by changing halide ions and layer number (Figs. 6(b)–6(d)). As a result, the color temperature of the STEs emission can be tuned, which would be beneficial for indoor illumination (Fig. 6(e)) [²⁵].

Fig.6 Optoelectronic application based on self-trapped excitons in 2D perovskites. (a) Fluorescence images of 2D perovskites with chloride ions (left) and bromide ions (right). (b)–(d) Absorption and fluorescence spectra of 2D perovskites with (b) chloride ions, (c) bromide ions, and (d) iodide ions. (e) Chromaticity coordinates diagram of the emission in (b)–(d). (f) Structure diagram of a 2D perovskite narrowband photodetector. (g) Narrowband photodetectors in a visible band based on 2D perovskites. (h) Polarization-dependent photocurrent of STEs. (a)–(e) Adapted with permission from Ref. [²⁵]. Copyright (2014), American Chemical Society. (f) and (g) Adapted with permission from Ref. [²²]. Copyright (2019), Nature Publishing. (h) Adapted with permission from Ref. [⁴⁶]. Copyright (2019), John Wiley & Sons

Full size|PPT slide

The STEs in 2D perovskites can also be applied to achieve narrowband photodetections based on charge collection narrowing (CCN) mechanism [²²]. Photons with energy higher than free excitons are absorbed in the surface of the crystals, which cannot significantly contribute to the photocurrent due to the large resistance of the organic layer. In contrast, photons with energy near STEs are absorbed inside the crystal and thus could contribute to photocurrent (Fig. 6(f)) [²²]. Therefore, narrowband photodetections using 2D perovskites can be realized by taking advantage of the STEs-assisted-enhanced absorption with the concept of CCN. By further tuning the bandgap of 2D perovskites, the response peak of the narrowband photodetectors can cover the whole visible spectrum (Fig. 6(g)) [²²]. STEs show an orientation preference because of the layered structure of 2D perovskites, which induces a polarization-dependent absorption coefficient (Fig. 6(h)) [³⁴]. Taking advantage of the polarization-dependent absorption coefficient of STEs in 2D perovskites, Li et al. [⁴⁶] have demonstrated the polarization-resolved narrowband photodetectors. The photodetectors possess the ability to simultaneously sense both the wavelength and the polarization of the light.

Conclusions and perspective

In conclusion, we have summarized the recent development of STEs in 2D perovskites. First, we introduced the basic characteristics of STEs in 2D perovskites. Next, we discussed the factors that can affect the emission intensity of STEs. Then, we represented the experimental techniques used to identify the STEs. Finally, we discussed the possible optoelectronic applications based on STEs in 2D perovskites.

Although great progress has been made on STEs in 2D perovskites, several challenges have to be addressed to explore more possible applications based on STEs in 2D perovskites. First, how the species of organic layer affect the formation of STEs in 2D perovskites is still unclear. Despite the electronic band structure of 2D perovskites that is largely determined by the inorganic layer, the organic layer can alter the electron–phonon coupling strength. As a result, the organic layer would also influence the formation of STEs. Second, the detailed formation of the STEs in 2D perovskites has rarely been studied. Understanding the formation process of STEs is essential for engineering STEs in materials for desired applications. Last, the decay process of STEs in 2D perovskites has not been fully investigated. Revealing the decay process of STEs would be beneficial for developing light-emitting devices based on STEs.

Acknowledgements

D. L. acknowledges the support from the National Basic Research Program of China (No. 2018YFA0704403), the National Natural Science Foundation of China (NSFC) (Grant No. 61674060), and Innovation Fund of Wuhan National Laboratory for Optoelectronics (WNLO).

References

1 Brenner T M, Egger D A, Kronik L, Hodes G, Cahen D. Hybrid organic-inorganic perovskites: low-cost semiconductors with intriguing charge-transport properties. Nature Reviews Materials, 2016, 1(1): 15007

2 Li W, Wang Z, Deschler F, Gao S, Friend R H, Cheetham A K. Chemically diverse and multifunctional hybrid organic-inorganic perovskites. Nature Reviews Materials, 2017, 2(3): 16099

3 National Renewable Energy Laboratory. NREL efficiency chart. 2020

4 Wang Z, Shi Z, Li T, Chen Y, Huang W. Stability of perovskite solar cells: a prospective on the substitution of the A cation and X anion. Angewandte Chemie International Edition, 2017, 56(5): 1190–1212

PMID

5 Dou L. Emerging two-dimensional halide perovskite nanomaterials. Journal of Materials Chemistry C, Materials for Optical and Electronic Devices, 2017, 5(43): 11165–11173

6 Etgar L. The merit of perovskite’s dimensionality; can this replace the 3D halide perovskite? Energy & Environmental Science, 2018, 11(2): 234–242

7 Grancini G, Nazeeruddin M K. Dimensional tailoring of hybrid perovskites for photovoltaics. Nature Reviews Materials, 2019, 4(1): 4–22

8 Li J, Wang J, Zhang Y, Wang H, Lin G, Xiong X, Zhou W, Luo H, Li D. Fabrication of single phase 2D homologous perovskite microplates by mechanical exfoliation. 2D Materials, 2018, 5(2): 021001

9 Fang C, Wang H, Shen Z, Shen H, Wang S, Ma J, Wang J, Luo H, Li D. High-performance photodetectors based on lead-free 2D Ruddlesden-Popper perovskite/MoS₂ heterostructures. ACS Applied Materials & Interfaces, 2019, 11(8): 8419–8427

PMID

10 Ma J, Fang C, Chen C, Jin L, Wang J, Wang S, Tang J, Li D. Chiral 2D perovskites with a high degree of circularly polarized photoluminescence. ACS Nano, 2019, 13(3): 3659–3665

PMID

11 Cao D H, Stoumpos C C, Farha O K, Hupp J T, Kanatzidis M G. 2D homologous perovskites as light-absorbing materials for solar cell applications. Journal of the American Chemical Society, 2015, 137(24): 7843–7850

PMID

12 Smith M D, Connor B A, Karunadasa H I. Tuning the luminescence of layered halide perovskites. Chemical Reviews, 2019, 119(5): 3104–3139

PMID

13 Gao Y, Shi E, Deng S, Shiring S B, Snaider J M, Liang C, Yuan B, Song R, Janke S M, Liebman-Peláez A, Yoo P, Zeller M, Boudouris B W, Liao P, Zhu C, Blum V, Yu Y, Savoie B M, Huang L, Dou L. Molecular engineering of organic-inorganic hybrid perovskites quantum wells. Nature Chemistry, 2019, 11(12): 1151–1157

PMID

14 Dou L, Wong A B, Yu Y, Lai M, Kornienko N, Eaton S W, Fu A, Bischak C G, Ma J, Ding T, Ginsberg N S, Wang L W, Alivisatos A P, Yang P. Atomically thin two-dimensional organic-inorganic hybrid perovskites. Science, 2015, 349(6255): 1518–1521

PMID

15 Straus D B, Kagan C R. Electrons, excitons, and phonons in two-dimensional hybrid perovskites: connecting structural, optical, and electronic properties. Journal of Physical Chemistry Letters, 2018, 9(6): 1434–1447

PMID

16 Blancon J C, Tsai H, Nie W, Stoumpos C C, Pedesseau L, Katan C, Kepenekian M, Soe C M, Appavoo K, Sfeir M Y, Tretiak S, Ajayan P M, Kanatzidis M G, Even J, Crochet J J, Mohite A D. Extremely efficient internal exciton dissociation through edge states in layered 2D perovskites. Science, 2017, 355(6331): 1288–1292

PMID

17 Chen Y, Sun Y, Peng J, Tang J, Zheng K, Liang Z. 2D Ruddlesden-Popper perovskites for optoelectronics. Advanced Materials, 2018, 30(2): 1703487

PMID

18 Wang J, Su R, Xing J, Bao D, Diederichs C, Liu S, Liew T C H, Chen Z, Xiong Q. Room temperature coherently coupled exciton-polaritons in two-dimensional organic-inorganic perovskite. ACS Nano, 2018, 12(8): 8382–8389

PMID

19 Yuan M, Quan L N, Comin R, Walters G, Sabatini R, Voznyy O, Hoogland S, Zhao Y, Beauregard E M, Kanjanaboos P, Lu Z, Kim D H, Sargent E H. Perovskite energy funnels for efficient light-emitting diodes. Nature Nanotechnology, 2016, 11(10): 872–877

PMID

20 Ha S T, Shen C, Zhang J, Xiong Q. Laser cooling of organic-inorganic lead halide perovskites. Nature Photonics, 2016, 10(2): 115–121

21 Straus D B, Hurtado Parra S, Iotov N, Gebhardt J, Rappe A M, Subotnik J E, Kikkawa J M, Kagan C R. Direct observation of electron-phonon coupling and slow vibrational relaxation in organic-inorganic hybrid perovskites. Journal of the American Chemical Society, 2016, 138(42): 13798–13801

PMID

22 Li J, Wang J, Ma J, Shen H, Li L, Duan X, Li D. Self-trapped state enabled filterless narrowband photodetections in 2D layered perovskite single crystals. Nature Communications, 2019, 10(1): 806

PMID

23 Wu X, Trinh M T, Niesner D, Zhu H, Norman Z, Owen J S, Yaffe O, Kudisch B J, Zhu X Y. Trap states in lead iodide perovskites. Journal of the American Chemical Society, 2015, 137(5): 2089–2096

PMID

24 Cortecchia D, Neutzner S, Srimath Kandada A R, Mosconi E, Meggiolaro D, De Angelis F, Soci C, Petrozza A. Broadband emission in two-dimensional hybrid perovskites: the role of structural deformation. Journal of the American Chemical Society, 2017, 139(1): 39–42

PMID

25 Dohner E R, Jaffe A, Bradshaw L R, Karunadasa H I. Intrinsic white-light emission from layered hybrid perovskites. Journal of the American Chemical Society, 2014, 136(38): 13154–13157

PMID

26 Mao L, Guo P, Kepenekian M, Hadar I, Katan C, Even J, Schaller R D, Stoumpos C C, Kanatzidis M G. Structural diversity in white-light-emitting hybrid lead bromide perovskites. Journal of the American Chemical Society, 2018, 140(40): 13078–13088

PMID

27 Mao L, Wu Y, Stoumpos C C, Wasielewski M R, Kanatzidis M G. White-light emission and structural distortion in new corrugated two-dimensional lead bromide perovskites. Journal of the American Chemical Society, 2017, 139(14): 5210–5215

PMID

28 Williams R T, Song K S. The self-trapped exciton. Journal of Physics and Chemistry of Solids, 1990, 51(7): 679–716

29 Smith M D, Karunadasa H I. White-light emission from layered halide perovskites. Accounts of Chemical Research, 2018, 51(3): 619–627

PMID

30 Smith M D, Jaffe A, Dohner E R, Lindenberg A M, Karunadasa H I. Structural origins of broadband emission from layered Pb-Br hybrid perovskites. Chemical Science (Cambridge), 2017, 8(6): 4497–4504

PMID

31 Stoumpos C C, Cao D H, Clark D J, Young J, Rondinelli J M, Jang J I, Hupp J T, Kanatzidis M G. Ruddlesden-Popper hybrid lead iodide perovskite 2D homologous semiconductors. Chemistry of Materials, 2016, 28(8): 2852–2867

32 Wang S, Ma J, Li W, Wang J, Wang H, Shen H, Li J, Wang J, Luo H, Li D. Temperature-dependent band gap in two-dimensional perovskites: thermal expansion interaction and electron-phonon interaction. Journal of Physical Chemistry Letters, 2019, 10(10): 2546–2553

PMID

33 Blancon J C, Stier A V, Tsai H, Nie W, Stoumpos C C, Traoré B, Pedesseau L, Kepenekian M, Katsutani F, Noe G T, Kono J, Tretiak S, Crooker S A, Katan C, Kanatzidis M G, Crochet J J, Even J, Mohite A D. Scaling law for excitons in 2D perovskite quantum wells. Nature Communications, 2018, 9(1): 2254

PMID

34 Li J, Ma J, Cheng X, Liu Z, Chen Y, Li D. Anisotropy of excitons in two-dimensional perovskite crystals. ACS Nano, 2020, 14(2): 2156–2161

PMID

35 Yu J, Kong J, Hao W, Guo X, He H, Leow W R, Liu Z, Cai P, Qian G, Li S, Chen X, Chen X. Broadband extrinsic self-trapped exciton emission in Sn-doped 2D lead-halide perovskites. Advanced Materials, 2019, 31(7): e1806385

PMID

36 Yangui A, Garrot D, Lauret J S, Lusson A, Bouchez G, Deleporte E, Pillet S, Bendeif E E, Castro M, Triki S, Abid Y, Boukheddaden K. Optical investigation of broadband white-light emission in self-assembled organic-inorganic perovskite (C₆H₁₁NH₃)₂PbBr₄. Journal of Physical Chemistry C, 2015, 119(41): 23638–23647

37 Zhou C, Lin H, Shi H, Tian Y, Pak C, Shatruk M, Zhou Y, Djurovich P, Du M H, Ma B. A zero-dimensional organic seesaw-shaped tin bromide with highly efficient strongly Stokes-shifted deep-red emission. Angewandte Chemie International Edition, 2018, 57(4): 1021–1024

PMID

38 Zhou G, Su B, Huang J, Zhang Q, Xia Z. Broad-band emission in metal halide perovskites: mechanism, materials, and applications. Materials Science and Engineering R Reports, 2020, 141(1): 100548

39 Yuan Z, Zhou C, Tian Y, Shu Y, Messier J, Wang J C, van de Burgt L J, Kountouriotis K, Xin Y, Holt E, Schanze K, Clark R, Siegrist T, Ma B. One-dimensional organic lead halide perovskites with efficient bluish white-light emission. Nature Communications, 2017, 8(1): 14051

PMID

40 Li X, Guo P, Kepenekian M, Hadar I, Katan C, Even J, Stoumpos C C, Schaller R D, Kanatzidis M G. Small cyclic diammonium cation templated (110)-oriented 2D halide (X= I, Br, Cl) perovskites with white-light emission. Chemistry of Materials, 2019, 31(9): 3582–3590

41 Mao L, Wu Y, Stoumpos C C, Traore B, Katan C, Even J, Wasielewski M R, Kanatzidis M G. Tunable white-light emission in single-cation-templated three-layered 2D perovskites (CH₃CH₂NH₃)₄Pb₃Br_{10−xClx. Journal of the American Chemical Society, 2017, 139(34): 11956–11963}

PMID

42 Gautier R, Paris M, Massuyeau F. Exciton self-trapping in hybrid lead halides: role of halogen. Journal of the American Chemical Society, 2019, 141(32): 12619–12623

PMID

43 Cortecchia D, Yin J, Bruno A, Lo S Z A, Gurzadyan G G, Mhaisalkar S, Brédas J L, Soci C. Polaron self-localization in white-light emitting hybrid perovskites. Journal of Materials Chemistry C, Materials for Optical and Electronic Devices, 2017, 5(11): 2771–2780

44 Luo J, Wang X, Li S, Liu J, Guo Y, Niu G, Yao L, Fu Y, Gao L, Dong Q, Zhao C, Leng M, Ma F, Liang W, Wang L, Jin S, Han J, Zhang L, Etheridge J, Wang J, Yan Y, Sargent E H, Tang J. Efficient and stable emission of warm-white light from lead-free halide double perovskites. Nature, 2018, 563(7732): 541–545

PMID

45 Li S, Luo J, Liu J, Tang J. Self-trapped excitons in all-inorganic halide perovskites: fundamentals, status, and potential applications. Journal of Physical Chemistry Letters, 2019, 10(8): 1999–2007

PMID

46 Li L, Jin L, Zhou Y, Li J, Ma J, Wang S, Li W, Li D. Filterless polarization-sensitive 2D perovskite narrowband photodetectors. Advanced Optical Materials, 2019, 7(23): 1900988