All-optical pseudo noise sequence generator using a micro-ring resonator

Abstract

A scheme for the generation of a pseudo noise (PN) sequence in the optical domain is proposed. The cascaded units of micro-ring resonator (MRR)-based D flip-flop are used to design the device. D flip-flops consist of a single MRR and share the same optical pump signal. Numerical analysis is performed, and simulated results are discussed. The proposed device can be used as a building block for optical computing and for creating an information processing system.

Key words： all-optical; D flip-flop; micro-ring resonator (MRR); optical communication; pseudo noise (PN) sequence

1 Introduction

In the last two decades, considerable research has been carried out to realize the digital logic computational techniques using different technologies. Physical wireless connectivity can be achieved using either radio frequency or optical signals. The radio frequency spectrum is congested, and services in new bands are difficult. Optical computation and optical devices are good alternatives to radio frequency communication systems. The wireless channel shows good capacity for optical communication [1]. Optical wireless networks are good candidates for the next generation communication systems [2]. A model of an intensity-modulated direct detection channel for the free-space optical communication has been proposed [3]. A complementary metal oxide semiconductor (CMOS) transimpedance amplifier for the optical wireless communication has been reported [4]. 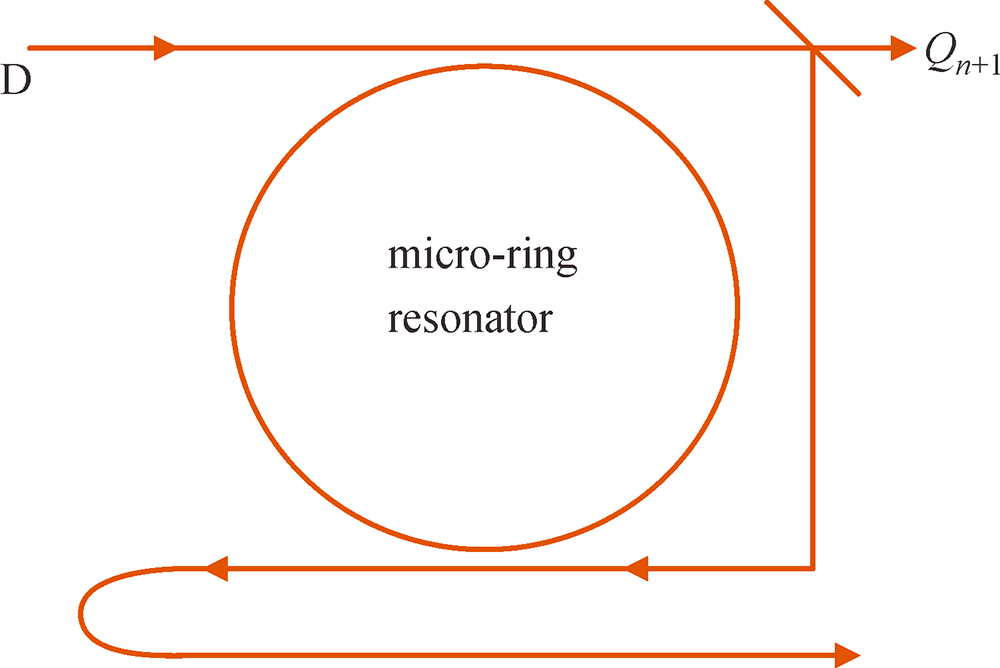A free-space optical channel has been analyzed from the perspective of information theory [5]. The main objectives of these efforts are to realize optical communication, where the entire operation depends only upon a photon rather than an electron. Several techniques have been proposed to utilize the higher transmission capacity of optical communication networks. Configurability, compactness, and programmability are the major concerns of the next generation communication systems. Ring resonators that use various fabricating materials have been reported such as a silicon-on-insulator (SOI)-based micro-ring resonator (MRR) [6], silicon MRR [7], and vertically coupled GaInAsP–InP MRR [8]. Silicon MRR is an excellent platform for performing all-optical signal processing [9]. MRR offers high-Q, ultra-fast switching, ultra-low power consumption, and ease of fabrication [7,10]. Many studies have investigated all-optical logic gates using MRR as a switch such as all-optical ultrafast NOT, XOR/XNOR logic gates [11], OR/NOR-directed logic devices [12], digital logic NOT, NOR, XOR, AND, and NAND [13,14]. A comparison of optical signals has been proposed using a cascaded MRR structure [15].

Thus, it is of great interest to analyze techniques related to MRR to realize combinational and sequential circuits. For the fast optical communication network, it is essential to generate a simple and efficient method to improve the performance of optical computation techniques.

All-optical devices can be applied to the next generation communication system. MRRs are used as building blocks for very large scale integrated optics. Their small size, filtering characteristics, and the ability of being used in complex and flexible configurations make these devices useful and efficient for integrated optics and photonics applications. The convergence of microelectronics and photonics allows to design high speed and compact devices [16]. The switching, compactness, and ability to integrate multiple MRRs are the main advantages of MRRs. The ultra-compact size and optical signal processing of MRR make it an ideal candidate for the very large scale integrated (VLSI) photonic circuits [11,17]. The integrated photonics technology is used to fabricate all-optical devices where optical devices are controlled by photons and do not need any optoelectronics conversion.

A synchronous pseudo noise (PN) code sequence generator has been introduced [12] and is applied to spread spectrum communication systems. The PN sequence has several advantages such as immunity to disturbance from other narrowband signals and low power spectrum. A rapid acquisition scheme with a new decision logic is proposed, where the average number of chips for acquisition is lower compared to that for conventional logic [14]. The device dimension is reduced using an optimized linear feedback shift register (LFSR) permutation [18]. The design of an all-optical PN sequence generator using MRR can considerably reduce the device dimension. The proposed device is a perfect example of interconnected optical switching elements. Because the proposed device is all-optical in nature, the undesirable latencies and speed limitations imposed by electrical to optical and optical to electrical conversion can be eliminated.

In this study, a considerable effort was made to design devices for the optical communication network. Section 1 presents an introduction to the optical communication network, research work carried out in the field of optical networking, as well as advantages and limitations of optical communication. Section 2 explores the operation of MRR. The design of optical D flip-flop is discussed. Section 3 deals with the operation of a PN sequence generator. A PN sequence generator is designed using MRR, and the simulated results are discussed. In Section 4, relevant conclusions are discussed.

2 Micro-ring resonator (MRR) and all-optical D flip-flop

MRR consists of a ring resonator and input–output waveguides. The operating principal of MRR is the coupling phenomena between the ring resonator and input–output waveguide. The coupling coefficient between the input waveguide and ring is k₁ and that between the ring and output waveguide is k₂. Figure 1 shows the diagram of MRR, where r is the ring radius. Constructive interference occurs if the path length of the round trip is an integer multiple of the wavelength. Constructive interference is known as “ON resonance”. At resonance, periodic fringes are observed at the output ports. Resonance condition include maximum and minimum power at through port and drop port respectively.

Fig.1 Single MRR

Full size|PPT slide

The resonance condition can be changed by varying the vertically applied pump signal. If the pump signal is applied vertically to MRR, it is known as a vertically coupled MRR (VCMRR); if the pump signal is applied latterly, it is known as a laterally coupled MRR (LCMRR).

When an appropriate intensity of the pump signal is applied to the resonator, the refractive index of the resonator changes. High-density carriers are generated when the optical ring is excited from the top of the ring and results in the complete absorption of light. This results in a decrease in the refractive index profile, and a blue-shift phenomenon is temporarily observed for the specific micro-resonance wavelengths. The resonance wavelength changes with a change in the refractive index, which can be used to switch the signal ON or OFF or turn the resonance ON or OFF for a specific wavelength. If the circumference of the ring is considered as L, k₁ is the coupling coefficient between the input and the ring, k₂ is the coupling coefficient between the ring and the output,α is the intensity attenuation coefficient of the ring, γ is the intensity insertion loss coefficient, and k_n is the wave propagation constant. k_n={\displaystyle \frac{\mathrm{2}\mathrm{\pi }}{\lambda }}{\eta }_{\mathrm{eff}},λ is the resonant wavelength of the ring, {\eta }_{\mathrm{eff}}=n_{\mathrm{0}}+n_{\mathrm{2}}I=n_{\mathrm{0}}+{\displaystyle \frac{n_{\mathrm{2}}}{A_{\mathrm{eff}}}}P, where n₀ and n₂ are the linear and nonlinear refractive indices, respectively. I and P are the intensity and power of the optical pump signal. E_i1 and E_i2 are assumed to be the input and add port field, respectively. The fields at the points a, b, c, and d are E_ra, E_rb, E_rc, and E_rd, respectively.

(1)E_{ra}={(\mathrm{1}-\gamma )}^{\raisebox{1ex}{$\mathrm{1}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{2}$}\right.}[\mathrm{j}\sqrt{k_{\mathrm{1}}}{E}_{\mathrm{i}\mathrm{1}}+\sqrt{(\mathrm{1}-k_{\mathrm{1}})}{E}_{rd}],

(2)E_{rb}=E_{ra}\exp (-\alpha {\displaystyle \raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$\mathrm{4}$}\right.})\exp \left(\mathrm{j}{k}_n{\displaystyle \raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$\mathrm{2}$}\right.}\right),

(3)E_{rc}={(\mathrm{1}-\gamma )}^{\raisebox{1ex}{$\mathrm{1}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{2}$}\right.}[\mathrm{j}\sqrt{k_{\mathrm{2}}}{E}_{\mathrm{i}2}+\sqrt{(\mathrm{1}-k_{\mathrm{2}})}{E}_{rb}],

(4)E_{rd}=E_{rc}\exp (-\alpha {\displaystyle \raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$\mathrm{4}$}\right.})\exp \left(\mathrm{j}{k}_n{\displaystyle \raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$\mathrm{2}$}\right.}\right).

The field at the through port is

(5)E_{\mathrm{t}}={(\mathrm{1}-\gamma )}^{\raisebox{1ex}{$\mathrm{1}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{2}$}\right.}[\sqrt{(\mathrm{1}-k_{\mathrm{1}})}{E}_{\mathrm{i}\mathrm{1}}+\mathrm{j}\sqrt{k_{\mathrm{1}}}{E}_{rd}].

The field at the drop port is

(6)E_{\mathrm{d}}={(\mathrm{1}-\gamma )}^{\raisebox{1ex}{$\mathrm{1}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{2}$}\right.}[\sqrt{(\mathrm{1}-k_{\mathrm{2}})}{E}_{\mathrm{i2}}+\mathrm{j}\sqrt{k_{\mathrm{2}}}{E}_{rb}].

For simplification, let us consider

D={(\mathrm{1}-\gamma )}^{\raisebox{1ex}{$\mathrm{1}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{2}$}\right.},x=D\exp (-\alpha {\displaystyle \frac{L}{\mathrm{4}}}),\mathrm{and}\varphi ={\displaystyle \frac{k_{n}L}{\mathrm{2}}}.

By solving Eqs. (1)–(6) [19,20], the through port (TP) and drop port (DP) fields are obtained as

(7)E_{\mathrm{t}}={\displaystyle \frac{D\sqrt{\mathrm{1}-k_{\mathrm{1}}}-D\sqrt{\mathrm{1}-k_{\mathrm{2}}}{x}^{\mathrm{2}}{\exp }^{\mathrm{2}}(j\varphi )}{\mathrm{1}-\sqrt{\mathrm{1}-k_{\mathrm{1}}}\sqrt{\mathrm{1}-k_{\mathrm{2}}}{x}^{\mathrm{2}}{\exp }^{\mathrm{2}}(j\varphi )}}{E}_{\mathrm{i1}}+{\displaystyle \frac{-D\sqrt{k_{\mathrm{1}}{k}_{\mathrm{2}}}\exp (\mathrm{j}\varphi )}{\mathrm{1}-\sqrt{\mathrm{1}-k_{\mathrm{1}}}\sqrt{\mathrm{1}-k_{\mathrm{2}}}{x}^{\mathrm{2}}{\exp }^{\mathrm{2}}(\mathrm{j}\varphi )}}{E}_{\mathrm{i2}},

(8)E_{\mathrm{d}}={\displaystyle \frac{-D\sqrt{k_{\mathrm{1}}{k}_{\mathrm{2}}}x\exp (\mathrm{j}\varphi )}{\mathrm{1}-\sqrt{\mathrm{1}-k_{\mathrm{1}}}\sqrt{\mathrm{1}-k_{\mathrm{2}}}{x}^{\mathrm{2}}{\exp }^{\mathrm{2}}(\mathrm{j}\varphi )}}{E}_{\mathrm{i1}}+{\displaystyle \frac{D\sqrt{\mathrm{1}-k_{\mathrm{1}}}-D\sqrt{\mathrm{1}-k_{\mathrm{2}}}{x}^{\mathrm{2}}{\exp }^{\mathrm{2}}(\mathrm{j}\varphi )}{\mathrm{1}-\sqrt{\mathrm{1}-k_{\mathrm{1}}}\sqrt{\mathrm{1}-k_{\mathrm{2}}}{x}^{\mathrm{2}}{\exp }^{\mathrm{2}}(\mathrm{j}\varphi )}}{E}_{\mathrm{i2}}.

The switching phenomenon of MRR can be described by the above mentioned equations. The cascaded arrangement of MRR is used further to design all-optical devices. Equations (7) and (8) can be used to analyze the switching phenomenon of MRR. A temporary blue shift phenomenon at the wavelength of 1550 nm is observed. The MRR structure consists of GaAs–AlGaAs; it is assumed that optical signal is not applied at the drop port. The coupling coefficients, k₁ and k₂, are assumed to be 0.25; attenuation coefficient \alpha =\mathrm{0.0005}\hspace{0.17em}{\mathrm{\mu m}}^{-\mathrm{1}}, insertion loss γ=5%, radius r = 3.05 µm, and the effective cross-sectional area is 29.20 µm².

Figure 2(a) shows the switching phenomenon of MRR, where the input optical signal switches between the output at through and drop ports.

Fig.2 (a) Switching phenomenon of MRR. (b) Normalized output power at through and drop ports at the wavelength of 1550 nm. (c) Variation in the phase shift with the average amount of pump power inside the ring resonator

Full size|PPT slide

However, a variation in the refractive index Δn is represented by Eq. (9) [21].

(9)△n=-[\mathrm{8.8}\times {\mathrm{10}}^{-\mathrm{22}}{\displaystyle \frac{\beta t_{\mathrm{p}}{}^{\mathrm{2}}}{\mathrm{2}h\nu \sqrt{\mathrm{\pi }{s}^{\mathrm{2}}}}}{p}^{\mathrm{2}}{}_{\mathrm{avg}}+\mathrm{8.5}\times {\mathrm{10}}^{-\mathrm{22}}{\left({\displaystyle \frac{\beta t_{\mathrm{p}}{}^{\mathrm{2}}}{\mathrm{2}h\nu \sqrt{\mathrm{\pi }{s}^{\mathrm{2}}}}}{p}^{\mathrm{2}}{}_{\mathrm{avg}}\right)}^{\mathrm{0.8}}].

Higher extinction ratio (ER) helps MRR to achieve ultra-fast switching. ER is defined as

(10)\mathrm{ER(dB})=\mathrm{10}\lg ({\displaystyle \frac{{{\displaystyle P}}_{\min }^{\mathrm{1}}}{{{\displaystyle P}}_{\max }^0}}),

where {{\displaystyle P}}_{\min }^{\mathrm{1}} and {{\displaystyle P}}_{\max }^{\mathrm{0}} represent the minimum and maximum peak intensities, i.e., high (1) and low (0), respectively [22].

Using Eqs. (1)–(9), an appropriate blue shift phenomenon is obtained at the resonance wavelength λ=1550 nm. The following parameters are considered for the simulation purpose: \beta =\mathrm{7.9}\times {\mathrm{10}}^{-\mathrm{10}}\mathrm{cm/W}, t (pulse width at half power peak) = 100 fs, t_p (photon life time) = 12.5 ns, h\nu =\mathrm{49.725}\times {\mathrm{10}}^{-\mathrm{20}}\mathrm{J} ,n_{\mathrm{2}}=\mathrm{4}\times {\mathrm{10}}^{-\mathrm{18}}{\mathrm{m}}^2\mathrm{/W}.The normalized output response at through and drop ports of MRR is shown in Fig. 2(b).

On the basis of the discussed parameters, a MATLAB simulation was performed for a different magnitude of the average pump power. Figure 2(c) suggests that the 2.552-mW amount of the average pump power is sufficient for the π amount of the phase shift; however, the average pump power of 1.82 mW has been reported [23,24]. Thus, the specified amount of power causes an appropriate blue shift, which is perfect for the switching module. This module is capable of driving the connected MRR structures.

Clocked optical D flip-flop is the basic building block of the proposed optical sequential circuit. D flip-flop is a transparent flip-flop. When the clock signal is low, the flip-flop remains disabled; when clock signal is high, the input is transferred to the output terminal. The truth table of the D flip-flop is shown in Table 1.

The basic layout diagram of the optical clocked D flip-flop using MRR is shown in Fig. 3, where D is the continuous optical signal, and the clock signal is applied in the form of an optical pump signal. Through and add ports are connected, and the output Q_n+1 is observed at the through port of MRR [25].

Tab.1 Truth table of D flip-flop

clock	D	Qn+1
0	X	Qn
1	0	0
1	1	1

Fig.3 All-optical clocked D flip-flop using the MRR structure

Full size|PPT slide

Fig.4 Simulation result of the D flip-flop

Full size|PPT slide

From the through port to the add port, an external feedback is applied. The main aim of the feedback is to maintain the flip-flop previous state in the absence of the clock signal. Figure 4 shows the numerical simulation of the proposed D flip-flop. The first row represents the input signal D, second row represents the applied clock pulse, an updated output signal in the presence of the clock pulse is shown in the third row. The result shows that when the clock signal is high and the input pulse is set to 1, the output terminal (Q_n+1) acquires the state of the input data D. When the clock signal is zero, the output maintains the previous state. This result shows that the proposed structure works as an all-optical D flip-flop.

3 Design of a PN sequence generator using MRR

The basic digital diagram of a 4-bit PN sequence generator is shown in Fig. 5. The circuit consists of serially cascaded four D flip-flops. The outputs Q₀ and Q₁ are applied to the XOR logic gate, and the output obtained from the XOR logic gate is applied as an input of the first D flip-flop.

Fig.5 Block diagram of the 4-bit PN sequence generator

Full size|PPT slide

The PN sequence generator generates a 4-bit random sequence, whose pattern is decided by the initial bit sequence. The specific arrangement generates 15 combinations of random bit patterns. If the initial bit sequence is considered as Q_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \mathrm{0001}, then the shifting of bit sequences generates a different bit sequence, as shown in Table 2.

Tab.2 Truth table of 4-bit PN sequence generator where the initial sequence is Q_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \mathrm{0001}

clock	Q3	Q2	Q1	Q0
0	0	0	0	1
1	1	0	0	0
2	0	1	0	0
3	0	0	1	0
4	1	0	0	1
5	1	1	0	0
6	0	1	1	0
7	1	0	1	1
8	0	1	0	1
9	1	0	1	0
10	1	1	0	1
11	1	1	1	0
12	1	1	1	1
13	0	1	1	1
14	0	0	1	1
15	0	0	0	1

Table 2 shows the output sequence of the 4-bit PN sequence generator obtained from the structure shown in Fig. 5. The main objective is to implement an all-optical PN sequence generator using the proper configuration of the MRR structure. The basic module of the proposed device is the D flip-flop.

The schematic diagram of the all-optical 4-bit PN sequence generator is shown in Fig. 6. The proposed device consists of six identical MRR structures. MRR-based all-optical clocked D flip-flops, MRR1–MRR4, are connected in such a manner that the output of the first MRR works as an input for the next MRR. MRR1– MRR4 are excited by the same.

An optical clocked pump signal in the form of pulsed laser is represented as the ‘CLK’ signal. The main objective of MRR1–MRR4 is to shift the optical signal from input port to the output port of the optically clocked D flip-flop. A continuous wave optical signal is applied at the input of MRR5. MRR5 is modulated by an optical pump pulse Q₁; at through and drop ports, Q₁ and {{\displaystyle \bar{Q}}}_{\mathrm{1}} are observed. The through port output of MRR5 works as an input for the input port of MRR6; the drop port output of MRR5 work as an input for the add port of MRR6. MRR6 is modulated with the pump signal Q₀; the optical pulse obtained at the drop port of MRR6 is the XOR equivalent of Q₀ and Q₁. Optical signals Q₁ and Q₀ can be amplified by the wavelength conversion mechanism using cross-gain and cross-phase modulation in a semiconductor optical amplifier [26]. The amplified signals are further applied to MRR6 and MRR5, respectively. The optical signal obtained from the drop port of MRR6 behaves as the input signal to the input port of MRR1. The operation of the proposed device is all-optical; optoelectronic conversion is not needed, and switching is in the picosecond range. The data rate of all-optical shift registers using MRR is reported as 100 Gb/s [24]. The proposed device is the further implementation of an all-optical shift register using MRR, although we are computing XOR between two optical signals Q₁ and Q₀; owing to this computation, some variation in speed is expected; thus, the data rate will be nearly 100 Gb/s. In addition, data rate can be calculated using Eq. (11) [24]. The obtained value depends on the coupling coefficient (k), dimensions of MRR, and the absorption coefficient (a),

(11)T={\displaystyle \frac{Y^{\mathrm{2}}}{\mathrm{1}-\mathrm{2}X\cos \varphi +X^{\mathrm{2}}}},

where X={\cos }^{\mathrm{2}}k\exp (-\alpha \mathrm{\pi }r),Y={\sin }^{\mathrm{2}}k\exp (-\alpha \mathrm{\pi }{\displaystyle \raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$\mathrm{2}$}\right.}),\hspace{0.17em}\mathrm{and}\hspace{0.17em}\varphi ={\eta }_{\mathrm{eff}}{\displaystyle \frac{\mathrm{4}{\mathrm{\pi }}^{\mathrm{2}}r}{\lambda }}.

Fig.6 Layout diagram of all-optical 4-bit PN sequence generator

Full size|PPT slide

The mathematical model of the proposed PN sequence generator can be described using Eqs. (1)–(8). The simulated result of the proposed device is shown in Fig. 7.

Fig.7 Simulated results describe the output state for the clock pulses 1 to 15. (a) Output state at the 0th clock pulse Q_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \text{'}\mathrm{0001}\text{'}. (b) Output state at the 1st clock pulse Q_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \text{'}\mathrm{1000}\text{'}. (c) Output state at the 2nd clock pulse Q_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \text{'}\mathrm{0100}\text{'}. (d) Output state at the 3rd clock pulse Q_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \text{'}\mathrm{0010}\text{'}. (e) Output state at the 4th clock pulse Q_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \text{'}\mathrm{1001}\text{'}.(f) Output state at the 5th clock pulseQ_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \text{'}\mathrm{1100}\text{'}. (g) Output state at the 6th clock pulseQ_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \text{'}\mathrm{0110}\text{'}.(h) Output state at the 7th clock pulse Q_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \text{'}1011\text{'}.(i) Output state at the 8th clock pulseQ_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \text{'}\mathrm{0101}\text{'}. (j) Output state at the 9th clock pulse Q_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \text{'}\mathrm{1010}\text{'}.(k) Output state at the 10th clock pulse Q_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \text{'}\mathrm{1101}\text{'}. (l) Output state at the 11th clock pulse Q_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \text{'}\mathrm{1110}\text{'}. (m) Output state at the 12th clock pulse Q_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \text{'}\mathrm{1111}\text{'}. (n) Output state at the 13th clock pulse Q_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \text{'}\mathrm{0111}\text{'}. (o) Output state at the 14th clock pulse Q_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \text{'}\mathrm{0011}\text{'}. (p) Output state at the 15th clock pulseQ_{\mathrm{3}}{Q}_{\mathrm{2}}{Q}_{\mathrm{1}}{Q}_{\mathrm{0}}\to \text{'}\mathrm{0001}\text{'}

Full size|PPT slide

The proposed MATLAB simulation result can be verified using Table 2, which shows that the proposed device is suitable for the generation of appropriate result associated with the 4-bit all-optical PN sequence generator.

4 Conclusions

An interesting concept for the generation of an all-optical PN sequence is presented, where the cascaded units of MRRs are used. The proposed scheme can be successfully extended and implemented for the higher order by the proper incorporation of MRR. The simplicity and flexibility of the proposed design make it suitable for practical applications. This device can revolutionize the all-optical communication network. The similarity between analytical and simulated results confirms the accuracy of the proposed device.

References

1 Haas S M, Shapiro J H. Capacity of wireless optical communications. IEEE Journal on Selected Areas in Communications, 2003, 21(8): 1346–1357

2 Maia Borges R, Cerqueira Sodre Junior A. Reconfigurable optical-wireless communications for future generations. IEEE Latin America Transactions, 2015, 13(11): 3580–3584

3 Chaaban A, Morvan J M, Alouini M S. Free-space optical communications: capacity bounds, approximations, and a new sphere-packing perspective. IEEE Transactions on Communications, 2016, 64(3): 1176–1191

4 Chen R Y, Yang Z Y. CMOS transimpedance amplifier for gigabit-per-second optical wireless communications. IEEE Transactions on Circuits and Wystems. II: Express Briefs, 2016, 63(5): 418–422

5 Anguita J A, Djordjevic I B, Neifeld M A, Vasic B V. Shannon capacities and error-correction codes for optical atmospheric turbulent channels. Journal of Optical Networking, 2005, 4(9): 586–601

6 Niehusmann J, Vörckel A, Bolivar P H, Wahlbrink T, Henschel W, Kurz H. Ultrahigh-quality-factor silicon-on-insulator microring resonator. Optics Letters, 2004, 29(24): 2861–2863

PMID

7 Bogaerts W, De Heyn P, Van Vaerenbergh T, De Vos K, Kumar Selvaraja S, Claes T, Dumon P, Bienstman P, Van Thourhout D, Baets R. Silicon microring resonators. Laser & Photonics Reviews, 2012, 6(1): 47–73

8 Grover R, Absil P P, Van V, Hryniewicz J V, Little B E, King O, Calhoun L C, Johnson F G, Ho P T. Vertically coupled GaInAsP--InP microring resonators. Optics Letters, 2001, 26(8): 506–508

PMID

9 Ding Y, Ou H, Xu J, Xiong M, An Y, Hu H, Galili M, Riesgo A L, Seoane J, Yvind K, Oxenløwe L K, Zhang X, Huang D, Peucheret C. Linear all-optical signal processing using silicon micro-ring resonators. Frontiers of Optoelectronics, 2016, 9(3): 362–376

10 Lipson M. Guiding, modulating, and emitting light on silicon-challenges and opportunities. Journal of Lightwave Technology, 2005, 23(12): 4222–4238

11 Xiao H, Li D, Liu Z, Han X, Chen W, Zhao T, Tian Y, Yang J. Experimental realization of a CMOS-compatible optical directed priority encoder using cascaded micro-ring resonators. Nanophotonics, 2018, 7(4): 727–733

12 Ishida K. Synchronous pseudo-noise code sequence generation circuit. U.S. Patent 5519736, 1996

13 Xu Q, Lipson M. All-optical logic based on silicon micro-ring resonators. Optics Express, 2007, 15(3): 924–929

PMID

14 Lee J H, Song I, Park S R, Lee J. Rapid acquisition of PN sequences with a new decision logic. IEEE Transactions on Vehicular Technology, 2004, 53(1): 49–60

15 Yang L, Guo C, Zhu W, Zhang L, Sun C. Demonstration of a directed optical comparator based on two cascaded microring resonators. IEEE Photonics Technology Letters, 2015, 27(8): 809–812

16 Zhao Y, Wang X, Gao D, Dong J, Zhang X. On-chip programmable pulse processor employing cascaded MZI-MRR structure. Frontiers of Optoelectronics, 2019, 12(2): 148–156

17 Little B E, Chu S T, Pan W, Kokubun Y. Microring resonator arrays for VLSI photonics. IEEE Photonics Technology Letters, 2000, 12(3): 323–325

18 Condo C, Gross W J. Pseudo-random Gaussian distribution through optimised LFSR permutations. Electronics Letters, 2015, 51(25): 2098–2100

19 Rabus D G. Realization of optical filters using ring resonators with integrated semiconductor optical amplifiers in GaInAsP /InP. Dissertation for the Doctoral Degree. Berlin: Technische Universität Berlin, 2002

20 Rakshit J K, Chattopadhyay T, Roy J N. Design of ring resonator based all-optical switch for logic and arithmetic operations–a theoretical study. Optik, 2013, 124(23): 6048–6057

21 Bharti G K, Rakshit J K. Design and performance analysis of high speed optical binary code converter using micro-ring resonator. Fiber and Integrated Optics, 2018, 37(2): 103–121

22 Houbavlis T, Zoiros K E, Kanellos G, Tsekrekos C. Performance analysis of ultrafast all-optical Boolean XOR gate using semiconductor optical amplifier-based Mach-Zehnder interferometer. Optics Communications, 2004, 232(1–6): 179–199

23 Rakshit J K, Roy J N. Silicon micro-ring resonator-based all-optical digital-to-analog converter. Photonic Network Communications, 2017, 34(1): 84–92

24 Rakshit J K, Roy J N. Design of all-optical universal shift register using nonlinear microring resonators. Journal of Computational Electronics, 2016, 15(4): 1450–1461

25 Rakshit J K, Roy J N, Chattopadhyay T. A theoretical study of all-optical clocked D flip flop using single micro-ring resonator. Journal of Computational Electronics, 2014, 13(1): 278–286

26 Asghari M, White I H, Penty R V. Wavelength conversion using semiconductor optical amplifiers. Journal of Lightwave Technology, 1997, 15(7): 1181–1190