

Frontiers of Optoelectronics >
Characteristics of laser induced discharge tin plasma and its extreme ultraviolet radiation
Received date: 16 Sep 2019
Accepted date: 23 Dec 2019
Published date: 15 Sep 2021
Copyright
In this paper, a CO2 laser induced discharge plasma extreme ultraviolet (EUV) source experimental device was established. The optical emission spectroscopy was used to diagnose the characteristics of the plasma, and the evolution of electron temperature and electron density with time was obtained. The influence of discharge voltage on plasma parameters was analyzed and discussed. The EUV radiation characteristics of the plasma were investigated by self-made grazing incidence EUV spectrometer. The EUV radiation intensity and conversion efficiency were discussed.
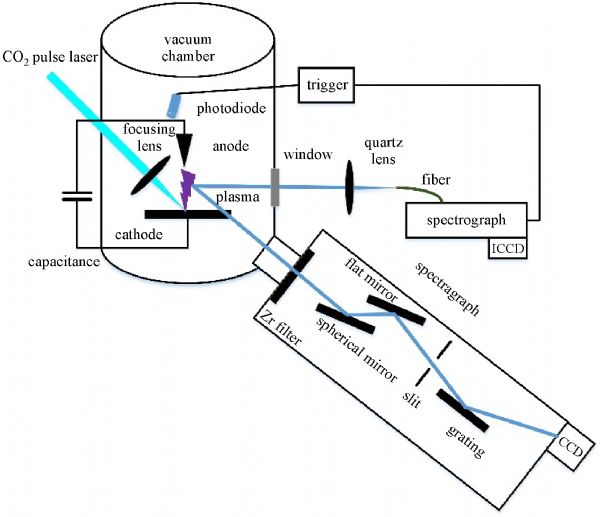
Junwu WANG , Xinbing WANG , Duluo ZUO . Characteristics of laser induced discharge tin plasma and its extreme ultraviolet radiation[J]. Frontiers of Optoelectronics, 2021 , 14(3) : 352 -359 . DOI: 10.1007/s12200-020-0964-8
| 1 |
Wagner C, Harned N. Lithography gets extreme. Nature Photonics, 2010, 4(1): 24–26
|
| 2 |
van de Kerkhof M, Jasper H, Levasier L, Peteers R, van Es R, Bosker J, Zdravkov A, Lenderink E, Evangelista F, Broman P, Bilski B, Last T. Enabling sub-10 nm node lithography: presenting the NXE: 3400B EUV scanner. In: Proceedings of SPIE 10143, Extreme Ultraviolet (EUV) Lithography VIII. San Jose: SPIE, 2017, 101430D
|
| 3 |
Meiling H, Buzing N, Cummings K, Harned N, Hultermans B, de Jonge R, Kessels B, Kürz P, Lok S, Lowisch M, Mallman J, Pierson B, Wagner C, van Dijk A, van Setten E, ZimmermSan an J. EUVL system: moving towards production. In: Proceedings of SPIE 7271, Alternative Lithographic Technologies. San Jose: SPIE, 2009, 727102
|
| 4 |
O’Sullivan G, Li B, D’Arcy R, Dunne P, Hayden P, Kilbane D, McCormack T, Ohashi H, O’Reilly F, Sheridan P, Sokell E, Suzuki C, Higashiguchi T. Spectroscopy of highly charged ions and its relevance to EUV and soft X-ray source development. Journal of Physics B, Atomic, Molecular, and Optical Physics, 2015, 48(14): 144025
|
| 5 |
Fomenkov I V, Ershov Al, Partlo W N,Myers D W, Sandstrom R L, Bowering N R, Vaschenko G O, Khodykin O V, Bykanov A N, Srivastava S N, Ahmad I, Rajyaguru C, Golich D J, Dea S D, Hou R r, O’Brien K M, Dunstan W J, Brandt D C. Laser-produced plasma light sources for EUVL. In: Proceedings of SPIE 7636, Extreme Ultraviolet (EUV) Lithography. San Jose: SPIE, 2010, 763639
|
| 6 |
Hotta E, Sakai Y, Hayashi Y, Niimi G, Huang B, Zhu Q S, Song I, Watanabe M. Extreme ultraviolet light sources and soft X-ray laser based on discharge produced plasma. In: Proceedings of SPIE 9524, International Conference on Optical and Photonic Engineering (icOPEN 2015). Singapore: SPIE, 2015, 95242U
|
| 7 |
Stamm U, Kleinschmidt J, Bolshukhin D, Brudermann J, Hergenhan G, Korobotchko V, Nikolaus B, Schürmann M C, Schriever G, Ziener C, Borisov V M. Development status of EUV sources for use in beta-tools and high-volume chip manufacturing tools. In: Proceedings of SPIE 6151. Emerging Lithographic Technologies X. San Jose: SPIE, 2006, 61510O
|
| 8 |
Beyene G A, Tobin I, Juschkin L, Hayden P, O’Sullivan G, Sokell E, Zakharov V S, Zakharov S V, O’Reilly F. Laser-assisted vacuum arc extreme ultraviolet source: a comparison of picosecond and nanosecond laser triggering. Journal of Physics D, Applied Physics, 2016, 49(22): 225201
|
| 9 |
Schriever G, Semprez O, Jonkers J, Yoshioka M, Apetz R. Laser-produced plasma versus laser-assisted discharge plasma: physics and technology of extreme ultraviolet lithography light sources. Journal of Micro/Nanolithography, MEMS, and MOEMS, 2012, 11(2): 021104
|
| 10 |
Teramoto Y, Narihiro Z, Yamatani D, Yokoyama T, Bessho K, Joshima Y. Development of Sn-fueled high-power DPP EUV source for enabling HVM. In: Proceedings of SPIE 6517, Emerging Lithographic Technologies XI. San Jose: SPIE, 2007, 65173R
|
| 11 |
Teramoto Y, Santos B, Mertens G, Kops R. High-radiance LDP source: clean, reliable, and stable EUV source for mask inspection. In: Proceedings of SPIE 9776, Extreme Ultraviolet (EUV) Lithography VII.San Jose: SPIE, 2016, 97760L
|
| 12 |
Tobin I, Juschkin L, Sidelnikov Y, O’Reilly F, Sheridan P, Sokell E, Lunney J G. Laser triggered Z-pinch broadband extreme ultraviolet source for metrology. Applied Physics Letters, 2013, 102(20): 203504
|
| 13 |
Turkot B, Carson S L, Lio A, Liang T, Phillips M, McCool B, Stenehjem E, Crimmins T, Zhang G J, Sivakumar S. EUV progress toward HVM readiness. In: Proceedings of SPIE 9776, Extreme Ultraviolet (EUV) Lithography VII.San Jose: SPIE, 2016, 977602
|
| 14 |
Teramoto Y, Santos B, Mertens G, Kops R. High-radiance LDP source for mask inspection application. In: Proceedings of SPIE 9048, Extreme Ultraviolet (EUV) Lithography V. San Jose: SPIE, 2014, 904813
|
| 15 |
Teramoto Y, Santos B, Mertens G, Kops R, Kops M, von Wezyk A, Bergmann K, Yabuta H, Nagano A, Ashizawa N, Taniguchi Y, Yamatani D, Shirai T, Kasama K. High-radiance LDP source for mask inspection and beam line applications. In: Proceedings of SPIE 10143, Extreme Ultraviolet (EUV) Lithography VIII. San Jose: SPIE, 2017, 101431L
|
| 16 |
Shaikh N M, Tao Y, Burdt R A, Yuspeh S, Amin N, Tillack M S. Spectroscopic analysis of temperature and density of Sn plasma produced by a CO2 laser. Journal of Applied Physics, 2010, 108(8): 083109
|
| 17 |
Wu T, Wang X, Zuo D, Lu P. Research of pulse CO2 laser produced tin plasma. In: Proceedings of SPIE 8603, High-Power Laser Materials Processing: Lasers, Beam Delivery, Diagnostics, and Applications II. San Francisco: SPIE, 2013, 86030Y
|
| 18 |
Kieft E R, van der Mullen J, Kroesen G M W, Banine V, Koshelev K N. Stark broadening experiments on a vacuum arc discharge in tin vapor. Physical Review E: Statistical, Nonlinear, and Soft Matter Physics, 2004, 70(6): 066402
|
| 19 |
Kieft E R, van der Mullen J, Kroesen G M W, Banine V, Koshelev K N. Characterization of a vacuum-arc discharge in tin vapor using time-resolved plasma imaging and extreme ultraviolet spectrometry. Physical Review E: Statistical, Nonlinear, and Soft Matter Physics, 2005, 71(2): 026409
|
| 20 |
Zhu Q, Muto T, Yamada J, Kishi N, Watanabe M, Okino A, Horioka K, Hotta E. Estimation of electron temperature and density of the decay plasma in a laser-assisted discharge plasma extreme ultraviolet source by using a modified Stark broadening method. Journal of Applied Physics, 2011, 110(12): 123302
|
| 21 |
Tobin I. Optical and EUV studied of laser triggered Z-pinch discharges. Dissertation for the Doctoral. Dublin, Ireland: Trinity College, 2014, 20–300
|
| 22 |
Djeniže S, Srećković A, Nikolić Z. On the Sn I and Sn II Stark broadening. Journal of Physics B, Atomic, Molecular, and Optical Physics, 2006, 39(14): 3037–30451
|
| 23 |
Griem H R. Semiempirical formulas for the electron-impact widths and shifts of isolated ion lines in plasmas. Physical Review, 1968, 165(1): 258–266
|
| 24 |
Aydin Ü, Roth P, Gehlen C D, Noll R. Spectral line selection for time-resolved investigations of laser-induced plasmas by an iterative Boltzmann plot method. Spectrochimica Acta Part B, Atomic Spectroscopy, 2008, 63(10): 1060–1065
|
| 25 |
Miller M H, Roig R A, Bengtson R D. Experimental transition probabilities and Stark-broadening parameters of neutral and singly ionized tin. Physical Review A, 1979, 20(2): 499–506
|
| 26 |
Coons R W, Harilal S S, Polek M, Hassanein A. Spatial and temporal variations of electron temperatures and densities from EUV-emitting lithium plasmas. Analytical and Bioanalytical Chemistry, 2011, 400(10): 3239–3246
|
| 27 |
Zhu Q, Yamada J, Kishi N, Hosokai T, Watanabe M, Okino A, Horioka K, Hotta E. Pinch dynamics of the 13.5 nm EUV-emitting plasma in a LA-DPP source. In: Proceedings of 2011 Academic International Symposium on Optoelectronics and Microelectronics Technology. Haerbin, 2011, 172–175
|
| 28 |
Zhang J, Gu P J. An approximate method for calculating ionization state of local thermodynamic equilibrium and nonlocal thermodynamic equilibrium plasma. Chinese Journal of Computational Physics, 1987, 4(1): 1–16 (in Chinese)
|
/
| 〈 |
|
〉 |