Interface phonon polariton coupling to enhance graphene absorption

Abstract

Here we present a graphene photodetector of which the graphene and structural system infrared absorptions are enhanced by interface phonon polariton (IPhP) coupling. IPhPs are supported at the SiC/AlN interface of device structure and used to excite interband transitions of the intrinsic graphene under gated-field tuning. The simulation results show that at normal incidence the absorbance of graphene or system reaches up to 43% or closes to unity in a mid-infrared frequency range. In addition, we found the peak-absorption frequency is mainly decided by the AlN thickness, and it has a red-shift as the thickness decreases. This structure has great application potential in graphene infrared detection technology.

Key words： interface phonon polariton (IPhP); infrared absorption enhancement; graphene photodetector

1 Introduction

Graphene, consisting of one monolayer of carbon atoms arranged in a honeycomb lattice, has important application prospects in materials science, micro-nano processing, energy, biomedicine and drug delivery [1–6]. It is considered to be a revolutionary material in the future with excellent optical, electrical and mechanical properties. Because of the special band structure of graphene, wide spectral absorption can be achieved, but its absorbance is only about 2.3% [7]. The low absorption issue is expected to be overcome for the high responsivity requirement of infrared photodetector.

Optical confinement effects of the surface plasmon polariton (SPP) and surface phonon polariton (SPhP) can be used to significantly enhance the light-matter interaction. As an important area of nanophotonic topic, SPP is widely used in the fields of enhanced sensing, optical radiation, photodetection, and surface-enhanced spectroscopy [8–14]. First of all, the SPP technology is under consideration for enhancing the graphene infrared absorption. However, SPP is generally excited on the surface of noble metals like Au, Ag, and Cu, etc., and a low quality-factor (Q-factor) is the characteristics when the SPP resonance works at an optical frequency, which limits the further development for SPP applications. It has been found that polar crystals like III-V semiconductors have a high reflectivity in the mid-infrared or far-infrared region. For example, SiC has a reflectance close to 100% in the wavelength range from λ = 10.32 to 12.61 mm [15]. In this spectral region, the polar crystal has a negative dielectric constant, and SPhP modes will be supported at its interface. Derived from optical phonons with long lifetimes, the SPhP mode inherits the characteristics of high Q-factor from phonons. Based on these unique advantages, SPhP becomes an alternative of SPP in the mid-infrared spectrum with a broad prospect.

Similar to SPP, the surface wave frequency must be near the SPhP characteristic frequency to produce significant absorption. The essence of SPhP is the atoms collective oscillation mode which is coupled with the incident electromagnetic wave. As the incident electromagnetic wave interacts with the lattice vibration in the semiconductor, it leads to the transition of the phonon state and the absorption of light. It is impossible to couple the incident light wave into SPhP directly because the propagation wave number of SPhP is far larger than that of free space light. Therefore, it is necessary to meet the wave vector matching condition with the coupling device or by introducing special structures to achieve exciting the SPhP mode. The common excitation approaches are prism coupling, grating coupling, and near-field excitation.

In this paper, we propose an infrared detector based on intrinsic graphene and utilize the optical confinement effect of interface phonon polaritons (IPhPs) to increase the graphene absorbance.

2 Design of the detector

We have designed a structure and explored the graphene and structural system absorption properties by the finite-difference time-domain (FDTD) method. The detector consists of Au gratings on the top of SiC/AlN/graphene/BN stacked structure as shown in Fig. 1. The SiC/AlN is used to support IPhP. The light source is selected as the plane wave which is incident from top to bottom, and periodic boundary conditions are adopted in the x-axis direction and perfect matched layer boundary conditions in the y-axis direction. Using the metal grating on the surface, the light meets the wave vector matching condition, and couples to SiC/AlN to excite IPhP. In consequence, it increases the graphene absorbance.

Fig.1 Schematic of device structure.  The thickness of SiC layer, graphene layer and BN layer are d_SiC = 350 mm, d_G = 2 nm, d_BN = 13 nm, respectively. d_AlN, which represents the thickness of AlN, is a variable. The Au grating has a period of p = 10 mm, a width of w = 5.72 mm, and a thickness of d_Au = 100 nm

Full size|PPT slide

In this simulation, the surface conductivity of graphene s_gis derived using the well-known Kubo formula and written as [16–20]

(1){{\displaystyle \sigma }}_g={\displaystyle \frac{{je}^{\mathrm{2}}}{\pi {\hslash }^{\mathrm{2}}(\omega -j\mathrm{2})}}{{\displaystyle \int }}_{\mathrm{0}}^{\infty }\xi \left({\displaystyle \frac{{{\displaystyle \partial f}}_d(\xi ,{{\displaystyle E}}_F,T)}{\partial \xi }}-{\displaystyle \frac{{{\displaystyle \partial f}}_d(-\xi ,{{\displaystyle E}}_F,T)}{\partial \xi }}\right)\mathrm{d}\xi -{\displaystyle \frac{{je}^{\mathrm{2}}(\omega -j\mathrm{2})}{\pi {\hslash }^{\mathrm{2}}}}{{\displaystyle \int }}_{\mathrm{0}}^{\infty }{\displaystyle \frac{{{\displaystyle \partial f}}_d(-\xi ,{{\displaystyle E}}_F,T)-{{\displaystyle f}}_d(\xi ,{{\displaystyle E}}_F,T)}{{(\omega -j\mathrm{2})}^{\mathrm{2}}-\mathrm{4}{(\xi /\hslash )}^{\mathrm{2}}}}\mathrm{d}\xi ,

(2){{\displaystyle f}}_d(\xi ,{{\displaystyle E}}_F,T)={(e^{(\xi -{{\displaystyle E}}_F)/{{\displaystyle k}}_{B}T}+\mathrm{1})}^{-\mathrm{1}}.

Here, e is the electron charge, k_B is the Boltzmann constant, ћ is reduced Planck constant, T is Kelvin temperature, E_F is the Fermi level, w is the angular frequency and G is the scattering rate, xis the energy of electrons. We take G as 16.67 ps^-1 [21], and assume room temperature T = 300 K, for all simulations.

And the dielectric constant of polar crystals is written as

(3){{\displaystyle ϵ}}_{\Vert ,\perp }={{\displaystyle ϵ}}_{\infty \Vert ,\perp }+{\displaystyle \frac{{{\displaystyle ϵ}}_{\infty \Vert ,\perp }\left({{\displaystyle \omega }}_{\mathrm{LO}\Vert ,\perp }^{\mathrm{2}}-{{\displaystyle \omega }}_{\mathrm{TO}\Vert ,\perp }^{\mathrm{2}}\right)}{{{\displaystyle \omega }}_{\mathrm{TO}\Vert ,\perp }^{\mathrm{2}}-{\omega }^{\mathrm{2}}-{{\displaystyle \mathrm{i}\omega \mathrm{\Gamma }}}_{\Vert ,\perp }}},

w_TO∥,^ and w_LO∥,^ are the transverse and longitudinal optic phonon frequencies, respectively, and G_∥,^ are the phonon damping constants. For SiC, we have e_∞^ = 6.4, e_∞∥ = 7.7, w_TO^ = 797 cm^-1, w_TO∥ = 782 cm^-1, w_LO^ = 971 cm^-1, w_LO∥ = 965 cm^-1, G_∥,^ = 2.8 cm^-1 [22]. The dielectric constant of SiC is shown in Fig. 2.

Fig.2 Dielectric constant of SiC in the x direction, i.e., perpendicular to the lattice C-axis (the parallel-directional values are not plotted here). The real part (in black dot) of dielectric constant is negative while the imaginary part (in red triangle) is positive

Full size|PPT slide

3 Results and discussion

With the change of the grating period p, the simulation results are shown in Fig. 3. The absorbance varies significantly with the change of the grating period while the location l of the absorption peak is unaltered. The grating provides an extra wave vector. It meets the wave vector matching as we set the grating period p = 10 mm, which leads to the strongest vibration. Meanwhile, the phonon is excited at the interface between SiC and AlN, and the energy of the phonon is coupled into the graphene, which improves the absorption of graphene. Figure 4 is an electric field distribution diagram of a grating period p = 10 mm and a light wavelength l = 10.57 mm. The most filed are distributed in AlN and SiC, which is a feature of phonon [23].

Absorption of graphene is written as [24]

(4){{\displaystyle A}}_{\mathrm{G}}={\displaystyle \frac{\mathrm{2}\pi }{{{\displaystyle \lambda }}_{\mathrm{0}}{\left|{{\displaystyle E}}_{\mathrm{0}}\right|}^{\mathrm{2}}S{{\epsilon }_G^{\text{'}}}^{\text{'}}}}{{\displaystyle \mathrm{\iiint }}}_V{\left|{{\displaystyle E}}_G\right|}^{\mathrm{2}}\mathrm{d}V.

Equation (4) indicates that the absorbance of graphene is proportional to imaginary part of dielectric constant.

Fig.3 Effect of different grating  period p on the absorbance of graphene. The main absorption peak is located at l= 10.57 mm. The inset shows that the peak location remains unchanged at l = 10.57 mm

Full size|PPT slide

Fig.4 Electric field distribution at  l = 10.57 mm. The fields are mainly confined within AlN and SiC

Full size|PPT slide

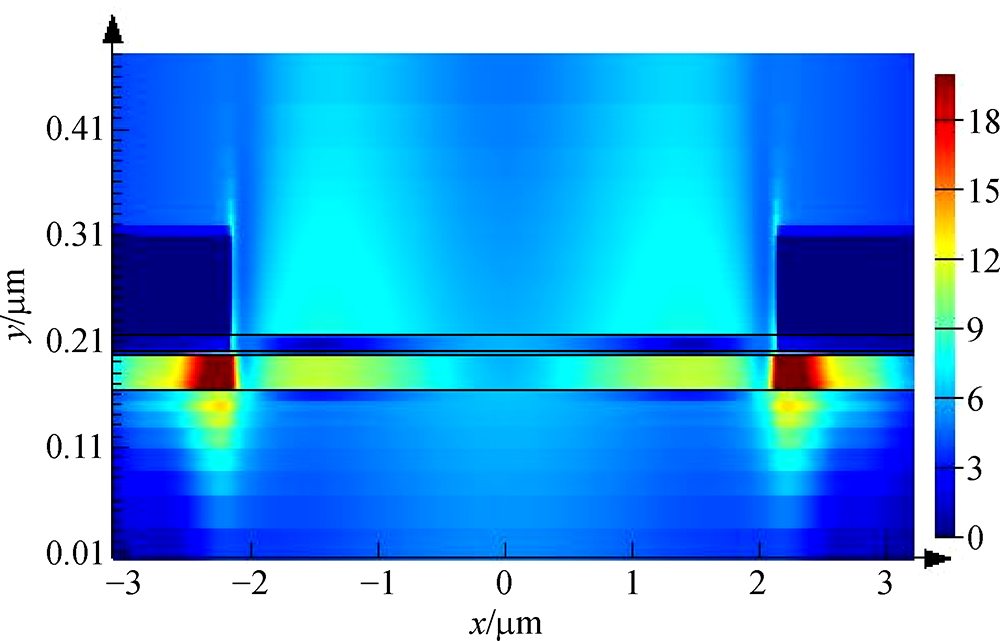
Then, we explore the influence on graphene absorption with different AlN thickness. The metal grating is chose as p = 10 mm, d_Au = 100 nm, and w = 5.72 mm. The thickness of AlN changes to d_AlN = 100, 80, 60, 40, 20 nm, while the other parameters keep unchanged. As shown in Fig. 5, the absorbance of system reaches close to 100% at l = 10.57 mm. In Fig. 6, the peak absorbance of graphene for the different AlN thickness are 28.3%, 30.8%, 34.0%, 37.5%, and 43.6%, respectively. As the thickness of AlN decreases, the absorbance of graphene increases. It is due to that as the thickness of AlN increases, the path of IPhP in AlN increases, which means more energy loss, and the energy that eventually couples into the graphene decreases. While the AlN becomes thinner, the propagation path of IPhP getting shorter, and the energy consumed by the AlN decreases; in consequence, the energy coupled into the graphene increases, resulting in an increase of the graphene absorption. In addition, we found that as the thickness of AlN decreases, the absorption peak shifts toward the long wavelength direction. This is due to that for multilayer dielectric film, the characteristic frequency of IPhP is not only related to the materials, but also to the thickness of each dielectric layer [25]. As the thickness of AlN decreases, it has an impact on the characteristic frequency of the interface phonon, which causes the resonance absorption peak red-shifted.

Fig.5 Absorbance of the structural  system with different AlN thicknesses d_AlN. The inset shows the absorption peak has a red shift as the d_AlN decreases

Full size|PPT slide

Fig.6 Graphene absorbance with  different AlN thicknesses d_AlN. The inset shows that the absorption peaks locate at l = 10.562, 10.568, 10.574, 10.580, and 10.596 mm are red-shifted with the decrease of AlN thickness

Full size|PPT slide

4 Conclusion

In summary, we presented the design of graphene photodetector based on IPhPs in mid-infrared region. With the extra wave vector provided by the grating, the light is coupled into the SiC/AlN interface to excite the IPhPs. Then, the optical confinement effects of IPhPs increase the graphene absorbance. As for the main absorption peak (l = 10.57 mm), the grating period (p) has no impact on the location, while the graphene absorbance is affected seriously. We found that the absorbance and absorption peak position of graphene change with the thickness of AlN (d_AlN), the graphene absorbance reaches 43.6% at the wavelength of l = 10.57 mm, meanwhile the system absorbance reaches 100%. Both graphene and the system’s absorption peak have a red shift as the d_AlN decreases. The remarkable enhancement in graphene absorption suggests that the IPhP structure is potentially helpful for designing high-performance graphene photodetectors.

Acknowledgements

This work was funded by the National Natural Science Foundation of China (NSFC) (Grant No. 61675080) and Fundamental Research Funds for the Central Universities (HUST: 2016YXMS021).

References

1 Parmar J, Patel S K, Ladumor M, Sorathiya V, Katrodiya D. Graphene-silicon hybrid chirped-superstructure bragg gratings for far infrared frequency. Materials Research Express, 2019, 6(6): 065606

2 Huck C, Tzschoppe M, Semenyshyn R, Neubrech F, Pucci A. Chemical identification of single ultrafine particles using surface-enhanced infrared absorption. Physical Review Applied, 2019, 11(1): 014036

3 Thomas L, Sorathiya V, Patel S K, Guo T. Graphene-based tunable near-infrared absorber. Microwave and Optical Technology Letters, 2019, 61(5): 1161–1165

4 Patel S K, Charola S, Parmar J, Ladumor M. Broadband metasurface solar absorber in the visible and near-infrared region. Materials Research Express, 2019, 6(8): 086213

5 Katrodiya D, Jani C, Sorathiya V, Patel S K. Metasurface based broadband solar absorber. Optical Materials, 2019, 89: 34–41

6 Hao R, Jin J, Wei X, Jin X, Zhang X, Li E. Recent developments in graphene-based optical modulators. Frontiers of Optoelectronics, 2014, 7(3): 277–292

7 Geim A K. Graphene: status and prospects. Science, 2009, 324(5934): 1530–1534

PMID

8 He X, Liu F, Lin F, Xiao G, Shi W. Tunable MoS₂ modified hybrid surface plasmon waveguides. Nanotechnology, 2019, 30(12): 125201

PMID

9 Shi C, He X, Peng J, Xiao G, Liu F, Lin F, Zhang H. Tunable terahertz hybrid graphene-metal patterns metamaterials. Optics & Laser Technology, 2019, 114: 28–34

10 Yi Z, Liang C, Chen X, Zhou Z, Tang Y, Ye X, Yi Y, Wang J, Wu P. Dual-band plasmonic perfect absorber based on graphene metamaterials for refractive index sensing application. Micromachines, 2019, 10(7): 443

PMID

11 Cen C, Zhang Y, Liang C, Chen X, Yi Z, Duan T, Tang Y, Ye X, Yi Y, Xiao S. Numerical investigation of a tunable metamaterial perfect absorber consisting of two-intersecting graphene nanoring arrays. Physics Letters A, 2019, 383(24): 3030–3035

12 Cen C, Yi Z, Zhang G, Zhang Y, Liang C, Chen X, Tang Y, Ye X, Yi Y, Wang J, Hua J. Theoretical design of a triple-band perfect metamaterial absorber in the THz frequency range. Results in Physics, 2019, 14: 102463

13 Patel S K, Ladumor M,Sorathiya V, Guo T. Graphene based tunable grating structure. Materials Research Express, 2019, 6(2): 025602

14 Patel S K, Ladumor M, Parmar J, Guo T. Graphene-based tunable reflector superstructure grating. Applied Physics. A, Materials Science & Processing, 2019, 125(8): 574

15 Le Gall J, Olivier M, Greffet J J. Experimental and theoretical study of reflection and coherent thermal emission by a SiC grating supporting a surface-phonon polariton. Physical Review B, 1997, 55(15): 9195–9199

16 Hanson G W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. Journal of Applied Physics, 2008, 103(6): 064302

17 He X, Liu F, Lin F, Shi W. Investigation of terahertz all-dielectric metamaterials. Optics Express, 2019, 27(10): 13831–13844

PMID

18 Achilli S, Cavaliere E, Nguyen T H, Cattelan M, Agnoli S. Growth and electronic structure of 2D hexagonal nanosheets on a corrugated rectangular substrate. Nanotechnology, 2018, 29(48): 485201

PMID

19 Hanson G W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. Journal of Applied Physics, 2008, 103(6): 064302

20 Peres N M R, Guinea F, Castro Neto A H. Electronic properties of disordered two-dimensional carbon. Physical Review B, 2006, 73(12): 125411

21 Zhang Q, Li X, Hossain M, Xue Y, Zhang J, Song J, Liu J, Turner M D, Fan S, Bao Q, Gu M. Graphene surface plasmons at the near-infrared optical regime. Scientific Reports, 2014, 4: 6559

22 Tiwald T E, Woollam J A, Zollner S, Christiansen J, Gregory R B, Wetteroth T, Wilson S R, Powell A R. Carrier concentration and lattice absorption in bulk and epitaxial silicon carbide determined using infrared ellipsometry. Physical Review B, 1999, 60(16): 11464–11474

23 Huang K C, Bienstman P, Joannopoulos J D, Nelson K A, Fan S. Phonon-polariton excitations in photonic crystals. Physical Review B, 2003, 68(7): 075209

24 Zhang Y, Meng D, Li X, Yu H, Lai J, Fan Z, Chen C. Significantly enhanced infrared absorption of graphene photodetector under surface-plasmonic coupling and polariton interference. Optics Express, 2018, 26(23): 30862–30872

PMID

25 Lee S C, Ng S S, Abu Hassan H, Hassan Z, Dumelow T. Calculation of dispersion of surface and interface phonon polariton resonances in wurtzite nsemiconductor multilayer system taking damping effects into accout. Thin Solid Films, 2014, 551: 114–119