Catalyst particle shapes and pore structure engineering for hydrodesulfurization and hydrodenitrogenation reactions

Abstract

Catalyst particle shapes and pore structure engineering are crucial for alleviating internal diffusion limitations in the hydrodesulfurization (HDS)/hydrodenitrogenation (HDN) of gas oil. The effects of catalyst particle shapes (sphere, cylinder, trilobe, and tetralobe) and pore structures (pore diameter and porosity) on HDS/HDN performance at the particle scale are investigated via mathematical modeling. The relationship between particle shape and effectiveness factor is first established, and the specific surface areas of different catalyst particles show a positive correlation with the average HDS/HDN reaction rates. The catalyst particle shapes primarily alter the average HDS/HDN reaction rate to adjust the HDS/HDN effectiveness factor. An optimal average HDS/HDN reaction rate exists as the catalyst pore diameter and porosity increase, and this optimum value indicates a tradeoff between diffusion and reaction. In contrast to catalyst particle shapes, the catalyst pore diameter and the porosity of catalyst particles primarily alter the surface HDS/HDN reaction rate to adjust the HDS/HDN effectiveness factor. This study provides insights into the engineering of catalyst particle shapes and pore structures for improving HDS/HDN catalyst particle efficiency.

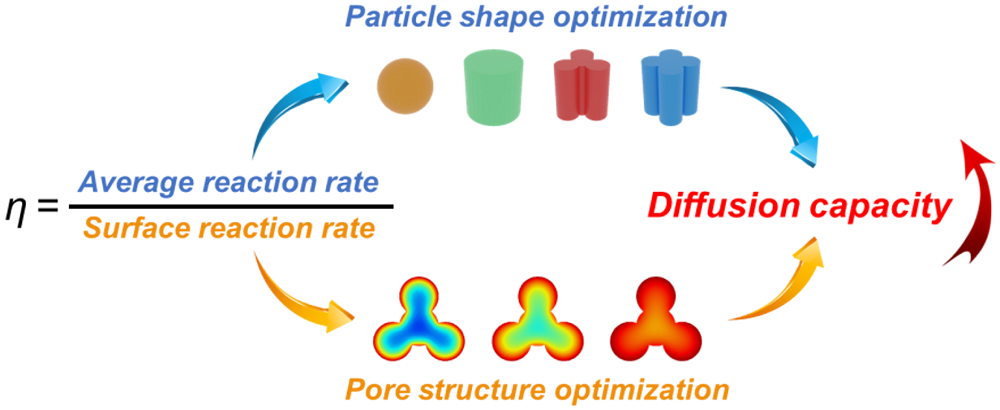
Key words： hydrodesulfurization; hydrodenitrogenation; particle shape; pore structure

1 Introduction

The hydrotreating (HDT) of heavy crude oil for removing undesired impurities (metal, sulfur, nitrogen, aromatics, etc.) is crucial in satisfying stricter fuel regulations, particularly for limiting the contents of sulfur and nitrogen compounds [1–8]. Hydrodesulfurization (HDS) and hydrodenitrogenation (HDN) technologies are typically employed to eliminate the corresponding sulfur and nitrogen impurities with extruded Co–Mo or Ni–Mo alumina-supported catalyst particles in commercial plants. Numerous experimental [9,10] and simulation studies [11–13] have been performed to optimize the properties of catalysts and reactor operation conditions to improve HDS and HDN performance.

Industrial HDS and HDN catalysts are typically pelletized into millimeter-sized particles of different shapes before being loaded into HDT reactors to reduce the reactor pressure drop. Meanwhile, HDS and HDN are relatively rapid reactions. Therefore, HDS and HDN are inevitably limited by internal diffusion. In this respect, the optimization of catalyst physical properties (particle shapes and pore structures) appears to be more urgent than the optimization of catalyst chemical compositions (active components, promoters, and supports) for maximizing catalyst utilization and prolong the catalyst lifetime.

Typical industrial HDS and HDN catalyst particle shapes are designed in trilobe and tetralobe shapes to reduce pressure drop and facilitate the diffusion of reactants, and numerous studies focusing on the relationship between particle shape and HDS/HDN reaction performance have been performed in recent decades [14–17]. Ancheyta et al. [14] developed theoretical equations to calculate the geometric volume and external area of HDT lobe-shaped catalyst particles; furthermore, they [15] investigated the effects of catalyst particles of different shapes on HDS performance. However, the particle shape was adjusted based on the particle equivalent diameter instead of the actual three-dimensional geometry. Hernández et al. [16] proposed an approach that simultaneously uses one-dimensional and generalized cylindrical models to evaluate the effectiveness factor of HDS trilobular catalyst particles. Kolitcheff et al. [17] reported that the particle shape factor and particle size distribution can significantly affect the mass transfer behavior of HDS catalyst supports; furthermore, they indicated that industrial catalysts with trilobe and tetralobe shapes are required for the simulation and optimization of HDS. Therefore, a more reliable model that simulates the HDS/HDN of catalyst particles with complex shapes should be developed.

In addition to the optimization of catalyst particle shapes, the pore structures of catalyst particles have been investigated extensively to alleviate the internal diffusion limitation [18–23]. Zhou et al. [22] synthesized a well-organized mesoporous NiMo/SiO₂ opal catalyst and discovered that the open-pore system of the catalyst rendered the reactive surface more accessible to the reactants during HDS. Lv et al. [23] discovered that CoMo/ZS-PL-γ-Al₂O₃ (CoMo/AZS-PL) catalysts with short unrestricted diffusion path lengths exhibited better HDS performance than CoMo/ZS-LR-γ-Al₂O₃ (CoMo/AZS-LR) catalysts with long meso-channels. However, compared with experimental investigations, the mathematical simulation of pore structure effects is less time-consuming and more economical. Hence, mathematical modeling can be developed to rationally design and optimize the pore structures of HDS/HDN catalyst particles to enhance the catalyst efficiency.

In this study, the effects of catalyst particle shapes (sphere, cylinder, trilobe, and tetralobe) and pore structures (pore diameter and porosity) on the reaction–diffusion behaviors of HDS/HDN at the particle scale were investigated via mathematical modeling. The effects of particle shape on HDS/HDN performance were first investigated, and the relationship between particle shape and effectiveness factor was established. Subsequently, the pore structures of trilobe catalyst particles, which exhibited the highest HDS/HDN effectiveness factor, were optimized to improve the catalyst particle efficiency. Finally, the effects of the catalyst pore diameter and porosity on the HDS/HDN effectiveness factors were further analyzed.

2 Mathematical model

A single catalyst particle model was employed to investigate the effects of catalyst particle geometries (sphere, cylinder, trilobe, and tetralobe) and pore structures (pore diameter and porosity) on the reaction–diffusion behavior of HDS and HDN reactions. A detailed description of the reaction kinetics and governing equations is provided below.

2.1 Single-particle model

A schematic diagram of HDS and HDN catalyst particles with four different shapes (sphere, cylinder, trilobe, and tetralobe) is shown in Fig. 1, in which the external and internal regions correspond to the fluid and catalyst particle domains, respectively. The height and radius of the entire reactor were set to 8 and 2.5 mm, respectively. The geometrical parameters of the four different particles are listed in Table 1, where H_P, D_P, S_P, V_P, and STV correspond to the single-particle’s height, excircle diameter, surface area, volume, and specific surface area, respectively. All the four different particles had the same excircle diameter of 2.54 mm, whereas the cylinder, trilobe and tetralobe particles had the same height of 2.54 mm.

Fig.1 Schematic diagram of HDS and HDN single-particle model for four different shapes.

Full size|PPT slide

Tab.1 Geometrical parameters of four different particles

Particle	HP/mm	DP/mm	SP/mm2	VP/mm3	STV/mm–1
Sphere	–	2.54	20.27	8.58	2.36
Cylinder	2.54		30.40	12.87	2.36
Trilobe			27.05	7.21	3.75
Tetralobe			29.30	9.48	3.09

2.2 Reaction kinetics

The HDS and HDN reactions of gas oil are expressed as follows [24]:

（1）\mathrm{Ar}-\mathrm{S}+{\mathrm{2H}}_{\mathrm{2}}\to \mathrm{Ar}-\mathrm{H}+{\mathrm{H}}_{\mathrm{2}}\mathrm{S}

（2）\mathrm{Ar}-\mathrm{N}+{\mathrm{3H}}_{\mathrm{2}}\to \mathrm{Ar}-\mathrm{H}+{\mathrm{NH}}_{\mathrm{3}}

where Ar-S, Ar-N, and Ar-H represent sulfur-containing, nitrogen-containing, and aromatic compounds, respectively. The kinetics of HDS and HDN obtained from Mederos et al. [24] were used to describe the reaction, as follows:

(3)R_{\mathrm{HDS}}=k_{\mathrm{HDS}}{\displaystyle \frac{{\left(c_{\mathrm{S}}\right)}^{\mathrm{1.8}}{\left(c_{{\mathrm{H}}_{\mathrm{2}}}\right)}^{\mathrm{0.96}}}{{\left(\mathrm{1}\mathrm{+}{K}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{S}}{c}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{S}}\right)}^{\mathrm{2}}}},

(4)k_{\mathrm{HDS}}=k_{\mathrm{0,HDS}}\exp \left(-{\displaystyle \frac{E_{\mathrm{HDS}}}{RT}}\right),

(5)K_{{\mathrm{H}}_{\mathrm{2}}\mathrm{S}}=\mathrm{5}.\mathrm{1}\mathrm{7}\exp \left({\displaystyle \frac{\mathrm{34020}}{RT}}\right),

(6)R_{\mathrm{HDN}}=k_{\mathrm{HDN}}{c}_{\mathrm{N}},

(7)k_{\mathrm{HDN}}=k_{\mathrm{0,HDN}}\exp \left(-{\displaystyle \frac{E_{\mathrm{HDN}}}{RT}}\right),

where R_HDS and R_HDN correspond to the HDS or HDN reaction rate, c_i corresponds to the molar concentration of species i (i = S, H₂, H₂S, N), k_HDS, k_HDN, k_0,HDS, and k_0,HDN are the HDS and HDN reaction rate constants and the corresponding pre-exponential factors, respectively. E_HDS, E_HDN, and K_{{\mathrm{H}}_{\mathrm{2}}\mathrm{S}} are the HDS, HDN reaction activation energies, and H₂S adsorption equilibrium constants. R and T are the molar gas constant and reaction temperature, respectively.

2.3 Governing equations

2.3.1 Random Spheres Model

Random Spheres Model (RSM) [25,26] was used to describe the pore structures of the catalyst particles, in which the catalyst pore diameter, porosity, and specific surface area were correlated, and all the parameters were associated with the number and radius of overlapping spherical particles. The catalyst porosity (\epsilon) is expressed as

(8)\epsilon =\exp \left(-{\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}\mathrm{\pi }{n}_{\mathrm{1}}{a}_{\mathrm{1}}^{\mathrm{3}}\right),

where n₁ and a₁ are the number and radius of the overlapping spherical particles, respectively. The surface area per unit volume of the catalyst particles \left(\sigma \right) can be defined as follows:

(9)\sigma =\mathrm{4}\mathrm{\pi }\epsilon n_{\mathrm{1}}{a}_{\mathrm{1}}^{\mathrm{2}}.

The surface area per unit mass of the catalyst particle (S) can be expressed as follows:

(10)S={\displaystyle \frac{\sigma }{{\rho }_{\mathrm{cat}}}},

where ρ_cat is the density of the catalyst particles. The catalyst pore diameter \left(d_{\mathrm{pore}}\right) is expressed as

(11)d_{\mathrm{pore}}={\displaystyle \frac{\mathrm{1}}{\mathrm{\pi }{n}_{\mathrm{1}}{a}_{\mathrm{1}}^{\mathrm{2}}}},

2.3.2 Momentum conservation equation

In this study, the laminar flow over the catalyst particle is expressed by the Navier–Stokes equation as follows:

(12){\rho }_{\mathrm{oil}}(\mathit{u}\cdot \nabla )\mathit{u}=\nabla \cdot (-p\mathit{l}+\mathit{K})+\mathit{F},

where ρ_oil, u, and K correspond to the density, velocity, and viscous stress tensor of gas oil, and F is the external force acting on gas oil. u, K and F are all vectors and l is unit vector.

2.3.3 Energy conservation equation

The energy conservation equation in the fluid domain is expressed as

(13)\nabla (u\cdot {\rho }_{\mathrm{oil}}\cdot C_{\mathrm{p,oil}}\cdot T)-\nabla ({\lambda }_{\mathrm{oil}}\cdot \nabla T)=\mathrm{0},

where C_p,oil and λ_oil are the specific heat capacity and thermal conductivity of the gas oil, respectively. The energy conservation equation in the particle domain is expressed as

(14)-\nabla ({\lambda }_{\mathrm{cat}}\cdot \nabla T)+{\rho }_{\mathrm{cat}}\cdot Q_i=\mathrm{0},

where λ_cat and Q_i are the particle effective thermal conductivity and reaction heat of HDS and HDN, respectively. λ_cat can be evaluated as follows:

(15){\lambda }_{\mathrm{cat}}=\epsilon \cdot {\lambda }_{\mathrm{oil}}+(\mathrm{1}-\epsilon )\cdot {\lambda }_{\mathrm{solid}},

where λ_solid is the effective thermal conductivity of the catalyst support.

2.3.4 Mass conservation equation

The mass conservation equation in the fluid domain is expressed as

(16)\nabla (-D_i\cdot \nabla c_i)\mathrm{+}u\cdot \nabla c_i=\mathrm{0,}

where D_i is the reactor-diffusion coefficient of species i. The mass conservation equation in the particle domain is expressed as

(17)\nabla (-D_{\mathrm{e},i}\cdot \nabla c_i)-R_i=\mathrm{0,}

where R_i corresponds to the reaction rate of species i. D_e,i is the particle diffusion coefficient of species i, which can be evaluated as follows [27]:

(18)D_{\mathrm{e,}i}={\displaystyle \frac{\epsilon }{\tau }}\left({\displaystyle \frac{\mathrm{1}}{\mathrm{1}/D_{\mathrm{M},i}+\mathrm{1}/D_{\mathrm{K},i}}}\right),

(19)\tau =\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\log \epsilon ,

where ε, τ, D_M,i, and D_K,i are the porosity and tortuosity of the catalyst particle, and the molecular and Knudsen diffusivities of species i within the particle domain, respectively.

D_M,i can be expressed as

(20)D_{\mathrm{M},i}=\mathrm{8}.\mathrm{9}\mathrm{3}{\mathrm{e}}^{-\mathrm{8}}\left({\displaystyle \frac{v_{\mathrm{L}}^{\mathrm{0.267}}}{v_i^{\mathrm{0.433}}}}\right)\cdot \left({\displaystyle \frac{T}{{\mu }_{\mathrm{L}}}}\right),

where ν_L is the critical molar volume of the gas oil, ν_i is the molar volume of species i, and μ_L is the viscosity of oil. D_K,i can be expressed as

(21)D_{\mathrm{K,}i}=\mathrm{4}\mathrm{8}.\mathrm{5}{d}_{\mathrm{pore}}{\left({\displaystyle \frac{T}{M_i}}\right)}^{\mathrm{0.5}},

where M_i is the molar mass of species i. Equations (13), (14), (16), and (17) can be solved using the boundary conditions listed in Table 2. c_{{\mathrm{H}}_{\mathrm{2}},0}, c_{\mathrm{S},0}, and c_{\mathrm{N},0} correspond to the initial molar concentration of species H₂, S and N. They can be expressed as follows:

(22)c_{{\mathrm{H}}_{\mathrm{2}}\mathrm{,}}{}_{\mathrm{0}}={\displaystyle \frac{{\left(p_{{\mathrm{H}}_{\mathrm{2}}}^{}\right)}_{\mathrm{0}}}{RT}},

(23)c_{\mathrm{S},\mathrm{0}}={\displaystyle \frac{{\left({\rho }_{\mathrm{oil}}{w}_{\mathrm{S}}\right)}_{\mathrm{0}}}{\mathrm{32}}},

(24)c_{\mathrm{N},\mathrm{0}}={\displaystyle \frac{{\left({\rho }_{\mathrm{oil}}{w}_{\mathrm{N}}\right)}_{\mathrm{0}}}{\mathrm{14}}},

where, p_{{\mathrm{H}}_{\mathrm{2}}}, w_S, and w_N represent the hydrogen pressure, sulfur, and nitrogen content, respectively.

Tab.2 Boundary conditions for solving Eqs. (13), (14), (16) and (17)^a)

Position	Temperature	Concentration
Reactor inlet (z= 0)	T = T0	ci = ci,0
Reactor outlet (z= LR)	{\displaystyle \frac{\partial T}{\partial z}}=\mathrm{0}	{\displaystyle \frac{\partial c_i}{\partial z}}=\mathrm{0}
Particle center (r= 0)	{\displaystyle \frac{\partial T}{\partial r}}=\mathrm{0}	{\displaystyle \frac{\partial c_i}{\partial r}}=\mathrm{0}
Particle external surface (r= RP)	T = Ts	ci = ci,s

a) Z and r are the distance from the reactor inlet and the center of the catalyst particle. LR and RP are reactor length and catalyst particle radius. ci,0 represents the initial concentration of species i. ci,s and Ts represent the molar concentration of species i and temperature of the catalyst particle surface.

The effectiveness factors (η) of the catalyst particles can be expressed as follows:

(25)\eta ={\displaystyle \frac{\mathrm{Average}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{reaction}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{rate}}{\mathrm{Surface}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{reaction}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{rate}}}\mathrm{ }\mathrm{ }\mathrm{ }={\displaystyle \frac{{\displaystyle \frac{\mathrm{1}}{V_{\mathrm{p}}}}{\displaystyle \underset{\mathrm{0}}{\overset{V_{\mathrm{p}}}{\int }}{R}_i}\mathrm{d}{V}_{\mathrm{p}}}{{\displaystyle \frac{\mathrm{1}}{S_{\mathrm{p}}}}{\displaystyle \underset{\mathrm{0}}{\overset{S_{\mathrm{p}}}{\int }}{R}_i}\mathrm{d}{S}_{\mathrm{p}}}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\left(i=\mathrm{HDS},\mathrm{HDN}\right),

where R_i corresponds to the HDS or HDN reaction rate; V_p and S_p correspond to the volume and surface area of the catalyst particle, respectively. All relevant parameters and variables used in this study are listed in Tables 3 and S1, respectively.

Tab.3 Parameters for simulation of HDS and HDN

Parameter	Symbol	Value	Unit
Inlet velocity	u0	0.01	m∙s–1
Hydrogen pressure	PH2	5.3	MPa
Temperature	T0	653	K
Sulfur content	ws	2.19	wt%
Nitrogen content	wN	330	ppm (×10−6)
Molar mass of oil	Mw	248.7	g∙mol–1
Average boiling point of oil	TMeABP	306.75	°C
Radius of overlapping spherical particles	a1	4.89	nm
True density of catalyst particle	ρs	3.36	g∙cm–3
Pre-exponential factor of HDS	k0,HDS	2.64e17	(cm3)m+n∙(mol(m+n–1) g∙s)–1
Activation energy of HDS	EHDS	150.10	kJ∙mol–1
Pre-exponential factor of HDN	k0,HDN	1.55e12	s–1
Activation energy of HDN	EHDN	172.280	kJ∙mol–1
Reaction heat of HDS	∆rHm,HDS	–34.89	kJ∙mol–1
Reaction heat of HDN	∆rHm,HDN	–21.62	kJ∙mol–1

2.4 Numerical methods

The reaction, momentum, energy, and mass conservation equations for simulating HDS and HDN were implemented in the commercial software COMSOL Multiphysics 4.3 using the finite element method to solve partial differential equations over a specified particle geometry. A mesh sensitivity analysis was performed to ensure the accuracy of the model (see Fig. S1, cf. Electronic Supplementary Material (ESM)). It was observed that even when the number of elements reached 1132738, the average reaction rate remained almost unchanged, indicating that increasing the elements until the abovementioned number did not affect the average reaction rate. Therefore, the setting of Mesh 5 was employed in further studies.

3 Results and discussion

3.1 Model validation

Single particle model is difficult to validate since it is hard to locally obtain the detailed information of temperature and concentration distribution within the single catalyst particle. Herein, two-dimensional reactor models (cf. ESM) of HDS and HDN were compared to verify their accuracies. Figure 2 shows the change in the outlet sulfur and nitrogen concentrations along the reactor length in the simulation. As shown, the differences in the outlet sulfur and nitrogen concentration between the experimental and simulated results were within the allowable range, indicating that the HDS and HDN kinetic models were reasonable and can be employed in subsequent investigations.

Fig.2 Comparison of outlet (a) sulfur and (b) nitrogen concentrations between experimental [24] and simulated results (T = 340 °C, P = 5.3 MPa, LHSV = 2.5 h^–1, z_L = 25.2 cm, u_L= 0.0181 cm∙s^–1, ρ_B = 0.9943).

Full size|PPT slide

3.2 Effects of particle shape

Because the HDS and HDN of gas oil are affected by severe internal diffusion limitations, and the optimal catalyst shape can effectively alleviate internal diffusion limitations, the effects of particle shape on the reaction-diffusion behavior of HDS and HDN were first investigated, as shown in Figs. 3 and 4. The operational conditions and properties of the catalyst particle are listed in Table 4.

Tab.4 Operational conditions and properties of catalyst particle

Parameter	Symbol	Value	Unit
Hydrogen pressure	PH2	5.3	MPa
Inlet temperature	T0	653	K
Inlet sulfur content	wS	2.19	wt%
Inlet nitrogen content	wN	330	ppm
Catalyst pore diameter	dpore	10.9	nm
Catalyst porosity	ε	0.55	–

Figure 3(a) shows the concentration distribution of sulfur-containing compounds in catalyst particles of different shapes, in which the upside and downside graphs were based on the central cross-section and longitudinal section perspectives, respectively. As shown, the sulfur concentration of all four catalyst particles decreased significantly along the catalyst particle radial direction, and the sulfur-containing compounds appeared only within a thin layer near the particle surface, indicating that the HDS reaction was severely restricted by internal diffusion and that most interior zones of the catalyst particles were not completely utilized. However, it was difficult to distinguish the sulfur concentration variation among the four different catalyst particles, as shown in Fig. 3(a). Hence, the average and surface HDS reaction rates of the different catalyst particles were further compared to understand the slight variation in the sulfur concentration, as shown in Fig. 3(b). It was clear that the average HDS reaction rates of the four catalyst particles changed more significantly than those of the surface HDS reaction rate, and the trilobe catalyst particle exhibited the lowest surface HDS reaction rate and the highest average HDS reaction rate.

The η of the four catalyst particles (defined as shown in Eq. (25)), which was used to evaluate the utilization efficiency of the catalyst particles, was further compared to assess the extent of the internal diffusion limitations. As shown in Fig. 3(c), the trilobe catalyst particles demonstrated the highest HDS effectiveness. This may be due to the large specific surface area of the trilobe catalyst particles, which can significantly reduce the diffusion path of the reactants and ease diffusion from the particle surface into the interior zone of the particle. Therefore, the trilobe catalyst particles afforded a significantly higher average HDS reaction rate and a slightly lower surface HDS reaction rate, thereby improving the HDS effectiveness factor and catalyst particle utilization.

Fig.3 (a) Concentration distribution of sulfur-containing compounds in catalyst particles of different shapes; (b) average and surface HDS reaction rates of different catalyst particles; (c) HDS effectiveness factors of different catalyst particles.

Full size|PPT slide

Figure 4(a) shows the concentration distribution of nitrogen-containing compounds in catalyst particles of different shapes. Compared with HDS, the reaction rate of HDN was relatively lower, which allowed the reactants to diffuse deeper into the interior zone of the catalyst particle. The particle shape significantly affected the nitrogen-containing compound concentration, and the trilobe catalyst particle showed the lowest concentration gradient, indicating the further utilization of the interior zone thereof. The average surface HDN reaction rate and HDN effectiveness factor of different catalyst particles are shown in Figs. 4(b) and 4(c), respectively. They exhibited the same trends compared with the HDS trends, i.e., the trilobe catalyst particle demonstrated a significantly higher average HDN reaction rate and a slightly lower surface HDN reaction rate, and hence the highest HDN effectiveness factor among all catalyst particles.

Fig.4 (a) Concentration distribution of nitrogen-containing compounds in catalyst particles of different shapes; (b) average and surface HDN reactions rate of different catalyst particles; (c) HDN effectiveness factors of different catalyst particles.

Full size|PPT slide

As discussed above, the particle shape significantly affects the reaction-diffusion behavior of HDS and HDN; therefore, a correlation between the reaction rate and specific surface area was established, as presented in Fig. 5. Figure 5(a) shows that the average HDS reaction rate increased linearly with the particle specific surface area, whereas the surface HDS reaction rate remained almost unchanged. Meanwhile, the HDS effectiveness factor was correlated positively with the particle specific surface area (see Fig. 5(b)). The HDN process exhibited the same trend, as shown in Figs. 5(c) and 5(d).

This is primarily because the increased particle specific surface area created a shorter diffusion path for the reactants to diffuse into the interior zone of the catalyst particle for further reaction, which improved the particle average reaction rate instead of the particle surface reaction rate, thereby enhancing the particle effectiveness factor and alleviating the internal diffusion limitation. It is noteworthy that the linearity of the curve shown in Fig. 5(b) was higher than that in Fig. 5(d), which was due to the more severe diffusion limitations caused by HDS as compared with HDN.

Fig.5 (a) Average and surface HDS reaction rates; (b) HDS effectiveness factor as a function of particle specific surface area; (c) average and surface HDN reaction rates; (d) HDN effectiveness factor as a function of particle specific surface area.

Full size|PPT slide

3.3 Effects of pore structure

Although the trilobe catalyst particles partially alleviated the internal diffusion limitations of HDS and HDN compared with the other three catalyst particles, the reactants still could not access the most interior zones of the trilobe catalyst particle, based on observing the concentration distributions shown in Figs. 3(a) and 4(a). Therefore, the pore structures of the trilobe catalyst particles were further investigated to improve the catalyst particle efficiency, as shown in Fig. 6.

Figures 6(a) and 6(b) show the average HDS and HDN reaction rates as a function of catalyst pore diameter and porosity, where the pore diameter varied within from 5 to 50 nm, and the porosity varied from 0.2 to 0.8. Based on the RSM, the catalyst pore diameter is dependent on the catalyst porosity and specific surface area, and the corresponding data are shown in Figs. 6(c) and 6(d). As shown, both the catalyst pore diameter and porosity significantly affected the average HDS and HDN reaction rates. The average HDS reaction rate increased to a maximum of 40.9 mol∙(m³∙s)^–1 as the catalyst pore diameter and porosity increased to 12 nm and 0.6, respectively, followed by a decrease in the average HDS reaction rate with a further increase in the catalyst pore diameter and porosity. The average HDN reaction rate with respect to the catalyst pore diameter and porosity show the same trends, as illustrated in Figs. 6(a) and (b), where the average HDN reaction rate increased to a maximum of 0.32 mol∙(m³∙s)^–1 as the catalyst pore diameter and porosity increased to 9 nm and 0.45, respectively. Boahene and Mouli et al. [28,29] synthesized four types of FeW/SBA-15 catalysts with different pore diameters ranging from 5 to 20 nm; they indicated that the FeW/SBA-15-supported catalyst with a pore diameter of approximately 10 nm demonstrated the highest HDS and HDN activities, which is consistent with our simulation results.

As shown in Figs. 6(c) and 6(d), the catalyst porosity increased with the catalyst pore diameter. Based on Eq. (18), the catalyst porosity is positively linearly correlated with the effective diffusion coefficient, indicating that increasing the catalyst pore diameter and porosity can significantly enhance the diffusion capacity of the reactants. When the catalyst pore diameter increased from 5 to 7 nm or the catalyst porosity increased from 0.2 to 0.35, the catalyst surface area per unit volume increased to 2.25 × 10⁸ m²∙m^–3, resulting in more active sites for reaction, and a further increase in the catalyst pore diameter and porosity will reduce the catalyst surface area per unit volume of catalyst, thereby resulting in fewer active sites for the reaction.

The effects of the catalyst pore diameter and catalyst porosity on the HDS/HDN reaction rate are shown in Fig. 6(e). In zone I, the HDS/HDN reaction rates were facilitated by the enhanced diffusion capacity of the reactants and improved active sites resulting from the increased catalyst pore diameter, porosity, and surface area. Subsequently, in zone II, the growth rates of the catalyst pore diameter and porosity began decelerating, whereas the catalyst surface area began to decrease gradually, which decelerated the growth of the HDS/HDN reaction rate. Finally, in zone III, the growth rate of the catalyst pore diameter decelerated further, and the catalyst surface area began to decline rapidly, which resulted in a significant decrease in the HDS/HDN reaction rate. Therefore, as shown in Figs. 6(a) and (b), an optimal average HDS/HDN reaction rate existed as the catalyst pore diameter and porosity increased, and this optimum value indicates a tradeoff between diffusion and reaction. It is noteworthy that the catalyst pore diameter or porosity corresponding to the optimal HDS reaction rate was greater than that corresponding to the optimal HDN reaction rate because HDS was affected more significantly by the severe diffusion limitations compared with HDN.

Fig.6 Average HDS and HDN reaction rate as a function of (a) catalyst pore diameter and (b) catalyst porosity; (c) catalyst pore diameter as a function of porosity and surface area; (d) catalyst porosity as a function of pore diameter and surface area; (e) schematic diagram showing effect of catalyst pore diameter and catalyst porosity on reaction rate.

Full size|PPT slide

The effects of pore structure on the HDS and HDN catalyst particle efficiency were investigated, as illustrated in Fig. 7. As shown, the HDS and HDN effectiveness factors increased with the catalyst pore diameter and porosity. Additionally, the variation trends of the HDS and HDN effectiveness factors differed from those of the HDS and HDN reaction rates.

Fig.7 HDS and HDN effectiveness factor as a function of (a) catalyst pore diameter and (b) catalyst porosity.

Full size|PPT slide

To understand the difference between the variation trends, the individual effects of the particle pore diameter and porosity on HDS and HDN were investigated, as shown in Figs. 8 and S3 (cf. ESM), respectively. The reaction-diffusion abilities of HDS and HDN with the increase in the pore diameter of the trilobe catalyst particles are shown in Fig. 8. The concentration distributions of sulfur-containing compounds in the trilobe catalyst particles of different catalyst pore diameters (5, 12 and 50 nm) are illustrated in Fig. 8(a). As shown, the surface concentration gradient decreased as the catalyst pore diameter increased. Meanwhile, Fig. 8(b) shows that as the catalyst pore diameter increased, the average HDS reaction rate first increased and then decreased, whereas the surface HDS reaction rate decreased gradually. This is different from the trend showing the effect of particle shape on the average and surface HDS reaction rates of gas oil.

The optimal particle pore diameter for the average HDS reaction rate indicated a tradeoff between diffusion and reaction, which has been discussed above. The trend of the surface HDS reaction rate was primarily a result of the increased catalyst pore diameter, which improved the diffusion coefficient of the reactants, as shown in Fig. 8(c). Consequently, the diffusion capacity of reactants increased, and more reactants were able to diffuse deeper into the interior zone of the trilobe catalyst particle, thereby decreasing the surface HDS reaction rate of the trilobe catalyst particles. Because the variation range of the surface HDS reaction rate was much larger than that of the average HDS reaction rate, the variation in the effectiveness factor was governed by that in the surface HDS reaction rate, which exhibited a negative linear correlation with the catalyst pore diameter, as shown in Fig. 8(c). Similarly, the trend showing the effects of the catalyst pore diameter on the HDN reaction rate and effectiveness factor (see Figs. 8(e) and 8(f)) were consistent with that for HDS. The concentration distributions of sulfur- and nitrogen-containing compounds in the trilobe catalyst particles of different catalyst porosities are illustrated in Fig. S3. Because the catalyst porosity was positively correlated with the catalyst pore diameter, the effects of porosity on HDS and HDN were consistent with that of the catalyst pore diameter.

Fig.8 (a) Concentration distribution of sulfur-containing compounds in trilobe catalyst particle of different pore diameters; (b) average and surface HDS reaction rate; (c) HDS effectiveness factor and diffusion coefficient with respect to pore diameter; (d) concentration distribution of nitrogen-containing compounds in trilobe catalyst particle of different pore diameters; (e) average and surface HDN reaction rate; (f) HDN effectiveness factor and diffusion coefficient with respect to pore diameter.

Full size|PPT slide

4 Conclusions

In summary, the effects of catalyst particle shapes and pore structures on the reaction–diffusion behaviors of HDS and HND were clarified in this study. It was discovered that the specific surface areas of different catalyst particles were positively correlated with the average HDS/HDN reaction rates, and that the catalyst particle shapes primarily altered the average HDS/HDN reaction rate to adjust the HDS/HDN effectiveness factor. The catalyst with a pore diameter of 12 nm and a porosity of 0.6 exhibited the highest average HDS reaction rate, whereas the catalyst with a pore diameter of 9 nm and a porosity of 0.45 exhibited the highest average HDN reaction rate. The optimal catalyst pore diameter and porosity for the average HDS/HDN reaction rate indicated a tradeoff between diffusion and reaction. In contrast to the catalyst particle shape, the pore diameter and porosity of the catalyst particles primarily altered the surface HDS/HDN reaction rate to adjust the HDS/HDN effectiveness factor. Our study provides insight into the engineering of catalyst particle shapes and pore structures for improving HDS/HDN catalyst particle efficiency.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China (Grant Nos. 22038003, 21922803, 22178100 and 21776077), the Innovation Program of Shanghai Municipal Education Commission, the Program of Shanghai Academic/Technology Research Leader (Grant No. 21XD1421000).

Electronic Supplementary Material

Supplementary material is available in the online version of this article at https://dx.doi.org/10.1007/s11705-021-2127-x and is accessible for authorized users.

References

1 Ancheyta-Juárez J, Aguilar-Rodríguez E, Salazar-Sotelo D, Betancourt-Rivera G, Leiva-Nuncio M. Hydrotreating of straight run gas oil light cycle oil blends. Applied Catalysis A, General, 1999, 180(1–2): 195–205

2 Marroquín-Sánchez G, Ancheyta-Juárez J. Catalytic hydrotreating of middle distillates blends in a fixed-bed pilot reactor. Applied Catalysis A, General, 2001, 207(1–2): 407–420

3 Schmitz C, Datsevitch L, Jess A. Deep desulfurization of diesel oil: kinetic studies and process-improvement by the use of a two-phase reactor with pre-saturator. Chemical Engineering Science, 2004, 59(14): 2821–2829

4 Novaes L da R, de Resende N S, Salim V M M, Secchi A R. Modeling, simulation and kinetic parameter estimation for diesel hydrotreatin. Fuel, 2017, 209: 184–193

5 Stanislaus A, Marafi A, Rana M S. Recent advances in the science and technology of ultra low sulfur diesel (ULSD) production. Catalysis Today, 2010, 153(1–2): 1–68

6 Mjalli F S, Ahmed O U, Al-Wahaibi T, Al-Wahaibi Y, Al Nashef I M. Deep oxidative desulfurization of liquid fuels. Reviews in Chemical Engineering, 2014, 30(4): 337–378

7 Breysse M, Djega-Mariadassou G, Pessayre S, Geantet C, Vrinat M, Pérot G, Lemaire M. Deep desulfurization: reactions, catalysts and technological challenges. Catalysis Today, 2003, 84(3–4): 129–138

8 Babich I V, Moulijn J A. Science and technology of novel processes for deep desulfurization of oil refinery streams: a review. Fuel and Energy Abstracts, 2003, 82(6): 607–631

9 Bej S K. Performance evaluation of hydroprocessing catalysts—a review of experimental techniques. Energy & Fuels, 2002, 16(3): 774–784

10 De Bruljn A, Naka I, Sonnemans J W M. Effect of the noncylindrical shape of extrudates on the hydrodesulfurization of oil fractions. Industrial & Engineering Chemistry Process Design and Development, 1981, 20(1): 40–45

11 Jarullah A T, Mujtaba I M, Wood A S. Kinetic parameter estimation and simulation of trickle-bed reactor for hydrodesulfurization of crude oil. Chemical Engineering Science, 2011, 66(5): 859–871

12 Mann P, Diez F V, Ordonez S. Fixed bed membrane reactors for WGSR-based hydrogen production: optimization of modelling approaches and reactor performance. International Journal of Hydrogen Energy, 2012, 37(6): 4997–5010

13 Farahani H F, Shahhosseini S. Simulation of hydrodesulfurization trickle bed reactor. Chemical Product and Process Modeling, 2011, 6(1): 1–19

14 Ancheyta J, Muñoz J A D, Macías M J. Experimental and theoretical determination of the particle size of hydrotreating catalysts of different shapes. Catalysis Today, 2005, 109(1–4): 120–127

15 Macías M J, Ancheyta J. Simulation of an isothermal hydrodesulfurization small reactor with different catalyst particle shapes. Catalysis Today, 2004, 98(1–2): 243–252

16 Macías Hernández M J, Morales R D, Ramírez-Lopez A. Simulation of the effectiveness factor for a tri-lobular catalyst on the hydrodesulfurization of diesel. International Journal of Chemical Reactor Engineering, 2009, 7(1): 91–97

17 Kolitcheff S, Jolimate E, Hugon A, Verstraete J, Rivallan M, Carrette P L, Couenne F, Tayakout-Fayolle M. Tortuosity and mass transfer limitations in industrial hydrotreating catalysts: effect of particle shape and size distribution. Catalysis Science & Technology, 2018, 8(10): 4537–4549

18 Shi Y, Yang C F, Zhao X Q, Cao Y Q, Qian G, Lu M K, Ye G H, Peng C, Sui B K, Lv Z H, . Engineering the hierarchical pore structures and geometries of hydrodemetallization catalyst pellets. Industrial & Engineering Chemistry Research, 2019, 58(23): 9829–9837

19 Yang L, Lu J F, Chen H Y, Ruckenstein E, Qin Y H, Wang T L, Sun W, Wang C W. Screening and improving porous materials for ultradeep desulfurization of gasoline. Industrial & Engineering Chemistry Research, 2020, 60(1): 604–613

20 Klimova T, Peña L, Lizama L, Salcedo C, Gutiérrez O Y. Modification of activity and selectivity of NiMo/SBA-15 HDS catalysts by grafting of different metal oxides on the support surface. Industrial & Engineering Chemistry Research, 2009, 48(3): 1126–1133

21 Salmas C E, Androutsopoulos G P. A novel pore structure tortuosity concept based on nitrogen sorption hysteresis data. Industrial & Engineering Chemistry Research, 2011, 40(2): 721–730

22 Zhou Z, Chen S L, Hua D, Zhang J H. Preparation and evaluation of a well-ordered mesoporous nickel-molybdenum/silica opal hydrodesulfurization model catalyst. Transition Metal Chemistry, 2011, 37(1): 25–30

23 Lv Y P, Wang X L, Gao D W, Ma X L, Li S N, Wang Y, Song G L, Duan A J, Chen G Z. Hierarchically porous ZSM-5/SBA-15 zeolite: tuning pore structure and acidity for enhanced hydro-upgrading of FCC gasoline. Industrial & Engineering Chemistry Research, 2018, 57(42): 14031–14043

24 Mederos F S, Ancheyta J, Elizalde I. Dynamic modeling and simulation of hydrotreating of gas oil obtained from heavy crude oil. Applied Catalysis A, General, 2012, 425–426: 13–27

25 Macé O, Wei J. Diffusion in random particle models for hydrodemetalation catalysts. Industrial & Engineering Chemistry Research, 1991, 30(5): 909–918

26 Rao S M, Coppens M O. Increasing robustness against deactivation of nanoporous catalysts by introducing an optimized hierarchical pore network—application to hydrodemetalation. Chemical Engineering Science, 2012, 83: 66–76

27 Topalian P J, Liyanage D R, Danforth S J, Aquino A I, Brock S L, Bussell M E. Effect of particle size on the deep HDS properties of Ni₂P catalysts. Journal of Physical Chemistry C, 2019, 123(42): 25701–25711

28 Boahene P E, Soni K, Dalai A K, Adjaye J. Application of different pore diameter SBA-15 supports for heavy gas oil hydrotreatment using FeW catalyst. Applied Catalysis A, General, 2011, 402(1–2): 31–40

29 Mouli K C, Soni K K, Dalai A K, Adjaye J. Effect of pore diameter of Ni-Mo/Al-SBA-15 catalysts on the hydrotreating of heavy gas oil. Applied Catalysis A, General, 2011, 404(1–2): 21–29