A “Sequential Design of Simulations” approach for exploiting and calibrating discrete element simulations of cohesive powders

Abstract

The flow behaviours of cohesive particles in the ring shear test were simulated and examined using discrete element method guided by a design of experiments methodology. A full factorial design was used as a screening design to reveal the effects of material properties of partcles. An augmented design extending the screening design to a response surface design was constructed to establish the relations between macroscopic shear stresses and particle properties. It is found that the powder flow in the shear cell can be classified into four regimes. Shear stress is found to be sensitive to particle friction coefficient, surface energy and Young’s modulus. A considerable fluctuation of shear stress is observed in high friction and low cohesion regime. In high cohesion regime, Young’s modulus appears to have a more significant effect on the shear stress at the point of incipient flow than the shear stress during the pre-shear process. The predictions from response surface designs were validated and compared with shear stresses measured from the Schulze ring shear test. It is found that simulations and experiments showed excellent agreement under a variety of consolidation conditions, which verifies the advantages and feasibility of using the proposed “Sequential Design of Simulations” approach.

Key words： discrete element method; cohesive materials; parameter calibration; ring shear cell; design of experiments

1 Introduction

The flow behaviour of cohesive particles has attracted increasing attention due to a wide range of applications across diverse areas including pharmaceutical, agriculture, food and chemical industries. A better understanding of the effect of the material properties on the flow behaviour of cohesive particles is beneficial to optimize and improve the relevant industrial applications. As the computer hardware and algorithms continue to improve, the discrete element method (DEM) has become a valuable technique for addressing powder handling equipment designs [1–3]. In DEM simulations, the position, velocity and force of individual particles are calculated directly using classical Newton’s law. Therefore, DEM allows direct incorporation of the cohesion forces between particles and can help understand the underlying mechanisms, which makes it an attractive tool [4].

The reliability of a DEM model mainly depends on the accuracy of the force-displacement law used in particle contacts and the choice of relevant simulation parameters [5]. One main challenge with DEM is how to select representative parameters at particle scale that can accurately reproduce realistic bulk behaviours of the granular powders. Currently, material properties like particle size, shape and density can be measured or estimated directly by experiments with enough confidence. However, there is still disagreement on the best methods to measure some rheological parameters required in constitutive contact models, such as the particle surface energy. Furthermore, experimental measurements usually leads to scatted values with powder samples. Additional assumptions need to be made in DEM simulations such as using a representative particle shape, a limit number of discretized particle size and an averaged coefficient of restitution over a range of impact velocities. Therefore, a so-called calibration process is required before DEM can be employed as a reliable predictive tool for industrial processes. The calibration process here is referred to as a procedure of determining simulation parameters at particle scale for DEM simulations to quantitatively match the bulk behaviour of powders in experiments.

The angle of repose is one of the most commonly used tests to calibrate DEM simulation parameters [6]. The static angle of repose from a powder pile and dynamic angle of repose in the rotating drum have been simulated and compared with experimental measurements to find the optimal parameters [7,8]. However, it is known that the angle of repose is sensitive to a variety of parameters such as particle sliding friction, rolling friction and surface energy [9,10]. It is possible that more than one set of parameters will produce a similar angle of repose measured in the experiments, which makes the calibration test problematic [11]. The shear cell test for powders has shown potentials to be an effective calibration method for DEM simulations [12,13]. It has long been used to characterize the flow properties of bulk solids and has the advantageous reproducibility for the flow behavious of cohesive powders. The principle of shear testing is to measure the yield stress locus of bulk powders under different consolidation stresses [14]. The ring shear cell tester can generate several yield stress points under different normal stresses, which can be used as multiple responses for calibrating more than one simulation parameter. Therefore, experiments and simulations of ring shear cell tester were investigated in this study.

Currently, DEM calibration processes are commonly carried out at a one-factor-at-a-time approach, where parameters are varied individually at each time and then the effects on the simulation responses are monitored. Simons et al. [12] studied the sensitivity of various material properties to the shear cell results by a one-factor-at-a-time approach. They found the shear results depend on more than one input parameter and suggest that the calibration process should include more than one experiment. Huang et al. [15] simulated and measured the shear resistance of ballast particles in the direct shear test. Numerous simulation cases were carried out with various the particle friction and contact stiffness to match the shear stress versus displacement curves measured in experiments. However, the optimal parameters are still obscure. While it is conceptually simple, the one-factor-at-a-time approach is often inefficient and of questionable accuracy when there are interactions between two input variables [16]. By contrast, the design of experiments (DoE) methodology allows investigators to systematically vary multiple factors within the context of one experimental design. It is also known as a multivariate experimental design and analysis [17]. DoE is now commonly used in industries as a tool to achieve quality by design and minimize the cost of various processes. Although DoE was originally designed for optimizing the performance of experimental processes, recently there have been proposals to apply DoE in the calibration process of DEM simulations [18,19]. To distinguish the difference between numerical experiments and lab physical experiments, the DoE methodology is referred to as the design of simulations (DoS) here.

This paper aims to present a sequential DoS (SDoS) methodology to computationally investigate the ring shear test and calibrate the material properties required in DEM simulations. The remainder of the paper is structured as follows. The powder material and the experimental procedure for Schulze ring shear testing in the lab are described in Section 2. The DEM contact model used in the simulations and methodology of SDoS are introduced in Section 3. The design results are then discussed in details in Section 4. Finally, Section 5 makes a summary of this work.

2 Experimental

2.1 Powder materials

The Tablettose 100 provided from Meggle (Molkerei MEGGLE Wasserburg GmbH & Co. KG, Germany) was used in the ring shear cell experiments. The Tablettose 100 is manufactured by a continuous spray agglomeration process. Its cumulative particle size distribution is given in the supplemental file.

2.2 Ring shear testing

The ring shear testing technique is commonly used for the evaluation of the flow properties of the powder samples. Each measurement was performed using the ring shear tester, RST-XS (Dietmar Schulze, Germany). The ring-shaped shear cell is 13 mm in height, with outer and inner diameters of 64 and 32 mm, respectively. The lids have vertical vanes of height 3 mm distributed azimuthally every 22.5° on the surfaces. At the beginning of the measurement, the powder sample was filled into the annular shear cell without applying force to the upper surface of the powder bed. The powder was then consolidated under a constant pre-shear normal stress ({\sigma }_{\mathrm{pre}}) and the lower portion of the cell was slowly rotated until a steady-state flow had been achieved where the shear stress becomes constant ({\tau }_{\mathrm{pre}}). This procedure is hereafter referred to as the pre-shear process. After the pre-shear process, the normal stress was first released and a lower constant normal stress ({\sigma }_{\mathrm{sh}}) was then applied to shear the powder until the incipient flow occurred in the powder sample. The shear stress at the incipient flow point is referred to as incipient flow shear stress ({\tau }_{\mathrm{sh}}). The layout of the experimental and simulated ring shear cell tester is provided in the supplemental file. The fundamental principles of ring shear tester measurements can be referred to the textbook of Schulze [14].

3 Models

3.1 DEM model

The Johnson-Kendall-Roberts (JKR) contact model is implemented in LIGGGHTS 3.7.0 [20,21] and used in this study for ring shear simulations. The schematic of the JKR contact force-displacement relationship can be found in the supplemental file. The contact force in JKR model could be calculated as a function of contact area [22]:

（1）F_n={\displaystyle \frac{\mathrm{4}{E}^{*}{a}^{\mathrm{3}}}{\mathrm{3}{R}^{*}}}-\sqrt{\mathrm{16}\mathrm{\pi }\gamma E^{*}{a}^{\mathrm{3}}},

where E^* is the effective Young’s modulus given by {\displaystyle \frac{\mathrm{1}}{E^{*}}}={\displaystyle \frac{\mathrm{1}-{\nu }_{\mathrm{1}}^{\mathrm{2}}}{E_{\mathrm{1}}}}+{\displaystyle \frac{\mathrm{1}-{\nu }_{\mathrm{2}}^{\mathrm{2}}}{E_{\mathrm{2}}}}. E_i and {\nu }_i (i = 1,2) denote Young’s moduli and Poisson’s ratios of the contacting spheres, respectively. \gamma is the surface energy. R^* is the effective radius given by {\displaystyle \frac{\mathrm{1}}{R^{*}}}={\displaystyle \frac{\mathrm{1}}{R_{\mathrm{1}}}}+{\displaystyle \frac{\mathrm{1}}{R_{\mathrm{2}}}}, where R_{\mathrm{1}} and R_{\mathrm{2}} are the radii of the two spheres, respectively. a is the contact radius during a collision. The contact radius a can be related to the overlap between particles, \delta, which is provided as follows:

(2)\delta ={\displaystyle \frac{a^{\mathrm{2}}}{R^{*}}}-\sqrt{{\displaystyle \frac{\mathrm{4}\mathrm{\pi }\gamma a}{E^{*}}}}.

The contact radius used in Eq. (1) is obtained by solving the equation of Eq. (2) with the overlap of each time step. Furthermore, a dashpot was added in the normal force to dissipate kinetic energy in the particle materials. The damping force in normal direction can be calculated as follows:

(3)F_{nd}={\eta }_n{\mathit{u}}_{n,ij},

(4){\eta }_n=-\mathrm{2}\sqrt{{\displaystyle \frac{\mathrm{5}}{\mathrm{6}}}}\beta \sqrt{S_n{m}^{*}},

(5)S_n=\mathrm{2}{E}^{*}a,

(6)\beta ={\displaystyle \frac{\mathrm{lne}}{\sqrt{{\ln }^{\mathrm{2}}\mathrm{e}+{\mathrm{\pi }}^{\mathrm{2}}}}}

Likewise, the tangential force is calculated as a sum of the tangential spring force and damping force:

(7)F_{\mathrm{t}}=F_{\mathrm{ts}}+F_{\mathrm{td}},

(8)F_{\mathrm{ts}}=F_{{\mathrm{ts}}_{(n-\mathrm{1})}}+\mathrm{\Delta }{F}_{\mathrm{ts}},

(9)F_{\mathrm{td}}=-\mathrm{2}\sqrt{{\displaystyle \frac{\mathrm{5}}{\mathrm{6}}}}\beta \sqrt{S_{\mathrm{t}}{m}^{*}}{\mathit{u}}_{\mathrm{t},ij},

(10)\mathrm{\Delta }{F}_{\mathrm{ts}}=-S_{\mathrm{t}}{\delta }_{\mathrm{t}},

where {\delta }_{\mathrm{t}} is the incremental tangential overlap and {\mathit{u}}_{\mathrm{t},ij} is the tangential component of relative velocity. S_{\mathrm{t}} is the tangential stiffness given as:

(11)S_{\mathrm{t}}=\mathrm{8}{G}^{*}a,

(12){\displaystyle \frac{\mathrm{1}}{G^{*}}}={\displaystyle \frac{\mathrm{2}-v_A}{G_A}}+{\displaystyle \frac{\mathrm{2}-v_B}{G_B}},

where G^{*} is the equivalent shear modulus and v is the Poisson’s ratio. The tangential force is limited by the Coulomb law of friction (F_{\mathrm{t},\max }={\mu }_{\mathrm{s}}{F}_{\mathrm{n}}), where {\mu }_{\mathrm{s}} is the static friction coefficient.

3.2 Design of simulations

The schematic diagram of the SDoS proposed in this work is shown in Fig. 1. The sequential design of the simulations approach can be broken down into three steps. A screening design is first performed to understand the ring shear process and extract significant factors that affect the shear stresses at pre-shear and shear processes. Subsequently, the screening design is augmented to be a response surface design supplemented with more runs on the significant factors. Predictions on the material properties can be made from the results of response surface design. New simulation cases would be carried out to verify the predictions and comparisons between experimental measurements and the simulations using the calibrated input parameters are made to test the performance of the model. If the performance is not satisfactory, it is possible to add the prediction point back to the enhancement design and make a new estimation on the optimal input parameters. All the design tables and analysis of the design results are generated using JMP® JMP [23].

Fig.1 A SDoS approach for studying and calibrating DEM simulations.

Full size|PPT slide

A screening design is carried out as the early step of the present SDoS, which is intended to facilitate the understanding of the process and determine a few significant factors from a list of many potential ones. The analysis of screening designs depends on the principle of effect sparsity. It is assumed that most of the variations in the responses can be explained by a small number of effects. Under this principle, hypothesis tests are performed to test whether the effects are active. A good screening design ensures that the main effects are orthogonal and uncorrelated with two-factor interactions. A two-level full factorial design is constructed in this work for screening design since it can identify major trends and easy to be augmented in a followed-up design. In the current full factorial design, each simulation factor has two levels, i.e., low and high values. The simulation runs include all combinations of these factor levels. In this study, we are going to investigate five input simulation parameters. Therefore, a total of 32 simulation cases will be conducted.

After screening experiments, an enhancement design can be followed up to provide more details on the relationships among the critical factors and the response variables. A central composite response surface design is adopted in this study. Each factor is set at three levels so that any nonlinear relationships between factors and responses can be detected. As shown in Fig. 1, the central composite design can be constructed by augmenting the existing two-level factorial design. This means that parts of the simulation results from the previous screening design can be re-used in the augmentation design, which can reduce the total computational costs. The response surface design uses an I-criterion optimality which minimizes the average variance of prediction over the design space. It is more appropriate than the factorial design if the primary design goal is to predict responses or determine regions in the design space where the response falls within an acceptable range. After performing the response surface design, a relationship between factors and responses is established and predictions on the optimal input parameter can be made. Finally, new simulation cases will be carried out to verify the predictions. Comparisons between experiment measurements and the simulations using the calibrated input parameters are made to test the performance of the model. If the performance is not satisfactory, it is possible to add the prediction point back to the enhancement design and make a new estimation on the optimal input parameters. Subsequently, simulations with the calibrated input parameters were followed up to verify the predictions and further validated with experiment target responses. In this work, additional cases with different consolidation conditions were also simulated and compared with the experimental measurements to test the feasibility of the proposed workflow.

4 Results and discussion

In this work, all the simulations were carried out using the DEM particle simulation code LIGGGHTS 3.7.0 [20]. Note that the default JKR model in LIGGGHTS is a simplified version that defines the cohesion force linearly proportional to the contact area. In this work, we did not use the simplified version because it was not sufficient to satisfactorily predict incipient flows in highly consolidated bulk powders [24,25]. Therefore, a full JKR contact model is implemented in all the simulations. The ring shear test in the DEM simulation performs the same procedures as the experimental setup. A normal force servo control is applied to the upper lid and rotation is set to the bottom cell. Following the ASTM standard [26], the shear stress in the simulation is calculated as follows:

(13)\tau ={\displaystyle \frac{M}{r_{\mathrm{m}}A}},

(14)r_{\mathrm{m}}={\displaystyle \frac{\mathrm{2}(r_{\mathrm{out}}^{\mathrm{3}}-r_{\mathrm{in}}^{\mathrm{3}})}{\mathrm{3}(r_{\mathrm{out}}^{\mathrm{2}}-r_{\mathrm{in}}^{\mathrm{2}})}},

where M is the torque on the top lid due to particles and r_{\mathrm{m}} is the moment arm, with r_{\mathrm{in}} and r_{\mathrm{out}} being the inner and outer radii of the top lid, respectively. A is the area of the top lid.

The material properties of the particle and the shear cell are shown in Table 1. The simulation time step is set to be 20% of the Rayleigh time step. Unless stated otherwise, the normal stress at the pre-shear process {\sigma }_{\mathrm{pre}} is set at 2000 Pa and the normal stress at the shear process {\sigma }_{\mathrm{sh}} is set at 400 Pa for the simulations carried out in this work. Further details of optimal numerical setup to accelerate the simulations are supplemented in the appendix.

Tab.1 Simulation parameters used in ring shear test

Property	Value
Particle density/(kg·m–3)	1600
Number of particles	~80000
Particle radius/\mathrm{\mu m}	125 (30%), 75 (61%), 60 (9%)
Surface energy/(J·m–2)	0.0001–0.1
Young’s modulus/GPa	0.13–1.3
Poisson’s ratio	0.1–0.5
Particle-particle friction coefficient	0.1–0.8
Particle-particle restitution coefficient	0.3–0.9
Wall Young’s modulus/GPa	1.3
Wall Poisson’s ratio	0.3
Particle-wall friction coefficient	0.1
Particle-wall restitution coefficient	0.6

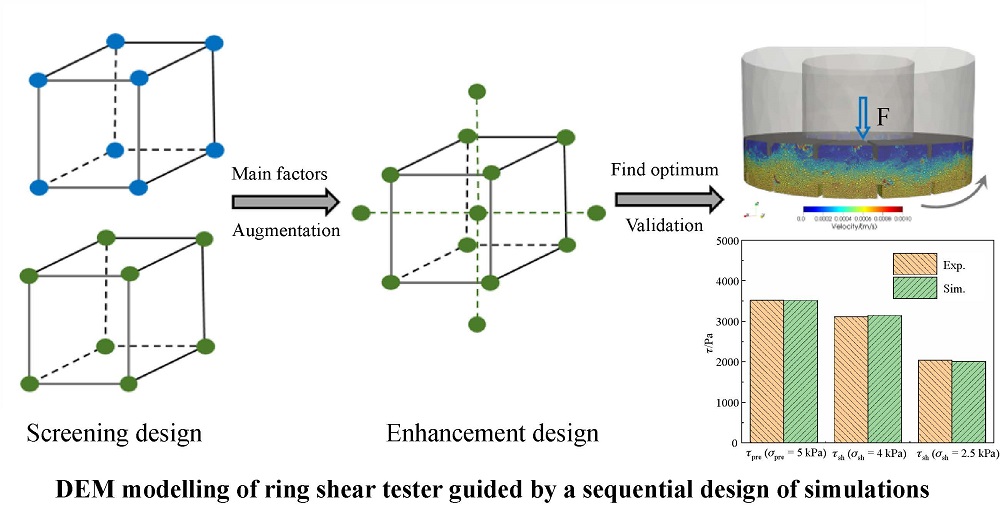
4.1 Screening design

As stated in the modelling section, screening design is an effective tool to identify a small number of highly influential factors that affect process responses. In this study, the numerical parameters in DEM simulation considered were the following: Young’s modulus (0.13–1.3 GPa); Poisson’s ratio (0.1–0.5); particle surface energy (0.0001–0.1 J·m^–2); particle restitution coefficient (0.3–0.9) and particle friction coefficient (0.1–0.8). The values are chosen to cover a relatively large parameter space for targeting typical pharmaceutical excipient powders including different types of lactose and microcrystalline cellulose particles. Note that the range of the values may need to be extended if the targeting material is active pharmaceutical ingredient poweders. The responses of the design are the predictions of the shear stress at the pre-shear process and shear stress at the incipient flow. The full factorial design is constructed and the generated numerical experimental design table is listed in Table 2. A total of 32 simulation cases were conducted. The simulated strain-stress results of all the full factorial design cases are shown in Fig. 2. It can be observed that the shear stresses at the pre-shear process and shear process significantly vary after changing the input parameters. More specifically, there are very large amplitudes of stress fluctuation in some of the cases.

Tab.2 Design table of the full factorial design used in this study

Pattern	Case ID	Young’s modulus/GPa	Poisson ratio	Friction coefficient	Restitution coefficient	Surface energy/(J·m–2)
++++−	1	1.3	0.5	0.8	0.9	0.0001
+−−++	2	1.3	0.1	0.1	0.9	0.1
++−++	3	1.3	0.5	0.1	0.9	0.1
++−−−	4	1.3	0.5	0.1	0.3	0.0001
+−+−−	5	1.3	0.1	0.8	0.3	0.0001
−++−−	6	0.13	0.5	0.8	0.3	0.0001
−+++−	7	0.13	0.5	0.8	0.9	0.0001
−−+−+	8	0.13	0.1	0.8	0.3	0.1
−−−+−	9	0.13	0.1	0.1	0.9	0.0001
−+−−−	10	0.13	0.5	0.1	0.3	0.0001
+−−−−	11	1.3	0.1	0.1	0.3	0.0001
+−−+−	12	1.3	0.1	0.1	0.9	0.0001
++−−+	13	1.3	0.5	0.1	0.3	0.1
+−+−+	14	1.3	0.1	0.8	0.3	0.1
−−−++	15	0.13	0.1	0.1	0.9	0.1
−−−−+	16	0.13	0.1	0.1	0.3	0.1
+−++−	17	1.3	0.1	0.8	0.9	0.0001
+−+++	18	1.3	0.1	0.8	0.9	0.1
−++++	19	0.13	0.5	0.8	0.9	0.1
−+−+−	20	0.13	0.5	0.1	0.9	0.0001
+−−−+	21	1.3	0.1	0.1	0.3	0.1
+++++	22	1.3	0.5	0.8	0.9	0.1
++−+−	23	1.3	0.5	0.1	0.9	0.0001
−+−−+	24	0.13	0.5	0.1	0.3	0.1
+++−+	25	1.3	0.5	0.8	0.3	0.1
−−−−−	26	0.13	0.1	0.1	0.3	0.0001
−−++−	27	0.13	0.1	0.8	0.9	0.0001
−−+−−	28	0.13	0.1	0.8	0.3	0.0001
−+−++	29	0.13	0.5	0.1	0.9	0.1
+++−−	30	1.3	0.5	0.8	0.3	0.0001
−−+++	31	0.13	0.1	0.8	0.9	0.1
−++−+	32	0.13	0.5	0.8	0.3	0.1

Fig.2 The simulated shear strain-stress results by the full factorial design.

Full size|PPT slide

Table 3 presents the effect summary for the shear stress at the pre-shear process by performing a significant test based on the simulation results of the full factorial design cases. The null hypothesis here is that the effect of a term is not important. Given the null hypothesis is true, a p-value is the probability of getting a result at least as extreme as the sample result assuming that the null hypothesis is correct. The p-value is calculated as:

(15)p\mathrm{-\; value}=P(\mathrm{X}\le \chi \mid H_{\mathrm{0}}\mathrm{is\; ture})=\mathrm{c}\mathrm{d}f(\chi ),

where H_{\mathrm{0}} is the null hypothesis, \mathrm{X} is the Chi-square, \chi is the value of the test statistic cacluated from the sample, and \mathrm{c}\mathrm{d}f(\chi ) is the cumulative distribution function of the Chi-square distribution under the null hypothesis [27]. If the p-value is lower than a pre-defined significance level, we reject the null hypothesis. If not, we conclude that it fails to reject the null hypothesis; namely, the term is not significant than a random guess. If the p-value is smaller than 0.05, it is referred to as statistically significant [28]. If the p-value smaller than 0.001, it is referred to as statistically highly significant. Table 3 illustrates that the effect of friction coefficient and surface energy on the pre-shear shear stress is statistically highly significant. The effect of Young’s modulus, Poisson ratio and coefficient of restitution are not statistically significant. To make it clearer, the LogWorth of the effect is also plotted in Table 3. The LogWorth is defined as –log₁₀(p-value). This transformation adjusts  p-values to provide an appropriate scale for graphing and comparisons. A LogWorth value that exceeds 2 is significant at the 0.01 level which is indicated as a blue line in Table 3. It can be clearly seen that the particle friction dominates the determination of the pre-shear shear stress in the simulation cases. This is confirmed in the box plot as shown in Fig. 3 which divides all the simulation cases into two groups. Increasing particle friction significantly increase pre-shear shear stress. The variation of the pre-shear shear stress within each group can be attributed to the additional effect of surface energy, which is shown in different colors of the points.

Tab.3 The effect summary for pre-shear shear stress predicted by the full factorial design

Effect	p-Value	LogWorth
Friction coefficient	4.2e−26	25.37
Surface energy	2.23e−9	8.65
Young's modulus	7.13e−2	1.14
Restitution coefficient	4.04e−1	0.39
Poisson ratio	9.55e−1	0.02

Fig.3 The simulated pre-shear shear stresses by the full factorial design.

Full size|PPT slide

It can be observed that the shear stress at incipient flow can be divided into six levels and thus it is divided into six groups shown in Fig. 4. Compared with the number of groups that appeared in the pre-shear shear stress, it indicates that there may be more than one factor that dominates the prediction of shear stress at incipient flow. The effect summary for shear stress at the incipient flow from full factorial design cases is shown in Table 4. It is identified that the surface energy, particle friction and Young’s modulus effects are statistically highly significant. Among them, the surface energy is the most important effect on the prediction of shear stress at incipient flow.

Tab.4 The effect summary for shear stress at the incipient flow predicted by the full factorial design

Effect	p-Value	LogWorth
Friction coefficient	9.0e−22	14.85
Surface energy	1.4e−15	21.05
Young’s modulus	8.07e−4	3.09
Restitution coefficient	7.42e−1	0.13
Poisson ratio	7.5e−1	0.12

Fig.4 The simulated shear stress at the incipient flow by the full factorial design.

Full size|PPT slide

Based on the fact that both particle friction and surface energy are statistically highly significant for the responses of pre-shear shear stress and shear stress at incipient flow, we classify the simulations cases into four flow regimes as shown in Fig. 5. It can be observed that the strain-stress behaviours are similar within each regime whereas distinctions are noticeable between different regimes. In particular, considerable fluctuations of stress are found in the high friction and low cohesion regimes. This is because frequent stick-slip is likely to occur in the fictional dry powder, as also confirmed in the literature [29,30]. The underlying mechanisms have not been fully clear, although some researchers believe it may be due to friction mobilization and shear band propagation [31,32]. It is found that the amplitude of fluctuation is larger at a higher particle restitution coefficient while adding cohesion will suppress the amplitude of the fluctuation. By comparing Fig. 5(a) with Fig. 5(b), it is clear that the pre-shear shear stress increases significantly with the increase of particle friction. By comparing Fig. 5(a) with Fig. 5(c), it can be seen that the surface energy have a significant effect on the shear stress at incipient flow. It is also noted that there are apparently two differential layers for the shear stresses at incipient flows in Figs. 5(c) and 5(b). By matching the case id, it is found that is caused by the effect of Young’s modulus. A higher Young’s modulus will result in smaller shear stress at incipient flow under high cohesion regimes. On the other hand, Young’s modulus shows minimal effects under low cohesion regimes as shown in Figs. 5(a) and 5(b). This highlights the advantage of using the DoE for facilitating analysis of the ring shear cell testing since the effect of Young’s modulus could be difficult to discover if a varying one-factor-at-a-time approach is applied.

Fig.5 Four different flow regimes extracted from the full factorial design. (a) Low particle friction and low cohesion; (b) high particle cohesion and low cohesion; (c) low particle friction and high cohesion; (d) high particle friction and high cohesion.

Full size|PPT slide

4.2 Enhancement design

After identifying the influencing factors, an enhancement design is followed up to explore more details on the relationships among the factors and the response variables. From the previous screening design, we know that particle friction, surface energy and Young’s modulus are significant effects on the prediction of the shear stress in ring shear cell simulations. The designs so far are a parametric study on the sensitivity of the effects of material properties on the ring shear test results, the conclusions can be applied to any test materials. In this session, we would like to calibrate the material properties for Tablettose 100 powders which have been used in our ring shear experiment in the lab. The Young’s modulus of the particle is set to be 1.3 GPa based on the micro-indentation test results [33]. A response surface design is carried out to find the optimal values of the particle friction coefficient and surface energy. The design table of the simulation cases is listed in Table 5.

Tab.5 Design table of the response surface design used in this study

Pattern	Case ID	Friction coefficient	Surface energy/(J·m–2)
−	1	0.1	0.0001
0a	2	0.45	0.0001
+−	3	0.8	0.0001
a0	4	0.1	0.05005
00	5	0.45	0.05005
A0	7	0.8	0.05005
−+	8	0.1	0.1
0A	9	0.45	0.1
++	10	0.8	0.1

After performing the simulations, two response surfaces can be constructed based on the simulation results. Figure 6 shows the surface plots of the shear stress at pre-shear and shear stress at incipient flow with varying surface energies and particle friction coefficients. The black mesh planes represent the experimental measurement values of the shear stresses. It can be seen from Fig. 6(a) that there are many combinations of friction coefficient and surface energy values given a pre-shear shear stress, which could be obtained through the intersection of black mesh plane and the response surface. However, there is one unique combination of the surface energy and friction coefficient if we combine both response surfaces of pre-shear shear stress and shear stress at incipient flow. The prediction formulas for the pre-shear shear stress and shear stress at the incipient flow can be obtained by fitting the response surfaces and removing the insignificant terms. The final prediction expressions are given as follows:

(16){\tau }_{\mathrm{pre}}=\mathrm{1020}+\mathrm{1908}\mu -\mathrm{1248}{\mu }^{\mathrm{2}}-\mathrm{1690}\gamma +\mathrm{28031}{\gamma }^{\mathrm{2}},

(17){\tau }_{\mathrm{sh}}=\mathrm{172}+\mathrm{577}\mu -\mathrm{381}{\mu }^{\mathrm{2}}+\mathrm{2326}\gamma +\mathrm{4685}{\gamma }^{\mathrm{2}},

Fig.6 The surface plots predicted by the response surface design (a) response surface of pre-shear stress by varying particle friction and surface energy (b) response surface of shear stress at incipient flow by varying particle friction and surface energy. The black mesh planes represent the experimental measurement values.

Full size|PPT slide

Figure 7 shows the DEM simulated stresses and predicted stresses based on the prediction expressions fitted by the response surface design. It can be seen that both the predictions for pre-shear shear stress and shear stress at the incipient flow are very good and with a very high coefficient of determination (R²>0.9), which means that most of the variations in the responses have been explained by the model. Normality tests for the residuals were also performed and results show that the distribution of residuals is a normal distribution with the mean close to zero.

Fig.7 The actual and predicted stress fitted by the response surface design (a) shear stress at pre-shear (b) shear stress at incipient flow. The line of fit is solid red and the confidence bands (95%) are shaded red. The dashed horizontal blue line is the mean stress of the simulation cases.

Full size|PPT slide

Figure 8 shows the prediction profiler based on the response surface design. It can be observed that the conclusions on the effects are the same as for the screening design. The interparticle friction coefficient is the most important factor for the prediction of pre-shear shear stress, which shows a steep slope. The effects of interparticle friction on the shear stress during pre-shear and under incipient flow are also confirmed to be non-linear. The shear stress initially increases with the increase of friction coefficient and then asymptotes to an upper limit. This asymptotic behaviour is also reported for the simulations of non-cohesive particles in the literature [12,34–36]. The optimal combination of the surface energy and particle friction can be calculated by solving the equation system shown above and is also shown in the prediction profiler. The calibrated particle friction for Tablettose 100 particles is 0.26 and surface energy is 0.052 J·m^–2.

Fig.8 The prediction profiler from the fitting of response surface design results.

Full size|PPT slide

4.3 Experimental validation

DEM simulations are carried out based on the estimation of the values of particle friction and surface energy to validate the model built from the response surface design. Figure 9 shows the overall validation results. Figure 9(a) presents the comparison between the experimental measurements and the DEM simulation results with the calibrated material properties. Good agreement has been achieved both for the predictions of the pre-shear stress and shear stress at the incipient flow. Note that if one is not satisfied with the predictions, it is possible to further refine the response surface design by adding this validation point to make a new estimation. Currently, the relative errors between the experimental measurements and simulation results are less than 10%. The validity of the calibrated material properties is further tested for the predictions of shear stress at the incipient flow under different normal stresses (the pre-shear normal stresses are kept the same). It can be seen from Fig. 9(b) that there is good agreement between the experimental measurements and simulation results.

Fig.9 (a) Validation of the pre-shear shear stress and shear stress at the incipient flow predicted from response surface design; (b) test of the validity of the calibrated material properties for the predictions of shear stress at the incipient flow under different normal stresses.

Full size|PPT slide

In previous designs, all the simulations are performed under a 2 kPa pre-consolidation normal stress. It would be useful to test the performance of the model under a different pre-consolidation normal stress which has not been trained by the design models. Figure 10 shows comparisons of the shear stresses from experimental measurements and DEM simulations using calibrated material properties under a 5 kPa pre-consolidation normal stress. It is very encouraging that the calibrated material properties brought the DEM simulation results for shear stress quite close to the experimental data, which further verifies the feasibility of using the proposed SDoS method for calibrating DEM simulation parameters.

Fig.10 Comparisons of the shear stresses from experimental measurement and DEM simulation using calibrated material properties under a 5 kPa pre-consolidation normal stress.

Full size|PPT slide

5 Conclusions

In this work, a SDoS approach has been proposed to systematically examine the effect of the material properties on measurements from the ring shear test and further used for calibrating the simulation parameters for cohesive lactose powder. JKR model was used in DEM to simulate the effect of cohesion at the interparticle level and shear stress calculated in the numerical simulation was compared with shear stress measured experimentally from ring shear test. The effects of Young’s modulus, surface energy, particle friction, Poisson ratio and restitution coefficient were used as the factors in SDoS. The shear stresses at the pre-shear process and the incipient flows were used as responses to characterize the ring shear tester simulations. The workflow of the SDoS approach includes three phases, namely, screening design, enhancement design and validations. This strategy draws lessons from the divide and conquers principle, that is, break a complicated problem into two or more sub-problems and established primary goals before establishing secondary goals.

As the first phase of the SDoS, a full factorial design is used as a screening design to identify a small number of influential factors that profoundly affect process responses. The design results indicate that the shear stress results from ring shear cell tester are sensitive to particle friction, surface energy and Young’s modulus. In particular, particle friction dominates the shear stress at the pre-shear process and surface energy is the most influencing factor on the shear stress at incipient flows. There is an interaction effect on the particle Young’s modulus and surface energy on the shear stress at incipient flow. Based on the simulation results of full factorial design, it is found that the simulation results can be divided into four flow regimes. Large fluctuation of shear stress is only observed in the high friction and low surface energy regime. The effect of Young’s modulus appears to have a more significant on the shear stress at incipient flow than the pre-shear process under high surface energy regime.

After identifying the influential factors from the screening design, an augment design converting existing screening design to a response surface design has been constructed to investigate a more detail relationship between the factors and the responses for a lactose powder used in the experiments. The optimal material properties were predicted from the response surface fitting and validated with the numerical simulation results. It is shown that the simulations with calibrated parameters can successfully predict the experimental shear stress locus under the training pre-consolidation normal stress. Moreover, additional test cases using the calibrated material properties to predict a different pre-consolidation normal stress condition have been performed and compared with experimental measurements. Good agreement has been achieved between simulations and experiments, which verifies the proposed SDoS workflow for studying and calibrating of cohesive particles. Further works on investigating the performance of using the calibrated material properties to predict the fluidization and entrainment behaviours of dry powder inhalation process are ongoing in our group. Finally, it is shown that a combination of dimesionless Bond number and Tabor number could help scale the DEM simulations of coarse-grained cohesive particles [21]. In the future, it would be interesting to investigate the strategy of using a group of dimesionless numbers for calibration of DEM simulations.

Acknowledgements

The project is funded through Advanced Manufacturing Supply Chain Initiative ‘Advanced Digital Design of Pharmaceutical Therapeutics’ (ADDoPT) project (Grant No. 14060) and the EPSRC grant INFORM 2020 (EP/N025075/1).

Open Access

This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

References

1 Sakai M. How should the discrete element method be applied in industrial systems?: a review. Kona Powder and Particle Journal, 2016, 33: 169–178

2 Guo Y, Curtis J S. Discrete element method simulations for complex granular flows. Annual Review of Fluid Mechanics, 2015, 47(1): 21–46

3 Zhu H, Zhou Z, Yang R, Yu A. Discrete particle simulation of particulate systems: a review of major applications and findings. Chemical Engineering Science, 2008, 63(23): 5728–5770

4 Jarray A, Habibi M, Scheper B J, Shi H, Luding S. Mixing of bidisperse cohesive granular materials in food processes. International Journal of Food Engineering, 2019, 5(3): 195–199

5 Coetzee C J. Review: calibration of the discrete element method. Powder Technology, 2017, 310: 104–142

6 Marigo M, Stitt E H. Discrete element method (DEM) for industrial applications: comments on calibration and validation for the modelling of cylindrical pellets. Kona Powder and Particle Journal, 2015, 32(0): 236–252

7 Roessler T, Katterfeld A. Scaling of the angle of repose test and its influence on the calibration of DEM parameters using upscaled particles. Powder Technology, 2018, 330: 58–66

8 Combarros M, Feise H, Zetzener H, Kwade A. Segregation of particulate solids: experiments and DEM simulations. Particuology, 2014, 12: 25–32

9 Yan Z, Wilkinson S, Stitt E, Marigo M. Discrete element modelling (DEM) input parameters: understanding their impact on model predictions using statistical analysis. Computational Particle Mechanics, 2015, 2(3): 283–299

10 Alizadeh M, Asachi M, Ghadiri M, Bayly A, Hassanpour A. A methodology for calibration of DEM input parameters in simulation of segregation of powder mixtures, a special focus on adhesion. Powder Technology, 2018, 339: 789–800

11 Wensrich C, Katterfeld A. Rolling friction as a technique for modelling particle shape in DEM. Powder Technology, 2012, 217: 409–417

12 Simons T A, Weiler R, Strege S, Bensmann S, Schilling M, Kwade A. A ring shear tester as calibration experiment for DEM simulations in agitated mixers—a sensitivity study. Procedia Engineering, 2015, 102: 741–748

13 Bednarek X, Martin S, Ndiaye A, Peres V, Bonnefoy O. Calibration of DEM parameters on shear test experiments using Kriging method. Powders and Grains 2017. Les Ulis: EDP Sciences, 2017, 15016

14 Schulze D. Powders and Bulk Solids: Behavior, Characterization, Storage and Flow. 1st ed. Berlin Heidelberg: Springer, 2008, 35–74

15 Huang H, Tutumluer E. Discrete element modeling for fouled railroad ballast. Construction & Building Materials, 2011, 25(8): 3306–3312

16 Rackl M, Hanley K J. A methodical calibration procedure for discrete element models. Powder Technology, 2017, 307: 73–83

17 Figard S D. The basics of experimental design for multivariate analysis. In: SAS Global Forum. Buckinghamshire: SAS Institute Inc., 2009, 284

18 Hanley K J, O’Sullivan C, Oliveira J C, Cronin K, Byrne E P. Application of Taguchi methods to DEM calibration of bonded agglomerates. Powder Technology, 2011, 210(3): 230–240

19 Johnstone M, Ooi J. Calibration of DEM models using rotating drum and confined compression measurements. In: 6th World Congress on Particle Technology. Nuremberg, 2010

20 Kloss C, Goniva C, Hager A, Amberger S, Pirker S. Models, algorithms and validation for opensource DEM and CFD-DEM. Progress in Computational Fluid Dynamics, an International Journal, 2012, 12(2-3): 140–152

21 Chen X, Elliott J A. On the scaling law of JKR contact model for coarse-grained cohesive particles. Chemical Engineering Science, 2020, 227: 115906

22 Johnson K, Kendall K, Roberts A. Surface energy and the contact of elastic solids. In: Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. London: The Royal Society, 1971, 301–313

23 Version J M P. 15. Buckinghamshire: SAS Institute Inc., 2019

24 Ajmal M, Roessler T, Richter C, Katterfeld A. Calibration of cohesive DEM parameters under rapid flow conditions and low consolidation stresses. Powder Technology, 2020, 374: 22–32

25 Pachón-Morales J, Do H, Colin J, Puel F, Perre P, Schott D. DEM modelling for flow of cohesive lignocellulosic biomass powders: model calibration using bulk tests. Advanced Powder Technology, 2019, 30(4): 732–750

26 ASTM International. Standard Test Method for Bulk Solids Using Schulze Ring Shear Tester. West Conshohocken, PA: ASTM International, 2016

27 Proust M. Design of Experiments Guide. 1st ed. Cary, NC: SAS Institute Inc., 2010, 298–300

28 Box G E, Hunter W G, Hunter J S. Statistics for Experimenters. 1st ed. New York: John Wiley and Sons, 1978, 173–200

29 Johnson P A, Savage H, Knuth M, Gomberg J, Marone C. Effects of acoustic waves on stick-slip in granular media and implications for earthquakes. Nature, 2008, 451(7174): 57–60

30 Dorostkar O, Carmeliet J. Potential energy as metric for understanding stick-slip dynamics in sheared granular fault gouge: a coupled CFD-DEM study. Rock Mechanics and Rock Engineering, 2018, 51(10): 3281–3294

31 Lieou C K, Daub E G, Guyer R A, Ecke R E, Marone C, Johnson P A. Simulating stick‐slip failure in a sheared granular layer using a physics‐based constitutive model. Journal of Geophysical Research. Solid Earth, 2017, 122(1): 295–307

32 Klaumünzer D N M. Stick-slip shear banding in metallic glasses. Dissertation for the Doctoral Degree. Zurich: Eidgenössische Technische Hochschule Zürich, 2012, 25–56

33 Cabiscol R, Finke J, Zetzener H, Kwade A. Characterization of mechanical property distributions on tablet surfaces. Pharmaceutics, 2018, 10(4): 184

34 Guo Y, Buettner K, Lane V, Wassgren C, Ketterhagen W, Hancock B, Curtis J. Computational and experimental studies of flexible fiber flows in a normal‐stress‐fixed shear cell. AIChE Journal. American Institute of Chemical Engineers, 2019, 65(1): 64–74

35 Aigner A, Schneiderbauer S, Kloss C, Pirker S. Determining the coefficient of friction by shear tester simulation. In: Proceedings of the 3rd International Conference on Particle-Based Methods. Barcelona: CIMNE, 2013, 335–342

36 Ketterhagen W R, Curtis J S, Wassgren C R, Hancock B C. Predicting the flow mode from hoppers using the discrete element method. Powder Technology, 2009, 195(1): 1–10