Design of bio-oil additives via molecular signature descriptors using a multi-stage computer-aided molecular design framework

Abstract

Direct application of bio-oil from fast pyrolysis as a fuel has remained a challenge due to its undesirable attributes such as low heating value, high viscosity, high corrosiveness and storage instability. Solvent addition is a simple method for circumventing these disadvantages to allow further processing and storage. In this work, computer-aided molecular design tools were developed to design optimal solvents to upgrade bio-oil whilst having low environmental impact. Firstly, target solvent requirements were translated into measurable physical properties. As different property prediction models consist different levels of structural information, molecular signature descriptor was used as a common platform to formulate the design problem. Because of the differences in the required structural information of different property prediction models, signatures of different heights were needed in formulating the design problem. Due to the combinatorial nature of higher-order signatures, the complexity of a computer-aided molecular design problem increases with the height of signatures. Thus, a multi-stage framework was developed by developing consistency rules that restrict the number of higher-order signatures. Finally, phase stability analysis was conducted to evaluate the stability of the solvent-oil blend. As a result, optimal solvents that improve the solvent-oil blend properties while displaying low environmental impact were identified.

Key words： computer-aided molecular design; bio-oil additives; molecular signature descriptor

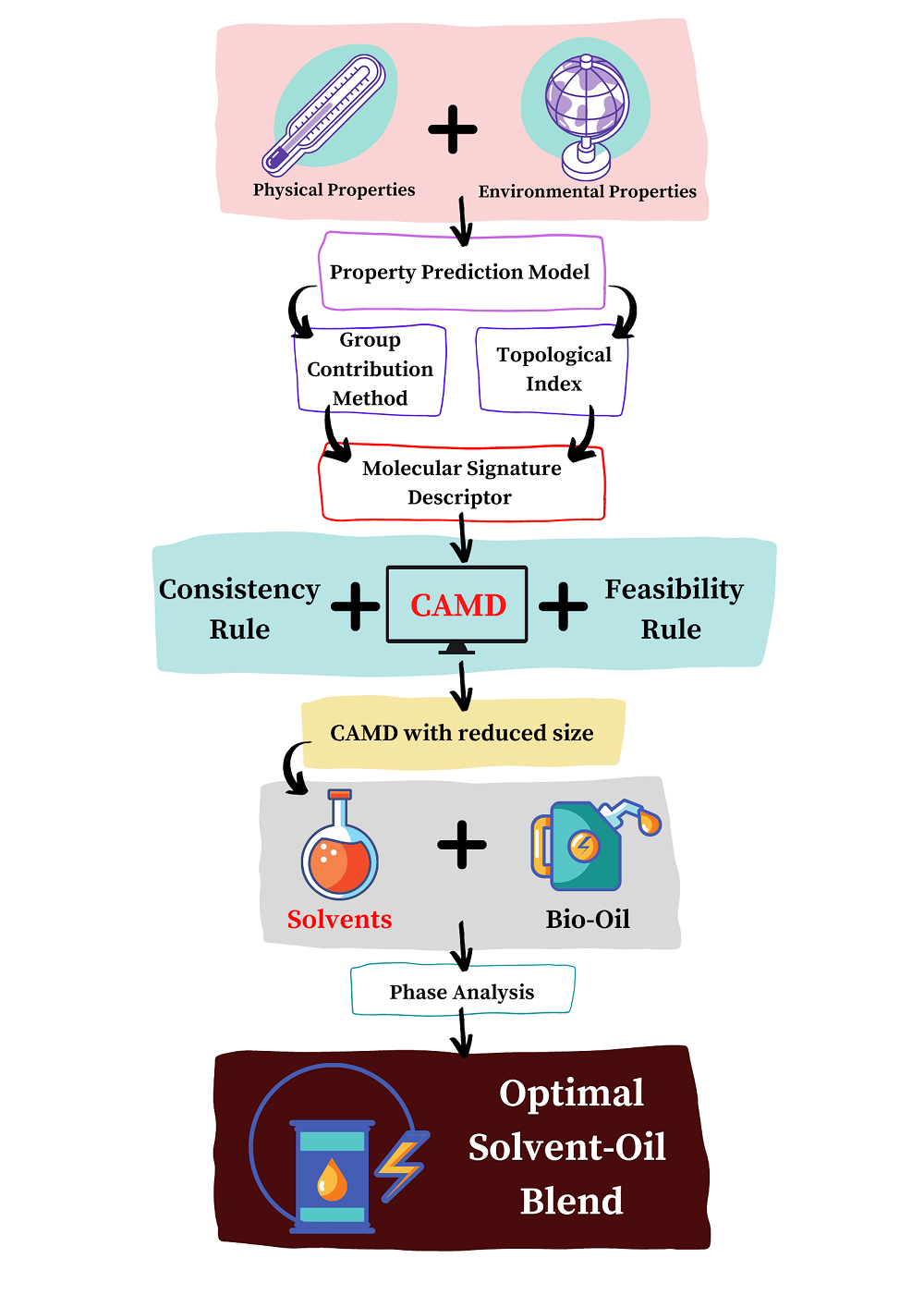
1 Introduction

Biomass is regarded as a relatively clean and renewable energy source originating from plants and animals, which has received increased attention as a potential alternative fuel. A comprehensive review on the state of the art technologies used for converting biomass to biofuel has been reported recently by Lee et al. [1] and Lewandowski et al. [2]. Both these papers review various biomass conversion pathways including thermochemical (i.e., combustion, gasification, liquefaction, pyrolysis and torrefaction) and biochemical (i.e., anaerobic digestion, alcoholic fermentation, fermentation and photobiological hydrogen production). Among these conversion processes, pyrolysis has the advantage of being a relatively simple and inexpensive technology [3]. With pyrolysis, solid biomass can be converted into bio-oil along with biochar and gaseous by-products. However, problems such as thermal and chemical instability, as well as immiscibility with petroleum fuels often hampers the direct application of bio-oil in diesel engines or gas turbines [4]. Besides, poor fuel properties of bio-oil from pyrolysis such as corrosiveness, high viscosity and low heating value limit its application as a biofuel [5]. Solvent addition is one of the most popular bio-oil upgrading methods as it is relatively simple and economically viable [6,7]. Lower viscosity, higher stability and homogenisation of bio-oil can be achieved with the addition of solvents [5]. Moreover, the heating value of bio-oil was found to increase due to the solvent addition [4]. Conventionally, the design of solvents involves a trial-and-error process within a large set of candidates which is tedious, time-consuming and costly [8]. Unlike traditional search and optimisation techniques, a more efficient solvent design can be carried out by utilising computer-aided molecular design (CAMD) tools where molecules possessing desired properties are identified based on the pre-determined product requirements.

CAMD is a reverse engineering approach in which the optimal molecules can be identified from a given set of molecular building blocks and a specified set of targeted properties [9]. In the past, CAMD has been widely incorporated in designing solvents for various applications [10]. A comprehensive review on the solution techniques, applications and future opportunities of CAMD tools are presented in the review articles of Austin et al. [11] and Ng et al. [12]. In addition, more detailed discussion on the development of CAMD applications in the design of solvents can be found in the review articles of Zhou et al. [13] and Chemmangattuvalappil [14]. Other than the abovementioned application areas, the use of CAMD in the design of biofuel additives was reported as well. Hada et al. [15] combined property clustering techniques and characterisation-based group contribution (GC) method in a reverse problem formulation for the design of bio-oil-diesel additives. Khor et al. [16] developed a fuzzy optimisation-based CAMD approach in the design of alternative solvents for recovery of palm pressed fibre’s residual oil. Physical properties of the potential solvent along with safety and health attributes were optimised in the study. Yunus et al. [17] applied CAMD in the solvent design for palm oil residual extraction from spent bleaching earth. The solvent candidates were screened and evaluated by using a simulation software. Mah et al. [18] developed a multi-objective optimisation based CAMD framework for bio-oil solvent design. The trade-off between low solvent ratio and high heating value was determined. Due to the rising awareness on environmental issues and stringent environmental regulations, the demand for green solvent has intensified in recent years [19]. Neoh et al. [20] proposed a two-stage multi-objective optimisation problem for the design of bio-oil additives where environmental, health and safety aspect and fuel functionality were optimised simultaneously. However, the environmental, health and safety aspects considered in this work were limited to those properties for which GC property prediction models are available.

Among the different types of property prediction models, some of the prediction models for environmental or non-thermodynamic properties are derived based on semi-empirical quantitative structure-property relationship (QSPR) and quantitative structure-activity relationship (QSAR) models. QSAR/QSPRs are predictive models derived mathematically, which convert the chemical structures into molecular descriptors that are relevant to a certain physical property or bioactivity [21]. They can be described in terms of GC method and topological index (TI) like connectivity, shape or wiener index. QSAR/QSPRs are often expressed in terms of more than one TI. Different properties may be expressed with different TI as well. However, different TIs exhibit different mathematical expression, which pose challenges in combining and solving it simultaneously on a common platform [22]. To overcome this issue, molecular signature descriptor was introduced, where various GC models and TIs can be expressed on a common platform [23].

Molecular signature descriptor is one of the two-dimensional (2D) fragment-based TI that systematically captures the structural information of a 2D structural formula. It describes the molecular atoms in terms of extended valencies up to a predefined height [24]. Owing to the fact that molecular signature descriptor is known as the canonical representation of a molecule, all other 2D classes of descriptors can be represented in terms of molecular signature [25]. In the past, molecular signature descriptors have been applied in various CAMD fields. QSPR based approach with molecular signature descriptor was applied in the design of novel polymers [26] and novel glucocorticoid receptor ligands with pulmonary selectivity [27]. In Weis and Visco.’s [28] work, ethyl lactate was identified as green industrial solvent by applying the CAMD approach with molecular signature descriptor. Chemmangattuvalappil et al. [29] redefined the TIs by incorporating molecular signature descriptors in the reverse problem formulation framework. The developed algorithm was then applied in the design of alkyl substituent of fungicide. Ng et al. [30] developed a novel two-stage optimisation approach for optimal mixture design in an integrated biorefinery.

Previous research on the design of bio-oil additives focused only on the property targets that can be predicted using GC prediction models with 1st order GCs. However, it is important to incorporate contributions from higher-order molecular groups in CAMD to account for the interactive effects of molecular groups [31]. In addition, the nonavailability of the required GC contributions restricted their applicability in CAMD problem [32]. Moreover, the selected GC model may not have all the model parameters required for the estimation of property of a specific chemical [33]. For this reason, TI approaches can be applied as they are a function of the entire molecular graph, which reflect the entire nature of the molecular structure [11]. Several contributions reported on the application of TIs in the modelling of properties in environmental, pharmacology and toxicology fields for its coverage of larger molecular topology [11]. The main reason for these limitations is because incorporating TI and GC models with higher-order group contributions together is computationally challenging. Thus, molecular signature-based algorithms were introduced in this work to incorporate higher-order molecular groups from GC models and multiple TIs on a common platform for CAMD. Signatures of different height can be used to represent different TI and GC models with higher-order contributions. However, coverage of TIs and higher-order GCs require signatures of higher height due to the requirement of higher structural information. Despite the high accuracy of estimation with the use of signatures of higher height, the complexity of CAMD increases due to the combinatorial nature of higher-order signatures. Having several building blocks will result in a large number of signatures at higher height, which leads to difficulties in modelling and solving the CAMD problem. Hence, the height of signatures has to be lowered in order to be used in a CAMD formulation. However, not all the signatures considered in the CAMD problem are consistent with each other to form a feasible molecule. Thus, a consistency rule was developed in this work to reduce the size of CAMD problem by excluding irrelevant molecular signature at a lower height from the building block sets. Infeasible signatures (signature that do not fulfil the consistency rules) are systematically eliminated at different levels and this can help to keep a manageable problem size. With the help of consistency rules, it is possible to apply molecular signature descriptors in designing molecules with all promising building blocks while also considering appropriate GC prediction models with higher-order contributions and QSPRs with different TIs. After determining all the possible additives, the accuracy of the estimated higher heating value of solvent candidates was verified through a database search. Other than the thermodynamic properties, Gibbs free energy of mixing was estimated to evaluate the miscibility of solvent-oil blend. Phase behaviour analysis on solvent-oil-water blend was presented by plotting the Gibbs phase ternary graphs. On the other hand, the stability of the solvent-oil blend was determined by computing tangent plane distance. Sensitivity analysis was conducted on bio-oil’s water content to investigate its effect on the solvent ratio and miscibility of the final solvent-oil blend. Finally, an optimum solvent that improves the solvent-oil blend properties and stability was generated.

2 Experimental

The main objective of this work is to develop a systematic multi-stage framework in reducing the size of CAMD problem due to the combinatorial nature of molecular signature descriptor. Solvents that form stable blends with bio-oil and possess optimal properties can be generated with this framework by considering physical, environmental and thermodynamic properties. An algorithm of GC method coupled with TI approach was used to solve the multiple property indexes involved in the CAMD problem. This framework can be divided into 4 main stages and their correlated sub-steps are shown in Fig. 1.

Fig.1 Framework for the development of CAMD model for the design of solvent.

Full size|PPT slide

2.1 Step 1: problem definition

Firstly, the problem definition was formulated, where the product needs were determined based on the requirements from regulations and specifications. This usually requires data on physical and thermodynamic properties as they contribute to the functionality of the product. In addition, environmental properties were considered to ensure that the generated solvent molecules have low environmental impact. The selected desired properties will serve as the design objective to generate molecules.

The identified product requirements were then translated into measurable quantitative target properties. For example, the flow consistency of solvent can be expressed in terms of its density and viscosity. These identified target properties will either be used as constraints or optimisation objective in the CAMD formulation stage. Upper and lower limits were defined for these target properties to ensure the designed solvents display similar physical characteristics as a conventional solvent.

2.2 Property prediction models

In this step, suitable property prediction models were identified to compute the target properties of the solvent. In this work, property prediction models in terms of GC method and TI were considered and expressed as a function of the molecular signature descriptor. For GC-based property prediction models, higher-order molecular groups show higher prediction quality compared to the 1st order approach. In this work, higher-order molecular groups (2nd and 3rd order groups) along with the basic molecular building blocks (1st order) have been considered. Molecular signatures of desirable heights were generated based on the root atoms and chemical families selected for the solvent design. The height and number of signatures required to describe the molecular group in GC models depend on the number of atoms present for the molecular structure and the nature of the final molecule. Thus, maximum signature height for the CAMD problem can be determined from the available property prediction models.

2.3 Step 2: CAMD formulation

The CAMD optimisation model was represented using the following set of generalised mathematical expressions [11]:

(1)F_{\mathrm{obj}}=\max F(x,p),

(2)p=f(x),

(3)h_{\mathrm{1}}(p,x)\le \mathrm{0},

(4)h_{\mathrm{2}}(p,x)=\mathrm{0},

(5)s_{\mathrm{1}}(x)\le \mathrm{0},

(6)s_{\mathrm{2}}(x)=\mathrm{0},

(7)p_k^{\mathrm{L}}\le p_k\le p_k^{\mathrm{U}}\forall k,

(8)x_d^{\mathrm{L}}\le x_d\le x_d^{\mathrm{U}}\forall d.

For the above expressions, p is the vector of properties and p_k is the property values for each property k. Meanwhile, n is the vector representing the structural information of designed molecules. The x_d vector indicates the number of occurrences of each molecular signature d. The function f then transforms this structural information into a property estimate using the appropriate QSPR relationship. Equation (1) is a general objective function for the CAMD problem. The F(x,p) is known as the vector of objective function which quantify the performance of the designed molecule based on its properties p. The F function can either be maximised or minimised depending on the design problem. Equation (2) is the function f which estimates vector of properties p from attributes such as number of molecular signatures. Equations (3) and (4) are the general function representing the inequality and equality constraints, respectively. These equations correspond to product design specifications such as property’s value for thermodynamic and environmental properties. As the property depends on the presence of signatures, these constraints can control the number of appearances of specific signatures in the designed molecule. As for Eqs. (5) and (6), they are the general function representing the inequality and equality constraints, respectively, related to the molecular structure generation. These structural constraints ensure the generated molecule is structurally feasible. Equations (7) and (8) are the boundaries set on property values and the number of signatures.p_k^{\mathrm{L}} and x_d^{\mathrm{L}} are the lower bounds for property k and x_d, respectively. Similarly, p_k^{\mathrm{U}} and x_d^{\mathrm{U}} are the upper bounds for property k and x_d, respectively.

For the CAMD problem, the function f(x)may be formulated as a mixed-integer nonlinear program. However, due to the increasing size of the mathematical problem, it is usually challenging to solve such a mixed-integer nonlinear program problems with the structural information included [34]. In this work, molecular signature descriptors were used to present the CAMD problem as an equivalent mixed-integer linear program. The 2D descriptor (both TI and GC models) of molecule G, TI(G) can be expressed as a dot product between two vectors,{}^h{\alpha }_g , the vector of occurrence number of atomic signatures of height h, and TI(\mathrm{root}({}^h{\sum }^{\mathrm{}})), the vector of predicted values from the model computed for each of the atomic signatures as shown in (Eq. (9)):

(9)TI(G)=k^h{\alpha }_g\cdot TI(\mathrm{root}({}^h{\sum }^{\mathrm{}})).

By using the signatures, the non-linear part of the mathematical formulation can be hidden inside the molecular signature building blocks. As shown in Eq. (9), the prediction model is expressed as linear equation, where the only variable is the number of respective building blocks, which are atomic signatures. In each of the building blocks, contribution to the property can be estimated using the original property prediction model. When GC model was used for property prediction, the term in the bracket refers to the property contribution from the signature that represents the set of molecular groups present in the higher-order groups. In CAMD, since the structure of molecule is not known prior to the design, the presence of higher-order groups is not known during the design. Molecular signatures were used to track the presence of all possible 2nd and 3rd order contributions by considering a signature height of 2 or 3. These models can be linear or non-linear. However, since these non-linear expressions were only used in the estimation of contribution of the building blocks, hence it will not be part of the variables. The only variable involved will be the number of appearances of each signature. Considering the prediction model for normal melting point, T_m as an example (Eq. (10)) [31].

\exp \left({\displaystyle \frac{T_m}{T_{m\mathrm{0}}}}\right)={\displaystyle {\sum }_i{N}_i{T}_{mi}}+{\displaystyle {\sum }_i{M}_j{T}_{mj}}+{\displaystyle {\sum }_i{O}_k{T}_{mk\mathrm{}}},

(10)

where N_i, M_j and O_kare the number of individual building blocks from 1st order, 2nd order and 3rd order groups, respectively. T_{mi}, T_{mj} and T_{mk}are the contributions for 1st order, 2nd order and 3rd order groups, respectively. T_m0 = 147.45 K; T_m is the normal melting point and was set to be lower than 298.15 K. The exponential term, \exp \left({\displaystyle \frac{T_m}{T_{m\mathrm{0}}}}\right) at the left-hand side of Eq. (10) contributes to the non-linearity of the expressions. By substituting and solving the left-hand side of the equation, the prediction model is now a linear equation, as shown in Eq. (11). The only variable in the equation is the number of building blocks.

(11)\mathrm{7.554}>{\displaystyle {\sum }_i{N}_i{T}_{mi}+}{\displaystyle {\sum }_i{M}_j{T}_{mj}+{\displaystyle {\sum }_i{O}_k{T}_{mk}}}

However, this approach will lead to the generation of a substantial amount of molecular signature building blocks to be considered for CAMD. To address this issue, a multi-level approach has been developed where the amount of generated molecular signature building blocks can be controlled.

2.3.1 Feasibility rules

To ensure the feasibility of the final molecule, the selected signature building blocks should fulfil the requirements to form effective solvents. An efficient, structured algorithm for joining groups to form feasible chemical compounds was integrated into the signature based CAMD [35,36]. Generally, molecules are reported to be unstable if two heteroatoms are bonded to the same carbon atom, and at least one of the atoms is also bonded to a hydrogen atom. Combination like heteroatom bonding with another should be avoided as these compounds are usually highly reactive and not suitable to be considered as solvents. Constraints from the work of van Dyk & Nieuwoudt [36] classified the groups of molecules according to the type of free bonds as shown in Table 1. In general, Table 2 can be summarised based on Eq. (12):

n_{\mathrm{4}}+n_{\mathrm{5}}\ge n_{\mathrm{1}}+n_{\mathrm{2}},

(12)

where n_{iis the total number of free bond group i in the molecule.}

Tab.1 Free bond groups in terms of signature of height 2

Group	Description	Example
I	Bonding atom is a heteroatom bonded to a hydrogen atom	O1(C2(CO))
II	Bonding atom is a heteroatom bonded to a carbon atom	O2(C2(CO)C3(CCO))
III	Bonding atom is a carbon atom bonded to a heteroatom, which is bonded to a hydrogen atom	C2(O1(C)C2(CC))
IV	Bonding atom is a carbon atom bonded to a heteroatom, which is bonded to a carbon atom	C2(O2(CC)C2(CC))
V	Bonding atom is a carbon atom bonded to another carbon atom	C2(C2(CC)C3(CCC))

Tab.2 Allowed combination of groups

Group	I	II	III	IV	V
I	×	×	×	×	√
II	×	×	×	√	√
III	×	×	√	√	√
IV	×	√	√	√	√
V	√	√	√	√	√

As some of the property prediction models used GC method, signature descriptors were translated and assigned to their corresponding groups from GC method. Only the root atom of each atomic signature was considered to prevent the overlapping issues during the property estimation. Taking the molecular signature C2(CC), the root atom C was connected to 2 carbon atoms by single bonds and the rest was bonded to hydrogen atoms. Thus ‘CH₂’ is the corresponding GC group for this signature. In another example, the signature C4 (=CCO) has the root atom C connected to an oxygen and two carbons by single and double bonds, respectively. To ensure no overlapping of groups, the simplest equivalent group was chosen. In this case, the group ‘C=C’ was chosen.

2.3.2 Structural constraints

Structural constraints are essential in a CAMD problem to ensure the formation of a complete molecular graph with all signatures connected in order to generate a feasible solution. The structural constraints used in molecular signature-based algorithms must follow a few rules in order to generate a complete structure [29]: (I) Signatures must be connected without any free bonds in the structure. Thus, the total number of available degrees (valencies) should be matching with the total number of vertices (atoms) in the graph (molecules). (II) The number of bonds in each signature should be consistent with the bonds of the rest of signatures.

Table 3 shows the mathematical expressions of structural constraints for rule (I) and (II). Equation 13 was developed to express the relation between the number of signatures and the bonds where n_{\mathrm{1}}, n_{\mathrm{2}}, n_{\mathrm{3}}, and n_{\mathrm{4}} are the number of signatures x_i with valency of one, two, three and four, respectively. Here N_{Di}, N_{Mi} and N_{Ti} are the signatures with one double bond, two double bond and one triple bond, respectively [29]. Meanwhile, rule (II) can be mathematically represented as equation 14, which must be fulfilled by all colour sequences, including colour sequences in which i=j at each height. The expression {(l_i\to l_j)}_h is for colouring sequence l_i\to l_j at level h [29].

Tab.3 Mathematical expression for structural constraints

Rule	Structural constraint	Equation
I	{\displaystyle \sum }_{i=\mathrm{1}}^{n_{\mathrm{1}}}{x}_i+\mathrm{2}{\displaystyle \sum }_{n_{\mathrm{1}}}^{n_{\mathrm{2}}}{x}_i+\mathrm{3}{\displaystyle \sum }_{n_{\mathrm{2}}}^{n_{\mathrm{3}}}{x}_i+\mathrm{4}{\displaystyle \sum }_{n_{\mathrm{3}}}^{n_{\mathrm{4}}}{x}_i=\mathrm{2}\left[\left({\displaystyle \sum }_{i=\mathrm{1}}^N{x}_i+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \sum }_{i=\mathrm{0}}^{N_D{}_i}{x}_i+{\displaystyle \sum }_{i=\mathrm{0}}^{N_M{}_i}{x}_i+{\displaystyle \sum }_{i=\mathrm{1}}^{N_T{}_i}{x}_i\right)-\mathrm{1}\right]	(13)
II	{\sum }^{\mathrm{}}{(l_i\to l_j)}_h={\sum }^{\mathrm{}}{(l_j\to l_i)}_h	(14)

2.3.3 Consistency rules

The CAMD problem was initially solved at height 1 level to identify promising signatures generated from the previous stage. Subsequently, height 2 signatures were generated based on the identified height 1 signatures. However, to ensure the final generated molecule is structurally feasible, only signatures that fulfil the structural constraints were considered.

To generate a feasible molecular structure from the signature building blocks, each signature must be connected to another signature that with the same structure at a level h−1. An example on the enumeration of molecular structures from signatures are shown in Table 4. The collection of signatures presented in this example is one of the solutions obtained for the bio-oil solvent case study in section 3.

Tab.4 Set of signatures for 2-octanol with its corresponding height 2 signatures

No.	Height 3 signature	Corresponding height 2 signature
1	C1(C3(C1(C)C2(CC)O1(C)))	C1(C3(CCO)
2	C1(C2(C1(C)C2(CC))	C1(C2(CC))
3	C2(C1(C2(CC))C2(C2(CC)C2(CC)))	C2(C1(C)C2(CC))
4	C2(C2(C1(C)C2(CC))C2(C2(CC)C2(CC)))	C2(C2(CC)C2(CC))
5	C2(C2(C2(CC)C2(CC))C2(C2(CC)C2(CC)))	C2(C2(CC)C2(CC))
6	C2(C2(C2(CC)C2(CC))C2(C2(CC)C3(CCO)))	C2(C2(CC)C2(CC))
7	C2(C2(C2(CC)C2(CC))C3(C1(C)C2(CC)O1(C)))	C2(C2(CC)C3(CCO))
8	C3(C1(C3(CCO))C2(C2(CC)C3(CCO))O1(C3(CCO)))	C3(C1(C)C2(CC)O1(C))
9	O1(C3(C1(C)C2(CC)O1(C)))	O1(C3(CCO))

Firstly, any signature of height 3 was selected. In this case, signature (1), C1(C3(C1(C)C2(CC)O1(C))) was selected. Next, it was inferred that there is only one signature possible from the first layer, which is C3(C1(C)C2(CC)O1(C)). From Table 4, it is observed that the height 2 signatures for signature (8), C3(C1(C3(CCO))C2(C2(CC)C3(CCO))O1(C3(CCO))) was exactly same as the signature from the first layer. Thus, signature (1) was connected with signature (8). The same procedure was then repeated on signature (8) to get the next bond. In this study, an algorithm was developed based on the graph signature enumeration method by Faulon [37].

In the developed approach, signatures of height h were generated based on the collection of height h−1 signatures identified from the CAMD problem. The first layer of signature generated must contain one of the height h−1 signatures from the previous result. For example, assuming the signatures C1(C), C2(CC), C2(CO) and C3(CCO) were identified as the promising height 1 signature from the CAMD problem, the generated height 2 signatures based on C1(C) are shown as below:

1. C1(C2(CC))

2. C1(C2(CO))

3. C1(C3(CCO))

With this approach, the total number of generated height 2 signatures was reduced from 13 signatures to 3 signatures. In another example, taking the collection of height 2 signatures, the following set is obtained:

1. C1(C3(CCO)

2. C1(C2(CC))

3. C2(C1(C)C2(CC))

4. C2(C2(CC)C2(CC))

5. C2(C2(CC)C3(CCO))

6. C3(C1(C)C2(CC)O1(C))

7. O1(C3(CCO))

In this case, height 3 signatures generated based on the signature (3), C2(C1(C)C2(CC)) are listed as:

1. C2(C1(C2(CC))C2(C1(C)C2(CC)))

2. C2(C1(C2(CC))C2(C2(CC)C2(CC)))

3. C2(C1(C2(CC))C2(C2(CC)C3(CCO)))

Similar approach was applied to the rest of signatures to generate the remaining height 3 signatures.

2.4 Step 3: verification

Verification step is crucial to ensure that the molecules generated from previous steps are feasible and practical. In this step, generated molecules were verified through database search from various platforms like ChemSpider, PubChem, etc. For compounds that exist in the database, comparison was made to verify the property values obtained from the CAMD result. As for compounds that do not exist in the database or proved to be infeasible, the previous step was repeated by modifying the property attributes and constraints.

2.5 Step 4: miscibility analysis

It is crucial to ensure the designed solvent is miscible with bio-oil-diesel blend to avoid phase separation in the final solvent-oil blend. Phase stability test was conducted by computing the tangent plane distance. For an n-component mixture at constant temperature and pressure, the phase stability analysis employed the Gibbs tangent plane distance function as shown in (Eq. (15)) [38]:

(15)d(x)={\displaystyle \sum }_{i=\mathrm{1}}^n{x}_i[\ln x_i{\gamma }_i(x)-\ln z_i{\gamma }_i(z)],

where, z is the compositions of component i in mole fractions of the tested phase, x is the composition component i of a trial phase and γ indicates the activity coefficient of component i in respective phase. For mixture that is stable and exhibits homogenous single-phase, the following (Eq. (16)) can be followed [38]:

(16)d(x)\ge \mathrm{0.}

The solvent-oil blend was said to be stable if the tangent plane distance is non-negative. If otherwise, step 1 to step 4 will be revisited by modifying the property attributes and constraints.

3 Results and discussion

3.1 Defining target properties and constraints

The main objective of the designed solvent is to improve the physical properties of the bio-oil. The designed solvent should always be in a liquid state at room temperature for ease of handling and storage. Thus, the constraints for normal melting and boiling points of solvent were set at 298.15 K and 400.15 K, respectively. On the other hand, a greater higher heating value is preferable for better fuel combustion. In present work, higher heating value for the designed solvent was maximized, which serves as the objective function. Besides, the final bio-oil-diesel blends are expected to display good continuous flow. Solvent additives should exhibit high miscibility in bio-oil to ensure the homogeneity of the final product. Finally, the solvent additive should also comply with environmental regulations set by authorities for low environmental impact. The generated solvents should possess low toxicity with minimal accumulation in both land and aquatic ecosystem. The final bio-oil-diesel blend should be environmentally sustainable, which is usually measured by the global warming potential [39]. In order to reduce the formation of photochemical smog, low photochemical oxidation potential is expected for the final bio-oil-diesel blend [40]. Constraints for the properties mentioned above were defined according to the ASTM D6751 and EN:14214 standards. Table 5 shows the respective targeted properties and identified constraints for each product requirements.

Tab.5 Translation of product requirements into target properties and constraints

Requirement/need	Targeted property	Constraint
Liquid state at room temperature	Normal boiling point/K	>400.15
	Normal melting point/K	<298.15
Fuel combustion quality	Higher heating value	To be maximised
Fuel flow consistency	Viscosity/(mPa·s)	1>\nu>6
	Density/(kg·m–3)	800>\rho>1000
Homogenous form	Tangent plane distance	To be determined
Environmental related properties and toxicology	Aquatic acute toxicity, LC50	>100
	Aquatic acute toxicity, EC50	>100
	Oral acute toxicity, LD50	>100
	Bioconcentration factor	<1000
	Soil-water partition coefficient/(L·kg–1)	<31622
	Global warming potential	<10
	Photochemical oxidation potential	<10

3.2 Selecting appropriate property prediction model

Based on the target properties identified in the previous section, the respective property prediction models were selected to estimate the properties of the designed solvents as shown in Table S1 (cf. Electronic Supplementary Material, ESM). In this case study, the chosen property prediction models were expressed in terms of GC method and connectivity index. These property prediction models require different degree of details on the structural knowledge to estimate the properties of the designed molecules. Different TI and GC models require different levels of structural information. Thus, the targeted signature height depends on the required structural information of the TI or GC models. Signatures with higher height contain more structural information of the molecules. It is possible to enumerate the lower order signature from a higher-order signature. Thus, signatures of lower height can be estimated as the sum of higher-order signatures. For GC models, higher-order (2nd and 3rd order) groups were considered as they can provide a better description on the interaction between 1st order groups and the effects of certain molecular group combinations to the property of a molecule. Despite the higher accuracy of estimation for complex compounds, higher-order GC groups require more details on structural knowledge. Generally, a 2nd order group from GC method can be represented in a molecular signature of height 2 or 3, with examples shown in Table 6. Other than GC models, the height of signature also dependents on the TI models. For instance, 1st order connectivity index requires signature of height 2; 2nd order connectivity index requires signature of height 3, etc. From Table S1, the prediction model for octanol/water partition coefficient requires connectivity index of 3rd order. Therefore, the maximum signature height required in this problem was set at 4. However, all possible height 4 signatures need to be generated to solve the CAMD problem using molecular signature descriptor. As the height of signature increases, the possible combination of molecular signature increases as well. In this case study, the number of generated height 4 signatures was expected to exceed 100000 signatures. Pre-screening was conducted by applying feasibility rules on the generated signatures. As a result, the total number of height 4 signatures was reduced to around 10000 signatures.

Tab.6 Example of 2nd order group expressed in terms of signature of height 2 or 3

2nd order group	Molecular signature
(CH3)2CH	C3(C1(C)C1(C)C2(CC))
CH(CH3)CH(CH3)	C3(C1(C3(CCC)) C1(C3(CCC)) C3(C3(CCC)C1(C)C1(C))
CH3COOCH	C4(C1(C4(=OOC) =O2(=C4(=OOC) O2(C4(=OOC)C2(CO)))

3.3 CAMD formulations

The atoms that are commonly present in solvents, which includes: H, C, N and O were chosen for the design of bio-oil additive. The hydrocarbon groups considered in this study were limited to alkanes, alkenes, alcohol, carboxylic acid, ketones, aldehyde, esters, ethers and nitriles which can be predominately found in solvents. The chemicals groups are listed in Table S2 (cf. ESM) [32].

In the first step, the signatures of height 1 were generated based on the selected atoms’ type and chemical families, resulting in a total of sixty five different molecular signature combinations. By applying feasibility rules mentioned in section 2.3.1, the set of height 1 signatures was then reduced to a total of twenty four signatures. As some of the property prediction models were expressed in GC method, signature descriptors were translated and assigned to their corresponding groups from GC method as shown in Table S3 (cf. ESM). The CAMD problem was then solved using global solver by LINGO extended version 18.0.56. By solving the CAMD problem, five height 1 signatures were identified as promising signature candidates as shown in Table 7.

Next, height 2 signatures were generated based on these five identified signatures of height 1. From Fig. 2, a total of one hundred and fourty seven height 2 signatures were generated if only pre-screening step was conducted. Taking C1(C) from the resulting signature of height 1 candidates as an example, a total of twenty three signatures were generated by considering only the feasibility rules. However, not all these twenty three signatures were consistent with each other to form a feasible molecule. By applying the consistency rule, only three signatures out of the twenty three signatures can fulfil the requirement, which include:

1. C1(C3(CCO))

2. C1(C2(CC))

3. C1(C2(CO))

Fig.2 Generation of height 2 signature based on the height 1 signature, CI(C).

Full size|PPT slide

Same approach was applied to the remaining four height 1 signatures as shown in Fig. 2. As a result, a total of seventeen height 2 signatures were generated by applying both feasibility and consistency rules. The generated height 2 signatures together with their corresponding GC group are shown in Table S4 (cf. ESM). The CAMD problem was then solved again for the seventeen height 2 signatures set. As a result, seven signatures from the height 2 set were identified as promising signature candidates. Similar methodology was then applied to generate height 3 and height 4 signatures. List of generated height 3 and height 4 signatures are shown in Tables S5 and S6 (cf. ESM). With this approach, the signature set size was reduced from a set of more than ten thousand height 4 signatures to the final twenty one height 4 signatures. Finally, the CAMD problem was solved and promising molecular signatures of height 4 identified are tabulated in Table 7.

Tab.7 Potential height 1, 2, 3 and 4 signatures generated

No.	Signature
	Height 1
S1	C1(C)
S4	C2(CC)
S5	C2(CO)
S11	C3(CCO)
S22	O1(C)
	Height 2
D1	C1(C3(CCO))
D2	C1(C2(CC))
D4	C2(C1(C)C2(CC))
D7	C2(C2(CC)C2(CC))
D9	C2(C2(CC)C3(CCO))
D14	C3(C1(C)C2(CC)O1(C))
D17	O1(C3(CCO))
	Height 3
T1	C1(C3(C1(C)C2(CC)O1(C)))
T2	C1(C2(C1(C)C2(CC)))
T4	C2(C1(C2(CC))C2(C2(CC)C2(CC)))
T7	C2(C2(C1(C)C2(CC))C2(C2(CC)C2(CC)))
T9	C2(C2(C2(CC)C2(CC))C2(C2(CC)C2(CC)))
T10	C2(C2(C2(CC)C2(CC))C2(C2(CC)C3(CCO)))
T12	C2(C2(C2(CC)C2(CC))C3(C1(C)C2(CC)O1(C)))
T13	C3(C1(C3(CCO))C2(C2(CC)C3(CCO))O1(C3(CCO)))
T14	O1(C3(C1(C)C2(CC)O1(C)))
	Height 4
Q1	C1(C3(C1(C3(CCO))C2(C2(CC)C3(CCO))O1(C3(CCO))))
Q2	C1(C2(C1(C2(CC))C2(C2(CC)C2(CC))))
Q3	C2(C1(C2(C1(C)C2(CC))C2(C2(C1(C)C2(CC))C2(C2(CC)C2(CC))))
Q7	C2(C2(C1(C2(CC))C2(C2(CC)C2(CC)))C2(C2(C2(CC)C2(CC))C2(C2(CC)C2(CC))))
Q12	C2(C2(C2(C1(C)C2(CC))C2(C2(CC)C2(CC)))C2(C2(C2(CC)C2(CC))C2(C2(CC)C3(CCO))))
Q15	C2(C2(C2(C2(CC)C2(CC))C2(C2(CC)C2(CC)))C2(C2(C2(CC)C2(CC))C3(C1(C)C2(CC)O1(C))))
Q18	C2(C2(C2(C2(CC)C2(CC))C2(C2(CC)C3(CCO)))C3(C1(C3(CCO))C2(C2(CC)C3(CCO))O1(C3(CCO))))
Q20	C3(C1(C3(C1(C)C2(CC)O1(C)))C2(C2(C2(CC)C2(CC))C3(C1(C)C2(CC)O1(C)))O1(C3(C1(C)C2(CC)O1(C))))
Q21	O1(C3(C1(C3(CCO))C2(C2(CC)C3(CCO))O1(C3(CCO))))

The molecular structures of promising solvents were generated from the identified height 4 signature building blocks. Database search for the feasible molecules was then carried out. The feasible solvent molecules were identified as 2-octanol, 2-heptanol, 2-hexanol and 2-pentanol, respectively. Higher heating value of the identified solvent candidates were verified through NIST’s (National Institute of Standards and Technology) database as shown in Table 8 [41]. The higher heating value estimated in present work for the abovementioned solvent candidates were close to the actual higher heating value obtained from NIST database, with less than 1% differences. According to Eq. (17), the higher heating value for the final solvent-oil blend was expected to increase as the amount of solvent fraction increases. However, the solvent-oil blend will be mixed with a large portion of diesel, forming a solvent-oil-diesel blend. Thus, effect of the amount of solvent added on the higher heating value of solvent-oil blend will be negligible as compared to the amount of diesel present in the blend.

(17)HH{V}_{\mathrm{mix}}={\sum }^{\mathrm{}}{x}_{i}HH{V}_i.

Tab.8 Higher heating values obtained from NIST’s database and present work for respective solvent candidates

Molecular name	Higher heating value from NIST/(MJ·kg–1)[41]	Higher heating value/(MJ·kg–1)
2-Octanol	40.66	40.89
2-Heptanol	39.72	40.00
2-Hexanol	38.98	38.92
2-Pentanol	37.72	37.50

Other than contributing to the higher heating value of bio-oil, the solvent candidates also play a major role in improving the miscibility of the final blend. With the absence of solvent, strong intermolecular forces of the bio-oil will attract the molecules instead of dispersing in aqueous phase and petroleum fraction [42]. However, the amphiphilic properties of the identified solvent candidates are capable to help in dispersion of the bio-oil. Phase stability was conducted by computing the tangent plane distance for the four identified solvent molecules. Sensitivity analysis on the phase behaviour of solvent-oil blend was also conducted for different water content. The average water mass fraction for crude pyrolysis bio-oil was reported to be around 38%–42% [43]. Thus, crude pyrolysis bio-oil containing 40 wt-% of water was considered as the maximum water content. In order to investigate the effect of water content on the final blend’s miscibility, bio-oil with reduced water content will also be considered in the analysis. The water content in bio-oil can be reduced to 16 wt-% by eliminating the aqueous phase. In addition, water content of 25 wt-% was taken as the median value and considered in the sensitivity analysis. Figure 3 shows the Gibbs energy and tangent plot for 2-octanol-oil blend at 16% (Fig. 3(a)), 25% (Fig. 3(b)) and 40% water content (Fig. 3(c)), respectively. The optimal mole fraction obtained for 2-octanol was 0.805, 0.83 and 0.85 at bio-oil’s water content of 16%, 25% and 40%, respectively. The amount of solvent required in the solvent-oil blend increases slightly as the water content in bio-oil increases. Similar trends were obtained for 2-heptanol-, 2-hexanol- and 2-pentanol-oil blends where the Gibbs energy and tangent plots for these solvent-oil blends are shown in Figs. S1–S3. From Figs. 3(a), 3(b) and 3(c), the blend of 2-octanol and bio-oil is stable and exhibit homogenous single-phase as the tangent line was plotted below the Gibbs curve. This could be explained by the presence of –OH group in the solvent’s molecular structure which aids in promoting miscibility of the blend.

Fig.3 Gibbs energy and tangent plot for 2-octanol and bio-oil (a) 16% water content, (b) 25% water content, and (c) 40% water content.

Full size|PPT slide

Besides, a ternary phase diagram was plotted for the mixtures of bio-oil, water and 2-octanol (solvent) to evaluate the miscibility of final blend at various mixing compositions. In the phase diagram (Fig. 4), the red dots represent the immiscible blend while the green dots represent the miscible blend. The solvent-oil-water blend was miscible over most of the composition range. However, the blend was immiscible at the mixing ratio, 2-octanol:bio-oil:water of 0:10:90 and 10:0:90. Similar results were obtained for 2-heptanol-, 2-hexanol- and 2-pentanol-oil-water blends, as shown in Fig. S4.

Fig.4 Gibbs phase ternary graph of bio-oil, water and 2-octanol.

Full size|PPT slide

Table 9 summarises the key properties and information of the identified candidate solvents. All the resulting molecules possess a higher heating value of at least 37.5 MJ·kg^–1. The solvent-oil blends were expected to be homogenous as the tangent plane distance calculated is non-negative for all solvent candidates. It can be concluded that 2-octanol is the most suitable solvent candidate with the highest higher heating value at 40.89 MJ·kg^–1.

Tab.9 The identified feasible solvent candidates

Molecular name	Formula	Molecular structure	Higher heating value/(MJ·kg–1)	Miscibility
2-Octanol	CH3(CH2)5CH(OH)CH3		40.89	Miscible
2-Heptanol	CH3(CH2)4CH(OH)CH3		40.00	Miscible
2-Hexanol	CH3(CH2)3CH(OH)CH3		38.92	Miscible
2-Pentanol	CH3(CH2)2CH(OH)CH3		37.50	Miscible

4 Conclusions

In this work, CAMD tools were developed to design an optimal solvent that can upgrade bio-oil while possessing low environmental impact. At the initial stage, additive requirements were determined and translated into target properties. Suitable property prediction models to estimate the targeted physicochemical and environmental properties were identified. Different property prediction models possess different structures and require different topological information. In this work, GC and TI based property prediction models were used for property estimations. Molecular signature descriptors were then applied in the problem to represent different indices in the prediction models. In addition, relevant structural constraints were incorporated in the model to ensure the feasibility of the designed molecules. To represent higher-order of GC groups, higher height of signature building blocks were needed. Multi-stage approach was used to reduce the size of problem due to the combinatorial nature of higher-order signatures. Moreover, consistency rules were applied to ensure only relevant and consistent signatures are generated. After generating feasible molecules, tangent plane distance was computed to evaluate the miscibility and stability of the solvent-oil blend. From the case study, 2-pentanol, 2-hexanol, 2-heptanol and 2-octanol were identified as the promising solvents candidates. Database verification was conducted on the higher heating value for all solvent candidates. Among the identified solvents, 2-octanol was selected as the most promising solvent candidate with a higher heating value of 40.89 MJ·kg^–1 along with other desirable attributes. To conclude, the developed methodology in this work can be applied in the design of solvents for any application. Further improvements can be made by considering the addition of emulsifiers and/or reactive solvents in the design of additives for bio-oil upgrading purposes. In addition, life cycle sustainability assessment should also be conducted to ensure the sustainability of solvent-oil blend.

Acknowledgements

The authors would like to express sincere gratitude to Ministry of Higher Education Malaysia for the realization of this research project under the Grant FRGS/1/2019/TK02/UNIM/02/1. However, only the authors are responsible for the opinion expressed in this paper and for any remaining errors.

Electronic Supplementary Material

Supplementary material is available in the online version of this article at https://dx.doi.org/10.1007/s11705-021-2056-8 and is accessible for authorized users.

References

1 Lee S Y, Sankaran R, Chew K W, Tan C H, Krishnamoorthy R, Chu D T, Show P L. Waste to bioenergy: a review on the recent conversion technologies. BMC Energy, 2019, 1(4): 1–22

2 Lewandowski W M, Ryms M, Kosakowski W. Thermal biomass conversion: a review. Processes, 2020, 8(5): 516

3 Fermoso J, Pizarro P, Coronado J M, Serrano D P. Advanced biofuels production by upgrading of pyrolysis bio-oil. Wiley Interdisciplinary Reviews. Energy and Environment, 2017, 6(4): 1–18

4 Khosravanipour Mostafazadeh A, Solomatnikova O, Drogui P, Tyagi R D. A review of recent research and developments in fast pyrolysis and bio-oil upgrading. Biomass Conversion and Biorefinery, 2018, 8(3): 739–773

5 Yang H, Yao J, Chen G, Ma W, Yan B, Qi Y. Overview of upgrading of pyrolysis oil of biomass. Energy Procedia, 2014, 61: 1306–1309

6 Zhang S, Yang X, Zhang H, Chu C, Zheng K, Ju M, Liu L. Liquefaction of biomass and upgrading of bio-oil: a review. Molecules, 2019, 24(2250): 1–30

7 Lian X, Xue Y, Zhao Z, Xu G, Han S, Yu H. Progress on upgrading methods of bio-oil: a review. International Journal of Energy Research, 2017, 41(13): 1798–1816

8 Venkatasubramanian V, Chan K, Caruthers J M. Computer-aided molecular design using genetic algorithms. Computers & Chemical Engineering, 1994, 18(9): 833–844

9 Gani R, Achenie L E K, Venkatasubramanian V. Chapter 1—Introduction to CAMD. Computer-Aided Chemical Engineering, 2003, 12: 3–21

10 Papadopoulos A I, Tsivintzelis I, Linke P, Seferlis P. Computer-aided molecular design: fundamentals, methods, and applications. Reference Module in Chemistry, Molecular Sciences and Chemical Engineering, 2018, 4–36

11 Austin N D, Sahinidis N V, Trahan D W. Computer-aided molecular design: an introduction and review of tools, applications, and solution techniques. Chemical Engineering Research & Design, 2016, 116: 2–26

12 Ng L Y, Chong F K, Chemmangattuvalappil N G. Challenges and opportunities in computer-aided molecular design. Computers & Chemical Engineering, 2015, 81: 115–129

13 Zhou T, McBride K, Linke S, Song Z, Sundmacher K. Computer-aided solvent selection and design for efficient chemical processes. Current Opinion in Chemical Engineering, 2020, 27: 35–44

14 Chemmangattuvalappil N G. Development of solvent design methodologies using computer-aided molecular design tools. Current Opinion in Chemical Engineering, 2020, 27: 51–59

15 Hada S, Solvason C C, Eden M R. Characterization-based molecular design of bio-fuel additives using chemometric and property clustering techniques. Frontiers in Energy Research, 2014, 2(20): 1–12

16 Khor S Y, Liam K Y, Loh W X, Tan C Y, Ng L Y, Hassim M H, Ng D K W, Chemmangattuvalappil N G. Computer aided molecular design for alternative sustainable solvent to extract oil from palm pressed fibre. Process Safety and Environmental Protection, 2017, 106: 211–223

17 Yunus N A, Zaki N M, Wan Alwi S R. Design of solvents for palm oil recovery using computer aided approach. Chemical Engineering Transactions, 2018, 63: 583–588

18 Mah A X Y, Chin H H, Neoh J Q, Aboagwa O A, Thangalazhy-Gopakumar S, Chemmangattuvalappil N G. Design of bio-oil additives via computer-aided molecular design tools and phase stability analysis on final blends. Computers & Chemical Engineering, 2019, 123: 257–271

19 Byrne F P, Jin S, Paggiola G, Petchey T H M, Clark J H, Farmer T J, Hunt A J, McElroy C R, Sherwood J. Tools and techniques for solvent selection: green solvent selection guides. Sustainable Chemical Processes, 2016, 4(7): 1–24

20 Neoh J Q, Chin H H, Mah A X Y, Aboagwa O A, Thangalazhy-Gopakumar S, Chemmangattuvalappil N G. Design of bio-oil additives using mathematical optimisation tools considering blend functionality and sustainability aspects. Sustainable Production and Consumption, 2019, 19: 53–63

21 Dimian A C, Bildea C S, Kiss A A. Chapter 12—Chemical Product Design. Computer-Aided Chemical Engineering, 2014, 35: 489–523

22 Chemmangattuvalappil N G, Eden M R. A novel methodology for property-based molecular design using multiple topological indices. Industrial & Engineering Chemistry Research, 2013, 52(22): 7090–7103

23 Visco D P Jr, Pophale R S, Rintoul M D, Faulon J L. Developing a methodology for an inverse quantitative structure-activity relationship using the signature molecular descriptor. Journal of Molecular Graphics & Modelling, 2002, 20(6): 429–438

24 Faulon J L, Visco D P, Pophale R S. The signature molecular descriptor. 1. Using extended valence sequences in QSAR and QSPR studies. Journal of Chemical Information and Computer Sciences, 2003, 43(3): 707–720

25 Visco D P Jr, Chen J J. The signature molecular descriptor in molecular design: past and current applications. Computer-Aided Chemical Engineering, 2016, 39: 315–343

26 Brown W M, Martin S, Rintoul M D, Faulon J L. Designing novel polymers with targeted properties using the signature molecular descriptor. Journal of Chemical Information and Modeling, 2006, 46(2): 826–835

27 Jackson J D, Weis D C, Visco D P Jr. Potential glucocorticoid receptor ligands with pulmonary selectivity using I-QSAR with the signature molecular descriptor. Chemical Biology & Drug Design, 2008, 72(6): 540–550

28 Weis D C, Visco D P. Computer-aided molecular design using the signature molecular descriptor: application to solvent selection. Computers & Chemical Engineering, 2010, 34(7): 1018–1029

29 Chemmangattuvalappil N G, Solvason C C, Bommareddy S, Eden M R. Reverse problem formulation approach to molecular design using property operators based on signature descriptors. Computers & Chemical Engineering, 2010, 34(12): 2062–2071

30 Ng L Y, Andiappan V, Chemmangattuvalappil N G, Ng D K S. A systematic methodology for optimal mixture design in an integrated biorefinery. Computers & Chemical Engineering, 2015, 81: 288–309

31 Marrero J, Gani R. Group-contribution based estimation of pure component properties. Fluid Phase Equilibria, 2001, 183-184: 183–208

32 Conte E, Martinho A, Matos H A, Gani R. Combined group-contribution and atom connectivity index-based methods for estimation of surface tension and viscosity. Industrial & Engineering Chemistry Research, 2008, 47(20): 7940–7954

33 Hukkerikar A S, Kalakul S, Sarup B, Young D M, Sin G, Gani R. Estimation of environment-related properties of chemicals for design of sustainable processes: development of group-contribution⁺ (GC⁺) property models and uncertainty analysis. Journal of Chemical Information and Modeling, 2012, 52(11): 2823–2839

34 Zhang L, Cignitti S, Gani R. Generic mathematical programming formulation and solution for computer-aided molecular design. Computers & Chemical Engineering, 2015, 78: 79–84

35 Gani R, Nielsen B, Fredenslund A. A group contribution approach to computer-aided molecular design. AIChE Journal. American Institute of Chemical Engineers, 1991, 37(9): 1318–1332

36 van Dyk B, Nieuwoudt I. A computer-aided molecular design of solvents for distillation processes. In: International Conference on Distillation and Absorption. Düsseldorf: Verein Deutscher Ingenieure e.V. (VDI), 2002,1

37 Faulon J L, Churchwell C J, Visco D P. The signature molecular descriptor 2 enumerating molecules from their extended valence sequences. Journal of Chemical Information and Computer Sciences, 2003, 43(3): 721–734

38 Prausnitz J M, Lichtenthaler R N, Azevedo E G. Molecular Thermodynamics of Fluid-Phase Equilibria. 3rd ed. Upper Saddle River: Prentice-Hall, 1999, 687–696

39 Pacheco R, Silva C. Global warming potential of biomass-to-ethanol: review and sensitivity analysis through a case study. Energies, 2019, 12(13): 2535

40 Ooi J, Ng D K S, Chemmangattuvalappil N G. Optimal molecular design towards an environmental friendly solvent recovery process. Computers & Chemical Engineering, 2018, 117: 391–409

41 Linstrom P J, Mallard W G. NIST Chemistry WebBook, NIST Standard Reference Database Number 69. Gaithersburg MD: National Institute of Standards and Technology, 2021

42 Manara P, Bezergianni S, Pfisterer U. Study on phase behavior and properties of binary blends of bio-oil/fossil-based refinery intermediates: a step toward bio-oil refinery integration. Energy Conversion and Management, 2018, 165: 304–315

43 Asadullah M, Ab Rasid N S, Kadir S A S A, Azdarpour A. Production and detailed characterization of bio-oil from fast pyrolysis of palm kernel shell. Biomass and Bioenergy, 2013, 59: 316–324