Computational design of structured chemical products

Abstract

In chemical product design, the aim is to formulate a product with desired performance. Ingredients and internal product structure are two key drivers of product performance with direct impact on the mechanical, electrical, and thermal properties. Thus, there is a keen interest in elucidating the dependence of product performance on ingredients, structure, and the manufacturing process to form the structure. Design of product structure, particularly microstructure, is an intrinsically complex problem that involves different phases of different physicochemical properties, mass fraction, morphology, size distribution, and interconnectivity. Recently, computational methods have emerged that assist systematic microstructure quantification and prediction. The objective of this paper is to review these computational methods and to show how these methods as well as other developments in product design can work seamlessly in a proposed performance, ingredients, structure, and manufacturing process framework for the design of structured chemical products. It begins with the desired target properties and key ingredients. This is followed by computation for microstructure and then selection of processing steps to realize this microstructure. The framework is illustrated with the design of nanodielectric and die attach adhesive products.

Key words： product design; performance; ingredients; structure; manufacturing process framework; structured chemical products; microstructure design

1 Introduction

The design and optimization of processes to produce chemicals has been the primary focus of traditional chemical engineering. Recently, this focus has been gradually shifting towards the design of performance-based products such as cosmetic, personal care, food, healthcare, pharmaceutical, and electronic products. The cynosure of these products is their performance characteristics, not just their physicochemical properties. Chemical product design emphasizes the identification of consumers’ needs, and conceptualization of viable products to meet them [1–7]. Many product design methods have been developed. For example, Wibowo and Ng proposed a procedure for product-oriented process synthesis that includes identification of product attributes, selection of ingredients and microstructure, performance analysis, and process design [8,9]. They applied the framework to design creams and pastes, and other chemical-based consumer products. Perspective on chemical product design was explored through case studies for different structured products [10]. Seider et al. discussed product design in a comprehensive manner considering house of quality, stage-gate product development process, and so on [11]. A consumer-integrated product design framework was presented by Smith and Ierapepritou who incorporated consumer input and economic criteria in product design and a case study on under eye cream was used to illustrate the method [12]. Gani and Ng proposed a multidisciplinary, hierarchical framework, which integrates the model-based computer-aided techniques with knowledge based and experimental approaches to design the four types of chemical products—molecular, formulated, functional, and device product [13].

Chemical product design was viewed as the inversion of quality, property, and process functions by Bernardo and Saraiva and the technique was illustrated using case studies on perfumes, moisturizing lotion, and pharmaceutical ointment [14]. A comprehensive design framework presented by Mattei et al. for emulsion-based products was applied for the design of sunscreen and hand-wash lotions [15]. The scope of product design has expanded over time to include marketing, economics, social responsibility, and finance [16,17]. To unify the disparate issues in product design, a grand product design (GPD) model has been proposed [18]. Zhang et al. has applied this concept to develop an integrated framework for designing formulated products [19]. Recently, GPD has been expanded to include product pricing [20], government policy [21], and supplier selection [22] as shown in Fig. 1. The multifaceted relationships of ingredients, structure and processing to realize the desired product quality based on consumer preference are surrounded by the dotted line.

Fig.1 Schematic representation of GPD Model. Red dotted line encircled the target technological area.

Full size|PPT slide

The prediction of the macro properties of heterogeneous media in which the size, geometry, and property of the phases vary widely has been an active research area in materials science for a while [23]. Recent developments in computational material design have provided promising modelling methods for the design of microstructure with desired properties [24–27].

With the increasing demand for high-quality chemical products, both experimental and computational approaches are needed to accelerate the product conceptualization process. However, little work has been done on the conceptual and computational design of structured products. To fill this gap, a systematic design framework—performance, ingredients, structure, and manufacturing process (PRISM) is proposed. The desired product properties and performance are achieved by selecting appropriate ingredients and identifying suitable product structures, which in turn need to be fabricated by a manufacturing process. The PRISM framework is embedded in the GPD model, which considers all the other issues related to product design such as sustainability, pricing, consumer desires, supply chain, corporate social responsibility, product cost, marketing, etc. Note that the GPD model is a living model that is expected to expand over time.

As many consumer-oriented chemical products are available, it is of utmost importance to define the products that come under the domain of structured chemical products. Gani and Ng classify chemical products into molecular products, formulated products, functional products, and devices as illustrated in Fig. 2 [13]. The function and performance of most functional products, and to some extent formulated products, are related to the physicochemical properties of constituents (or phases) and the resultant product structure, which fit into the description of structured chemical products such as composite, emulsion, powders (e.g., granulated and compressed), extruded solids, suspensions, and so on. Therefore, molecular products and devices are not the focus of this paper.

Fig.2 Classification of consumer-oriented chemical products.

Full size|PPT slide

The paper is organized as follows. The PRISM framework is discussed in Section 2. At the outset, the physicochemical phenomena of relevance to product performance are identified (Section 2.1). This is followed by selection of the ingredients in Section 2.2. Product structure is described by product form, macrostructure, and microstructure (Section 2.3). Analytical models and computational methods for structural design are reviewed in Section 2.4 and 2.5, respectively. The processes for fabricating the desired structures are reviewed in Section 2.6. The PRISM framework has been applied on nanodielectrics in Section 3.1 and die attach adhesive (DAA) in Section 3.2. Concluding remarks are provided in Section 4.

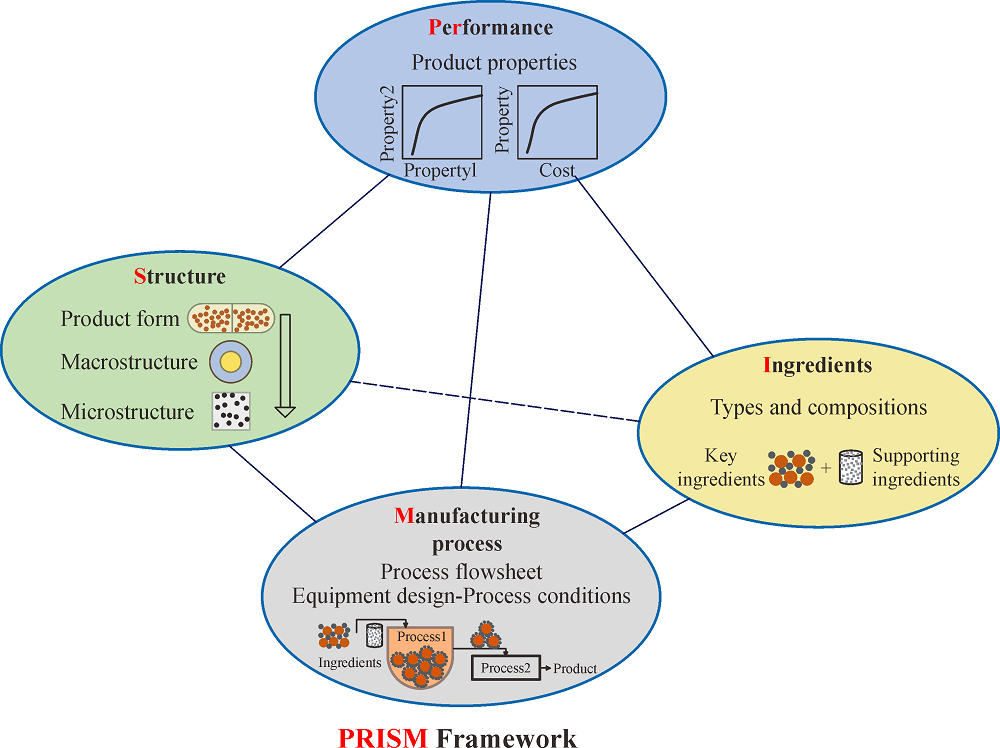
2 The PRISM framework

Figure 3 shows a PRISM indicating that product performance is dependent on ingredients, structure, and manufacturing process. Product performance is decided by consumer preference and/or market requirements. They tend to be qualitative in nature and are related to the technical requirements using the house of quality. It is more than the physicochemical properties of the product. Both ingredient type and composition in a product should be considered. Products with two or more phases possess a structure. The overall physicochemical properties of the product depend on the properties of the constituents and the spatial distribution, composition, size, and shape of the phases in the product. Finally, the manufacturing process is designed to realize the desired product structure.

Fig.3 The PRISM framework.

Full size|PPT slide

Figure 4 shows a workflow diagram for systematically executing the PRISM framework. It begins with market survey to identify the consumer preferences. Information on market needs, market size, competing products, and so on is collected. This is followed by identification of product attributes and product use conditions, which account for the fact that the product quality depends on how it is used. For example, the quality of an ink for a screen printer cannot be exactly defined until the design and operating conditions of the printer are fixed. In general, a product must go through a series of rigorous tests to validate its performance. If the performance does not meet the expectations, another product concept will be identified, and the workflow is repeated. The key elements of the PRISM framework are discussed below in details.

Fig.4 A workflow diagram of computation-based PRISM framework of product design.

Full size|PPT slide

2.1 Product performance and relevant physicochemical phenomena

Product performance is often characterized by a single or a group of parameters. For example, the performance of a DAA is governed by the physicochemical phenomena—heat conduction, which can be quantified by its thermal conductivity,k. However, it may also be necessary to specify its specific stiffness, E/ρ, where E is elastic modulus and ρ is density. For many products, decision making often requires a compromise among multiple criteria such as product performance and product cost. A trade-off is usually sought between multiple criteria using multi-objective optimization (i.e., Pareto optimal solution using epsilon-constraint method) [28]. Table 1 lists a number of structural products along with their key functions, desired performance, relevant physicochemical phenomena, and types of ingredients.

Tab.1 Intended functions, desired performance, relevant physicochemical phenomena, and ingredients information of structural products

Product	Intended (main) function	Desired performance	Relevant physicochemical phenomena	Types of ingredients
				Key ingredients	Supporting ingredients
DAA [29]	Provides heat management	Enhanced heat transfer	Heat conduction	Filler Polymer matrix	Solvent
Nanodielectrics [30]	Resists the flow of electric charges through a material	Enhanced dielectric properties	Electrostatics	Filler Polymer matrix	Dispersing agent Solvent
Mosquito repellent mat [31]	Stores the repellent solution and releases it to air when being heated	Controlled diffusion	Mass transfer (diffusion)	Active ingredient Solvent Propellant	Fragrance Emollients
Sound absorption foam [32]	Absorbs noise from the environment	High sound absorption	Acoustics absorption	Polymer matrix Foaming agent	Surfactant
Thermal barrier coating [33]	Protects the metallic component from heat	High heat resistance	Heat conduction/ convection	Coating material Substrate	−
Solar cell encapsulant film [34]	Provides electrical insulation and heat management	Electrical resistance and enhanced heat transfer	Electrical conduction Heat conduction	Filler Polymer matrix	Coupling agent Solvent
Electromagnetic interference (EMI) shield [35]	Adsorbs and reflects electromagnetic waves	EMI shielding effectiveness	Electromagnetics	Filler Polymer matrix	Solvent
Piezoresistive sensor [36]	Changes electrical resistivity when compressed or strained	High Piezoresistive sensitivity (gauge factor)	Electrical conduction Elasticity	Filler Polymer matrix	Solvent

The relevant governing equations model the overall product performance based on the identified physicochemical phenomena. At steady state with no generation or destruction of energy, the divergence of a generic flux F is zero.

(1)\nabla \cdot F=\mathrm{0.}

The constitutive equation for a gradient-based phenomenon relates the flux to a material property P and the corresponding state variable φ.

(2)F=P\cdot \nabla \phi .

Consider the DAA in Table 1. It is a polymer composite with silver microparticles used for attaching a light emitting diode (LED) chip to a substrate. The polymer serves as an adhesive while the silver particles facilitate the conduction of heat from the chip to the substrate. For DAA, F represents the heat flux which is related to the thermal conductivity k and the temperature gradient \nabla T. Similarly, for nanodielectrics, the electric flux is related to the relative permittivity and the gradient of the electric field.

The combination of Eq. (1) and Eq. (2) provides the governing equation. In accordance with the GPD model [18], product quality (\underset{\_}{q}) can then be expressed as a function of its structure (\underset{\_}{s}), material properties (\underset{\_}{p}), and product use conditions (\underset{\_}{u}), which is mathematically represented in Fig. 1 as

(3)\underset{\_}{q}\leftarrow T_q(\underset{\_}{p},\underset{\_}{s},\underset{\_}{u}).

The selection of the ingredients and their properties are discussed next.

2.2 Ingredients and physicochemical properties

Selection of ingredients for a specific product requires different considerations. In addition to meeting performance requirements, cost is an important factor. International, national, and local regulations regarding the use of the selected ingredients have to be followed as some ingredients may be banned due to toxicity and health concerns. Fabrication requirements such as ease of machining, corrosion effect on the equipment, etc. should be considered. Environmental issues include the impact of the chosen material on waste gas, water, and solids. Other requirements include availability, recyclability, and sustainability.

The ingredients are divided into two categories, as shown in Table 1. Key ingredients are the constituents whose properties are directly related to the primary function of the product; e.g., metallic filler and polymer in DAA. Supporting ingredients are the constituents whose properties are not directly linked to the primary product function; however, their addition is needed to enhance product performance, facilitate manufacturing, etc. For example, ethanol has to be added to aid fillers dispersion in the DAA.

Ingredient selection often starts with a materials database, typical compositions for the product, and selection heuristics. Then, the formulation is fixed by experimental iteration using a causal table to guide the process. This traditional approach was systematized and illustrated using a skin-care cream [16]. Alternatively, theoretical calculations are used to screen various base-case formulations, followed by experimental verification. This approach was adopted by Conte et al. for the formulation of an insect repellent spray [37,38]. In practice, both approaches are used in ingredient selection depending on the availability, suitability, relevance, and reliability of the theoretical models. It is particularly difficult to find models for selecting ingredients that involve the prediction of the five senses—touch, taste, smell, hearing, and sight although progress is being made with the advent of machine learning models [39].

2.3 Product structure

Product structure is the spatial distribution of the constituents and is related to product quality and processing. Knowledge of the number of phases, their nature, phase fraction, and geometrical features is essential for property prediction and structural optimization. To understand product structure, it is convenient to arrange the structural information in three different scales—product form, macrostructure, and microstructure, as shown in Table 2. A brief description is provided below. Note that this is only one way, among others, to classify the product structure.

Tab.2 Different levels of product structure

Product structure	Structure representation/categorization	Descriptions
Product form	Solid	Composite, tablet, encapsulate, powder, granules, film
	Semi-solid	Paste, cream
	Liquid	Emulsion, liquid foam, suspension, mixture
	Gas	Aerosol
Macrostructure	Composition	No. of phases, volume fraction
	Phase distribution/arrangement	Dispersed, porous, segregated, patterned (honeycomb, lamellar, layered, onion)
Microstructure	Phase fraction	Local volume fraction
	Phase distribution/arrangement	Local dispersion (orientation, distance between the inclusions)
	Shape of inclusion	Sphere, needle, cubic, disk, rod, fiber
	Size of inclusion	Micro, nano
	Interfacial interaction	Interfacial layer
	Crystallinity	Single crystalline, polycrystalline, amorphous
	Porosity	Pore size

Product form. Product form is what a layman uses to describe a product. The product can be a solid, a semi-solid, liquid, or gas, and can be a film, powder, foam, paste, cream as well as other physical forms. For more science-oriented consumers, the product can be classified as composite, emulsion, solution, mixture, and so on.

Macrostructure. Macrostructure refers to the gross structure of the product, which reveals how the ingredients are arranged spatially as observed with an unaided eye or using a light microscope (i.e., at≤10 × magnification). In this paper, macrostructure refers to product features of a length scale>100 \mathrm{\mu m}. For mixtures, it can be described as homogeneous or heterogeneous. The latter can be further described as isotropic or anisotropic. Its phase distribution can be dispersed, porous, segregated, patterned, etc. The patterned products can be further classified as honeycomb, lamellar, layered structure, and so on. Based on phase distribution, four common types of macrostructure in structural chemical products are described below, and the examples are listed in Table 3. Note that a product can be of different macrostructures. For example, dispersed structure is more common for EMI shield. However, more EMI shields are developed with segregated structure recently because of the low volume fraction of fillers in the segregated structure [35].

Tab.3 Common macrostructures in structural products

Macrostructure	Description	Examples of products
Dispersed	One phase is dispersed in a continuous phase	DAA nanodielectrics
Porous	Presence of pores within a structure	Mosquito repellent mat Sound absorption foam
Lamellar	A structure composed of thin, flat, and interchanging lamellae of different materials	Thermal barrier coating Solar cell encapsulant film
Segregated	One phase forms a continuous network in the structure	EMI shield Piezoresistive sensor

Dispersion is common in multiphase materials such as composites. The way that fillers dispersed in a composite affects its material properties such as mechanical strength, effective thermal conductivity, etc. [40]. A well-dispersed structure is generally desirable; however, agglomeration and aggregation are the major problems associated with a dispersion [41]. A porous structure is characterized in terms of the size and interconnectivity of the pores. If the pores are connected, fluid flow in these porous channels is possible and the product is a bi-continuous structure. Recently, hierarchical design and synthesis of porous materials has gained considerable interest [42,43]. Lamellar structure composes of thin, flat, and interchanging layers (lamellae) of different phases/materials. Structural parameters such as particle size, lamellar spacing, and the orientation of the lamellar layers determine the properties of a lamellar structure [44]. A segregated structure is the opposite of a dispersed structure. The fillers form a continuous network even at a low mass fraction [45]. The percolation threshold can be further lowered using a double percolation strategy. First, polymer A forms a continuous path in polymer B. Then, the fillers form a continuous path in polymer A [46].

Microstructure. In this paper, microstructure refers to the phase features of a product viewed under a microscope at>25× magnification, and with a length scale ranging from 0.01 to 100 \mathrm{\mu m}. Table 4 summarizes the microstructural features having strong impact on product performance such as phase fraction, shape of inclusion, size of inclusion, phase distribution, and so on.

Tab.4 Key microstructural features of composite material

Microstructural features	Examples of microstructural features parameters	Graphical representation
Phase fraction	Weight fraction, volume fraction	‒
Shape of inclusion	Aspect ratio, roundedness, rectangularity	Particulate	Fibrous
Size of inclusion	Equivalent diameter, particle size distribution	Microparticles	Nanoparticles
Phase distribution	Average nearest center/surface distance between inclusion (interconnectivity), orientation	Preferred orientation	Interconnected
Interfacial interaction	Thickness of interfacial layer	‒

Figure 5 schematically illustrates the three levels of product structure by three examples. The first one is a nanodielectric, which is a nanoparticle-loaded polymer composite. The product form is a solid and the macrostructure is a dispersed system. The key microstructural features include the amount, shape, size, and size distribution of the nanoparticles. Another example is a DAA, which is a polymer-based composite loaded with filler particles. The product form is a solid layer with a dispersed macrostructure. The important microstructural parameters include the loading of the filler particles, the shape, size, and distribution of the nano- and micron-sized filler particles. The third example is a piezoresistive sensor which is a piezoresistive film with a segregated macrostructure. The key microstructural features include amount, size, and size distribution of nanotubes as well as the size of polymer particles.

Fig.5 Schematic illustration of levels of structures in (a) Nanodielectrics, (b) DAA, (c) piezoresistive sensor.

Full size|PPT slide

2.4 Analytical models

A number of analytical models are available for predicting the structure-property relationship. For a rough estimate, the linear mixing rule can be used to calculate the effective property {\lambda }_{\mathrm{e}} of a composite:

(4){\lambda }_{\mathrm{e}}={\lambda }_{\mathrm{1}}(\mathrm{1}-\varphi )+\varphi {\lambda }_{\mathrm{2}},

where \varphi is the volume fraction of the dispersed phase, {\lambda }_{\mathrm{1}} and {\lambda }_{\mathrm{2}} are the property of the continuous phase and dispersed phase, respectively. It provides reasonable values for properties such as density while deviates significantly for other properties that are strongly dependent on structural arrangements. Table 5 summarizes basic models for predicting the effective property of two-phase structural products possessing various macroscopic structures. Improvements to these basic models have been proposed for heat conduction phenomenon that led to 1) models with empirical parameters to account for certain structural features [48–50]; 2) combined models in which combination of two or more basic models are utilized for complex structures [51,52]; 3) network models that decompose a complex microstructure into a network formed by a large number of parallel and series models [53,54].

Tab.5 Analytical models for predicting the effective properties of two-phase structural products [47]

Models	Expressions a)
Parallel model	{\lambda }_{\mathrm{e}}=(\mathrm{1}-\varphi ){\lambda }_{\mathrm{1}}+\varphi {\lambda }_{\mathrm{2}}
Series model	{\lambda }_{\mathrm{e}}={\left[{\displaystyle \frac{\mathrm{1}-\varphi }{{\lambda }_{\mathrm{1}}}}+{\displaystyle \frac{\varphi }{{\lambda }_{\mathrm{2}}}}\right]}^{-\mathrm{1}}
Effective medium theory (EMT) model	{\lambda }_{\mathrm{e}}=(\mathrm{1}-\varphi ){\displaystyle \frac{{\lambda }_{\mathrm{1}}-{\lambda }_{\mathrm{e}}}{{\lambda }_{\mathrm{1}}+\mathrm{2}{\lambda }_{\mathrm{e}}}}+\varphi {\displaystyle \frac{{\lambda }_{\mathrm{2}}-{\lambda }_{\mathrm{e}}}{{\lambda }_{\mathrm{2}}+\mathrm{2}{\lambda }_{\mathrm{e}}}}
Maxwell model	{\displaystyle \frac{{\lambda }_{\mathrm{e}}}{{\lambda }_{\mathrm{1}}}}={\displaystyle \frac{\mathrm{1}+\mathrm{3}(\alpha -\mathrm{1})\varphi }{(\alpha +\mathrm{2})-(\alpha -\mathrm{1})\varphi }}
Hamilton model	{\displaystyle \frac{{\lambda }_{\mathrm{e}}}{{\lambda }_{\mathrm{1}}}}={\displaystyle \frac{\alpha +(n-\mathrm{1})+(n-\mathrm{1})(\alpha -\mathrm{1})\varphi }{\alpha +(n-\mathrm{1})+(\mathrm{1}-\alpha )\varphi }}
Reciprocity model	{\displaystyle \frac{{\lambda }_{\mathrm{e}}}{{\lambda }_{\mathrm{1}}}}={\displaystyle \frac{\mathrm{1}+(\sqrt{\alpha }-\mathrm{1})\varphi }{\mathrm{1}+(\sqrt{\mathrm{1}/\alpha }-\mathrm{1})\varphi }}

a) \alpha ={\displaystyle \frac{{\lambda }_{\mathrm{2}}}{{\lambda }_{\mathrm{1}}}} = property ratio, n = shape factor of the dispersed phase.

2.5 Computation-driven framework/methods/techniques

The models described above are intended for analysis; that is, the product structure is fixed, and the model simply predicts the effective properties. This section focuses on synthesis; that is, after selecting the ingredients, the model determines the ingredient composition and microstructure to fulfill the desired product performance. Various mathematical frameworks/techniques for structure generation have been proposed and can be divided into two main groups. The first one is a microstructure characterization and reconstruction (MCR) technique that deals with the structure-property calculation in two steps. It starts by generating/reproducing the microstructure based on experimental/simulation data using appropriate computer algorithm, followed by solving the relevant governing equations to predict the performance. These methods are applied when the structural information is not physically well defined, but can be quantified statistically. In other words, the MCR technique first captures the microstructural information (characterization), then generates statistically equivalent microstructures (reconstruction) [47]. The second group is microstructure design optimization, which solves the microstructure problem and the relevant transport equations together. A well-defined microstructure in terms of structure type and parameters is essential to start the optimization problem [55]. Some of these methods are briefly described below, and the first three methods are MCR technique.

2.5.1 Correlation function (CF)-based reconstruction

CF-based methods reconstruct statistically equivalent digitized microstructure via various statistical functions that capture the degree of spatial correlation related to the morphological features of the microstructure. Basic steps of CF-based reconstruction are depicted in Fig. 6 [56]. Note that the physical descriptors-based method to be described below basically follow the same reconstruction steps.

Fig.6 The basic framework of CF-based reconstruction methods.

Full size|PPT slide

First, during image transformation, the contrast adjustment and noise filtration of grey-scale images are performed before digitization of the image. Volume fraction-based transformation strategy is commonly adopted to convert the adjusted greyscale images to the binary images that maintain the volume fraction consistency [23,56]. The binary image is then quantified via various statistical CFs. These functions capture the statistical information through an indicator function I(X) to check the material presence (e.g., phase of interest) at some randomly chosen point, X, within the design domain.

(5)I(X)=\{\begin{array}{ll}\mathrm{1,}& \mathrm{X}\in \mathrm{p}\mathrm{articular}\mathrm{\hspace{0.17em}}\mathrm{phase/region}\\ \mathrm{0,}& \mathrm{otherwise}\end{array}.

The indicator function has different role for different CFs. For example, in two-point CF, S₂, it is used to provide the probability that two randomly chosen points, X_{\mathrm{1}}, X_{\mathrm{2}}, lie in phase of interest, i via Eq. (6).

(6)

After selecting the statistical CFs, microstructure reconstruction (i.e., phase distribution within the microstructure domain) is carried out through appropriate techniques [23]. Reconstruction of a microstructure is equivalent to identifying a set of CFs f_j(r) that match the experimentally/user defined determined CFs {\widehat{f}}_j(r) [27].

(7)E={\displaystyle {\sum }_{j=\mathrm{1}}^m}{\displaystyle {\sum }_{r=\mathrm{0}}^l}{\alpha }_j{\left[{\widehat{f}}_j(r)-f_j(r)\right]}^{\mathrm{2}},

where m is the total number of statistical functions involved in reconstruction, {\alpha }_j is the weighting factor used to quantify the function’s importance, while l is the maximum length of r at which the functions are equated. The generated microstructure is closer to target if E (refer as energy) is very small. By using appropriate computational procedure (e.g., mesh generation to solve discretized version of governing equations), the generated microstructures are then used to perform numerical modelling to predict their effective properties [56,57].

One of the major limitations associated with CFs is its infinite dimensions and the absence of a physical meaning in the CFs. Therefore, the relation of CF to sensible microstructural features is yet to be established. The statistical characterization step is only applicable to isotropic microstructures, and has limitation on anisotropic microstructures. This method is also computationally expensive for use in iterative microstructure design. Despite its limitations, the CF-based method is still an important MCR technique as it facilitates the inverse design of a microstructure. It has been widely applied in the microstructure reconstruction of various complex, heterogeneous, porous, and polycrystalline structures such as composite [58], cathode materials [59], and foods [60].

2.5.2 Physical descriptors-based reconstruction

In physical descriptors-based reconstruction methods, the morphology is characterized using a small set of microstructure descriptors similar to the parameters listed in Table 4, the statistical estimates of these descriptors are then used to reconstruct statistically equivalent microstructure [61–63]. The generic workflow of physical-based reconstruction follows what is shown in Fig. 6, except that in the characterization step the physical descriptors are identified using appropriate software techniques [61]. The descriptors having a single value assigned to all microstructure images are called deterministic descriptors; e.g., volume fraction. For a random structure, direct measurement of some descriptors is not feasible.

After determining the physical descriptors, optimization-based techniques such as simulated annealing are then used to determine the location of particle center by matching dispersion descriptors; i.e., nearest center distance between clusters/particles, while phase fraction and geometry descriptors (size and shape of inclusion) determine the number of cluster/particles. After specifying particles centers’ locations, reconstruction of the particle shape profile is carried out by geometry descriptors (randomly generated value; e.g., exponential distribution of nanoparticle’s diameter). Lastly, the output geometry in the form of pixelated image is then discretized by using a suitable mesh technique to perform property simulation. Despite having clear physical meaning of the microstructure descriptors, the use of this method for complex microstructures with irregular geometries is still a challenge.

2.5.3 Machine learning (ML)

With advancement in high-throughput computing technology in recent years, ML has found numerous applications in materials design and discovery [64,65]. As a data driven approach, ML provides comprehensive relationship between key structural descriptors and properties of interest. The generic process of ML for microstructure design is shown in Fig. 7 followed by description of the basic steps.

Fig.7 Generic workflow of microstructure design using ML.

Full size|PPT slide

Data generation: similar to previous approaches, a large amount of data is required that can be generated either from experiments or rigorous mechanistic models [65]. For example, computer aided tools such as COMSOL can be used to run various simulation to obtain a structure-property database that incorporates important structural parameters [18]. For certain chemical products, the structure-property database is publicly available (e.g., matweb, materials project, etc.) which expedites the design process of chemical products [65].

Descriptor generation and identification: generate a set of descriptors to describe the microstructures. Descriptors can be statistical or physical. The input data is the values of descriptors and output data is properties. Descriptors can be highly related to each other. Therefore, it is necessary to pre-process the high-dimensional input datasets with dimension reduction tools prior to the construction of ML models.

Model construction and validation: ML model is then built, mostly using supervised learning (i.e., artificial neural network, support vector machine, etc.), to correlate identified descriptors and properties of interest [27]. The evaluation or validation process is then applied to check the performance of the model algorithm. For different problems, different evaluation standards are available. However, cross-validation and bootstrapping are the commonly used evaluation methods for microstructure design [65].

Microstructure prediction and experimental verification: generate-and-test and mathematical optimization are the common approaches for microstructure prediction and verification. The former is to generate all possible microstructure leading to desired properties and then compare the predicted ones with the experimental values. The latter is to formulate the design problem as an optimization problem where properties are maximized or minimized by optimizing the descriptors. The problem can be solved using deterministic or stochastic algorithms and only the optimal solutions are verified [65].

ML techniques are considered fast and flexible in dealing complex microstructures and have shown good reconstruction accuracy in many applications such as for bioinspired composite [66], renewable energy materials [67], and food materials [68]. However, no explicit microstructure descriptors or features in the model, and large amount of required data (unavailable in most material design cases) are the major issues in ML for microstructure design.

2.5.4 Microstructure design optimization

Microstructure design optimization, e.g., topology optimization, is a mathematical framework that provides the optimal spatial distribution of the target materials within the design space (representative volume element (RVE)). First, the RVE is divided into a large number of finite elements. An optimization problem is solved to distribute the materials within the RVE such that the objective function f(x) representing the effective property of a microstructure is either maximized or minimized subject to various constraints [23]. A generic microstructure design optimization problem can be expressed by Eq. (8) [69].

\mathrm{min/max}\mathrm{\hspace{0.17em}}f(x)

(8)\mathrm{s}\mathrm{.t}\mathrm{.}\mathrm{\hspace{0.17em}}{g}_k(x)\le \mathrm{0},\mathrm{\hspace{0.17em}}k=\mathrm{1},\mathrm{...},\mathrm{\hspace{0.17em}}{n}_g,

x_i\in [\mathrm{0},\mathrm{1}]

where n_g is total number of constraints. The design variable x_i is binary to represent whether the material is present or absent in a particular element i.

A number of approaches such as homogenization, solid isotropic material with penalization (SIMP), evolutionary structural optimization, and level set method are available to solve the microstructure design optimization [70–73]. For example, a smooth penalty function with a penalty parameter is added to the objective function in the SIMP method. This helps to enhance the convergence to 0–1 solutions and transform the original problem into a smoother objective function with fewer local minima [74].

Microstructure design optimization, i.e., topology optimization, can be considered as a multiscale hierarchical design technique to optimize the product performance and the distribution of the materials at a micro-level simultaneously [75]. The key challenge associated with the microstructure design optimization is on how to incorporate the structural parameters in Table 4 in the design problem. Also, getting stable and rapid convergence with reduced sensitivity while handling various numerical instabilities can be challenging [76]. Some progress has been made recently to handle these challenges [55]. Microstructure design optimization has been widely applied to design cellular materials [77] and composite materials [78].

2.6 Manufacturing process design

The fourth element of the PRISM framework is the manufacturing process. To execute process design, the process flowsheets as well as the processing techniques that produce the product with the desired structure are first identified. Next, equipment type, dimensions, and operating conditions are specified. An example on polypropylene/aluminum nitride (AlN) conductive polymer composite (CPC) is illustrated in Table 6 [79]. Two processing techniques that are able to produce a segregated structure are identified based on experience. Experiments were then conducted to identify the optimal flowsheet and its operating conditions. AlN network was well connected in the composite fabricated using mechanical grinding, as the AlN coating forms a continuous path upon hot pressing of the AlN-coated polymer resin particles. Experimental data show that, with 10 vol% AlN, the mechanical grinding approach offered a higher thermal conductivity (0.37 W∙m^–1∙K^–1) than the composites prepared by melt mixing (0.30 W∙m^–1∙K^–1).

Tab.6 Structure-processing-property relationship in CPC [79]

Product structure		Processing routes			Property and resultant structure a)
Macro-structure	Microstructural features	Key processing techniques	Equipment design	Operating conditions
Segregated	Volume fraction, size and shape of inclusion, interconnectivity	Mechanical grinding, Hot pressing	Dimensions of mechanical grinder, and its blade design	Time and speed of grinding, time, temperature and pressure for hot pressing	Thermal conductivity= 0.37 W∙m–1∙K–1
		Melt mixing Hot pressing	Dimensions of the mixer, and its mixing blade design	Time, temperature and mechanical power of mixing time, temperature and pressure for pressing	Thermal conductivity= 0.30 W∙m–1∙K–1

a) Yellow dots represent the distribution of AlN in the polymer network.

The integration of processing technique in microstructure design optimization is still missing, as the manufacture of most structural products cannot be processed by conventional unit operations in which process design and simulation is well-developed. Progress has been made in this area by introducing microstructure-sensitive design [80], in which the optimal processing route can be selected for a product with the desired performance, given an initial material design and a desired product structure [24]. More research effort has to be made along this direction.

3 Examples

In this section, two examples, namely nanodielectrics and DAA, are used to illustrate how the PRISM framework is used to design the structured chemical products. MCR technique is used for the computational design of nanodielectrics, whereas the microstructure design optimization is used to design DAA.

3.1 Nanodielectrics

The PRISM framework is applied to design a nanodielectric product depicted in Fig. 4(a).

3.1.1 Product performance and relevant physicochemical phenomena

A nanodielectric is a multi-component dielectric nanostructure that leads to the change in dielectric properties, and is characterized by its relative permittivity and dielectric loss factor. A typical desired permittivity of nanodielectrics is around 4 and the dielectric loss factor should be kept at minimal [81]. Other properties such as thermal conductivity, mechanical strength, adhesion, and so on are also important, but they are not considered in this example.

3.1.2 Ingredients and physicochemical properties

Table 1 shows that the key ingredients in a nanodielectric are the polymer matrix and filler. The type of filler, its morphology, loading, etc. affect the dielectric property. Metal oxides, metal nitride, glass, and minerals are common fillers used in nanodielectrics [81]. Silica is selected as the filler in this example as it provides the desired dielectric performance as well as improved thermal and mechanical characteristics, whereas epoxy is commonly used as the polymer matrix [41,82]. Glycidoxypropyltrimethoxysilane (GPTMS) and ethanol are selected as the coupling agent and solvent, respectively [83].

3.1.3 Product structure

Figure 4(a) shows that the product form is a solid layer, in which the fillers are dispersed in a polymer matrix. The amount, size, and its distribution in the polymer are important microstructural parameters to be considered [84,85].

3.1.4 Analytical models

EMT based models such as Maxwell Garnett model can be used to estimate the volume fraction of the filler particles such that the resultant permittivity matches with the desired product performance. This volume fraction can be used as the initial guess or bound for the computation-driven method in the next step [86].

3.1.5 Computation-driven framework/methods/techniques

Zhang et al. [62] applied physical descriptors-based reconstruction method to determine the target properties. Physical descriptors such as volume fraction, cluster area, aspect ratio, and nearest center distance are extracted from a 2-D image of the sample. As the volume fraction of filler in the polymer matrix is low (0.5%–3%) and with uneven distribution of aggregates within the design domain, a decomposition and re-assembly strategy is applied to preserve the structural information at local positions. The image is first divided into multiple equal-sized sub-blocks. The descriptor-based reconstruction method is applied in each sub-block, which is then re-assembled to get the fully reconstructed microstructure. Finite element simulations are then performed to calculate the effective relative permittivity and the dielectric loss factor. The computational results show that smaller cluster area and larger volume fraction provide the desired dielectric performance. The nearest center distance has minimal impact on the target properties as clusters are sparsely distributed in the matrix.

3.1.6 Manufacturing process design

The process used to manufacture the nanodielectrics is depicted in Fig. 8, and the key process parameters for each processing techniques are summarized in Table 7 [84,87]. The computational results showed that a smaller cluster area is desired. Thus, silica nanoparticles are mixed with ethanol and GPTMS in a sonication bath to modify the surface of the nanoparticles and to form a stable dispersion with minimal fillers aggregation. Epoxy resin is then added to the dispersion, which is then dried to remove the coupling agent and solvent. Curing agent is then added to produce the composite, followed by vacuum degassing to remove air bubbles. Finally, casting and curing are conducted to obtain the final product.

Fig.8 Process flowsheet for the manufacture of nanodielectrics.

Full size|PPT slide

Tab.7 Processing techniques, equipment and process parameters for the manufacture of nanodielectrics

Processing techniques	Equipment	Functions	Process parameters
Sonication	Ultrasonicator	Disperse nanoparticles, surface modification of nanoparticles to prevent agglomeration	Sonic power, time
Mixing	Shear mixer	Disperse the silica nanoparticles in epoxy, control particle size	Mechanical speed, time
Drying	Vacuum oven	Remove solvent and coupling agent	Temperature, time
Mixing	Shear mixer	Mix the curing agent with the polymer mixture	Mechanical speed, time
Degassing	Vacuum desiccator	Remove air bubbles and moisture	Time
Casting and curing	Pre-defined mold oven	Form the solid composite	Temperature, time

3.2 Die attach adhesive

The PRISM framework is applied to design the DAA depicted in Fig. 4(b).

3.2.1 Product performance and relevant physicochemical phenomena

DAA is a polymer-based composite loaded with filler particles. The primary purpose of a DAA is to conduct heat from the LED chip to the heat sink. In addition, it should provide sufficient adhesion and electrical resistance. To simplify the simulation later on, only thermal conductivity is considered as the target property with a minimal value of 3 W∙m^–1∙K^–1 [29,88].

3.2.2 Ingredients and physicochemical properties

Polymer matrix and the highly conductive filler particles are the key ingredients, whereas solvent is the supporting ingredient that assists the dispersion of the filler particles in the matrix. Based on our experience and the previous studies [29], silver micro-particles and nano-particles are selected as the filler particles, whereas epoxy and ethanol are chosen as the polymer matrix and the solvent, respectively, in this example.

3.2.3 Product structure

The product form is a solid layer with a dispersed macrostructure. The silver micro-particles and nano-particles are distributed in the polymer matrix. The key microstructural parameters include the loading, shape and size of the filler particles, and its size distribution in the polymer matrix.

3.2.4 Analytical models

The parallel and series models in Table 5 determine the upper and lower bounds of the effective thermal conductivity, respectively, which are set as the constraints of the microstructure design optimization in the next step.

3.2.5 Computation-driven framework/methods/techniques

The microstructure design optimization was applied to design the product microstructure with the desired performance [28]. A 2-D RVE (length= width= 8 \mathrm{\mu m}) that discretized into 80 × 80 elements is used in the simulation. The four corners in an RVE are occupied by the silver micro-particles, equivalent to 42% volume loading if they are homogenously distributed. The temperatures at the top and bottom surfaces of the DAA are set at 403 K and 402 K, respectively. The microstructure design optimization is formulated as a mixed-integer nonlinear programming (MINLP) problem for maximizing the heat conductivity subject to various constraints including the conservation equation and the constitution equation, as well as constraints on the volume fraction of the filler particles, the size and orientation of the filler particles, and the minimum separation among filler particles. The design variable of the optimization problem is whether or not the filler is present at a specific element in the RVE. Readers can refer to [28] for the detailed equations of the optimization problem. As the MINLP problem involves a large number of binary variables, the widely used SIMP method is applied and a smooth penalty function is added to help converging the optimization problem. The optimization problem was solved using GAMS 24.7 with the DICOPT solver.

Two simulations were conducted. Figure 9(a) shows the distribution of the rod-shaped nanoparticles for achieving a higher thermal conductivity (i.e., 3.65 W∙m^–1∙K^–1). The rod-shaped nanoparticles are located closer to the center of the RVE. If an additional constraint is added such that the rod-shaped nanoparticles are homogeneously distributed within the RVE, a lower thermal conductivity at 3.19 W∙m^–1∙K^–1 is obtained and the distribution of the rod-shaped nanoparticles is illustrated in Fig. 9(b).

Fig.9 Optimal DAA microstructure.

Full size|PPT slide

3.2.6 Manufacturing process design

The process used to manufacture the DAA is depicted in Fig. 10, and the key process parameters for each processing techniques are summarized in Table 8 [29]. The silver microparticles and nanoparticles are first mixed with ethanol and epoxy in a mechanical stirrer, followed by homogenization and sonication to form a dispersion. Solvent is then removed in a dryer. Finally, curing agent is added and the final product is obtained after molding and curing. Note that the alignment of the rod-shaped nanoparticles can be achieved during processing by modifying the surface of the nanoparticles with magnetic compounds and mixing the nanoparticles and the polymer matrix under magnetic field [89]. This also illustrates that product design is an iterative process.

Fig.10 Process flowsheet for the manufacturing of DAA.

Full size|PPT slide

Tab.8 Processing techniques, equipment and process parameters for the manufacturing of DAA

Processing techniques	Equipment	Functions	Process parameters
Mixing	Mechanical stirrer	Mix the particles with epoxy	Mechanical speed, time
Homogenization	Homogenizer	Disperse fillers in the polymer matrix	Mechanical speed, time
Sonication	Ultrasonicator	Disperse fillers in the polymer matrix	Sonic power, time
Drying	Oven	Remove solvent	Temperature, time
Mixing	Mixer	Mix the curing agent with the polymer mixture	Mechanical speed, time
Molding and curing	Pre-defined mold oven	Form the solid composite	Temperature, time

4 Conclusions

Product structure has a significant impact on the performance of a chemical product. Limited research has been conducted in the PSE community to systematically design the product structure of a chemical product. This review attempts to integrate various aspects related to product structure and come up with the PRISM framework. Computational methods that can be used to synthesize the required product structure are discussed and its limitations highlighted. The PRISM framework developed in this review points to an important research area of integrating ingredients selection, product structure, and manufacturing process design to obtain a chemical product with the desired performance.

References

1 Cussler E L, Moggridge G D. Chemical Product Design. 1st ed. Cambridge: Cambridge University Press, 2001, 1–416

2 Gani R. Chemical product design: challenges and opportunities. Computers & Chemical Engineering, 2004, 28: 2441–2457

3 Costa R, Moggridge G D, Saraiva P M. Chemical product engineering. An emerging paradigm within chemical engineering. AIChE Journal, 2006, 52: 1976–1986

4 Hill M. Chemical product engineering—the third paradigm. Computers & Chemical Engineering, 2009, 33: 947–953

5 Smith B V, Ierapepritou M G. Integrative chemical product design strategies: reflecting industry trends and challenges. Computers & Chemical Engineering, 2010, 34: 857–865

6 Ng K M, Gani R. Chemical product design: advances in and proposed directions for research and teaching. Computers & Chemical Engineering, 2019, 126: 147–156

7 Olson G B. Designing a new material world. Science, 2000, 288: 993–998

8 Wibowo C, Ng K M. Product-oriented process synthesis and development: creams and pastes. AIChE Journal, 2001, 47: 2746–2767

9 Wibowo C, Ng K M. Product-centered processing: manufacture of chemical-based consumer products. AIChE Journal, 2002, 48: 1212–1230

10 Ng K M, Gani R, Johansen K D. Chemical Product Design: Towards a Perspective Through Case Studies. 1st ed. Amsterdam: Elsevier, 2007, 165–490

11 Seider W D, Widagdo S, Seader J D, Lewin D R. Perspectives on chemical product and process design. Computers & Chemical Engineering, 2009, 33: 930–935

12 Smith B V, Ierapepritou M G. Framework for consumer-integrated optimal product design. Industrial & Engineering Chemistry Research, 2009, 48: 8566–8574

13 Gani R, Ng K M. Product design—molecules, devices, functional products, and formulated products. Computers & Chemical Engineering, 2015, 81: 70–79

14 Bernardo F P, Saraiva P M. A Conceptual model for chemical product design. AIChE Journal, 2015, 61: 802–815

15 Mattei M, Kontogeorgis G M, Gani R. A comprehensive framework for surfactant selection and design for emulsion based chemical product design. Fluid Phase Equilibria, 2014, 362: 288–299

16 Cheng Y S, Lam K W, Ng K M, Ko R K M, Wibowo C. An integrative approach to product development—a skin-care cream. Computers & Chemical Engineering, 2009, 33: 1097–1113

17 Bagajewicz M J. On the role of microeconomics, planning, and finances in product design. AIChE Journal, 2007, 53: 3155–3170

18 Fung K Y, Ng K M, Zhang L, Gani R. A grand model for chemical product design. Computers & Chemical Engineering, 2016, 91: 15–27

19 Zhang L, Fung K Y, Zhang X, Fung H K, Ng K M. An integrated framework for designing formulated products. Computers & Chemical Engineering, 2017, 107: 61–76

20 Chan Y C, Fung K Y, Ng K M. Product design: a pricing framework accounting for product quality and consumer awareness. AIChE Journal, 2018, 64: 2462–2471

21 Zhang X, Zhang L, Fung K Y, Rangaiah G P, Ng K M. Product design: impact of government policy and consumer preference on company profit and corporate social responsibility. Computers & Chemical Engineering, 2018, 118: 118–131

22 Zhang X, Zhang L, Fung K Y, Ng K M. Product design: incorporating make-or-buy analysis and supplier selection. Chemical Engineering Science, 2019, 202: 357–372

23 Torquato S. Random heterogeneous materials: microstructure and macroscopic properties. Interdisciplinary Applied Mathematics, 2002, 16: 1–656

24 Fullwood D T, Niezgoda S R, Adams B L, Kalidindi S R. Microstructure sensitive design for performance optimization. Progress in Materials Science, 2010, 55: 477–562

25 Brough D B, Wheeler D, Warren J A, Kalidindi S R. Microstructure-based knowledge systems for capturing process-structure evolution linkages. Current Opinion in Solid State and Materials Science, 2017, 21: 129–140

26 Cecen A, Dai H, Yabansu Y C, Kalidindi S R, Song L. Material structure-property linkages using three-dimensional convolutional neural networks. Acta Materialia, 2018, 146: 76–84

27 Bostanabad R, Zhang Y, Li X, Kearney T, Brinson L C, Apley D W, Liu W K, Chen W. Computational microstructure characterization and reconstruction: review of the state-of-the-art techniques. Progress in Materials Science, 2018, 95: 1–41

28 Mushtaq F. Computation-based microstructure design of structured chemical products. Dissertation for the Doctoral Degree. Hong Kong: The Hong Kong University of Science and Technology, 2020, 50–90

29 Lu D, Liu C, Lang X, Wang B, Li Z, Lee W M P, Lee S W R. Enhancement of thermal conductivity of die attach adhesive (DAAs) using nanomaterials for high brightness light emitting diode (HBLED). In: 2011 IEEE 61st Electronic Components and Technology Conference (ECTC), Lake Buena Vista, FL: IEEE, 2011, 667–672

30 Anandraj J, Joshi M G. Fabrication, performance and applications of integrated nanodielectric properties of materials: a review. Composite Interfaces, 2018, 25: 455–489

31 Muñoz V, Buffa F, Molinari F, Hermida L G, García J J, Abraham G A. Electrospun ethylcellulose-based nanofibrous mats with insect-repellent activity. Materials Letters, 2019, 253: 289–292

32 Cao L, Fu Q, Si Y, Ding B, Yu J. Porous materials for sound absorption. Composites Communications, 2018, 10: 25–35

33 Li G R, Wang L S, Yang G J. Achieving self-enhanced thermal barrier performance through a novel hybrid-layered coating design. Materials & Design, 2019, 167: 107647

34 Lee B, Liu J Z, Sun B, Shen C Y, Dai G C. Thermally conductive and electrically insulating EVA composite encapsulants for solar photovoltaic (PV) cell. Express Polymer Letters, 2008, 2: 357–363

35 Cui C H, Yan D X, Pang H, Xu X, Jia L C, Li Z M. Formation of a segregated electrically conductive network structure in a low-melt-viscosity polymer for highly efficient electromagnetic interference shielding. ACS Sustainable Chemistry & Engineering, 2016, 4: 4137–4145

36 Wang M, Zhang K, Dai X X, Li Y, Guo J, Liu H, Li G H, Tan Y J, Zeng J B, Guo Z. Enhanced electrical conductivity and piezoresistive sensing in multi-wall carbon nanotubes/polydimethylsiloxane nanocomposites via the construction of a self-segregated structure. Nanoscale, 2017, 9: 11017

37 Conte E, Gani R, Ng K M. Design of formulated products: a systematic methodology. AIChE Journal, 2011, 57: 2431–2449

38 Conte E, Gani R, Cheng Y S, Ng K M. Design of formulated products: experimental component. AIChE Journal, 2012, 58: 173–189

39 Zhang X, Zhou T, Zhang L, Fung K Y, Ng K M. Food product design: a hybrid machine learning and mechanistic modeling approach. Industrial & Engineering Chemistry Research, 2019, 58: 16743–16752

40 Király A, Ronkay F. Effect of filler dispersion on the electrical conductivity and mechanical properties of carbon/polypropylene composites. Polymer Composites, 2013, 34: 1195–1203

41 Fu S, Sun Z, Huang P, Li Y, Hu N. Some basic aspects of polymer nanocomposites: a critical review. Nano Materials Science, 2019, 1: 2–30

42 Yang X Y, Chen L H, Li Y, Rooke J R, Sanchezc C, Su B L. Hierarchically porous materials: synthesis strategies and structure design. Chemical Society Reviews, 2017, 46: 481–558

43 Slater A G, Cooper A I. Function-led design of new porous materials. Science, 2015, 348: aaa8075

44 Liu Q, Ye F, Gao Y, Liu S, Yang H, Zhou Z. Fabrication of a new SiC/2024Al co-continuous composite with lamellar microstructure and high mechanical properties. Journal of Alloys and Compounds, 2014, 585: 146–153

45 Pang H, Xu L, Yan D X, Li Z M. Conductive polymer composites with segregated structures. Progress in Polymer Science, 2014, 39: 1908–1933

46 Pang H, Chen C, Bao Y, Chen J, Ji X, Lei J, Li Z M. Electrically conductive carbon nanotube/ultrahigh molecular weight polyethylene composites with segregated and double percolated structure. Materials Letters, 2012, 79: 96–99

47 Wang M, Pan N. Predictions of effective physical properties of complex multiphase materials. Materials Science and Engineering, 2008, 63: 1–30

48 Nan C W, Birringer R, Clarke D R, Gleiter H. Effective thermal conductivity of particulate composites with interfacial thermal resistance. Journal of Applied Physics, 1997, 81: 6692–6699

49 Nan C W, Shi Z, Lin Y. A simple model for thermal conductivity of carbon nanotube-based composites. Chemical Physics Letters, 2003, 37: 666–669

50 Singh K J, Singh R, Chaudhary D R. Heat conduction and a porosity correction term for spherical and cubic particles in a simple cubic packing. Journal of Physics. D, Applied Physics, 1998, 31: 1681–1687

51 Carson J K, Lovatt S J, Tanner D J, Cleland A C. Thermal conductivity bounds for isotropic, porous materials. International Journal of Heat and Mass Transfer, 2005, 48: 2150–2158

52 Wang J F, Carson J K, North M F, Cleland D J. A new approach to modelling the effective thermal conductivity of heterogeneous materials. International Journal of Heat and Mass Transfer, 2006, 49: 3075–3083

53 Agari Y, Uno T. Estimation on thermal conductivities of filled polymers. Journal of Applied Polymer Science, 1986, 32: 5705–5712

54 Liang X G, Ji X. Thermal conductance of randomly oriented composites of thin layers. International Journal of Heat and Mass Transfer, 2000, 43: 3633–3640

55 Mushtaq F, Zhang X, Fung K Y, Ng K M. Product design: an optimization-based approach for targeting of particulate composite microstructure. Computers & Chemical Engineering, 2020, 140: doi:10.1016/j.compchemeng.2020.106975

56 Liu Y, Greene M S, Chen W, Dikin D A, Liu W K. Computational microstructure characterization and reconstruction for stochastic multiscale material design. Computer Aided Design, 2013, 45: 65–76

57 Mukherjee P P, Wang C Y. Stochastic microstructure reconstruction and direct numerical simulation of the PEFC catalyst layer. Journal of the Electrochemical Society, 2006, 153: A840–A849

58 Sheidaei A, Baniassadi M, Banu M, Askeland P, Pahlavanpour M, Kuuttila N, Pourboghrat F, Drzal L T, Garmestani H. 3-D microstructure reconstruction of polymer nano-composite using FIBSEM and statistical correlation function. Composites Science and Technology, 2013, 80: 47–54

59 Wu W, Jiang F. Microstructure reconstruction and characterization of PEMFC electrodes. International Journal of Hydrogen Energy, 2014, 39: 15894–15906

60 Derossi A, Gerke K M, Karsanina M V, Nicolai B, Verboven P, Severini C. Mimicking 3D food microstructure using limited statistical information from 2D cross-sectional image. Journal of Food Engineering, 2019, 241: 116–126

61 Xu H, Li Y, Brinson C, Chen W. A descriptor-based design methodology for developing heterogeneous microstructural materials system. Journal of Mechanical Design, 2014, 136: 051007

62 Zhang Y, Zhao H, Hassinger I, Brinson L C, Schadler L, Chen W. Microstructure reconstruction and structural equation modeling for computational design of nanodielectrics. Integrating Materials and Manufacturing Innovation, 2015, 4: 209–234

63 Hassinger I, Li X, Zhao H, Xu H, Huang Y, Prasad A, Schadler L, Chen W, Brinson L C. Toward the development of a quantitative tool for predicting dispersion of nanocomposites under non-equilibrium processing conditions. Journal of Materials Science, 2016, 51: 4238–4249

64 Lu W, Xiao R, Yang J, Li H, Zhang W. Data mining-aided materials discovery and optimization. Journal of Materiomics, 2017, 3: 191–201

65 Zhou T, Song Z, Sundmacher K. Big data creates new opportunities for materials research: a review on methods and applications of machine learning for materials design. Engineering, 2019, 5: 1017–1026

66 Gu G X, Chen C T, Richmond D J, Buehler M J. Bioinspired hierarchical composite design using machine learning: simulation, additive manufacturing, and experiment. Materials Horizons, 2018, 5: 939–945

67 Gu G H, Noh J, Kim I, Jung Y. Machine learning for renewable energy materials. Journal of Materials Chemistry. A, Materials for Energy and Sustainability, 2019, 7: 17096–17117

68 Besseris G J. Taguchi-generalized regression neural network micro-screening for physical and sensory characteristics of bread. Heliyon, 2018, 3: e00551

69 Bendsøe M P, Sigmund O. Topology Optimization: Theory, Methods, and Applications. 2nd ed. New York: Springer-Verlag Berlin Heidelberg, 2004, 1–318

70 Suzuki K, Kikuchi N. A homogenization method for shape and topology optimization. Computer Methods in Applied Mechanics and Engineering, 1991, 93: 291–318

71 Bendsøe M P, Sigmund O. Material interpolation schemes in topology optimization. Archive of Applied Mechanics, 1999, 69: 635–654

72 Xie Y M, Steven G P. A simple evolutionary procedure for structural optimization. Computers & Structures, 1993, 49: 885–896

73 Wang M Y, Wang X, Guo D. A level set method for structural topology optimization. Computer Methods in Applied Mechanics and Engineering, 2003, 192: 227–246

74 Murray W, Ng K M. An algorithm for nonlinear optimization problems with binary variables. Computational Optimization and Applications, 2010, 47: 257–288

75 Xia L, Breitkopf P. Multiscale structural topology optimization with an approximate constitutive model for local material microstructure. Computer Methods in Applied Mechanics and Engineering, 2015, 286: 147–167

76 Sigmund O, Maute K. Topology optimization approaches. Structural and Multidisciplinary Optimization, 2013, 48: 1031–1055

77 Zheng J, Luo Z, Li H, Jiang C. Robust topology optimization for cellular composites with hybrid uncertainties. International Journal for Numerical Methods in Engineering, 2018, 115: 695–713

78 Chu S, Gao L, Xia M, Li H. Design of sandwich panels with truss cores using explicit topology optimization. Composite Structures, 2019, 210: 892–905

79 Hu M, Feng J, Ng K M. Thermally conductive PP/AlN composites with a 3-D segregated structure. Composites Science and Technology, 2015, 110: 26–34

80 Adams B L, Henrie A, Henrie B, Lyon M, Kalidindi S R, Garmestani H. Microstructure-sensitive design of a compliant beam. Journal of the Mechanics and Physics of Solids, 2001, 49: 1639–1663

81 Tan D, Irwin P. Polymer Based Nanodielectric Composites, Advances in Ceramics—Electric and Magnetic Ceramics, Bioceramics, Ceramics and Environment. London: IntechOpen, 2011, 115–132

82 Lee D W, Yoo B R. Advanced silica/polymer composites: materials and applications. Journal of Industrial and Engineering Chemistry, 2016, 38: 1–12

83 Yu Z Q, You S L, Baier H. Effect of organosilane coupling agents on microstructure and properties of nanosilica/epoxy composites. Polymer Composites, 2012, 33: 1516–1524

84 Tanaka T, Montanari G C, Mülhaupt R. Polymer nanocomposites as dielectrics and electrical insulation-perspectives for processing technologies, material characterization and future applications. IEEE Transactions on Dielectrics and Electrical Insulation, 2004, 11: 763–784

85 Cai Z, Wang X, Luo B, Hong W, Wu L, Li L. Dielectric response and breakdown behavior of polymer-ceramic nanocomposites: the effect of nanoparticle distribution. Composites Science and Technology, 2017, 145: 105–113

86 Sarami M A, Moghadam M, Gilani A G. Modified dielectric permittivity models for binary liquid mixture. Journal of Molecular Liquids, 2019, 277: 546–555

87 Bellucci F, Fabiani D, Montanari G C, Testa L. The processing of nanocomposites. In: Dielectric Polymer Nanocomposites. New York: Springer Science and Business Media, 2010, 31–64

88 Seider W D, Lewin D R, Seader J D, Widegado S, Gani R, Ng K M. Product and Process Design Principles: Synthesis, Analysis and Evaluation. 4th ed. New York: Wiley, 2017, 674–681

89 Romero A S, Chen B. Strategies for the preparation of polymer composites with complex alignment of the dispersed phase. Nanocomposites, 2018, 4: 137–155