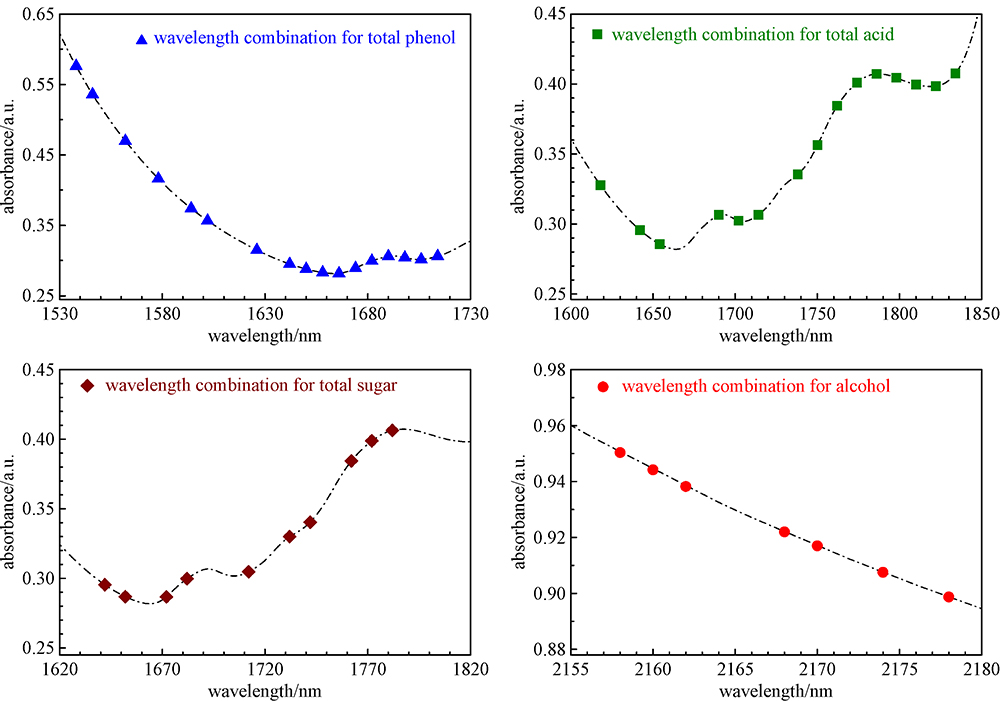
Alcohol, total sugar, total acid, and total phenol contents are the main indicators of wine quality detection. This study aims to establish simultaneous analysis models for the four indicators through near-infrared (NIR) spectroscopy with wavelength optimization. A Norris derivative filter (NDF) platform with multiparameter optimization was established for spectral pretreatment. The optimal parameters (i.e., derivative order, number of smoothing points, and number of differential gaps) were (2, 9, 3) for alcohol, (1, 19, 5) for total sugar, (1, 17, 11) for total acid, and (1, 1, 1) for total phenol. The equidistant combination-partial least squares (EC-PLS) was used for large-scale wavelength screening. The wavelength step-by-step phase-out PLS (WSP-PLS) and exhaustive methods were used for secondary optimization. The final optimization models for the four indicators included 7, 10, 15, and 13 wavelengths located in the overtone or combination regions, respectively. In an independent validation, the root mean square errors, correlation coefficient for prediction (i.e., SEP and RP), and ratio of performance-to-deviation (RPD) were 0.41 v/v, 0.947, and 3.2 for alcohol; 1.48 g/L, 0.992, and 6.8 for total sugar; 0.68 g/L, 0.981, and 5.1 for total acid; and 0.181 g/L, 0.948, and 2.9 for total phenol. The results indicate high correlation, low error, and good overall prediction performance. Consequently, the established reagent-free NIR analytical models are important in the rapid and real-time quality detection of the wine fermentation process and finished products. The proposed wavelength models provide a valuable reference for designing small dedicated instruments.