1 Introduction
1.1 Background introduction
Graves’ ophthalmopathy, also called thyroid-associated ophthalmopathy (TAO), is an eyelid disease associated with thyroid dysfunction and immune system disorder [1]. Graves’ ophthalmopathy extensively affects the soft tissue of the eyelids, which can also lead to eyeball protrusion, eye movement disorder, optic nerve damage, reduced vision, and even blindness. The pathogenesis and diagnosis of Graves’ ophthalmopathy have always been the research hotspot. Computed tomography (CT), magnetic resonance imaging (MRI), ultrasound (US) and related laboratory tests can be used for a screening check for thyroid dysfunction. However, some patients who had thyroid-associated ophthalmopathy did not show abnormalities in the thyroid screening test [2]. Cakir reported one case of TAO, no thyroid-related autoantibodies were detected in the blood and thyroid function was also normal [3]. No single clinical or laboratory examination is the gold standard for diagnosing thyroid eye disease for now [4]. To overcome this problem, a more stable and accurate diagnosis method is needed.
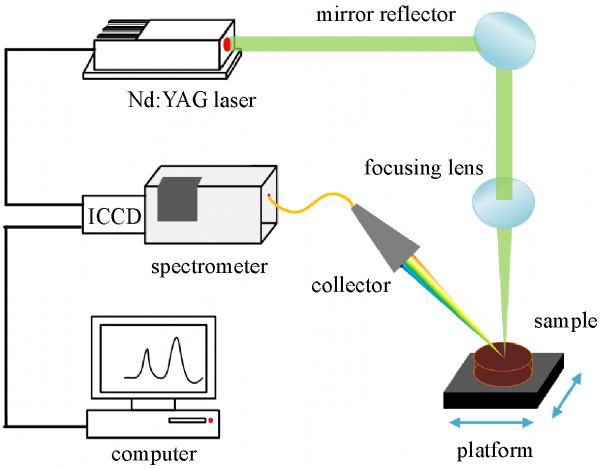
Laser-induced breakdown spectroscopy (LIBS) is an atomic and ionic emission spectroscopy technique [5]. LIBS has been widely used in meat species identification, wood species classification, soil samples analysis, oil detection, red wine classification, and material analysis and other fields [6–13], etc. In recent ten years, many researchers have explored the application of LIBS in the biomedical field. Chen et al. diagnosed human malignancies such as lymphoma and multiple myeloma (MM) using LIBS in combination with chemometric method [14]. Ghasemi et al. used LIBS for the diagnosis of several malignant tissue samples including breast, colon, Larynx, and tongue [15]. Gaudiuso et al. diagnosed melanoma using LIBS combined with linear discriminant analysis (LDA), fisher discriminant analysis (FDA), support vector machines (SVM) and gradient boosting [16]. Chu et al. discriminated nasopharyngeal carcinoma serum using LIBS combined with extreme learning machine (ELM) and random forest (RF) [17]. To our best knowledge, no studies have been reported about identifying Graves’ ophthalmology by using LIBS. Moreover, LIBS combined with generalized regression neural network (GRNN) algorithm for solving classification problems has not been investigated.
In this study, we identified between TAO paraffin embedding samples and healthy controls using LIBS combined with the LDA, SVM, k-nearest neighbor (kNN), and GRNN, respectively. We first realized the identification of Graves’ ophthalmology by using LIBS combined with machine learning method, and first applied the GRNN algorithm to classify biomedical tissues combined with LIBS. The spectral lines were used as the input of classifications. The average accuracy rate, sensitivity, specificity, area under the curve (AUC), and coefficient of variation (CV) were used to evaluate the identification performance of the model.
1.2 Algorithm introduction
LDA is a classic linear supervised learning method, and it was first proposed by Fisher in 1936 on the second classification problem, also known as Fisher linear discriminant [18]. It is still one of the most widely adopted and extremely effective methods in the application of dimension reduction and pattern classification [19,20]. Compared with the neural network method, LDA does not need to adjust parameters, so there is no need such as learning parameters, optimization weights, and selection of neuron activation functions. And it is not sensitive to normalization or randomization of patterns, and this is more prominent among the various algorithms based on gradient descent.
SVM is a generalized linear classifier that classifies data in a supervised manner, it can be nonlinearly classified by using the kernel method, which is one of the common kernel learning methods [21]. SVM classification is only related to several support vectors and has strong stability and a high degree of robustness. The SVM was used for classification and regression analysis problems such as text recognition, face image recognition, plant species identification and tumor detection in machine learning and soft computing tasks [22,23].
kNN algorithm is one of the supervised learning methods [24]. When classifying test samples, the training samples set is first scanned, k samples that are most similar to the test samples set are found, and test samples are determined according to the category of k samples. The algorithm is not sensitive to abnormal data, simple and easy to implement. It is widely used in gender prediction, text recognition, tumor detection, and so on [25,26].
GRNN is a kind of radial basis function neural network. The network structure of GRNN has input layer, pattern layer, summation layer, and output layer [27]. It is widely used in engine performance evaluation, worsted yarn quality, and target tracking fields [28–30]. GRNN model has strong nonlinear capability and high degree of fault tolerance and robustness. As long as the training set is determined, the corresponding network structure and the connection weight between neurons are also determined accordingly. The training process of GRNN is also the process of optimizing smooth parameter s, the parameter Spread is used to express the smooth parameter s [31].
2 Experimental
2.1 Experimental setup
The experiment instruments are composed of a Q-switched Nd:YAG laser, a Czerny-Turner spectrometer, and an intensified charge-coupled device (ICCD) camera mainly. The Q-switched Nd:YAG laser emitted laser beam which focused on the surface of sample by a focal lens and produced the plasma. The plasma emission spectra were collected through the spectrometer and ICCD camera. The parameters about the instruments are as follows: the Q-switched Nd:YAG laser (wavelength: 532 nm; pulse energy: 3 mJ; repetition rate: 10 Hz; French, Quantel., Brilliant B), the Czerny-Turner spectrometer (grating: 1200 lines/mm, sparkling wavelength: 700 nm, resolution: 0.07 nm, acquisition bandwidth: 46 nm, UK, Andor Tech., Shamrock 500i) and ICCD camera (UK, Andor Tech., iStar 320T). The gate delay and the gate width of the ICCD camera were set to be 1 and 9 ms, respectively. The number of laser shots and the number of replicates were 5 and 10, respectively. The experiment instruments are shown in Fig. 1.
2.2 Sample pre-treatment
Experimental samples were collected from graves’ ophthalmopathy patients and healthy controls at the Cancer Center, Union Hospital, Tongji Medical College. In total, 6 paraffin-embedded samples were donated by 3 healthy controls and 3 TAO patients. The TAO patients were diagnosed previously. It is necessary to pretreat the biological tissue samples for the analysis by LIBS. The pre-treatment steps are described below:
1) Paraffin embedding. The collected tissue was saved at -80°C first and was sent to Biossci biotechnology company Ltd (Hubei, China) to make paraffin embedding. Paraffin-embedded samples are shown in Fig. 2. Figures 2(c)–2(e) were healthy controls, and the rest was Graves’ ophthalmology samples.
2) Slice. Paraffin-embedded tissue was sliced with a paraffin slicer. Each sample was sliced to 10 pieces, and every piece was 40 mm thick. Then they were placed on a glass slide, dried and stored.
The laser beam scanned a round area on the sample surface and a single spectrum was obtained by accumulating all pulses in the round area. We collected only one spectrum from one piece and 10 spectra from each sample. A total of 60 spectra were analyzed.
3 Results and discussion
3.1 Analytical line selection
The LIBS spectra from the TAO samples and healthy samples are shown in Fig. 3. We determined the elements corresponding to the observed spectral lines by comparing the National Institute of Standards and Technology (NIST) spectral database [32]. The observed elements included metallic elements (Na, K, Al, Ca), non-metallic element (O) and molecular bands ((C-N), (C-O)). The 14 spectra from one non-metallic element, two molecular bands, and four metallic elements were chosen. These 14 spectra are listed in Table 1.
Tab.1 Analytical lines used as input variables for the classifier |
| element | wavelength/nm | |
|---|---|---|
| molecular bands | C-N | 385.09, 385.47, 386.19, 387.14 388.34 |
| C-O | 389.31 | |
| O | 383.03, 383.59 | |
| metallic elements | Na | 588.99, 589.59 |
| K | 766.49, 769.90 | |
| Al | 394.40, 396.15 | |
| Ca | 393.37, 396.85 |
3.2 Identification of TAO samples with the linear model
We collected ten spectra from each paraffin embedding sample. In total, 60 spectra from 3 healthy controls and 3 TAO patients are used. For each paraffin embedding sample, seven spectra were selected randomly as a training set, and the other three spectra were selected as test set. There are 42 spectra constitute to training set, and 18 spectra constitute to test set totally. The operation of random selection spectra, model training and testing were repeated 100 times. The average accuracy, precision, sensitivity, specificity, and CV were used to evaluate the model [33]. The identification results of the LDA model are shown in Table 2. The identification accuracy of the LDA model was 76.33%. The sensitivity, specificity, and precision were 75.89%, 76.78%, and 76.57%, respectively. The CV of the model was 0.0010.
Tab.2 Confusion matrix of the LDA model |
| predicted class | true class | |
|---|---|---|
| TAO | normal | |
| TAO | 683 | 209 |
| normal | 217 | 691 |
The results showed that the LDA is not suitable for the identification of TAO samples. This is because LDA is a simple linear classifier that does not satisfy the classification of these data.
3.3 Identification of TAO samples with the nonlinear model
In the SVM model, the radial basis function (RBF) kernel function and grid search for parameter optimization were used. The parameter optimization results were shown in Fig. 4. The results showed that the best log2g and log2c were 6 and -1, respectively. The average accuracy rate of SVM model was 96.28%. The identification results of the SVM model are shown in Table 3. The sensitivity, specificity, and precision of the SVM model were 93.78%, 98.78%, and 98.71%, respectively. The CV of the SVM model was 0.0499.
Tab.3 Confusion matrix of the SVM model |
| predicted class | true class | |
|---|---|---|
| TAO | normal | |
| TAO | 844 | 11 |
| normal | 56 | 889 |
kNN model only has one parameter k that can be adjusted, and the parameter optimization result of k is shown in Fig. 5. When the k-value was 3, the kNN model had the best accuracy rate 96.56% and the lowest CV 0.0373. This means the model is efficient and stable. The identification results of the kNN model are shown in Table 4. The sensitivity, specificity, and precision of the kNN model were 96.78%, 96.33%, and 96.35%, respectively.
Tab.4 Confusion matrix of the kNN model |
| predicted class | true class | |
|---|---|---|
| TAO | normal | |
| TAO | 871 | 33 |
| normal | 29 | 867 |
The parameter optimization result of the Spread-value about GRNN is shown in Fig. 6. The Spread-value was from 0.01 to 0.20 and interval increased by 0.01. When the Spread-values were 0.01, 0.02, 0.03, and 0.04, the best accuracy rate was 96.33%, respectively, while the CV was 0.0378, respectively. The Spread-value reflects the approximation ability of the neutral network to the sample data. The larger Spread-value, the smoother approximation process can be acquired. To avoid overfitting, we chose 0.04 as the best Spread-value. The identification results of the GRNN model are shown in Table 5. The sensitivity, specificity, and precision of the GRNN model were 96.67%, 96.00%, and 96.03%, respectively.
Tab.5 Confusion matrix of the GRNN model |
| predicted class | true class | |
|---|---|---|
| TAO | normal | |
| TAO | 870 | 36 |
| normal | 30 | 864 |
Then we compared the three nonlinear models using receiver operating characteristic (ROC) curve, and area under the curve (AUC) to evaluate the quality of the models. The ROC curves of the three models are shown in Fig. 7. The AUC of the SVM, kNN, and GRNN models were 0.9791, 0.9695, and 0.9665, respectively. The AUC, sensitivity, and specificity of the three models are listed in Table 6.
Tab.6 Indicators of the nonlinear identification models |
| AUC | sensitivity | specificity | |||||||
|---|---|---|---|---|---|---|---|---|---|
| SVM | kNN | GRNN | SVM | kNN | GRNN | SVM | kNN | GRNN | |
| test set | 0.9791 | 0.9695 | 0.9665 | 0.9378 | 0.9678 | 0.9667 | 0.9878 | 0.9633 | 0.9600 |
| training set | 1 | 0.9699 | 1 | 1 | 1 | 1 | 1 | 0.9671 | 1 |
4 Conclusions
In summary, a new approach of diagnosing Graves’ ophthalmology was proposed based on LIBS combined with machine learning method. One linear model (LDA) and three nonlinear models (SVM, kNN, GRNN) were compared in this article. The results showed that the average accuracy rate of LDA was only 76.33%, the average accuracy rate of SVM, kNN and GRNN were 96.28%, 96.56%, and 96.33%, respectively, so the kNN model had the best average accuracy rate. The sensitivity of the three nonlinear models were 93.78%, 96.78%, and 96.67%, respectively and the specificity of the three nonlinear models were 98.78%, 96.33%, and 96.00%, respectively. The kNN model had the best sensitivity, but its specificity was slightly worse than the SVM model’s. Sensitivity means the percentage of positive samples detected, whereas specificity means the percentage of negative samples detected. For the detection of biomedical samples, we pay more attention to the detection rate of positive samples. Therefore, we can conclude that kNN is slightly better than SVM. Moreover, the various evaluation indicators of the kNN model were slightly better than those of the GRNN model. Among the four models, the kNN model had the best performance. Therefore, LIBS combined with machine learning method can be an effective way to distinguish Graves’ ophthalmology.