Toward the implementation of a universal angle-based optical indoor positioning system

Abstract

There is an emerging market today for indoor positioning systems capable of working alongside global navigation satellite systems, such as the global positioning system, in indoor environments. Many systems have been proposed in the literature but all of them have fundamental flaws that hold them back from widescale implementation. We review angle-of-arrival (AOA) and angle-difference-of-arrival (ADOA) optical indoor positioning systems which have been proven to be robust, accurate, and easily implementable. We build an AOA/ADOA optical indoor positioning system out of a simple commercial high-speed camera and white light light emitting diodes (LEDs) which operate over a working area of 1 m³, and compare its performance to other indoor positioning methods. The AOA and ADOA systems achieve positioning with low errors of 1.2 and 3.7 cm, respectively.

Key words： angle-of-arrival (AOA); angle-difference-of-arrival (ADOA); indoor positioning; optical positioning

1 Introduction

The global positioning system (GPS) is the heart of a multibillion dollar (annual) industry [1]. Commercial products utilizing GPS have become commonplace in everyday life over the past few decades. We rely on accurate positioning data for a wide range of applications including vehicular navigation, city planning, and personal recreation. Unfortunately, this powerful system has a fundamental challenge in that GPS operation becomes unreliable when the user is either indoors or underground. This is due to the lack of line-of-sight links between the system’s satellites and the user [2]. Since most people spend much of their day indoors (i.e., homes, places of employment, places of recreation), a new positioning technology must be adapted for indoor environments.

Literature in recent decades has provided an abundance of indoor positioning systems [3,4], but none of these systems have seen wide-scale adoption due to practical challenges. These challenges either stem from the cost of implementing the system or from technical considerations. Most indoor positioning systems found in the literature make use of one of three general positioning techniques: received signal strength (RSS) [5–12], time of arrival (TOA)/time-difference of arrival (TDOA) [13–18], or angle of arrival (AOA)/angle-difference of arrival (ADOA) [19–23]. Such techniques can be implemented with ultrasonic, radio-frequency (RF), or optical (visible or infrared) signaling to realize the desired indoor positioning system.

Current ultrasonic indoor positioning systems make use of the TOA/TDOA technique with ultrasonic signaling [14,15]. These systems have low position error, below 1 cm [14,24], but require complex signal coding schemes [14,15]. Additionally, these systems typically require many transmitters and a customized receiver, leading to high cost. Finally, the position error of these systems often increases in real environments due to distortion of the received signal by ambient acoustic noise, temperature fluctuations [24], and multipath. This sensitivity to the environment and their cost make TOA/TDOA-ultrasonic positioning systems impractical.

A second well-known form of indoor positioning system makes use of RSS or TOA/TDOA techniques with RF signaling. The performance and utility of such RF indoor positioning systems greatly depend upon which RF transmitter technology is used. Systems based upon Wi-Fi, Bluetooth, and ultra-wideband technologies have all been demonstrated. Indoor positioning systems based on Wi-Fi technology use an RSS receiver and have a position error greater than 1 m [8,9], which is poor. These systems also typically rely upon mapping RSS levels from multiple Wi-Fi transmitters in an area beforehand, making them sensitive to dynamic objects, such as people, in the positioning environment, as well as changes to the environment itself. Indoor positioning systems based upon Bluetooth technology tend to be more accurate than systems based on Wi-Fi; however, they still yield a position error on the order of meters [25]. In addition, Bluetooth systems utilize the same RSS mapping technique as Wi-Fi systems, so they are also sensitive to error from dynamic objects in the positioning environment and changes to the environment. From a practical standpoint, Wi-Fi and Bluetooth receivers exist in consumer devices making these types of indoor positioning systems easier to implement. In fact, some simple consumer indoor positioning systems that use Wi-Fi technology already exist from companies such as Infsoft [26]. Unfortunately, their low accuracy limits their use to applications where meter-level accuracy is adequate and environments having existing Wi-Fi or Bluetooth transmitters, such as airports. Indoor positioning systems using ultra-wideband technology are the most accurate of the RF indoor positioning systems [27–29]. Such systems use TOA/TDOA receivers to achieve position errors of 0.5 to 2.5 cm [28,29]. Unfortunately, the TOA/TDOA technique requires precise synchronization between all transmitters to obtain good performance. Thus, the practicality of ultra-wideband technology can suffer from the high cost of installing and synchronizing transmitters as well as the cost of adding ultra-wideband receivers to consumer devices.

A newer form of indoor positioning system makes use of RSS, TOA/TDOA, or AOA/ADOA techniques with optical signaling [4,6,7,11,12,19–23]. The performance of these systems is greatly dependent upon the positioning technique that is used. Fortunately, the technologies used in many of these indoor optical systems are similar to each other. Transmitters are implemented using light emitting diodes (LEDs), and receivers are implemented using optical detectors. When positioning is carried out using an RSS receiver, theoretical position errors typically ranges from 5 to 20 cm [5,6,10,12,30,31], while experimental position errors range from around 5 cm for idealized environments [7] to 40 cm for more practical systems [32]. This is typically the least accurate of the optical indoor positioning systems due to its error caused by multipath effects and power fluctuations of the transmitters. When positioning is carried out using a TOA/TDOA receiver, the position error is on the order of 2 mm [13,16], which is vastly superior. Unfortunately, this system faces the challenges mentioned above for the TOA/TDOA technique. The requirement for precise transmitter synchronization makes this technique both difficult and expensive to implement. When positioning is carried out using an AOA or ADOA receiver, a position error ranging between 1 and 4 cm can be achieved [19–22,33]. While this error is larger than those of systems based upon the TOA/TDOA technique, optical indoor positioning systems based on the AOA/ADOA technique have no transmitter synchronization requirement. In addition, these systems are immune to errors caused by variations in transmitter output power making them more robust than their RSS counterparts. The main challenge with optical AOA and ADOA receivers is their increased hardware complexity, in comparison to the other two positioning techniques. For example, a simple photodiode can be used as the optical receiver in both the RSS and TOA/TDOA techniques, while multiple photodiodes or even a camera is required for the AOA/ADOA technique. While the added complexity may seem to be a disadvantage, many consumer devices already contain high quality cameras that are ideal optical receivers. In light of this, AOA and ADOA technology appears to be a strong candidate for future indoor positioning systems [34].

In this paper, we will review several recent advances in AOA and ADOA based optical indoor positioning systems and demonstrate several simple yet accurate implementations. The aim of this work is to bring together these advances in AOA and ADOA based optical indoor positioning systems. We show how they are cheaper to implement while maintaining accuracy in practice in comparison to other indoor positioning technologies making AOA and ADOA optical indoor positioning system the ideal candidate for a universal optical indoor positioning system. The work is laid out as follows: Section 2 introduces the AOA and ADOA optical positioning system and gives an analysis of optical receiver architectures; Section 3 outlines design considerations of practical AOA based optical positioning systems and presents some key positioning results; Section 4 outlines design considerations of practical ADOA based optical positioning systems and presents some key positioning results; Section 5 draw conclusions from the presented work.

2 System overview

While the operation of AOA and ADOA based optical indoor positioning systems are somewhat different, there are some commonalities. These commonalities are primarily based on the capabilities of the optical receiver. In this section, we will discuss the common operation principles between the AOA and ADOA based optical indoor positioning systems. We will then investigate two suitable optical receiver architectures.

2.1 Positioning environment

At its most fundamental level, an AOA or ADOA based optical indoor positioning system consists of a network of fixed optical beacons, which are the transmitters, and a mobile optical receiver as shown in Fig. 1. The entire system contains two coordinate frames: the global coordinate frame, which is aligned with the room that the indoor positioning system is installed in, and the local coordinate frame, which is attached to the optical receiver. These coordinate frames are denoted by x, y, and z axes and x_b, y_b, and z_b axes in Fig. 1, respectively. For simplicity, Fig. 1 assumes that the local and global coordinate frames share the same orientation. Within the global coordinate frame, the ith optical beacon, denoted in the figure by hollow circles, is positioned at (x_i, y_i, z_i) where the z_i is typically the same for all optical beacons. Physically, these optical beacons are typically white light or infrared LEDs, which are mounted on the ceiling. The layout of the optical beacons depends on whether an AOA or ADOA system is used. As such, the layout of optical beacons will be treated in the AOA and ADOA sections in further depth. The position of the mobile optical receiver, denoted in the figure by the solid circle, is located in the global coordinate frame at (x, y, z). It is this position that must be identified.

Fig.1 An AOA optical indoor positioning system with two optical beacons, at (x₁, y₁, z₁) and (x₂, y₂, z₂), and an optical receiver, at (x, y, z). The global frame, having x, y, and z axes, and local frame, having x_b, y_b, and z_b axes, are shown with azimuthal, f, and polar, q, angles in the local frame. © [2017] IEEE. Reprinted, with permission, from Ref. [21]

Full size|PPT slide

To solve for its position, the optical receiver must be able to discern two sets of information. The first set of information is a list of the AOAs between itself and the optical beacons. Each long-dashed line in Fig. 1 between an optical beacon and the optical receiver is called a line of position (LOP). The angles at which each LOP intersects the origin of the optical receiver’s local coordinate frame can be described by two angles in the local frame: the azimuthal angle, f, and the polar angle, q. In Fig. 1, the azimuthal and polar angles for the ith optical beacon in the local coordinate frame are denoted by f_i and q_i, respectively. The second set of information that the optical receiver must discern is the identity of each optical beacon. Each optical beacon must transmit a unique identifier, which is cross-referenced to a table containing the coordinates of each optical beacon in the global frame. This table is assumed to be known a priori by the optical receiver. There are multiple methods of optical beacon identification, but the one used typically depends upon the characteristics of the optical receiver architecture. Such architectures are discussed in the following subsection.

2.2 Optical receiver architectures

The two main optical receiver architectures found in the literature are the multi-photodiode architecture and the camera architecture. The multi-photodiode architecture typically consists of three orthogonally mounted photodiodes in a corner-cube configuration [19,33], although other forms have been proposed [22]. The corner-cube configuration is advantageous as it is compact, uses a minimal number of photodiodes, and is capable of retro-reflection modulation if the optical indoor positioning system is also used for light based communications [35]. The camera architecture consists of an image sensor with a lens mounted above it to produce an image of the optical beacons. This architecture can be found in many consumer devices, such as smartphones. To assess receiver performance, we will now take a deeper look at how each architecture carries out AOA measurements and optical beacon identification.

2.2.1 Multi-photodiode architecture

The multi-photodiode architecture is a simple, yet effective, architecture for both measuring AOAs and identifying their optical beacons. For simplicity, we will consider a corner-cube configuration since it shares many of the advantages and disadvantages of the other configurations. The inset of Fig. 2 shows a corner-cube of photodiodes with its corresponding azimuthal and polar angles. Since each photodiode is oriented in a different direction, the intensity of the incident optical signal will be different for each of the three photodiodes. As such, the photocurrent from the three photodiodes can be used together to uniquely calculate the AOA of the given optical beacon. This is done using the equations and procedures found in Ref. [35].

In a practical multi-photodiode optical receiver, the measured AOAs will contain error, which is then transferred to the estimated position. This occurs regardless of whether AOA or ADOA positioning is used. Consequently, these AOA errors must be minimized to carry out positioning with the highest accuracy. Such errors are introduced by the photodiodes being at improper angles, asymmetries in the detection circuitry for each photodiode, or partial illumination of the structure. In Ref. [19], a corner-cube configuration was used to measure AOAs for positioning, and an AOA error of 2.4° was found. Another limiting factor in AOA measurement is the field of view (FOV) of the optical receiver. A practical multi-photodiode optical receiver has a somewhat limited FOV due to the physical placement of the photodiodes. In a corner-cube configuration, the optical receiver can only measure optical beacons within a solid angle of roughly p/2 steradians, which corresponds to a half angle for the FOV of approximately 20.7°. This is rather limited. However, several corner-cubes can be arranged to increase the FOV, as has been proposed for communications [36].

In addition to accurately measuring AOAs, the multi-photodiode optical receiver must be able to discern which AOAs correspond to which optical beacon. The most common way to do this is to modulate the emitted power of each optical beacon at a unique frequency and have the optical receiver run a series of electronic bandpass filters on each photodiode to differentiate the signals from each optical beacon [19]. This frequency identification method is advantageous due to its simple operation and reliability. By making the frequencies sufficiently high and spacing them sufficiently far apart in frequency, the receiver is unlikely to mistake one optical beacon for another. In Ref. [19], frequency identification was used in an AOA optical indoor positioning system. Figure 2 shows the fast Fourier transform (FFT) of the signals from two optical beacons on all three photodiodes in a corner-cube configuration.

Fig.2 Frequency spectra of the photocurrents measured from the three photodiodes (PDs) of a corner-cube multi-photodiode architecture. Photocurrents I₂ and I₃ are vertically shifted for clarity. Two optical beacons, one transmitting at 1.2 kHz and the other transmitting at 1.4 kHz, are being detected. © [2012] IEEE. Reprinted, with permission, from Ref. [19]

Full size|PPT slide

Here we can see that photodiodes 1 and 2 detect significant photocurrents at 1.2 and 1.4 kHz, while photodiode 3 detects virtually no signal at either frequency. Finally, the signal-to-noise ratio (SNR) of these photocurrents is large, making the possibility of false optical beacon detection negligible.

2.2.2 Camera architecture

The camera architecture is a slightly more complex, but much more accurate, optical receiver architecture. Its main advantage is its low AOA error, typically below 1° [20–22,37]. A representative camera architecture taken from Ref. [22] is shown in Fig. 3. In this figure, we see that a lens is used to focus the incoming optical intensity to a small focal spot on the image sensor.

Fig.3 Schematic of the camera architecture from Ref. [22]. In this figure, the local frame is denoted x' y' z', O_c is the center of the image sensor, f is the focal length of the lens, and P is the location of the focal spot. The points Q, T, and L were used in Ref. [22] but are not used in this analysis. © [2017] IEEE. Reprinted, with permission, from Ref. [22]

Full size|PPT slide

The location of the center of the focal spot on the image sensor, denoted by P in the figure, is measured in pixels from the center of the image sensor, denoted by O_c in Fig. 3. From the location of the focal spot, the azimuth angle as measured on the image sensor, f ', can be calculated simply as

(1)\varphi \text{'}=\arctan \left({\displaystyle \frac{B_x}{B_y}}\right),

where B_x and B_y are the x and y coordinates of the focal spot in units of pixels. The polar angle measured on the image sensor, q′, is slightly more difficult to calculate. If we assume that the focusing lens is an ideal thin lens, the polar angle as measured by the image sensor, q′, is

(2)\theta \text{'}=\arctan \left({\displaystyle \frac{k\sqrt{B_x^2+B_y^2}}{f}}\right),

where k is a scaling factor that typically must be calibrated and f is the focal length of the lens. When using systems containing more complicated lens geometries, or if lens aberrations are to be considered, this expression is inadequate. In those cases, Eq. (2) will typically be approximated by linearization or the entire system will be modeled to obtain a more accurate definition of the polar angle. This is typically required for wide FOV architectures because error in the polar angle as measured by the image sensor grows as the angle increases [21,37]. Another source of error for both angles is the pixel quantization caused by the discrete nature of the pixels on the image sensor. It can be shown that this error is reduced as the number of pixels on the image sensor increases and this error grows as the focal spot approaches the origin on the image sensor [21]. For the system modeled in Ref. [21] the total AOA error is measured to be approximately 1° if the polar angle, q, is in the range 15°<q<50°. This angle is used to define the FOV of the optical receiver, meaning that it can measure optical beacons within a solid angle of just over 2p steradians. This not only allows the camera architecture to see more optical beacons than the multi-photodiode architecture, but it also allows the optical receiver to operate at large tilted angles while still seeing the ceiling mounted optical beacons.

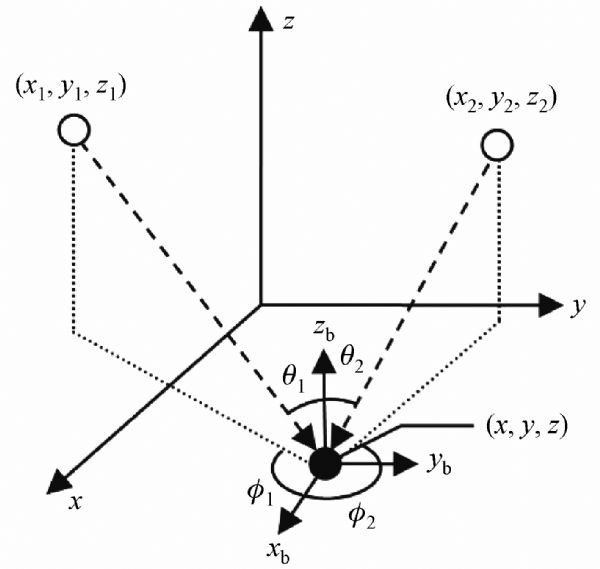
The improved AOA accuracy and FOV of the camera architecture comes at the cost of an increased difficulty in identifying optical beacons. The frequency identification method used for the multi-photodiode architecture is difficult to implement with the camera architecture due to the low frame rate of most current image sensors. While newer cameras such as the GoPro Black are capable of capturing slow-motion video at frame rates up to 240 Hz, frequency identification is still challenging due to a user’s ability to see light modulation up to 65 Hz [38]. This frequency, called the flicker frequency, limits the minimum frequency and minimum frequency spacing. To overcome this limitation, the techniques in Ref. [21] can be applied. There, two additional capabilities of the camera architecture are leveraged to identify optical beacons. First, the camera architecture can spatially separate incoming signals meaning that optical beacons can reuse identifier frequencies so long as each optical beacon has a unique combination of identifier frequencies, i.e., frequency 1 or frequency 2 or both frequencies 1 and 2. This was not possible in the photodiode architecture since each photodiode measured the incoming signals from all beacons simultaneously. Second, most image sensors today can detect color using separate pixels that are sensitive to red, green, and blue (RGB) light. Also, since certain white light LEDs are comprised of separate RGB diodes, the system can transmit different identifier frequencies on different colors of the same optical beacon, e.g., frequency 1 on red, direct current (DC) on green, and both frequencies 1 and 2 on blue. In this system, a DC signal acts as no frequency. Combining these two identification methods with the frequency based method, the authors in Ref. [21] arrived at the color-frequency detection method. In this method, given a certain number of frequencies, n_f, and a certain number of colors, n_c, the number of unique identifiers is {({\mathrm{2}}^{n_{\mathrm{f}}}-\mathrm{1})}^{n_{\mathrm{c}}}. This is because each optical beacon must have at least one identifier frequency on at least one color. The authors of Ref. [21] had a camera with a frame rate of 187 Hz, which restricted the number of possible identifier frequencies to two. However, in that work, it was assumed that frequencies above the Nyquist frequency could not be used due to aliasing. Recently, we have now found that this is not the case. By under-sampling higher frequencies, we can increase the number of useable identifier frequencies so long as the image sensor in the optical receiver does not have an antialiasing filter and care is taken to ensure that any alias frequencies arising from the under-sampling of the identifier frequencies do not fall too close to other identifier frequencies. This allows the system to use identifier frequencies up to and even above the sampling rate. We call this new technique under-sampled frequency-color identification for optical beacons.

We implemented a camera based optical receiver with under-sampled frequency-color identification using a GoPro Black 3. The sampling rate of this optical receiver was 240 Hz, allowing it to detect frequencies up to 120 Hz without aliasing. Allowing alias frequencies, we can detect identifier frequencies above 300 Hz, albeit at a lower SNR. Figure 4 shows the detected signal from a single optical beacon modulated at 70, 207, and 319 Hz.

Fig.4 Frequency spectra in dB of three optical beacons as measured by a GoPro Black 3. The optical beacons are modulated at 70, 207, and 319 Hz. Due to the frame rate of the GoPro Black 3, the 207 Hz signal is the alias frequency of 32 Hz, and the 319 Hz signal is the alias frequency of 78 Hz

Full size|PPT slide

We can see from these results that there are noticeable peaks at 32, 70, and 78 Hz. The 32 Hz peak is the alias frequency of 207 Hz and the 78 Hz peak is the alias frequency of 319 Hz. While the amplitudes differ, the SNR for all frequencies is still more than sufficient to reliably determine their presence.

2.2.3 Architecture summary

In this section, we reviewed the basic operating principles common to both AOA and ADOA optical positioning systems as well as the two main optical receiver architectures seen in the literature. We found that, for both systems, the optical receiver must accurately determine the AOAs associated with each optical beacon and identify which optical beacon each AOA is associated with. Based on the results found in the literature for multi-photodiode and camera architectures, we conclude that the camera architecture is a superior candidate for the optical receiver in both AOA and ADOA optical positioning systems, due to its better accuracy and compatibility with consumer devices.

3 AOA based positioning

Having identified the superior optical receiver for both optical AOA and ADOA positioning systems, we turn to the specific details of an AOA based optical positioning system. We first look at the basic algorithm to carry out AOA based optical positioning. Next, we look at how the optical beacon geometry affects the accuracy of the position solution. Finally, we look at some positioning results obtained using the GoPro Black 3 optical receiver introduced in the previous section.

3.1 AOA positioning algorithm

To determine the optical receiver’s position in the global frame of an AOA based optical positioning system, a set of nonlinear equations must be solved. With the aid of Fig. 1, we follow the derivations shown in Ref. [37] to obtain the following azimuthal and polar angle equations for the ith optical beacon (based upon the position of that optical beacon and the position of the optical receiver):

(3){\varphi }_i=\arctan \left({\displaystyle \frac{y-y_i}{x-x_i}}\right),

(4){\theta }_i=\arctan \left({\displaystyle \frac{\Vert r_i\Vert }{\left|z-z_i\right|}}\right).

In this expression, r_i=(x-x_i)\widehat{x}+(y-y_i)\widehat{y} is the vector between the optical receiver and the point on the z plane of the optical receiver that is directly below the ith optical beacon, where \Vert r_i\Vert is the second norm of r_i. Note that these equations give the azimuthal and polar angles in the global frame. As such, the local coordinate frame of the optical receiver must share the same orientation as the system’s global frame. Note, as well, that these equations cannot be simply inverted to solve for the position of the optical receiver. A nonlinear least squares (LS) algorithm must be used instead. Following the derivations of Ref. [37], we first linearize Eqs. (3) and (4) and write them in matrix form giving

(5)[\mathit{H}]=\left[{\displaystyle \frac{\begin{array}{lll}{\displaystyle \frac{(y_{\mathrm{1}}-y)}{{\Vert r_{\mathrm{1}}\Vert }^{\mathrm{2}}}}& {\displaystyle \frac{(x-x_{\mathrm{1}})}{{\Vert r_{\mathrm{1}}\Vert }^{\mathrm{2}}}}& \mathrm{0}\\ ⋮& ⋮& ⋮\\ {\displaystyle \frac{(y_i-y)}{{\Vert r_i\Vert }^{\mathrm{2}}}}& {\displaystyle \frac{(x-x_i)}{{\Vert r_i\Vert }^{\mathrm{2}}}}& \mathrm{0}\\ ⋮& ⋮& ⋮\\ {\displaystyle \frac{(y_n-y)}{{\Vert r_n\Vert }^{\mathrm{2}}}}& {\displaystyle \frac{(x-x_n)}{{\Vert r_n\Vert }^{\mathrm{2}}}}& \mathrm{0}\end{array}}{\begin{array}{lll}{\displaystyle \frac{|z_{\mathrm{1}}-z|(x_{\mathrm{1}}-x)}{\Vert r_{\mathrm{1}}\Vert {\Vert R_{\mathrm{1}}\Vert }^{\mathrm{2}}}}& {\displaystyle \frac{|z_{\mathrm{1}}-z|(y_{\mathrm{1}}-y)}{\Vert r_{\mathrm{1}}\Vert {\Vert R_{\mathrm{1}}\Vert }^{\mathrm{2}}}}& {\displaystyle \frac{\Vert r_{\mathrm{1}}\Vert }{{\Vert R_{\mathrm{1}}\Vert }^{\mathrm{2}}}}\\ ⋮& ⋮& ⋮\\ {\displaystyle \frac{|z_i-z|(x_i-x)}{\Vert r_i\Vert {\Vert R_i\Vert }^{\mathrm{2}}}}& {\displaystyle \frac{|z_i-z|(y_i-y)}{\Vert r_i\Vert {\Vert R_i\Vert }^{\mathrm{2}}}}& {\displaystyle \frac{\Vert r_i\Vert }{{\Vert R_i\Vert }^{\mathrm{2}}}}\\ ⋮& ⋮& ⋮\\ {\displaystyle \frac{|z_n-z|(x_n-x)}{\Vert r_n\Vert {\Vert R_n\Vert }^{\mathrm{2}}}}& {\displaystyle \frac{|z_n-z|(y_n-y)}{\Vert r_n\Vert {\Vert R_n\Vert }^{\mathrm{2}}}}& {\displaystyle \frac{\Vert r_n\Vert }{{\Vert R_n\Vert }^{\mathrm{2}}}}\end{array}}}\right].

In this expression, H is called the system design matrix and R_i=(x-x_i)\widehat{x}+(y-y_i)\widehat{y}+(z-z_i)\widehat{z}. The system design matrix is shown as an augmented matrix containing both the azimuthal and polar partial derivatives. Next, we obtain a vector of azimuthal and polar angle errors from the ith optical beacon, df_i and dq_i, respectively. We do this by calculating the azimuthal and polar angles expected at our current estimate of the position and subtracting them from the measured azimuthal and polar angles. We then use an initial position estimate to obtain constant values for the system design matrix. Next, we solve the LS equation,

(6)\left[\begin{array}{l}\partial x\\ \partial y\\ \partial z\end{array}\right]={({\mathit{H}}^{\mathrm{T}}\mathit{H})}^{-\mathrm{1}}{\mathit{H}}^{\mathrm{T}}\left[\begin{array}{l}\partial {\varphi }_{\mathrm{1}}\\ ⋮\\ \partial {\varphi }_i\\ ⋮\\ {\displaystyle \frac{\partial {\varphi }_n}{\partial {\theta }_{\mathrm{1}}}}\\ ⋮\\ \partial {\theta }_i\\ ⋮\\ \partial {\theta }_n\end{array}\right],

to obtain the vector [dx dy dz]^T, which is an estimate of the error in the current position estimate. Finally, we add that estimated error to the current position estimate and iterate through the whole process until the estimated position error falls below an acceptable threshold.

3.2 Dilution of precision

As stated earlier, error in the measured AOAs will introduce error in the final estimated position. From Eq. (6), we can see that the proportionality between the measured AOA errors and the position errors depends upon the system design matrix, H. According to Ref. [39], we can define a quantity called the dilution of precision (DOP) which is calculated from the design matrix, H, as

(7)\mathrm{D}\mathrm{O}\mathrm{P}(x,y,z)=\sqrt{\mathrm{tr}{({\mathit{H}}^{\mathrm{T}}\mathit{H})}^{-\mathrm{1}}}={\displaystyle \frac{{{\displaystyle \sigma }}_{\mathrm{p}}(x,y,z)}{{{\displaystyle \sigma }}_{\mathrm{a}}}}.

This expression calculates DOP from the system’s design matrix, H, for a given point in the global frame and equates it to the ratio of the position error at the point in the global frame, s_p(x, y, z), to the AOA error of the optical receiver, s_a. Thus, DOP acts as a scaling factor between angle error and position error, and it is a function of position in space.

The system design matrix in Eq. (5) is highly dependent upon the locations of the optical beacons relative to the optical receiver. In Ref. [37], several different optical beacon configurations were tested and the DOP values over a constant z plane below the optical beacons were calculated. The results of that analysis are shown in Fig. 5. The three optical beacon configurations tested were a triangle, shown in Fig. 5(a), a square, shown in Fig. 5(b), and a hexagon, shown in Fig. 5(c). The optical beacons were fixed on a plane at z = 100 cm and all DOP calculations were carried out on the plane of z = 0. The area coverage for each optical beacon configuration was determined by making the optical power density equal for each configuration and the position error was calculated assuming an AOA error of s_a = 1°.

Fig.5 Curves for DOP and position error for the (a) triangle, (b) square, and (c) hexagon optical beacon geometries. Optical beacons are indicated by hollow white circles. The position error is calculated from the DOP using an AOA error of 1°. © [2015] IEEE. Reprinted, with permission, from Ref. [37]

Full size|PPT slide

These results indicate that by transitioning from the triangle configuration to the hexagon configuration, a roughly 30% improvement can be made in positioning accuracy. While this is not orders of magnitude, it does highlight the fact that proper optical beacon placement is necessary to maximize the capabilities of an optical AOA positioning system.

3.3 AOA positioning results

An optical AOA indoor positioning system was built and the GoPro Black 3 optical receiver described in Section 2.22 was used as the optical receiver. Nine optical beacons in a square configuration were used in this system, as shown in Fig. 6.

Fig.6 AOA optical indoor positioning system. The optical beacons are denoted by hollow circles and the optical receiver is denoted by the x-y-z coordinate frame. This figure is from the thesis of M. Bergen. It is owned by UBC under a creative commons license and the authors are free to reuse it here (given the publisher’s approval) since it is openly available through cIRcle

Full size|PPT slide

The positioning results for this system are shown in Fig. 7 for 31 arbitrary positions over a 1 m³ working area. The average position error for this system is 1.2 cm. This agrees with the errors obtained in Ref. [21] using a camera architecture and a similar working area, and is superior to the 5 cm error obtained in Ref. [33], which used a corner-cube architecture in a smaller system with fewer optical beacons. As expected, the error increases as the optical receiver moves toward the periphery of the system, due to large polar angles, and at the center of the system, as it is directly below an optical beacon so one of the azimuthal angles is undefined.

Fig.7 Positioning results for an AOA optical indoor positioning system using a GoPro Black 3 as the optical receiver. Estimated positions are indicated by orange ´’s; true positions are indicated by blue circles

Full size|PPT slide

4 ADOA based positioning

The main challenge faced by optical indoor positioning systems based solely on AOA measurements is the requirement to know the optical receiver’s orientation. This means that the optical receiver is either limited to certain orientations, as was the case in the previous section, or must integrate accelerometers and gyroscopes to determine its orientation accurately, which is costly. One solution is an optical indoor positioning system based on ADOA instead of AOA. In this section, we will review the relevant theory for optical indoor positioning systems based on ADOA, then show experimental results for such a system.

4.1 ADOA positioning algorithm

An ADOA optical indoor positioning system makes use of the fact that by differencing AOAs, the dependence on which coordinate frame the AOAs are measured in is removed. In an ADOA system, AOAs are measured just as they were for the standard AOA system; however, instead of calculating the optical receiver’s position from that information alone, the angles are differenced to give a new set of measurements. An example of an ADOA system is shown in Fig. 8. This figure shows the mth and nth optical beacon and the ADOA, g, which is the angle that subtends the vectors between the mth and nth optical beacons and the optical receiver.

Fig.8 Schematic of an ADOA optical indoor positioning system. The mth and nth optical beacons are denoted by the hollow circles at (x_m, y_m, z_m) and (x_n, y_n, z_n), respectively. The optical receiver is denoted by the a solid circle at (x, y, z), and the ADOA between the mth and nth optical beacon is denoted by g_m,n. Note that there is no coordinate frame attached to the optical receiver as this information is irrelevant

Full size|PPT slide

Following the work done in Ref. [22], the equation to calculate an ADOA based on the locations of the optical beacons and the optical receiver is

(8){\gamma }_{m,n}=\arccos \left({\displaystyle \frac{r_m·r_n}{\Vert r_m\Vert \Vert r_n\Vert }}\right).

If the entirety of Eq. (8) is independent of the orientation of the measurement frame, the ADOA angle, g, is also independent of the orientation of the measurement frame. The numerator of Eq. (8) is the inner product of the vector between the optical receiver and the mth optical beacon, and the vector between the optical receiver and the nth optical beacon. Inner product calculations are independent of the measurement frame so long as both vectors are in the same frame, thus satisfying our requirement. The denominator of Eq. (8) is the magnitude of the distance between the optical receiver and the two optical beacons. Since this is a scalar quantity, it is independent of measurement frame, thus satisfying our requirement. The interested reader can find a more quantitative treatment of this analysis in Ref. [22].

Now that the ADOAs have been related to the locations of the optical beacons and the location of the optical receiver, they must be related to the measured AOAs. To do so, we again follow the analysis in Ref. [22], which derives the expression for the relationship between the ADOAs and the AOAs to be

(9)\begin{array}{l}\cos ({\gamma }_{m,n})=\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{[\sin (\theta {\text{'}}_m)\cos (\varphi {\text{'}}_m)-\sin (\theta {\text{'}}_n)\cos (\varphi {\text{'}}_n)]}^{\mathrm{2}}\\ -{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{[\sin (\theta {\text{'}}_m)\sin (\varphi {\text{'}}_m)-\sin (\theta {\text{'}}_n)\sin (\varphi {\text{'}}_n)]}^{\mathrm{2}}\\ -{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{[\cos (\varphi {\text{'}}_m)-\cos (\varphi {\text{'}}_n)]}^{\mathrm{2}}.\end{array}

We must now use Eqs. (8) and (9) to solve for the position of the optical receiver. The complexity of these equations prevents us from using the LS method that was introduced for AOA systems; therefore, we must introduce a new method of solving these equations. The route taken in Ref. [22] is to use an exhaustive search within a bounded positioning region to find the position whose ADOAs best match the measured ADOAs. While this method is computationally expensive, it eliminates the possibility of non-convergence that can plague LS calculations. The solution time is greatly dependent on the size of the search area and the size of each spatial step. The accuracy of this algorithm is directly influenced by the spatial step size.

4.2 ADOA positioning results

The positioning results presented in Section 3.3 have been reprocessed using an ADOA algorithm instead of the AOA algorithm used previously. The ADOA algorithm uses a spatial step size of 1 cm to obtain its position estimates. The results are shown in Fig. 9. In the figure, the blue circles denote actual positions, while the green squares denote the estimated positions.

Fig.9 Positioning results for an ADOA optical indoor positioning system using a GoPro Black 3 as the optical receiver. Estimated positions are indicated by green squares; true positions are indicated by blue circles

Full size|PPT slide

It can be seen that an ADOA optical indoor positioning system is capable of low position error. The average error for the 31 random locations investigated is 4.3 cm; however, eliminating the one obvious blunder in the data reduces the position error to approximately 3.7 cm. While the position error of the ADOA system is higher than an AOA system, it is still superior to the position error for RSS systems. Moreover, it sheds the requirement to know the receiver’s orientation, which limits the AOA system’s usefulness. Table 1 illustrates the accuracy of AOA and ADOA-based optical indoor positioning methods by comparing it to other indoor positioning system methods.

Tab.1 Comparison of optical positioning methods

method	reference	year	theoretical accuracy	experimental accuracy	transmitter/receiver technology
optical AOA	this work	2018		1.2 cm	LEDs/high speed camera
optical ADOA	this work	2018		3.7 cm	LEDs/high speed camera
optical RSS	[5]	2014	5−20 cm
optical RSS	[7]	2012		4.4 cm	LEDs/photodiode
RF RSS	[8]	2015		100−300 cm	Wi-Fi
optical TDOA	[13]	2011		0.2 cm	LEDs/photodiode
ultrasonic TOA	[14]	2015		<1 cm	specialized ultrasonic equipment
optical TOA	[16]	2013	2−5 cm
optical AOA	[21]	2017		1.7 cm	LEDs/high speed camera
optical ADOA	[22]	2018		3.2 cm	LEDs/smartphone
RF RSS	[25]	2014		200−400 cm	bluetooth low energy
RF TOA	[29]	2017		0.5−2.5 cm	ultra wideband
optical AOA	[37]	2015	1−3 cm

5 Conclusion

Indoor positioning systems are emerging from research environments into commercial systems. However, there is still a need for a single implementation that can operate in all indoor environments. Optical AOA/ADOA indoor positioning systems show great promise for this because of their versatility. They are independent of the transmitter power, transmitter synchronization, acoustic noise, temperature, and humidity and provide superior accuracy, with errors on the order of 1−5 cm. Moreover, AOA/ADOA indoor positioning systems can be implemented with simple LEDs and commercially-available cameras—making them strong candidates for future indoor positioning systems.

Acknowledgements

This work was supported in part by the Natural Science and Engineering Research Council of Canada, the Canadian Foundation for Innovation, and Western Economic Diversification Canada.

References

1 Leveson I. The economic value of GPS: preliminary assessment. Leveson Consulting. 2015

2 Global Positioning System Standard Positioning Service Performance Standard. 4 ed, 2008

3 Liu H, Darabi H, Banerjee P, Liu J. Survey of wireless indoor positioning techniques and systems. IEEE Transactions on Systems, Man and Cybernetics, Part C, Applications and Reviews, 2007, 37(6): 1067–1080

4 Luo J, Fan L, Li H. Indoor positioning systems based on visible light communication: state of the art. IEEE Communications Surveys and Tutorials, 2017, 19(4): 2871–2893

5 Zhang X, Duan J, Fu Y, Shi A. Theoretical accuracy analysis of indoor visible light communication positioning system based on received signal strength indicator. Journal of Lightwave Technology, 2014, 32(21): 4180–4186

6 Kim Y, Hwang J, Lee J, Yoo M. Position estimation algorithm based on tracking of received light intensity for indoor visible light communication systems. In: Proceedings of International Conference on Ubiquitous & Future Networks. Dalian, China: IEEE, 2011, 131–134

7 Jung S Y, Hann S, Park S, Park C S. Optical wireless indoor positioning system using light emitting diode ceiling lights. Microwave and Optical Technology Letters, 2012, 54(7): 1622–1626

8 Ma R, Guo Q, Hu C, Xue J. An improved WiFi indoor positioning algorithm by weighted fusion. Sensors (Basel), 2015, 15(9): 21824–21843

PMID

9 Taniuchi D, Liu X, Nakai D, Maekawa T. Spring model based collaborative indoor position estimation with neighbor mobile devices. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(2): 268–277

10 Lim J. Ubiquitous 3D positioning systems by led-based visible light communications. IEEE Wireless Communications, 2015, 22(2): 80–85

11 Gu W J, Aminikashani M, Deng P, Kavehrad M. Impact of multipath reflections on the performance of indoor visible light positioning systems. Journal of Lightwave Technology, 2016, 34(10): 2578–2587

12 Rahaim M, Prince G B, Little T D C. State estimation and motion tracking for spatially diverse VLC networks. In: Proceedings of IEEE Globecom Workshops (GC Wkshps). Anaheim, CA, USA: IEEE, 2012, 1249–1253

13 Jung S Y, Hann S, Park C S. TDOA-based optical wireless indoor localization using LED ceiling lamps. IEEE Transactions on Consumer Electronics, 2011, 57(4): 1592–1597

14 De Angelis A, Moschitta A, Carbone P, Calderini M, Neri S, Borgna R, Peppucci M. Design and characterization of a portable ultrasonic indoor 3-D positioning system. IEEE Transactions on Instrumentation and Measurement, 2015, 64(10): 2616–2625

15 Lindo A, Garcia E, Ureña J, del Carmen Perez M, Hernandez A. Multiband waveform design for an ultrasonic indoor positioning system. IEEE Sensors Journal, 2015, 15(12): 7190–7199

16 Wang T Q, Sekercioglu Y A, Neild A, Armstrong J. Position accuracy of time-of-arrival based ranging using visible light with application in indoor localization systems. Journal of Lightwave Technology, 2013, 31(20): 3302–3308

17 Do T H, Yoo M. TDOA-based indoor positioning using visible light. Photonic Network Communications, 2014, 27(2): 80–88

18 Panta K, Armstrong J. Indoor localization using white LEDs. Electronics Letters, 2012, 48(4): 228–230

19 Arafa A, Jin X, Klukas R. Wireless indoor optical positioning with a differential photosensor. IEEE Photonics Technology Letters, 2012, 24(12): 1027–1029

20 Arafa A, Jin X, Bergen M H, Klukas R, Holzman J F. Characterization of image receivers for optical wireless location technology. IEEE Photonics Technology Letters, 2015, 27(18): 1923–1926

21 Bergen M H, Jin X, Guerrero D, Chaves H A L F, Fredeen N V, Holzman J F. Design and implementation of an optical receiver for angle-of-arrival-based positioning. Journal of Lightwave Technology, 2017, 35(18): 3877–3885

22 Zhu B, Cheng J, Wang Y, Yan J, Wang J. Three-dimensional VLC positioning based on angle difference of arrival with arbitrary tilting angle of receiver. IEEE Journal on Selected Areas in Communications, 2018, 36(1): 8–22

23 Yasir M, Ho S W, Vellambi B N. Indoor position tracking using multiple optical receivers. Journal of Lightwave Technology, 2016, 34(4): 1166–1176

24 Wu J, Zhu J, Yu Z, Zhuge J. Three-dimensional temperature field compensation technology for large-scale ultrasonic positioning system. Transactions of the Institute of Measurement & Control, 2016, 39(12): 0142331216648375

25 Zhao X, Xiao Z, Markham A, Trigoni N, Ren Y. Does BTLE measure up against WiFi? A comparison of indoor location performance. In: Proceedings of20th European Wireless Conference on European Wireless. Barcelona, Spain: IEEE, 2014, 1–6

26 Infsoft GmbH. Indoor Positioning, Tracking and Indoor Navigation with Wi-Fi. 2017

27 Gezici S, Tian Z, Giannakis G B, Kobayashi H, Molisch A F, Poor H V, Sahinoglu Z. Localization via ultra-wideband radios: a look at positioning aspects for future sensor networks. IEEE Signal Processing Magazine, 2005, 22(4): 70–84

28 Sadi F, Johnson T, Klukas R. Simulation of a non-coherent UWB transceiver design–noise and impairment analysis. International Journal of Ultra Wideband Communications and Systems, 2012, 2(4): 216–224

29 Bharadwaj R, Swaisaenyakorn S, Parini C G, Batchelor J C, Alomainy A. Impulse radio ultra-wideband communications for localization and tracking of human body and limbs movement for healthcare applications. IEEE Transactions on Antennas and Propagation, 2017, 65(12): 7298–7309

30 Zhang W, Chowdhury M I S, Kavehrad M. Asynchronous indoor positioning system based on visible light communications. Optical Engineering, 2014, 53(4): 045105

31 Wu D, Ghassemlooy Z, Zhong W D, Khalighi M A, Minh H L, Chen C, Zvanovec S, Boucouvalas A C. Effect of optimal Lambertian order for cellular indoor optical wireless communication and positioning systems. Optical Engineering (Redondo Beach, Calif.), 2016, 55(6): 066114

32 Li L, Hu P, Peng C, Shen G, Zhao F. Epsilon: a visible light based positioning system. In: Proceedings of 11th USENIX Conference on Networked Systems Design and Implementation. Seattle, WA, USA: ACM, 2014, 331–343

33 Arafa A, Dalmiya S, Klukas R, Holzman J F. Angle-of-arrival reception for optical wireless location technology. Optics Express, 2015, 23(6): 7755–7766

PMID

34 Armstrong J, Sekercioglu Y A, Neild A. Visible light positioning: a roadmap for international standardization. IEEE Communications Magazine, 2013, 51(12): 68–73

35 Jin X, Holzman J F. Differential retro-detection for remote sensing applications. IEEE Sensors Journal, 2010, 10(12): 1875–1883

36 Collier C M, Jin X, Holzman J F, Cheng J. Omni-directional characteristics of composite retroreflectors. Journal of Optics A, Pure and Applied Optics, 2009, 11(8): 085404

37 Bergen M H, Arafa A, Jin X, Klukas R, Holzman J F. Characteristics of angular precision and dilution of precision for optical wireless positioning. Journal of Lightwave Technology, 2015, 33(20): 4253–4260

38 Davis J, Hsieh Y H, Lee H C. Humans perceive flicker artifacts at 500 Hz. Scientific Reports, 2015, 5(1): 7861

PMID

39 Dempster A G. Dilution of precision in angle-of-arrival positioning systems. Electronics Letters, 2006, 42(5): 291–292