Cuprous oxide/copper oxide interpenetrated into ordered mesoporous cellulose-based carbon aerogels for efficient photocatalytic degradation of methylene blue

Abstract

The casual discharge of dyes from industrial settings has seriously polluted global water systems. Owing to the abundance of biomass resources, preparing photocatalysts for photocatalytic degradation of dyes is significant; however, it still remains challenging. In this work, a cuprous oxide/copper oxide composite was interpenetrated onto carbon nanosheets of cellulose-based flexible carbon aerogels (Cu₂O/CuO@CA_x) via a simple freeze-drying-calcination method. The introduction of the carbon aerogel effectively prevents the aggregation of the cuprous oxide/copper oxide composite. In addition, Cu₂O/CuO@CA_0.2 has a larger specific surface area, stronger charge transfer capacity, and lower recombination rate of photogenerated carriers than copper oxide. Moreover, Cu₂O/CuO@CA_0.2 exhibited high photocatalytic activity in decomposing methylene blue, with a degradation rate reaching up to 99.09% in 60 min. The active oxidation species in the photocatalytic degradation process were systematically investigated by electron spin resonance characterization and poisoning experiments, among which singlet oxygen played a major role. In conclusion, this work provides an effective method for preparing photocatalysts using biomass resources in combination with different metal oxides. It also promotes the development of photocatalytic degradation of dyes.

Key words： carbon aerogel; photocatalysis; dye degradation; biomass; cuprous oxide/copper oxide

1 Introduction

Rapid developments in industry and agriculture have considerably improved the global economy and accelerated the development of society while detrimentally affecting the environment [1,2]. In particular, the discharge of dye wastewater on a global scale has resulted in the pollution of water bodies and the depletion of drinkable water, threatening the survival of humans, animals and plants [3]. Methylene blue, first synthesized by Heinrich Caro in 1800, has an aromatic heterocyclic structure with the molecular formula C₁₆H₁₈N₃ClS and is the most commonly used dye in the textile industry [4]. It is highly soluble in water, readily forms stable solutions with water at room temperature and is commonly used to dye cotton, silk and paper. In addition, methylene blue is often used as a bacterial stain and indicator [5] and has been further utilized in the medical field to treat bacterial malaria [6]. However, methylene blue is toxic, carcinogenic and mutagenic, with exposure to its low concentrations resulting in diarrhea, nausea and vomiting [7]. When methylene blue concentration reaches a certain level in water bodies around the globe, mass extinction of aquatic life may occur. Moreover, the presence of methylene blue in water results in the production of deep-colored by-products, which reduce sunlight transmittance through the water. Consequently, there is a decrease in the levels of dissolved oxygen in water, affecting the survival of aquatic organisms [8]. Therefore, eliminating such pollutants from water is vital for achieving sustainable industrial and agricultural development.

Currently, the typical methods used for dye treatment are physical (adsorption and membrane separation) [9], biological (phytoremediation and aerobic) [10] and chemical methods (electrochemical oxidation, chemical precipitation and advanced oxidation) [11]. Physical methods proceed via a simple reaction mechanism, are easy to operate, and do not cause secondary water pollution. The popular materials used in physical methods include activated carbon [12], bentonite [13] and nanofiber membranes [14]. Although these materials are low cost and efficient, they have limited adsorption capacity and reusability. Biological methods use microorganisms to chemically react with pollutants, converting organic pollutants into harmless inorganic substances, thereby achieving water purification [15]. However, although biological methods consume low energy, do not produce secondary water pollution and require low investment, their high environmental pH and temperature requirements greatly limit their application [16]. Chemical methods are based on the chemical reactions between chemical reagents and dyes to produce precipitates or simple compounds or on the degradation of dyes by redox substances and using an external electric field. These methods are currently popular because they are simple, efficient and controllable. However, they also have many limitations, such as high costs, production of secondary pollutants and high energy consumption [11]. Therefore, it would be beneficial to develop a new environmentally friendly, pollution-free technology for treating dyes with low cost, high efficiency and low energy consumption.

Photocatalysis is a green technology with significant application prospects in the energy and environmental fields. It has been widely used in the synthesis of organic acids [17] and furfuryl alcohol [18], hydrogen generation [19] and carbon dioxide (CO₂) reduction [20]. Photocatalysis is the most promising technology for eliminating organic pollutants from wastewater owing to its environmental friendliness, low energy consumption, low cost and reusability, especially for methylene blue degradation. The key to achieving this goal is to develop an efficient and economical photocatalyst. Numerous photocatalysts have been developed, such as metal-free semiconductors [21] and metal oxides/sulfides [22]. Copper oxide-based nanoparticles have been widely used in photocatalysis owing to their wide range of light absorption, antimicrobial properties, excellent electrical and thermal conductivities, and suitable optical bandgap [23]. Typically, copper oxide (CuO) is an indirect bandgap semiconductor with a bandgap of 1.7 eV and a carrier diffusion length of 200 nm [24]. However, pure CuO exhibits low photocatalytic degradation of organic dyes in practical applications due to photocorrosion and rapid recombination of photogenerated carriers. Due to the synergistic geometrical and electronic aspects or strain and ligand effects, nanocomposites composed of two metal oxides exhibit superior catalytic activity compared to single metal oxides [25]. The disadvantages of single-component CuO photocatalysts can be modified by combining with other components (e.g., cerium oxide, cuprous oxide, titanium dioxide, ferric oxide) [26‒29]. As we known, Cu₂O is a direct bandgap semiconductor with a bandgap of 2.2 eV and a carrier diffusion length of 500 nm. As a typical p-type semiconductor photocatalyst with a suitable band gap, low toxicity and a wide visible light absorption range, Cu₂O has attracted a lot of interest. Meanwhile, the photocatalytic performance of photocatalysts depends on the intrinsic carrier dynamics such as carrier mobility, life-time, diffusion length and density. Surprisingly, the carrier mobility of Cu₂O is 30‒130 cm²·V^‒1·s^‒1, which is significantly higher than that of other photocatalysts (e.g., titanium dioxide, bismuth vanadium oxide, ferric oxide, and tungsten trioxide) [30]. Moreover, some researches have shown that CuO and Cu₂O can be interconverted, which avoids the addition of other functional materials, leading to the low production costs [31]. However, the nanocatalysts often suffered from aggregation/clumping due to the high surface energies of the particles, resulting in poor photocatalytic activity. Moreover, nanoscale catalysts are difficult to be recycled. Therefore, developing a new process for synthesizing highly active, stable and recyclable CuO/Cu₂O-based photocatalysts is of great significance.

Carbon aerogels are recognized as excellent carrier materials for loaded heterogeneous catalysts owing to their high porosity, excellent electronic conductivity and physicochemical stability [32]. The materials commonly used for preparing carbon aerogels include graphene oxide [33], graphitic carbon nitride [34] and metal-organic frameworks [35]. However, the carbon precursors of these materials are mainly derived from non-renewable fossil resources, leading to the high cost. To this end, a more efficient and economical routes to fabricate new carbon aerogels with high performance would be advantageous. The developments of biomass-based carbon aerogels with abundant renewable raw materials, low cost and environmental friendliness make them expected to be a sustainable alternative for non-renewable carbon materials [36]. Carboxymethylcellulose sodium (CMC) and cellulose nanofibers (CNFs) produced from decomposing plant cellulose are the most abundant and sustainable biopolymers on earth, which are ideal precursors for synthesizing biomass-based carbon aerogels. The obtained CMC/CNF-based carbon aerogels have low density, three-dimensional interconnected pores, high electrical conductivity and excellent adsorption capacity. Moreover, the CMC and CNF structures have natural compatibility, with the introduction of CNF giving CMC/CNF-based carbon aerogels excellent compressibility and elasticity [37]. While other biomass precursors used to prepare carbon aerogels include alginate [38], chitosan [39], and starch [40], the poor thermal stability of these biomass polymers results in the carbon aerogels prepared being fragile and incompressible [41], which greatly limits the practical application of them. Hence, the combination of heterogeneous catalysts with CMC/CNF-based carbon aerogels to prepare novel photocatalysts has great potential.

Herein, we report the interpenetration of a Cu₂O/CuO composite into cellulose-based carbon nanosheets (named Cu₂O/CuO@CA_x) using a simple freeze-drying-calcination method for photocatalytic degradation of methylene blue, where CuO nanobelt precursor was partly reduced to Cu₂O. We carefully investigated the optimal reaction conditions for the photocatalytic degradation of methylene blue. In addition, the active oxidation species produced in the photocatalytic degradation of methylene blue were investigated by electron spin resonance (ESR) characterization and poisoning experiments. The possible reaction mechanism of the photocatalytic degradation methylene blue process was further elucidated. Overall, this study effectively combines biomass resources with different types of metal oxide nanomaterials, which shows great potential in treating dyes in wastewater.

2 Experimental

2.1 Preparation of CuO

First, 110.0 g of sodium hydroxide (NaOH) was slowly added to 0.9 L of deionized water. Following the complete dissolution of NaOH, 20.0 g of hexadecyl trimethyl ammonium bromide (CTAB) was slowly added in the obtained solution under magnetic stirring conditions. Subsequently, the mixed system was heated to 60 °C to obtain NaOH-CTAB solution. Additionally, 3.1 g of cupric nitrate was precisely weighed and dissolved in 0.1 L of deionized water. The obtained solution was injected into the NaOH-CTAB solution and stirred magnetically for 1 h. The system was then filtered at 60 °C, and the filter cake was washed with ethanol and deionized water to neutral. The black solid samples were dried in an open oven at 50 °C for 12 h. Finally, these dried black powders were further calcined under N₂ atmosphere (350 °C, 120 min) to obtain CuO.

2.2 Preparation of Cu₂O/CuO@CA_x

Different CuO dosages (0.1 g, 0.2 g and 0.3 g) were added to 20 mL of deionized water and dispersed adequately, respectively. Then, 1.0 g of CMC was dissolved into the above dispersion. After that, 1.0 g of CNF was slowly added, and the obtained solution was mechanically stirred for 120 min. The mixed samples were freeze-dried and then calculated at 500 °C for 120 min under nitrogen atmosphere to obtain Cu₂O/CuO@CA_x (named as Cu₂O/CuO@CA_0.1, Cu₂O/CuO@CA_0.2 and Cu₂O/CuO@CA_0.3, respectively).

2.3 Photocatalytic activity measurements

The photocatalytic properties of Cu₂O/CuO@CA_0.2 were studied by degradation of methylene blue dye under the irradiation of a 300 W Xenon lamp. The influences of pH values on the photocatalytic degradation of methylene blue were first investigated. Specifically, methylene blue solutions (100 ppm) with pH values of 7, 8, 9, 10, and 11 were prepared and then 10 mg of Cu₂O/CuO@CA_0.2 was added. The mixed system was first stirred at 500 r·min⁻¹ for 40 min under darkness to reach adsorption/desorption equilibrium. Then, the reaction was reacted for 60 min under the irradiation of visible light. The reacted solution was filtered through a microporous filter (0.22 μm) and the concentrations were measured with a ultraviolet−visible spectrophotometer at a wavelength of 664 nm. Under the optimal pH, the effects of Cu₂O/CuO@CA_0.2 dosages, irradiation time and CuO addition in CuO/CuO@CA_x on the photocatalytic degradation of methylene blue were also investigated. All the above reactions were carried out at room temperature.

The degradation efficiency of methylene blue was calculated by the following equation:

\mathrm{R}\mathrm{e}\mathrm{m}\mathrm{o}\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{y}\left(\mathrm{\%}\right)=\frac{C_{\mathrm{e}}-C_{\mathrm{t}}}{C_{\mathrm{e}}}\times 100\mathrm{\%},

where C_e (mg·L^‒1) and C_t (mg·L^‒1) represented the methylene blue concentrations before and after being degraded for a certain time, respectively.

3 Results and discussion

3.1 Catalyst synthesis and characterization

The preparation schematic, scanning electron microscopy (SEM) images, elemental mapping images and the energy-dispersive X-ray spectroscopy (EDS) of Cu₂O/CuO@CA_0.2 are shown in Fig.1. The preparation of Cu₂O/CuO@CA_x is illustrated in Fig.1(a), mainly including directional freezing-casting, vacuum freeze-drying, and calcination strategies. First, CMC and CNF were used as carbon sources and dissolved in a dispersion of CuO nanobelt, followed by directional freezing-casting and vacuum freeze-drying to obtain Cu₂O/CuO@CA_x precursors. Lastly, a controllable calcination was carried out to acquire Cu₂O/CuO@CA_x with vertically aligned layered structure. The morphology of the prepared Cu₂O/CuO@CA_0.2 was studied by SEM. It is apparent from the images in Fig.1(b) and Fig.1(c) that Cu₂O/CuO@CA_0.2 exhibits a structure with vertically aligned layers; this structure ensures the stability and flexibility of the material. Fig.1(d) and Fig.1(e) show the uniform distribution of interpenetrated Cu species into ordered mesoporous cellulose-based carbon aerogels. In addition, the elemental mapping images (Fig.1(f)–Fig.1(i)) show a uniform distribution of C, N, O and Cu in the composites, indicating that the Cu species were successfully interpenetrated into the carbon nanosheets in carbon aerogels. Furthermore, EDS data (Fig.1(j)) show C, N, O and Cu contents of 68.52, 0.10, 15.94 and 10.95 wt%, respectively.

Fig.1 (a) Schematic of Cu₂O/CuO@CA_x preparation. (b–e) Scanning electron microscopy images of Cu₂O/CuO@CA_0.2. Elemental mapping images of Cu₂O/CuO@CA_0.2: (f) C, (g) N, (h) O and (i) Cu. (j) Energy-dispersive X-ray spectroscopy of Cu₂O/CuO@CA_0.2.

Full size|PPT slide

Fig.2 shows the N₂ adsorption–desorption isotherms and Fourier transform infrared (FTIR) spectra of CuO and Cu₂O/CuO@CA_0.2. To better illustrate the interpenetrating effect of Cu₂O/CuO into carbon nanosheets in case of carbon aerogels on the surface area and pore size distribution, CuO and Cu₂O/CuO@CA_0.2 were subjected to N₂ adsorption−desorption measurements. As shown in Fig.2(a), both materials exhibit IV-type isotherms, indicating an abundance of mesopores in their structures (Fig.2(b)). Moreover, the specific surface area of Cu₂O/CuO@CA_0.2 (26.71 m²·g^–1) was considerably higher than CuO (7.79 m²·g^–1). This phenomenon can be attributed to the combination of a Cu₂O/CuO compound with a carbon aerogel exhibiting a layered structure, which is consistent with the SEM results. Meanwhile, the higher specific surface area of Cu₂O/CuO@CA_0.2 compared to CuO may enhance the adsorption and mass transfer properties of the photocatalyst, improving its photocatalytic efficiency.

Fig.2 (a) N₂ adsorption−desorption isotherms and (b) Barret−Joyner−Halenda pore size distributions of copper oxide (CuO) and Cu₂O/CuO@CA_0.2; (c) Fourier transform infrared (FTIR) spectra of CuO and Cu₂O/CuO@CA_0.2 and (d) its local zoom of FTIR spectrum for Cu₂O/CuO@CA_0.2.

Full size|PPT slide

To investigate the Cu species on the prepared materials, the functional groups on the material’s surface were investigated using FTIR spectroscopy. As shown in Fig.2(c), the characteristic absorption band at 3442 cm^–1 is attributed to the stretching vibration of O–H. The characteristic peak at 494 cm^–1 in the FTIR spectrum of CuO is because of the bending vibration of Cu–O [42]. The band at 672 cm⁻¹ in the FTIR spectrum of Cu₂O/CuO@CA_0.2 shown in Fig.2(d) is associated with the stretching vibration of Cu–O in Cu₂O, while the peak at 521 cm⁻¹ is attributed to the stretching vibration of Cu–O in CuO. This result further indicated the successful preparation of Cu₂O/CuO@CA_0.2.

To further verify the successful fabrication of the Cu₂O/CuO@CA_0.2, X-ray diffraction (XRD) characterizations of CuO and Cu₂O/CuO@CA_0.2 were performed. In addition, the elemental composition and chemical states of Cu₂O/CuO@CA_0.2 were investigated using X-ray photoelectron spectroscopy (XPS). The XRD and XPS results are shown in Fig.3. In Fig.3(a), the typical diffraction peaks of CuO can be observed (PDF#44-0706-CuO). With regards to the Cu₂O/CuO@CA_0.2, the diffraction peaks at 35.4° and 38.3° correspond to the (110) and (111) crystallographic planes of CuO, respectively, and those at 36.3°, 42.3°, 61.4° and 73.5° correspond to the (111), (200), (220) and (311) crystallographic planes of Cu₂O (PDF#77-0199), respectively. Thus, the results indicate that partial Cu₂O was formed during CuO calcination. The composite formed by the two compounds was interpenetrated into the carbon nanosheets of the carbon aerogels, which is consistent with the FTIR and SEM results.

Fig.3 (a) X-ray diffraction patterns of copper oxide and Cu₂O/CuO@CA_0.2; X-ray photoelectron spectroscopy (XPS) spectra of Cu₂O/CuO@CA_0.2: (b) XPS survey spectrum, (c) C 1s, (d) N 1s, (e) O 1s and (f) Cu 2p.

Full size|PPT slide

In the survey spectrum of Cu₂O/CuO@CA_0.2 shown in Fig.3(b), the binding energy peaks for C, N, O and Cu can be observed. In the C 1s spectrum shown in Fig.3(c), three diffraction peaks located at 284.8, 285.7 and 290.3 eV can be attributed to C–C, O–C and O=C bonding, respectively [43]. The peaks at 399.5 and 401.6 eV in the N 1s spectrum correspond to NH₂/N–C and NH³⁺, respectively (Fig.3(d)). The high-resolution O 1s spectrum was fitted into three peaks, identified as O–Cu (531.1 eV), O=C (532.8 eV) and H–O (534.7 eV) (Fig.3(e)) [44]. The presence of Cu²⁺ was confirmed by the peaks of Cu 2p_3/2 and Cu 2p_1/2 at 933.4 and 953.2 eV, respectively, in the Cu 2p spectrum. The presence of Cu⁺ was confirmed by the peaks at 932.0 and 951.8 eV, indicating Cu₂O formation [43]. The aforementioned results are consistent with those of SEM, FTIR and XRD, indicating the successful preparation of Cu₂O/CuO@CA_0.2.

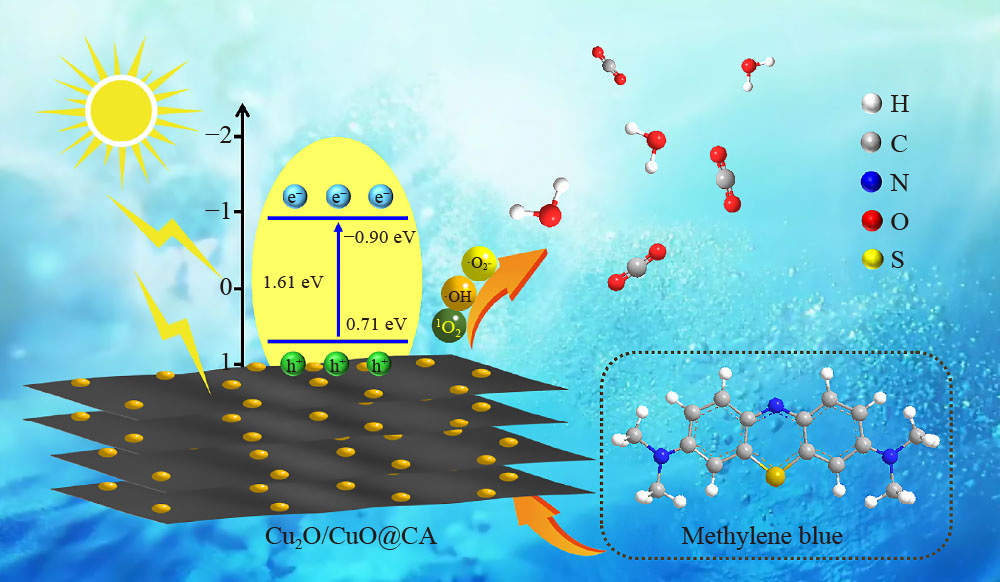
Fig.4 shows the Mott−Schottky, ultraviolet photoelectron spectroscopy (UPS), photocurrent response and electrochemical impedance spectroscopy (EIS) results of CuO and Cu₂O/CuO@CA_0.2. The energy band structure of semiconductors is closely related to their redox properties, which essentially determine their charge separation efficiency. To elucidate the energy band structure of Cu₂O/CuO@CA_0.2, Mott−Schottky plots were constructed and UPS measurements were performed. As shown in Fig.4(a) and Fig.4(b), the positive slope of the Mott−Schottky curves indicated that both CuO and Cu₂O/CuO@CA_0.2 are n-type semiconductors. Based on the horizontal intercepts obtained from the maximum slope, the flat-band potentials of CuO and Cu₂O/CuO@CA_0.2 were −0.98 and −0.90 V, respectively. The conduction band of the n-type semiconductor is 0.2 V more negative than the flat-band potential [45]. Thus, the conduction bands of CuO and Cu₂O/CuO@CA_0.2 were −0.78 and −0.7 V vs. Ag/AgCl, respectively. The conversion of the reference electrode of the conduction band to a normal hydrogen electrode (NHE) was achieved using the Nernst formula (E_NHE = E_Ag/AgCl + 0.197 and pH = 7), and the calculated conduction bands for CuO and Cu₂O/CuO@CA_0.2 were calculated as −0.98 and −0.90 V, respectively. In addition, UPS was used to study the electronic states and valence band (VB) of the photocatalysts. Fig.4(c) and Fig.4(d) show the UPS results of CuO and Cu₂O/CuO@CA_0.2, respectively. The work function (Φ) was first calculated according to Φ = 21.20 − E_cutoff, where 21.20 is the UV excitation energy, and E_cutoff was derived from the point of intersection at high binding energy. E_cutoff values for CuO and Cu₂O/CuO@CA_0.2 were 16.20 and 16.02 eV, respectively. The Φ values of CuO and Cu₂O/CuO@CA_0.2 were calculated using its formula as 5.00 and 5.18 eV, respectively. The VB positions were calculated based on E_VB (vs. vacuum) = Φ + E_edge, where E_edge is the intersection point at low binding energy. E_edge values for CuO and Cu₂O/CuO@CA_0.2 were 0.30 and − 0.03 eV, and the calculated E_VB (vs. vacuum) values were 0.86 and 0.71 eV, respectively. Finally, the reference was transformed into NHE using the equation: E_VB (vs. NHE) = E_VB (vs. vacuum) − 4.44. The VBs of CuO and Cu₂O/CuO@CA_0.2 vs. NHE were calculated to be 0.86 and 0.71 V, respectively. According to the Mott–Schottky and UPS results, the bandgaps of CuO and Cu₂O/CuO@CA_0.2 were calculated to be 1.84 and 1.61 eV, respectively. The charge separation of CuO and Cu₂O/CuO@CA_0.2 was investigated by recording transient photocurrent curves. As shown in Fig.4(e), Cu₂O/CuO@CA_0.2 exhibits a higher photocurrent response than CuO, indicating that Cu₂O/CuO@CA_0.2 has a higher photogenerated charge separation ability. Moreover, the EIS results showed that the arc radius of Cu₂O/CuO@CA_0.2 is smaller than that of CuO (Fig.4(f)), indicating that the charge transfer resistance of Cu₂O/CuO@CA_0.2 is significantly lower, allowing for the efficient separation and migration of photoinduced excitons [46].

Fig.4 Mott−Schottky plots of (a) copper oxide (CuO) and (b) Cu₂O/CuO@CA_0.2; (c, d) ultraviolet photoelectron spectroscopy of CuO and Cu₂O/CuO@CA_0.2; (e) periodic ON/OFF photocurrent response of CuO and Cu₂O/CuO@CA_0.2 in 0.1 mol·L⁻¹ Na₂SO₄ electrolyte under visible light irradiation (λ > 420 nm) at 0.5 V vs. Ag/AgCl electrode; (f) electrochemical impedance spectroscopy Nyquist plots in the visible light illumination of CuO and Cu₂O/CuO@CA_0.2.

Full size|PPT slide

3.2 Photocatalytic activity tests

To increase methylene blue degradation, experiments were conducted to determine the optimal process conditions. The results are shown in Fig.5. The pH value affects the photocatalyst surface properties, such as the surface charge and dissociation of contaminants [47]. Meanwhile, methylene blue is a cationic dye; an alkaline system is beneficial for its degradation. In this work, the photocatalytic degradation methylene blue activity was monitored by measuring the absorbance of the solution at different pH values (7, 8, 9, 10 and 11). Initially, Cu₂O/CuO@CA_0.2 (10 mg) was added to a methylene blue solution (10 mL and 100 ppm) and reacted in the dark with magnetic stirring for 40 min to reach adsorption/desorption equilibrium, followed by irradiation for 60 min. As shown in Fig.5(a), the degradation rate of methylene blue reached 99.08% when pH increased to 8. The degradation of methylene blue remained constant upon further increasing the pH values. Therefore, pH = 8 was selected as the best pH value from the perspective of green chemistry.

Fig.5 The effects of (a) pH and (b) catalyst dosage on the photocatalytic degradation of methylene blue using Cu₂O/CuO@CA_0.2; the effect of (c) reaction time on the photocatalytic degradation of methylene blue using Cu₂O/CuO@CA_x; photocatalytic degradation kinetics of methylene blue using (d, g) Cu₂O/CuO@CA_0.1, (e, h) Cu₂O/CuO@CA_0.2 and (f, i) Cu₂O/CuO@CA_0.3.

Full size|PPT slide

Next, the amount of catalyst significantly impacts the degradation efficiency and oxidation capacity. Here, a series of experiments were performed with different Cu₂O/CuO@CA_0.2 dosages for the photocatalytic degradation of methylene blue. As shown in Fig.5(b), the degradation rate of methylene blue reached 99.09% when the Cu₂O/CuO@CA_0.2 dosage was 5 mg. However, the degradation rate of methylene blue slightly decreased upon increasing the amount of Cu₂O/CuO@CA_0.2. This phenomenon can be attributed to the increased turbidity of the nanoparticles, which causes more scattering effects and less visible light penetration [2].

A series of tests were performed to investigate the effect of CuO addition in CuO/CuO@CA_x on the degradation of methylene blue. Similarly, the experiments were first treated in dark conditions for 40 min to reach adsorption/desorption equilibrium. Afterwards, the reactions were carried out under the irradiation with 300 W Xenon lamp. Obviously, all samples displayed excellent photocatalytic degradation performance (Fig.5(c)). Among them, Cu₂O/CuO@CA_0.2 exhibited the best photocatalytic performance, with the degradation rate of methylene blue reaching 90.98% when irradiated for 20 min, which was higher than those of CuO/CuO@CA_0.1 and CuO/CuO@CA_0.3 systems. In the following, the effects of reaction times on their photocatalytic degradation efficiencies of methylene blue were studied. As shown in Fig.5(c), the degradation rate of methylene blue was significantly increased upon exposure to a 300 W xenon lamp irradiation for 20 min, showing a linear trend. A slight increase in degradation efficiency was observed between 20 and 60 min. However, it was almost constant between 60 and 120 min due to the gradual occupation of the active catalyst sites as the reaction proceeded, which reduced the efficiency of the system [2]. Among the tested photocatalysts, Cu₂O/CuO@CA_0.2 exhibited the highest photocatalytic degradation efficiency, degrading ≥ 90% of methylene blue in 60 min. To further demonstrate the performance of the photocatalysts, kinetic curve fitting was performed. Fig.5(d)–Fig.5(i) fitting results revealed that the degradation process followed first-order reaction kinetics. In addition, as shown in Fig.5(d)–Fig.5(f), the rate constant of Cu₂O/CuO@CA_0.2 was determined to be 0.05047, which is higher than those of Cu₂O/CuO@CA_0.1 (0.03937) and Cu₂O/CuO@CA_0.3 (0.04523), indicating that Cu₂O/CuO@CA_0.2 demonstrated the best photocatalytic degradation performance.

To investigate the effect of photo corrosion on the photocatalyst, the content of copper ions released from Cu₂O/CuO@CA_0.2 after the reaction was also explored. Here, 5 mg of Cu₂O/CuO@CA_0.2 was added to 10 mL of methylene blue solution with a concentration of 100 ppm (the copper content was 54.75 mg·L^–1), and the mixed system was stirred for 40 min under dark conditions and then irradiated by visible light for 60 min. After that, the contents of copper ions were detected by inductively coupled plasma mass spectrometry, and 0.1919 mg·L^–1 of copper ions was observed, indicating that the Cu₂O/CuO@CA_0.2 has an excellent stability.

To better understand the photocatalytic efficiency of Cu₂O/CuO@CA_0.2, the efficiency of Cu₂O/CuO@CA_0.2 and the reported catalysts on the photocatalytic degradation of methylene blue were investigated. Obviously, the Cu₂O/CuO@CA_0.2 has excellent photocatalytic activity in the methylene blue degradation as compared with the reported catalysts (Table S1, cf. Electronic Supplementary Material) [26–29,33,48]. As for the MgFe₂O₄/CuO/GO, the reaction time is lower than that of this work (Table S1, entries 1 and 2). However, the initial concentration of methylene blue in the Cu₂O/CuO@CA_0.2 (100 mg·L^–1) photocatalytic system is higher than that of MgFe₂O₄/CuO/GO (10 mg·L^–1). Meanwhile, the MgFe₂O₄/CuO/GO has large preparation costs and tedious preparation processes when compared with Cu₂O/CuO@CA_0.2. Overall, this photocatalytic system shows excellent photocatalytic performance and has a promising application in the treatment of methylene blue.

3.3 ESR characterization and poisoning experiments

To investigate the photocatalytic degradation mechanism of methylene blue using Cu₂O/CuO@CA_0.2, ESR trapping experiments were conducted. The results are shown in Fig.6. The electrons (e⁻), holes (h⁺), superoxide radical (·O₂⁻), hydroxyl radical (·OH) and singlet oxygen (¹O₂) signals of Cu₂O/CuO@CA_0.2 were detected in the absence of catalysts in the dark and upon exposure to catalysts for 5 and 10 min. Initially, 2,2,6,6-tetramethylpiperidine-N-oxide (TEMPO) was used to detect e⁻ and h⁺. As shown in Fig.6(a), a stable triplet peak with a 1:1:1 intensity was generated using TEMPO (in the absence of a catalyst or in the dark with a catalyst). After 5 min of irradiation, TEMPO was converted, and the corresponding peak intensity decreased, indicating the production of e⁻. When irradiated for 10 min, the peak intensity was further reduced, indicating more e⁻ were generated. The signal intensity trends of h⁺ were similar to those of e⁻ (Fig.6(b)) owing to the pair formation of e⁻ and h⁺.

Fig.6 2,2,6,6-Tetramethylpiperidine-N-oxide electron spin resonance (ESR) spin labeling for (a) electrons and (b) holes, 5,5-dimethyl-1-pyrroline-N-oxide ESR spin trapping for (c) superoxide radical and (d) hydroxyl radical as well as 2,2,6,6-tetramethyl-4-piperidone-1-yloxy ESR spin labeling for (e) singlet oxygen (control: under the dark conditions or irradiation without samples); (f) the effect of different active oxidation species on methylene blue’s degradation.

Full size|PPT slide

Furthermore, 5,5-dimethyl-1-pyrroline-N-oxide (DMPO) was used to monitor the generated ·O₂⁻ and ·OH during the photocatalytic degradation processes. In Fig.6(c), ·O₂⁻ signals were not detectable in the absence of catalysts when irradiated using visible light or in the darkness with photocatalysts, indicating that visible light is necessary for producing ·O₂⁻. Under visible light irradiation, the signals of DMPO/·O₂⁻ with an intensity of 1:1:1:1 were detected in the Cu₂O/CuO@CA_0.2 system, indicating that ·O₂⁻ was generated. Similarly, the signal intensity of DMPO/·O₂⁻ increased with the irradiation time, suggesting more ·O₂⁻ was produced. For ·OH, all the trends were similar to those of ·O₂⁻, except for the DMPO/·OH intensity of 1:2:2:1 (Fig.6(d)).

¹O₂ is also a typical oxidatively active species, with 2,2,6,6-tetramethyl-4-piperidone-1-yloxy commonly used as a trapping agent in ESR measurements to investigate the production of ¹O₂. As displayed in Fig.6(e), no signals were observed in the system without Cu₂O/CuO@CA_0.2 irradiated by visible light or in darkness. However, a triplet peak with an intensity of 1:1:1 was generated when visible light was irradiated on the Cu₂O/CuO@CA_0.2 system. The corresponding signal intensity increased with a longer exposure time to light, indicating the production of ¹O₂ and its contents increasing with irradiation time.

To determine the effects of the main active species produced by the Cu₂O/CuO@CA_0.2 photocatalytic system for the degradation of methylene blue, a series of poisoning experiments were performed over Cu₂O/CuO@CA_0.2 under optimal conditions (5 mg Cu₂O/CuO@CA_0.2, pH = 8, 100 ppm of methylene blue solution and exposure to the dark for 40 min and visible light irradiation for 60 min). The effects of ·OH, ¹O₂, ·O₂⁻ and h⁺ on the photocatalytic degradation of methylene blue were investigated using isopropyl alcohol, tryptophan, p-benzoquinone and potassium iodide as sacrificial agents. As shown in Fig.6(f), adding p-benzoquinone, isopropyl alcohol and tryptophan inhibited the photocatalytic degradation of methylene blue compared to the Cu₂O/CuO@CA_0.2 photocatalytic system without a sacrificial agent. Moreover, compared with the other two sacrificial agents, the addition of tryptophan resulted in the lowest degradation rate of methylene blue, indicating that ¹O₂ was the main active species involved in the photocatalytic degradation of methylene blue. However, after adding potassium iodide, the degradation rate of methylene blue was slightly enhanced, indicating that the h⁺ inhibited the degradation of methylene blue.

3.4 Possible mechanism of photocatalytic degradation of methylene blue via Cu₂O/CuO@CA_0.2

Based on previously reported data and the results of ESR spectroscopy measurements as well as poisoning experiments, a possible reaction pathway for the photocatalytic degradation of methylene blue using Cu₂O/CuO@CA_0.2 was proposed [49]. Initially, the different potentials of the VBs and conduction bands of CuO and Cu₂O result in the transfer of photogenerated e⁻ and h⁺ between CuO and Cu₂O. In case of visible light irradiation, e⁻ is transferred from Cu₂O to CuO, while h⁺ is transferred from CuO to Cu₂O [50]. Furthermore, carbon aerogels have excellent conductivity and superior charge carrier mobility, resulting in enhanced charge separation. The pathways for the generation of active oxidation species are postulated as follows:

{\mathrm{O}}_2+{\mathrm{e}}^{-}\to \cdot {{\mathrm{O}}_2}^{-}

\cdot {{\mathrm{O}}_2}^{-}+{\mathrm{h}}^{+}\to {}^1{\mathrm{O}}_2

\mathrm{O}{\mathrm{H}}^{-}/{\mathrm{H}}_2\mathrm{O}+{\mathrm{h}}^{+}\to \cdot \mathrm{O}\mathrm{H}

The excited e⁻ reacts with the O₂ adsorbed on the catalyst surface to form ·O₂⁻, as shown in Fig.7. Some of the ·O₂⁻ further reacts with h⁺ to form ¹O₂. Moreover, h⁺ can combine with OH⁻ and H₂O to form ·OH. Eventually, methylene blue adsorbed on the catalyst surface was degraded to CO₂ and H₂O under their comprehensive effects.

Fig.7 The possible photocatalytic mechanism for degradation of methylene blue using Cu₂O/CuO@CA_0.2.

Full size|PPT slide

4 Conclusions

In summary, Cu₂O/CuO@CA_0.2 with a vertically aligned layered structure was successfully prepared via a freeze-drying-calcination method. Cu₂O/CuO@CA_0.2 exhibited a narrower bandgap and faster photogenerated carrier separation/migration than CuO. According to the first-order kinetics equation, photocatalytic experiments demonstrated that Cu₂O/CuO@CA_0.2 displays excellent photocatalytic degradation of methylene blue. The optimised reaction conditions yielded an optimal degradation rate of 99.09% in 60 min (Cu₂O/CuO@CA_0.2 dosage: 5 mg, pH 8 and methylene blue solution concentration: 100 ppm). The usage of free radical scavengers and tracking probes revealed that ¹O₂ is the main active oxidation species involved in the degradation process. Therefore, this study proposed a simple, effective and controllable method for preparing biomass-based photocatalysts loaded with metal oxides to facilitate the application of photocatalytic technology in the field of environmental protection.

Acknowledgements

This work was supported by the Foundation of National Natural Science Foundation of China (Grant No. 22008018), NSFC-CONICFT Joint Project (Grant No. 51961125207), China Postdoctoral Science Foundation (Grant No. 2020M670716), Liaoning Province “Xingliao Talent Plan” Outstanding Talent Project (Grant No. XL YC1901004), Innovation Support Program for High-level Talents of Dalian (Top and Leading Talents) (Grant No. 201913), the Foundation of Guangxi Key Laboratory of Clean Pulp & Papermaking and Pollution Control, College of Light Industry and Food Engineering, Guangxi University (Grant No. 2021KF08), Dalian City Outstanding Talent Project (Grant No. 2019RD13), Start-up Fund for Doctoral Research of Dalian Polytechnic University (Grant No. 2020-07), the Foundation of State Key Laboratory of Biobased Material and Green Papermaking (Grant No. KF201914), Qilu University of Technology, Shandong Academy of Sciences, and the Foundation of Key Laboratory of State Forestry and Grassland Administration for Plant Fiber Functional Materials (Grant No. 2020KFJJ06). We also thank the Shiyanjia laboratory for the XPS analysis.

Electronic Supplementary Material

Supplementary material is available in the online version of this article at https://doi.org/10.1007/s11705-023-2305-0 and is accessible for authorized users.

References

1 Gusain R, Gupta K, Joshi P, Khatri O P. Adsorptive removal and photocatalytic degradation of organic pollutants using metal oxides and their composites: a comprehensive review. Advances in Colloid and Interface Science, 2019, 272: 102009

2 Ebrahimi R, Maleki A, Zandsalimi Y, Ghanbari R, Shahmoradi B, Rezaee R, Safari M, Joo S W, Daraei H, Harikaranahalli Puttaiah S, Giahi O. Photocatalytic degradation of organic dyes using WO₃-doped ZnO nanoparticles fixed on a glass surface in aqueous solution. Journal of Industrial and Engineering Chemistry, 2019, 73: 297–305

3 de Oliveira Guidolin T, Possolli N M, Polla M B, Wermuth T B, Franco de Oliveira T, Eller S, Klegues Montedo O R, Arcaro S, Cechinel M A P. Photocatalytic pathway on the degradation of methylene blue from aqueous solutions using magnetite nanoparticles. Journal of Cleaner Production, 2021, 318: 128556

4 Sahu S, Pahi S, Sahu J K, Sahu U K, Patel R K. Kendu (diospyros melanoxylon Roxb) fruit peel activated carbon—an efficient bioadsorbent for methylene blue dye: equilibrium, kinetic, and thermodynamic study. Environmental Science and Pollution Research International, 2020, 27(18): 22579–22592

5 Borghei Y S, Hosseini M, Ganjali M R. Visual detection of miRNA using peroxidase-like catalytic activity of DNA-CuNCs and methylene blue as indicator. Clinica Chimica Acta, 2018, 483: 119–125

6 Lu G, Nagbanshi M, Goldau N, Mendes Jorge M, Meissner P, Jahn A, Mockenhaupt F P, Müller O. Efficacy and safety of methylene blue in the treatment of malaria: a systematic review. BMC Medicine, 2018, 16(1): 59

7 Hosseini H, Zirakjou A, McClements D J, Goodarzi V, Chen W H. Removal of methylene blue from wastewater using ternary nanocomposite aerogel systems: carboxymethyl cellulose grafted by polyacrylic acid and decorated with graphene oxide. Journal of Hazardous Materials, 2022, 421: 126752

8 Ren L F, Tang Z, Du J Y, Chen L, Qiang T T. Recyclable polyurethane foam loaded with carboxymethyl chitosan for adsorption of methylene blue. Journal of Hazardous Materials, 2021, 417: 126130

9 Li L X, Lv Y, Wang J, Jia C, Zhan Z S, Dong Z L, Liu L L, Zhu X D. Enhance pore structure of cyanobacteria-based porous carbon by polypropylene to improve adsorption capacity of methylene blue. Bioresource Technology, 2022, 343: 126101

10 Sharma R, Saini H, Paul D R, Chaudhary S, Nehra S P. Removal of organic dyes from wastewater using Eichhornia crassipes: a potential phytoremediation option. Environmental Science and Pollution Research International, 2021, 28(6): 7116–7122

11 Giwa A R A, Bello I A, Olabintan A B, Bello O S, Saleh T A. Kinetic and thermodynamic studies of fenton oxidative decolorization of methylene blue. Heliyon, 2020, 6(8): e04454

12 Jiang F H, Cao D F, Hu S X, Wang Y, Zhang Y, Huang X H, Zhao H, Wu C N, Li J G, Ding Y L, Liu K. High-pressure carbon dioxide-hydrothermal enhance yield and methylene blue adsorption performance of banana pseudo-stem activated carbon. Bioresource Technology, 2022, 354: 127137

13 Benhouria A, Islam M A, Zaghouane-Boudiaf H, Boutahala M, Hameed B H. Calcium alginate-bentonite-activated carbon composite beads as highly effective adsorbent for methylene blue. Chemical Engineering Journal, 2015, 270: 621–630

14 Zhao R, Li Y Z, Sun B L, Chao S, Li X, Wang C, Zhu G S. Highly flexible magnesium silicate nanofibrous membranes for effective removal of methylene blue from aqueous solution. Chemical Engineering Journal, 2019, 359: 1603–1616

15 Bedekar P A, Kshirsagar S D, Gholave A R, Govindwar S P. Degradation and detoxification of methylene blue dye adsorbed on water hyacinth in semi continuous anaerobic−aerobic bioreactors by novel microbial consortium-SB. RSC Advances, 2015, 5(120): 99228–99239

16 Ong S A, Toorisaka E, Hirata M, Hano T. Treatment of methylene blue-containing wastewater using microorganisms supported on granular activated carbon under packed column operation. Environmental Chemistry Letters, 2007, 5(2): 95–99

17 Liu K N, Ma J L, Yang X P, Jin D N, Li Y C, Jiao G J, Yao S Q, Sun S L, Sun R C. Boosting electron kinetics of anatase TiO₂ with carbon nanosheet for efficient photo-reforming of xylose into biomass-derived organic acids. Journal of Alloys and Compounds, 2022, 906: 164276

18 Zhao H Q, Zhu Q, Zhuang Y, Zhan P, Qi Y O, Ren W Q, Si Z H, Cai D, Yu S S, Qin P Y. Hierarchical ZnIn₂S₄ microspheres as photocatalyst for boosting the selective biohydrogenation of furfural into furfuryl alcohol under visible light irradiation. Green Chemical Engineering, 2022, 3(4): 385–394

19 Liu Z D, Liu K N, Sun R C, Ma J L. Biorefinery-assisted ultra-high hydrogen evolution via metal-free black phosphorus sensitized carbon nitride photocatalysis. Chemical Engineering Journal, 2022, 446: 137128

20 Yang R G, Fu Y M, Wang H N, Zhang D P, Zhou Z, Cheng Y Z, Meng X, He Y O, Su Z M. ZIF-8/covalent organic framework for enhanced CO₂ photocatalytic reduction in gas−solid system. Chemical Engineering Journal, 2022, 450: 138040

21 Wang T Q, Tian B B, Han B, Ma D R, Sun M Z, Hanif A, Xia D H, Shang J. Recent advances on porous materials for synergetic adsorption and photocatalysis. Energy and Environmental Materials, 2022, 5(3): 711–730

22 Balbuena J, Carraro G, Cruz M, Gasparotto A, Maccato C, Pastor A, Sada C, Barreca D, Sánchez L. Advances in photocatalytic NO_x abatement through the use of Fe₂O₃/TiO₂ nanocomposites. RSC Advances, 2016, 6(78): 74878–74885

23 Li J K, Lv C P, Liu X H, Jiao Z B, Liu N. Highly durable Ag-CuO heterostructure-decorated mesh for efficient oil/water separation and in situ photocatalytic dye degradation. Energy and Environmental Materials, 2021, 4(4): 611–619

24 Masudy-Panah S, Zhuk S, Tan H R, Gong X, Dalapati G K. Palladium nanostructure incorporated cupric oxide thin film with strong optical absorption, compatible charge collection and low recombination loss for low cost solar cell applications. Nano Energy, 2018, 46: 158–167

25 Dai Y H, Wang Y, Liu B, Yang Y H. Metallic nanocatalysis: an accelerating seamless integration with nanotechnology. Small, 2015, 11(3): 268–289

26 Raees A, Jamal M A, Ahmed I, Silanpaa M, Saad Algarni T. Synthesis and characterization of CeO₂/CuO nanocomposites for photocatalytic degradation of methylene blue in visible light. Coatings, 2021, 11(3): 305

27 Bayat F, Sheibani S. Enhancement of photocatalytic activity of CuO-Cu₂O heterostructures through the controlled content of Cu₂O. Materials Research Bulletin, 2022, 145: 111561

28 Ma J G, Tian Z J, Li L, Lu Y, Xu X L, Hou J W. Loading nano-CuO on TiO₂ nanomeshes towards efficient photodegradation of methylene blue. Catalysts, 2022, 12(4): 383

29 Nuengmatcha P, Porrawatkul P, Chanthai S, Sricharoen P, Limchoowong N. Enhanced photocatalytic degradation of methylene blue using Fe₂O₃/graphene/CuO nanocomposites under visible light. Journal of Environmental Chemical Engineering, 2019, 7(6): 103438

30 Toe C Y, Scott J, Amal R, Ng Y H. Recent advances in suppressing the photocorrosion of cuprous oxide for photocatalytic and photoelectrochemical energy conversion. Journal of Photochemistry and Photobiology C: Photochemistry Reviews, 2019, 40: 191–211

31 Jiang D H, Xue J B, Wu L Q, Zhou W, Zhang Y G, Li X H. Photocatalytic performance enhancement of CuO/Cu₂O heterostructures for photodegradation of organic dyes: effects of CuO morphology. Applied Catalysis B: Environmental, 2017, 211: 199–204

32 Ge J L, Zhang Y F, Park S J. Recent advances in carbonaceous photocatalysts with enhanced photocatalytic performances: a mini review. Materials, 2019, 12(12): 1916

33 Waheed I F, Al-Janabi O Y T, Foot P J S. Novel MgFe₂O₄-CuO/GO heterojunction magnetic nanocomposite: synthesis, characterization, and batch photocatalytic degradation of methylene blue dye. Journal of Molecular Liquids, 2022, 357: 119084

34 He B, Feng M, Chen X Y, Zhao D W, Sun J. One-pot construction of chitin-derived carbon/g-C₃N₄ heterojunction for the improvement of visible-light photocatalysis. Applied Surface Science, 2020, 527: 146737

35 Zhang L X, Wang C L, Jiu H F, Xu Q W, Li X, Song W, Luo S Y, Zhao J H. Metal-organic framework derived carbon-encapsulated hollow CuO/Cu₂O heterostructure heterohedron as an efficient electrocatalyst for hydrogen evolution reaction. Dalton Transactions, 2022, 51(8): 3349–3356

36 Rangarajan G, Jayaseelan A, Farnood R. Photocatalytic reactive oxygen species generation and their mechanisms of action in pollutant removal with biochar supported photocatalysts: a review. Journal of Cleaner Production, 2022, 346: 131155

37 Shan Y W, Guo Y, Wang Y, Du X R, Yu J, Luo H, Wu H, Boury B, Xiao H, Huang L L, Chen L. Nanocellulose-derived carbon/g-C₃N₄ heterojunction with a hybrid electron transfer pathway for highly photocatalytic hydrogen peroxide production. Journal of Colloid and Interface Science, 2021, 599: 507–518

38 Yang W, Yang W, Zou R, Huang Y F, Lai H H, Chen Z H, Peng X W. Cellulose nanofiber-derived carbon aerogel for advanced room-temperature sodium-sulfur batteries. Carbon Energy, 2022, 5(1): e203

39 Wang L, Wu Q, Zhao B Z, Li Z L, Zhang Y H, Huang L, Yu S T. Multi-functionalized carbon aerogels derived from chitosan. Journal of Colloid and Interface Science, 2022, 605: 790–802

40 Peydayesh M, Vogt J, Chen X L, Zhou J T, Donat F, Bagnani M, Müller C R, Mezzenga R. Amyloid-based carbon aerogels for water purification. Chemical Engineering Journal, 2022, 449: 137703

41 Jiao G J, Ma J L, Zhang J Q, Zhou J H, Sun R C. High-efficiency capture and removal of phosphate from wastewater by 3D hierarchical functional biomass-derived carbon aerogel. Science of the Total Environment, 2022, 827: 154343

42 Zhao X L, Tan Y X, Wu F C, Niu H Y, Tang Z, Cai Y Q, Giesy J P. Cu/Cu₂O/CuO loaded on the carbon layer derived from novel precursors with amazing catalytic performance. Science of the Total Environment, 2016, 571: 380–387

43 Bai W D, Wu M B, Du X L, Gong W L, Ding Y H, Song C H, Liu L. Synergistic effect of multiple-phase rGO/CuO/Cu₂O heterostructures for boosting photocatalytic activity and durability. Applied Surface Science, 2021, 544: 148607

44 Dubale A A, Ahmed I N, Zhang Y J, Yang X L, Xie M H. A facile strategy for fabricating C@Cu₂O/CuO composite for efficient photochemical hydrogen production with high external quantum efficiency. Applied Surface Science, 2020, 534: 147582

45 Gao X C, Feng J, Su D W, Ma Y C, Wang G X, Ma H Y, Zhang J T. In-situ exfoliation of porous carbon nitride nanosheets for enhanced hydrogen evolution. Nano Energy, 2019, 59: 598–609

46 Xu Y S, Fan M J, Yang W J, Xiao Y H, Zeng L T, Wu X, Xu Q H, Su C L, He Q J. Homogeneous carbon/potassium-incorporation strategy for synthesizing red polymeric carbon nitride capable of near-infrared photocatalytic H₂ production. Advanced Materials, 2021, 33(39): 2101455

47 Toloman D, Popa A, Stan M, Stefan M, Vlad G, Ulinici S, Baisan G, Silipas T D, Macavei S, Leostean C, Pruneanu S, Pogacean F, Suciu R C, Barbu-Tudoran L, Pana O. Visible-light-driven photocatalytic degradation of different organic pollutants using Cu doped ZnO-MWCNT nanocomposites. Journal of Alloys and Compounds, 2021, 866: 159010

48 Sathiyavimal S, Vasantharaj S, Kaliannan T, Pugazhendhi A. Eco-biocompatibility of chitosan coated biosynthesized copper oxide nanocomposite for enhanced industrial (azo) dye removal from aqueous solution and antibacterial properties. Carbohydrate Polymers, 2020, 241: 116243

49 Serrà A, Gómez E, Michler J, Philippe L. Facile cost-effective fabrication of Cu@Cu₂O@CuO-microalgae photocatalyst with enhanced visible light degradation of tetracycline. Chemical Engineering Journal, 2021, 413: 127477

50 Zhang W W, Chen X, Zhao X T, Yin M Y, Feng L P, Wang H. Simultaneous nitrogen doping and Cu₂O oxidization by one-step plasma treatment toward nitrogen-doped Cu₂O@CuO heterostructure: an efficient photocatalyst for H₂O₂ evolution under visible light. Applied Surface Science, 2020, 527: 146908