Reduction kinetics of SrFeO_3−δ/CaO∙MnO nanocomposite as effective oxygen carrier for chemical looping partial oxidation of methane

Abstract

Chemical looping reforming of methane is a novel and effective approach to convert methane to syngas, in which oxygen transfer is achieved by a redox material. Although lots of efforts have been made to develop high-performance redox materials, a few studies have focused on the redox kinetics. In this work, the kinetics of SrFeO_3−δ–CaO∙MnO nanocomposite reduction by methane was investigated both on a thermo-gravimetric analyzer and in a packed-bed microreactor. During the methane reduction, combustion occurs before the partial oxidation and there exists a transition between them. The weight loss due to combustion increases, but the transition region becomes less inconspicuous as the reduction temperature increased. The weight loss associated with the partial oxidation is much larger than that with combustion. The rate of weight loss related to the partial oxidation is well fitted by the Avrami–Erofeyev equation with n = 3 (A3 model) with an activation energy of 59.8 kJ∙mol^‒1. The rate law for the partial oxidation includes a solid conversion term whose expression is given by the A3 model and a methane pressure-dependent term represented by a power law. The partial oxidation is half order with respect to methane pressure. The proposed rate law could well predict the reduction kinetics; thus, it may be used to design and/or analyze a chemical looping reforming reactor.

Key words： chemical looping reforming; SrFeO_3−δ/CaO·MnO nanocomposite; reduction kinetics; Avrami–Erofeyev model; pressure-dependent term

1 Introduction

Methane (CH₄), the main component of natural gas, is widely used in heating, power generation, transportation, and manufacture as a fuel due to its low carbon footprint and high heat value [1–4]. Over the past decades, large reserves of coal-bed methane, natural gas hydrates, and shale gas have been discovered and exploited, providing an opportunity for further methane valorization [5–7]. In general, there are two routes for converting methane into valuable products, the direct conversion route and the indirect one [3,8]. The former directly transforms methane into the desired products, such as methanol, ethylene, and benzene [9–11], which are probably more reactive than methane, resulting in low yield and carbon efficiency [12]. The latter, also known as syngas (a mixture of CO and H₂) route, involves multiple steps and has been widely used for large-scale commercial transformations of natural gas [13,14]. Starting from syngas that is produced by methane reforming, a variety of commercially viable products including liquid fuels and oxygenates can be obtained by the well-established technologies such as Fischer–Tropsch synthesis or methanol synthesis [5,15,16].

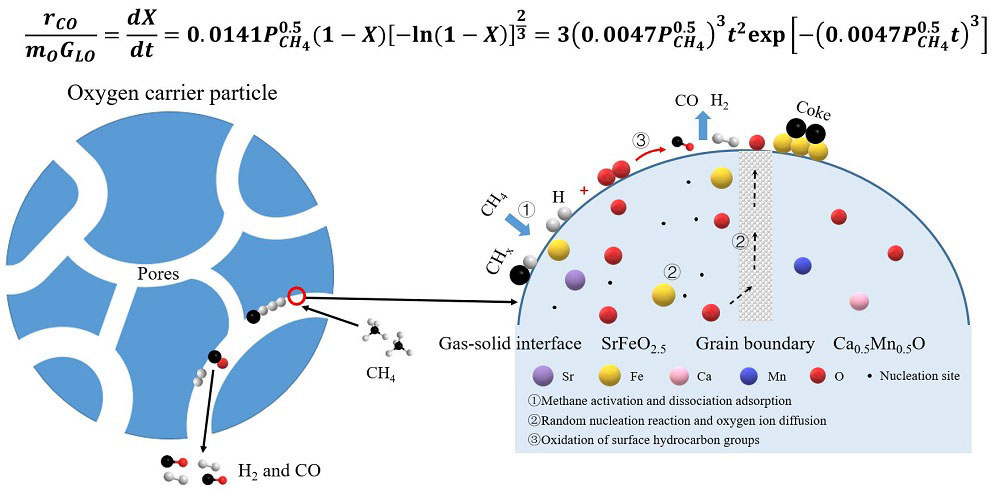
As a novel and efficient transformation route, chemical-looping reforming of methane (CLRM), which uses a redox material that not only activates a stable C–H bond of CH₄ (bond energy of 438.8 kJ∙mol^‒1) but also provides oxygen species that combine with carbon atoms [2,17], has attracted tremendous attentions in recent years [18,19]. Mixed metal oxides and perovskites have been intensively investigated as redox materials [20,21], because they prefer C–H activation. AFeO_3−δ (A = La, Eu or Sr) perovskites have exhibited high activity toward methane partial oxidation [21–23], the main reaction in the reduction step of CLRM. Among these perovskites, LaFeO₃ and SrFeO_3−δ exhibit nearly 90% and 100% syngas selectivity at 900 and 980 °C, respectively [15,21]. These findings have further encouraged studies on perovskites as the redox materials for CLRM. Specifically, SrFeO_3−δ is one of the most attractive candidate materials because it is cheap, readily available, and easily tunable [24–26]. To further enhance its redox performance, several strategies have been explored, such as anchoring or depositing it on another material [27,28]. Li et al. [29] prepared a nanocomposite composed of SrFeO_3−δ as the active phase and CaO as the dispersing medium, and found that methane conversion and syngas selectivity reached 90% and 89% at 980 °C, respectively, and CaO phase significantly enhanced both the redox kinetics and the cyclability. The composition-performance relationship of nanocomposites and the effect of dispersing medium were further investigated [15]. In the reduction step, the nanocomposite containing 10 wt % SrFeO_3−δ exhibited the highest CH₄ conversion (88%) and syngas production rate (1.8 mol∙kg_SFO⁻¹∙min⁻¹), but the one containing 80 wt % SrFeO_3−δ showed the highest syngas productivity (27.3 mol∙kg_SFO⁻¹). Besides, MnO and CaO∙MnO were also investigated as the dispersing medium [30]. Among these three nanocomposites, SrFeO_3−δ–CaO∙MnO (SF–CM) exhibited the maximum instantaneous CH₄ conversion (66.2%) and syngas selectivity (91.5%) at 900 °C.

Although these efforts provide valuable clues on the rational design of high-performance redox materials, the redox properties of perovskite-containing nanocomposites remain poorly understood, especially the redox mechanism and kinetics that can not only provide information about the rate at which reactions proceed but also shed light on the reaction mechanism. To date, the kinetics of gas–solid reactions involved in chemical looping methane reforming has yet to be thoroughly investigated. In this context, we studied the kinetics of SrFeO_3−δ-containing nanocomposite reduction by methane and focused on the reduction mechanism to establish the corresponding rate equation. The reduction mechanism was inferred from the weight loss curves at 3 different temperatures with the same methane concentration at atmospheric pressure. Subsequently, an empirical rate law was proposed, whose parameters were obtained from CO evolution profiles with 5 different methane pressures at 900 °C and 1 atm (1.013 × 10⁵ Pa) by using the linear regression technique. Finally, the equation was used to predict the reduction rate. The results suggest the proposed rate law can well predict the reduction kinetics. Thus, it may be used to design and analyze a chemical looping reforming reactor.

2 Experimental

2.1 Synthesis and characterization

SF–CM (30 wt % SrFeO_3−δ) was prepared by the sol–gel method using Sr(NO₃)₂ (99.5% purity), Fe(NO₃)₃·9H₂O (98.5% purity), Ca(NO₃)₂∙4H₂O (99.0% purity), Mn(NO₃)₂ solution (49.0–51.0 wt %), citric acid (99.5% purity), and ethylene glycol (99.0% purity) purchased from SINOPHARM without further purification. Nitrate salts, whose relative mass ratio was determined by the stoichiometry of desired product, were dissolved into deionized water and heated up to 80 °C under agitation (600 r·min⁻¹) until a gel formed. After that, the gel was dried at 120 °C for 12 h to evaporate the residual water and then treated at 400 °C in the air for 4 h. Finally, the precursor was calcined at 1000 °C in the flowing air for 12 h. The detailed characterization of the SF–CM nanocomposite, including X-ray diffraction, scanning electron microscope, and high-resolution transmission electron microscopy and energy dispersive spectroscopy mapping, was given in a previous study [30].

2.2 Reduction kinetics

The isothermal reduction at 1 atm was carried out on a thermo-gravimetric analyzer (SDT Q600, TA Instruments). In a typical run, about 30 mg of SF–CM was put into the sample cup. Before measurements, the sample was treated at 900 °C for 1 h in Ar (100 STP·mL∙min^‒1). After the pre-treatment, argon was switched to a gas mixture (10 vol % CH₄ balance with Ar, gas flowrate = 100 STP·mL∙min^‒1). The reduction at 850 and 950 °C with the same methane concentration was performed on the same equipment.

The reduction kinetics at the atmospheric pressure with different methane concentrations was conducted in a fixed-bed flow quartz tubular reactor (ID = 8 mm) that was externally heated by an electric furnace with a K-type thermocouple monitoring the furnace temperature. Typically, 1.00 g of SF–CM particles (200–450 μm) was placed on the top of the quartz wool plug. The temperature of reactor was ramped up to 900 °C at 10 °C∙min^‒1 in Ar (100 STP·mL∙min^‒1). Once it reached the targeted value, argon was switched to a gas mixture (Y vol % CH₄/(110-Y) vol % Ar, Y = 15, 20, 30, 40 and 50, gas flowrate = 110 STP·mL∙min^‒1). After the reduction step, the oxygen carriers were purged with Ar (100 STP∙mL·min^‒1) for 30 min and then oxidized by a gas mixture of CO₂ and Ar (20% CO₂ in Ar, 100 STP·mL∙min^‒1). The gas composition at the outlet of reactor was monitored by an on-line mass spectrometer (LC-D200M, Tilon).

2.3 Reduction rate law

The kinetics of nanocomposite reduction by methane was investigated based on the solid-state reactions [31,32]. The reaction rate is given by Eq. (1):

(1)\frac{\mathrm{d}X}{\mathrm{d}t}=k^{{}^{\prime }}\left(T\right)f\left(X\right),

where, kʹ(T) is the rate constant that may also depend on the morphology and density of solid in some cases, and X is the fraction of converted solid which is calculated by Eq. (2):

(2)X=\frac{m_0-m_{\mathrm{t}}}{m_0-m_{\mathrm{\infty }}},

where m₀ is the initial weight, m_t is the weight at time t, and m_∞ is the final weight.

For the gas–solid reactions, the reaction rate is also dependent on the partial pressure of the gaseous reactant [33]. Therefore, a pressure term should be incorporated into the rate law. It is reasonable to assume that the pressure-dependent term can be represented by the following equation:

(3)h\left(P\right)={P_{\mathrm{B}}}^{\beta } .

Inserting the pressure term into the rate law for solid-state reactions can yield the rate law for gas–solid reactions:

(4)\frac{\mathrm{d}X}{\mathrm{d}t}=k^{{}^{\prime }}\left(T\right)f\left(X\right)h\left(P\right)=A{\mathrm{e}}^{-\frac{E_{\text{α}}}{RT}}f\left(X\right){P_{\mathrm{B}}}^{\beta } ,

where A and E_a are the pre-exponential factor and activation energy (kJ∙mol^‒1), respectively, T is the absolute temperature (K), R is the ideal gas constant (8.314 J∙mol^‒1∙K^‒1), and P_B is the partial pressure of gaseous reactant B (atm). A close examination of Eq. (4) reveals that it has the same form as that for the rate law of homogenous and heterogenous catalytic reactions. To some extent, f (X) and h (P) functions can be called the concentration terms of solid and gaseous reactants, respectively.

Under isothermal conditions with a constant partial pressure of the gaseous reactant, separating variables and integrating Eq. (4) gives the integral form of the isothermal rate laws:

(5)g\left(X\right)={\int }_0^X\frac{\mathrm{d}X}{f\left(X\right)}=\left(A{\mathrm{e}}^{-\frac{E_{\text{α}}}{RT}}{P_{\mathrm{B}}}^{\beta }\right)t=k\left(T,P_{\mathrm{B}}\right)t.

Several reaction models (f(X) and g(X)) are listed in Table S1 (cf. Electronic Supplementary Material, ESM). For the reduction reaction under a specific condition (both the temperature and the partial pressure are fixed), the reaction rate is only dependent on the reaction model. Thus, the appropriate model can be visually determined by comparing the theoretical graphical shape of isothermal curves (dX/dt vs. X plot) and the measured one. Because difference in the dX/dt vs. X plots of each model group is significantly pronounced, it is relatively easy to infer the appropriate model group from the plot. Additionally, the shapes of one model group are similar, e.g., the Avrami–Erofeyev models (A2, A3, and A4) exhibit a bell-shaped relationship between the reduction rate and X. The most appropriate model is then determined by non-linear least-square analysis. The activation energy E_a is obtained from the plot of lnk vs. 1/T according to the following equation:

(6)\mathrm{l}\mathrm{n}k= \beta \mathrm{l}\mathrm{n}{P}_{\mathrm{B}}+ \mathrm{l}\mathrm{n}A- \frac{E_{\mathrm{a}}}{RT}.

3 Results and discussion

3.1 Activation energy of partial oxidation of methane

According to Eq. (6), the activation energy of reduction can be estimated from thermal gravity analysis at several different isothermal conditions under which the change in the partial pressure of methane (P_B) is ignorable. Fig.1 illustrates the reduction of SF−CM nanocomposite by methane. Fig.1(a) is the plots of weight loss vs. reduction time at 850, 900, and 950 °C, and the corresponding loss rates (‒dW/dt) are presented in Fig.1(b). On the rate profiles, there are two peaks−a large peak, and an ensuing small one. Moreover, it seems that there exists a transition region between the two peaks. Based on the continuous weight loss in Fig.1(a) and the previous study [30], coking is negligible and the first peak is associated with the complete oxidation of methane, while the second one is attributed to partial oxidation of methane [30,34–36]. As can be seen, the second peak becomes increasingly pronounced as the reduction temperature decreases, which is accompanied by a decrease in the first peak.

Fig.1 (a) TG, (b) DTG and (c) dX/dt vs. X curves of SF–CM reduction by methane at three temperatures, and (d) Arrhenius plot; reaction conditions: m_SF–CM = 27 mg, F = 110 STP∙mL∙min^‒1 (10 vol % CH₄), P = 1 atm.

Full size|PPT slide

It is believed that complete oxidation involves surface oxygen species. If this is the case, the area of the first peak, which is proportional to the weight loss related to the complete oxidation, should maintain unchanged or decrease as the reduction temperature increases. This is because the amount of surface oxygen species cannot increase as the reduction temperature rises [37]. Therefore, other factors could play a role in complete oxidation. From the viewpoint of thermodynamics, only the oxygen species with high chemical potential can completely oxidize methane. However, whether oxygen species can perform the complete oxidation partially depends on their concentration at the solid/gas interface where the oxidation reaction takes place. If it is low, the complete oxidation cannot occur even if the oxygen species (lattice oxygen) in the bulk phase could perform the complete oxidation. The second peak, associated with partial oxidation of methane, becomes sharp but the transition region gets less inconspicuous as the reduction temperature increases. To estimate the activation energy of partial oxidation, its starting points, which were obtained from extrapolating the observed rate backward, should be identified. In Fig.1(b), the rate profile of weight loss solely related to partial oxidation of methane is composed of the dash line (extrapolated data) and a portion of the solid line (measured data). The corresponding plots of dX/dt vs. X at three reduction temperatures are presented in Fig.1(c).

Obviously, the partial oxidation of methane by lattice oxygen species of SF–CM conforms to the Avrami–Erofeyev model, which is referred to as the nucleation and nuclei growth model. This reaction model involves two restrictions on nuclei growth–the first is driven by the ingestion that facilitates the elimination of a potential nucleation site by the growth of an existing nucleus; the second is coalescence—the loss of the reactant/product interface when two or more growing nuclei merges. The Avrami–Erofeyev model has a general expression:

(7)\frac{\mathrm{d}X}{\mathrm{d}t}=k n\left(1-X\right){\left[-\mathrm{l}\mathrm{n}\left(1-X\right)\right]}^{\frac{\left(n-1\right)}{n}},

where n (> 1) is the order of nucleation. Usually, n is an integer but it is not in some cases. For n = 2 (1D nuclei growth, A2), 3 (2D nuclei growth, A3), and 4 (3D nuclei growth, A4), the nuclei are rod-shaped, disc-shaped, and spherical, respectively [38]. Non-integer n values between 2 and 4 are indicative of irregularly shaped nuclei. When n is equal to 4, the reaction mechanism is also interpreted as autocatalytic nucleation [39]. The order of nucleation can be obtained from the linear plot of ln t vs. ln[‒ ln(1 ‒ X)] according to the following equation:

(8)\mathrm{l}\mathrm{n}t= \frac{1}{n}\mathrm{l}\mathrm{n}\left[-\mathrm{l}\mathrm{n}\left(1-X\right)\right]+\mathrm{l}\mathrm{n}k.

At three reduction temperatures, the partial oxidation kinetics is best fitted by the A3 model (Avrami–Erofeyev equation with n = 3); the activation energy (E_a), estimated from the slope of the Arrhenius plot (Fig.1(d)), is 59.8 kJ∙mol^‒1, which is much higher than the activated energy for the reaction is strongly gaseous diffusion-limited (8–24 kJ∙mol^‒1) [40]. For SF–CM nanocomposites prepared at relatively high temperatures (e.g., 1000 °C and above), their porosity is usually very low and can be considered as nonporous materials. Therefore, both external and internal gaseous diffusion can be ignored under the experimental conditions. The activation energy over SF–CM oxygen carrier is close to those for 10% Co/mesoporous alumina and Sr_2.45La_0.55FeCoO_7‒δ but lower than that over NiO/MgAl₂O₄ (Table S2, cf. ESM).

3.2 Dependence of partial oxidation on methane pressure

Most rate laws for gas–solid reactions exclude a pressure-dependent term of the gaseous reactant. However, our preliminary investigations demonstrate that the reduction of SF–CM by methane is strongly dependent on the partial pressure of methane. A recent work also suggests that hydrogen pressure has a significant effect on the reduction of CaMn_0.9Fe_0.1O₃ that is a redox material for chemical looping oxidative dehydrogenation of ethane [33]. From these observations, one could infer the rate-determining step of gas–solid reactions. For SF–CM oxygen carrier, the active phase is SrFeO_2.5 under the reaction conditions [30]. It was suggested that SrFeO_2.5 is a stoichiometric compound, which is reduced to SrO and Fe by methane in the reduction step and then oxidized back to SrFeO_2.5 by water or CO₂ in the oxidation step. Producing syngas from the reduction of SF–CM by methane involves the following steps: methane activation that generates intermediates (e.g., CH_x with x = 4, 3, 2, 1, or 0), the reaction of the intermediates with oxygen species (CH_x + O → CO + x/2H₂), and the solid-state transformation (SrFeO_2.5→ SrO + Fe + 1.5 O) that produces oxygen species (Fig.2).

Fig.2 Schematic diagram of SF–CM reduction by methane.

Full size|PPT slide

The pressure-dependent term is also known as the accommodation function, whose various forms have been derived and used in solid–gas systems. A generalized form was proposed to describe the kinetics of solid–gas reactions is [40]:

(9)h\left(P\right)={\left(\frac{P_{\mathrm{G}}}{P^{\text{Ɵ}}}\right)}^{-a}\left[1-{\left(\frac{P_{\mathrm{G}}}{P_{\mathrm{E}}}\right)}^b\right],

where a and b are the constants, P_G is the partial pressure of the gaseous product (atm), P^Ɵ is the standard pressure (= 1 atm), and P_E is the equilibrium pressure at the operating temperature (atm). Based on the above discussion, the reduction of SF–CM by methane could be considered as a thermal decomposition process that involves the transformation of one solid into a gas and two solids, and the gas reacts with methane once it forms. In the absence of a reducing agent, the partial pressure of oxygen in the system cannot be reduced lower than the equilibrium one. When methane is introduced to the system, the partial pressure of oxygen becomes very low (P_G ˂˂ P_E) and thus the reduction is accelerated. In this case, the partial pressure of oxygen is negatively proportional to the partial pressure of methane. Therefore, the rate SF–CM reduction can be described in terms of methane pressure by Eq. (4).

If other reactions except the partial oxidation of methane are ignorable in SF–CM reduction by methane, the production rate of CO or the instantaneous CO flowrate is:

(10)r_{\mathrm{C}\mathrm{O}}=F_{\mathrm{C}\mathrm{O}}=m_{\mathrm{o}}{\mathrm{\Gamma }}_{\mathrm{L}\mathrm{O}}\frac{\mathrm{d}X}{\mathrm{d}t}= m_{\mathrm{o}}{\mathrm{\Gamma }}_{\mathrm{L}\mathrm{O}}\times 3k \left(1-X\right){\left[-\mathrm{l}\mathrm{n}\left(1-X\right)\right]}^{\frac{2}{3}},

where F_CO is the instantaneous CO flowrate (mol∙s^‒1), m_o is the mass of redox material (kg), and Γ_LO is the oxygen storage capacity (mol∙kg^‒1). In this work, the instantaneous flowrate, F_CO, was measured. The conversion of redox material at t can be calculated:

(11)X=\frac{{{\displaystyle \int }}_0^t{F}_{\mathrm{C}\mathrm{O}}\mathrm{d}t}{{{\displaystyle \int }}_0^{t_{\mathrm{r}\mathrm{e}\mathrm{d}}}{F}_{\mathrm{C}\mathrm{O}}\mathrm{d}t}=\frac{{{\displaystyle \int }}_0^t{F}_{\mathrm{C}\mathrm{O}}\mathrm{d}t}{m_{\mathrm{o}}{\Gamma }_{\mathrm{L}\mathrm{O}}},

where t_red is the reduction time, which elapsed between the starting point when CO was detected in the output stream and a time when CO flowrate dropped to 1% of its maximum value.

Fig.3 shows the kinetics of SF–CM reduction at three different methane partial pressures. The CO flowrate as a function of time for methane pressures of 0.15, 0.30, and 0.50 atm at 900 °C is illustrated Fig.3(a). As can be seen, the reduction period becomes shorter as the partial pressure of methane increases. Specifically, it decreases from 16 to 9.5 min when P_{{\mathrm{C}\mathrm{H}}_4} varies from 0.15 to 0.5 atm. Correspondingly, the maximum CO flowrate increases with the increase in methane pressure. The maximum one at 0.5 atm of methane is nearly twice as high as that at 0.15 atm of methane. It should be mentioned here that the partial pressure of methane is referred to the one at the beginning of reduction. The integration of the measured CO flowrate yielded the conversion of redox material as a function of time, which is shown in Fig.3(b). The plots of dX/dt vs.X are presented in Fig.3(c), which is obtained by differentiating the conversion-time data.

Fig.3 Kinetics of SF–CM reduction at three methane partial pressures: (a) CO flowrate as a function of time, (b) conversion of redox material as a function of time, (c) plots of dX/dt vs. X, and (d) the plots of ln[‒ln(1 ‒ X)] as function of time t; reaction conditions: m_SF–CM = 1 g, T = 900 °C, F = 110 STP∙mL·min^‒1, P = 1 atm.

Full size|PPT slide

For the A3 model, the conversion of redox material as a function of time is:

(12)X=1-{\mathrm{e}}^{-{\left(kt\right)}^3}=1-{\mathrm{e}}^{-{\left(k^{{}^{\prime }}{P}_{{\mathrm{C}\mathrm{H}}_4}^{\beta }t\right)}^3}.

Differentiating the above equation with respect to t yields the rate law for reduction:

(13)\frac{\mathrm{d}X}{\mathrm{d}t}=3 k^{{}^{\prime }}{P}_{{\mathrm{C}\mathrm{H}}_4}^{\beta } \left(1-X\right){\left[-\mathrm{l}\mathrm{n}\left(1-X\right)\right]}^{\frac{2}{3}}.

Rearranging Eq. (12) and then taking the natural logarithm twice can obtain the following formula:

(14)\mathrm{l}\mathrm{n}\left[-\mathrm{l}\mathrm{n}\left(1-X\right)\right]=3\mathrm{l}\mathrm{n}t+3\mathrm{l}\mathrm{n}\left(k^{{}^{\prime }}{P}_{{\mathrm{C}\mathrm{H}}_4}^{\beta }\right).

The plot of ln[‒ ln(1 ‒ X)] as function of time t should be a straight line with an intercept of 3ln(kʹP_CH4^β) and a slope of 3. However, it seems that not all data points fall on one straight line (Fig.3(d) and S1, cf. ESM). A close examination of the plot reveals the conversion at a range of 0.1 to 0.9 visually falls on a straight line. After taking into large uncertainty associated with low conversions, only the conversion between 0.1 and 0.9 was used to calculate β and kʹ at 900 °C, and the plots of ln[‒ ln(1 ‒ X)] vs. lnt for five methane pressures are presented in Fig. S2 (cf. ESM). The values of ln(k^{{}^{\prime }}{P}_{{\mathrm{C}\mathrm{H}}_4}^{\beta }) obtained from the linear regression for five pressures are listed in Tab.1. From the slope and the intercept of the line given in Fig.4, β is found to be 0.5 and kʹ to be 0.0047 s^‒1 at 900 °C. Thus, the rate law for SF–CM reduction by methane at 900 °C:

Tab.1 Values of ln(k^{{}^{\prime }}{P}_{{\mathrm{C}\mathrm{H}}_4}^{\beta }) and runs test for 5 methane partial pressures

Methane pressure/atm	ln(k^{{}^{\prime }}{P}_{{\mathrm{C}\mathrm{H}}_4}^{\beta })	Expected runs	Number of runs
0.15	‒6.2842	170	168
0.20	‒61896	150	150
0.30	‒5.9663	116	116
0.40	‒5.7943	100	96
0.50	‒5.7244	95	95

Fig.4 Plot of ln(k^{{}^{\prime }}{P}_{{\mathrm{C}\mathrm{H}}_4}^{\beta }) vs. lnP_{{\mathrm{C}\mathrm{H}}_4}.

Full size|PPT slide

(15)\begin{array}{rl}\frac{\mathrm{d}X}{\mathrm{d}t}=& 0.0141P_{{\mathrm{C}\mathrm{H}}_4}^{0.5}\left(1-X\right){\left[-\mathrm{l}\mathrm{n}\left(1-X\right)\right]}^{\frac{2}{3}}\\ =& {\left(0.0047P_{\mathrm{C}{\mathrm{H}}_4}^{0.5}\right)}^3{t}^2\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left(0.0047P_{\mathrm{C}{\mathrm{H}}_4}^{0.5}t\right)}^3\right].\end{array}

The predicted and measured reduction rates as a function of time for five methane partial pressures are illustrated in Fig.5 and Fig. S3 (cf. ESM). As can be seen, the above equation fits the reduction data well, which is further confirmed by the runs test and the Q–Q plot.

Fig.5 The predicted and measured reduction rates for four methane partial pressures: (a) 0.15, (b) 0.30, (c) 0.40, and (d) 0.50 atm; reaction conditions: m_SF–CM = 1 g, T = 900 °C, F = 110 STP∙mL∙min^‒1, P = 1 atm.

Full size|PPT slide

The runs test determines whether the data systematically deviate from the model. A run is a consecutive series of data points whose residuals are either all positive or all negative. The number of runs is equal to 1 + 2N_pN_n/(N_p + N_n), where N_p and N_n are the number of data points below and above the curve, respectively. Theoretically, there are equal number of data points below and above the curve; thus, the expected number of runs is about 1 + N/2 (N is the total number of data points). The numbers of runs for 5 methane pressures are listed in Tab.1. The Q–Q plot is useful for determining if the residuals follow a normal distribution. If the data values in the plot fall along a roughly straight line at a 45-degree angle, the data are normally distributed. The Q–Q plots for five methane pressures are presented in Fig.6 and Fig. S4 (cf. ESM). Virtually, the data values roughly fall along the straight line at a 45-degree angle. Therefore, we conclude that the parameter values of the proposed rate law may be reliable.

Fig.6 The Q–Q plot for four methane partial pressures: (a) 0.15, (b) 0.30, (c) 0.40, and (d) 0.50 atm; reaction conditions: m_SF–CM = 1 g, T = 900 °C, F = 110 STP∙mL∙min^‒1, P = 1 atm.

Full size|PPT slide

4 Conclusions

In this work, the kinetics of SF–CM nanocomposite reduction by methane was first investigated on a thermo-gravimetric analyzer and then in a packed-bed reactor, in which both complete and partial oxidation of methane were involved but methane cracking was negligible. The complete oxidation occurred before the partial oxidation and there existed a transition between them. As the reduction temperature increased, the weight loss due to the complete oxidation increased but the transition region became less inconspicuous. At 850, 900 and 950 °C, the weight loss associated with the partial oxidation was much larger than that with the complete oxidation. The rate of weight loss from the partial oxidation as a function of time is well fitted by the A3 model, with the activation energy of 59.8 kJ∙mol^‒1. The rate law for methane partial oxidation includes a methane pressure-dependent term and another term related to the solid conversion whose expression is given by the A3 model; the former is represented by a power law. The partial oxidation is half order with respect to methane pressure. Although the reduction rate is well fitted by the proposed rate law, careful considerations should be taken when using it to design and analyze a chemical-looping reforming reactor. This is because the rate constant depends not only on the operating temperature but also on the morphology and density of nanocomposite particles.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China (Grant No. 21978230) and Shaanxi Creative Talents Promotion Plan−Technological Innovation Team (Grant No. 2019TD-039).

Electronic Supplementary Material

Supplementary material is available in the online version of this article at https://dx.doi.org/10.1007/s11705-022-2188-5 and is accessible for authorized users.

References

1 Caballero A, Pérez P J. Methane as raw material in synthetic chemistry: the final frontier. Chemical Society Reviews, 2013, 42(23): 8809–8820

2 Sun L, Wang Y, Guan N, Li L. Methane activation and utilization: current status and future challenges. Energy Technology, 2020, 8(8): 1900826

3 Song H, Meng X, Wang Z J, Liu H, Ye J. Solar-energy-mediated methane conversion. Joule, 2019, 3(7): 1606–1636

4 Olivos-Suarez A I, Szécsényi À, Hensen E J M, Ruiz-Martinez J, Pidko E A, Gascon J. Strategies for the direct catalytic valorization of methane using heterogeneous catalysis: challenges and opportunities. Chemical Reviews, 2016, 6(5): 2965–2981

5 Schwach P, Pan X, Bao X. Direct conversion of methane to value-added chemicals over heterogeneous catalysts: challenges and prospects. Chemical Reviews, 2017, 117(13): 8497–8520

6 Li X, Pei C, Gong J. Shale gas revolution: catalytic conversion of C₁–C₃ light alkanes to value-added chemicals. Chem, 2021, 7(7): 1755–1801

7 Mistré M, Crénes M, Hafner M. Shale gas production costs: historical developments and outlook. Energy Strategy Reviews, 2018, 20: 20–25

8 Tang P, Zhu Q, Wu Z, Ma D. Methane activation: the past and future. Energy & Environmental Science, 2014, 7(8): 2580–2591

9 Guo X, Fang G, Li G, Ma H, Fan H, Yu L, Ma C, Wu X, Deng D, Wei M, Tan D, Si R, Zhang S, Li J, Sun L, Tang Z, Pan X, Bao X. Direct, nonoxidative conversion of methane to ethylene, aromatics, and hydrogen. Science, 2014, 344(6183): 616–619

10 Liu Y, Deng D, Bao X. Catalysis for selected C1 chemistry. Chem, 2020, 6(10): 2497–2514

11 Sushkevich V L, Palagin D, Ranocchiari M, van Bokhoven J A. Selective anaerobic oxidation of methane enables direct synthesis of methanol. Science, 2017, 356(6337): 523–527

12 Haribal V P, Wang X J, Dudek R, Paulus C, Turk B, Gupta R, Li F. Modified ceria for “low-temperature” CO₂ utilization: a chemical looping route to exploit industrial waste heat. Advanced Energy Materials, 2019, 9(41): 1901963

13 Lin T, Yu F, An Y, Qin T, Li L, Gong K, Zhong L, Sun Y. Cobalt carbide nanocatalysts for efficient syngas conversion to value-added chemicals with high selectivity. Accounts of Chemical Research, 2021, 54(8): 1961–1971

14 Liu H, Li Y, He D. Recent progress of catalyst design for carbon dioxide reforming of methane to syngas. Energy Technology (Weinheim), 2020, 8(8): 1900493

15 Yu W, Wang X, Liu Y, Wei J, Zhang J. Effect of composition on the redox performance of strontium ferrite nanocomposite. Energy & Fuels, 2020, 34(7): 8644–8652

16 Damma D, Smirniotis P G. Recent advances in the direct conversion of syngas to oxygenates. Catalysis Science & Technology, 2021, 11(16): 5412–5431

17 Zhu Z, Guo W, Zhang Y, Pan C, Xu J, Zhu Y, Lou Y. Research progress on methane conversion coupling photocatalysis and thermocatalysis. Carbon Energy, 2021, 3(4): 519–540

18 Niu J, Guo F, Ran J, Qi W, Yang Z. Methane dry (CO₂) reforming to syngas (H₂/CO) in catalytic process: from experimental study and DFT calculations. International Journal of Hydrogen Energy, 2020, 45(55): 30267–30287

19 Zhang R, Cao Y, Li H, Zhao Z, Zhao K, Jiang L. The role of CuO modified La_0.7Sr_0.3 FeO₃ perovskite on intermediate-temperature partial oxidation of methane via chemical looping scheme. International Journal of Hydrogen Energy, 2020, 45(7): 4073–4083

20 Zhu X, Imtiaz Q, Donat F, Müller C R, Li F. Chemical looping beyond combustion—a perspective. Energy & Environmental Science, 2020, 13(3): 772–804

21 Zeng L, Cheng Z, Fan J A, Fan L S, Gong J. Metal oxide redox chemistry for chemical looping processes. Nature Reviews. Chemistry, 2018, 2(11): 349–364

22 Zheng Y, Li K, Wang H, Tian D, Wang Y, Zhu X, Wei Y, Zheng M, Luo Y. Designed oxygen carriers from macroporous LaFeO₃ supported CeO₂ for chemical-looping reforming of methane. Applied Catalysis B: Environmental, 2017, 202: 51–63

23 Zhu H, Zhang P, Dai S. Recent advances of lanthanum-based perovskite oxides for catalysis. ACS Catalysis, 2015, 5(11): 6370–6385

24 Wang X, Krzystowczyk E, Dou J, Li F. Net electronic charge as an effective electronic descriptor for oxygen release and transport properties of SrFeO₃-based oxygen sorbents. Chemistry of Materials, 2021, 33(7): 2446–2456

25 Sedykh V D, Rybchenko O G, Suvorov E V, Ivanov A I, Kulakov V I. Oxygen vacancies and valence states of iron in SrFeO_3–δ compounds. Physics of the Solid State, 2020, 62(10): 1916–1923

26 Ji K, Dai H, Dai J, Deng J, Wang F, Zhang H, Zhang L. PMMA-templating preparation and catalytic activities of three-dimensional macroporous strontium ferrites with high surface areas for toluene combustion. Catalysis Today, 2013, 201: 40–48

27 Yang J, Li L, Yang X, Song S, Li J, Jing F, Chu W. Enhanced catalytic performances of in situ-assembled LaMnO₃/δ-MnO₂ hetero-structures for toluene combustion. Catalysis Today, 2019, 327: 19–27

28 Chen J, Buchanan T, Walker E A, Toops T J, Li Z, Kunal P, Kyriakidou E A. Mechanistic understanding of methane combustion over Ni/CeO₂: a combined experimental and theoretical approach. ACS Catalysis, 2021, 11(15): 9345–9354

29 Zhang J S, Haribal V, Li F X. Perovskite nanocomposites as effective CO₂-splitting agents in a cyclic redox scheme. Science Advances, 2017, 3(8): e1701184

30 Wang X H, Du X C, Yu W B, Zhang J S, Wei J J. Coproduction of hydrogen and methanol from methane by chemical looping reforming. Industrial & Engineering Chemistry Research, 2019, 58(24): 10296–10306

31 Khawam A, Flanagan D R. Solid-state kinetic models: basics and mathematical fundamentals. Journal of Physical Chemistry B, 2006, 110(35): 17315–17328

32 Li G, Lv X, Ding C, Zhou X, Zhong D, Qiu G. Non-isothermal carbothermic reduction kinetics of calcium ferrite and hematite as oxygen carriers for chemical looping gasification applications. Applied Energy, 2020, 262: 114604

33 Tian Y, Dudek R B, Westmoreland P R, Li F. Effect of sodium tungstate promoter on the reduction kinetics of CaMn_0.9Fe_0.1O₃ for chemical looping-oxidative dehydrogenation of ethane. Chemical Engineering Journal, 2020, 398: 125583

34 Zhao K, Zheng A, Li H, He F, Huang Z, Wei G, Shen Y, Zhao Z. Exploration of the mechanism of chemical looping steam methane reforming using double perovskite-type oxides La_1.6Sr_0.4FeCoO₆. Applied Catalysis B: Environmental, 2017, 219: 672–682

35 Zhao K, Li L, Zheng A, Huang Z, He F, Shen Y, Wei G, Li H, Zhao Z. Synergistic improvements in stability and performance of the double perovskite-type oxides La_2−xSr_xFeCoO₆ for chemical looping steam methane reforming. Applied Energy, 2017, 197: 393–404

36 Tang M, Xu L, Fan M. Progress in oxygen carrier development of methane-based chemical-looping reforming: a review. Applied Energy, 2015, 151: 143–156

37 Gao Y, Neal L M, Li F. Li-promoted La_xSr_2–xFeO_4−δ core-shell redox catalysts for oxidative dehydrogenation of ethane under a cyclic redox scheme. ACS Catalysis, 2016, 6(11): 7293–7302

38 Cheng F, Dupont V, Twigg M V. Direct reduction of nickel catalyst with model bio-compounds. Applied Catalysis B: Environmental, 2017, 200: 121–132

39 Fedunik-Hofman L, Bayon A, Donne S W. Kinetics of solid–gas reactions and their application to carbonate looping systems. Energies, 2019, 12(15): 2981

40 Fogler H S. Elements of Chemical Reaction Engineering. 5th ed. New York: Pearson Education Inc., 2016,