An integrated approach for machine-learning-based system identification of dynamical systems under control: application towards the model predictive control of a highly nonlinear reactor system

Abstract

Advanced model-based control strategies, e.g., model predictive control, can offer superior control of key process variables for multiple-input multiple-output systems. The quality of the system model is critical to controller performance and should adequately describe the process dynamics across its operating range while remaining amenable to fast optimization. This work articulates an integrated system identification procedure for deriving black-box nonlinear continuous-time multiple-input multiple-output system models for nonlinear model predictive control. To showcase this approach, five candidate models for polynomial and interaction features of both output and manipulated variables were trained on simulated data and integrated into a nonlinear model predictive controller for a highly nonlinear continuous stirred tank reactor system. This procedure successfully identified system models that enabled effective control in both servo and regulator problems across wider operating ranges. These controllers also had reasonable per-iteration times of ca. 0.1 s. This demonstration of how such system models could be identified for nonlinear model predictive control without prior knowledge of system dynamics opens further possibilities for direct data-driven methodologies for model-based control which, in the face of process uncertainties or modelling limitations, allow rapid and stable control over wider operating ranges.

Key words： nonlinear model predictive control; black-box modeling; continuous-time system identification; machine learning; industrial applications of process control

1 Introduction

Against a backdrop of data proliferation and a surging enthusiasm in the applications of artificial intelligence in industry, there has been a growing interest in the community to incorporate the latest results reported in the machine learning (ML) literature to infer dynamical systems from data more effectively [1]. This inference of dynamical systems is also known as system identification (SysID). This discipline has vital industrial pertinence because it yields representations of the process that, firstly, improve system understanding, and secondly, enable the simulation of complex systems to obtain time-series predictions. While this discipline is anchored in statistics and applied mathematics and is thus well-situated to take advantage of the data-driven industry 4.0 revolution, it remains an art form in practice, not least due to the numerous design decisions that practitioners encounter as well as the large number of parameters and hyperparameters that need to be estimated.

1.1 Model predictive control

A prominent application of SysID can be found in advanced model-based process control strategies such as model predictive control (MPC). MPC incorporates knowledge about the process through a system model and solves a dynamic optimization problem at each time step to yield an optimal control sequence. It then applies the first control action in this sequence to the system before proceeding to re-solve the optimization problem at the next time step [2]. MPC can be especially useful because, unlike common applications of conventional process controllers, it natively supports multiple-input multiple-output (MIMO) formulations. It also allows system constraints, which represent process limits, to be directly included in the problem formulation, thereby ensuring plant safety and reliability in an explicit manner [3]. MPC has seen successful adoption in industry to ensure safe, reliable, and profitable system operation, with key examples present in process manufacturing, the control of complex machinery, as well as other value-adding activities [3].

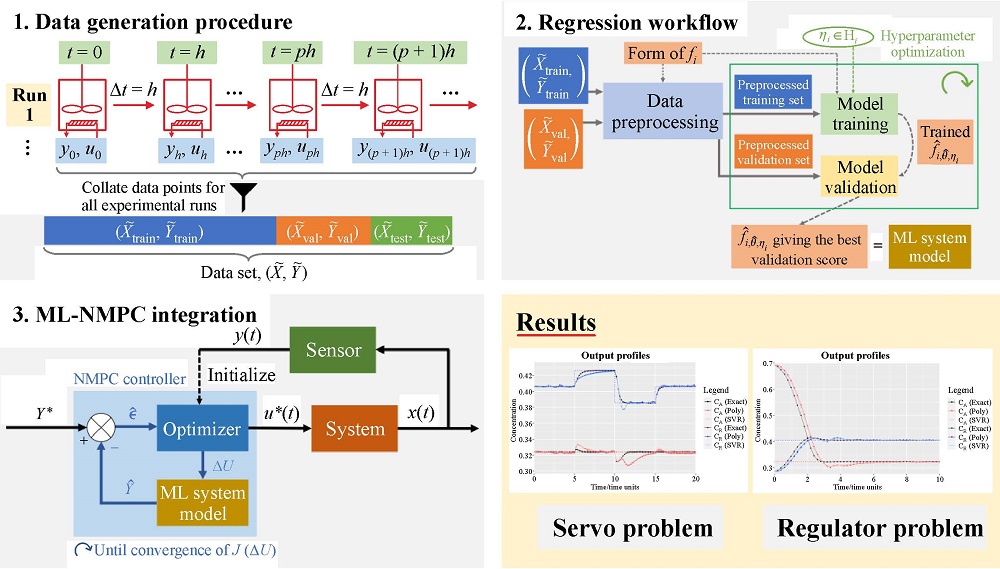
The system model plays a determinant role in MPC. It should adequately describe the process dynamics across the controller operating range while remaining simple enough to allow fast optimization [4]. These models could either be constructed from first principles, which might be difficult and costly for complex processes [5], or directly inferred from empirical data [6]. These models could also have different forms: linear, nonlinear, hybrid or nonparametric, among others. MPC products have typically relied on linear models to exploit efficient optimization algorithms [7]. However, such linear MPCs might struggle to offer effective control outside a limited operating range [5,8]. Indeed, achieving tight control across a process’ entire operating range is generally difficult, with other conventional applications of widely-used methods like proportional-integral-derivative controllers also ill-equipped to handle systems that are highly nonlinear around their operating points [9,10]. Nonlinear MPCs (NMPCs) can overcome these limitations by employing nonlinear system models and system constraints, which have more flexible forms that permit better representation of the process over a wider operating range. This comes however at the expense of needing to solve non-convex optimization problems quickly and precisely [11]. References [3] and [12] describe successful applications of different MPC formulations in a broad class of academic and industrial problems.

Recent advances in computing and statistics have generated novel techniques that could further improve the viability of black-box nonlinear SysID methods for model-based control. Such black-box methods are useful when process understanding is limited to begin with, or when mechanistic models derived from first principles take prohibitively long to evaluate for fast-sampling applications. Reference [13] demonstrated the neural network-based identification of single-input single-output system models for a pH neutralization process and showed that the resulting NMPC was able to track set-point changes better than a linear MPC. References [14] and [15] reported the use of recurrent neural networks and ensemble techniques to generate MIMO system models for NMPC of a continuous stirred tank reactor (CSTR) system, showing that these NMPCs performed better than linear MPCs at rejecting process disturbances.

1.2 Key contributions

Related works in the SysID literature have typically focused on presenting methodologies with special properties. Reference [1] reported a specific methodology for learning efficient models through sparse regression, for instance. The present work is instead designed to be expository and comprehensive in nature, and its main contribution is to articulate an integrated, overarching approach for learning the dynamics of continuous-time systems under control. This work is targeted at interested or starting practitioners in need of a systematic, integrated, and rigorous methodology for applying ML SysID techniques for model-based control purposes.

The key steps of this integrated approach are as follows: (i) the experimental design for data generation, (ii) the regression workflow which consists of data preprocessing techniques and the critical but often overlooked hyperparameter optimization (HO) phase, and (iii) the integration of the learnt model into an ML-NMPC controller. To formalize the goals at each step of this framework, a rigorous exposition of the ML techniques employed at each step, which include feature generation and Bayesian optimization (BO), is provided. While this framework imposes a logical structure to the flow of the data-driven tasks, it remains sufficiently flexible to allow different techniques to be employed at each stage, which future-proofs this framework in the face of further advances in ML.

This approach is exemplified through the case study of a highly nonlinear MIMO CSTR process. The resulting ML-NMPCs were evaluated based on both control performance and solution times on both servo and regulator problems to ensure the solution’s applicability and practicality in real-world industrial settings. The resulting ML-NMPCs were finally benchmarked against an NMPC that employs the true system model. This NMPC is demonstrated to be able to solve all the control problems effectively.

This work is organized as follows. Section 2 formalizes the proposed integrated approach. Section 3 details the CSTR case study, presents the three control scenarios, and reports practical details in implementing this approach. Section 4 presents results and discussions. Section 5 concludes this piece and offers recommendations for future research.

2 Methodology

In the following exposition, x\in {\mathcal{K}}^q is a column vector, with \mathcal{K} representing some field and q\ge \mathrm{1}. The notation \left[a,b\right] represents a row vector when \left(a,b\right)\in {\mathcal{K}}^{\mathrm{2}}, and the \mathrm{T} superscript represents the vector transpose operation, such that {\left[a,b\right]}^{\mathrm{T}} is a column vector. The ╫ symbol represents column vector concatenation, and it returns another column vector, such that x_{\mathrm{1}}╫x_{\mathrm{2}}={\left[x_{\mathrm{1}}^{\mathrm{T}},x_{\mathrm{2}}^{\mathrm{T}}\right]}^{\mathrm{T}} and {╫}_{i\in \left\{\mathrm{1},...,n\right\}}{x}_i={\left[x_{\mathrm{1}}^{\mathrm{T}},...,x_n^{\mathrm{T}}\right]}^{\mathrm{T}}, where x_i\in {\mathcal{K}}^{q_i}. An n\times p matrix with values in \mathcal{K} is denoted {\mathcal{M}}_{n,p}\left(\mathcal{K}\right), while n-order square matrices are {\mathcal{M}}_n\left(\mathcal{K}\right). The ╫ symbol is also used to represent the vertical concatenation of matrices with the same number of columns, such that {╫}_{i\in \left\{\mathrm{1},...,n\right\}}{B}_i={\left[B_{\mathrm{1}}^{\mathrm{T}},...,B_n^{\mathrm{T}}\right]}^{\mathrm{T}}, where B_i\in {\mathcal{M}}_{q_i,p}\left(\mathcal{K}\right). Sets are represented by \left\{\mathrm{1},...,k\right\}. Closed intervals are defined as \left[\alpha \mathrm{;}\beta \right], with \alpha and \beta real numbers. Left and right half-open intervals are \left]\alpha \mathrm{;}\beta \right] and \left[\alpha \mathrm{;}\beta \right[ respectively, with open intervals denoted as \left]\alpha \mathrm{;}\beta \right[. Given x\left(t\right)\in {\mathcal{K}}^q a continuous-time vector-valued quantity, where t\in {ℝ}_{+}, x\left[k\right] represents its value associated with the discrete time-step k, such that x\left[k\right]=x\left(t_k\right), where t_k is the real time associated with the discrete time-step k. \mathrm{\Delta } finally represents the difference operator, such that \mathrm{\Delta }x\left[k\right]:=x\left[k+\mathrm{1}\right]-x\left[k\right].

Equations (1) and (2) describe a general continuous-time state representation for a dynamical system.

(1)\dot{x}=f\left(x,u\right),

(2)y=g\left(x,u\right)+ϵ,

where x\in {ℝ}^a, u\in {ℝ}^b and y\in {ℝ}^c are the state, control, and output vectors respectively, with f:{ℝ}^a\times {ℝ}^b\to {ℝ}^a a general nonlinear state equation and g:{ℝ}^a\times {ℝ}^b\to {ℝ}^c a general nonlinear output equation; ϵ is a random variable corresponding to measurement noise. In what follows, we assume complete state information, such that y=x+ϵ. For a MIMO system, a, b and c are integers that are strictly greater than 1.

If f is a highly nonlinear function, conventional applications of widely-used strategies like proportional-integral-derivative control and linear MPC might not offer effective control beyond a limited range. This motivates the study of nonlinear control strategies like NMPC, which the following subsection describes.

2.1 Nonlinear model predictive control

Given a discrete-time controller, Eq. (3) defines the cost function J at any given discrete time-step k\in \mathbb{N}:

(3)J\left(\mathrm{\Delta }U\right):=\mathrm{tr}\left({\left(Y-Y^{\mathrm{*}}\right)}^{\mathrm{T}}Q\left(Y-Y^{\mathrm{*}}\right)\right)+\mathrm{tr}\left(\mathrm{\Delta }{U}^{\mathrm{T}}R\mathrm{\Delta }U\right),

where \mathrm{\Delta }U:={\left[\mathrm{\Delta }u\left[k\right],\mathrm{\Delta }u\left[k+\mathrm{1}\left],...,\mathrm{\Delta }u\right[k+m-\mathrm{1}\right]\right]}^{\mathrm{T}}\in {\mathcal{M}}_{m,b}\left(ℝ\right) is the control sequence over the control horizon m\in {\mathbb{N}}^{\mathrm{*}}, Y:={\left[y\left[k+\mathrm{1}\left|k\left],...,y\right[k+p\right|k\right]\right]}^{\mathrm{T}}\in {\mathcal{M}}_{p,c}\left(ℝ\right) is the output trajectory over the prediction horizon p\in {\mathbb{N}}^{\mathrm{*}}, Y^{\mathrm{*}}\in {\mathcal{M}}_{p,c}\left(ℝ\right) is the system set-point over p, Q\in {\mathcal{M}}_c\left({ℝ}_{+}\right) and R\in {\mathcal{M}}_b\left({ℝ}_{+}\right) are diagonal non-negative weight matrices whose coefficients reflect the relative importance of the corresponding terms in the cost function, and \mathrm{tr}(·) represents the trace of the matrix. The control actions are applied in a zero-order hold fashion throughout the sampling interval, such that u\left(t\right)=u\left[k\right],\mathrm{\hspace{0.17em}}\forall t\in \left[t_k\mathrm{;}{t}_{k+\mathrm{1}}\right].

Equations (4–8) formulate the NMPC problem, which is solved in a receding horizon fashion:

(4)\underset{\mathrm{\Delta }U}{\min }J\left(\mathrm{\Delta }U\right)\mathrm{},

(5)s.t.\mathrm{\hspace{0.17em}}Y=\mathcal{F}\left(x\left[k\right],u\left[k\right],\mathrm{\Delta }U╫{\mathrm{0}}_{p-m,b}\right),

(6)\mathrm{\Delta }{u}_{\min }\le \mathrm{\Delta }u\left[l\right]\le \mathrm{\Delta }{u}_{\max },\mathrm{\hspace{0.17em}}\forall l\in \left\{k,...,k+m-\mathrm{1}\right\},

(7)u_{\min }\le u\left[l\right]\le u_{\max },\mathrm{\hspace{0.17em}}\forall l\in \left\{k,...,k+m-\mathrm{1}\right\},

(8)y_{\min }\le y\left[l\right]\le y_{\max },\mathrm{\hspace{0.17em}}\forall l\in \left\{k+\mathrm{1},...,k+p\right\},

where \mathcal{F} is a nonlinear function which generates the discrete-time output trajectory given the system’s initial state and the control sequence, and {\mathrm{0}}_{p-m,b} is a zero matrix of dimension \left(p-m\right)\times b. The concatenation of {\mathrm{0}}_{p-m,b} is equivalent to defining \mathrm{\Delta }u\left[l\right]=\mathrm{0},\forall l\in \left\{k+m,...,k+p-\mathrm{1}\right\}, then appending these zero values to \mathrm{\Delta }U such that the resulting matrix has p rows. Therefore, u remains constant after the control horizon. \mathcal{F} can be generated from f as Eq. (9) shows:

(9)\mathcal{F}\left(x\left[k\right],u\left[k\right],\mathrm{\Delta }U╫{\mathrm{0}}_{p-m,b}\right)={\left[\mathcal{G}\left(\mathrm{1}\right),...,\mathcal{G}\left(p\right)\right]}^{\mathrm{T}},

where \mathcal{G}\left(l\right):=x\left(t_k\right)+\underset{t_k}{\overset{t_{k+l}}{\int }}f\left(x\left(\tau \right),u\left(\tau \right)\right)\mathrm{\hspace{0.17em}}\mathrm{d}\tau ,\forall l\in \left\{\mathrm{1},...,p\right\}. Equations (6–8) represent constraints on the control actions’ rates of change, constraints on their magnitude, and constraints on system outputs, respectively.

This NMPC problem is a constrained nonlinear optimization problem which can be solved using active set or interior point methods. As f and \mathcal{G} both return the same vector Y, they are equivalent from the controller’s perspective. We thus refer to f as the NMPC system model in what follows. The continuous-time SysID approach was pursued here because it may be more intuitive to scientists and engineers [16]. With that said, the proposed approach is potentially also amenable to discrete-time formulations after suitable modifications.

If f or \mathcal{F} is not known a priori, it becomes necessary to first identify it from empirical data. The following subsection describes how recent advances in ML could be applied in the context of a broader integrative SysID approach for nonlinear control.

2.2 Black-box direct continuous-time SysID

Figure 1 illustrates the three-step framework for directly identifying f as NMPC system models from empirical data. The data generation procedure involves performing experiments that perturb the system across the controller’s operating region to reveal system dynamics. The regression workflow then proceeds to infer nonlinear continuous-time functions as NMPC system models. These system models are finally integrated into the ML-NMPC controllers, which are subsequently tested to evaluate their closed-loop control performance.

Fig.1 Integrated data-driven approach for identification of continuous-time NMPC system models.

Full size|PPT slide

2.2.1 Data generation procedure

The design of the input signal is critical to generating a rich data set, and the signal proposed in this work consists of simultaneous random step changes for all manipulated variables. The experimental sampling time h is also an important parameter as the following discussion will show.

To generate an input signal of time length t_{\mathrm{sim}}\in {ℝ}_{+}^{*} for a single manipulated variable, a partition of the interval \left[\mathrm{0}\mathrm{;}{t}_{\mathrm{sim}}\right] is first performed by performing a random jump forward in time from the start of the interval, with the jump length in time units (tus) sampled from a discrete uniform distribution \mathcal{U}\left(\left\{l_{\min },l_{\min }+h,...,l_{\max }\right\}\right), where l_{\min } and l_{\max } are the minimum and maximum jump lengths in tus respectively and are both integer multiples of h, then repeating these jumps until t_{\mathrm{sim}} is reached. The value of the manipulated variable at each subinterval is then sampled from a continuous uniform distribution \mathcal{U}\left(\left[u_{\min }\mathrm{;}{u}_{\max }\right]\right), where u_{\min } and u_{\max } are the lower and upper bounds of the manipulated variable as specified in the NMPC formulation, respectively. This process is repeated for each manipulated variable.

Figure 2 shows an example of an input signal and the system response when the input signal is applied to the system. As the control values reached are uniformly represented across the controller’s operating region, it facilitates the learning of ML models that interpolate well to give good dynamical predictions within this region.

Fig.2 Example input signal (green) and system response (red), where t=\mathrm{10000}, l_{\min }=\mathrm{10}, l_{\max }=\mathrm{100}, u_{\min }=\mathrm{0}, u_{\max }=\mathrm{1}.

Full size|PPT slide

Given an input signal {\left(u_i\right)}_{i\in \left\{\mathrm{0},...,t_{\mathrm{sim}}/h\right\}} and the system response {\left(y_i\right)}_{i\in \left\{\mathrm{0},...,t_{\mathrm{sim}}/h\right\}}, where u_i and y_i are potentially multidimensional, we pose {\tilde{x}}_i:=y_i╫u_i and {\tilde{y}}_i:= \left[\left(y_{i+\mathrm{1}}-y_i\right)/h\right], \forall i\in \left\{\mathrm{0},...,t_{\mathrm{sim}}/h-\mathrm{1}\right\}.  {\tilde{x}}_i and  {\tilde{y}}_i represent data points and their corresponding labels, which are alternatively the independent and dependent variables respectively, and this supervised learning task is formalized in Section 2.2.2.

As  {\tilde{y}}_i contain first-order approximations of the continuous derivatives representing the system dynamics, values for h that are small with respect to the system’s characteristic time would be ideal, i.e., at least an order of magnitude smaller. In this work, the initial process values are taken to be the set-point values. Combining data points from multiple experimental runs is also straightforward, and it is indeed desirable to use as many data points as could possibly be collected. This is because, in general, model variance decreases as the number of data points increases, such that more precise estimates for the model parameters are achieved.

2.2.2 Regression workflow

We pose \tilde{X}:={\left[{\tilde{x}}_i\right]}_{i\in \left\{\mathrm{1},...,N\right\}}^{\mathrm{T}} the design matrix with {\left\{{\tilde{x}}_i\right\}}_{i\in \left\{\mathrm{1},...,N\right\}} the data set of size N\in {\mathbb{N}}^{\mathrm{*}}, and \tilde{Y}:={\left[{\tilde{y}}_i\right]}_{i\in \left\{\mathrm{1},...,N\right\}}^{\mathrm{T}} the labels matrix with {\left\{{\tilde{y}}_i\right\}}_{i\in \left\{\mathrm{1},...,N\right\}} the set of labels associated to \left\{{\tilde{x}}_i\right\}.

Before performing the regression task, the data set is split into training, validation, and test sets. The training set contains the data used to fit a given model. The validation set contains the data used to provide an unbiased evaluation of a model fit on the training set while tuning the model hyperparameters. The test data finally contains the data used to provide an unbiased evaluation of the tuned models. The validation and test sets are “held out” from the training set to prevent data leakage, which is when information outside the training set is used to create the model. Data leakage causes the estimates of the final model’s general predictive power to be overly optimistic. We note I_{\mathrm{train}}, I_{\mathrm{val}} and I_{\mathrm{test}} the set of indices of \tilde{X} corresponding to these sets, with \mathrm{card}\left(I_{\mathrm{train}}\right)=N_{\mathrm{train}}, \mathrm{card}\left(I_{\mathrm{val}}\right)=N_{\mathrm{val}} and \mathrm{card}\left(I_{\mathrm{test}}\right)=N_{\mathrm{test}}, such that N_{\mathrm{train}}+N_{\mathrm{val}}+N_{\mathrm{test}}=N. {\tilde{X}}_{\mathrm{train}}:={\left[{\tilde{x}}_i\right]}_{i\in I_{\mathrm{train}}}^{\mathrm{T}} is the training design matrix with {\tilde{Y}}_{\mathrm{train}}:={\left[{\tilde{y}}_i\right]}_{i\in I_{\mathrm{train}}}^{\mathrm{T}} its labels matrix. {\tilde{X}}_{\mathrm{val}}, {\tilde{Y}}_{\mathrm{val}}, {\tilde{X}}_{\mathrm{test}} and {\tilde{Y}}_{\mathrm{test}} are defined similarly.

Data preprocessing encompasses a broad set of strategies that prepares the data set for the model training phase in such a way as to facilitate the learning of models that generalize well. It generally involves data cleaning, which removes outliers that might have resulted from sensor faults or data input errors, and feature engineering, which encompasses other techniques like feature transformation, feature generation, and feature extraction. In this work, we focus on the generation of polynomial and interaction features, which represent higher-order and coupled nonlinear terms in the system dynamics. We pose \tilde{X}={\left[{\tilde{X}}_j\right]}_{j\in \left\{\mathrm{1},...,N_f\right\}}, where {\tilde{X}}_{j\in \left\{\mathrm{1},...,N_f\right\}} are feature vectors with N_f\in \mathbb{N} the number of features. Equation (10) formalizes the feature generation procedure of degree d\in {\mathbb{N}}^{*}:

(10)

To illustrate this procedure, suppose that \tilde{X}=\left[{\tilde{X}}_{\mathrm{1}},{\tilde{X}}_{\mathrm{2}}\right]. A feature generation of degree 2 yields the following matrix:

(11){\tilde{X}}^{\left(\mathrm{2}\right)}=\left[\mathrm{1},{\tilde{X}}_{\mathrm{1}},{\tilde{X}}_{\mathrm{2}},{\tilde{X}}_{\mathrm{1}}^{\mathrm{2}},{\tilde{X}}_{\mathrm{1}}{\tilde{X}}_{\mathrm{2}},{\tilde{X}}_{\mathrm{2}}^{\mathrm{2}}\right].

Data standardization is also performed to allow all features to be considered equally during model training. Equation (12) describes this operation:

(12){\tilde{X}}_{·,std}^{\left(d\right)}={\left[{\displaystyle \frac{{\tilde{X}}_{·,j}^{\left(d\right)}-{\overline{\tilde{X}}}_{�,j}^{\left(d\right)}}{{\widehat{\sigma }}_{�,j}}}\right]}_{j\in \left\{\mathrm{1},...,N_f^{\left(d\right)}\right\}},

where {\tilde{X}}_{·,j}^{\left(d\right)} represents the j-th column of {\tilde{X}}_{·}^{\left(d\right)}, {\overline{\tilde{X}}}_{�,j}^{\left(d\right)} the sample mean of {\tilde{X}}_{�,j}^{\left(d\right)}, {\widehat{\sigma }}_{�,j} the population standard deviation of {\tilde{X}}_{�,j}^{\left(d\right)}, and N_f^{\left(d\right)}\in {\mathbb{N}}^{�} the total number of polynomial and interaction features. · is a placeholder referring either to the training, validation, or test sets. If · refers to either {\tilde{X}}_{\mathrm{train}} or {\tilde{X}}_{\mathrm{val}}, then � refers to {\tilde{X}}_{\mathrm{train}}. If · refers to {\tilde{X}}_{\mathrm{test}}, then � refers to . This mapping of · to � is done to prevent data leakage.

The model training phase corresponds to solving for a prediction function f such that \tilde{y}�f\left(\tilde{x}\right). Suppose that we have n candidate models, i.e., n different regression forms for f. For each f_{i\in \left\{\mathrm{1},...,n\right\}}, we solve the mean squared error (MSE) minimization problem in Eq. (13):

(13){\widehat{\theta }}_i=\underset{{\theta }_i\in {\mathrm{\Theta }}_i}{\arg \mathrm{\hspace{0.17em}}\min }{\displaystyle \frac{\mathrm{1}}{N_{\mathrm{train}}}}{\sum }_{j\in I_{\mathrm{train}}}{\left({\tilde{y}}_j-f_{i,{\theta }_i}\left(\widetilde{x_j}\right)\right)}^{\mathrm{2}},

where {\mathrm{\Theta }}_i represents the parameter space for f_i. f_{i,{\widehat{\theta }}_i} finally represents the solution to this regression problem, and this procedure is repeated for each f_i. Let {\eta }_i\in {\mathrm{H}}_i be the set of hyperparameters for f_i. HO involves training f_i with different {\eta }_i, then selecting {\widehat{\eta }}_i which satisfies Eq. (14):

(14){\widehat{\eta }}_i=\underset{{\eta }_i\in {\mathrm{H}}_i}{\arg \mathrm{\hspace{0.17em}}\min }{\displaystyle \frac{\mathrm{1}}{N_{\mathrm{val}}}}{\sum }_{j\in I_{\mathrm{val}}}{\left({\tilde{y}}_j-f_{i,{\widehat{\theta }}_i\mathrm{;}{\eta }_i}\left(\widetilde{x_j}\right)\right)}^{\mathrm{2}}.

BO is employed in this work for HO, with exhaustive grid searches used instead if the hyperparameter space is countable and sufficiently small. BO is a class of optimization techniques that applies Bayes Theorem to quickly find the global optima of a general nonlinear multidimensional function [17]. Unlike grid and random searches, BO takes past evaluations into account by using them to build a probabilistic surrogate model of the HO objective function. It uses this model to select the most promising hyperparameters at each iteration. The objective function is then evaluated at those hyperparameters, with this result subsequently used to update the surrogate model. This iterative procedure therefore yields posteriors that better approximate the HO objective function with each evaluation, from which the best hyperparameters can be hoped to be more easily located [17]. As function evaluations for Eq. (14) are expensive, since an iteration involves training an entire model, such a principled approach which balances exploration of the hyperparameter space and exploitation of best found values is desirable [18,19].

The formalization of BO consists of five key elements. The first element is {\mathrm{H}}_i, the hyperparameter space, and the second is the HO objective function, which was present in Eq. (14) and is explicated here:

(15)\mathcal{J}\left({\eta }_i\right):={\displaystyle \frac{\mathrm{1}}{N_{\mathrm{val}}}}\sum _{j\in I_{\mathrm{val}}}{\left({\tilde{y}}_j-f_{i,{\widehat{\theta }}_i\mathrm{;}{\eta }_i}\left(\widetilde{x_j}\right)\right)}^{\mathrm{2}}.

The third element is the surrogate model, which is an alternative probabilistic representation of the objective function that is cheaper to evaluate. The fourth is the acquisition function which is defined over {\mathrm{H}}_i and is computed from the surrogate model, and it quantifies the desirability of sampling a given point in {\mathrm{H}}_i next. The final element is the BO history, which is a set containing the s samples drawn from \mathcal{J} so far. The surrogate model is referred to as the posterior distribution when it is conditioned by {\mathcal{D}}_{\mathrm{BO},s}, and is represented by p_{{\mathcal{D}}_{\mathrm{BO},s}}. We also drop the i subscript in an abuse of notation for the remaining technical development of BO.

Common acquisition functions include the probability of improvement, expected improvement (EI), entropy search, and lower confidence bound. At the \left(s+\mathrm{1}\right)-th iteration, these functions have the generic form shown in Eq. (16):

(16)A_{s+\mathrm{1}}\left(\eta \right)={\mathcal{E}}_{{\mathcal{D}}_{\mathrm{BO},s}}\left[u_{s+\mathrm{1}}\left(\eta \right)\right],

where u_{s+\mathrm{1}}:\mathrm{H}\to ℝ is a utility function to maximize. EI is the most common acquisition function and is used in this study, and it has the following utility function at the \left(s+\mathrm{1}\right)-th iteration:

(17)u_{EI,s+\mathrm{1}}\left(\eta \right)=\max \left(\mathrm{0},{\mathcal{J}}_s^{\mathrm{*}}-\mathcal{J}\left(\eta \right)\right),

where {\mathcal{J}}_s^{*}:=\underset{v\in \left\{\mathrm{1},...,s\right\}}{\min }\mathcal{J}\left({\eta }_v\right) is the best value for \mathcal{J} found after s iterations. The acquisition function A_{EI,s+\mathrm{1}}\left(\eta \right) at the \left(s+\mathrm{1}\right)-th evaluation is thus:

(18)A_{EI,s+\mathrm{1}}\left(\eta \right)={\int }_{-\infty }^{\infty }\max \left(\mathrm{0},{\mathcal{J}}_s^{\mathrm{*}}-\mathcal{J}\right)\mathrm{\hspace{0.17em}}{p}_{{\mathcal{D}}_{BO,s}}\left(\mathcal{J}\mathrm{|}\eta \right)\mathrm{\hspace{0.17em}}\mathrm{d}\mathcal{J}={\int }_{-\infty }^{{\mathcal{J}}_s^{\mathrm{*}}}\left({\mathcal{J}}_s^{\mathrm{*}}-\mathcal{J}\right)\mathrm{\hspace{0.17em}}{p}_{{\mathcal{D}}_{BO,s}}\left(\mathcal{J}\mathrm{|}\eta \right)\mathrm{\hspace{0.17em}}\mathrm{d}\mathcal{J}.

This finally yields the following maximization problem at the \left(s+\mathrm{1}\right)-th evaluation:

(19){\eta }_{s+\mathrm{1}}=\underset{\eta \in \mathrm{H}}{\arg \mathrm{\hspace{0.17em}}\max }{A}_{EI,s+\mathrm{1}}\left(\eta \right)=\underset{\eta \in \mathrm{H}}{\arg \mathrm{\hspace{0.17em}}\max }{\int }_{-\infty }^{{\mathcal{J}}_s^{\mathrm{*}}}\left({\mathcal{J}}_s^{\mathrm{*}}-\mathcal{J}\right)\mathrm{\hspace{0.17em}}{p}_{{\mathcal{D}}_{BO,s}}\left(\mathcal{J}\mathrm{|}\eta \right)\mathrm{\hspace{0.17em}}\mathrm{d}\mathcal{J}.

This therefore corresponds to finding \eta \in \mathrm{H} which is expected to improve on {\mathcal{J}}_s^{*} the most, given the current surrogate model p_{{\mathcal{D}}_{BO,s}}\left(\mathcal{J}\mathrm{|}\eta \right).

Common forms for the surrogate model include Gaussian processes and Tree-Parzen estimators (TPEs), with the latter being applied in this work. Technical details for the structure of TPEs and how EI is optimized in the TPE algorithm can be found in ref. [18]. The degree for polynomial feature generation is considered as a hyperparameter for all candidate models, with d_i\in \left\{\mathrm{1},...,\mathrm{10}\right\}, \forall i.

Each candidate model f_i whose best hyperparameters {\widehat{\eta }}_i have been found is then trained on {\tilde{X}}_{\mathrm{train}}{\cup }^{\mathrm{}}{\tilde{X}}_{\mathrm{val}} and tested on {\tilde{X}}_{\mathrm{test}} to determine its test MSE, which serves as an indicator of the model’s general predictive ability with respect to other candidate models after hyperparameter tuning. Before integration into ML-NMPC, the models are initialized with their best hyperparameters {\widehat{\eta }}_i and trained on the full data set  \tilde{X}.

In situations where data is sparse, it would be useful to apply cross-validation techniques to obtain better estimates for the model’s general predictive power during HO. K-fold cross-validation involves, firstly, extracting {\tilde{X}}_{\mathrm{test}} from \tilde{X}, then splitting the remaining data into K equal folds, i.e., {\left\{{\tilde{X}}_i\right\}}_{i\in \left\{\mathrm{1},...,K\right\}}, where K\le N-N_{\mathrm{test}}. K number of models are then trained for each hyperparameter configuration, with each run l\in \left\{\mathrm{1},...,K\right\} having {\displaystyle {\cup }_{i\in \left\{\mathrm{1},...,K\right\}\backslash l}}{\tilde{X}}_l as the training set and {\tilde{X}}_l as its validation set. This technique returns K validation MSEs, which can be averaged to obtain a less biased estimate of the model’s goodness. K is typically selected to be 5 or 10. Leave-one-out cross-validation involves selecting K=N-N_{\mathrm{test}} and, while it is the most computationally expensive, returns the least biased estimate of the model’s goodness. As it is assumed that enough data has been generated, cross-validation techniques are not employed in this work.

2.2.3 Integration of ML model into NMPC

In the last step of this framework, the models f_{i,{\widehat{\theta }}_i\mathrm{;}{\widehat{\eta }}_i} obtained from the regression workflow are integrated into the ML-NMPC as system models and used to generate predictions for \dot{x}, which themselves are used to evolve x in time to generate Y given \mathrm{\Delta }U. To solve this system of first-order ordinary differential equations, numerical methods like Runge-Kutta methods and linear multistep methods can be used.

Tuning of the ML-NMPC control parameters is done before testing its closed-loop performance on the case study. In this work, this consists of modifying m to minimize the weighted integrated absolute error (WIAE) for a ±5% set-point step experiment:

(17)\mathrm{WIAE}:={\int }_{t_{\mathrm{0}}}^{t_f}W\Vert y\left(t\right)-y^{\mathrm{*}}{\left(t\right)\Vert }_{\mathrm{1}}\mathrm{\hspace{0.17em}}\mathrm{d}t,

where W\in {\mathcal{M}}_c\left({ℝ}_{+}\right) is a weight matrix, and t_{\mathrm{0}}\in {ℝ}_{+} and t_f\in {ℝ}_{+} are the start and end times of the experiment, respectively. p=\mathrm{5} was taken to be fixed in this work. The WIAE was selected as the figure of merit for its simple interpretation, though other controller tuning statistics that explicitly include \mathrm{\Delta }U or that have more elaborate forms could also be used without any loss of generality of this procedure (see ref. [20] for other statistics that could be used in place of the WIAE). The controller’s sampling time h_{\mathrm{NMPC}} is typically chosen to be 5 to 10 times faster than the system’s characteristic time as a rule of thumb [21].

3 Case study

3.1 Plant model

The case study, which was also studied in ref. [22], consists of a single CSTR system which houses a reversible chemical reaction described in Eq. (20), where A is the feed species, R the desired product, and S the undesired byproduct. Non-dimensionalized expressions for the system’s dynamical behavior are shown in Eqs. (21–23):

(20)A{\rightleftharpoons }_{k_{\mathrm{4}}}^{k_{\mathrm{1}}}R{\rightleftharpoons }_{k_{\mathrm{3}}}^{k_{\mathrm{2}}}S,

(21){\displaystyle \frac{\mathrm{d}{C}_A}{\mathrm{d}t}}=q\left[C_{A\mathrm{0}}-C_A\right]-k_{\mathrm{1}}{C}_A+k_{\mathrm{4}}{C}_R,

(22){\displaystyle \frac{\mathrm{d}{C}_R}{\mathrm{d}t}}=q\left[\mathrm{1}-C_{A\mathrm{0}}-C_R\right]+k_{\mathrm{1}}{C}_A+k_{\mathrm{3}}\left[\mathrm{1}-C_A-C_R\right]-\left[k_{\mathrm{2}}+k_{\mathrm{4}}\right]C_R,

(23)k_j=k_{\mathrm{0},j}\exp \left\{{\left[-{\displaystyle \frac{E}{R{T}_{\mathrm{0}}}}\right]}_j\left[{\displaystyle \frac{\mathrm{1}}{T}}-\mathrm{1}\right]\right\},\mathrm{\hspace{0.17em}}j\in \left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\right\},

where C_{i\in \left\{A,R,S\right\}}\in {ℝ}_{+} is the species’ reactor concentration, C_{A\mathrm{0}}\in {ℝ}_{+} is the feed concentration of A, q\in {ℝ}_{+} is the feed and the exit flow rate, k_{j\in \left\{\mathrm{1},...,\mathrm{4}\right\}}\in {ℝ}_{+} are the reaction rate constants, k_{\mathrm{0},j\in \left\{\mathrm{1},...,\mathrm{4}\right\}}\in {ℝ}_{+} are the Arrhenius pre-exponential constants, {\left[E/R{T}_{\mathrm{0}}\right]}_{j\in \left\{\mathrm{1},...,\mathrm{4}\right\}}\in {ℝ}_{+} are the normalized activation energies, and T\in {ℝ}_{+} is the system temperature. q and T are the manipulated variables in this study. The values for the model parameters are reported in Appendix A (cf. Electronic Supplementary Material, ESM).

Figure 3 schematizes the CSTR plant and plots the system’s steady-state conditions as a function of T when q is 0.8 and at its nominal point. To simplify the system, it is assumed that the low-level flow and temperature control loops have negligible dead times and present no steady-state errors. The system’s set-point was selected to maximize the ratio of C_R to C_A. This corresponds also to maximizing product yield and minimizing any downstream separations costs. There are strong non-linearities in how both C_A and C_R vary with T at the set-point. There is also input multiplicity, since two different values of T could yield the same value for C_R, which suggests that there are sign changes in the determinant of the steady-state gain matrix within the operating region that make linear controllers with integral action unstable [23]. The control of this system at this set-point is therefore a relevant and interesting problem.

Fig.3 (a) Schematic diagram of CSTR plant, where q^{*} and T^{*} represent set-points for q and T respectively; (b) system steady-state conditions for q=\mathrm{0.8} (“Reactor startup” and “Upset recovery” refer to start points for the control problems in Section 3.2).

Full size|PPT slide

To numerically simulate this system, a linear multistep method implemented through the LSODA option in integrate.solve_ivp in the SciPy package (version 1.5) was used [24]. A Gaussian noise �\sim \mathcal{N}\left(\mathrm{0},{\mathrm{10}}^{-\mathrm{3}}\right) was included in every measurement of C_A and C_R to simulate measurement noise. Given the range of values for C_A and C_R, this corresponds to a measurement error of ca. 1%.

3.2 Control scenarios

Controller performance was evaluated based on 3 scenarios. The first scenario was a servo control problem representing ±5% step changes to the C_R set-point. This step size was selected because the control actions needed to stabilize the system at the new set-points are large enough to pose a control problem that is challenging enough to be studied meaningfully. Each experimental run began at the set-point and was followed by the +5% step and the −5% step before reverting to the set-point, such that the experiment had the following C_R profile: \left[\mathrm{0.406},\mathrm{\hspace{0.17em}}\mathrm{0.426},\mathrm{\hspace{0.17em}}\mathrm{0.386},\mathrm{\hspace{0.17em}}\mathrm{0.406}\right]. Each step lasted for 5 tus for a total experimental length of 20 tus.

The second and third scenarios were regulator control problems corresponding to “reactor startup” and “upset recovery” respectively. These two process disturbances lay at opposite sides of the set-point, with the former having low T and C_R values and the latter having an abnormally high T value. A process controller would therefore need to optimize correctly for T values within an extended range of 0.8 and 1.1 to perform well in both these scenarios. All experimental runs for these two scenarios lasted for 10 tus.

3.3 Framework application

To infer f for this case study, we pose {\tilde{x}}_i:={\left[C_A,C_R,q,T\right]}_i^{\mathrm{T}} and {\tilde{y}}_i:={\left[\mathrm{d}{C}_A/\mathrm{d}t,\mathrm{d}{C}_R/\mathrm{d}t\right]}_i^{\mathrm{T}}. Note that the polynomial and interaction features for {\tilde{x}}_j up to degree d would be appended to this vector before the model training phase as part of the feature generation procedure described in Section 2.2.2. In this work, h=\mathrm{0.1} tu, t_{\mathrm{sim}}=\mathrm{1000}, l_{\min }=\mathrm{1}, l_{\max }=\mathrm{10}, q_{\min }=\mathrm{0.5}, q_{\max }=\mathrm{0.9}, T_{\min }=\mathrm{0.7} and T_{\max }=\mathrm{1.1}. 5 runs were performed, and an example of an experimental run is shown in Fig. 4.

Fig.4 Example system response (top) to an input signal (bottom) for the CSTR case study.

Full size|PPT slide

In this work, a 60%, 20%, 20% split for the training, validation and test sets was used. The polynomial feature generation and data standardization operations were performed with preprocessing.PolynomialFeatures and preprocessing.StandardScaler from scikit-learn (version 0.23) respectively [25]. The scikit-learn package was also used to perform model training for different candidate models. The optuna package (version 2.3) in Python 3.8 was used to perform BO [26]. The f_i studied in this work are common regression forms and include linear regression, which we henceforth refer to as “polynomial” regression, support vector regression (SVR), decision tree (DT) regression, extra trees (ET) regression and gradient boosted (GB) regression. The model hyperparameters {\eta }_i for each f_i are reported in Appendix B (cf. ESM).

The NMPC problem was solved using the sequential least squares quadratic programming method which was implemented in optimize.minimize from SciPy (version 1.5) [24]. The constraints on the control actions’ magnitude and system outputs, which are Eqs. (7) and (8) respectively, were manifested as soft constraints, with the coefficients of their penalty terms in the objective function taken to be 1000. The nonlinear optimizer was initialized with values sampled from \mathcal{U}\left(\left[-{\mathrm{10}}^{-\mathrm{3}},{\mathrm{10}}^{-\mathrm{3}}\right]\right) at the first time step and was warm-started with the solution from the previous time step in subsequent time steps. In this study h_{\mathrm{NMPC}}=\mathrm{0.2} tu.

To evolve the system in time with the ML models in the ML-NMPC, the RK23 solver in optimize.minimize from SciPy (version 1.5) was used. W=\mathrm{diag}\left(\left[\mathrm{1},\mathrm{3}\right]\right) was chosen for the WIAE to punish C_R deviations 3 times more heavily than C_A deviations.

4 Results and discussion

We report firstly the closed-loop performances of an NMPC controller with the exact system model, which will serve as a benchmark for ML-NMPC. The performance of the ML models from the SysID procedure will be quantified through their validation and test R^{\mathrm{2}} and MSE values, following which the closed-loop performances of these ML-NMPCs on the control scenarios will be presented.

In what follows, we refer to the NMPC with the exact system model as the “exact NMPC”. For the ML-NMPCs, we use the shorthand “polynomial-NMPC” to refer to ML-NMPCs with a system model that is linear in the polynomial and interaction features, “DT-NMPC” to refer to ML-NMPCs with a DT system model, and so on for the other ML models. All calculations were performed in a Python 3.8 environment on a computer with 16 GB of RAM and a 4-core Intel® Core™ i7-4790 CPU running at 3.60 GHz.

4.1 Nonlinear MPC with exact system model

Figure 5 shows the results for the exact NMPC with p=\mathrm{5} and different values of m, and it can be observed that m=\mathrm{1} offers the lowest WIAE on the step experiments while also taking the least time to solve. Figure 6 shows the performance for the tuned exact NMPC on the three control scenarios. Stable closed-loop performance was achieved for all control scenarios. The servo, startup, and recovery problems took 3.65, 2.24 and 1.82 s to solve respectively for the m=\mathrm{1} case, demonstrating average per-iteration solution times in the order of 10 ms. This therefore validates the use of the exact NMPC as a useful benchmark for rapid and stable control of this system. Appendix C (cf. ESM) reports the parameters for this exact NMPC.

Fig.5 (a) WIAE for exact NMPC with p=\mathrm{5}; (b) exact NMPC solution times with p=\mathrm{5}.

Full size|PPT slide

Fig.6 Exact NMPC performance for p=\mathrm{5} and m=\mathrm{1}: (a) servo problem, (b) startup problem, and (c) upset recovery problem.

Full size|PPT slide

While it is expected that greater values of m provide tighter control, albeit with longer solution times, m=\mathrm{1} was shown to give lower values for WIAE. However, this came with more aggressive control actions, as Fig. 7 shows. The larger the value for m, the smoother the control profiles, with this demonstrating how the changes in the control action constitute an important term in the NMPC objective function. Having selected WIAE as our figure of merit for the sake of interpretability, we keep m=\mathrm{1} as the tuned m value, making again a further mention that other statistics for tuning m could also be employed which explicitly considers the control actions. The ML-NMPCs presented in Section 4.3 will also take m=\mathrm{1} as their tuned m value.

Fig.7 Exact NMPC performance for m=\mathrm{1},\mathrm{\hspace{0.17em}}\mathrm{3},\mathrm{\hspace{0.17em}}\mathrm{5} for the servo problem: (a) output profiles, and (b) control profiles.

Full size|PPT slide

4.2 HO

Figure 8 plots the validation and test R^{\mathrm{2}} scores, and the test MSE scores, for each candidate model. Figure 9 presents more insights into the BO procedure as illustrated through the optimization history plots and slice plots, taking SVR as an example. Appendix D (cf. ESM) reports the best hyperparameters {\widehat{\eta }}_i for each f_i found through BO.

Fig.8 (a) Validation and test R^{\mathrm{2}} scores for each candidate model; (b) test MSE score for each candidate model (“Poly” refers to the polynomial regression model).

Full size|PPT slide

Fig.9 (a) Optimization history for BO of SVR; (b) slice plot for � hyperparameter for SVR (objective value is validation R^{\mathrm{2}}).

Full size|PPT slide

The tuned polynomial model gave the highest test R^{\mathrm{2}} value and the lowest test MSE value, suggesting that it would return better estimates for \mathrm{d}{C}_A/\mathrm{d}t and \mathrm{d}{C}_R/\mathrm{d}t than other candidate models for this case study. The tuned SVR model gave slightly poorer R^{\mathrm{2}} and MSE scores than the polynomial model, with the tree-based models, i.e., DT, ET, and GB, performing even more poorly than SVR. It is worth noting that different candidate models possess different structures that permit them to model some dynamical systems more efficiently than others. The validation and test results of each model relative to other models can therefore be expected to differ from one case study to another.

The optimization history in Fig. 9(a) illustrates how the BO procedure balances exploration of the hyperparameter space with the exploitation of best found values. The first few trials gave models that returned poor validation scores, and as better hyperparameter configurations were encountered the validation scores of subsequent models remained around similarly good values, suggesting that the sampling strategy began focusing on points close to the best-found hyperparameters. Figure 9(b) reinforces this observation by showing how later trials focused on the region around �=\mathrm{0.02}, with sporadic evaluations at values outside of that region.

4.3 Closed-loop control results

After HO, the tuned candidate models were integrated into ML-NMPC controllers and tested against the three control scenarios. Figure 10 shows the results for ML-NMPC. Figures 11, 12 and 13 show concentration and control paths from the polynomial-NMPC and SVR-NMPC for the servo, startup, and upset recovery problems, respectively. These paths are compared against those from the exact NMPC. Figure 14 shows GB-NMPC performance on all three control problems, with these results being representative of the performances of ML-NMPC employing tree-based system models. The results from the two stable ML-NMPCs, the polynomial-NMPC and SVR-NMPC, are finally benchmarked against the exact NMPC in Tables 1 and 2.

Fig.10 ML-NMPC performance for p=\mathrm{5} and : (a) WIAE, and (b) solution times.

Full size|PPT slide

Fig.11 Exact, polynomial- and SVR- NMPC performance for the servo problem: (a) output profiles, and (b) control profiles.

Full size|PPT slide

Fig.12 Exact, polynomial- and SVR- NMPC performance for the startup problem: (a) output profiles, and (b) control profiles.

Full size|PPT slide

Fig.13 Exact, polynomial- and SVR- NMPC performance for the upset recovery problem: (a) output profiles, and (b) control profiles.

Full size|PPT slide

Fig.14 GB-NMPC performance for p=\mathrm{5} and m=\mathrm{1}: (a) servo problem, (b) startup proble, and (c) upset recovery problem.

Full size|PPT slide

Tab.1 Comparison of WIAEs for polynomial- and SVR- NMPCs against exact NMPC for p=\mathrm{5} and m=\mathrm{1}

Item	Controller performance in WIAE
	Polynomial	SVR	Exact
Servo	0.209	0.200	0.094
Startup	1.090	1.031	0.870
Upset recovery	0.392	0.774	0.326

Tab.2 Comparison of solution times for Polynomial- and SVR- NMPCs against exact NMPC for p=\mathrm{5} and m=\mathrm{1}

Item	Solution times in seconds
	Polynomial	SVR	Exact
Servo	11.9	69.0	3.50
Startup	6.63	72.2	2.33
Upset recovery	5.88	41.0	1.83

Polynomial- and SVR- NMPCs succeeded in achieving tight control for all three control problems, as Figs. 11–13 show. In the servo problem, C_A and C_R values took slightly longer to settle at their new set-point values for the two ML-NMPCs, with this due to these controllers offering q control which is less aggressive. This suggests that the quality of the continuous-time model identified from the data is sensitive to the selection of the experimental sampling time h for the data generation procedure. While h=\mathrm{0.1} tu was sufficient to generate data that allowed the polynomial and SVR models to learn the right “signs” for the time-derivatives characterizing the dynamical system, smaller h values might offer even better first-order approximations for these time-derivatives that ML models could learn from, potentially allowing the ML-NMPC to solve more accurately for smaller time-steps to achieve tighter control. The control paths in the regulator problems in Figs. 12 and 13 also reveal q and T control for ML-NMPC which lagged slightly behind those for the exact NMPC.

These two ML-NMPCs required an order of magnitude more time per iteration than the exact NMPC, though they remained fast in the order of 0.1 s per iteration. The SVR-NMPC required more time than the polynomial-NMPC due to its increased model complexity, with it taking between 5 and 7 times longer while not offering any consistent improvement in WIAE performance over the polynomial-NMPC. Taking both control performance and evaluation times into account, the polynomial-NMPC would be preferable to the SVR-NMPC for this case study.

The tree-based ML-NMPCs were ineffective in control for all three control problems, as Fig. 14 shows, though an exception exists in ET-NMPC for upset recovery. Tree-based models might not be suitable as system models for ML-NMPC in this study because their piece-wise constant nature [27] could prevent optimizers like SLSQP, which depend on local gradient or Hessian approximations, from functioning well. Understanding this observation for tree-based models lies beyond the scope of this work and can be pursued in a future study.

The results above validate the ability of the proposed integrative SysID approach to identify system models for NMPC that allow effective control of a highly nonlinear MIMO CSTR system for control problems across a wider operating range. Further comments made on observations from this case study reinforce the importance of selecting a suitable h for the data generation procedure, highlight the usefulness of simpler models with shorter ML-NMPC solution times, and hint towards more advanced applications of ML that achieve better bias-variance tradeoffs through this framework. Examples illustrating the latter point include incorporating expert system knowledge to impose a prior structure on the candidate models, thereby reducing model bias. Such models are known as grey-box models. Feature selection techniques such as principal component analysis can also be incorporated along with other model regularization techniques to reduce model variance.

5 Conclusions

In this work, an integrated SysID procedure for deriving black-box nonlinear continuous-time MIMO system models for NMPC was articulated. This procedure was validated through the successful identification of NMPC system models that enabled effective control of a highly nonlinear MIMO CSTR system across a wider operating range. This framework is sufficiently flexible and allows practitioners to employ different data generation methods, apply different HO methods, as well as test different candidate models. The choices presented here reflect the current state-of-the-art or what is reasonable, based on the authors’ experience.

It is hoped that these results can motivate further research in direct data-driven methodologies for SysID for MPC. Future directions include the following:

1.‚Applying more advanced ML techniques to this framework such as feature selection, model regularization. Other candidate models that involve local regression or ensemble methods could also be studied in greater detail. This abundance of ML techniques could be exploited to achieve better bias-variance tradeoffs and yield better system models.

2.‚Studying the impact of measurement noise, the amount of data available, and the experimental and NMPC controller sampling times on this SysID procedure to quantify its sensitivity to the quality of data and other design decisions.

3.‚Exploring how a discrete-time model could be derived from a well-learnt continuous-time model, which could serve as a fit-for-purpose NMPC system model requiring smaller solution times.

Acknowledgements

The authors thank the MOE AcRF Grant in Singapore for financial support of the projects on Precision Healthcare Development, Manufacturing and Supply Chain Optimization (Grant No. R-279-000-513-133) and Advanced Process Control and Machine Learning Methods for Enhanced Continuous Manufacturing of Pharmaceutical Products (Grant No. R-279-000-541-114).

Code Availability Statement

ƒAccess to the GitHub repository containing the source code for this project is available upon request.

Electronic Supplementary Material

ƒSupplementary material is available in the online version of this article at https://dx.doi.org/10.1007/s11705-021-2058-6 and is accessible for authorized users.

References

1 Kaiser E, Kutz J N, Brunton S L. Sparse identification of nonlinear dynamics for model predictive control in the low-data limit. Proceedings—Royal Society. Mathematical, Physical and Engineering Sciences, 2018, 474(2219): 20180335

2 Sommeregger W, Sissolak B, Kandra K, von Stosch M, Mayer M, Striedner G. Quality by control: towards model predictive control of mammalian cell culture bioprocesses. Biotechnology Journal, 2017, 12(7): 1600546

3 Qin S J, Badgwell T A. A survey of industrial model predictive control technology. Control Engineering Practice, 2003, 11(7): 733–764

4 Öner M, Montes F C C, Ståhlberg T, Stocks S M, Bajtnerb J E, Sin G. Comprehensive evaluation of a data driven control strategy: experimental application to a pharmaceutical crystallization process. Chemical Engineering Research & Design, 2020, 163: 248–261

5 Al Seyab R K, Cao Y. Nonlinear system identification for predictive control using continuous time recurrent neural networks and automatic differentiation. Journal of Process Control, 2008, 18(6): 568–581

6 Ljung L. Perspectives on system identification. Annual Reviews in Control, 2010, 34(1): 1–12

7 Mokhatab S, Poe W A. Handbook of Natural Gas Transmission and Processing. 2nd ed. Boston: Gulf Professional Publishing, 2012, 473–509

8 Venkateswarlu C, Venkat Rao K. Dynamic recurrent radial basis function network model predictive control of unstable nonlinear processes. Chemical Engineering Science, 2005, 60(23): 6718–6732

9 Štampar S, Sokolič S, Karer G, Žnidaršič A, Škrjanc I. Theoretical and fuzzy modelling of a pharmaceutical batch reactor. Mathematical and Computer Modelling, 2011, 53(5-6): 637–645

10 Alanis A Y, Arana-Daniel N, López-Franco C. Artificial Neural Networks for Engineering Applications. Washington: Academic Press, 2019, 55–63

11 Pan Y, Wang J. Model predictive control of unknown nonlinear dynamical systems based on recurrent neural networks. IEEE Transactions on Industrial Electronics, 2012, 59(8): 3089–3101

12 Schoukens J, Ljung L. Nonlinear system identification: a user-oriented road map. IEEE Control Systems, 2019, 39: 28–99

13 Arefi M, Montazeri A, Poshtan J, Jahed-Motlagh M. Nonlinear model predictive control of chemical processes with a wiener identification approach. In: 2006 IEEE International Conference on Industrial Technology. Mumbai: IEEE, 2006, 1735–1740

14 Wu Z, Tran A, Rincon D, Christofides P D. Machine learning-based predictive control of nonlinear processes. Part I: theory. AIChE, 2019, 65(11): e16729

15 Wu Z, Tran A, Rincon D, Christofides P D. Machine-learning-based predictive control of nonlinear processes. Part II: computational implementation. AIChE, 2019, 65(11): e16734

16 Garnier H. Direct continuous-time approaches to system identification. Overview and benefits for practical applications. European Journal of Control, 2015, 24: 50–62

17 Frazier P I. A tutorial on Bayesian optimization. arXiv:1807.02811 [stat.ML], 2018

18 Bergstra J, Bengio Y. Random search for hyper-parameter optimization. Journal of Machine Learning Research, 2012, 13: 281–305

19 Berk J, Nguyen V, Gupta S, Rana S, Venkatesh S. Exploration enhanced expected improvement for bayesian optimization. In: Berlingerio M, Bonchi F, Gärtner T, Hurley N, Ifrim G, eds. Machine Learning and Knowledge Discovery in Databases. Cham: Springer International Publishing, 2019, 621–637

20 Seborg D E, Mellichamp D A, Edgar T F, Doyle F J III. Process dynamics and control. 3rd ed. New York: John Wiley & Sons, 2010

21 Binder B J T, Johansen T A, Imsland L. Improved predictions from measured disturbances in linear model predictive control. Journal of Process Control, 2019, 75: 86–106

22 Wong W C, Chee E, Li J, Wang X. Recurrent neural network-based model predictive control for continuous pharmaceutical manufacturing. Mathematics, 2018, 6(11): 242

23 Koppel L B. Input multiplicities in nonlinear, multivariable control systems. AIChE, 1982, 28(6): 935–945

24 Virtanen P, Gommers R, Oliphant T E, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, Bright J, . SciPy 1.0: fundamental algorithms for scientific computing in Python. Nature Methods, 2020, 17(3): 261–272

25 Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, . Scikit-learn: machine learning in Python. Journal of Machine Learning Research, 2011, 12: 2825–2830

26 Akiba T, Sano S, Yanase T, Ohta T, Koyama M. Optuna: a next-generation hyperparameter optimization framework. In: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: Association for Computing Machinery, 2019, 2623–2631

27 Shi Y, Li J, Li Z. Gradient boosting with piece-wise linear regression trees. arXiv:1802.05640 [cs.LG], 2019