Molecular level understanding of CO₂ capture in ionic liquid/polyimide composite membrane

Abstract

Ionic liquid (IL)/polyimide (PI) composite membranes demonstrate promise for use in CO₂ separation applications. However, few studies have focused on the microscopic mechanism of CO₂ in these composite systems, which is important information for designing new membranes. In this work, a series of systems of CO₂ in 1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide composited with 4,4-(hexafluoroisopropylidene) diphthalic anhydride (6FDA)-based PI, 6FDA-2,3,5,6-tetramethyl-1,4-phenylene-diamine, at different IL concentrations were investigated by all-atom molecular dynamics simulation. The formation of IL regions in PI was found, and the IL regions gradually became continuous channels with increasing IL concentrations. The analysis of the radial distribution functions and hydrogen bond numbers demonstrated that PI had a stronger interaction with cations than anions. However, the hydrogen bonds among PI chains were destroyed by the addition of IL, which was favorable for transporting CO₂. Furthermore, the self-diffusion coefficient and free energy barrier suggested that the diffusion coefficient of CO₂ decreased with increasing IL concentrations up to 35 wt-% due to the decrease of the fractional free volume of the composite membrane. However, the CO₂ self-diffusion coefficients increased when the IL contents were higher than 35 wt-%, which was attributed to the formation of continuous IL domain that benefitted the transportation of CO₂.

Key words： carbon dioxide; ionic liquid; 6FDA-TeMPD; composite membrane; molecular dynamics simulation

1 Introduction

Global warming has received considerable worldwide attention and is mainly caused by an increase in atmospheric CO₂ from the release of flue gas, the burning of natural gas and so on [1,2]. On the other hand, CO₂ is an important carbon source for producing high-value chemicals. Therefore, the capture and separation of CO₂ has become a very important issue [3,4].

Polymer membranes have some advantages in gas separation, such as environmental friendliness, low energy requirement, high separation efficiency and compact operation [5,6] and have been regarded as potential membranes for the separation of CO₂. Polyimides (PIs) are one of the most commonly used polymer membranes and show good performance for gas separation [7,8]. Many researchers have explored the permeability and selectivity of gas in PI by experiments. It has been found that fluorine-containing PIs are particularly effective in the separation of CO₂ because of their high fractional free volume (FFV) [9]. Kanehashi et al. [10] reported that 4,4-(hexafluoroisopropylidene) diphthalic anhydride (6FDA)-2,3,5,6-tetramethyl-1,4-phenylene diamine (TeMPD) had a CO₂ permeability of 1156 barrer, and the selectivity of CO₂/N₂ was 15.5. Tong et al. [8] found that the CO₂/N₂ selectivity was 20.1, but the permeability coefficient was only 142.61 barrer for the 6FDA-α,α-bis(4-amino-3,5-dimethyphenyl)-1-(3′,4′,5′-trifluorophenyl) methane (BATFM) membrane. Weigelt et al. [11] prepared thin-film composite membranes for CO₂ separation and reported that the CO₂/CH₄ selectivity was 47.6, and the CO₂ permeability was only 53.4 barrer for thick films of 6FDA-4,4′-(hexafluoroisopropylidene) dianiline. Therefore, most polymer membranes usually exhibit a trade-off between selectivity and perme-ability.

In recent decades, ionic liquids (ILs) have been increasingly studied for separating CO₂ due to their good thermal stability, low volatility, designability and high solubility [12,13]. Moreover, compared with traditional amines, the special functional groups and correspondingly outstanding properties of ILs can decrease the energy consumption required for CO₂ separation [14]. Jalili et al. [15] found that the order of the solubility of CO₂ in imidazolium-based ILs was bis(trifluoromethylsulfonyl)imide ([Tf₂N]^–)>trifluoromethylsulfonate ([OTf]^–)>hexafluorophosphate ([PF₆]^–)>tetrafluoroborate ([BF₄]^–) for physical absorption. 1,1,3,3-Tetramethylguanidinium imidazole was found to capture 1.01 mol CO₂ per mol IL, which was likely due to the reaction between CO₂ and the imidazole anion [16]. Wang et al. [17] reported that the NH₃/CO₂ selectivity was 50 in bis(1-butyl-3-methylimidazolium) tetrachloridocupraten ([BMIM]₂[CuCl₄]). However, ILs still have some drawbacks, such as their high viscosity and cost. Thus, many researchers have tried to combine ILs with polymer membranes to overcome the limitations of both ILs and polymer membranes for enhancing gas separation efficiency.

Recently, researchers have focused on preparing IL/PI composite membranes for CO₂ separation [18,19]. For example, Kanehashi et al. [10] studied the separation of CO₂ in the [BMIM][Tf₂N]/PI membrane and reported that the CO₂ permeability was 501 barrer and the selectivity of CO₂/N₂ was 27.6. Ito et al. [20] found that the CO₂ permeability was 412 barrer and the selectivity of CO₂/N₂ was 27 in sulfonated polyimide (SPI)/[BMIM][Tf₂N] composite membranes at 303 K. The CO₂ permeability selectivity in SPI/[BMIM][PF₆] was lower than that in SPI/[BMIM][Tf₂N]. Monteiro et al. [21] reported that IL/metal-organic framework/Matrimid®5218 mixed matrix membranes could effectively improve the selectivity and permeability of CO₂/N₂.

Although many experiments have been adopted to investigate the separation of CO₂ in IL/PI composite membranes, little research has focused on studying the microscopic mechanisms. Molecular dynamics simulation is a widely used tool to explore microscopic mechanisms [22,23]. For example, Lourenco et al. [24] studied the structures and interactions between a system of 1-ethyl-3-methylimidazolium ([Tf₂N]) and CO₂ by molecular dynamics simulation. They found that the total volume of the system increased as the CO₂ concentration increased, and the solubility of CO₂ in ILs was higher than that in water due to the stronger interaction between anions and CO₂. Balçık et al. [22] found that the F atoms of 6FDA and O atoms of 3,3,4,4-benzophenone tetracarboxyclic dianhydride were the main sites of CO₂ adsorption through grand canonical Monte Carlo and molecular dynamics simulations. Abedini et al. [25] found that N atoms in the ionic PI chains had a strong interaction with CO₂, and the [BF₄]^–-based system showed high selectivity for CO₂/CH₄. For CO₂/N₂, the [Tf₂N]^–-based system had higher selectivity than the [BF₄]^–-based system. Nevertheless, a molecular-level understanding regarding the separation of CO₂ with IL/PI composite membranes is rare, and the microscopic mechanism is still not clear.

In this work, all-atom molecular dynamics simulations of CO₂ in a composite system composed of 6FDA-TeMPD PI and different concentrations of [BMIM][Tf₂N] were performed at 503 K and 1 bar. This system was chosen because it shows good performance for CO₂ separation, and [BMIM][Tf₂N] and 6FDA-TeMPD PI are a typical IL and polymer for separating CO₂, respectively. The main contents of this work are organized as follows. First, the interactions and microstructures of IL/PI systems with different IL contents were studied. The radial distribution function (RDF), coordination numbers, hydrogen bond numbers and FFV were calculated. Second, the dynamic properties and interactions of CO₂ with IL/PI systems were investigated by analyzing the interaction energy, RDFs, spatial distribution function (SDF), self-diffusion coefficient and potential of mean force (PMF). Finally, the conclusions are summarized.

2 Experimental

An all-atom force field was employed to simulate the mixtures of CO₂ in 6FDA-TeMPD PI and [BMIM][Tf₂N] by using the GROMACS 5.1.1 software package [26,27]. The functional form for the total energy is provided as follows:

(1)E={\displaystyle \sum _{\text{bonds}}}\frac{1}{2}{k}_{\mathrm{b}}{(r-r_0)}^2+{\displaystyle \sum _{\text{angles}}}\frac{1}{2}{k}_{\mathrm{a}}{(\theta -{\theta }_0)}^2+{\displaystyle \sum _{\text{dihedrals}}}\frac{k_i}{2}[1+\cos (n\varphi -{\varphi }_0\left)\right]+{\displaystyle \sum 4{\epsilon }_{ij}}\left[{\left(\frac{{\sigma }_{ij}}{r_{ij}^{12}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}^6}\right)}^6\right]+{\displaystyle \sum \frac{q_i{q}_j}{4\mathrm{\pi }{\epsilon }_0{r}_{ij}}},

where the first three terms represent the bond interaction, and the last two terms describe the van der Waals and Coulombic interactions, respectively. The all-atom force field parameters for [BMIM]⁺ and [Tf₂N]^– were obtained from Liu et al. [28] and Lopes et al. [29], respectively, and have been successfully employed to study many IL mixtures. The charge parameters of 6FDA-TeMPD PI were taken from Tanis’s work [30], and the other force field parameters of 6FDA-TeMPD PI were generated from general AMBER force field [31]. The detailed force field parameters for 6FDA-TeMPD PI and the atom types are presented in Table S1 and Fig. S1 (cf. Electronic Supplementary Material, ESM), respectively. The simulated densities and experimental data [10] for the mixture of [BMIM][Tf₂N] and 6FDA-TeMPD PI are listed in Table S2 (cf. ESM). From Table S2, it can be found that the simulated densities were consistent with the experimental results as a whole, which indicated that the force fields used here were reliable. The chemical structures of [BMIM]⁺, [Tf₂N]^– and 6FDA-TeMPD PI are shown in Fig. 1.

Fig.1 Chemical structures of (a) [BMIM]⁺, (b) [Tf₂N]^–, (c) the 6FDA-TeMPD monomer and (d) the PI chain composed of 8 monomers of 6FDA-TeMPD. Color code: H atoms, white; C atoms, cyan; N atoms, blue; S atoms, yellow; O atoms, red; F atoms, pink.

Full size|PPT slide

In all simulated systems, 30 PI chains with each chain made up of 8 monomers of 6FDA-TeMPD were adopted. The weight percentages of [BMIM][Tf₂N] were 0, 10, 20, 30, 35, 40, 50 and 100 wt-%. Detailed information about the numbers of [BMIM][Tf₂N] and PI are listed in Table 1. The initial configurations of [BMIM][Tf₂N] and PI mixtures were prepared by Packmol [32] with three-dimensional periodic boundaries. The particle mesh Ewald method [33] was used to calculate the long-range electrostatic interaction with a cutoff radius of 1.2 nm. The cutoff radius was also set to 1.2 nm for the van der Waals potential and short-range neighbor list. All the bonds were restricted by the LINCS algorithm [34]. A Parrinello-Rahman barostat [35] was used to control the pressure at 1 bar with a coupling constant of 2.0 ps, and a Nose-Hoover thermostat [36] was carried out to maintain the temperature with a time constant of 0.2 ps.

Tab.1 Simulated IL/PI systems

IL concentration/wt-%	0	10	20	30	35	40	50	100
Amount of IL	0	39	93	160	201	250	372	400
Amount of PI	30	30	30	30	30	30	30	0

The initial configurations of the mixtures of IL and PI were first minimized by energy minimization with the steepest descent method for removing possible overlapping structures. The minimum force was set to 100 kJ·mol^–1·nm^–1. Then, the canonical ensemble was performed for 1 ns at 503 K to equilibrate the system. Finally, the systems were simulated under the isobaric-isothermal (NPT) ensemble with an annealing simulation. All the systems were heated to 600 K for 10 ns, heated to 700 K for 20 ns, and then gradually cooled to 503 K in 20 ns. The equilibration time lasted for 30 ns. Finally, another 60 ns was run to analyze the results. The equilibrium trajectories were collected every 20 ps. In addition, it is well known that molecular dynamics simulations are time consuming. It was found that the system of [BMIM][Tf₂N] and 6FDA-TeMPD PI moved very slowly under experimental conditions (308 K) because 30 PI chains with each chain made up of 8 monomers of 6FDA-TeMPD were adopted. It could be hard for 6FDA-TeMPD PI to cross the potential barrier at 308 K. Therefore, to quickly reach dynamic equilibrium and reduce the simulation time, the temperature was set to 503 K, which is below the decomposition temperature of [BMIM][Tf₂N] and 6FDA-TeMPD PI. Moreover, the RDF analysis of cation-anion and PI-cation with 20, 35 and 50 wt-% IL at 308 K were calculated. The calculated results are compared with those at 503 K. As shown in Fig. S2 (cf. ESM), the first peak and valley positions for RDFs of the cation-anion and PI-cation at 308 K and 503 K are almost the same. These results suggest that compared with the simulation at 308 K, the simulation at 503 K has almost no effect on structure, and hence, on properties.

To investigate the dynamic properties and interactions of CO₂ in IL/PI systems, 50 CO₂ molecules were inserted into the equilibrium structures of IL/PI systems. The force field of CO₂ was obtained from Shi and Maginn [37] The systems of CO₂ in IL/PI were equilibrated in the NPT ensemble for 50 ns, and another 50 ns was run for further analysis.

PMF of CO₂ in [BMIM][Tf₂N]/PI systems was calculated by an umbrella sampling [38] and weighted histogram analysis method (WHAM) [39] through GROMACS 5.1.1 software [27]. Two CO₂ molecules were inserted into the equilibrium structures of [BMIM][Tf₂N]/PI systems with different IL concentrations. In this study, the reaction coordinate was chosen as the distance between two CO₂. The configurations were simulated further for 10 ns, and the 26 windows were set from 0.05 to 1.3 nm under a force constant of 5000 kJ·mol^–1·nm^–2.

3 Results and discussion

3.1 IL/PI systems

3.1.1 Microstructure

It is necessary to study the microscopic structure of the IL/PI composite system because it can directly reflect changes in the membrane [40]. Snapshots of the equilibrated microscopic structures of [BMIM][Tf₂N] and PI with increasing IL concentrations are shown in Fig. 2. From Fig. 2, it can be seen that the ILs are scattered and not connected at low concentrations, while ILs are gradually connected to each other and form continuous channels at high concentrations, indicating that the ILs could better disperse in PI chains with increasing IL concentration. Similarly, it was reported that ILs could form continuous domains in [BMIM][BF₄]/Nafion [41] and IL/polyvinylidene fluoride (PVDF) systems [42] by molecular simulation. In addition, it was experimentally found that the IL domain could form in [BMIM][Tf₂N]/PI composite membranes when IL concentrations were higher than 35 wt-% [10].

Fig.2 Snapshots of IL/PI systems at different concentrations: (a) 10 wt-%, (b) 20 wt-%, (c) 30 wt-%, (d) 35 wt-%, (e) 40 wt-% and (f) 50 wt-%. The white and red represent PI and IL, respectively.

Full size|PPT slide

3.1.2 Interaction

RDF describes the probability of other atoms or sites around a central atom or site separated by a distance r, which can be calculated by Eq. (2),

(2)g\left(r\right)={\displaystyle \frac{n\left(r\right)}{\mathrm{4}\rho \mathrm{\pi }{r}^{\mathrm{2}}}},

where \rho is the local density of the target atom or site around the central atom or site, r is the radius of the sphere, and n\left(r\right) is the number of target particles along the radius r.

The center-of-mass RDFs of cation-anion and site-site RDFs of cation-PI and anion-PI were computed and presented in Fig. 3. Figure 3(a) shows the center-of-mass RDFs between cations and anions in [BMIM][Tf₂N]/PI at different concentrations of IL. Figure 3(a) clearly shows that the first peak and valley positions between cations and anions are almost the same for all IL concentrations. The positions of the first peaks between cations and anions for all IL concentrations were at approximately 0.5 nm, and the first peak value gradually decreased as the concentration of IL increased. These results indicated that the IL preferred to gradually disperse in the [BMIM][Tf₂N]/PI composite membrane with increasing IL concentration, which was consistent with the microstructures in Fig. 2.

To study the interaction between the IL and PI chains, the site-site RDFs of cations-PI and anions-PI with different IL concentrations were calculated. The site-site RDFs for H5 atoms in [BMIM]⁺ around the O and F atoms in PI are shown in Figs. 3(b) and 3(c), respectively. Figure 3(d) shows the site-site RDFs between O1 atoms in [Tf₂N]^– and H atoms in PI. From Fig. 3(b), it can be found that the RDFs between H5 atoms in [BMIM]⁺ and O atoms in PI had a sharp peak value at approximately 0.25 nm for all IL concentrations, which meant that hydrogen bonds were formed between the O atoms in PI and the H5 atoms in [BMIM]⁺. However, as displayed in Figs. 3(c) and 3(d), the distributions of H5 atoms in cations around the F1 atoms in PI and the distributions of O1 atoms in anions around the H atoms in PI were very weak. These results revealed that the interaction between the H5 atoms in [BMIM]⁺ and O atoms in PI was the strongest and was much higher than that between the O1 atoms in anions and H atoms in PI.

Fig.3 (a) Center-of-mass RDFs of cation-anion and site-site RDFs for (b) the H5 atoms in cations and O atoms in PI; (c) the H5 atoms in cations and F1 atoms in PI; (d) the O1 atoms in anions and H atoms in PI at different IL concentrations.

Full size|PPT slide

Since the interaction between the O atoms in PI and H5 atoms in cations is the strongest, the coordination number between the O atoms in PI and H5 atoms in cations was calculated to investigate the effect of IL concentration on the interaction of PI-cations. The coordination number can be obtained by the following equation:

(3)N\left(r\right)={\displaystyle {\int }_{\mathrm{0}}^r}\rho g\left(r\right)\mathrm{4}\mathrm{\pi }{r}^{\mathrm{2}}\mathrm{d}r.

The calculated coordination numbers of O–H5 at different concentrations of [BMIM][Tf₂N] are depicted in Fig. 4. As seen in Fig. 4, the coordination number of O–H5 gradually increased with increasing IL concentration, suggesting that the interaction between PI chains and cations was enhanced, and the cations were more dispersed around the PI chains with increasing IL concentration. Kanehashi et al. [10] also found that [BMIM][Tf₂N] could be well-dispersed in a IL/PI composite membrane by attenuated total reflection infrared spectrometry.

Fig.4 Coordination numbers of the H5 atoms in [BMIM]⁺ around O atoms in PI at different IL concentrations.

Full size|PPT slide

3.1.3 Hydrogen bond

Hydrogen bonds are an important intermolecular interaction [43,44], which is one of the factors for forming polymer complexes with excellent mechanical properties. The number of hydrogen bonds for PI-PI, PI-cations and PI-anions were calculated for all IL concentrations. A hydrogen bond is considered to form when the donor and acceptor distance is no more than 0.35 nm and the angle of the donor-hydrogen-acceptor is less than 30° [27]. Here, the possible donors were hydrogen atoms in the PI chains and [BMIM]⁺. The potential acceptors were oxygen and fluorine atoms in the PI chains and [Tf₂N]^–. As shown in Fig. 5, the number of hydrogen bonds for PI-cations and PI-anions gradually increased as the IL concentration increased. Moreover, the hydrogen bond numbers between the PI and cations were larger than those between the PI and anions at all IL concentrations, which agreed with the results in Fig. 3. However, the number of hydrogen bonds among the PI chains decreased as the IL concentration increased, which was due to the formation of strong hydrogen bonds between the PI-cations and PI-anions. These results indicated that the IL provided a shielding effect. The destroyed hydrogen bond network among the PI chains due to the IL addition was beneficial for the transportation of CO₂. Similarly, the hydrogen bond numbers among the PVDF chain were also found to decrease with increasing IL concentration [42].

Fig.5 Hydrogen bond numbers of PI-PI, PI-cations and PI-anions at different IL concentrations.

Full size|PPT slide

3.1.4 FFV

The FFVs of the IL/PI composite systems at different IL concentrations were calculated by GROMACS 5.1.1 software [27]. When the distance between the probe and any atom was less than the sums of the van der Waals radii of both atoms, the position would be considered occupied. The van der Waals radii obtained from Bondi’s work [45] were adopted for the calculation. The FFV is obtained by the following equation [46]:

(4)FFV=\mathrm{1}-{\displaystyle \frac{\mathrm{1.3}{V}_{\mathrm{vdw}}}{V_{\mathrm{m}}}},

where V_{\mathrm{vdw}} is the van der Waals volume of the molecule and V_{\mathrm{m}} is the molar volume. Figure 6 presents the FFVs of the IL/PI composite systems at different IL concentrations. Figure 6 shows that the FFV of the IL/PI systems gradually decreased with increasing IL concentrations. However, when the IL concentration was more than 35 wt-%, the rate of decrease of FFV was very low. For example, the FFV was 0.282 and 0.258 for 20 and 35 wt-% IL, respectively. However, the FFV was 0.258 and 0.244 for 35 and 50 wt-% IL, respectively. The –C(CF₃)₂– group of 6FDA in PI occupies a large molecular space and induces chain stiffness, leading to the large FFV and low mobility of PI [47]. Therefore, the FFV of the IL/PI composite membrane continued to decrease with increasing IL content from 0 to 35 wt-%, indicating that the IL filled the voids of the PI chains. However, as illustrated in Section 3.1.1, when the IL concentration was more than 35 wt-%, a continuous IL channel was formed, resulting in the lower rate of decrease of FFV.

Fig.6 FFVs of the IL/PI composite systems at different IL concentrations.

Full size|PPT slide

3.2 IL/PI-CO₂ system

3.2.1 Interaction energy

To study the CO₂ with IL/PI system, the interaction energies of IL-CO₂ and PI-CO₂ were calculated. The interaction energy is the sum of the van der Waals and Coulombic energy. The interaction energies of IL-CO₂ and PI-CO₂ in the IL/PI composite systems at different IL concentrations are shown in Fig. 7. It is clear that the interaction energy between PI and CO₂ decreased with increasing IL concentration, while the interaction energy between IL and CO₂ increased with increasing IL concentration. Furthermore, compared with the interaction energy between IL and CO₂, the interaction energy between PI and CO₂ was stronger. In general, the interaction between IL-CO₂ and PI-CO₂ in the IL/PI system was competitive.

Fig.7 Interaction energies of (a) PI-CO₂ and (b) IL-CO₂ at different IL concentrations.

Full size|PPT slide

3.2.2 Distributions of CO₂ around IL and PI

To understand the distribution of CO₂ in the IL/PI composite system, the RDFs of CO₂-IL and CO₂-PI were analyzed. Here, the F1, H and O atoms are the PI sites, H5 atoms are the cation sites, N atoms are the anion sites, and C atoms were chosen to represent CO₂. Figure 8 shows the RDFs of CO₂-PI, CO₂ cations, and CO₂ anions at 50 wt-% IL. As shown in Fig. 8(a), the distribution of the C atoms of CO₂ around the O atoms of PI was higher than those around the H and F1 atoms of PI, indicating that CO₂ was mainly distributed around the O atoms of PI. Similarly, Balçık et al. [22] found that the O atoms of PI were the preferential sites for CO₂ sorption. As seen in Fig. 8(b), the distribution of the C atoms of CO₂ around the N atoms of the anion was slightly higher than that around the H5 atoms of the cation. However, as a whole, the distribution of CO₂ around PI was generally stronger than that around the anions and cations, which suggested that the interaction of CO₂-PI was stronger than that of CO₂-IL. These results were in accordance with the interaction energies of IL-CO₂ and PI-CO₂ in Fig. 7.

Fig.8 Site-site RDFs of (a) PI-CO₂ and (b) IL-CO₂ at 50 wt-% IL.

Full size|PPT slide

The microstructure of the composite system can be more intuitively reflected by three-dimensional SDFs. The SDFs of the O atoms of PI, C atoms of CO₂ and N atoms of anions around cations in the IL/PI systems at 20, 35 and 50 wt-% IL are shown in Fig. 9. The N atoms of anions are primarily distributed around the H5 and H4 atoms of cations at 20 wt-% IL. Additionally, the distribution of N atoms of anions gradually spreads from the H5/H4 position to the position above the imidazole of cations as the IL concentration increases. The high-density areas for the O atoms of PI around cations were found around H5 and H4 and above and below the imidazole of cations. Some areas, such as H5 and H4, for the O atoms of PI and N atoms of anions around cations overlapped, suggesting that PI and anions were competitive in these areas. However, the C atoms of CO₂ were mainly distributed around H4 and the –(CH₃) group of cations. Overall, the cations were mainly surrounded by anions and PI, which was likely due to the negative atomic charges of the O atoms of PI and anions.

Fig.9 Three-dimensional probable distribution of the O atoms of PI (blue), C atoms of CO₂ (white), and N atoms of anions (green) around the cations in IL/PI composite systems at (a) 20 wt-% IL with average densities of 2.0, 2.0 and 10.0, respectively, (b) 35 wt-% IL with average densities of 2.0, 2.0 and 7.0, respectively, and (c) 50 wt-% IL with average densities of 2.2, 2.0 and 5.0, respectively.

Full size|PPT slide

3.2.3 Self-diffusion coefficient

The self-diffusion coefficient is one of the most important properties for evaluating the performance of IL/polymer composite membranes. The self-diffusion coefficients of cations and anions of the IL and CO₂ in all simulated systems are obtained by the Einstein relation:

(5)D={\displaystyle \frac{\mathrm{1}}{\mathrm{6}N}}\underset{t\to \infty }{\lim }{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\langle {\displaystyle {\sum }_{i=\mathrm{1}}^N{\left[r_i\right(t)-r_i(\mathrm{0}\left)\right]}^{\mathrm{2}}}\rangle ,

where the angle bracket is the ensemble-averaged mean square displacement (MSD) of the center of mass of molecules, r_i is the center of mass positions of the molecules, and N is the total number of molecules. It is important to define the appropriate time range for calculating the self-diffusion coefficient. To more accurately calculate the MSDs, the NPT equilibrium trajectory of the final 50 ns was analyzed. As shown in Fig. S3 (cf. ESM), the MSDs of all simulated systems were linear from 50 to 100 ns, which indicated that the obtained self-diffusion coefficients of the cations, anions, and CO₂ were reliable. Figure 10 shows the diffusion coefficients of the cations, anions of IL and CO₂ in the IL/PI systems at different IL concentrations. As shown in Fig. 10(a), the self-diffusion coefficients of the cations and anions increased with increasing IL concentrations. For example, the self-diffusion coefficients of [BMIM]⁺ and [Tf₂N]^– were 0.29 × 10^–11 and 0.17 × 10^–11 m²·s^–1 after the addition of 20 wt-% IL, whereas they were 1.9 × 10^–11 and 1.22 × 10^–11 m²·s^–1 with the addition of 50 wt-% IL, respectively.

The self-diffusion coefficients of CO₂ in IL/PI systems are displayed in Fig. 10(b). When the IL concentration was less than 35 wt-%, the self-diffusion coefficient of CO₂ gradually decreased with increasing IL concentration. For example, the self-diffusion coefficient of CO₂ in pure PI was 131.22 × 10^–11 m²·s^–1, while it was 50.61 × 10^–11 m²·s^–1 with the addition of 35 wt-% IL. The decreasing trend of the self-diffusion coefficient of CO₂ was in accordance with the decreasing trend of FFV. Cheng et al. also reported that the FFV had a positive effect on the capture of nonpolar solutes [48]. After that, the diffusivity of CO₂ gradually increased with increasing IL concentration. For example, the self-diffusion coefficients of CO₂ were 75 × 10^–11 and 90 × 10^–11 m²·s^–1 at 40 and 50 wt-% IL, respectively. In addition, the CO₂ diffused faster in pure IL than in pure PI. This simulated result was consistent with the reported experimental phenomena [10]. Therefore, it could be concluded that the diffusion of CO₂ was dependent on the voids in the composite membrane when the IL concentration was less than 35 wt-%, and the IL provided a blocking effect toward CO₂ diffusion. However, when the concentration of IL was more than 35 wt-%, the diffusion of CO₂ mainly relied on the continuous domains of the IL, and the IL played a role of spreading effect for the transportation of CO₂ in the composite membrane.

Fig.10 Self-diffusion coefficients of the (a) cations and anions of IL and (b) CO₂ in the IL/PI composite systems at different IL concentrations.

Full size|PPT slide

3.2.4 PMF of CO₂

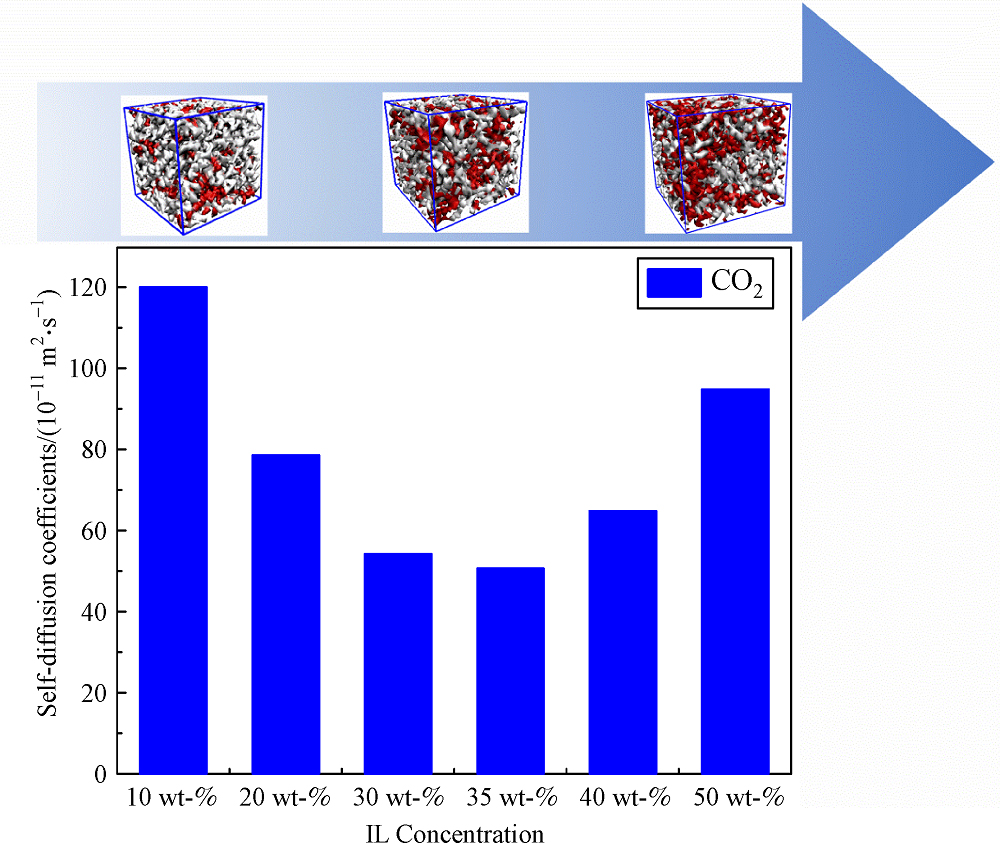
The PMF values of CO₂ in [BMIM][Tf₂N]/PI at different IL concentrations were calculated. The WHAM [29] was used to analyze the sampling results. The simulated histogram for calculating the PMF of CO₂ is displayed in Fig. S4 (cf. ESM). From Fig. S4, it could be found that every histogram was well crossed together, which indicated that the simulated PMF of CO₂ was reliable. Figure 11 shows the PMF of CO₂ in [BMIM][Tf₂N]/PI at different IL concentrations. It was clear that the positions of the lowest PMF of CO₂ for 10, 20, 30, 35, 40 and 50 wt-% IL are at approximately 0.40 nm. However, the first peak positions for PMF at different IL concentrations were different. Therefore, the free energy barrier obtained by the difference between the first valley and peak in the PMF was calculated and was then employed to study many systems [49,50]. The free energy barriers of CO₂ in [BMIM][Tf₂N]/PI with 10, 20, 30, 35, 40 and 50 wt-% IL were 3.68, 3.96, 4.36, 4.41, 4.32 and 4.30 kJ·mol^–1, respectively. When the IL concentration was lower than 35 wt-%, the order of the free energy barrier for CO₂ at different IL concentrations was 10 wt-% IL<20 wt-% IL<30 wt-% IL<35 wt-% IL. However, when the IL concentration was higher than 35 wt-%, the sequence of the free energy barrier for CO₂ at different IL concentrations was 50 wt-% IL<40 wt-% IL. It is well known that when the free energy barrier is low, gas molecules will need less energy and can be more easily transported in the membrane. Therefore, it could be concluded that when the IL concentration was less than 35 wt-%, the sequence of CO₂ passing through the IL/PI membrane at different IL concentrations was 10 wt-% IL>20 wt-% IL>30 wt-% IL>35 wt-% IL. However, when the IL concentration was more than 35 wt-%, CO₂ was easier to diffuse in the IL/PI system at 50 wt-% IL than that at 40 wt-% IL.

Fig.11 PMF values of CO₂ in the [BMIM][Tf₂N]/PI composite systems at different IL concentrations.

Full size|PPT slide

4 Conclusions

In this work, the systems of CO₂ with [BMIM][Tf₂N]/PI at different IL concentrations were studied by all-atom MD simulations. The concentrations of IL were 0, 10, 20, 30, 35, 40, 50 and 100 wt-%. It was found that the ILs were scattered in the [BMIM][Tf₂N]/PI system at low concentrations. However, the scattered IL regions tended to connect with each other and gradually form continuous channels with increasing IL concentration, which suggested that the ILs were well-dispersed in the [BMIM][Tf₂N]/PI composite system. The RDF and hydrogen bond number results showed that PI had a stronger interaction with cations than anions. The hydrogen bond numbers of PI-cation and PI-anion gradually increased as the IL concentration increased. However, the hydrogen bond numbers among PI chains decreased with increasing IL concentrations, which could be attributed to the shielding effect of the IL; thus, the quick transportation of CO₂ was facilitated.

Furthermore, the dynamic properties and interactions of CO₂ in the IL/PI composite systems were investigated. The RDFs and interaction energies suggested that the interaction between PI and CO₂ was stronger than that between IL and CO₂, and the O atoms of PI were the main sites for attracting CO₂. The interaction energy of PI-CO₂ decreased, while the interaction energy of IL-CO₂ increased with increasing IL concentration. Moreover, the self-diffusion coefficients and PMF values were calculated. The self-diffusion coefficients of the cations and anions in the IL increased with increasing IL concentration, which was beneficial for the diffusion of CO₂. However, the composite system with 35 wt-% IL was the turning point for the self-diffusion coefficient of CO₂. The self-diffusion coefficient of CO₂ first decreased and then increased. The decrease in the self-diffusion coefficient of CO₂ was attributed to the decreased FFV of the IL/PI composite system, and the IL exhibited a blocking effect. The increase in the self-diffusion coefficient of CO₂ originated from the formation of continuous IL domains at high IL concentrations, and the IL played a role of spreading effect. These studies provide a molecular level understanding of CO₂ capture in an IL/polymer membrane and also provide useful information for designing new membranes.

Acknowledgments

This work was supported by the National Key R & D Program of China (Grant No. 2018YFB0605802), the National Natural Science Foundation of China (Grant Nos. 51674234, 21978293, U1704251), “Transformational Technologies for Clean Energy and Demonstration”, Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA 21030500), NSFC-NRCT joint project (Grant No. 51661145012), and CAS Pioneer Hundred Talents Program.

Electronic Supplementary Material

Supplementary material is available in the online version of this article at https://dx.doi.org/10.1007/s11705-020-2009-7 and is accessible for authorized users.

References

1 Deng L Y, Kvamsdal H. CO₂ capture: challenges and opportunities. Green Energy & Environment, 2016, 1(3): 179–179

2 Quale S, Rohling V. The European carbon dioxide capture and storage laboratory infrastructure (ECCSEL). Green Energy & Environment, 2016, 1(3): 180–194

3 Boothandford M E, Abanades J C, Anthony E J, Blunt M J, Brandani S, Dowell N M, Fernandez J R, Ferrari M, Gross R, Hallett J P. Carbon capture and storage update. Energy & Environmental Science, 2014, 7(1): 130–189

4 Vitillo J G, Smit B, Gagliardi L. Introduction: carbon capture and separation. Chemical Reviews, 2017, 117(14): 9521–9523

5 Li M, Jiang X, He G. Application of membrane separation technology in postcombustion carbon dioxide capture process. Frontiers of Chemical Science and Engineering, 2014, 8(2): 233–239

6 Kanehashi S, Scholes C A. Perspective of mixed matrix membranes for carbon capture. Frontiers of Chemical Science and Engineering, 2020, 14(3): 1–10

7 Pandiyan S, Brown D, Neyertz S, van der Vegt N F A. Carbon dioxide solubility in three fluorinated polyimides studied by molecular dynamics simulations. Macromolecules, 2010, 43(5): 2605–2621

8 Tong H, Hu C, Yang S, Ma Y, Guo H, Fan L. Preparation of fluorinated polyimides with bulky structure and their gas separation performance correlated with microstructure. Polymer, 2015, 69: 138–147

9 O’Harra K E, Kammakakam I, Devriese E M, Noll D M, Bara J E, Jackson E M. Synthesis and performance of 6FDA-based polyimide-ionenes and composites with ionic liquids as gas separation membranes. Membranes, 2019, 9(7): 79–96

10 Kanehashi S, Kishida M, Kidesaki T, Shindo R, Sato S, Miyakoshi T, Nagai K. CO₂ separation properties of a glassy aromatic polyimide composite membranes containing high-content 1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ionic liquid. Journal of Membrane Science, 2013, 430: 211–222

11 Weigelt F, Escorihuela S, Descalzo A, Tena A, Escolastico S, Shishatskiy S, Serra J M, Brinkmann T. Novel polymeric thin-film composite membranes for high-temperature gas separations. Membranes, 2019, 9(4): 51–64

12 Zhang X, Feng H, Liu Z, Wang W, Maginn E J. Absorption of CO₂ in the ionic liquid 1-n-hexyl-3-methylimidazolium tris(pentafluoroethyl)trifluorophosphate ([Hmim][FEP]): a molecular view by computer simulations. Journal of Physical Chemistry B, 2009, 113(21): 7591–7598

13 Zhang X, Liu Z, Wang W. Screening of ionic liquids to capture CO₂ by COSMO-RS and experiments. AIChE Journal. American Institute of Chemical Engineers, 2008, 54(10): 2717–2728

14 Haghtalab A, Shojaeian A. High pressure measurement and thermodynamic modelling of the solubility of carbon dioxide in N-methyldiethanolamine and 1-butyl-3-methylimidazolium acetate mixture. Journal of Chemical Thermodynamics, 2015, 81: 237–244

15 Jalili A H, Mehdizadeh A, Shokouhi M, Sakhaeinia H, Taghikhani V. Solubility of CO₂ in 1-(2-hydroxyethyl)-3-methylimidazolium ionic liquids with different anions. Journal of Chemical Thermodynamics, 2010, 42(6): 787–791

16 Lei X, Xu Y, Zhu L, Wang X. Highly efficient and reversible CO₂ capture through 1,1,3,3-tetramethylguanidinium imidazole ionic liquid. RSC Advances, 2014, 4(14): 7052–7054

17 Wang J, Zeng S, Huo F, Shang D, He H, Bai L, Zhang X, Li J. Metal chloride anion-based ionic liquids for efficient separation of NH₃. Journal of Cleaner Production, 2019, 206: 661–669

18 Li P, Coleman M R. Synthesis of room temperature ionic liquids based random copolyimides for gas separation applications. European Polymer Journal, 2013, 49(2): 482–491

19 Mittenthal M S, Flowers B S, Bara J E, Whitley J W, Spear S K, Roveda J D, Wallace D A, Shannon M S, Holler R, Martens R, Daly D T. Ionic polyimides: hybrid polymer architectures and composites with ionic liquids for advanced gas separation membranes. Industrial & Engineering Chemistry Research, 2017, 56(17): 5055–5069

20 Ito A, Yasuda T, Ma X, Watanabe M. Sulfonated polyimide/ionic liquid composite membranes for carbon dioxide separation. Polymer Journal, 2017, 49(9): 671–676

21 Monteiro B, Nabais A R, Almeida Paz F A, Cabrita L, Branco L C, Marrucho I M, Neves L A, Pereira C C L. Membranes with a low loading of metal-organic framework-supported ionic liquids for CO₂/N₂ separation in CO₂ capture. Energy Technology (Weinheim), 2017, 5(12): 2158–2162

22 Balçık M, Ahunbay M G. Prediction of CO₂-induced plasticization pressure in polyimides via atomistic simulations. Journal of Membrane Science, 2018, 547: 146–155

23 Zhang X, Liu Z, Liu X. Understanding the interactions between tris(pentafluoroethyl)-trifluorophosphate-based ionic liquid and small molecules from molecular dynamics simulation. Science China. Chemistry, 2012, 55(8): 1557–1565

24 Lourenco T C, Coelho M F, Ramalho T C, Van Der Spoel D, Costa L T. Insights on the solubility of CO₂ in 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide from the microscopic point of view. Environmental Science & Technology, 2013, 47(13): 7421–7429

25 Abedini A, Crabtree E, Bara J E, Turner C H. Molecular simulation of ionic polyimides and composites with ionic liquids as gas-separation membranes. Langmuir, 2017, 33(42): 11377–11389

26 Spoel D V D, Lindahl E, Hess B, Groenhof G, Berendsen H J C. GROMACS: fast, flexible, and free. Journal of Computational Chemistry, 2005, 26(16): 1701–1718

27 Hess B, Kutzner C, Van Der Spoel D, Lindahl E. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. Journal of Chemical Theory and Computation, 2008, 4(3): 435–447

28 Liu Z P, Huang S P, Wang W C. A refined force field for molecular simulation of imidazolium-based ionic liquids. Journal of Physical Chemistry B, 2004, 108(34): 12978–12989

29 Lopes J N C, Pádua A A H. Molecular force field for ionic liquids composed of triflate or bistriflylimide anions. Journal of Physical Chemistry B, 2004, 108(43): 16893–16898

30 Tanis I, Brown D, Neyertz S J, Heck R, Mercier R. A comparison of homopolymer and block copolymer structure in 6FDA-based polyimides. Physical Chemistry Chemical Physics, 2014, 16(42): 23044–23055

31 Wang J, Wolf R M, Caldwell J W, Kollman P A, Case D A. Development and testing of a general amber force field. Journal of Computational Chemistry, 2004, 25(9): 1157–1174

32 Martínez L, Andrade R, Birgin E G, Martínez J M. PACKMOL: a package for building initial configurations for molecular dynamics simulations. Journal of Computational Chemistry, 2009, 30(13): 2157–2164

33 Essmann U, Perera L, Berkowitz M L, Darden T, Lee H, Pedersen L G. A smooth particle mesh Ewald method. Journal of Chemical Physics, 1995, 103(19): 8577–8593

34 Hess B, Bekker H, Berendsen H J C, Fraaije J G E M. LINCS: a linear constraint solver for molecular simulations. Journal of Chemical Theory and Computation, 1997, 18(12): 1463–1472

35 Parrinello M, Rahman A. Polymorphic transitions in single crystals: a new molecular dynamics method. Journal of Applied Physics, 1981, 52(12): 7182–7190

36 Braga C, Travis K P. A configurational temperature Nosé-Hoover thermostat. Journal of Computational Physics, 2005, 123(13): 134101–134116

37 Shi W, Maginn E J. Atomistic simulation of the absorption of carbon dioxide and water in the ionic liquid 1-n-hexyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide [hmim] [Tf2N]. Journal of Physical Chemistry B, 2008, 112(7): 2045–2055

38 Torrie G M, Valleau J P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: umbrella sampling. Journal of Computational Physics, 1977, 23(2): 187–199

39 Kumar S, Rosenberg J M, Bouzida D, Swendsen R H, Kollman P A. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. Journal of Computational Chemistry, 1992, 13(8): 1011–1021

40 Wang Y, Wang C, Zhang Y, Huo F, He H, Zhang S. Molecular insights into the regulatable interfacial property and flow behavior of confined ionic liquids in graphene nanochannels. Small, 2019, 15(29): 1804508–1804518

41 Sun D L, Zhou J. Ionic liquid confined in nafion: toward molecular-level understanding. AIChE Journal. American Institute of Chemical Engineers, 2013, 59(7): 2630–2639

42 Song T, Zhang X, Li Y, Jiang K, Zhang S, Cui X, Bai L. Separation efficiency of CO₂ in ionic liquids/poly(vinylidene fluoride) composite membrane: a molecular dynamics study. Industrial & Engineering Chemistry Research, 2019, 58(16): 6887–6898

43 Zhang X, Huo F, Liu X, Dong K, He H, Yao X, Zhang S. Influence of microstructure and interaction on viscosity of ionic liquids. Industrial & Engineering Chemistry Research, 2015, 54(13): 3505–3514

44 Dong K, Liu X, Dong H, Zhang X, Zhang S. Multiscale studies on ionic liquids. Chemical Reviews, 2017, 117(10): 6636–6695

45 Bondi A. Van der Waals volumes and radii. Journal of Physical Chemistry, 1964, 68(3): 441–451

46 Lee W M. Selection of barrier materials from molecular-structure. Polymer Engineering and Science, 1980, 20(1): 65–69

47 Tanaka K, Kita H, Okano M, Okamoto K. Permeability and permselectivity of gases in fluorinated and non-fluorinated polyimides. Polymer, 1992, 33(3): 585–592

48 Cheng H, Zhang J, Qi Z. Effects of interaction with sulphur compounds and free volume in imidazolium-based ionic liquid on desulphurisation: a molecular dynamics study. Molecular Simulation, 2018, 44(1): 55–62

49 Cantley L, Swett J L, Lloyd D, Cullen D A, Zhou K, Bedworth P V, Heise S, Rondinone A J, Xu Z P, Sinton S, Bunch J S. Voltage gated inter-cation selective ion channels from graphene nanopores. Nanoscale, 2019, 11(20): 9856–9861

50 Zhou K, Xu Z P. Ion permeability and selectivity in composite nanochannels: engineering through the end effects. Journal of Physical Chemistry C, 2020, 124(8): 4890–4898