Energy distribution between liquid hydrogen and liquid oxygen temperatures in a Stirling/pulse tube refrigerator

Abstract

A two-stage gas-coupled Stirling/pulse tube refrigerator (SPR), whose first and second stages respectively involve Stirling and pulse tube refrigeration cycles, is a very promising spaceborne refrigerator. The SPR has many advantages, such as a compact structure, high reliability, and high performance, and is expected to become an essential refrigerator for space applications. In research regarding gas-coupled regenerative refrigerator, the energy flow distribution between the two stages, and optimal phase difference between the pressure wave and volume flow, are two critical parameters that could widely influence refrigerator performance. The effects of displacer displacement on the pressure wave, phase difference, acoustic power distribution, and inter-stage cooling capacity shift of the SPR have been investigated experimentally. Notably, to obtain the maximum first-stage cooling capacity, an inflection point in displacement exists. When the displacer displacement is larger than the inflection point, the cooling capacity could be distributed between the first and second stages. In the present study, an SPR was designed and manufactured to work between the liquid hydrogen and liquid oxygen temperatures, which can be used to cool small-scale zero boil-off systems and space detectors. Under appropriate displacer displacement, the SPR can reach a no-load cooling temperature of 15.4 K and obtain 2.6 W cooling capacity at 70 K plus 0.1 W cooling capacity at 20 K with 160 W compressor input electric power.

Key words： Stirling/pulse tube refrigerator; displacer displacement; space application; phase shift; energy distribution

1 Introduction

A low-temperature environment is essential for space detectors to reduce thermal noise and background radiation while improving the accuracy and breadth of detection [1–3]. Cryogenic propellants like liquid hydrogen and liquid oxygen are essential for long-duration missions. The substantial boil-off losses due to low storage temperatures can be eliminated by high-performance refrigerators [4]. Considering the heat transfer loss, the cooling temperatures of liquid hydrogen and liquid oxygen are respectively selected as 20 and 70 K. To date, Stirling refrigerators and pulse tube refrigerators have been widely applied in space explorations [5, 6]. The refrigerator normally requires a multi-stage structure for cooling temperatures below 20 K. However, the Stirling and pulse tube refrigerators have limitations owing to their structural characteristics [7–14]. Thus, by avoiding the disadvantages of Stirling and pulse tube refrigerators and combining their advantages, the Stirling/pulse tube refrigerator (SPR) can achieve the space requirements for high efficiency, long lifetime, and compactness.

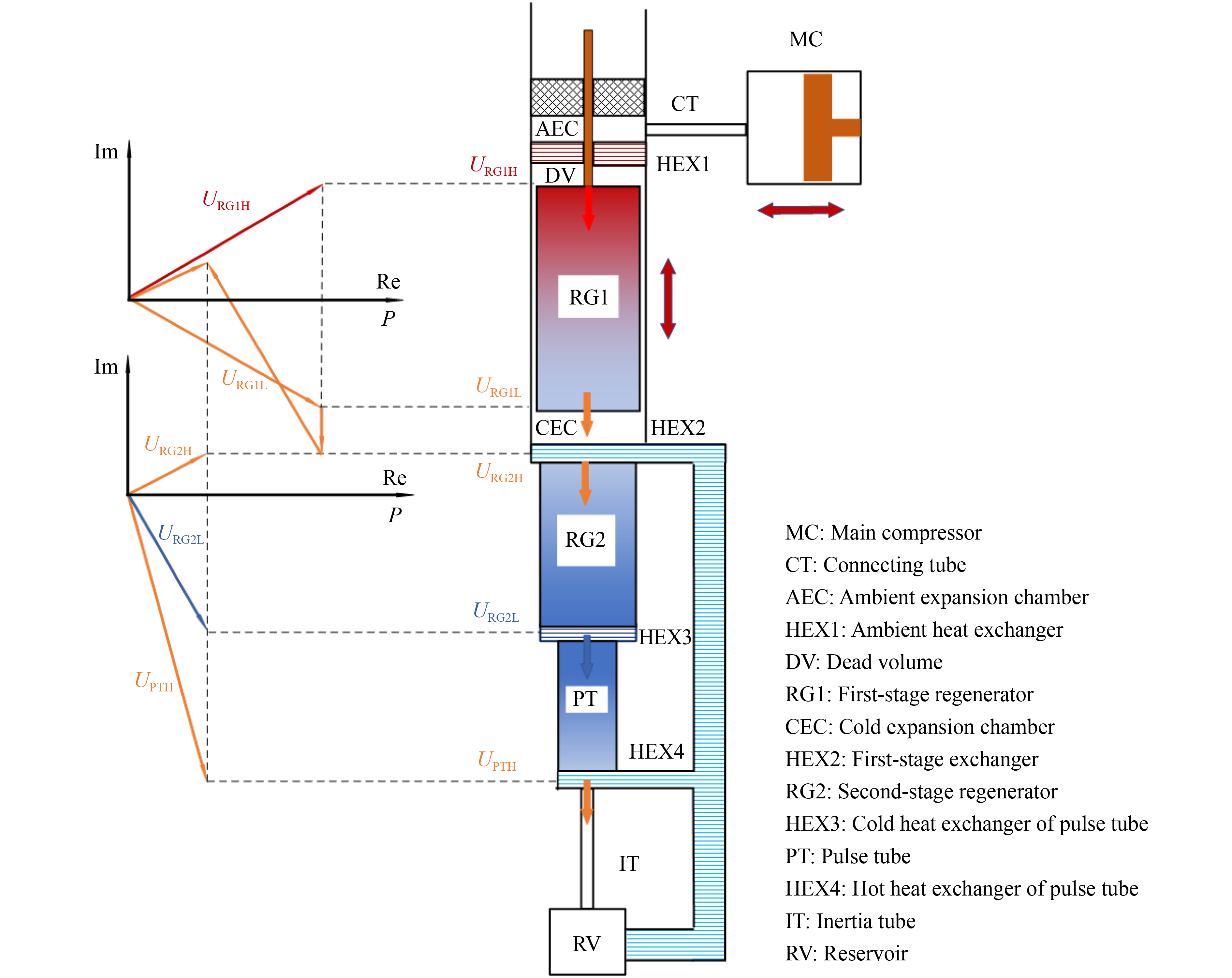
Interestingly, the SPR proposed by Raytheon in 1999 [15–17] has been studied for over 20 years. To satisfy the requirements of different working temperatures and cooling capacities, Raytheon has developed three types of SPR as follows: High Capacity Raytheon Stirling/Pulse Tube 2-Stage (HC-RSP2) working at 35 K/85 K, Mid Capacity Raytheon Stirling/Pulse Tube 2-Stage (MC-RSP2) working at 58 K/110 K, and Low Temperature Raytheon Stirling/Pulse Tube 2-Stage (LT-RSP2) working at 10 K/55 K [18]. In 2014, Raytheon designed a Compact Inline Stirling/pulse tube two-stage refrigerator (CI-RSP2), which can provide 4.5 W power at 70 K plus 0.25 W power at 20 K with an input power of 208 W [19]. During the design of the SPR, Raytheon proposed that the SPR has unique thermodynamic advantages in its ability to shift cooling capacity between its two stages through the dynamic adjustment of the first Stirling stage displacer phase, thereby giving the SPR a degree of working flexibility. Further, Guo et al. developed an ideal thermodynamic model of SPR to analyze the effect of the displacer phase on cooling capacity shift [20]. Moreover, Chao et al. proposed five different working states of SPR, and also established the boundary range [21]. In 2019, Liu et al. designed an SPR working at 35 K/85 K, and the cooling capacity of the SPR was 1.16 W at 35 K plus 7.25 W at 85 K with an input power of 234.6 W [22]. In 2021, Liu et al. proposed a theoretical model considering the significant factors affecting the overall performance, as well as a numerical model of the SPR [23, 24].

An SPR has a unique ability to shift its cooling capacity between its first and second stages by actively controlling the displacer, which is the principal phase shifter. The inter-stage cooling capacity shift allows the SPR to adapt efficiently to the changing requirements without requiring trim heaters. Hence, the loss of overall efficiency is minimal during operation load shift. However, previous research mainly focused on the cooling capacity shift by adjusting the displacer phase between the compressor piston and displacer, ignoring the impact of the displacer displacement. The displacer displacement affects two parameters of the SPR, which are the phase shift and energy distribution. The mechanism of the effects has been discussed based on theoretical analysis, and has been verified by experiment. An SPR was tested under optimum displacer displacement, and the experimental results agreed well with the theoretical analysis and numerical simulation.

2 Experiment system and performance

2.1 Structure of the SPR

Fig.1 is a schematic of the SPR. The two-stage SPR is gas-coupled and driven by a main linear compressor. The first Stirling stage includes the main compressor (MC), connecting tube (CT), ambient expansion chamber (AEC), ambient heat exchanger (HEX1), dead volume (DV), cold expansion chamber (CEC), and a displacer filled with stainless steel mesh as the first-stage regenerator (RG1). The second pulse tube stage includes the second regenerator (RG2), pulse tube (PT), low-temperature inertance tube (IT), and gas reservoir (RV). The second stage adopts a coaxial pulse tube, which is instrumental in improving the compactness. In the first stage, the working gas is compressed by the main linear compressor piston. Thereafter, the gas flows across the first-stage regenerator into the first-stage expansion space, and is simultaneously precooled. The working gas expands in the expansion chamber to realize a first-stage cooling capacity, thereby substantially reducing the volume flow amplitude and acoustic power at the outlet of the expansion chamber. Subsequently, the working gas flows across the first-stage exchanger into the second-stage pulse tube. The phase diagram on the left side of Fig.1 was obtained using a thermoacoustic analytical model, which is based on ideal assumptions. The phase diagram shows that the phase shift and energy distribution of the SPR occur in the cold expansion chamber, where the amplitude and phase of the volume flow change significantly. The influence of the displacer displacement on the phase difference and energy distribution is discussed separately below. The phasors U_{\mathrm{R}\mathrm{G}1\mathrm{H}}, U_{\mathrm{R}\mathrm{G}1\mathrm{L}}, U_{\mathrm{R}\mathrm{G}2\mathrm{H}}, U_{\mathrm{R}\mathrm{G}2\mathrm{L}}, and U_{\mathrm{P}\mathrm{T}\mathrm{H}} denote the volume flows at the end of the regenerator and pulse tube, as indicated by the nomenclature.

Fig.1 Schematic and phase diagram of the SPR.

Full size|PPT slide

2.2 Experiment setup and structure dimensions

A 20 K/70 K SPR was designed, manufactured, and tested. To investigate the effect of displacer displacement on phase difference and energy distribution, the maximum displacement of the first-stage displacer was designed to reach 4 mm (from the equilibrium position to maximum value), which can be actively controlled by the expander motor. The piston diameter of the main linear compressor is 35 mm, and the maximum displacement is 5 mm (from the equilibrium position to the maximum value). The displacer phase between the displacer and the compressor piston can be actively controlled. As shown in Fig.2, the ambient heat exchanger is connected to the compressor through the connecting tube. The first Stirling and second pulse tube stages are gas coupled through the cold expansion chamber. The second pulse tube is coaxial, using a low-temperature inertance tube and gas reservoir as the phase shifter. The gas reservoir adopts an annular structure precooled by the first Stirling stage through the first-stage heat exchanger. The main parameters of the 20 K/70 K SPR are listed in Tab.1.

Tab.1 Main structure dimensions

Name	First-stage	Second-stage
Regenerator inner diameter	34 mm	21.2 mm
Regenerator length	63 mm	44 mm
Pulse tube outer diameter	–	7.9 mm
Pulse tube length	–	58 mm
Reservoir	–	150 mL
Stainless steel mesh	350#SS304	500#SS304

Fig.2 Photograph of the 20 K/70 K SPR without inertance tube, gas reservoir, compressor, and connecting tube.

Full size|PPT slide

A one-dimensional numerical model was built to study the impact of the displacer displacement. The numerical simulation was based on the energy conservation equation, continuity equation, momentum equation, and experimental formulas, considering the flow resistance, non-ideal heat transfer loss, axial heat conduction loss, and radiation loss. The pressure wave, volume flow, and temperature fluctuation at the end of each node were definite. The numerical model of the SPR was based on previous studies of our research group and was verified experimentally [23]. The one-dimensional conservation of mass, momentum, and energy equations are shown.

(1)\frac{\mathrm{\partial }\rho A_{\mathrm{f}}}{\mathrm{\partial }t}+\frac{\mathrm{\partial }\rho u{A}_{\mathrm{f}}}{\mathrm{\partial }x}=0,

(2)\frac{\mathrm{\partial }\rho u{A}_{\mathrm{f}}}{\mathrm{\partial }t}+\frac{\mathrm{\partial }u\rho u{A}_{\mathrm{f}}}{\mathrm{\partial }x}+\frac{\mathrm{\partial }P}{\mathrm{\partial }x}{A}_{\mathrm{f}}+ \frac{f}{d_{\mathrm{h}}}\frac{\rho u\left|u\right|}{2}{A}_{\mathrm{f}}=0,

(3)\frac{\mathrm{\partial }\rho e{A}_{\mathrm{f}}}{\mathrm{\partial }t}+P\frac{\mathrm{\partial }{A}_{\mathrm{f}}}{\mathrm{\partial }t}+\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(u\rho e{A}_{\mathrm{f}}+uP{A}_{\mathrm{f}}+q\right)-Q_{\mathrm{W}}=0.

The friction factor of the stainless-steel mesh is expressed as

(4)f=\frac{129}{Re}+2.91{Re}^{-0.103}.

Fig.3 shows a diagram of the experimental apparatus. The SPR is driven by the main compressor with an operating frequency of 40 Hz. Two calibrated linear variable differential transformer (LVDT) displacement transducers are applied to measure the vector amplitude and phase of the compressor piston and displacer. A pressure sensor is used to measure the pressure wave between the main compressor and cold finger. A Cernox thermometer is installed at the second-stage cold end heat exchanger to measure the second-stage temperature and is suitable for temperatures below 30 K. Three PT100 Platinum resistance temperature sensors are separately installed in the first-stage exchanger, inertance tube, and gas reservoir. Two thermal resistances are anchored to the two-stage heat exchangers as the thermal load. The temperature uncertainty is analyzed by considering the second-stage cooling temperature as 20 K as an example. The maximum uncertainty of the temperature measurement can be expressed as

Fig.3 Schematic diagram of the SPR measuring system.

Full size|PPT slide

(5)\delta =\sqrt{{{\delta }_1}^2+{{\delta }_2}^2+{{\delta }_3}^2}=15.67\mathrm{m}\mathrm{K},

where {\delta }_1, {\delta }_2, {\delta }_3 are the calibration error, instrument error, and random error, which are \pm 8 \mathrm{m}\mathrm{K}, \pm 3.1 \mathrm{m}\mathrm{K}, and \pm 13.11 \mathrm{m}\mathrm{K}, respectively. The uncertainties of the temperature, pressure, displacement, and phase measurements are listed in Tab.2.

Tab.2 Measurement parameters and uncertainty

Type of measurement parameters	Uncertainty
Temperature of the second cold end	15.67 mK
Pressure	0.5%
Displacement	0.3%
Phase	2%

2.3 Validation of the performance of the SPR working at 20 K/70 K by experiment

Fig.4 shows the cooling capacity with different displacer phase {\theta }_{\mathrm{d}} and input electric power. With an input electric power of 160 W and a displacer phase of 70°, the SPR achieves a cooling capacity of 0.1 W at 20 K plus 2.6 W at 70 K. As shown in Fig.4, under certain conditions, the displacer phase θ_d would actively shift the cooling capacity of the two stages. Under the 160 W input electric power, following the displacer phase {\theta }_{\mathrm{d}} decreases from 80° to 60°, the first-stage cooling capacity decreases from 3.05 to 1.16 W, and the second-stage cooling capacity increases from 0.06 to 0.16 W. The trend of the experimental data with different displacer phases is consistent with the thermoacoustic model established by Guo et al. [20] and experimental data measured by Raytheon [6, 15, 17].

Fig.4 Cooling capacities of the two stages.

Full size|PPT slide

As shown by the solid lines in Fig.5, for an average pressure of 2.15 MPa, frequency of 40 Hz, and displacer displacement of 3.0 mm, the no-load second temperature is 15.4 K, and the first-stage temperature is 55.4 K. Additionally, it takes approximately 5 h to stabilize temperature. Furthermore, when the displacer displacement is only 1 mm, which is less than the appropriate value, the improper energy distribution and phase difference deteriorate the absolute performance of the machine. As shown by the dotted lines in Fig.5, the two stages could not achieve the desired objective temperatures with a displacer displacement of 1 mm. The cold mass of the first stage is large because this stage is required to precool the entire second stage, and has a low cooling capacity. Thus, the first-stage cooling rate was found to be very slow, and it took approximately 10 h to reach stability. The experimental results show that it’s necessary to determine the optimum displacer displacement to improve the overall performance of the machine.

Fig.5 Cooling-down curves of the SPR.

Full size|PPT slide

3 Results and discussion

3.1 Effect of the displacer displacement on phase shift

3.1.1 The pressure wave

The displacements of the compressor piston and displacer are expressed as

(6)X_{\mathrm{c}}= \left|X_{\mathrm{c}}\right|\mathrm{c}\mathrm{o} \mathrm{s}\left(\omega t\right)=\mathrm{R} \mathrm{e}\left[{\mathit{X}}_{\mathbf{c}}{e}^{\mathrm{i}\omega t}\right],

(7)X_{\mathrm{d}}= \left|X_{\mathrm{d}}\right|\mathrm{c}\mathrm{o} \mathrm{s}\left(\omega t+{\theta }_{\mathrm{d}}\right)=\mathrm{R}\mathrm{e} \left[{\mathit{X}}_{\mathbf{d}}{e}^{\mathrm{i}\omega t}\right].

The relationship between the pressure wave and movement of the two moving parts (compressor piston and displacer) is expressed as follows [24]:

(8)\mathit{p}={\mathit{a}}_{\mathbf{1}}{\mathit{X}}_{\mathbf{c}}+ {\mathit{a}}_{\mathbf{2}}{\mathit{X}}_{\mathbf{d}},

where {\mathit{a}}_{\mathbf{1}} and {\mathit{a}}_{\mathbf{2}} are phasor constants, which are respectively related to the structural and working parameters of the SPR. The phasor constants {\mathit{a}}_{\mathbf{1}} and {\mathit{a}}_{\mathbf{2}} are calculated using Ref. [24].

For both stages to obtain a cooling capacity, the displacer phase {\theta }_{\mathrm{d}} should be ahead of the compressor piston. Meanwhile, the pressure phase should lie between the phase of the compressor piston and the displacer. If the pressure phase is greater than the displacer phase, the first stage of the SPR would generate heat instead of a cooling effect [20]. Fig.6 shows the experimental amplitude and pressure phase in the main compressor chamber. The pressure phase is between the displacer phase of 65° and compressor piston of 0°, as shown in Fig.6, which is necessary for the SRP to obtain the cooling capacity at both stages based on the theoretical analysis. The amplitude and phase of the pressure increase with an increase in the displacer displacement. When the displacement of the main compressor is 4 mm, with an increase in the displacer displacement from 2 to 2.5 mm, the amplitude of the pressure increases from 0.134 to 0.148 MPa, and the phase of the pressure increases from 53.4° to 55.6°. This is because according to Eq. (3), as the displacer displacement increases, the pressure phase approaches the displacer phase, which is ahead of the phase of the compressor piston.

Fig.6 Amplitude and phase of the pressure with different displacer displacements.

Full size|PPT slide

3.1.2 The axial distribution of the phase difference

Fig.7 shows the axial distribution of the phase difference with varying displacer displacements calculated using the numerical simulation. The phase difference in the ambient expansion chamber and dead volume spontaneously increases owing to the empty and variable volumes. The phase difference in the cold expansion chamber rapidly decreases because the empty volume is far less than that of the ambient expansion chamber and the phase of the variable volume is opposite to that of the ambient expansion chamber. In the first- and second-stage regenerators, the phase difference increases owing to the empty volume, flow resistance, and axial temperature gradient. In heat exchangers, the empty volume and flow resistance are small, and thus, the phase difference slightly deviates. In the pulse tube, the phase difference quickly increases because of the empty volume and the temperature gradient.

Fig.7 Axial distribution of the phase difference.

Full size|PPT slide

The phase difference in the first stage increases slightly when the displacer displacement increases, and the trend is highly consistent with the experimental pressure phase shown in Fig.6. When the displacer displacement increases from 2 to 2.8 mm, the phase difference at the hot end of RG1 increases from −10.2° to 9.2°, and the phase difference at the cold end of the RG1 increases from 45.4° to 57.5°. This implies that with an increase in displacer displacement, the phase difference at the middle point of the first-stage regenerator increasingly deviates from the zero point, indicating that the efficiency of the regenerator is decreasing [25].

As the displacer displacement increases from 2 to 2.8 mm, the phase difference at the inlet of the second stage varies from −64.3° to −62.5°, which shows that the phase difference at this stage has a negligible contribution toward the displacer displacement. This is attributed to the empty volume of the entire second stage, including the regenerator, pulse tube, heat exchangers, inertance tube, and gas reservoir, which can be regarded as a part of the cold expansion chamber; therefore, the influence of the relatively small cold expansion volume change on the second-stage inlet phase difference is minimal. In contrast, the phase difference in the second stage is mainly determined by the second-stage phase shifter (inertance tube and gas reservoir).

3.2 Effect of the displacer displacement on energy distribution

3.2.1 The acoustic power

The volume of the compressor space is expressed as

(9)V_{\mathrm{c}}= V_{\mathrm{c}\mathrm{m}}+\frac{1}{2}{A}_{\mathrm{c}}\left|X_{\mathrm{c}}\right|\left(1-\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t\right)\right).

The acoustic power in the compressor space is expressed as

(10)W_{\mathrm{c}}= \frac{\omega }{2\text{π}}\propto p\frac{\mathrm{d}{V}_{\mathrm{c}}}{\mathrm{d}t}\mathrm{d} t=\frac{1}{2}\omega A_{\mathrm{c}}\left|X_{\mathrm{c}}\right|\left|p\right| \mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{\mathrm{p}}.

The volume of the displacer space is expressed as

(11)V_{\mathrm{d}}= {V_{\mathrm{d}\mathrm{m}}+\frac{1}{2}A}_{\mathrm{d}}\left|X_{\mathrm{d}}\right|\left(1-\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t+{\theta }_{\mathrm{d}}\right)\right).

The expansion power at the cold end of the displacer is expressed as

(12)W_{\mathrm{d}}= -\frac{\omega }{2\text{π}}\propto p\frac{\mathrm{d}{V}_{\mathrm{d}}}{\mathrm{d}t}\mathrm{d} t=\frac{1}{2}\omega A_{\mathrm{d}}\left|X_{\mathrm{d}}\right|\left|p\right| \mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{d}}-{\theta }_{\mathrm{p}}\right).

The following assumptions are made: both regenerators are ideal, with no pressure drop inside any component and no leakage or friction within the clearance seals. The acoustic power at the inlet of the second stage is expressed as

(13)\begin{array}{rl}{W}_{\mathrm{p}\mathrm{t}}=& \frac{T_{\mathrm{L}1}}{T_{\mathrm{m}}}\left(W_{\mathrm{c}}+W_{\mathrm{d}}\right)-W_{\mathrm{d}}\\ =& \frac{1}{2}\omega \left|p\right|[\frac{T_{\mathrm{L}1}}{T_{\mathrm{m}}}{A}_{\mathrm{c}}\left|X_{\mathrm{c}}\right|\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{\mathrm{p}}\\ & +\left(\frac{T_{\mathrm{L}1}}{T_{\mathrm{m}}}-1\right)A_{\mathrm{d}}\left|X_{\mathrm{d}}\right|\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{d}}-{\theta }_{\mathrm{p}}\right)].\end{array}

The ratio of second-stage acoustic power to the first stage can be expressed as

(14)\epsilon =\frac{W_{\mathrm{p}\mathrm{t}}}{W_{\mathrm{d}}}=\frac{T_{\mathrm{L}1}}{T_{\mathrm{m}}} \frac{\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{\mathrm{p}}}{\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{d}}-{\theta }_{\mathrm{p}}\right)}\alpha +\left(\frac{T_{\mathrm{L}1}}{T_{\mathrm{m}}}-1\right),

where \alpha is the ratio of swept volume of compressor piston to displacer.

In the ideal theoretical model, the acoustic power at the first and second stages is determined by the first stage and ambient temperature, the swept volume of the compressor piston and displacer, the displacer phase, and the pressure phase. In real-world situations, the acoustic power distribution is affected by some additional factors, such as the irreversible losses and non-ideal effects, and should also follow Eqs. (7), (8), and (9).

Fig.8 shows the axial distribution of the acoustic power with different displacer displacements calculated by numerical simulation, and the local enlarged drawing of the cold expansion chamber is shown in the upper right corner. In the ambient expansion chamber, the acoustic power increases because of the recovery of acoustic power by the displacer. In the cold expansion chamber, the acoustic power decreases rapidly owing to the energy generated through displacer expansion. In other components, the acoustic power decreases owing to the flow resistance and temperature gradient.

Fig.8 Axial distribution of acoustic power.

Full size|PPT slide

As shown in Fig.8, the acoustic power in both the first and second stages increases with an increase in displacer displacement. When the displacer displacement increases from 2 to 2.8 mm, the acoustic power at the cold end of the first stage increases from 16 to 20 W, and the acoustic power distributed to the second stage increases from 4.3 to 6.5 W. Meanwhile, the acoustic power distributed to the first stage increases from 11.7 to 13.5 W, meanwhile, the ratio of second-stage acoustic power to the first stage \epsilon increases from 0.37 to 0.48, which implies that with the increase of the displacer displacement, more acoustic power is distributed into the second stage.

With an increase in displacer displacement, under similar compressor displacement, the input acoustic power of the compressor increases, implying that the impedance matching between the compressor and cold finger becomes more efficient. When the displacer displacement increases from 2 to 2.8 mm, the acoustic power in the cold finger increases from 66.3 to 83.8 W, and the recycled acoustic power at the ambient expansion chamber (AEC) increases from 12.1 to 16 W, which is larger than the expansion power at the cold end of the displacer since the amplitude of the pressure at AEC is larger than CEC in reality. Since the acoustic power can be recovered efficiently at the first stage, and the recycled acoustic power accounts for approximately 18% of the total input acoustic power, the SPR is more efficient than the pulse tube refrigerator.

3.2.2 The inter-stage cooling capacity shift

The actual cooling capacity is determined not only by the cold end acoustic power, but also by the various losses in the regenerator. The first-stage cooling capacity of SPR is given by

(15){⟨\dot{Q}⟩}_{\mathrm{n}\mathrm{e}\mathrm{t}}=W_{\mathrm{d}}- {⟨\dot{Q}⟩}_{\mathrm{r}\mathrm{e}\mathrm{g}}-{⟨\dot{Q}⟩}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{\_}\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}}-{⟨\dot{Q}⟩}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{\_}\mathrm{s}\mathrm{c}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{n}}-{⟨\dot{Q}⟩}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{\_}\mathrm{g}\mathrm{a}\mathrm{s}},

where W_{\mathrm{d}} is the expansion power at the cold end of the first-stage regenerator, {⟨\dot{Q}⟩}_{\mathrm{r}\mathrm{e}\mathrm{g}} is the irreversible heat exchanger loss at the first-stage regenerator, {⟨\dot{Q}⟩}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{\_}\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}} is the axial conduction loss along the regenerator wall, {⟨\dot{Q}⟩}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{\_}\mathrm{s}\mathrm{c}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{n}} is the axial conduction loss along the regenerator mesh, and {⟨\dot{Q}⟩}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{\_}\mathrm{g}\mathrm{a}\mathrm{s}} is the axial conduction loss along the working gas.

Based on the above analysis of the phase difference in Fig.7, it can be observed that as the displacer displacement increases from 2 to 2.8 mm, the first-stage regenerator efficiency decreases. To fully investigate the losses of the regenerator, the various losses were recalculated using REGEN 3.3, which is widely used to simulate the regenerator. As shown in Fig.9, the maximal loss of the first-stage regenerator is that dissipated by pressure drop due to the flow resistance in the regenerator. With the increase in displacer displacement from 2 to 2.8 mm, the pressure drop loss increases from 9.5 to 13 W because of the increase in volume flow amplitude. The sum of axial conduction loss along the regenerator wall and mesh is approximately 2.7 W, which is mainly determined by the temperature gradient. The sum of the non-ideal heat exchanger and non-ideal gas loss increases from 5.7 to 7.5 W when the displacer displacement increases from 2 to 2.8 mm. The efficiency of the regenerator decreases with an increase in the displacer displacement, which is due to the inappropriate phase difference as shown in Fig.7.

Fig.9 Losses at the first-stage regenerator.

Full size|PPT slide

The performance of the refrigerator in simulation and experiment is shown in Fig.10. It can be observed that the second-stage cooling capacity increases, whereas the first-stage cooling capacity initially increases and decreases thereafter with an increase in the displacer displacement. When the displacer displacement is 2.2 mm, the first-stage cooling capacity obtains the maximum value of the experiment and numerical simulation. The simulation trend is highly consistent with that of the experiment. In experiment under the compressor displacement piston of 4 mm, the first- and second-stage cooling capacities increases from 0.62 to 0.72 W and 30 to 59 mW, respectively, following an increase in the displacer displacement from 2 to 2.2 mm. However, when the displacer displacement increases from 2.2 to 2.5 mm, the first-stage cooling capacity decreases from 0.72 to 0.65 W, and the second-stage cooling capacity increases from 59 to 80 mW.

Fig.10 Comparing cooling capacity between simulation and experiment with different displacer displacement.

Full size|PPT slide

The reason is that based on the above analysis of phase shift and energy distribution, the first-stage expansion energy increases relative to an increase in the displacer displacement. However, the losses of the first-stage regenerator and second-stage precooling also demand increase. The first-stage cooling capacity is a result of comprehensive effects, thus, it would not always increase with an increase in the displacer displacement. Therefore, there is an inflection point at which the maximum first-stage cooling capacity is obtained. Since the acoustic power distributed into the second stage increases and there is little change in the second-stage phase difference, the second-stage cooling capacity increases with an increase in the displacer displacement, although this is limited. With the increase in displacer displacement, the first-stage cooling capacity gradually decreases until the designed first-stage precooling temperature is not maintained, resulting in a reduction in the second-stage cooling capacity.

When the displacer displacement is greater than the inflection point of 2.2 mm, with an increase in the displacer displacement, the cooling capacity can be distributed from the first stage to the second stage, thus, the inter-stage cooling capacity shift by the displacer displacement can be realized. If the cooling requirement of the second stage increases, the SPR can actively increase the displacer displacement to shift the first-stage cooling capacity to the second stage.

3.3 The performance of the SPR with different working parameters and dimensional parameters

3.3.1 Different compressor piston displacements

Fig.11 shows the cooling capacity of the two stages and the relative Carnot efficiency with different compressor pistons and displacer displacements obtained experimentally. The relative Carnot efficiency (rCOP) is calculated as

Fig.11 The two stages’ cooling capacity and rCOP with different displacement of displacer and compressor piston.

Full size|PPT slide

(16)\mathrm{r}\mathrm{C}\mathrm{O}\mathrm{P}={\displaystyle \frac{\left[\left({\displaystyle \frac{T_{\mathrm{H}}-T_{\mathrm{L}1}}{T_{\mathrm{L}1}}}\right)Q_1+\left({\displaystyle \frac{T_{\mathrm{H}}-T_{\mathrm{L}2}}{T_{\mathrm{L}2}}}\right)Q_2\right]}{W}}.

As shown in Fig.11, the inflection points of the displacer displacements obtaining the maximum value of the first-stage cooling capacity are 2.2, 2.4, and 2.5 mm when the displacements of compressor piston are 4, 4.3, and 4.6 mm, respectively. The reason why the inflection points increase with an increase in the compressor piston displacement is that, based on Eq. (9), the ratio of the second-stage acoustic power to the first-stage acoustic power α is determined by the ratio of the swept volume of the compressor piston to the displacer α. Because α increases with an increase in the compressor piston displacement, to maintain a constant α, the displacer displacement is expected to increase.

The rCOP initially increases, and thereafter decreases with an increase in the displacer displacement. The trend is similar to that of the first-stage cooling capacity because the cooling capacity of the first stage is far greater than that of the second stage. The displacer displacements helping achieve the maximum value of rCOP, 3.52%, 5.09%, and 5.90% are 2.3, 2.5, and 2.6 mm, respectively, while the compressor piston displacements are 4.0, 4.3, and 4.6 mm, respectively.

3.3.2 Different lengths of inertance tube

The low-temperature inertance tube and gas reservoir are the phase shifters of the second pulse tube stage. Notably, two different lengths of inertance tube (1.8 and 2.1 m), were tested. Fig.12 shows the two stages’ cooling capacity with different inertance tube lengths and displacer displacements. With an increase in the inertance tube length, the flow resistance increases, causing an increase in the second-stage inlet impedance, resulting in more acoustic power being distributed to the first stage, thus, the first-and second-stage cooling capacities increase and decrease, respectively.

Fig.12 Cooling capacity of the two stages with different inertance tube lengths.

Full size|PPT slide

Fig.12 shows that when the length of the inertance tube increases from 1.8 to 2.1 m, the first-stage cooling capacity increases from 0.96 to 1.39 W, and the second-stage cooling capacity decreases from 0.21 to 0.11 W with a displacer displacement of 2.2 mm. The trend of the two stages cooling capacity is consistent with different lengths of inertance tube. It proves that the inertance tube can also adjust the cooling capacity of the two stages. However, the phase adjustment cannot be actively controlled, and the operation is both trivial and troublesome, which needs to replace the inertance tube with different structural parameters in the vacuum chamber.

4 Conclusions

The impact of displacer displacement in a SPR on the phase shift and energy distribution is discussed. The influence of the displacer displacement on the first-stage phase distribution is greater than that on the second stage. Within limits, more acoustic power enters the first and second stages with an increase in displacer displacement. Consequently, the second-stage cooling capacity increases linearly owing to the greater acoustic power distributed to the second stage. The first-stage cooling capacity initially increases, and thereafter decreases with the increase in displacer displacement. Moreover, there is an inflection point of displacer displacement that helps achieve the maximum first-stage cooling capacity, which is due to a combination of the increases associated with expansion, losses of the first-stage regenerator, and the second-stage precooling demand. Furthermore, when the displacer displacement is greater than the inflection point, it can actively distribute the inter-stage cooling capacity.

An SPR operating between liquid hydrogen and liquid oxygen temperatures was designed. Notably, when stainless steel mesh is applied as the regenerative material in the two-stage regenerator, the SPR can reach a no-load cooling temperature of 15.4 K, and obtains 2.6 W at 70 K plus 0.1 W at 20 K with 160 W compressor input electric power under the appropriate displacer displacement, which can be applied to small-scale zero boil-off systems and space detectors. The effects of displacer displacement with different compressor piston displacements and inertance tube lengths on the SPR performance were investigated. The experiment results are consistent with the theoretical analysis and numerical simulation. The work presented in this paper would aid in the future design of SPR.

5 Notations

A	Area/m2
a1	Phasor constant defined in Eq. (8)
a2	Phasor constant defined in Eq. (8)
dh	Hydraulic diameter/m
f	Friction factor
p	Pressure phasor/Pa
Q1	First-stage cooling capacity/W
Q2	Second-stage cooling capacity/W
Re	Reynolds number
rCOP	Relative Carnot efficiency
T	Temperature/K
t	Time/s
u	Volume flow/(m3·s−1)
URG1H	Volume flow at the hot end of the first-stage regenerator/(m3·s−1)
URG1L	Volume flow at the cold end of the first-stage regenerator/(m3·s−1)
URG2H	Volume flow at the hot end of the second-stage regenerator/(m3·s−1)
URG2L	Volume flow at the cold end of the second-stage regenerator/ (m3·s−1)
UPTH	Volume flow at the hot end of the pulse tube/(m3·s−1)
V	Volume/m3
Vcm	Dead volume of the compressor space/m3
Vdm	Dead volume of the displacer space/m3
W	Work power/W
X	Displacement/m
X	Displacement phasor/m
α	Swept volume ratio between compressor and displacer
δ	Uncertainty
ω	Angular frequency/(deg·s−1)
θ	Phase angle/(° )
ρ	Density/(kg·m−3)
c	Compressor
d	Displacer
L1	The first stage
L2	The second stage
m	Mean value
p	Pressure wave
	Magnitude of phasor
⟨\cdot ⟩	Time average
Re[ ]	Real part
Im[ ]	Imaginary part

Acknowledgements

This work was supported by the Hundred Talents Program of the Chinese Academy of Sciences, the National Natural Science Foundation of China (Grant No. 51806231), and the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB35000000, XDB35040102).

Competing interests

The authors declare that they have no competing interests.

References

1 Bruno C, Giucci S. Cryogenic technology to improve electric thrusters. Acta Astronautica, 2002, 51(12): 855–863

2 RossR G. Aerospace coolers: a 50-year quest for long life cryogenic cooling in space. In: Timmerhaus K D, Reed R P, eds., Cryogenic Engineering: Fifty Years of Progress. New York: Springer, 2007

3 Getie M Z, Lanzetta F, Bégot S. . Reversed regenerative Stirling cycle machine for refrigeration application: a review. International Journal of Refrigeration, 2020, 118: 173–187

4 Plachta D W, Johnson W L, Feller J R. Zero boil-off system testing. Cryogenics, 2016, 74: 88–94

5 Wang B, Gan Z H. A critical review of liquid helium temperature high frequency pulse tube cryocoolers for space applications. Progress in Aerospace Sciences, 2013, 61: 43–70

6 Conrad T, Schaefer B, Bellis L. . Raytheon long life cryocoolers for future space missions. Cryogenics, 2017, 88: 44–50

7 PriceK DKirkconnell C S. Two Stage Hybrid Cryocooler Development. Cryocoolers 12. Boston: Springer US, 2003, 233–239

8 KirkconnellC SPriceK DBarrM C, . A Novel Multi-stage Expander Concept. Cryocoolers 11. Boston: Springer US, 2002, 259–263

9 Yang L W, Thummes G. High frequency two-stage pulse tube cryocooler with base temperature below 20 K. Cryogenics, 2005, 45(2): 155–159

10 Gan Z H, Fan B Y, Wu Y Z. . A two-stage Stirling-type pulse tube cryocooler with a cold inertance tube. Cryogenics, 2010, 50(6–7): 426–431

11 Dietrich M, Thummes G. Two-stage high frequency pulse tube cooler for refrigeration at 25 K. Cryogenics, 2010, 50(4): 281–286

12 Chao Y, Wang B, Li H. . A two-stage thermally-coupled pulse tube cryocooler working at 35 K for space application. Acta Astronautica, 2022, 191: 193–203

13 Liu S, Chen X, Zhang A. . Investigation on phase shifter of a 10 W/70 K inertance pulse tube refrigerator. International Journal of Refrigeration, 2017, 74: 450–457

14 Zhi X, Qiu L, Pfotenhauer J M. . Refrigeration mechanism of the gas parcels in pulse tube cryocoolers under different phase angles. International Journal of Heat and Mass Transfer, 2016, 103: 382–389

15 Kirkconnell C S, Hon R C, Kesler C H. . Raytheon Stirling/pulse tube cryocooler development. AIP Conference Proceedings, 2008, 985(1): 909–916

16 KennethD PCarl S KStepthenC N. Single fluid Stirling pulse tube hybrid expander. US Patent, 6167707: B1, 2001

17 Finch A T, Price K D, Kirkconnell C S. Raytheon Stirling/pulse tube two-stage (RSP2) cryocooler advancements. AIP Conference Proceedings, 2004, 710(1): 1285–1292

18 Hon R C, Kirkconnell C S, Shrago J A. . Raytheon RSP2 cryocooler low temperature testing and design enhancements. AIP Conference Proceedings, 2010, 1218(1): 371–380

19 Schaefer B R, Bellis L, Ellis M J. . Raytheon’s next generation compact inline cryocooler architecture. AIP Conference Proceedings, 2014, 1537(1): 371–377

20 Guo Y, Chao Y, Wang B. . The thermodynamic characteristics of a Stirling/pulse tube hybrid cryocooler. Cryogenics, 2018, 96: 133–143

21 Chao Y, Guo Y, Wang Y. . Thermodynamic analysis of the working states of the Stirling/pulse tube hybrid cryocooler. Applied Thermal Engineering, 2020, 170: 115024

22 Liu B, Jiang Z, Ying K. . A high efficiency Stirling/pulse tube hybrid cryocooler operating at 35 K/85 K. Cryogenics, 2019, 101: 137–140

23 Liu B, Jiang Z, Ying K. . Numerical and experimental study on a Stirling/pulse tube hybrid refrigerator operating around 30 K. International Journal of Refrigeration, 2021, 123: 34–44

24 Liu B, Jiang Z, Ying K. . Theoretical model of a Stirling/pulse tube hybrid refrigerator and its verification. Applied Thermal Engineering, 2021, 189: 116587

25 RadebaughR. Development of the pulse tube refrigerator as an efficient and reliable cryocooler. Institute of Refrigeration Proceedings, 2000