Active-reactive power scheduling of integrated electricity-gas network with multi-microgrids

Abstract

Advances in natural gas-fired technologies have deepened the coupling between electricity and gas networks, promoting the development of the integrated electricity-gas network (IEGN) and strengthening the interaction between the active-reactive power flow in the power distribution network (PDN) and the natural gas flow in the gas distribution network (GDN). This paper proposes a day-ahead active-reactive power scheduling model for the IEGN with multi-microgrids (MMGs) to minimize the total operating cost. Through the tight coupling relationship between the subsystems of the IEGN, the potentialities of the IEGN with MMGs toward multi-energy cooperative interaction is optimized. Important component models are elaborated in the PDN, GDN, and coupled MMGs. Besides, motivated by the non-negligible impact of the reactive power, optimal inverter dispatch (OID) is considered to optimize the active and reactive power capabilities of the inverters of distributed generators. Further, a second-order cone (SOC) relaxation technology is utilized to transform the proposed active-reactive power scheduling model into a convex optimization problem that the commercial solver can directly solve. A test system consisting of an IEEE-33 test system and a 7-node natural gas network is adopted to verify the effectiveness of the proposed scheduling method. The results show that the proposed scheduling method can effectively reduce the power losses of the PDN in the IEGN by 9.86%, increase the flexibility of the joint operation of the subsystems of the IEGN, reduce the total operation costs by $32.20, and effectively enhance the operation economy of the IEGN.

Key words： combined cooling; heating; and power (CCHP); integrated energy systems (IES); natural gas; power distribution system; gas distribution system

1 Introduction

Nowadays, the conflict between energy consumption and climate change has become increasingly obvious [1, 2]. Driven by this conflict, the energy transition is becoming more urgent [3]. Against this backdrop, the concept of integrated electricity-gas network (IEGN) [4–6] is proposed. Playing on the strength of tightly coupling the gas distribution network (GDN) and the power distribution network (PDN) [7], the IEGN is proven to overcome the shortage of independent design and operation among its subsystems, efficiently improve the integration of the multiple energy, and increase the energy efficiency and renewable energy share [8].

Consisting of the PDN and the GDN, traditional IEGN subsystems have been operated separately because each subsystem has been specialized in one product without sharing information [9, 10]. However, with the development of technology and gas availability, mainly represented by the combined cooling, heating, and power (CCHP) technology [11], more gas turbines (GT) and gas boilers (GB) have linked to the PDN and the GDN in the IEGN as distributed generators (DG), breaking the independent operation of the PDN and the GDN, and significantly improving the energy utilization efficiency of the entire IEGN. Besides, with microgrids emerging at the end-user, the pattern of the IEGN with multi-microgrids (MMGs) is also believed to be promising, which can promote the process of energy coupling and interconnection [12–14], further accelerating renewable energy integration and boosting the flexibility of the IEGN. However, the tight coupling between the PDN and the GDN can also pose new challenges to the power dispatch and scheduling of the PDN which can be affected by gas technical restrictions in the GDN, and aggravate the difficulty of joint optimization among the IEGN with MMGs. Hence, it is necessary to study the optimal scheduling and coordinated operation of the IEGN with MMGs.

Several works toward the optimal scheduling and joint operation of the IEGN have been investigated. Considering the uncertainty caused by the high penetration of wind power in the IEGN, Yang et al. [15] presented a distributionally robust frequency constrained scheduling, in which both frequency constraint and demand response joint chance constraints are considered to reduce the impact of the uncertainty of wind power. Focusing on the potential congestion in power lines and gas pipelines, Yang et al. [16] developed an optimal electricity-gas flow (OEGF) framework to maximize social welfare while relieving congestion. Considering the application of flexible energy resource suppliers in the PDN, electric vehicles (EVs) optimal sizing, intelligent charging planning and power sharing are considered in Refs. [17–19], which is proven effective in moderating the fluctuations of renewable energy and improving the system economy. From a computational point of view, a new Benders decomposition-based (IBD) algorithm is presented in Ref. [20] to overcome the difficulty caused by the nonconvexity of the commonly used the integrated electricity-gas system (IEGS) operation model. Chen et al. [21] introduced the feasibility margin and the infeasibility degree to identify the solvability of the optimal energy flow of IEGNs to avoid the unsolvable situation. From the discussion above, the optimal scheduling of PDN-based IEGN toward active power is studied. Still, the above works have neither considered the balance of reactive power nor taken the reactive power generation in the IEGN as a given value, which is not in line with the actual operation of the IEGN.

Reactive power is vital in ensuring reliable active power delivery, maintaining system voltage security, and reducing power loss. Higher penetration of distributed energy resources in the IEGN can also cause a bottleneck in power delivery, which poses new challenges to reactive power and voltage issues. To overcome this shortage, Zhang and Ren [22] proposed an optimal reactive power dispatch (ORPD) model to minimize energy loss without surging the cost of equipment investment and manpower for operation and maintenance. Introducing market mechanisms, a two-level framework for the operation of a competitive market for reactive power ancillary services is proposed in Ref. [23], in which the pricing policy for reactive power is utilized to improve trading efficiency. To overcome the difficulties brought by the nonlinearity of the alternating current power flow (ACPF), a linear approximating method for the ACPF is investigated in Ref. [24]. In Ref. [25], the border PMU measurements are utilized to guarantee the accuracy of the equivalent optimal reactive power flow model. However, the considered reactive power resources in the mentioned work are mainly synchronous generators, shunt capacitors, and flexible AC transmission system (FACTS) controllers; the potential reactive power capabilities of the distributed power sources in the IEGN with microgrids are not considered, which may cause a capacity waste.

In practice, most of the distributed energy resources in the IEGN with MMGs are grid-connected through inverters. If the inverters operate in the variable power output control mode, the inverters can provide reactive power for the IEGN. This means that the inverters of DGs have the potential to change the energy distribution of the whole IEGN. Accordingly, considering the reactive power control capacity of the PV and wind turbine (WT)-driven doubly-fed induction generators, a reactive power optimization algorithm to minimize the active loss and node voltage deviation is presented in Ref. [26]. In Refs. [27,28], the function of the power conditioning system (PCS) of an electrical battery to generate both active and reactive power in all four quadrants is innovatively discussed. Then, an active-reactive optimal power flow (A-R-OPF) in the DPN with embedded ESS utilizing the nature of the PCS is proposed in Ref. [29]. In addition, relevant results show that reasonable in situ reactive power compensation for power systems with high penetration distributed power sources can effectively reduce network loss and improve the grid operation economy [30,31]. Although the potentialities of the inverter of the DG have been exploited to enrich the content of the optimal operation of the reactive power, there are still drawbacks in the existing research. Mainly focusing on a single power network, the above work does not take the real multi-energy coupling relationship of the IEGN into consideration. In addition, it is likely to cause an economic degradation of the IEGN without considering the electrical coupling relationship and full utilization of its internal active-reactive power sources.

Considering the interaction between the multi-energy flow and the coupling relationship between subsystems of the IEGN, a day-ahead active-reactive power scheduling model of the IEGN is proposed in this paper by using the potential reactive power provision of the DG to balance the reactive power and reduce the operating cost of the IEGN. This paper is contributive because a day-ahead active-reactive power scheduling model of the IEGN with MMGs is proposed to minimize the total operation cost. Through the coupling relationship between the PDN and the GDN, the potentialities of the IEGN with MMGs toward the multi-energy cooperative interaction is optimized. In addition, compared with Refs. [4,5], the utilization of the optimal inverter dispatch (OID) of the inverter-based DG is considered. Not only active power but also reactive power can be generated by the DG, which further maximizes the utilization of capacity of the DG in the IEGN. The proposed model is formulated into an A-R-OPF problem, which can achieve a considerable reduction of power losses. Moreover, considering the non-convex characteristics of the network constraints of the PDN and the GDN, second-order cone (SOC)-convex optimization is introduced to convert the original model into a mixed integer convex optimization problem, which can effectively improve the efficiency of calculation by invoking the commercial solver.

A summary of the recently mentioned literature is presented in Tab.1 which emphasizes the contribution of this paper.

Tab.1 Summary of recent related literature

References	Introduction of IEGN	Practical constraints of reactive power	Multi-energy coupling	Potential reactive power capabilities the DG
[15,16, 19‒21]	√	×	√	×
[17,18]	×	×	×	×
[22‒25]	×	√	×	×
[26‒31]	×	√	×	√
Proposed scheduling method	√	√	√	√

2 Energy coupling in the IEGN with MMGs

The architecture of the IEGN with MMGs is shown in Fig.1, which mainly consists of three subsystems: a power distribution system, a gas distribution system, and a CCHP-dominated MMG. In the CCHP-dominated MMG, there are many DGs and energy conversion equipment, such as the GT, the GB, WTs, the heat storage system (HSS), the waste heat boiler (WHB), electric chillers (ECs), and absorption chillers (ACs). The PDN is equipped with distributed photovoltaic (DPV) and an ESS to generate power and flexibility. The extensive configuration of the distributed energy resources in the IEGN with MMGs ensures the supply of the multi-energy load, including electricity, heating, cooling, and gas. As can be observed in Fig.1, the CCHP-dominated MMGs supply their internal heating and cooling load by the CCHP units. In the GDN, the gas load is supplied by the gas source through the gas network. Owning ample energy conversion devices, the electricity load supplement in subsystems is not only directly achieved by the DG in the PDN and MMGs. Note that the components of the GDN are simplified because it is not the focus of this paper.

Fig.1 Energy flow in IEGN with MMGs.

Full size|PPT slide

Based on the proposed architecture in Fig.1, the electricity-gas coupling between the PDN and the GDN in the IEGN is indirectly achieved by the CCHP-dominated MMGs. In the MMGs, the GT obtains the natural gas as fuel from the gas source through the GDN, and generates electricity to the electricity load through the PDN. The schematic diagram of the GT is demonstrated in Fig.2. First, the GT draws in the pressurized, heated air from the outside atmosphere, and the compressed air is pressed into the combustion chamber to mix with the natural gas injected from the GDN to produce high temperature and high-pressure gas. The high temperature and high-pressure gas expands and does work, which partially converts the chemical energy of the natural gas into mechanical energy and outputs electrical work. Then the smoke waste heat and jacket water are absorbed by the WHB for transforming into the heating flow, and the exhaust gas is discharged into the atmosphere for natural exotherm [32]. In this way, the gas turbine converts the chemical energy of the fuel into thermal energy and part of the thermal energy into mechanical energy. In addition, there are other couplings between the energy flows in the IEGN with MMGs: The GB realizes the coupling between the natural gas flow and the heating flow. The AC couples the heating and the cooling flow, and the EC couples the electricity and the cooling flow.

Fig.2 Schematic diagram of GT.

Full size|PPT slide

As the most critical secondary energy in the IEGN, reactive power supply cannot be ignored as much as active power. Equipped with inverter-based DGs, the IEGN with the self-sufficiency of MMGs toward active and reactive power should be fully exploited. In addition to the traditional utilization of DGs to generate active power, the ability of the DG inverter to provide reactive power is also significant. During the DG generation period, a portion of the adjustable capacity remains unused while the inverter provides a certain amount of active power to the PDN. This remaining inverter adjustable capacity makes it possible for the inverter to be used to absorb or generate reactive power. Through the OID [25], the DG can utilize the quick-acting characteristic of power electronics and reasonably operates its inverter in the PCS to generate a phase mismatch between the reference current and the grid voltage. Introducing the OID into the scheduling of the IEGN, it is promising to realize the independent and rapid control of active and reactive power production.

The presence of the coupled internal devices MMGs deeply couples the PDN and the GDN, provides abundant energy for the IEGN, and makes it possible for the IEGN to achieve its internal energy complementarity. Besides, by utilizing the flexibly scheduled feature of DGs, the optimal scheduling of the IEGN toward active-reactive power can be more feasible and easier to be implemented. Based on the above discussion, the input-output scheme of the proposed active-reactive power scheduling process of the IEGN with MMGs is depicted in Fig.3.

Fig.3 Input-output scheme of active-reactive power scheduling of IEGN with MMGs.

Full size|PPT slide

3 Modeling of scheduling method of IEGN

With important components models elaborated in the PDN, the GDN, and the coupled MMG, the active-reactive power scheduling model of the IEGN with MMGs considering the OID of the DG is formulated in this Section.

3.1 Objective function

The objective function of the active-reactive power scheduling of the IEGN with MMGs is to minimize the total operating costs. Hence, the objective function can be formulated as

(1)min\left\{\sum _{i\in D}\sum _{m\in M}\sum _{t\in T}(C_t^{\mathrm{P}}{P}_t^{\mathrm{G}}+C_t^{\mathrm{Q}}{Q}_t^{\mathrm{G}}+C_{i,t}^{\mathrm{D}\mathrm{P}\mathrm{V}}+C_{i,t}^{\mathrm{E}\mathrm{S}\mathrm{S}}+M_{m,t}^{\mathrm{o}\mathrm{p}}+C_{m,t}^{\mathrm{g}\mathrm{a}\mathrm{s}})\right\},

which consists of the expenses incurred in transporting electricity from the utility grid, the running and maintenance cost of the DPV, the ESS, and MMGs coupled with the PDN, and the cost of purchased gas for the cogeneration unit. The items in Eq. (1) are further calculated in Eqs. (2) to (4).

(2)\begin{array}{rl}C{M}_{m,t}^{\mathrm{o}\mathrm{p}}=& M_{m,t}^{\mathrm{W}\mathrm{T}}+M_{m,t}^{\mathrm{H}\mathrm{S}\mathrm{S}}+M_{m,t}^{\mathrm{A}\mathrm{C}}+M_{m,t}^{\mathrm{E}\mathrm{C}}+M_{m,t}^{\mathrm{W}\mathrm{H}\mathrm{B}}\\ =& M_{m,t}^{\mathrm{W}\mathrm{T}}+c{m}_m^{\mathrm{H}\mathrm{S}\mathrm{S}}(H_{m,t}^{\mathrm{c}}+H_{m,t}^{\mathrm{d}})+c{m}_m^{\mathrm{W}\mathrm{H}\mathrm{B}}\cdot H_{m,t}^{\mathrm{W}\mathrm{H}\mathrm{B}}\\ & +c{m}_m^{\mathrm{A}\mathrm{C}}\cdot H_{m,t}^{\mathrm{A}\mathrm{C}}+c{m}_m^{\mathrm{E}\mathrm{C}}\cdot P_{m,t}^{\mathrm{E}\mathrm{C}},\mathrm{\forall }t,\mathrm{\forall }m,\end{array}

(3)C_{m,t}^{\mathrm{g}\mathrm{a}\mathrm{s}}=m_{\mathrm{g}\mathrm{a}\mathrm{s}}\left(\frac{P_{m,t}^{\mathrm{G}\mathrm{T}}}{{\eta }_m^{\mathrm{G}\mathrm{T}}}\cdot \frac{1}{L_{\mathrm{N}\mathrm{G}}}+\frac{H_{m,t}^{\mathrm{G}\mathrm{B}}}{{\eta }_m^{\mathrm{G}\mathrm{B}}}\cdot \frac{1}{L_{\mathrm{N}\mathrm{G}}}\right),\mathrm{\forall }t,\mathrm{\forall }m,

(4)C_{i,t}^{\mathrm{E}\mathrm{S}\mathrm{S}}=m_i^{\mathrm{E}\mathrm{S}\mathrm{S}}(B_{i,t}^{\mathrm{c}}+B_{i,t}^{\mathrm{d}}),\mathrm{\forall }t,\mathrm{\forall }i.

The model should also satisfy the following constraints.

3.2 Constraints of PDN operating constraints

According to Ref. [33], the operating constraints of the PDN are formulated as an alternating current optimal power flow (ACOPF) model. Note that the PDN is radical.

(5)\begin{array}{rl}{P}_{ij,t}-& I_{ij,t}^2{r}_{ij}-\sum _k^J{P}_{jk,t}-P_{j,t}^{\mathrm{D}}+K_{\mathrm{G}}{P}_t^{\mathrm{G}}+K_{\mathrm{E}\mathrm{S}\mathrm{S}}\left(B_{i,t}^{\mathrm{d}}-B_{i,t}^{\mathrm{c}}\right)\\ & +K_{\mathrm{D}\mathrm{P}\mathrm{V}}{P}_{i,t}^{\mathrm{D}\mathrm{P}\mathrm{V}}+K_m{P}_{m,t}=0,\mathrm{\forall }t,\mathrm{\forall }\text{i},\mathrm{\forall }ij,\mathrm{\forall }m,\end{array}

(6)\begin{array}{rl}{Q}_{ij,t}-& I_{ij,t}^2{x}_{ij}-\sum _k^J{Q}_{jk,t}-Q_{j,t}^{\mathrm{D}}+K_{\mathrm{G}}{Q}_t^{\mathrm{G}}+K_{\mathrm{D}\mathrm{P}\mathrm{V}}{Q}_t^{\mathrm{D}\mathrm{P}\mathrm{V}}\\ & +K_m{Q}_{m,t}=0,\mathrm{\forall }t,\mathrm{\forall }\text{i},\mathrm{\forall }ij,\mathrm{\forall }m,\end{array}

(7)P_{t,min}^{\mathrm{G}}⩽P_t^{\mathrm{G}}⩽P_{t,max}^{\mathrm{G}},

(8)Q_{t,min}^{\mathrm{G}}⩽Q_t^{\mathrm{G}}⩽Q_{t,max}^{\mathrm{G}},\mathrm{\forall }t,

(9)\begin{array}{rl}{V}_{j,t}^2=& V_{i,t}^2-2(r_{ij}{P}_{ij,t}^{}+x_{ij}{Q}_{ij,t}^{})+((r_{ij,t}^{}{)}^2\\ & +(x_{ij,t}^{}{)}^2){I_{ij,t}}^2,\mathrm{\forall }t,\mathrm{\forall }b,\mathrm{\forall }ij,\end{array}

(10)V_{i,t}^{min}⩽V_{i,t}⩽V_{i,t}^{max},\mathrm{\forall }t,\mathrm{\forall }i,

(11)\frac{P_{ij,t}^2+Q_{ij,t}^2}{V_{i,t}^2}=I_{ij,t}^2,\mathrm{\forall }t,\mathrm{\forall }b,\mathrm{\forall }ij.

The active and reactive power balance equations at each node are restricted in Eqs. (5) and (6), respectively. The transmission capacity limitations of the active and reactive power transferred from the utility grid are restricted in Eqs. (7) and (8). To ensure system security, Eq. (9) defines the node voltage equation, and Eq. (10) defines the voltage limits. Equation (11) is the line power flow constraint.

Equations (12) to (19) are the operation constraints of the equipped DGs, which the PDN should also satisfy.

(12)0⩽P_{i,t}^{\mathrm{D}\mathrm{P}\mathrm{V}}⩽P_{i,t}^{\mathrm{D}\mathrm{P}\mathrm{V},max},\mathrm{\forall }t,\mathrm{\forall }i,

(13)-P_{i,t}^{\mathrm{D}\mathrm{P}\mathrm{V}}\frac{\sqrt{1-{(k{f}_i^{\mathrm{D}\mathrm{P}\mathrm{V}})}^2}}{k{f}_i^{\mathrm{D}\mathrm{P}\mathrm{V}}}⩽Q_{i,t}^{\mathrm{D}\mathrm{P}\mathrm{V}}⩽P_{i,t}^{\mathrm{D}\mathrm{P}\mathrm{V}}\frac{\sqrt{1-{(k{f}_i^{\mathrm{D}\mathrm{P}\mathrm{V}})}^2}}{k{f}_i^{\mathrm{D}\mathrm{P}\mathrm{V}}},\mathrm{\forall }t,\mathrm{\forall }i,

(14)\sqrt{P{{}_{i,t}^{\mathrm{D}\mathrm{P}\mathrm{V}}}^2+Q{{}_{i,t}^{\mathrm{D}\mathrm{P}\mathrm{V}}}^2}⩽1.1S_i^{\mathrm{D}\mathrm{P}\mathrm{V}},\mathrm{\forall }t,\mathrm{\forall }i,

(15)0⩽B_{i,t}^{\mathrm{c}}⩽B_{i,max}^{\mathrm{c}},\mathrm{\forall }t,\mathrm{\forall }i,

(16)0⩽B_{i,t}^{\mathrm{d}}⩽B_{i,max}^{\mathrm{d}},\mathrm{\forall }t,\mathrm{\forall }m,

(17)E_{i,t+1}^{\mathrm{E}\mathrm{S}\mathrm{S}}=E_{i,t}^{\mathrm{E}\mathrm{S}\mathrm{S}}+\left({\eta }_i^{\mathrm{c},\mathrm{E}\mathrm{S}\mathrm{S}}{B}_{i,t}^{\mathrm{c}}-B_{i,t}^{\mathrm{d}}/{\eta }_i^{\mathrm{d},\mathrm{E}\mathrm{S}\mathrm{S}}\right)\mathrm{\Delta }t,\mathrm{\forall }t,\mathrm{\forall }i,

(18){SOC}_{i,min}^{\mathrm{E}\mathrm{S}\mathrm{S}}⩽E_{i,t}^{\mathrm{E}\mathrm{S}\mathrm{S}}/E_{i,t}^{\mathrm{E}\mathrm{S}\mathrm{S},max}⩽{SOC}_{i,max}^{\mathrm{E}\mathrm{S}\mathrm{S}},\mathrm{\forall }t,\mathrm{\forall }i,

(19)E_{i,0}^{\mathrm{E}\mathrm{S}\mathrm{S}}=E_{i,T}^{\mathrm{E}\mathrm{S}\mathrm{S}},\mathrm{\forall }m.

Equations (12) to (14) describe the operation constraints of the DPV [26]. In the variable power output control mode, Eqs. (12) and (13) are the active and reactive power output restrictions of the DPVs, where weather-based generating capabilities and physical constraints determine the maximum active power output of the DPVs. Equation (14) explains the connections among the active power output, the reactive power output, and the inverter capacity.

Equations (15) to (19) describe the operation constraints of the ESS (Ref. [34]). Equations (15) and (16) are the power constraints of the ESS charge/discharge. Equation (17) restricts the energy storage dynamics between time slots t and t+1. Equation (18) represents state of charge (SOC) limitations of the ESS. Equation (19) decouples daily electric energy storage operation across multiple days and guarantees continuous operations of the ESS.

3.3 Operating constraints of MMGs

The microgrid, as a whole, consists of the DG, the energy storage device and energy conversion device, etc. It is an autonomous system that can realize self-control, protection, and management. As seen in Fig.1, the operating constraints of CCHP-dominated MMGs are modeled below [34]:

a) Cooling, heating, active and reactive power balance

(20)CO{P}_{\mathrm{A}\mathrm{C}}\cdot H_{m,t}^{\mathrm{A}\mathrm{C}}+CO{P}_{\mathrm{E}\mathrm{C}}\cdot P_{m,t}^{\mathrm{E}\mathrm{C}}=C_{m,t}^{\mathrm{D}},\mathrm{\forall }t,\mathrm{\forall }m,

(21){\eta }_m^{\mathrm{W}\mathrm{H}\mathrm{B}}{H}_{m,t}^{\mathrm{G}\mathrm{T}}-H_{m,t}^{\mathrm{A}\mathrm{C}}+{\eta }_m^{\mathrm{G}\mathrm{B}}{H}_{m,t}^{\mathrm{G}\mathrm{B}}+H_{m,t}^{\mathrm{d}}=H_{m,t}^{\mathrm{c}}+H_{m,t}^{\mathrm{D}},\mathrm{\forall }t,\mathrm{\forall }m,

(22)P_{m,t}^{\mathrm{W}\mathrm{T}}+P_{m,t}^{\mathrm{G}\mathrm{T}}=P_{m,t}^{\mathrm{D}}+P_{m,t}^{\mathrm{E}\mathrm{C}}+P_{m,t},\mathrm{\forall }t,\mathrm{\forall }m,

(23)Q_{m,t}^{\mathrm{W}\mathrm{T}}=Q_{m,t}^{\mathrm{D}}+Q_{m,t},\mathrm{\forall }t,\mathrm{\forall }m.

Equations (20) to (23) are the cooling, heating, active and reactive power load balance equations that describe the energy flow relationship in Fig.1, respectively.

b) Installed capacity of CCHP

(24)P_{m,min}^{\mathrm{G}\mathrm{T}}⩽P_{m,t}^{\mathrm{G}\mathrm{T}}⩽P_{m,max}^{\mathrm{G}\mathrm{T}},\mathrm{\forall }t,\mathrm{\forall }m,

(25)P_{m,min}^{\mathrm{E}\mathrm{C}}⩽P_{m,t}^{\mathrm{E}\mathrm{C}}⩽P_{m,max}^{\mathrm{E}\mathrm{C}},\mathrm{\forall }t,\mathrm{\forall }m,

(26)P_{m,min}^{\mathrm{A}\mathrm{C}}⩽P_{m,t}^{\mathrm{A}\mathrm{C}}⩽P_{m,max}^{\mathrm{A}\mathrm{C}},\mathrm{\forall }t,\mathrm{\forall }m,

(27)H_{m,min}^{\mathrm{W}\mathrm{H}\mathrm{B}}⩽H_{m,t}^{\mathrm{W}\mathrm{H}\mathrm{B}}⩽H_{m,max}^{\mathrm{W}\mathrm{H}\mathrm{B}},\mathrm{\forall }t,\mathrm{\forall }m,

(28)H_{m,min}^{\mathrm{G}\mathrm{B}}⩽H_{m,t}^{\mathrm{G}\mathrm{B}}⩽H_{m,max}^{\mathrm{G}\mathrm{B}},\mathrm{\forall }t,\mathrm{\forall }m.

Equations (24) to (28) denote the lower and upper bounds of the installed capacity of the equipment in MMGs.

c) HSS

(29)0⩽H_{m,t}^{\mathrm{c}}⩽H_m^{\mathrm{c},max},\mathrm{\forall }t,\mathrm{\forall }m,

(30)0⩽H_{m,t}^{\mathrm{d}}⩽H_m^{\mathrm{d},max},\mathrm{\forall }t,\mathrm{\forall }m,

(31)H_{m,t+1}^{\mathrm{H}\mathrm{S}\mathrm{S}}=H_{m,t}^{\mathrm{H}\mathrm{S}\mathrm{S}}+\left({\eta }_m^{\mathrm{c},\mathrm{H}\mathrm{S}\mathrm{S}}{H}_{m,t}^{\mathrm{c}}-H_{m,t}^{\mathrm{d}}/{\eta }_m^{\mathrm{d},\mathrm{H}\mathrm{S}\mathrm{S}}\right)\mathrm{\Delta }t,\mathrm{\forall }t,\mathrm{\forall }m,

(32)S_{m,0}^{\mathrm{H}\mathrm{S}\mathrm{S}}=S_{m,T}^{\mathrm{H}\mathrm{S}\mathrm{S}},\mathrm{\forall }m.

Similar to the ESS in the PDN, the relevant constraint of the HSS is expressed in Eqs. (29) to (32).

d) WT

(33)0⩽P_{m,t}^{\mathrm{W}\mathrm{T}}⩽P_{m,t}^{\mathrm{W}\mathrm{T},max},\mathrm{\forall }t,\mathrm{\forall }m,

(34)-P_{m,t}^{\mathrm{W}\mathrm{T}}\frac{\sqrt{1-{(k{f}_m^{\mathrm{W}\mathrm{Y}\mathrm{T}})}^2}}{k{f}_m^{\mathrm{W}\mathrm{T}}}⩽Q_{m,t}^{\mathrm{W}\mathrm{T}}⩽P_{m,t}^{\mathrm{W}\mathrm{T}}\frac{\sqrt{1-{(k{f}_m^{\mathrm{W}\mathrm{T}})}^2}}{k{f}_m^{\mathrm{W}\mathrm{T}}},\mathrm{\forall }t,\mathrm{\forall }m,

(35)\sqrt{P{{}_{m,t}^{\mathrm{W}\mathrm{T}}}^2+Q{{}_{m,t}^{\mathrm{W}\mathrm{T}}}^2}⩽1.1S_m^{\mathrm{W}\mathrm{T}},\mathrm{\forall }t,\mathrm{\forall }m.

Similar to the DPV, the operational constraints of the WT are restricted from Eqs. (33) to (35).

e) Limitations of point of common coupling (PCC)

(36)-P_{m,t}^{\mathrm{P}\mathrm{C}\mathrm{C},max}⩽P_{m,t}⩽P_{m,t}^{\mathrm{P}\mathrm{C}\mathrm{C},max},\mathrm{\forall }t,\mathrm{\forall }m,

(37)-Q_{m,t}^{\mathrm{P}\mathrm{C}\mathrm{C},max}⩽Q_{m,t}⩽Q_{m,t}^{\mathrm{P}\mathrm{C}\mathrm{C},max},\mathrm{\forall }t,\mathrm{\forall }m.

There is a two-way energy flow between the multi-microgrid and its coupled PDN. Equations (36) and (37) indicate the limitation of exchanged electricity at PCCs.

3.4 Operating constraints of natural gas system

The GDN consists of natural gas wells, pipelines, and compressors. The steady-state model of the radical natural gas network is formulated as [35]

(38)w_t^{well}+w_{uv,t}-\sum _v^Z{w}_{vk,t}-w_{u,t}^{\mathrm{G}\mathrm{T}}-w_{u,t}^{\mathrm{G}\mathrm{B}}=0,\mathrm{\forall }t,\mathrm{\forall }u,\mathrm{\forall }v,

(39){\psi }_{min}^2⩽{\psi }_{u,t}^{\text{2}}⩽{\psi }_{max}^2,\mathrm{\forall }t,\mathrm{\forall }u,

(40)w_{min}^{\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}}⩽w_t^{\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}}⩽w_{max}^{\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}},\mathrm{\forall }t,\mathrm{\forall }u,\mathrm{\forall }v,

(41)w_{uv,t}=C_{uv}\sqrt{\left|{\psi }_{u,t}^2-{\psi }_{v,t}^2\right|},\mathrm{\forall }t,\mathrm{\forall }u,\mathrm{\forall }v,

(42){\psi }_{ct,t}⩽{\rho }_c{\psi }_{cf,t},\mathrm{\forall }t.

The nodal balancing equations in the natural gas system are denoted in Eq. (38), where the gas delivered to gas-fired generators is regarded as a gas load. Equations (39) and (40) limit the upper and lower bounds of the gas nodal pressure and gas supply of the gas well. The Weymouth gas flow equation of passive pipelines is represented in Eq. (41), in which it is assumed that the pipeline gas flow directions are fixed under typical working conditions. Equation (42) represents the relationship between the magnitudes of the gas nodal pressure on both sides of the compressor.

3.5 Constraints of energy coupling node

The energy coupling node in the IEGN is the center for multi-energy conversion and integration of the electricity and natural networks. The major multi-energy conversion equipment in energy coupling nodes is the CHP unit and the gas furnace in the MMGs. The main multi-energy conversion restrictions are illustrated as follow:

(43)w_{m,t}^{\mathrm{G}\mathrm{T}}=\frac{P_{m,t}^{\mathrm{G}\mathrm{T}}}{{\eta }_m^{\mathrm{G}\mathrm{T}}}\cdot \frac{1}{L_{\mathrm{N}\mathrm{G}}},\mathrm{\forall }t,\mathrm{\forall }m,

(44)w_{m,t}^{\mathrm{G}\mathrm{B}}=\frac{H_{m,t}^{\mathrm{G}\mathrm{B}}}{{\eta }_m^{\mathrm{G}\mathrm{B}}}\cdot \frac{1}{L_{\mathrm{N}\mathrm{G}}},\mathrm{\forall }t,\mathrm{\forall }m,

(45)H_{m,t}^{\mathrm{G}\mathrm{T}}={\alpha }_m^{\mathrm{G}\mathrm{T}}{P}_{m,t}^{\mathrm{G}\mathrm{T}},\mathrm{\forall }t,\mathrm{\forall }m.

Equations (43) and (44) describe the relationship between the power production and gas consumption of the GT and the GB, respectively. Equation (45) describes the relationship between the electric power production and the by-product heating power of the GT.

3.6 Convexification of the model

Based on an A-R-OPF problem, the formulation of the proposed model is a non-convex programming problem, which is difficult to be solved due to its nonlinear items of constraints. To address this problem, the technique of SOC-convex optimization is introduced to convert the original model into a convex optimization problem, which can effectively improve the calculation efficiency by invoking the commercial solver [36]. The specific relaxation of the SOC techniques is plotted in Fig.4, where the original problem is a nonconvex problem, whose nonconvex feasible region is transformed into a convex SOC feasible region after the relaxation. If the optimal solution after relaxation is still within the original nonconvex feasible region, the relaxation can be considered accurate; if the optimal solution is outside the original nonconvex feasible region, the relaxation is considered inaccurate [37].

Fig.4 SOC relaxation process.

Full size|PPT slide

Utilizing the SOC technique, the relaxation form of the nonconvex items in Eq. (11) in the ACOPF is transformed in Eq. (46):

(46)\{\begin{array}{l}{\Vert 2P_{ij,t}2Q_{ij,t}{l}_{ij,t}-U_{i,t}\Vert }_2\le l_{it,t}+U_{i,t},\\ l_{ij,t}=I_{ij,t}{}^2,\\ U_{i,t}=V_{i,t}^2,\end{array}\mathrm{\forall }t,\mathrm{\forall }b,\mathrm{\forall }ij.

Accordingly, the following modifications to Eqs. (5), (6), (9), and (10) in the model are transformed:

(47)\begin{array}{rl}{P}_{ij,t}-& l_{ij,t}{r}_{ij}-\sum _k^J{P}_{jk,t}-P_{j,t}^{\mathrm{D}}+K_{\mathrm{G}}{P}_t^{\mathrm{G}}+K_{\mathrm{E}\mathrm{S}\mathrm{S}}{P}_{i,t}^{\mathrm{E}\mathrm{S}\mathrm{S}}\\ & +K_{\mathrm{D}\mathrm{P}\mathrm{V}}{P}_{i,t}^{\mathrm{D}\mathrm{P}\mathrm{V}}+K_m{P}_{m,t}=0,\mathrm{\forall }t,\mathrm{\forall }i,\mathrm{\forall }j,\end{array}

(48)\begin{array}{rl}{Q}_{ij,t}-& l_{ij,t}{x}_{ij}-\sum _k^J{Q}_{jk,t}-Q_{j,t}^{\mathrm{D}}+K_{\mathrm{G}}{Q}_t^{\mathrm{G}}+K_{\mathrm{D}\mathrm{P}\mathrm{V}}{Q}_t^{\mathrm{D}\mathrm{P}\mathrm{V}}\\ & +K_m{Q}_{m,t}=0,\mathrm{\forall }t,\mathrm{\forall }i,\mathrm{\forall }j,\end{array}

(49)\begin{array}{rl}{U}_{j,t}=& U_{i,t}-2(r_{ij}{P}_{ij,t}+x_{ij}{Q}_{ij,t})\\ & +((r_{ij,t}{)}^2+(x_{ij,t}{)}^2)l_{ij,t},\mathrm{\forall }t,\mathrm{\forall }b,\mathrm{\forall }ij,\end{array}

(50)V_{i,t}^{min2}\le U_{i,t}\le V_{i,t}^{min2},\mathrm{\forall }t,\mathrm{\forall }i.

Likewise, Eq. (41) are transformed as

(51){\Vert \begin{array}{c}{w}_{uv,t}\\ {\text{C}}_{uv}{\psi }_{u,t}\end{array}\Vert }_2⩽{\text{C}}_{uv}{\psi }_{v,t},\mathrm{\forall }t,\mathrm{\forall }u,\mathrm{\forall }v.

After the transformations, the final form of the scheduling model is obtained in Eq. (52).

(52)\begin{array}{rl}& min\{\sum _{i\in D}\sum _{m\in M}\sum _{t\in T}(C_t^{\mathrm{P}}{P}_t^{\mathrm{G}}+C_t^{\mathrm{Q}}{P}_t^{\mathrm{G}}+C_{i,t}^{\mathrm{D}\mathrm{P}\mathrm{V}}+C_{i,t}^{\mathrm{E}\mathrm{S}\mathrm{S}}+M_{m,t}^{\mathrm{o}\mathrm{p}}+C_{m,t}^{\mathrm{g}\mathrm{a}\mathrm{s}})\}\\ & s.t.\text{Eqs}.(2)-(4),(7)-(8),(10),(12)-(40),\\ & (42)-(45),(46)-(51).\end{array}

As of here, the active-reactive power scheduling model of the IEGN has been transformed into a convex optimization problem, which can be efficiently solved by the commercial solver. To verify the accuracy of the SOC relaxation method, Eqs. (53) and (54) are used to define the error indicators.

(53){\epsilon }_{ij,t}^{\mathrm{P}\mathrm{D}\mathrm{N}}=\left|l_{ij,t}-\frac{{\left(P_{ij,t}\right)}^2+{\left(Q_{ij,t}\right)}^2}{U_{i,t}^{}}\right|,\mathrm{\forall }t,\mathrm{\forall }i,\mathrm{\forall }ij,

(54){\epsilon }_{uv,t}^{\mathrm{G}\mathrm{D}\mathrm{N}}=\left|{\left(C_{uv}{\psi }_{v,t}\right)}^2-{\left(w_{uv,t}\right)}^2-{\left({\text{C}}_{uv}{\psi }_{u,t}\right)}^2\right|,\mathrm{\forall }t,\mathrm{\forall }u,\mathrm{\forall }uv.

4 Case study

In this Section, an IEGN with CCHP-dominated MMGs [34] test system constructed by the IEEE 33-node PDN [33] and the 7-node GDN [35] is used to evaluate the performance of the proposed method. In this test system, there are two DPVs and three microgrids located in the PDN, and each microgrid contains gas-fired units that couple the PDN and the GDN, such as the GT or the GB. In the PDN, the total base loads are 4.09 MW and 2.53 Mvar, the base voltage is set at 12.66 kV, and the voltage limits are set as [0.95, 1.05] p.u.. The GDN has two gas wells, an electric compressor, and five passive pipelines. The topology of the text system is plotted in Fig.5. For sufficient calculation, the MOSEK 8.0 solver with the CVX toolbox in MATLAB is applied to solve the proposed model. The simulations are conducted on a computer with Intel Core i5 2.70 GHz CPU and 16 GB RAM.

Fig.5 Topology of the IEGN modified with the IEEE-33 node PDN and the 7-node GDN.

Full size|PPT slide

The data required for the PDN and the GDN in the IEGN and its coupled MMGs are listed in Tab.2 and Tab.3. For calculation purposes, the relevant configurations of the three microgrids are the same. As with the loads, the IEGN uses electricity and natural gas prices that fluctuate over time. The trends of load [34], price [38], and predictive output of related devices [39] are presented in Fig.6 to Fig.8.

Tab.2 Installed capacity of the devices in the IEGN with MMGs

Devices	Installed capacity/kW
WT	300
GT	100
GB	100
ESS	400
HSS	100
WHB	120
DPV1	800
DPV2	900
AC	150
EC	150

Tab.3 Common parameters in the IEGN with MMGs

Parameters	Value		Parameters	Value		Parameters	Value
{\alpha }_m^{\mathrm{G}\mathrm{T}}	1.2		COPAC	1.2		{\eta }_m^{\mathrm{c},\mathrm{H}\mathrm{S}\mathrm{S}}	0.92
{\eta }_m^{\mathrm{G}\mathrm{B}}	0.9		COPEC	3		{\eta }_m^{\mathrm{d},\mathrm{H}\mathrm{S}\mathrm{S}}	0.92
{\eta }_m^{\mathrm{W}\mathrm{H}\mathrm{B}}	0.73		{\eta }_m^{\mathrm{c},\mathrm{E}\mathrm{S}\mathrm{S}}	0.95		{\eta }_m^{\mathrm{d},\mathrm{H}\mathrm{S}\mathrm{S}}	0.95

Fig.6 Predictive load and output of DPVs.

Full size|PPT slide

Fig.7 Time-of-use electricity and natural gas price.

Full size|PPT slide

Fig.8 Multi-energy loads and the predictive output of the internal WT in the MMGs.

Full size|PPT slide

To illustrate the validity of the scheduling method, four cases of operation of the IEGN are employed:

Case 1: Only active power scheduling is applied to the IEGN, and the utilization of the inverter of the DG to generate reactive power is not considered.

Case 2: Considering the utilization of the inverter of the DG to generate reactive power, the proposed active-reactive power scheduling is applied to the IEGN. Only the ESS is equipped in the PDN as a flexible device.

Case 3: Considering the utilization of the inverter of the DG to generate reactive power, the proposed active-reactive power scheduling is applied to the IEGN. Only the HSS is equipped with MMGs as a flexible device.

Case 4: Considering the utilization of the inverter of the DG to generate reactive power, the proposed active-reactive power scheduling is applied to the IEGN. Moreover, the ESS and the HSS are equipped as flexible devices in the PDN and MMGs.

4.1 Day-ahead scheduling results of the IEGN with MMGs

The quantity of the active power transported from the utility grid to the PDN in Cases 1 to 4 is compared in Fig.9. Correlatively, the charging state of the ESS equipped in the IEGN in Case 4 is depicted in Fig.10. The purchased costs of the active power of the IEGN in Cases 1 to 4 is tabulated in Tab.4. It can be seen in Fig.9 that Cases 1, 3, and 4 have the same value toward the transferred active power from the utility grid because the scheduling methods and equipment configurations in Cases 1, 3, and 4 have the same impact on the active power. At the same time, they are partially different from Case 2. For narrative purposes, only Cases 2 and 4 will be compared subsequently. It is observed that at the utilized test parameters, compared to Case 2, the active power transported from the utility grid in Case 4 increases by 31.98% from 11:00 pm to 4:00 am and decreases by 33.16% from 4:00 pm to 7:00 pm. Further analysis can be conducted in combination with the charging state of the ESS in Case 4 in Fig.10. It is clearly observed that the increasing/decreasing phenomenon is correlated with the charging state of the ESS. Flexibly responding to the time-of-use tariffs, the ESS performs active power charging at lower active power price periods, such as from 11:00 pm to 3:00 pm, and the ESS discharges at the higher active power price periods, such as from 3:00 pm to 6:00 pm. According to Tab.4, more conclusions can be drawn that the IEGN with MMGs in Case 4, after applying the proposed scheduling method and equipment configurations toward active power, can arrange the charging and discharging of the ESS flexibly to take advantage of the difference of the active power price between different periods during a day. Taking advantage of the ability of the ESS to shift and smooth the active power load, the PDN in the IEGN with MMGs can get more usable flexibility and further cut the active power cost by $32.20 (compared to Case 2).

Tab.4 Active power purchased costs in the IEGN with MMGs

Cases	Active power cost/$
Case 1	2439.60
Case 2	2452.00
Case 3	2441.00
Case 4	2419.80

Fig.9 Quantity of the active power transported from the utility grid to the PDN in Cases 1 to 4.

Full size|PPT slide

Fig.10 Charging state of the ESS in the IEGN with MMGs in Case 4.

Full size|PPT slide

The quantity of purchased gas of the GDN in Cases 1 to 4 is compared in Fig.11, and the heat storage and heat release results of the HSS in microgrid 3 is shown in Fig.12. Relatively, Tab.5 records a comparison of the gas consumption costs. Similar to the former analysis toward active power, the following comparisons are only discussed between Case 3 and 4 to highlight the impact of the response capability of the HSS in MMGs. However, the gas consumption cost in Case 4 is $20.30 higher compared to that in Case 3. The reason for this is that the missing HSS makes the gas consumption of the IEGN less economical, and thus the IEGN with MMGs in Case 3 chooses to use less gas to reduce its total costs. It can be concluded that without the HSS, instead of consuming more natural gas to produce heating power, the IEGN with the dependence of MMGs on the electricity transported from the PDN has been improved to a certain extent.

Tab.5 Comparison of the gas consumption costs of the IEGN with MMGs in Cases 1 to 4

Cases	Gas consumption cost/$
Case 1	423.95
Case 2	423.95
Case 3	403.65
Case 4	423.95

Fig.11 Quantity of the purchased natural gas in the GDN of the IEGN with MMGs.

Full size|PPT slide

Fig.12 Heat storage and heat release results of the HSS in microgrid 3.

Full size|PPT slide

Fig.13 and Fig.14 show the quantity of the reactive power delivered from the utility and power loss of the PDN within a 24 h time slot. Tab.6 calculates the purchased cost of the reactive power, the total power loss, and the total operating cost of the IEGN with MMGs in Cases 1 to 4. To simplify the representation, only Case 1 is taken as the base case and Case 4 as the experimental comparison. It is shown in Fig.13 and Fig.14 that compared to Case 2, there is a significant drop both in the purchased reactive power and the power loss of Case 4 within a 24 h time slot, up by 32.15% and 38.9% at the utilized test parameters, respectively. Moreover, it is obviously noticed in Tab.6 that after applying the proposed scheduling method, the power loss in the PDN can be reduced by 0.41 kW per day (compared to Case 1). Besides, when it comes to the comparisons of the total operating cost of the IEGN with MMGs in Cases 1 to 4, it can be seen that the proposed scheduling method in Case 4 can decrease the total operating cost by $19.80, $32.20, and $21.20 compared to that of Cases 1, 2, and 3, respectively. It can be concluded that with the consideration of the active-reactive power output of the inverter by applying the OID and the installation of flexible devices like the ESS and the HSS, the proposed active-reactive power scheduling method of the IEGN can effectively reduce the total operating cost.

Tab.6 Reactive power cost, power loss, and the total operating cost of the IEGN with MMGs in Cases 1 to 4

Cases	Purchased cost of reactive power/$	Power loss of the PDN/kW	Total operating cost/$
Case 1	1091.90	4.16	3943.79
Case 2	953.12	3.76	3817.15
Case 3	953.29	3.78	3795.42
Case 4	952.99	3.75	3785.08

Fig.13 Quantity of the reactive power transported from the utility grid in the PDN of the IEGN with MMGs in Cases 1 and 4.

Full size|PPT slide

Fig.14 Quantity of the power loss of the PDN in the IEGN with MMGs in Cases 1 and 4.

Full size|PPT slide

4.2 Error verification for SOC relaxation

The SOC relaxation errors of the power and gas networks are shown in Fig.15, it can be seen that the SOC relaxation error of each branch in the PDN is of an order of 10⁻³ at each time, while the SOC relaxation error of each pipeline in the GDN is of order 10⁻⁷ at each time. The relaxation deviation is small enough to meet the scheduling requirements, which verifies the accuracy and effectiveness of the SOC relaxation.

Fig.15 Relaxation errors in Case 4.

Full size|PPT slide

4.3 Discussion of scenarios with power to gas (P2G) equipped in the IEGN with MMGs

In the IEGN, in addition to converting natural gas into electricity with the help of the GT and other equipment, electricity can also be converted into natural gas or hydrogen by the P2G technology, so as to realize the bidirectional flow of energy between the power network and the natural gas network. For further research, the power loss with and without the P2G devices in MMGs is compared. The capacity of the P2G devices in each microgrid is 100 kW, and the conversion efficiency of the P2G is set to 0.6 [40, 41]. It is shown in Fig.16 that the equipping P2G devices in the IEGN with MMGs can significantly reduce the power loss, especially during peak hours of the gas price. The reason for this is that the P2G devices are more inclined to convert the excess electricity into natural gas at the time of high-power generation and high gas price periods in MMGs to reduce the total operating cost, thereby reducing the quantity of power flow in the PDN and further reducing the power loss.

Fig.16 Quantity comparison of the power loss of the PDN in the scenarios with and without P2G.

Full size|PPT slide

5 Conclusions

This paper proposes a day-ahead active-reactive power scheduling method of the IEGN with MMGs. In view of the coupling relationship between the PDN and the GDN, the characteristic of CCHP-dominated MMGs, and the interaction between multi-energy flows, this method guides the scheduling results of the IEGN with MMGs by utilizing their internal flexibility resources and realizing energy share to minimize the total operating cost. Considering the non-convex characteristics of the PDN and the constraints of the GDN, the technique of SOC-convex optimization is introduced to convert the original model into the convex optimization problem for efficient calculation under the premise of ensuring accuracy. The test case of the proposed model in four different scenarios is investigated to demonstrate the feasibility and efficiency of the propose method. The key conclusions made from the case studies are as follows:

1) The proposed scheduling method can decrease the total operating costs by $19.80, $32.20, and $21.20 compared to the control group. Besides, the proposed method has a reduction of 9.86% of the total power losses, and the maximum power loss reduction in a single moment can be up to 38.9% in the case study.

2) It can be concluded that by considering the active and reactive power support capacity of the DG, the active-reactive power scheduling of the IEGN with MMGs can realize the collaborative optimization of its subsystems, improve the flexibility and economy of system operation, and effectively reduce the energy loss in the transmission network.

3) Taking advantage of the OID of the DG to generate active and reactive power, the maximized consumption capacities of the WT and the active power of the DPV is achieved along with maximizing the amount of their available reactive power.

The uncertainty of renewable energy is not considered in this paper, which is a limit of this work. In the future, the model can be extended with the introduction of uncertainty of renewable energy in the IEGN.

Acknowledgments

This work was partially supported by the National Natural Science Foundation of China (Grant Nos. 51877033, 52061635103, 52007026, and 52077028).

Notations

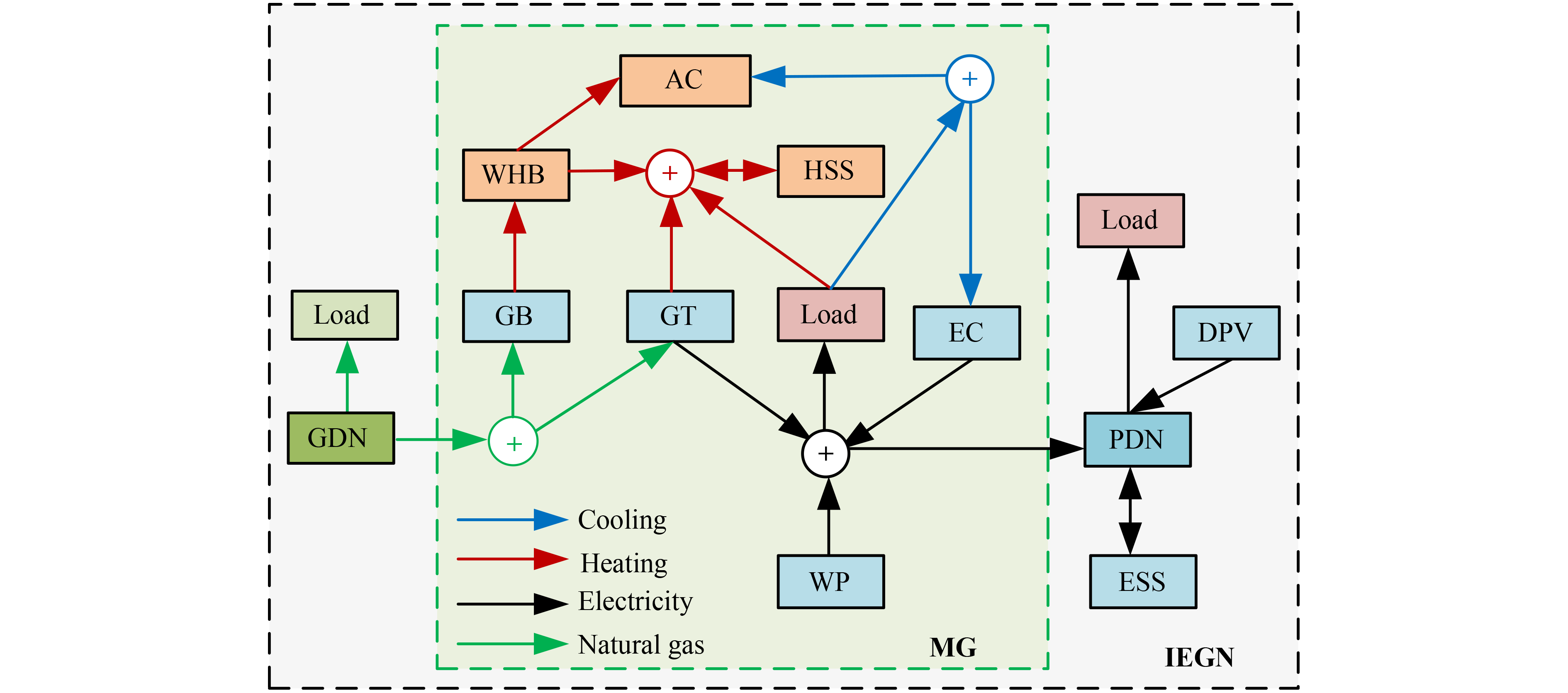
Acronyms
A-R-OPF	Active-reactive optimal power flow
AC	Absorption chillers
ACOPF	Alternating current optimal power flow
CCHP	Combined cooling, heating, and power
DG	Distributed generators
DPV	Distributed photovoltaic
EC	Electric chillers
GB	Gas boilers
GDN	Gas distribution network
GT	Gas turbines
HSS	Heat storage systems
IEGN	Integrated electricity-gas network
MMG	Multi-microgrids
OID	Optimal inverter dispatch
PCS	Power conditioning systems
PDN	Power distribution network
P2G	Power to gas
SOC	Second-order cone
WHB	Waste heat boilers
Indices
i/j	Index of nodes in the PDN
ij	Index of branches in the PDN
I/J	Set of the beginning/ending nodes of the branches in the PDN
m	Index of the microgrids
M	Set of the nodes of the PDN where the microgrids are located
t	Index of time slots
uv	Index of branches in the GDN
u/v	Index of nodes in the GDN
U/V	Set of the beginning/ending nodes of the pipelines in the GDN
Parameters
B_{i,t}^{\mathrm{c}}/B_{i,t}^{\mathrm{d}}	Charging/discharging power of the power storage system of node i of the PDN at the tth hour
Cuv	Weymouth equation coefficient
C_t^{\mathrm{P}}/C_t^{\mathrm{Q}}	Active/reactive power price of the utility grid at the tth hour
C_{i,t}^{\mathrm{D}\mathrm{P}\mathrm{V}}	Operation cost of the distributed photovoltaic of node i in the distribution network, which is assumed to be a constant
COPAC	Coefficient of performance of the absorption chiller in the mth microgrid
COPEC	Performance coefficient of the electrical chiller in the mth microgrid
c{m}_m^{\mathrm{H}\mathrm{S}\mathrm{S}}	Coefficient of the cost function of the heat storage system in the mth microgrid
c{m}_m^{\mathrm{E}\mathrm{C}}/c{m}_m^{\mathrm{A}\mathrm{C}}	Coefficient of the cost function of the electrical chiller/absorption chiller in the mth microgrid
c{m}_m^{\mathrm{W}\mathrm{H}\mathrm{B}}	Coefficient of the cost function of the waste heat boiler in the mth microgrid
C_{m,t}^{\mathrm{g}\mathrm{a}\mathrm{s}}	Purchased gas cost of the mth microgrids at the tth hour
C_{i,t}^{\mathrm{D}\mathrm{P}\mathrm{V}}	Operation cost of the distributed photovoltaic of node i in the distribution network
C_{i,t}^{\mathrm{E}\mathrm{S}\mathrm{S}}	Operation cost of the ESS of node i in the distribution network
E_{i,t}^{\mathrm{E}\mathrm{S}\mathrm{S}}	Amount of electricity stored in the energy storage system of node i of the PDN at the tth hour
H_{m,t}^{\mathrm{G}\mathrm{B}}	Heating power production of the gas boiler of the mth microgrid at the tth hour
H_{m,t}^{\mathrm{A}\mathrm{C}}	Heating power absorption of the absorption chiller of the mth microgrid at the tth hour
H_{m,t}^{\mathrm{c}}/H_{m,t}^{\mathrm{d}}	Charging/discharging power of the heat storage system in the mth microgrid at the tth hour
H_{m,t}^{\mathrm{D}}/C_{m,t}^{\mathrm{D}}	Heating and cooling power loads of the mth microgrid at the tth hour
H_{m,min}^{\mathrm{A}\mathrm{C}}/H_{m,max}^{\mathrm{A}\mathrm{C}}	Minimum/maximum heating power consumption of the absorption chiller in the mth microgrid
H_{m,min}^{\mathrm{W}\mathrm{H}\mathrm{B}}/H_{m,max}^{\mathrm{W}\mathrm{H}\mathrm{B}}	Minimum/maximum heating power absorption of the waste heat boiler in the mth microgrid
H_{m,min}^{\mathrm{G}\mathrm{B}}/H_{m,max}^{\mathrm{G}\mathrm{B}}	Minimum/maximum heating power generation of the gas boiler in the mth microgrid
H_{m,min}^{\mathrm{c}}/H_{m,max}^{\mathrm{c}}	Minimum/maximum heating power charging of the heat power storage in the mth microgrid
H_{m,min}^{\mathrm{d}}/H_{m,max}^{\mathrm{d}}	Minimum/maximum heating power discharging of the heat power storage in the mth microgrid
Iij,t	Current flowing in branch ij in the distribution network at the tth hour
k{f}_i^{\mathrm{D}\mathrm{P}\mathrm{V}}	Minimum power factor of the distributed photovoltaic inverter of node i in the PDN
KG/Km	Utility grid/microgrids located nodes correlation matrix
KESS/KDPV	ESS/distributed photovoltaic located nodes correlation matrix
lij,t	Square of the current flowing in branch ij in the distribution network at the tth hour
LNG	Heating value of natural gas
m_i^{\mathrm{E}\mathrm{S}\mathrm{S}}	Coefficient of the cost function of the node i of the electricity storage system (ESS) in the PDN
M_{m,t}^{\mathrm{o}\mathrm{p}}	Operation cost of the mth the microgrids at the tth hour
M_{m,t}^{\mathrm{H}\mathrm{S}\mathrm{S}}	Operation cost of the heat storage system in the mth microgrid at the tth hour
M_{m,t}^{\mathrm{W}\mathrm{H}\mathrm{B}}	Operation cost of waste heat boiler in the mth microgrid at the tth hour
M_{m,t}^{\mathrm{W}\mathrm{T}}	Operation cost of the wind turbine of the mth microgrid at the tth hour, which is assumed to be a constant
M_{m,t}^{\mathrm{A}\mathrm{C}}/M_{m,t}^{\mathrm{E}\mathrm{C}}	Operation cost of the absorption chiller/electrical chiller of the mth microgrid at the tth hour
Pij,t	Active power flow in branch ij in the distribution network at the tth hour
P_{m,t}^{\mathrm{E}\mathrm{C}}	Active power consumption of the electrical chiller of the mth microgrid at the tth hour
P_{i,t}^{\mathrm{D}\mathrm{P}\mathrm{V},\mathrm{m}\mathrm{a}\mathrm{x}}	Maximum forecasted active power production of the distributed photovoltaic of node i in the PDN at the tth hour
P_{m,t}^{\mathrm{D}}/Q_{m,t}^{\mathrm{D}}	Active and reactive power loads of the mth microgrid at the tth hour
P_t^{\mathrm{G}}/Q_t^{\mathrm{G}}	Active/reactive power transported from the utility grid at the tth hour
P_{i,t}^{\mathrm{D}}/Q_{i,t}^{\mathrm{D}}	Active and reactive power of node i of the PDN at the tth hour
P_{m,max}^{\mathrm{P}\mathrm{C}\mathrm{C}}/Q_{m,max}^{\mathrm{P}\mathrm{C}\mathrm{C}}	Maximum amount of active/reactive power traded at the point of common coupling between the mth microgrid and the PDN
P_{m,min}^{\mathrm{G}\mathrm{T}}/P_{m,max}^{\mathrm{G}\mathrm{T}}	Minimum/maximum active power production of the gas turbine in the mth microgrid
P_{m,min}^{\mathrm{E}\mathrm{C}}/P_{m,max}^{\mathrm{E}\mathrm{C}}	Minimum/maximum active power consumption of the electrical chiller in the mth microgrid
P_{t,min}^{\mathrm{G}}/P_{t,max}^{\mathrm{G}}	Minimum/maximum active power transported from the utility grid at the tth hour
P_{m,max}^{\mathrm{P}\mathrm{C}\mathrm{C}}/Q_{m,max}^{\mathrm{P}\mathrm{C}\mathrm{C}}	Maximum amount of active/reactive power traded at the point of common coupling between the mth microgrid and the PDN
Pm,t/Qm,t	Transported quantity of the mth microgrid of active/reactive power at the tth hour
P_{m,t}^{\mathrm{G}\mathrm{T}}/H_{m,t}^{\mathrm{G}\mathrm{T}}	Active/heating power production of the gas turbine at the tth hour
P_{i,t}^{\mathrm{D}\mathrm{P}\mathrm{V}}/Q_{i,t}^{\mathrm{D}\mathrm{P}\mathrm{V}}	Active/reactive power production of the distributed photovoltaic of node i of the PDN at the tth hour
Qij,t	Reactive power flowing in branch ij in the distribution network at the tth hour
Q_{t,min}^{\mathrm{G}}/Q_{t,max}^{\mathrm{G}}	Minimum/maximum reactive power transported from the utility grid at the tth hour
rij,t/xij,t	Resistance/reactance of branch ij in the distribution network
S_i^{\mathrm{D}\mathrm{P}\mathrm{V}}	Capacity of the distributed photovoltaic inverter of node i of the PDN
S_{m,t}^{\mathrm{H}\mathrm{S}\mathrm{S}}	Amount of heat stored in the electrical chiller at the tth hour
SO{C}_{i,min}^{\mathrm{E}\mathrm{S}\mathrm{S}}/SO{C}_{i,max}^{\mathrm{E}\mathrm{S}\mathrm{S}}	Minimum/maximum state of charge of the ESS in the node i in the PDN
Vmin,i,t/Vmax,i,t	Voltage limitations of node i in the distribution network
Vi,t	Nodal voltage in node i in the distribution network at the tth hour
Ui,t	Square of nodal voltage in node i in the distribution network at the tth hour
Ub,t	Voltage drop in branch b in the distribution network at the tth hour
w_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}}/w_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}}	Limitations of the gas supplied quantity from the gas well at the tth hour
wuv,t	Gas flow from node u to node v in the GDN at the tth hour
w_t^{\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}}	Gas production by node u in the gas well at the tth hour
w_{u,t}^{\mathrm{G}\mathrm{T}}/w_{u,t}^{\mathrm{G}\mathrm{B}}	Gas consumption by GT/GB at node u in the gas distribution system at the tth hour
ψmin/ψmax	Limitations of the gas nodal pressure in the GDN at the tth hour
ρc	Compression factor of the compressor
ψu,t	Gas nodal pressure in node u in the gas distribution network at the tth hour
ψct,t/ψcf,t	Gas nodal pressure of the inlet and outlet of the compressor in the GDN at the tth hour
{\eta }_m^{\mathrm{G}\mathrm{T}}	Efficiency of the gas turbine in the mth microgrid
{\eta }_m^{\mathrm{G}\mathrm{B}}	Efficiency of the gas boiler in the mth microgrid
{\eta }_m^{\mathrm{W}\mathrm{H}\mathrm{B}}	Efficiency of the waste heat boiler in the mth microgrid
{\eta }_i^{\mathrm{c},\mathrm{E}\mathrm{S}\mathrm{S}}/{\eta }_i^{\mathrm{d},\mathrm{E}\mathrm{S}\mathrm{S}}	Charging/discharging efficiency of the ESS of node i in the PDN
{\eta }_m^{\mathrm{c},\mathrm{H}\mathrm{S}\mathrm{S}}/{\eta }_m^{\mathrm{d},\mathrm{H}\mathrm{S}\mathrm{S}}	Charging/discharging efficiency of the heat storage system in the mth microgrid

References

1 Zhu M, Xu C, Dong S. . Integrated multi-energy flow calculation method for electricity-gas-thermal integrated energy systems. Protection and Control of Modern Power Systems, 2021, 6(1): 1–12

2 Amanpour S, Huck D, Kuprat M. . Integrated energy in Germany—a critical look at the development and state of integrated energies in Germany. Frontiers in Energy, 2018, 12(4): 493–500

3 Nasiri N, Zeynali S, Najafi Ravadanegh S. . A tactical scheduling framework for wind farm integrated multi-energy systems to take part in natural gas and wholesale electricity markets as a price setter. IET Generation, Transmission & Distribution, 2022, 16(9): 1849–1864

4 AbomazidA MEl-TaweelN AFaragH E Z. Energy management system for minimizing hydrogen production cost using integrated battery energy storage and photovoltaic systems. In: 2021 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, D.C., USA, 2021

5 Koirala B, Hers S, Morales-España G. . Integrated electricity, hydrogen and methane system modeling framework: application to the Dutch Infrastructure Outlook 2050. Applied Energy, 2021, 289: 116713

6 Wang H, Hou K, Zhao J B. . Planning-oriented resilience assessment and enhancement of integrated electricity-gas system considering multi-type natural disasters. Applied Energy, 2022, 315: 118824

7 Liu H Z, Shen X W, Guo Q L. . A data-driven approach towards fast economic dispatch in electricity–gas coupled systems based on artificial neural network. Applied Energy, 2021, 286: 116480

8 Chen S, Conejo A J, Sioshansi R. . Investment equilibria involving gas-fired power units in electricity and gas markets. IEEE Transactions on Power Systems, 2020, 35(4): 2736–2747

9 Ahmad F, Iqbal A, Ashraf I. . Optimal location of electric vehicle charging station and its impact on distribution network: a review. Energy Reports, 2022, 8: 2314–2333

10 Clegg S, Mancarella P. Integrated electrical and gas network flexibility assessment in low-carbon multi-energy systems. IEEE Transactions on Sustainable Energy, 2016, 7(2): 718–731

11 Liu M X, Shi Y, Fang F. A new operation strategy for CCHP systems with hybrid chillers. Applied Energy, 2012, 95: 164–173

12 Ahmadi S E, Sadeghi D, Marzband M. . Decentralized bi-level stochastic optimization approach for multi-agent multi-energy networked micro-grids with multi-energy storage technologies. Energy, 2022, 245(15): 123223

13 Nasiri N, Zeynali S, Ravadanegh S N. . A hybrid robust-stochastic approach for strategic scheduling of a multi-energy system as a price-maker player in day-ahead wholesale market. Energy, 2021, 235(15): 121398

14 Kazemi-Razi S M, Askarian Abyaneh H, Nafisi H. . Enhancement of flexibility in multi-energy microgrids considering voltage and congestion improvement: robust thermal comfort against reserve calls. Sustainable Cities and Society, 2021, 74: 103160

15 Yang L, Xu Y, Zhou J. . Distributionally robust frequency constrained scheduling for an integrated electricity-gas system. IEEE Transactions on Smart Grid, 2022, 13(4): 2730–2743

16 Yang L, Xu Y, Sun H. . Two-stage convexification-based optimal electricity-gas flow. IEEE Transactions on Smart Grid, 2020, 11(2): 1465–1475

17 Baherifard M A, Kazemzadeh R, Yazdankhah A S. . Intelligent charging planning for electric vehicle commercial parking lots and its impact on distribution network’s imbalance indices. Sustainable Energy, Grids and Networks, 2022, 30: 100620

18 Sadeghi D, Amiri N, Marzband M. . Optimal sizing of hybrid renewable energy systems by considering power sharing and electric vehicles. International Journal of Energy Research, 2022, 46(6): 8288–8312

19 Cao Z, Wang J, Zhao Q. . Decarbonization scheduling strategy optimization for electricity-gas system considering electric vehicles and refined operation model of power-to-gas. IEEE Access: Practical Innovations, Open Solutions, 2021, 9: 5716–5733

20 Gao H, Li Z. A benders decomposition based algorithm for steady-state dispatch problem in an integrated electricity-gas system. IEEE Transactions on Power Systems, 2021, 36(4): 3817–3820

21 Chen S, Wei Z, Sun G. . Identifying optimal energy flow solvability in electricity-gas integrated energy systems. IEEE Transactions on Sustainable Energy, 2017, 8(2): 846–854

22 Zhang Y, Ren Z. Optimal reactive power dispatch considering costs of adjusting the control devices. IEEE Transactions on Power Systems, 2005, 20(3): 1349–1356

23 El-Samahy I, Bhattacharya K, Canizares C. . A procurement market model for reactive power services considering system security. IEEE Transactions on Power Systems, 2008, 23(1): 137–149

24 Li Z, Yu J, Wu Q H. Approximate linear power flow using logarithmic transform of voltage magnitudes with reactive power and transmission loss consideration. IEEE Transactions on Power Systems, 2018, 33(4): 4593–4603

25 Yu J, Dai W, Li W. . Optimal reactive power flow of interconnected power system based on static equivalent method using border PMU measurements. IEEE Transactions on Power Systems, 2018, 33(1): 421–429

26 LiWLiangZMaC, . Reactive power optimization in distribution network considering reactive power regulation capability and fuzzy characteristics of distributed generators. In: 2019 4th International Conference on Power and Renewable Energy (ICPRE), Chengdu, China, 2019

27 MillerN WZrebiecR SHuntG, . Design and commissioning of a 5 MVA, 2.5 MWh battery energy storage system. In: Proceedings of 1996 Transmission and Distribution Conference and Exposition, Los Angeles, USA, 1996

28 Walker L H. 10-MW GTO converter for battery peaking service. IEEE Transactions on Industry Applications, 1990, 26(1): 63–72

29 Gabash A, Li P. Active-reactive optimal power flow in distribution networks with embedded generation and battery storage. IEEE Transactions on Power Systems, 2012, 27(4): 2026–2035

30 YangKGongYZhangP, . A reactive power compensation method based on tracing the power flow and loss function of power system. In: 2015 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Changsha, China, 2015

31 WangYWangTZhouK P, . Reactive power optimization of wind farm considering reactive power regulation capacity of wind generators. In: 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 2019

32 Zhang X, Sugishita H, Ni W. . Economics and performance forecast of gas turbine combined cycle. Tsinghua Science and Technology, 2005, 10(5): 633–636

33 Chen H H, Wang D, Zhang R F. . Optimal participation of ADN in energy and reserve markets considering TSO-DSO interface and DERs uncertainties. Applied Energy, 2022, 308(15): 118319

34 Wang C, Hong B, Guo L. . A general modeling method for optimal dispatch of combined cooling, heating and power microgrid. Proceedings of the CSEE, 2013, 33(31): 26–33

35 Li G Q, Yan K F, Zhang R F. . Resilience-oriented distributed load restoration method for integrated power distribution and natural gas systems. IEEE Transactions on Sustainable Energy, 2022, 13(1): 341–352

36 Farivar M, Low S H. Branch flow model: relaxations and convexification—parts I. IEEE Transactions on Power Systems, 2013, 28(3): 2554–2564

37 Chen H H, Fu L B, Bai L Q. . Distribution market-clearing and pricing considering coordination of DSOs and iso: an EPEC approach. IEEE Transactions on Smart Grid, 2021, 12(4): 3150–3162

38 Bai L, Wang J, Wang C. . Distribution locational marginal pricing (DLMP) for congestion management and voltage support. IEEE Transactions on Power Systems, 2018, 33(4): 4061–4073

39 Chen H H, Li H Y, Lin C. . An integrated market solution to enable active distribution network to provide reactive power ancillary service using transmission–distribution coordination. IET Energy Systems Integration, 2022, 4(1): 98–115

40 Chen Z, Zhang Y, Ji T. . Coordinated optimal dispatch and market equilibrium of integrated electric power and natural gas networks with P2G embedded. Journal of Modern Power Systems and Clean Energy, 2018, 6(3): 495–508

41 Teodor O. Coordination of battery energy storage and power-to-gas in distribution systems. Protection and Control of Modern Power Systems, 2017, 2(1): 1–8