Flow and thermal modeling of liquid metal in expanded microchannel heat sink

Abstract

Liquid metal-based microchannel heat sinks (MCHSs) suffer from the low heat capacity of coolant, resulting in an excessive temperature rise of coolant and heat sink when dealing with high-power heat dissipation. In this paper, it was found that expanded space at the top of fins could distribute the heat inside microchannels, reducing the temperature rise of coolant and heat sink. The orthogonal experiments revealed that expanding the top space of channels yielded similar temperature reductions to changing the channel width. The flow and thermal modeling of expanded microchannel heat sink (E-MCHS) were analyzed by both using the 3-dimensional (3D) numerical simulation and the 1-dimensional (1D) thermal resistance model. The fin efficiency of E-MCHS was derived to improve the accuracy of the 1D thermal resistance model. The heat conduction of liquid metal in Z direction and the heat convection between the top surface of fins and the liquid metal could reduce the total thermal resistance (R_t). The above process was effective for microchannels with low channel aspect ratio, low mean velocity (U_m) or long heat sink length. The maximum thermal resistance reduction in the example of this paper reached 36.0%. The expanded space endowed the heat sink with lower pressure, which might further reduce the pumping power (P). This rule was feasible both when fins were truncated (h₂ < 0, h₂ is the height of expanded channel for E-MCHS) and when over plate was raised (h₂ > 0).

Key words： liquid metal cooling; heat sink; expanded microchannel; flow and thermal modeling

1 Introduction

The heat generated from heat sources, such as chips, should be dissipated by the heat exchange between heat sinks and the coolant to ensure the regular operation of the equipment [1,2]. The heat dissipation process could be divided into three parts: the heat conduction in the heat sink, the heat transfer between the coolant and the heat sink, and the coolant flowing out the heat sink.

Substantial research efforts have focused on earning a higher nusselt number (Nu) to improve the heat transfer between the coolant and the heat sink. Optimizing the structure of the heat sink and improving the thermal properties of the coolant are the two main approaches. Structural optimization mainly focuses on passive techniques, such as adding ribs [3–6], changing configurations of channel [7–12], using vortex generators [13–16], segmented microchannel [17], and optimized rib structure and arrangement [18–20]. These ways are primarily suitable for the coolant with a low conductivity, i.e., water, and are generally accompanied by the complex structure and larger pressure drop [21]. Improving the thermal conductivity (k) of coolant can significantly advance heat transfer. Novel coolants with a higher k, such as nanofluid [22–24] and liquid metal [25–29], have received more attention. Nanofluids are usually composed of nanoparticles with a high k (Al₂O₃ [30], TiO₂ [31], Cu [32], and Ag [33]) and base fluids with a low viscosity. The Nu of nanofluids is usually higher than that of base fluid. However, it is difficult for nanofluids to avoid sedimentation completely. In addition, their heat transfer performance is still unable to cope with the condition with a high heat flux. Liquid metal has been applied to microchannel heat sink to achieve more efficient and stable heat dissipation [34,35]. It is proved that the liquid gallium-based heat sink could obtain a better cooling performance than the water-based one when the length of the heat sink is smaller than the critical length [36]. Sarafraz et al. found that the thermal performance of gallium is superior to CuO-water nanofluid when applied to cool the central processing unit (CPU) [37]. In recent years, the structure or system suitable for liquid metals has been gradually proposed, such as the centrifugal pump driven by rotating permanent magnets [38], the electromagnetic induction pump [21], the integrated liquid metal cooling system [39,40] and the two-stage multichannel liquid-metal cooling system [29]. These cases indicate that liquid metal is a candidate for the new generation of chip heat dissipation.

Notably, Fig.1 shows the flow and thermal performance of liquid metals are different from those of both water and nanofluids because of the differences between thermophysical properties (Fig.1). The high k makes the Nu of the liquid metal higher than that of the conventional fluids. But liquid metal coolant suffers a large temperature rise due to its weak specific heat capacity (C_p). For example, Liu et al. compared the total thermal resistance (R_t) of water-based and gallium-based microchannel heat sinks (MCHSs) with the same dimension. As the length of the heat sink increases, the temperature of the water-based heat sink almost remains constant but that of gallium-based heat sinks increases significantly [36]. According to Newton’s cooling formula (q = h_c·ΔT), the temperature difference (ΔT) between the wall and the coolant is equal to the ratio of the heat flux (q) to the convective heat transfer coefficient (h_c). When the flow and the heat transfer reach steady-state, the q and the h_c at some point in the heat sink are constant, resulting in the constant ΔT. Therefore, the temperature surge of the coolant arising from the low heat capacity will lead to the heat sink temperature rise and the uneven temperature distribution. Clearly, unlike that of water-based MCHSs, the optimization of liquid metal-based MCHSs should focus on decreasing the temperature rise of the liquid metal, i.e., reducing the resistance of heat capacity rather than the resistance of convection [28,41,42]. This requires more coolant to flow through the heat sink, which could be achieved by increasing the flow rate, increasing the width and height of the heat sink, or reducing the thickness of the fins. However, these ways are often accompanied by problems such as larger pumps, larger volumes or structural instability.

Fig.1 Comparison of thermophysical properties of nanofluids (Al₂O₃/methanol [45], TiO₂/water [46], silver nanoparticles/ethylene glycol-water [33], Cu-fly ash/water [32]) and liquid metals (gallium and Ga₆₈In₂₀Sn₁₂ [47]) and pure substances (water, methanol and ethanol [48]).

Full size|PPT slide

Interestingly, it is found by the authors of this paper that the convection at the end of the fins is not significant for heat transfer enhancement. By cutting the fin ends and thus reserving expanded space to increase the flow rate of coolant in the fixed size, the heat transfer will be much more effective. This expanded microchannel heat sink (E-MCHS) allows more cooling medium to flow through without changing the size of the heat sink, increasing the difficulty of processing, and destroying the stability of the heat sink. In this paper, the cooling performance of liquid metal for single-phase laminar heat transfer in the expanded microchannel is studied by using both the revised empirical correlations and the numerical analysis methods. Navier-Stokes and Energy equations with slip boundary conditions (velocity slip and temperature jump) are solved to study the hydraulic and heat transfer performances of the microchannels.

2 Material and methods

Generally, fins in MCHS are directly in contact with a cover plate. The expanded microchannel structure has been used in microchannel flow boiling to reduce the flow reversal and suppressed the flow instability [43,44]. There is an apparent difference between the heat transfer mechanism of the boiling heat transfer and the single-phase laminar heat transfer. This structure cannot reduce the thermal resistance of the water-based single-phase flow heat sink. However, it is suitable for reducing the excessive temperature rise of liquid metal in a microchannel. Fig.2(a) and Fig.2(b) present the structure of MCHS and E-MCHS. E-MCHS could be obtained by raising the cover plate (h₂ > 0, h₂ is the height of expanded channel for E-MCHS) or truncating the fins (h₂ < 0) of MCHS (Fig.2(a)−Fig.2(c)). For E-MCHSs, the height between the top of the fins and the bottom of the cover plate is named h₂ and the remaining height of the fins is h₁ (h₁ is height of fins for E-MCHS). The total channel height H is the sum of h₁ and h₂. Of note, H of E-MCHSs at h₂ < 0 and MCHS is the same.

Fig.2 The structure of MCHS and E-MCHS.

Full size|PPT slide

Compared to MCHSs, E-MCHSs provide expanded space for coolant. When h₂ < 0, E-MCHSs could earn an n\times W_{\text{w}}\times L of area for heat transfer at the cost of 2n\times h_2\times L area, in which n is the channel number, W_w is the fin width, L is the heat sink length. Therefore, when h_2 is smaller than W_{\text{w}}/2, the heat transfer area of the fins increases. The fin efficiency decreases with height increasing, thereby the heat transfer capacity arising from 2n\times h_2\times L is inferior to that from n\times W_{\text{w}}\times L. The narrow space at the top may increase the intensity of convective heat transfer. Thus, truncating fins may have a negligibly bad impact on the heat exchange between the coolant and the heat sink. Similarly, E-MCHSs could earn an n\times W_{\text{w}}\times L of area for heat transfer when h₂ > 0. More coolant means a smaller thermal resistance and a lower outlet temperature. Although more fluid requires a higher pumping power (P), the expansion of the channel also reduces the pressure drop. E-MCHSs could achieve a better cooling performance at a low P.

3 Theory and calculation of flow and thermal characteristics of MCHS/E-MCHS

The revised empirical correlations 1-dimensional (1D) thermal resistance model and numerical simulation were used to calculate the heat transfer and flow performance of MCHSs and E-MCHSs. The fin efficiency of E-MCHS was calculated to make the 1D thermal resistance model more accurate.

3.1 Theory of thermal resistance calculation

3.1.1 1D thermal resistance model

To clearly illustrate this process, the total thermal resistance R_{\mathrm{t}} is introduced, and the lower R_t refers to a better cooling performance. R_t could be deemed as the sum of the R_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}} (thermal resistance of heat conduction), R_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}} (thermal resistance of convection) and R_{\mathrm{c}\mathrm{a}\mathrm{l}} (thermal resistance of heat capacity). 1D resistance analysis has been proved to represent the physics of the heat transfer problem, and is suitable for use in the design and optimization of practical MCHS [7,49].

1) R_{\text{cond}} of MCHSs and E-MCHSs could be calculated as follows, in which t is the heat sink base thickness, A is the area of heat sink.

(1)R_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{\_}\mathrm{M}\mathrm{C}\mathrm{H}\mathrm{S}}=R_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{\_}\mathrm{E}\text{-}\mathrm{M}\mathrm{C}\mathrm{H}\mathrm{S}}=\frac{t}{kA}.

2) R_{\mathrm{c}\mathrm{a}\mathrm{l}} of MCHSs and E-MCHSs could be calculated as follows, in which ρ is the mass density, W_c is the channel width,U_m is the mean velocity, q_m is the mass flow.

(2)R_{\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{\_}\mathrm{M}\mathrm{C}\mathrm{H}\mathrm{S}}=\frac{1}{q_{\mathrm{m}}{C}_{\mathrm{p}}}=\frac{1}{\rho C_{\mathrm{p}}n{U}_{\mathrm{m}}H{W}_{\mathrm{c}}},

(3)R_{\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{\_}\mathrm{E}\mathrm{M}\mathrm{C}\mathrm{H}\mathrm{S}}=\frac{1}{q_{\mathrm{m}}{C}_{\mathrm{p}}}=\frac{1}{\rho C_{\mathrm{p}}n{U}_{\mathrm{m}}\left((h_1+h_2)W_{\mathrm{c}}+W_{\mathrm{w}}{h}_2\right)}.

In this paper, U_m was set as 1 m/s to simplify the calculation.

3) R_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}} of MCHS and E-MCHS could be calculated as follows, in which {\eta }_{\mathrm{M}\mathrm{C}\mathrm{H}\mathrm{S}} is the MCHS of fin efficiency, h is the height of fins for the MCHS or initial high of fins for E-MCHS.

(4)R_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}\mathrm{\_}\mathrm{M}\mathrm{C}\mathrm{H}\mathrm{S}}=\frac{1}{nhL\left(2{\eta }_{\mathrm{M}\mathrm{C}\mathrm{H}\mathrm{S}}{h}_{\mathrm{c}}+W_{\mathrm{c}}\right)},

(5)R_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}\mathrm{\_}\mathrm{E}\mathrm{M}\mathrm{C}\mathrm{H}\mathrm{S}}=\frac{1}{nhL\left(2{\eta }_2{h}_1+{\eta }_3{W}_{\mathrm{w}}+W_{\mathrm{c}}\right)},

where {\eta }_2 and {\eta }_3 refer to the heat exchange efficiency of the fins in E-MCHS, which will be introduced in Section 3.1.2.

The h_c can be calculated as follows, in which D_h is the hydrodynamic diameter (2W_cH/(W_c + H)).

(6)h_{\mathrm{c}}=\frac{Nuk}{D_{\mathrm{h}}}.

The thermal entry effect must be considered, and the dimensionless thermal entrance length is defined as follows, in which Re is the Reynolds number, Pr is the Prandtl number.

(7)x^{\text{*}}=\frac{x}{D_{\mathrm{h}}RePr}.

The Nu can be obtained by using Eqs. (8) and (9) [50], and \alpha is the width ratio of the fin to channel (W_w/W_c).

(8)

(9)

If x^{\ast } ≥ 0.1, the coolant could be deemed as the thermally fully developed flow while the local Nu can be calculated as [51]

(10)\begin{array}{rl}Nu=& 8.235(1-\frac{2.0421}{\alpha }+\frac{3.0853}{{\alpha }^2}-\frac{2.4765}{{\alpha }^3}\\ & +\frac{1.0578}{{\alpha }^4}-\frac{0.1861}{{\alpha }^5}).\end{array}

The Pr of the liquid metal is low and the short thermal entrance region is short, thus the thermal entry effect of liquid metal could be ignored. The Nu of the liquid metal could be calculated by using Eq. (10). In combination with Eq. (6), the convective h_c can be obtained. Therefore, R_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}} can be calculated after obtaining \eta.

3.1.2 Revised fin efficiency of MCHSs and E-MCHSs

The thermal differential equation of fins in MCHS could be simplified as follows, in which \theta represents T-T_{\mathrm{\infty }}.

(11)\frac{{\mathrm{\partial }}^2\theta }{\mathrm{\partial }{x}^2}=m^2\theta .

For MCHSs, the heat flow at the top of fins is 0. Thus, the boundary conditions are (Fig.2(d)):

(12)x=0;T=T_0,

(13)x=H-k\frac{\mathrm{\partial }\theta }{\mathrm{\partial }x}=h{\theta }_{\mathrm{H}}.

The efficiency of the traditional fin is as follows, in which m is the intermediate variable (-\sqrt{hP/k_{\mathrm{s}}{W}_{\mathrm{w}}}).

(14){\eta }_{\mathrm{M}\mathrm{C}\mathrm{H}\mathrm{S}}=\frac{\tan h\left(mH\right)}{mH}.

However, heat transfer between fins and coolant occurs on the top surface of fins in E-MCHS. Thus, the boundary conditions should be

(15)x=0;{\theta }_0=T_0-T_{\mathrm{\infty }},

(16)x=h_1-k\frac{\mathrm{\partial }\theta }{\mathrm{\partial }x}=h{\theta }_{h_1}.

The temperature of the truncated fin is as follows, in which B is the intermediate variable (-\sqrt{h{A}_{\mathrm{c}}/k_{\mathrm{s}}P}),

(17)\theta =\frac{{\theta }_0\mathrm{c}\mathrm{o}\mathrm{s}h\left(m{h}_1-mx\right)+B{\theta }_{h_1}\mathrm{s}\mathrm{i}\mathrm{n}h\left(mx\right)}{\mathrm{c}\mathrm{o}\mathrm{s}h\left(m{h}_2\right)}.

Thus,

(18){\overline{\varphi }}_{x=0}=k{A}_{\mathrm{c}}m{\theta }_0\mathrm{t}\mathrm{a}\mathrm{n}h\left(m{h}_1\right)+\frac{2A_{\mathrm{c}}h{\theta }_0}{\cos h\left(2m{h}_1\right)-B\mathrm{s}\mathrm{i}\mathrm{n}h\left(2m{h}_1\right)}.

The fin efficiency is defined as the ratio of the actual heat loss of fins to the hypothetical heat loss of fins surface at fin-base temperature. Here, to compare with traditional fins, it is assumed that the hypothetical heat loss of fins in E-MCHSs and the conventions fins is equal, and the efficiency of truncated fins is divided into two parts: η₂ indicates the heat transfer efficiency of the side of the fin and η₃ is the heat transfer efficiency of the top surface of fins.

(19)\begin{array}{rl}{\eta }_{\mathrm{E}\text{-}\mathrm{M}\mathrm{C}\mathrm{H}\mathrm{S}}=& {\eta }_2+{\eta }_3=\frac{\mathrm{t}\mathrm{a}\mathrm{n}h\left(m{h}_1\right)}{m{h}_1}\\ & +\frac{2A_{\mathrm{c}}}{P{h}_1\left(1+\cos h\left(2m{h}_1\right)-B\mathrm{s}\mathrm{i}\mathrm{n}h\left(2m{h}_1\right)\right)}.\end{array}

3.1.3 3-dimensional (3D) numerical model of the heat sink

A 3D flow and heat transfer conjugate numerical model was established. The simulation domain consists of the solid heat sink and the fluid domain, as is shown in Fig.3(a). In most of the following simulations, Re is lower than 2300, hence the laminar flow is considered for all of the cases. To simplify the analysis, it is assumed that the flow is steady and laminar [9]. The fluid is Newtonian and incompressible. The thermophysical properties are constant. There is no slip condition at walls. The heat sink is negligible radiative and natural convective heat transfer. There is no viscous dissipation. Body forces are neglected.

Fig.3 3D conjugated numerical simulation model.

Full size|PPT slide

Based on the above assumption, Eqs. (20)–(23) could be solved to compute velocity and the temperature distribution, in which T represents the temperature in the equations and \mu is the dynamic viscosity.

In the fluid zone:

(20)\frac{\mathrm{\partial }{u}_{i}T}{\mathrm{\partial }{x}_i}=\frac{k}{\rho C_{\mathrm{p}}}\frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{x}_i^2},

(21)\frac{\mathrm{\partial }{u}_i}{\mathrm{\partial }{x}_i}=0,

(22)\frac{\mathrm{\partial }\left(\rho u_i{u}_i\right)}{\mathrm{\partial }{x}_i}=-\frac{\mathrm{\partial }p}{\mathrm{\partial }{x}_j}+\mu \frac{{\mathrm{\partial }}^2{u}_j}{\mathrm{\partial }{x}_i^2}.

In the solid zone:

(23)k\frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{x}_i^2}=0.

The inlet was set as consistent U_m and the outlet was a free pressure outlet. The q was set to be 100 W/cm² at the bottom of the heat sink. The thermal insulation boundary condition was applied on the other channel walls. The numerical simulations were completed by using COMSOL-Multiphysics 5.4a, which solved the governing equations using the finite element method.

Based on the simulation results, the R_t of the heat sink was calculated through the calculated temperature. The R_t could be divided into R_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}}, R_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}}, and R_{\mathrm{c}\mathrm{a}\mathrm{l}} [52] as

(24)R_{\mathrm{t}}=\frac{T_{\mathrm{m}\mathrm{a}\mathrm{x}}-T_{\mathrm{i}\mathrm{n}}}{Q},

(25)R_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}}=\frac{t}{k_{\mathrm{s}}A},

(26)R_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}}=\frac{T_{\mathrm{b}}-T_{\mathrm{m}}}{Q}-R_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}},

(27)R_{\mathrm{c}\mathrm{a}\mathrm{l}}=\frac{T_{\mathrm{m}}-T_{\mathrm{i}\mathrm{n}}}{Q}.

The R_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}} calculated by numerical simulation is similar to that by revised empirical correlations.

The flow and thermal modeling of MCHS and E-MCHS were analyzed. The Ga₆₈In₂₀Sn₁₂ was selected as the coolant whose thermophysical properties can be referred to in Tab.1. First, to verify the numerical model, comparisons were made with a numerical study of the same system in Ref. [53], and correlations (8) and (9). The working conditions are that q = 100 W/m², W_c = W_w = 50 μm, L = 1 cm, t = 100 μm, and U_m = 1 m/s. The numerical results were in good agreement with the data of correlations (8) and (9) and the theoretical data in Ref. [53] at all given H. The maximum difference of numerical simulation was 2.9%. When H is less than 500 μm, the difference between the calculated results and the empirical formula is less than 1.25%, which verifies of the numerical model (Fig.3(b) and Fig.3(c)).

Tab.1 Thermo-physical properties of the working fluids and structural materials

Material	ρ/(kg·m−3)	Cp/(J·kg−1·K−1)	µ/(mPa·s)	k/(W·m−1·K−1)	Pr
Water	998.2	4182	1.003	0.6	6.99
Ga68In20Sn12	6363	366	2.22	39	0.02
Silicon	2328	700	–	148	–
Copper	8978	381	–	387.6	–

4 Result and discussion

4.1 Main effects plot

There are many factors affecting the performance of MCHS, such as L, W_c, h of fins, U and the thermal conductivity of heat sink. The influence of the velocity and the thermal conductivity can be determined empirically, i.e., the heat transfer performance is positively related to the velocity and thermal conductivity, but others are not. For E-MCHS, the effect of the h₂ of E-MCHSs is also uncertain. Orthogonal experiments are an effective way to determine the degree of influence of factors on the results with a minimum number of experiments [54]. Four main factors, including h, δ (δ equals to h₂/H), L, and W_c, were selected for orthogonal experimental analysis. The values of the design variables were obtained in COMSOL simulations with 5 different values of the 4 variables. The orthogonal design table L₂₅(5⁴) is listed in Tab.2.

Tab.2 Orthogonal array for simulations

Design No.	h/μm	δ	h×δ	L/cm	Wc/μm
1	200	−0.5	1	0.5	50
2	200	−0.1	3	4	1200
3	200	0	5	1	800
4	200	0.1	2	5	400
5	200	0.5	4	2	200
6	400	−0.5	5	4	400
7	400	−0.1	2	1	200
8	400	0	4	5	50
9	400	0.1	1	2	1200
10	400	0.5	3	0.5	800
11	1000	−0.5	4	1	1200
12	1000	−0.1	1	5	800
13	1000	0	3	2	400
14	1000	0.1	5	0.5	200
15	1000	0.5	2	4	50
16	2000	−0.5	3	5	200
17	2000	−0.1	5	2	50
18	2000	0	2	0.5	1200
19	2000	0.1	4	4	800
20	2000	0.5	1	1	400
21	4000	−0.5	2	2	800
22	4000	−0.1	4	0.5	400
23	4000	0	1	4	200
24	4000	0.1	3	1	50
25	4000	0.5	5	5	1200

Note: The h×δ column is the interaction between h and δ where the values 1‒5 represent the number of levels rather than specific parameter indicators.

Fig.4 displays the main effect of four factors on the five level cases at a maximum temperature. In Fig.4, the horizontal axis is the four factors (X1 to X4) and the interaction between h and δ, and the vertical axis is the mean response for each setting of each factor. The value of range could be used to infer the strength of the influence of factor on the thermal performance. h and L are the two most important influencing factors in regulating the thermal performance of E-MCHSs. δ (δ equals to h₂/H) and W_c have a close value of range, indicating that the regulation of both for maximum temperature is close. The interaction of δ and h does not have a stronger effect on the maximum temperature. The variation of the maximum temperature with h and L is monotonic while the variation with δ is more complex, which will be explained later. The orthogonal analysis shows that the effect of δ is close to that of width on thermal resistance, indicating that the expanded channel could be an important means of regulating the performance of the heat sink.

Fig.4 Main effect of different factors on the maximum temperature.

Full size|PPT slide

4.2 Influence of different factors on liquid metal based E-MCHSs

The orthogonal analysis has demonstrated the main factors affecting the maximum temperature of E-MCHS, but the effect of single factors on the thermal resistance, pressure drop, and P of the heat sink is still unclear, which will be analyzed in this section. The heat sink was made of silicon or copper. q of 100 W/cm² was imposed on a 4 cm (W) × 4 cm (L) footprint portion of a 0.5 mm thick (t).

4.2.1 Effect of h₂

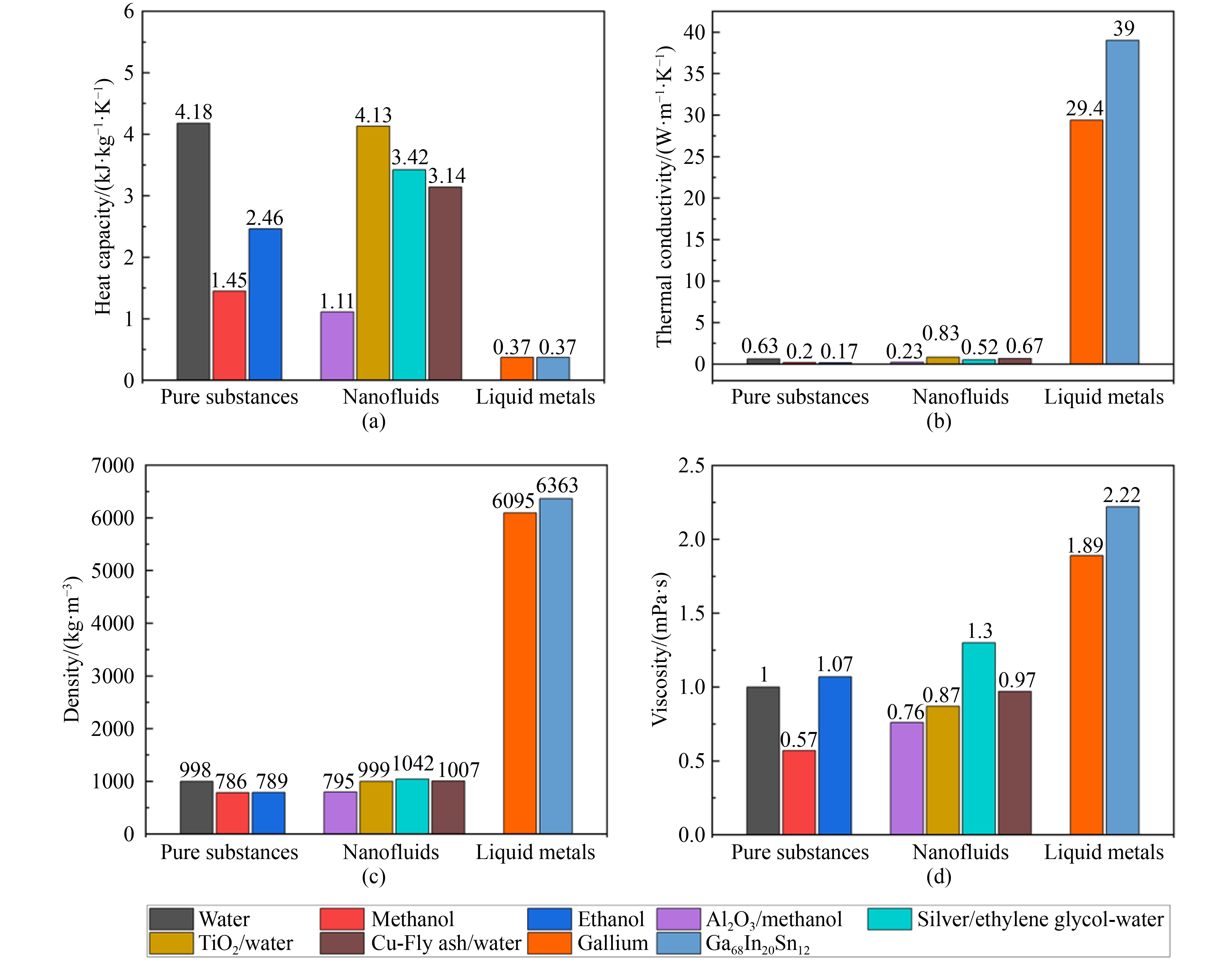
Compared to MCHSs, E-MCHSs introduce a new structural parameter (h₂) which changes the heat transfer performance and the thermal resistance ratio. Fig.5 presents the influence of h₂ ranging from −0.7 to 0.7 mm on the thermal resistance, pressure drop, and P. The weak ability of the liquid metal to take away the heat (low C_p) is the main reason to induce the larger thermal resistance. Thus, creating a gap to allow more liquid metal through the heat sink at a lower pressure drop and a lower P is beneficial for reducing the thermal resistance. Obviously, the R_t of E-MCHS decreases with the increase in the absolute value of h₂ (i.e., |h₂|). The R_t is reduced by 22.1% and 15.3% respectively at h₂ = 0.6 mm and h₂ = −0.6 mm when n = 50. The wider channels (smaller n) could also provide a larger space for the coolant. Thus, the gain of E-MCHSs gradually decreases as n decreases. When n = 30, the thermal resistance decreases by 7.7% and 5.5% when h₂ is equal to 0.2 and −0.2 mm, respectively. However, there is a limit to increasing the total height (H) and width of the heat sink to obtain a better performance. For example, the H of fins will reach 6 mm for the 4 cm (W) × 4 cm (L) heat sinks with n = 10 and β (channel aspect ratio, H/W_c)= 3. The heat sink is not suitable for heat dissipation in a small space. Therefore, although the thermal resistance still seems to decrease as n increases, the performance of E-MCHSs with a smaller n has not been simulated. For the case where the size of the heat dissipation space is determined (H and W are fixed), the h₂ becomes the new structural parameter for heat dissipation optimization. The revised empirical correlations are also used to calculate the heat transfer of E-MCHS and MCHSs. The result calculated by the revised empirical correlations shows the same trend as that of the simulation. But there exists a distinct deviation as n increases. The authors of this paper conjecture that it is the limitation of the empirical correlations (8)‒(10) instead of the correction of fin efficiency that causes this deviation. The flow of liquid metal is thermally developed. Thus, hydrodynamic development and the thermally fully developed heat transfer correlation are inaccurate under this condition [53]. When the coolant is changed to water, the revised empirical correlations are consistent with the simulation results. Therefore, the correction of fin efficiency is retained.

Fig.5 Variation of R_t, the pressure drop, and P at different h₂ values in the geometrical parameters and flow condition of β = 3, α = 1, U_m = 1 m/s.

Full size|PPT slide

Interesting changes in pressure and P also occur. When the gap between the top surface of fins and the cover plate is small, i.e., when the expanded space is small, microchannels have a greater friction resistance. Thus, the pressure drop and the P both increase and subsequently decrease as |h₂| increases. The low-pressure drop makes the structure more stable and reduces the difficulty of packaging. A low P means more efficiency and energy-saving. The R_t and P of E-MCHS and MCHS were compared with the same size, and an interesting conclusion appears: E-MCHS may exhibit a better thermal performance and a lower P when H is the same. Although there is more coolant in the E-MCHS at the same U_m, the total P is still reduced due to the obvious attenuation of pressure drops. In the range of β from 2 to 6, this rule always applies (Fig.6). However, as the total number of runners increases, this advantage of the expanded channel will become smaller, even disappear. In Fig.6, the geometrical parameters and flow condition are: α = 1, n = 50, U_m = 1 m/s, and β ranges from 2 to 7. The H of E-MCHS with β = X + 1 and h₂ = 0.4 mm is equal to that of MCHS with β = X.

Fig.6 R_t versus the P to measure the thermal performance of MCHSs and E-MCHSs.

Full size|PPT slide

4.2.2 Impact of channel aspect ratio

More coolant passing through E-MCHSs to reduce the temperature rise of the coolant is the key to improving the heat transfer performance. If the temperature rise of the heat sink is low, the enhancement effect of the expanded channel will be less. Thus, increasing β (i.e., H) will reap less revenue of E-MCHSs. Fig.7 shows the corresponding plot of the R_t and the P against \beta. The red and black solid lines indicate the R_t and the P of the MCHS (h₂ = 0), respectively. The geometrical parameters and flow condition are: α = 1, U_m = 1 m/s. As β increases, the R_t of E-MCHSs is closer to that of MCHS, and the enhancement generated from the truncated fins structure gradually decreases. The R_t of E-MCHSs is 36.0% lower than that of MCHSs at β = 2, but is only 4.0% lower when β = 6.

Fig.7 Variation of R_t and the pump power with β.

Full size|PPT slide

4.2.3 Effect of U_m

Similar to enlarging \beta, increasing U_m will reduce the profitability of the expanded channel. Fig.8 shows the effect of U_m on P and R_t, where the red and black solid lines indicate the R_t and the P of the MCHS (h₂ = 0), respectively, and the geometrical parameters and flow condition are: β = 3, α = 1. The increase in U_m increases the coolant passing through the heat sink per unit time, indicating that R_cal is lower. When U_m is only 0.5 m/s, the E-MCHSs can obtain a 29.2% lower R_t, and this data are reduced to 15% when U_m increase to 1.5 m/s.

Fig.8 Variation of R_t and the pump power with U_m.

Full size|PPT slide

4.2.4 Effect of structural composite on R_t

In this part, the influence of the structural material for the expanded channel is discussed (Fig.9). The structural materials are silicon and copper, and the geometrical parameters and flow condition are: β = 3, α = 1, U_m = 1 m/s. The R_t decreases about 20% after changing the structural material from silicon to copper, which is consistent with Liu’s conclusion [53]. The Cu-E-MCHSs have similar enhancements to the Si-E-MCHSs. The R_t of Cu-E-MCHS also decreases with the increase in the |h₂|. Similar to Si-E-MCHSs, the R_t seems to decrease as n increases. Therefore, the expanded channel structure have no advantages for Cu based heat sinks because the Cu-MCHSs with high \beta can be fabricated by using laser welding to reduce the R_cal. However, the co-designing electronics with MCHS have been an important structural type of electronic equipment [55]. Generally, silicon rather than copper functions as a microchannel cooling or fluid-distribution network in codesigning electronics. Thus, the cooling system of liquid metal and silicon has an important research significance.

Fig.9 Variation of R_t, the pressure drop and the P at different h₂ values.

Full size|PPT slide

4.2.5 Impact of length on R_t

The temperature rise of the coolant along the Z-direction is more pronounced. Liu et al. have proved that the temperature of water-based heat sink almost remains constant but that of the gallium-based heat sinks increases significantly as the length of the heat sink increases [36]. As a result, the gain of the expanded channel is superior when the length of the flow channel is increased (Fig.10). Fig.10 shows the relationship between R_t and length, where the geometrical parameters and flow condition are W_w = W_c = 400 μm, β = 3, α = 1, U_m = 1 m/s. Clearly, when the length reaches 6 cm, the R_t of E-MCHSs with h₂ = 0.4 mm can be reduced by about 26%.

Fig.10 Variation of R_t at different L values.

Full size|PPT slide

4.3 Change of R_cal, R_conv, and R_t

E-MCHSs could provide more space for the coolant and earn an additional area (n×W_w×L) for heat transfer. For the liquid metal based E-MCHS with h₂ < 0, the heat dissipation capacity of the fin will not be significantly reduced because a new convective heat transfer surface appears in the expansion space. To show the impact of h₂ on the heat transfer performance, the relationship between R_t, R_cal and R_conv at different h₂ values was plotted in Fig.11 where the geometrical parameters and flow condition are: β = 3, α = 1, U_m = 1 m/s. As |h₂| increases, R_t and R_cal decrease while R_conv decreases first and then increases. Although the R_conv of E-MCHS is still higher than R_cal in the absence of the enhancement of convection heat transfer, the change of h₂ can significantly reduce the heat capacity and thermal resistance. At the same time, the convective heat transfer resistance also has interesting changes. Although the height of the fin (h₂ < 0) is reduced, the R_conv is increased to a certain extent. A better cooling performance of E-MCHS is not at the expense of convection capacity, but converts the excess convection capacity into the ability to take away the heat. Thus, as h₂ increases from 0.3 to 0.7 mm, R_conv increases. An increase in h₂ provides more space for the coolant, and R_cal gradually decreases. As h₂ increases, the increase of R_conv will be greater than the decrease of R_cal.

Fig.11 Variation of R_t, R_cond, R_conv and R_cal with n.

Full size|PPT slide

For E-MCHSs without passive techniques to destroy the boundary layer, the velocity boundary layer is thicker due to the higher viscosity of the liquid metal and the longer L of the heat sink (Fig.12(a)). This may account for the fact that even in the liquid metal-based E-MCHS, R_conv is still high. Therefore, for the heat sink with passive techniques, the expanded flow channel structure may be an important route to further improve the total heat transfer performance because the expanded flow channel does not sacrifice the convective heat transfer capability of the heat sink.

Fig.12 Velocity and temperature contours of the outlet of E-MCHS.

Full size|PPT slide

Increasing |h₂| can continuously reduce the R_cal, and decrease the R_conv in a certain interval. The reduction of R_conv is arising from the increase in area for convective heat transfer and the enhancement of convective heat transfer in the expanded space. When h₂ > 0, the area for convection heat transfer is increased by n\times W_{\text{w}}\times L. However, a large expanded space (large h₂) may weaken the convective heat transfer efficiency of the microchannel. When h₂ < 0, E-MCHSs earn the additional area (n\times W_{\text{w}}\times L) for heat transfer at the cost of the area of truncated sidewall (2n\times h_2\times L). Therefore, when h₂ is smaller than W_w/2, the heat transfer area of E-MCHSs increases. Moreover, the convective heat transfer in the expanded space is intense. Increasing h₂ further than W_w/2 does not provide more benefit to reducing R_conv. The truncated fins lose more area for heat transfer once h₂ is larger than W_w/2, making the overall convective heat transfer capacity weaker. The reduced R_cal mainly results from the expanded channel allowing more liquid metal to pass through. This expansion space has little effect on water with a high heat capacity and a low thermal conductivity [49]. The liquid metal in the expanded channel can absorb heat through the Z-direction heat conduction and the convective heat transfer at the upper and top of fins.

Fig.13 shows the 3D isotherms and the 2D isotherms on different sections. Compared with conventional MCHSs, more coolant could be involved in the heat dissipation process. Obviously, the coolant in the expanded channel absorbs and takes away more heat from the heat sink. Therefore, the expanded channel obviously changes the gradient of temperature in the heat sink (Fig.13(c)). The outlet temperature and the average temperature of the coolant are reduced at the same heat flux density, and thereby the maximum temperature of the base of heat sink is finally lowered (Fig.13(b) and Fig.13(d)).

Fig.13 Temperature contour of E-MCHSs and MCHSs.

Full size|PPT slide

5 Conclusions

The flow and thermal performance of liquid metal in the expanded MCHS have been investigated by using numerical simulation and the 1D thermal resistance model. The conclusions can be drawn as follows:

1) Orthogonal experiments show that the expanded channel could be an important way of regulating the performance of E-MCHS with liquid metal.

2) The h₂ in the proper range (about W_w/2 < h₂ < 0, h₂ > 0) endows the E-MCHS with a better cooling capacity under the condition of constant inlet flow rate. A new convective heat transfer surface appears on top of the fins, while more coolant can absorb the heat in the expansion space. Therefore, the thermal resistance of E-MCHS must be smaller than that of MCHS. In actual working conditions, E-MCHS still has a better cooling performance under certain working conditions, even with pressure or pump power as the evaluation index.

3) For the heat sink with a high R_cal, such as that with low fins, a narrow-space, or under low flow rate conditions, the expanded flow channel has a significant improvement. For the microchannels using liquid metal as coolant, high fins are not necessary because the main contradiction is that liquid metal has a poor heat storage capacity rather than heat absorption capacity. The expanded channel can efficiently reduce the temperature rise of the coolant along the flow direction and the decrease of R_t of the heat sink at both lower pressure drop and lower P. There is an optimum value of h₂, which changes with different fin parameters and coolant thermal properties.

Acknowledgements

Thanks to Jing LIU, Zhongshan DENG and Yixin ZHOU for their guidance and suggestions on this work.

Notations

A	Area of heat sink
B	Intermediate variable/(-\sqrt{h{A}_{\text{c}}/k_{\text{s}}P})
Cp	Specific heat capacity/(J·kg−1·K−1)
Dh	Hydrodynamic diameter/(2WcH/(Wc + H))
H	Distance from the bottom of the fins to the cover plate
h	Height of fins for the MCHS or initial high of fins for E-MCHS
h1	Height of fins for E-MCHS
h2	Height of expanded channel for E-MCHS
hc	Heat transfer coefficient
k	Thermal conductivity
L	Heat sink length
m	Intermediate variable/(-\sqrt{hP/k_{\text{s}}{W}_{\text{w}}})
Nu	Nusselt number
n	Channel number
P	Pumping power
Pr	Prandtl number
q	Heat flux
qm	Mass flow
Rt	Total thermal resistance
Rcal	Thermal resistance of heat capacity
Rcov	Thermal resistance of convection
Rcond	Thermal resistance of heat conduction
Re	Reynolds number
T	Temperature
t	Heat sink base thickness
Um	Mean velocity
W	Heat sink width
Ww	Fin width
Wc	Channel width
x, y, z	Rectangular coordinates
Greek letters
α	Ww/Wc, width ratio of the fin to channel
β	H/Wc, channel aspect ratio
δ	h2/H
η	Fin efficiency
θ	T−T∞
μ	Dynamic viscosity
ρ	Mass density
Subscripts
b	Heat sink base
c	Channel
cal	Capacity
conv	Convection
cond	Conduction
f	Fluid

References

1 Elghool A, Basrawi F, Ibrahim T K. . A review on heat sink for thermo-electric power generation: Classifications and parameters affecting performance. Energy Conversion and Management, 2017, 134: 260–277

2 Li Q, Liu J. Liquid metal printing opening the way for energy conservation in semiconductor manufacturing industry. Frontiers in Energy, 2022, 16(4): 542–547

3 Di Capua H M, Escobar R, Diaz A J. . Enhancement of the cooling capability of a high concentration photovoltaic system using microchannels with forward triangular ribs on sidewalls. Applied Energy, 2018, 226: 160–180

4 Chai L, Wang L, Bai X. Thermohydraulic performance of microchannel heat sinks with triangular ribs on sidewalls – Part 1: Local fluid flow and heat transfer characteristics. International Journal of Heat and Mass Transfer, 2018, 127: 1124–1137

5 Derakhshanpour K, Kamali R, Eslami M. Improving performance of single and double-layered microchannel heat sinks by cylindrical ribs: A numerical investigation of geometric parameters. International Communications in Heat and Mass Transfer, 2021, 126: 105440

6 Lori M S, Vafai K. Heat transfer and fluid flow analysis of microchannel heat sinks with periodic vertical porous ribs. Applied Thermal Engineering, 2022, 205: 118059

7 Kim S M, Mudawar I. Analytical heat diffusion models for different micro-channel heat sink cross-sectional geometries. International Journal of Heat and Mass Transfer, 2010, 53(19−20): 4002–4016

8 Ermagan H, Rafee R. Numerical investigation into the thermo-fluid performance of wavy microchannels with superhydrophobic walls. International Journal of Thermal Sciences, 2018, 132: 578–588

9 Chiam Z L, Lee P S, Singh P K. . Investigation of fluid flow and heat transfer in wavy micro-channels with alternating secondary branches. International Journal of Heat and Mass Transfer, 2016, 101: 1316–1330

10 Ma D D, Xia G D, Li Y F. . Design study of micro heat sink configurations with offset zigzag channel for specific chips geometrics. Energy Conversion and Management, 2016, 127: 160–169

11 Ma D D, Xia G D, Wang J. . An experimental study on hydrothermal performance of microchannel heat sinks with 4-ports and offset zigzag channels. Energy Conversion and Management, 2017, 152: 157–165

12 Wu R, Zhang X, Fan Y. . A bi-layer compact thermal model for uniform chip temperature control with non-uniform heat sources by genetic-algorithm optimized microchannel cooling. International Journal of Thermal Sciences, 2019, 136: 337–346

13 Raihan M F B, Al-Asadi M T, Thompson H M. Management of conjugate heat transfer using various arrangements of cylindrical vortex generators in micro-channels. Applied Thermal Engineering, 2021, 182: 116097

14 Al-Asadi M T, Alkasmoul F S, Wilson M C T. Heat transfer enhancement in a micro-channel cooling system using cylindrical vortex generators. International Communications in Heat and Mass Transfer, 2016, 74: 40–47

15 Al-Asadi M T, Alkasmoul F S, Wilson M C T. Benefits of spanwise gaps in cylindrical vortex generators for conjugate heat transfer enhancement in micro-channels. Applied Thermal Engineering, 2018, 130: 571–586

16 Mohammed Hussein H A, Zulkifli R, Mahmood W M F B W. . Structure parameters and designs and their impact on performance of different heat exchangers: A review. Renewable and Sustainable Energy Reviews, 2022, 154: 111842

17 Naqiuddin N H, Saw L H, Yew M C. . Numerical investigation for optimizing segmented micro-channel heat sink by Taguchi-Grey method. Applied Energy, 2018, 222: 437–450

18 Xiao H, Liu Z, Liu W. Conjugate heat transfer enhancement in the mini-channel heat sink by realizing the optimized flow pattern. Applied Thermal Engineering, 2021, 182: 116131

19 Yang D, Jin Z, Wang Y. . Heat removal capacity of laminar coolant flow in a micro channel heat sink with different pin fins. International Journal of Heat and Mass Transfer, 2017, 113: 366–372

20 Bahiraei M, Mazaheri N, Daneshyar M R. Employing elliptical pin-fins and nanofluid within a heat sink for cooling of electronic chips regarding energy efficiency perspective. Applied Thermal Engineering, 2021, 183: 116159

21 Liu C, He Z. High heat flux thermal management through liquid metal driven with electromagnetic induction pump. Frontiers in Energy, 2022, 16(3): 460–470

22 Bahiraei M, Heshmatian S. Thermal performance and second law characteristics of two new microchannel heat sinks operated with hybrid nanofluid containing graphene–silver nanoparticles. Energy Conversion and Management, 2018, 168: 357–370

23 Bahiraei M, Heshmatian S. Electronics cooling with nanofluids: A critical review. Energy Conversion and Management, 2018, 172: 438–456

24 Ijam A, Saidur R, Ganesan P. Cooling of minichannel heat sink using nanofluids. International Communications in Heat and Mass Transfer, 2012, 39(8): 1188–1194

25 Deng Y, Liu J. A liquid metal cooling system for the thermal management of high power LEDs. International Communications in Heat and Mass Transfer, 2010, 37(7): 788–791

26 Hodes M, Zhang R, Lam L S. . On the potential of galinstan-based minichannel and minigap cooling. IEEE Transactions on Components, Packaging, and Manufacturing Technology, 2014, 4(1): 46–56

27 Zhang X D, Yang X H, Zhou Y X. . Experimental investigation of galinstan based minichannel cooling for high heat flux and large heat power thermal management. Energy Conversion and Management, 2019, 185: 248–258

28 Yang X H, Liu J. Advances in liquid metal science and technology in chip cooling and thermal management. In: Greene G A, Cho Y I, Hartnett J P, eds. Advances in Heat Transfer. Elsevier, 2018, 50: 187–300

29 Deng Y, Zhang M, Jiang Y. . Two-stage multichannel liquid-metal cooling system for thermal management of high-heat-flux-density chip array. Energy Conversion and Management, 2022, 259: 115591

30 Ataei M, Sadegh Moghanlou F, Noorzadeh S. . Heat transfer and flow characteristics of hybrid Al₂O₃/TiO₂–water nanofluid in a minichannel heat sink. Heat and Mass Transfer, 2020, 56(9): 2757–2767

31 Arshad W, Ali H M. Experimental investigation of heat transfer and pressure drop in a straight minichannel heat sink using TiO₂ nanofluid. International Journal of Heat and Mass Transfer, 2017, 110: 248–256

32 Kanti P, Sharma K V, Revanasiddappa M. . Thermophysical properties of fly ash-Cu hybrid nanofluid for heat transfer applications. Heat Transfer, 2020, 49(8): 4491–4510

33 Selvam C, Mohan Lal D, Harish S. Thermophysical properties of ethylene glycol-water mixture containing silver nanoparticles. Journal of Mechanical Science and Technology, 2016, 30(3): 1271–1279

34 Fu J, Zhang C, Liu T. . Room temperature liquid metal: Its melting point, dominating mechanism and applications. Frontiers in Energy, 2020, 14(1): 81–104

35 Xing Z, Fu J, Chen S. . Perspective on gallium-based room temperature liquid metal batteries. Frontiers in Energy, 2022, 16(1): 23–48

36 Xiang X, Yang J, Fan A. . A comparison between cooling performances of water-based and gallium-based micro-channel heat sinks with the same dimensions. Applied Thermal Engineering, 2018, 137: 1–10

37 Sarafraz M M, Arya A, Hormozi F. . On the convective thermal performance of a CPU cooler working with liquid gallium and CuO/water nanofluid: A comparative study. Applied Thermal Engineering, 2017, 112: 1373–1381

38 Ye J, Qin P, Xing Z R. . Liquid metal hydraulic actuation and thermal management based on rotating permanent magnets driven centrifugal pump. International Communications in Heat and Mass Transfer, 2022, 139: 106472

39 Zhu J Y, Thurgood P, Nguyen N. . Customised spatiotemporal temperature gradients created by a liquid metal enabled vortex generator. Lab on a Chip, 2017, 17(22): 3862–3873

40 Zhu J Y, Tang S Y, Khoshmanesh K. . An integrated liquid cooling system based on galinstan liquid metal droplets. ACS Applied Materials & Interfaces, 2016, 8(3): 2173–2180

41 Rui Z, Hodes M, Lower N. . Water-based microchannel and galinstan-based minichannel cooling beyond 1 kW/cm² heat flux. IEEE Transactions on Components, Packaging, and Manufacturing Technology, 2015, 5(6): 762–770

42 Chen Z, Qian P, Huang Z. . Study on flow and heat transfer of liquid metal in the microchannel heat sink. International Journal of Thermal Sciences, 2023, 183: 107840

43 Balasubramanian K, Lee P S, Jin L W. . Experimental investigations of flow boiling heat transfer and pressure drop in straight and expanding microchannels: A comparative study. International Journal of Thermal Sciences, 2011, 50(12): 2413–2421

44 Yin L, Jiang P, Xu R. . Heat transfer and pressure drop characteristics of water flow boiling in open microchannels. International Journal of Heat and Mass Transfer, 2019, 137: 204–215

45 Elias M M, Mahbubul I M, Saidur R. . Experimental investigation on the thermo-physical properties of Al₂O₃ nanoparticles suspended in car radiator coolant. International Communications in Heat and Mass Transfer, 2014, 54: 48–53

46 Khaleduzzaman S S, Sohel M R, Mahbubul I M. . Exergy and entropy generation analysis of TiO₂–water nanofluid flow through the water block as an electronics device. International Journal of Heat and Mass Transfer, 2016, 101: 104–111

47 Yang X H, Tan S C, Liu J. Thermal management of Li-ion battery with liquid metal. Energy Conversion and Management, 2016, 117: 577–585

48 Golzar K, Amjad-Iranagh S, Modarress H. Prediction of thermophysical properties for binary mixtures of common ionic liquids with water or alcohol at several temperatures and atmospheric pressure by means of artificial neural network. Industrial & Engineering Chemistry Research, 2014, 53(17): 7247–7262

49 Liu D, Garimella S V. Analysis and optimization of the thermal performance of microchannel heat sinks. International Journal of Numerical Methods for Heat & Fluid Flow, 2005, 15(1): 7–26

50 Harms T M, Kazmierczak M J, Gerner F M. Developing convective heat transfer in deep rectangular microchannels. International Journal of Heat and Fluid Flow, 1999, 20(2): 149–157

51 ShahR KLondonA L. Laminar Flow Forced Convection in Ducts: A Source Book for Compact Heat Exchanger Analytical Data. Salt Lake City: Academic Press, 2014

52 Vajdi M, Sadegh Moghanlou F, Ranjbarpour Niari E. . Heat transfer and pressure drop in a ZrB₂ microchannel heat sink: A numerical approach. Ceramics International, 2020, 46(2): 1730–1735

53 Yang X H, Tan S C, Ding Y J. . Flow and thermal modeling and optimization of micro/mini-channel heat sink. Applied Thermal Engineering, 2017, 117: 289–296

54 Zhang C, Chen L, Tong Z. Multi-objective optimization of heat sink with multi-cross-ribbed-fins for a motor controller. Journal of Engineering and Applied Sciences (Asian Research Publishing Network), 2022, 69(1): 34

55 van Erp R, Soleimanzadeh R, Nela L. . Co-designing electronics with microfluidics for more sustainable cooling. Nature, 2020, 585(7824): 211–216