High performance solid-state thermoelectric energy conversion via inorganic metal halide perovskites under tailored mechanical deformation

Abstract

Solid-state thermoelectric energy conversion devices attract broad research interests because of their great promises in waste heat recycling, space power generation, deep water power generation, and temperature control, but the search for essential thermoelectric materials with high performance still remains a great challenge. As an emerging low cost, solution-processed thermoelectric material, inorganic metal halide perovskites CsPb(I_1–xBr_x)₃ under mechanical deformation is systematically investigated using the first-principle calculations and the Boltzmann transport theory. It is demonstrated that halogen mixing and mechanical deformation are efficient methods to tailor electronic structures and charge transport properties in CsPb(I_1–xBr_x)₃ synergistically. Halogen mixing leads to band splitting and anisotropic charge transport due to symmetry-breaking-induced intrinsic strains. Such band splitting reconstructs the band edge and can decrease the charge carrier effective mass, leading to excellent charge transport properties. Mechanical deformation can further push the orbital energies apart from each other in a more controllable manner, surpassing the impact from intrinsic strains. Both anisotropic charge transport properties andZT values are sensitive to the direction and magnitude of strain, showing a wide range of variation from 20% to 400% (with a ZT value of up to 1.85) compared with unstrained cases. The power generation efficiency of the thermoelectric device can reach as high as approximately 12% using mixed halide perovskites under tailored mechanical deformation when the heat-source is at 500 K and the cold side is maintained at 300 K, surpassing the performance of many existing bulk thermoelectric materials.

Key words： inorganic metal halide perovskites; mechanical deformation; thermoelectrics; first-principle calculations; Boltzmann transport theory

1 Introduction

The development and progress of the modern society highly depend on the acquisition and efficient use of energy, especially when constrained by the current global energy crisis and environmental pollution problems [1–4]. According to recent studies, the global energy consumption of fossil fuels is growing rapidly, and 30%–60% of the energy consumed is wasted in the form of heat [5]. Therefore, recycling the waste heat and increasing the energy efficiency in industries and power plants are becoming more important. Thermoelectric generators have drawn attentions as they can directly convert heat into electricity based on the Seebeck effect [6–8], which is considered as a simple, effective, and environmentally friendly approach to harvest waste heat. Without moving parts, thermoelectric generators can also be greatly applied in space power generation, deep water power generation, and temperature control (see Fig.1, Fig.1) due to their long-term stability and the noiseless feature [9–11]. The power generation conversion efficiency of thermoelectric generators is mainly dependent on the performance of thermoelectric materials (see Fig.1), where the figure of merit (ZT) can measure such thermoelectric performance and a higher ZT corresponds to a high energy conversion efficiency. ZT is defined as ZT=S²σT/(k_e + k_l), where S, σ,T ,k_e and k_l are the Seebeck coefficient, electric conductivity, temperature, electronic and lattice thermal conductivity, respectively. The coupling of these parameters poses a great challenge to development of thermoelectric materials with a high performance.

Fig.1 Schematic diagram of perovskite-based thermoelectric materials, devices, and their potential applications.

Full size|PPT slide

Among the numerous thermoelectric materials, emerging metal halide perovskites and their derivatives have attracted much attention since they were first introduced into the thermoelectric field [12–14]. Eperon et al. [15] first demonstrated that cubic CsPbI₃ perovskite is very stable at low temperature for 200 days when stored in inert air. Kulbak et al. [16] found that devices fabricated with CsPbBr₃ are more stable than MAPbBr₃-based ones. Wang et al. [17] discovered that compositional tuning of perovskites (such as the X-site halide substitution) can further improve their moisture stability. In addition, recent experimental studies have demonstrated the more improved material stability of all-inorganic mixed halide perovskites CsPb(I_1–xBr_x)₃ than their pure counterparts [18]. Moreover, to suppress unwanted phase transition, stabilize the perovskite crystal structure, and tailor the thermoelectric performance, mechanical deformation treatment (see Fig.1) has been extensively utilized and investigated [19,20]. Li et al. [21] proposed that strain engineering strategy can effectively prevent the phase transition of CsPbI₃ based on DFT calculation results. Furthermore, Yalamdha et al. [22] found that CsSnX₃ (X = I, Br, Cl) displays a surprising band inversion behavior under pressures. Zitouni et al. [23] predicted the reduced band gaps in CsPbX₃ compounds under strains using first principles. Rahman and Giri [24] found that uniaxial tensile strain leads to ultra-low thermal conductivities for hybrid organic-inorganic perovskites, indicating the potential of mechanical deformation engineering to tune the physical properties of perovskites. For other thermoelectric material systems, many research groups found that the thermoelectric properties can be highly enhanced via mechanical deformation using first-principles calculations in combination with the Boltzmann transport theory [25–28]. Moreover, in situ machines have been widely developed to apply compressive and extensive strains on the bulk materials in experiment [29,30], suggesting that it is urgent and necessary to understand the mechanical deformation effects. However, there are still several unresolved issues regarding mechanical deformation problems. Particularly, there are very few investigations and discussions on the effects of mechanical deformation and compositional tuning on the thermoelectric properties of inorganic metal halide perovskites.

Motivated by the little existing understanding of the effect of mechanical deformation, the authors of this paper investigated the transport properties of the mixed halide perovskites. Combining first-principles density functional theory (DFT) calculations and the Boltzmann transport theory, they explored the compressive and extensive strain effect on the anisotropic carrier (electron/hole) transport and thermoelectric properties of mixed halide perovskites CsPb(I_1–xBr_x)₃. The electronic band structures revealed that halogen mixing alone, even without mechanical deformation, would lead to orbital splitting at the band edge due to symmetry-breaking, leading to a remarkable thermoelectric ZT of up to approximately 1.7 at 300 K. Upon mechanical deformation (within ±2% strain, as considered here), the splitting of energy levels of the three-fold degenerated 6p_x, 6p_y, and 6p_z orbitals of Pb at the conduction band minimum (CBM) were observed. The energy level of the corresponding splitting orbital would increase with an extensive strain or decrease with a compressive strain. Moreover, mechanical deformation induces a dramatic reconstruction of the CBM, changing the effective mass and the transport properties significantly. The Seebeck coefficient (S) tends to decrease upon splitting of the degenerated p-orbitals of Pb, while the electric conductivity (σ) along corresponding direction tends to increase if the orbital energy level decreases at lower carrier concentrations. Interestingly, mechanical deformation could reduce the optimal carrier concentration for achieving the maximum ZT at 300 K by more than 10 times, which would be beneficial to the doping process in real experimental design [31,32]. Anisotropic ZT values are very sensitive to the direction and magnitude of mechanical deformation, showing a wide-range variation of 20% to 400% (within ±2% strains, as considered herein, with a ZT value of up to 1.85) compared with the unstrained cases. This work highlights the fundamental mechanism and importance of mechanical deformation in the performance of metal halide perovskite devices.

2 Computational methods

The power generation efficiency of the thermoelectric device is mainly dependent on the performance of the thermoelectric materials of both N and P types as shown in Fig.1. The power generation conversion efficiency of the thermoelectric device is expressed as \eta = {\displaystyle \frac{T_{\mathrm{h}}-T_{\mathrm{c}}}{T_{\mathrm{h}}}}{\displaystyle \frac{\sqrt{1+{ZT}_{\mathrm{a}\mathrm{v}\mathrm{e}}}}{\sqrt{1+{ZT}_{\mathrm{a}\mathrm{v}\mathrm{e}}}+T_{\mathrm{c}}/T_{\mathrm{h}}}}, where T_h and T_c are the heat-source (hot-side) and heat-sink (cold-side) temperature of the device, and ZT_ave is the average ZT of the thermoelectric material, which can be tailored effectively via alloy engineering and mechanical deformation effect. In Ref. [33], it is demonstrated that the halide perovskite CsPbI₃ is a promising N-type thermoelectric material, and the Br atom substitutes the I halogen atom, forming the mixed halide perovskites alloy CsPb(I_1–xBr_x)₃, is promising to enhance the thermoelectric performance. First, the substitutions are from a starting pseudo-cubic supercell with 2 × 1 × 1 expansion of the cubic unit cell of CsPbI₃, and it causes 21 symmetry-nonequivalent polymorphic structures. A complete set of the optimized CsPb(I_1–xBr_x)₃ structures are demonstrated in Fig. S1. Then, mechanical deformation was imposed to tailor the transport properties further. The mechanical deformation (external strain) ε_i was introduced by varying the length of each supercell along axis i with the other two axes remaining unstrained, while the nuclei and electrons are allowed to relax freely in order to minimize internal forces and energies. The external strains applied on the inorganic metal halide perovskites range from –2% to 2% with an interval of 0.5%.

For DFT calculations, the Perdew-Burke-Ernzerhof (PBE) [34] functional and the projector augmented-wave (PAW) [35] formalism were used to conduct the geometry optimization and electronic structure calculations using the VASP [36] package. A plane-wave energy cutoff of 500 eV was used, and a pseudo-cubic supercell based on the 2 × 1 × 1 expansion of a cubic unit cell was treated with a Γ-centered 4 × 8 × 8 k-point mesh. Using the quasi-Newton (variable metric) algorithm [37], the lattice volume, shape, and the atomic positions of each configuration were fully optimized to minimize atomic forces below 1.0 meV/Å. The energy convergence criterion is 10^–5 eV for the self-consistent field iteration. A denser 6 × 12 × 12 k-point mesh was used for electronic band structure calculation. The scissor-operator approach [38] was applied to correct the PBE band gaps to the experiment values of CsPbI₃ (1.6 eV) [39] and CsPbBr₃ (2.25 eV) [40], since the PBE functional is known to underestimate the band gaps.

The thermoelectric transport properties (including relaxation time-normalized electric conductivity σ/τ and the Seebeck coefficient S, as well as the resulting power factors PF = S²σ) were calculated according to the Boltzmann transport theory using BoltzTraP [41] based on the relaxation time approximation. To estimate the carrier relaxation time τ, the deformation potential theory [42–46], the Fröhlich model [47], and the Brooks-Herring approach [48] were used to describe the scattering processes between charge carriers with longitudinal acoustic (LA) phonons, polar longitudinal optical (LO) phonons, and ionized impurities, respectively, and the details are presented in Electronic Supplementary Material. Note that τ was estimated using external strain-free CsPb(I_1–xBr_x)₃ structures as the reference in the deformation potential theory because only small strains (up to ±2%) within the elastic deformation region of metal halide perovskites [49] were considered here. Since the above three relaxation time models do not involve mechanical deformation effect, the τ values predicted for unstrained CsPb(I_1–xBr_x)₃ were used here, whose details can be found in Ref. [33].

The Klemens phonon model [50,51] and the Wiedemann-Franz law [52] were used to calculate the lattice thermal conductivity and electronic thermal conductivity (based on the computed electric conductivity), respectively. The Klemens phonon model was used to describe variations in the lattice thermal conductivity due to halogen mixing, while the mechanical deformation effect on lattice thermal conductivity was not considered here. Generally, since the lattice thermal conductivity normally decreases with tensile strain for bulk semiconductors, it is expected that even higher ZT values can be achieved if the mechanical deformation effect is considered in phonon transport. Therefore, the underestimated (lower-limit) ZT values were reported only due to enhanced electronic transport properties under tensile strain [53,54]. But it should also be noted that, for more special materials, such as two-dimensional materials, anomalous responses in thermal conductivity by tensile strains have been discovered [55–59]. For example, Hu et al. [56] found that the thermal conductivity of silicene first increases with extensive strain and then fluctuates at an elevated plateau. Tabarraei and Wang [59] also found that the thermal conductivity of boron nitride nanoribbons first increases and then decreases under stretching. Therefore, further investigations about the thermal conductivities under strain effect are expected.

3 Results and discussion

3.1 Electronic structures and mechanical properties under mechanical deformation

The electronic band structures of pure and mixed halide perovskites CsPb(I_1–xBr_x)₃ (21 polymorphs) without mechanical deformation effect were studied first to understand the effect of halogen mixing. As exhibited in Fig. S2, the band gap tends to increase as the Br composition x increases, while the valence band maximum (VBM) and the CBM (band gap + VBM) decrease as x increases, consistent with previous computational studies [60,61]. As discussed in Ref. [33], for pure halide perovskites (CsPbI₃, CsPbBr₃), the CBM is dominated by the three-fold degenerated 6p_x, 6p_y, and 6p_z orbitals of Pb (see Fig. S3(a)). However, in contrary to the degenerated CBM in the pure halide perovskites, the splitting of 6p_x, 6p_y, and 6p_z orbitals is observed in the CBM of mixed halide perovskites [33] (see Fig. S3(b)), indicating that the electronic structures and band gaps can be tailored by halogen mixing. Such orbital splitting is attributed to the intrinsic strains/stresses resulting from the different van der Waals (vdW) radii of the I and Br halogen ions [33]. However, since the intrinsic strains due to halogen mixing are inhomogeneous, there is no clear trend in the shifts of the 6p_x, 6p_y, and 6p_z orbitals of Pb upon halogen mixing. Therefore, the shifts in the band edge depend highly on the actual atomic arrangement of halogen atoms in each polymorph. Nevertheless, such orbital splitting is also traceable based on the detailed halogen arrangement in each polymorph. For the pseudo-cubic supercell considered here, the CsPb(I_1–xBr_x)₃ polymorphs can be categorized into three groups based on different splitting characters of the Pb-6p orbitals without strains: (i) three-fold degenerated with energy levels of 6p_x, 6p_y, and 6p_z orbitals remain the same, (ii) energy level of only one orbital 6p_x/6p_y/6p_z shifts, while the other two almost remain the same as being two-fold degenerated, and (iii) all three orbitals split. In this paper, only one pure CsPbI₃ (three-fold degenerated) and one mixed CsPbIBr₂ (two-fold degenerated with maximum ZT value) perovskites were taken as examples to investigate the mechanical deformation effects because of the space limitation and the similar varying tendency of the mechanical deformation effects on the transport properties for the other perovskites (see the ESM). The optimized structures of the pure (CsPbI₃) and the mixed (CsPbIBr₂) perovskites are shown in Fig.1(c), Fig.1(d) and the detailed lattice constants are listed in Table S1.

Interestingly, the band edge splitting is also observed when mechanical deformation is applied on even pure CsPbI₃ and CsPbBr₃. Taking the electronic structures of CsPbI₃ for example (see Fig.2–Fig.2), the 6p_x/6p_y/6p_z orbital of Pb shifts up (down) when the strain along the X/Y/Z direction is negative (positive), showing a clear trend due to the controllable strain direction. To understand the origin of the trend above, the contour plots of the electron density projected onto the XY plane are displayed in Fig.2 and the density of states (DOS) in Fig. S5. From the projected DOS, it can also be seen that the Pb-6p_x orbital shifts up or down, attributing to the Rashba-type band splitting effect caused by electron polarization under mechanical deformation [62]. From the electron density, the overlap between Pb-s and I-p orbitals is more pronounced, caused by the applied negative (compressive) strain and the decreased interatomic distance. On the contrary, the electron density is more localized under positive (extensive) strain due to the increased interatomic distance and reduced interactions. Furthermore, the downward shift in the 6p_i orbital of Pb will reconstruct the CBM, leading to a dramatic change in the curvature of CBM along the corresponding direction i. For example, the CBM at the T-point of CsPbI₃ changes from the 6p_y and 6p_z orbitals to the 6p_x orbital under extensive strain along the X direction (see Fig.2), leading to the energy band bending (larger curvature) along the T-R (X) direction and a lower electron effective mass, while the band along the other two directions (T-Y and T-Z) remain almost unaffected compared with the unstrained case. The strain effect on CsPbBr₃ is not focused here due to the previously reported low ZT values of CsPbBr₃ compared with CsPbI₃ and mixed halide perovskites [33].

Fig.2 Tailored electronic structures and electron densities of CsPbI₃ under mechanical deformations.

Full size|PPT slide

Mechanical deformation-induced band edge splitting is also observed in mixed halide perovskites, while it is entangled with the symmetry-breaking-induced band edge splitting due to halogen mixing (causing internal strains). For the mixed CsPbIBr₂ perovskite, there are two I atoms along X direction, while two Br atoms along Y and two Br atoms along Z directions, leading to a high intrinsic compressive strain along Y andZ directions. Therefore, for mixed halide CsPbIBr₂ perovskite, the CBM is dominated by the 6p_x orbital of Pb, while the other two-fold degenerated 6p_y and 6p_z orbital is on a higher energy level (Here, the band edge splitting in the unstrained mixed halide perovskites is depicted in Fig. S3(b) for reference and comparison.). Consequently, an extensive strain along X in the CsPbIBr₂ polymorph (Fig.3) will strengthen the splitting due to the downward shift of the 6p_x orbital. However, the extensive strains alongY or Z direction would make the original two-fold 6p_y and 6p_z orbitals become all three orbitals split. It is interesting to find that the mechanical deformation-induced band edge splitting in mixed halide perovskite can either reinforce or cancel out (weaken) the symmetry breaking-induced band edge splitting, depending on the direction, magnitude, and sign (compressive or extensive) of the strain. In addition, similar to the pure halide perovskites, a clear trend is found in mixed halide perovskites: extensive (compressive) strains along direction i will lead to downward (upward) shifts of the corresponding 6p_i-orbital of Pb. However, for the mixed halide perovskite CsPbIBr₂, the mechanical deformation along both X, Y, and Z directions would not dominate over the intrinsic strain, and the Pb-6p_x orbital maintains the CBM. For some other perovskites, however, the mechanical deformation effect would dominate over the intrinsic strain-induced band edge shifting (see Figs. S6–S8 and Supplementary Note) and the carrier effective mass will suddenly change under strain if the mechanical deformation can overcome the symmetry-breaking effect to reconstruct the CBM, which depends on the actual atomic arrangement in each polymorph [33], and therefore, lead to a very clear trend in the resulting band edge shifting.

Fig.3 Tailored electronic properties of CsPbIBr₂ under mechanical deformations.

Full size|PPT slide

The Young’s modulus, Shear modulus, Bulk modulus, and Poisson ratio of the two representative perovskites with and without mechanical deformation effect were then calculated, as it is essential to understand the mechanical properties for the device fabrications and engineering applications [63], especially the crack problems in thermoelectric device caused by the thermo-mechanical stresses. As is well known, the Young’s modulus is used to determine the stiffness of the crystal, whereas Shear modulus, Bulk modulus, and Poisson ratio to deal with the material rigidity, plastic deformation, and ductile properties, respectively. Without mechanical deformation, as is shown in Fig.4, the values of mechanical properties in the mixed halide perovskite CsPbIBr₂ are slightly higher than those of pure halide perovskite CsPbI₃, attributing to the higher strength of the Pb-Br bond than that of the Pb-I bond. In addition, the different chemical bond type makes the mixed halide perovskite CsPbIBr₂ present anisotropic compared with the isotropic mechanical properties (along X, Y, and Z directions) of pure halide perovskite CsPbI₃. Furthermore, the mechanical deformation can also destroy the isotropic mechanical properties of the pure perovskite CsPbI₃ (see Fig.4) or aggravate/reduce the degree of the anisotropic properties of the mixed halide perovskite CsPbIBr₂ (see Fig.4), which can also be verified from the electron density (Fig.2). Generally, the mechanical properties along the corresponding direction would increase (decrease) when the bond length decreases (increases) under negative (positive) strains, indicating that the mechanical properties can also be well tailored under mechanical deformation. The mechanical properties under mechanical deformation along other directions are shown in Figs. S9 to S10, and Table S2 summarizes detailed values of the mechanical properties.

Fig.4 Surface contours of the mechanical properties of CsPbI₃ and CsPbIBr₂.

Full size|PPT slide

3.2 Band edges, gaps, and carrier effective masses under mechanical deformation

The mechanical deformation-induced band edge splitting significantly modifies the band edges, band gaps, and carrier effective masses of both pure and mixed halide perovskites. Taking CsPbI₃ for example (Fig.5), the mechanical deformation-induced variations in VBM and CBM do not depend on the direction of strain, showing an isotropic strain effect due to its high crystalline symmetry. The VBM of CsPbI₃ exhibits a linear correlation with strain along all three directions (Fig.5), attributing to the strain-proportional bonding/antibonding character of the Pb-6s and I-5p orbitals which are determined by the interatomic distance (see Fig.2). However, the CBM and the band gap of CsPbI₃ (Fig.5–Fig.5) exhibit a nonlinear trend with strain (showing a maximum at zero strain), attributing to the splitting of the degenerated Pb-6p orbitals. Specifically, as shown in Fig.5, the energy levels of the Pb-6p_y and 6p_z orbitals remain two-fold degenerated with or without strain along the X direction, while they constitute the CBM under zero or compressive strains due to their positive linear correlation with strain. The energy of the split Pb-6p_x orbital crosses the energies of the Pb-6p_y and 6p_z orbitals at zero strain, and becomes the new CBM under extensive strain along X (the same trend is observed under the strain along Y or Z direction as shown in Fig. S11) due to its negative linearly correlation with strain. Such a crossover in the band edge orbital energies leads to different curvatures at the CBM as a function of strain (see Fig.2–Fig.2), which exhibits a sudden decrease in the electron effective mass along the same direction of the extensive strain (see Fig.5). The effective mass computed from the band structure is expressed as m^{\ast }={\hslash }^2/ {\displaystyle \frac{{\mathrm{\partial }}^{2}E}{{\mathrm{\partial }k}^2}}, and therefore, the larger the curvature at the CBM, the smaller the effective mass value. Smaller electron effective masses lead to a higher electron mobility which is beneficial to the thermoelectric transport performance.

Fig.5 Mechanical deformation-tunable band edges, band gaps, and carrier effective masses in CsPbI₃.

Full size|PPT slide

The same trend in band edge splitting and orbital energy shifting is observed in mixed halide perovskite CsPbIBr₂, as shown in Fig.6, synergistically contributed by the symmetry-breaking and the mechanical deformation effects. It is noted that the mechanical deformation-induced variations in VBM do not depend on the direction of strain even in a highly anisotropic structure (see Fig.6), attributing to the same strain effect (Fig.2) involving the overlap between the Pb-6s and I-5p orbitals. On the other hand, the CBM and the resulting band gap present anisotropic properties, as a result of the combination of the band splitting caused by the mechanical deformation effect and the original splitting caused by halogen mixing for the Pb-6p orbitals (see Fig.6–Fig.6). That is, the energy level of the Pb-6p_x orbital (CBM) would decrease under strain along X direction, while slightly increase along Y direction (see Fig.6, Fig.6) (the same trend is observed under strain along Z direction as shown in Fig. S12). Furthermore, the electron effective masses of the representative mixed halide perovskite as a function of strain applied along different directions are shown in Fig.6 and Fig.6. Generally, the effective mass along the corresponding direction tends to slightly increase (decrease) with extensive (compressive) strain, while keeping steady along the other two directions for the mixed halide perovskite CsPbIBr₂ because there is no crossover of the orbitals (Pb-p_x maintain the CBM). However, the carrier effective mass will suddenly change under strain if the mechanical deformation effect can overcome the symmetry-breaking effect to reconstruct the CBM (see Fig. S8).

Fig.6 Mechanical deformation-tunable band edges, band gaps, and carrier effective masses in CsPbIBr₂.

Full size|PPT slide

Structures with three-fold degenerated orbitals present the isotropic properties, and the two-fold degenerated orbital structures exhibit the same properties along the corresponding two directions, while the properties of the structures with all orbitals split are mostly anisotropic. In addition, the band structures, band gaps, and even anisotropic transport properties (such as the effective mass) can be modulated by the splitting and shifts of the 6p_x, 6p_y, and 6p_z orbitals of Pb near the CBM. While this can be readily realized by intrinsic strains upon halogen mixing, mechanical deformation could enable controllable enhancement in transport properties along any direction needed. Therefore, to achieve the maximum transport properties, the magnitude, direction, and sign of the mechanical deformation should be analyzed concretely and applied according to specific polymorphs.

3.3 Thermoelectric transport properties under mechanical deformation

As the band structures, band gaps, and carrier effective masses are strain-tunable in mixed halide perovskites, it is expected that thermoelectric transport properties, including the Seebeck coefficient, electrical conductivity, power factor, and the resulting ZT values are controllable as well. In this paper, the mechanical deformation effect in n-doped (with electron as the charge carrier) mixed halide perovskites at 300 K was mainly focused on because band splitting occurs at the CBM and higher ZT values were predicted in n-doped CsPb(I_1–xBr_x)₃ in Ref. [33]. It is expected that a similar temperature dependence would hold in thermoelectric transport properties of n-doped CsPb(I_1–xBr_x)₃ under mechanical deformation. Herein, “I-J” was used to denote the strain direction I and the resulting thermoelectric transport properties along dimension J. For the pure halide perovskite CsPbI₃ (three-degenerated Pb-6p orbital), the change in transport properties along a direction when a strain is applied along that same direction shares the same trend (i.e., X-X, Y-Y, and Z-Z cases are the same). This also applies to the orthogonal I-J cases, i.e., the change in transport properties for the X-Y (X-Z) case is similar to those for the Y-X (Y-Z) and Z-X (Z-Y) cases. Therefore, for the pure halide perovskite CsPbI₃, the mechanical deformation effect is shown only along one direction and it is presumed that the other two are similar.

For the CsPbI₃ perovskite with three-fold degenerated Pb-6p orbitals, the magnitude of the Seebeck coefficient S decreases as the magnitude of the strain increases along X because of the decreased level of degeneracy from three-fold to two-fold at 300 K (see Fig.7–Fig.7). The Seebeck coefficient along . decreases more than those along X-Y and X-Z. A very different trend is observed in the electric conductivity σ, in which σ along X-X (X-Y and X-Z) increases (decreases significantly) when enlarging the strain at lower carrier concentrations, while that along X-X (X-Y and X-Z) decreases (increases slightly) gradually when enlarging the compressive strain (see Fig.7–Fig.7), attributing to the combination of the carrier relaxation time-normalized electric conductivity σ/τ and the estimated carrier relaxation time τ (see Fig. S13). The carrier relaxation time-normalized electric conductivity σ/τ along X-X (X-Y and X-Z) increases (decreases significantly) when enlarging the extensive strain, while that along X-X (X-Y and X-Z) decreases (increases slightly) gradually when enlarging the compressive strain. The relaxation time remains stable as the strain varies, while it changes sharply when the effective mass changes dramatically (see Fig. S13(d)), which can be attributed to the fact that the polar optical relaxation time is dominant at a lower concentration, and the relaxation time would therefore increase sharply due to the small effective mass (almost massless) as the mechanical deformation applies.

Fig.7 Transport properties of CsPbI₃ at 300 K under mechanical deformations.

Full size|PPT slide

The decrease in S and increase in σ along X-X with mechanical deformation reduce the optimal carrier concentration n_e for achieving the maximum ZT value significantly, by one order of magnitude from 10¹⁹ to 10¹⁸ cm^–3 (see Fig.7). This is beneficial to meet the longstanding challenge in doping halide perovskites at high carrier concentrations in experiment due to their self-compensating nature [31,32], although the maximum ZT values along X-X are only slightly enhanced from 0.5 without strain to 0.55 at an extensive strain of 2%. But it should also be noted that, even though the optimal carrier concentration decreases significantly, it poses a challenge to heavily dope perovskites in existing experiments. Therefore, further investigations on the impact from defects and heterovalent doping methods are expected. Interestingly, Kang and Wang [64] proposed that, for CsPbBr₃, most of the intrinsic defects induce shallow transition levels and small formation energies, which may lead to a high carrier concentration. Recently, Zhang et al. [65] have proposed that the deep defect level engineering concept is a strategy to optimize the carrier concentration. Ren et al. [66] also proposed that by introducing an intermediate-level impurity, the carrier concentration can be tailored and optimized simultaneously over a wide temperature range.

On the other hand, the maximum ZT values along X-Y and X-Z decrease quite a lot under extensive strains because of the slightly decreased Seebeck coefficient and significantly reduced electric conductivity, while the ZT values are only slightly enhanced under compressive strains (Fig.7(h), Fig.7(i)).

For the mixed halide perovskite of CsPbIBr₂, with only one Pb-6p_x orbital shifts while the other two remain at the same energy level without mechanical deformation, such that transport properties along Y and Z directions are similar. Since the mechanical deformation-induced variations in S and σ follow the same trend mentioned above (resulting from orbital shifts), the computed anisotropic ZT values are only shown as a function of carrier concentration n_e when strains are applied along different directions (The detailed transport properties are shown in Figs. S14–S17). As shown in Fig.8 and S17, the varies in transport properties and the resulting ZT values for the Y-Y (Y-Z, X-Y) case are similar to those for theZ-Z (Z-Y, X-Z) cases because of the two-fold degenerated Pb-6p_y and 6p_z orbitals. Then, as discussed above, extensive strains shifting down the 6p_y and 6p_z orbital or compressive strains shifting up the 6p_x orbital would weaken the symmetry-breaking effect, however, the mechanical deformation effect is not strong enough to cancel out the symmetry-breaking effect completely. Therefore, the ZT values and the optimized carrier concentration to achieve the maximum ZT values exhibit little deformation effect, regardless of the strain direction, because of the steady effective mass and the maintained CBM (Pb-6p_x orbital). On the contrary, the sharply change of the optimal carrier concentration and the transport properties will be exhibited when the mechanical deformation covers the intrinsic strain effect (see Figs. S18–S20). Finally, the maximum ZT value can be achieved from about 1.7 (no strain) to 1.85 (under extensive strain along X or compressive strain along Y and Z directions) along X direction.

Fig.8 Anisotropic ZT values of CsPbIBr₂ at 300 K under mechanical deformations.

Full size|PPT slide

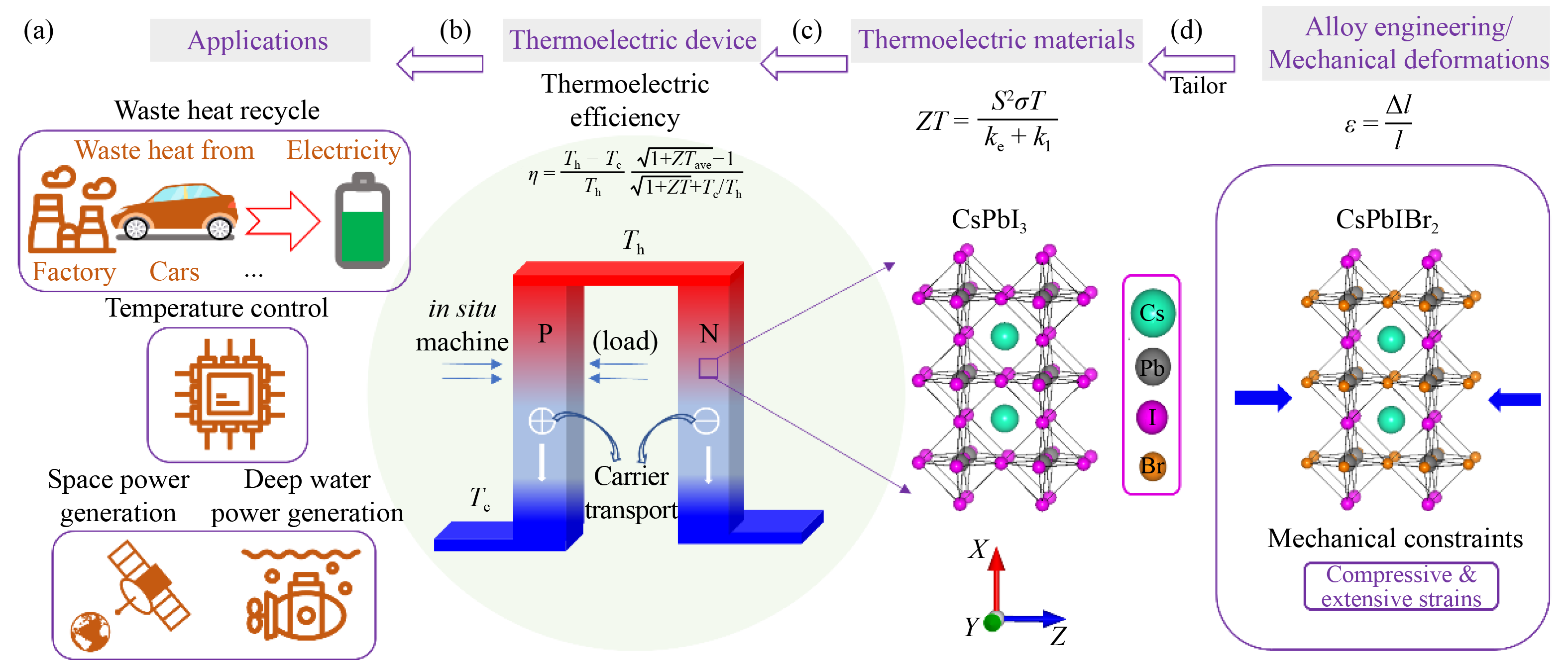
The thermoelectric transport properties and ZT values are mechanical deformation-tunable in inorganic metal halide perovskites, either by mechanical deformation or intrinsic strains caused by halogen mixing. These two factors can be combined synergistically to achieve remarkable ZT values in CsPb(I_1–xBr_x)₃. For pure CsPbI₃ perovskite with three-fold degenerated Pb-6p orbitals, the maximum ZT values can be enhanced from about 0.5 without strain to 0.55 with a strain of ±2% (e.g., X-X, Y-Y and Z-Z). For mixed halide CsPbIBr₂ perovskite with two-fold degenerated Pb-6p orbitals, the maximum ZT values can be enhanced from 1.7 without strain to 1.85 with a strain of ±2% (e.g., X-X and Y-X/Z-X). Such high ZT values (1.85 at 300 K) is even higher than the best commercialized and most reported Bi₂Te₃ based materials at room temperature, where the highest reports are the Fe-doped Bi_0.4Sb_1.6Te₃ (experimental ZT = ~1.4) [67], and Bi_0.5Sb_1.5Te₃ (experimental ZT = 1.72) [68]. For metal halide perovskites, the majority of the experimental reports on ZT values are Sn-based [14]. In contrast, the reported ZT values are still low (below 0.2) for metal halide perovskites, and the highest reported ZT value is 0.19 for (F4-TCNQ)-doped FASnI₃ [69]. Therefore, more investigations and effects are urgently needed to experimentally verify the appealing theoretical reports [14]. Finally, the power generation efficiency of the thermoelectric device as a function of the hot-side temperatures coming from different heat sources (room temperature at the cold-side) was estimated. As shown in Fig.9, the conversion efficiency is highly enhanced from CsPbI₃ (ZT = 0.5) to CsPbIBr₂ (ZT =1.85) under intrinsic strains and mechanical deformation, especially at high temperatures. Such high efficiency is comparable or even higher than many promising bulk thermoelectric materials [70], (besides the Bi₂Te₃ series) including the multicomponent oxides series, CuSe composites series, SnSe series, half-Heusler series, GeTe/PbTe series, and etc. Herein, one experimental report of the promising thermoelectric materials among each series is chosen as examples, such as BiCuSeO (ZT = ~0.45 at 300 K) [71], α-Cu_2+xSe (experimental average ZT = ~0.6 between 300 and 400 K) [72], SnSe (ZT = 0.8 at 300 K) [73], TaFeSb (average ZT = 0.93 between 300 and 973 K) [74], Pb_0.98Na_0.02Te-8%SrTe (average ZT = 1.2 between 300 and 800 K) [75]. The power generation efficiency can reach as high as 4.9% (CsPbI₃) to 12% (CsPbIBr₂ under 1% extensive strain) at 500 K, and these enhancements suggest that mechanical deformation in combination with the alloy engineering are efficient and controllable strategies, and the thermoelectric device with such high efficiency is promising to be applied in thermoelectrical fields and recycle the waste heat.

Fig.9 Thermoelectric energy conversion efficiency of inorganic halide perovskites compared with other thermoelectric materials. (Efficiency of CsPbI₃ without strain, and CsPbIBr₂ under 1% extensive strain as a function of the hot-side temperature, compared with other experimental reports of other promising thermoelectric materials, including BiCuSeO (ZT = ~0.45 at 300 K) [71], α-Cu_2+xSe (average ZT = ~0.6 between 300 and 400 K) [72], SnSe (ZT = 0.8 at 300 K) [73], TaFeSb (average ZT = 0.93 between 300 and 973 K) [74], Pb_0.98Na_0.02Te-8%SrTe (average ZT = 1.2 between 300 and 800 K) [75], Fe-doped Bi_0.4Sb_1.6Te₃ (ZT = ~1.4 at 300 K) [67], and Bi_0.5Sb_1.5Te₃ (ZT = 1.72 at 300 K) [68]).

Full size|PPT slide

4 Conclusions

In summary, it is discovered in this paper that mechanical deformation can fine-tune electronic band structures, anisotropic thermoelectric transport properties, and ZT values of mixed halide perovskites CsPb(I_1–xBr_x)₃. While halide mixing can readily introduce splitting of the original three-fold degenerated Pb-6p orbitals in pure halide perovskites (CsPbI₃ and CsPbBr₃) due to symmetry-breaking induced intrinsic strains, the shifts of these orbitals are highly anisotropic and challenging to control in various mixed halide perovskite polymorphs. In meeting this challenge, mechanical deformation can further push the orbital energies apart from each other in a more controllable manner, and therefore, the CBM can be effectively controlled through mechanical deformation, out-running the impact from the pre-existed intrinsic strains. For example, the directional dependent Pb-6p orbital energy levels would shift down with extensive strain or shift up with compressive strain. The resulting carrier effective mass would vary dramatically due to the reconstruction of the CBM, attributing to the downward shifted Pb-6p_x, 6p_y or 6p_z orbital that replaces the original CBM orbital. The carrier effective masses would then correlate inversely with the carrier relaxation time to influence other electronic transport properties. As a result, the Seebeck coefficient decreases as the three-fold degenerated orbitals split, while the electric conductivity along a direction would increase at lower carrier concentrations, when the orbital energy level along that same direction decreases. More interestingly, the reduced Seebeck coefficient and increased electric conductivity result in a significant reduction of the optimal carrier concentration to achieve maximum ZT values, providing a new avenue to meet the longstanding challenges in doping perovskites at higher carrier concentrations. Finally, the thermoelectric energy conversion efficiency can be tailored from (CsPbI₃) 4.9% to 12% (CsPbIBr₂ under 1% extensive strain) under intrinsic strains and mechanical deformation at 500 K. It is believed that this paper will provide fundamental insights into the synergetic strategy to combine halogen mixing (symmetry-breaking) and mechanical deformation to enhance the thermoelectric performance and optimize the doping process in mixed halide perovskites.

Acknowledgements

This work was financially supported by the Thousand Talent Young Scholar Program (BE0200006), Shanghai Aerospace Science and Technology Innovation Fund (USCAST2020-13), the Oceanic Interdisciplinary Program from Shanghai Jiao Tong University (SL2020MS008), and the National Natural Science Foundation of China (Grant No. 51776041).

Electronic Supplementary Material

Supplementary material is available in the online version of this article at https://doi.org/10.1007/s11708-022-0831-y and is accessible for authorized users.

References

1 WangH, HeJ. China’s pre-2020 CO₂ emission reduction potential and its influence. Frontiers in Energy, 2019, 13( 3): 571– 578

2 SemieniukG, TaylorL, RezaiA. . Plausible energy demand patterns in a growing global economy with climate policy. Nature Climate Change, 2021, 11( 4): 313– 318

3 PathakL, ShahK. Renewable energy resources, policies and gaps in BRICS countries and the global impact. Frontiers in Energy, 2019, 13( 3): 506– 521

4 ZhangX, GengY, TongY W. . Trends and driving forces of low-carbon energy technology innovation in China’s industrial sectors from 1998 to 2017: from a regional perspective. Frontiers in Energy, 2021, 15( 2): 473– 486

5 GarofaloE, BevioneM, CecchiniL. . Waste heat to power: technologies, current applications, and future potential. Energy Technology (Weinheim), 2020, 8( 11): 2000413

6 ZhaoC, ZhangZ, ZhangX. Special issue: nanotechnology in energy. Frontiers in Energy, 2018, 12( 1): 1– 4

7 LiuJ, GuoZ. Unconventional energy: seeking the ways to innovate energy science and technology. Frontiers in Energy, 2018, 12( 2): 195– 197

8 LiuZ, YuanS, YuanY. . A thermoelectric generator and water-cooling assisted high conversion efficiency polycrystalline silicon photovoltaic system. Frontiers in Energy, 2021, 15( 2): 358– 366

9 TwahaS, ZhuJ, YanY. . A comprehensive review of thermoelectric technology: materials, applications, modelling and performance improvement. Renewable & Sustainable Energy Reviews, 2016, 65 : 698– 726

10 JiaD, LiuJ. Human power-based energy harvesting strategies for mobile electronic devices. Frontiers of Energy and Power Engineering in China, 2009, 3( 1): 27– 46

11 LinS, ChenC, ZhaoL. . Molecular insights into water vapor adsorption and interfacial moisture stability of hybrid perovskites for robust optoelectronics. International Journal of Heat and Mass Transfer, 2021, 175 : 121334

12 HeY, GalliG. Perovskites for solar thermoelectric applications: a first principle study of CH₃NH₃AI₃ (A = Pb and Sn). Chemistry of Materials, 2014, 26( 18): 5394– 5400

13 TangG, GhosezP, HongJ. Band-edge orbital engineering of perovskite semiconductors for optoelectronic applications. Journal of Physical Chemistry Letters, 2021, 12( 17): 4227– 4239

14 HuS, RenZ, DjurišićA B. . Metal halide perovskites as emerging thermoelectric materials. ACS Energy Letters, 2021, 6( 11): 3882– 3905

15 EperonG E, PaternòG M, SuttonR J. . Inorganic caesium lead iodide perovskite solar cells. Journal of Materials Chemistry. A, Materials for Energy and Sustainability, 2015, 3( 39): 19688– 19695

16 KulbakM, GuptaS, KedemN. . Cesium enhances long-term stability of lead bromide perovskite-based solar cells. Journal of Physical Chemistry Letters, 2016, 7( 1): 167– 172

17 WangZ, ShiZ, LiT. . Stability of perovskite solar cells: a prospective on the substitution of the A cation and X anion. Angewandte Chemie International Edition, 2017, 56( 5): 1190– 1212

18 WangX, LingY, LianX. . Suppressed phase separation of mixed-halide perovskites confined in endotaxial matrices. Nature Communications, 2019, 10( 1): 695

19 YuH, SunQ, ZhangT. . Is the strain responsible to instability of inorganic perovskites and their photovoltaic devices? Materials Today. Energy, 2021, 19 : 100601

20 MoloneyE G, YedduV, SaidaminovM I. Strain engineering in halide perovskites. ACS Materials Letters, 2020, 2( 11): 1495– 1508

21 LiZ, QinY, DongL. . Elastic and electronic origins of strain stabilized photovoltaic gamma-CsPbI₃. Physical Chemistry Chemical Physics, 2020, 22( 22): 12706– 12712

22 YalamehaS, SaeidiP, NourbakhshZ. . Insight into the topological phase and elastic properties of halide perovskites CsSnX₃ (X  = l, Br, Cl) under hydrostatic pressures. Journal of Applied Physics, 2020, 127( 8): 085102

23 ZitouniH TahiriN El BounaguiO, . How the strain effects decreases the band gap energy in the CsPb X₃ perovskite compounds ? Phase Transitions, 2020, 93( 5): 455– 469

24 RahmanM A, GiriA. Uniquely anisotropic mechanical and thermal responses of hybrid organic-inorganic perovskites under uniaxial strain. Journal of Chemical Physics, 2021, 155( 12): 124703

25 DingG, GaoG Y, YuL. . Thermoelectric properties of half-Heusler topological insulators MPtBi (M = Sc, Y, La) induced by strain. Journal of Applied Physics, 2016, 119( 2): 025105

26 LuoX, SullivanM B, QuekS Y. First-principles investigations of the atomic, electronic, and thermoelectric properties of equilibrium and strained Bi₂Se₃ and Bi₂Te₃ including van der Waals interactions. Physical Review B: Condensed Matter and Materials Physics, 2012, 86( 18): 184111

27 PalK, AnandS, WaghmareU V. Thermoelectric properties of materials with nontrivial electronic topology. Journal of Materials Chemistry. C, Materials for Optical and Electronic Devices, 2015, 3( 46): 12130– 12139

28 ZouC, LeiC, ZouD. . Uniaxial tensile strain induced the enhancement of thermoelectric properties in n-type BiCuOCh (Ch = Se, S): a first principles study. Materials (Basel), 2020, 13( 7): 1755

29 BhaskarL K, KumarG, SrinivasanN. . Design and development of a miniaturized multiaxial test setup for in situ X-ray diffraction experiments. Review of Scientific Instruments, 2021, 92( 1): 015116

30 KleberX, RouxP, MorinM. Sensitivity of the thermoelectric power of metallic materials to an elastic uniaxial strain. Philosophical Magazine Letters, 2009, 89( 9): 565– 572

31 HaqueM A, KeeS, VillalvaD R. . Halide perovskites: thermal transport and prospects for thermoelectricity. Advanced Science (Weinheim, Baden-Wurttemberg, Germany), 2020, 7( 10): 1903389

32 NayakP K, SendnerM, WengerB. . Impact of Bi³⁺ heterovalent doping in organic-inorganic metal halide perovskite crystals. Journal of the American Chemical Society, 2018, 140( 2): 574– 577

33 YanL, WangM, ZhaiC. . Symmetry-breaking induced anisotropic carrier transport and remarkable thermoelectric performance in mixed halide perovskites CsPb(I_1–xBr_x)₃. ACS Applied Materials & Interfaces, 2020, 12( 36): 40453– 40464

34 PerdewJ P, BurkeK, ErnzerhofM. Generalized gradient approximation made simple. Physical Review Letters, 1996, 77( 18): 3865– 3868

35 TorrentM, JolletF, BottinF. . Implementation of the projector augmented-wave method in the ABINIT code: application to the study of iron under pressure. Computational Materials Science, 2008, 42( 2): 337– 351

36 KresseG, FurthmüllerJ. Efficient iterative schemes for Ab initio total-energy calculations using a plane-wave basis set. Physical Review B: Condensed Matter, 1996, 54( 16): 11169– 11186

37 PulayP. Convergence acceleration of iterative sequences: the case of SCF iteration. Chemical Physics Letters, 1980, 73( 2): 393– 398

38 FiorentiniV V, BaldereschiA. Dielectric scaling of the self-energy scissor operator in semiconductors and insulators. Physical Review B: Condensed Matter, 1995, 51( 23): 17196– 17198

39 YinW J, YanY, WeiS H. Anomalous alloy properties in mixed halide perovskites. Journal of Physical Chemistry Letters, 2014, 5( 21): 3625– 3631

40 StoumposC C, MalliakasC D, PetersJ A. . Crystal growth of the perovskite semiconductor CsPbBr₃: a new material for high-energy radiation detection. Crystal Growth & Design, 2013, 13( 7): 2722– 2727

41 MadsenG K H, SinghD J. BoltzTraP. A code for calculating band-structure dependent quantities. Computer Physics Communications, 2006, 175( 1): 67– 71

42 XiJ, LongM, TangL. . First-principles prediction of charge mobility in carbon and organic nanomaterials. Nanoscale, 2012, 4( 15): 4348– 4369

43 TangL, LongM, WangD. . The role of acoustic phonon scattering in charge transport in organic semiconductors: a first-principles deformation-potential study. Science in China. Series B, Chemistry, 2009, 52( 10): 1646– 1652

44 WangD, ShiW, ChenJ. . Modeling thermoelectric transport in organic materials. Physical Chemistry Chemical Physics, 2012, 14( 48): 16505– 16520

45 WangD, TangL, LongM. . First-principles investigation of organic semiconductors for thermoelectric applications. Journal of Chemical Physics, 2009, 131( 22): 224704

46 LuY B, KongX, ChenX. . Piezoelectric scattering limited mobility of hybrid organic-inorganic perovskites CH₃NH₃PbI₃. Scientific Reports, 2017, 7( 1): 41860

47 FröhlichH. Electrons in lattice fields. Advances in Physics, 1954, 3( 11): 325– 361

48 ChattopadhyayD, QueisserH J. Electron scattering by ionized impurities in semiconductors. Reviews of Modern Physics, 1981, 53( 4): 745– 768

49 YuJ, WangM, LinS. Probing the soft and nanoductile mechanical nature of single and polycrystalline organic–inorganic hybrid perovskites for flexible functional devices. ACS Nano, 2016, 10( 12): 11044– 11057

50 KlemensP G. Thermal resistance due to point defects at high temperatures. Physical Review, 1960, 119( 2): 507– 509

51 WangH, WangJ, CaoX. . Thermoelectric alloys between PbSe and PbS with effective thermal conductivity reduction and high figure of merit. Journal of Materials Chemistry. A, Materials for Energy and Sustainability, 2014, 2( 9): 3169– 3174

52 JonsonM, MahanG D. Mott’s formula for the thermopower and the Wiedemann-Franz law. Physical Review B: Condensed Matter, 1980, 21( 10): 4223– 4229

53 YangJ, MeisnerG P, ChenL. Strain field fluctuation effects on lattice thermal conductivity of ZrNiSn-based thermoelectric compounds. Applied Physics Letters, 2004, 85( 7): 1140– 1142

54 MaF, ZhengH B, SunY J. . Strain effect on lattice vibration, heat capacity, and thermal conductivity of graphene. Applied Physics Letters, 2012, 101( 11): 111904

55 DingB, LiX, ZhouW. . Anomalous strain effect on the thermal conductivity of low-buckled two-dimensional silicene. National Science Review, 2021, 8( 9): nwaa220

56 HuM, ZhangX, PoulikakosD. Anomalous thermal response of silicene to uniaxial stretching. Physical Review B: Condensed Matter and Materials Physics, 2013, 87( 19): 195417

57 LiH, ChengG, LiuY. . Anomalous thermal response of graphene kirigami induced by tailored shape to uniaxial tensile strain: a molecular dynamics study. Nanomaterials (Basel, Switzerland), 2020, 10( 1): 126

58 MortazaviB, LeM Q, RabczukT. . Anomalous strain effect on the thermal conductivity of borophene: a reactive molecular dynamics study. Physica E, Low-Dimensional Systems and Nanostructures, 2017, 93 : 202– 207

59 TabarraeiA, WangX. Anomalous thermal conductivity of monolayer boron nitride. Applied Physics Letters, 2016, 108( 18): 181904

60 QianJ, XuB, TianW. A comprehensive theoretical study of halide perovskites ABX₃. Organic Electronics, 2016, 37 : 61– 73

61 YuanY, XuR, XuH T. . Nature of the band gap of halide perovskites ABX₃ (A = CH₃NH₃, Cs; B = Sn, Pb; X = Cl, Br, I): first-principles calculations. Chinese Physics B, 2015, 24( 11): 116302

62 LeppertL, Reyes-LilloS E, NeatonJ B. Electric field- and strain-induced rashba effect in hybrid halide perovskites. Journal of Physical Chemistry Letters, 2016, 7( 18): 3683– 3689

63 LiaoM, LiuY, CuiP. . Modeling of alloying effect on elastic properties in BCC Nb-Ti-V-Zr solid solution: from unary to quaternary. Computational Materials Science, 2020, 172 : 109289

64 KangJ, WangL W. High defect tolerance in lead halide perovskite CsPbBr₃. Journal of Physical Chemistry Letters, 2017, 8( 2): 489– 493

65 ZhangQ, SongQ, WangX. . Deep defect level engineering: a strategy of optimizing the carrier concentration for high thermoelectric performance. Energy & Environmental Science, 2018, 11( 4): 933– 940

66 RenW, SongQ, ZhuH. . Intermediate-level doping strategy to simultaneously optimize power factor and phonon thermal conductivity for improving thermoelectric figure of merit. Materials Today Physics, 2020, 15 : 100250

67 ShinW H, RohJ W, RyuB. . Enhancing thermoelectric performances of bismuth antimony telluride via synergistic combination of multiscale structuring and band alignment by FeTe₂ incorporation. ACS Applied Materials & Interfaces, 2018, 10( 4): 3689– 3698

68 KimS I, LeeK H, MunH A. . Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics. Science, 2015, 348( 6230): 109– 114

69 ZhengL, ZhuT, LiY. . Enhanced thermoelectric performance of F₄-TCNQ doped FASnI₃ thin films. Journal of Materials Chemistry. A, Materials for Energy and Sustainability, 2020, 8( 47): 25431– 25442

70 WeiJ, YangL, MaZ. . Review of current high-ZT thermoelectric materials. Journal of Materials Science, 2020, 55( 27): 12642– 12704

71 LanJ L, LiuY C, ZhanB. . Enhanced thermoelectric properties of Pb-doped BiCuSeO ceramics. Advanced Materials, 2013, 25( 36): 5086– 5090

72 LiuH, YuanX, LuP. . Ultrahigh thermoelectric performance by electron and phonon critical scattering in Cu₂Se_1–xI_x. Advanced Materials, 2013, 25( 45): 6607– 6612

73 QinB, WangD, HeW. . Realizing high thermoelectric performance in p-type SnSe through crystal structure modification. Journal of the American Chemical Society, 2019, 141( 2): 1141– 1149

74 ZhuH, MaoJ, LiY. . Discovery of TaFeSb-based half-Heuslers with high thermoelectric performance. Nature Communications, 2019, 10( 1): 270

75 XingT, SongQ, QiuP. . Superior performance and high service stability for GeTe-based thermoelectric compounds. National Science Review, 2019, 6( 5): 944– 954