Analysis and stabilization control of a voltage source controlled wind farm under weak grid conditions

Abstract

This paper investigates and discusses the interaction stability issues of a wind farm with weak grid connections, where the wind turbines (WTs) are controlled by a new type of converter control strategy referred to as the voltage source (VS) control. The primary intention of the VS control method is to achieve the high-quality inertial response capability of a single WT. However, when it is applied to multiple WTs within a wind farm, its weak-grid performance regarding the stability remains concealed and needs to be clarified. To this end, a frequency domain model of the wind farm under the VS control is first developed. Based on this model and the application of a stability margin quantification index, not only the interactions between the wind farm and the weak grid but also those among WTs will be systematically assessed in this paper. A crucial finding is that the inertial response of VS control has negative impacts on the stability margin of the system, and the dominant instability mode is more related to the interactions among the WTs rather than the typical grid-wind farm interaction. Based on this knowledge, a stabilization control strategy is then proposed, aiming for stability improvements of VS control while fulfilling the demand of inertial responses. Finally, all the results are verified by time-domain simulations in power systems computer aided design/electromagnetic transients including DC(PSCAD/EMTDC).

Key words： weak grids; voltage source (VS) control; wind turbine (WT); stabilization control; wind farm; inertial response

1 Introduction

With the increasing penetration of renewable power generations [1,2], such as wind power in the power systems [3–5], the relative strength of grids is becoming weak in two aspects: lack of rotational inertia and the non-stiff grid voltage [6]. The former characterizes the weak grid effect from the electromechanical perspective while the latter interprets the weak grid effect from an electrical viewpoint. Specific to the wind power case, it is known that wind turbines (WTs) under the conventional vector control almost provide no inertial response to the grid [7,8], which can lead to the transient frequency instability of the power system if its penetration is high. On the other hand, a large-capacity WT connected to the end of a distributed power grid is another scenario. The electrical weak grid effect will occur due to the long-distance transmission line and the transformer leakage reactance existing between the WT and the synchronous generator (SG) [9]. Furthermore, integrating large-scale wind power is equivalent to decreasing the short circuit ratio (SCR) of the grid, which further aggravates the weak grid effect, causing various abnormal interaction issues, e.g., the low-frequency oscillations in wind farm [10], subsynchronous oscillations generated by the wind farm connected to the grid through the high-voltage direct current (HVDC) transmission [11], and the high-frequency harmonic oscillations generated by the interaction between the converter control and the grid impedance [12,13], etc. Therefore, there is an urgent need to reshape the behavior of WTs and improve their ability in weak grid operations. These challenges can be overcome from two aspects, corresponding to the afore-mentioned two types of weak grid effects as below: one is to solve interactive instability issues between the WT converter and the grid impedance, i.e., the electrical aspect; the other one is to make the WT exhibit a voltage source (VS) behavior similar to that of the SG, so that an autonomous inertial response can be realized, i.e., the electromechanical aspect.

With respect to the mitigation of oscillation issues caused by the interaction between Type-IV WTs and the weak grid, many endeavors have been made in recent years. For the wind power converter with the conventional vector control, the influence of grid impedance is generally ignored when designing the inner current loop. Nevertheless, the effective control bandwidth of the current loop decreases with the increase of grid impedance in a weak grid, which leads to the abnormal interaction between the current control loop and the phase locked loop (PLL) [14]. Zhang et al. [15] pointed out that the current control loop was equivalent to introducing a positive feedback term in the PLL, and the positive feedback effect was positively correlated to the grid impedance, which results in the instability of the converter under weak grid conditions. In Ref. [16], the output impedance model of grid-side converter (GSC) was established in the rotated d-q frame. The impedance-based analysis result showed that the q-q impedance of the vector-controlled inverter exhibited the negative resistance characteristic within the PLL bandwidth, which caused oscillations with the grid impedance. To decouple the control bandwidth of PLL from that of the current loop, Zhou et al. [17] proposed a robust control method by reducing the gain of PLL. However, the tracking and transient performance of the converter deteriorated with the decrease of the PLL bandwidth. Chen et al. [18] proposed a converter output impedance reshaping method based on phase compensation, which provided a sufficient stability margin at the intersection frequency between the grid impedance and converter output impedance. In Ref. [19], an active damping scheme through capacitor current feedback control was proposed to improve the stability of inductor-capacitor-inductor (LCL)-type converter against the resonant frequency variation. The designed parameters of stabilization control schemes proposed in Refs. [18,19] are mainly valid for the specific steady-state operation point. However, the robustness of the converter against large-scale variations of grid impedance is poor.

With respect to the inertial response that cannot be readily fulfilled by the conventional vector-controlled Type-IV WT, one type of solutions is to add an inertia extraction loop to the vector control structure, which does not change the current source of the external characteristics of WT [20,21]. Therefore, there still exist interactive instability issues in the weak grid environment. On the other hand, a kind of control method called the virtual SG (VSG) was adopted for converter control in Refs. [22,23], which simulated the electromechanical equation of a SG so that the converter had the electrical external characteristics of the SG. Yazdani et al. [24] and Harnefors et al. [25] studied the converter control method called power synchronization, which simulated the rotor motion equation of the SG and introduced the concept of virtual inertia. The power synchronization method can provide an inertial response to the grid, and the PLL is omitted, which avoids the instability caused by the PLL. Wu et al. [26] discussed the operation stability of VSG in a weak grid, and the analysis result showed that the sequence impedance of the VSG exhibited the same inductance characteristic as the grid impedance, which could guarantee the stable operation of the converter under extremely weak grid conditions. The control target of Refs. [22–26] is the output power of the converter. For the GSC of Type-IV WT whose control target is the DC-link voltage, the application of the strategies in Refs. [22–26] requires the introduction of an outer DC-link voltage control loop. However, the switching frequency of a high-capacity wind power converter is typically low (e.g., around 3 kHz), making it difficult to tune the multi-loops control parameters of VSG.

On the other hand, different from the typical VSG implementation by emulating the swing equation of the SG, another type of self-synchronization control scheme of Type-IV WT by using the intrinsic dynamics of DC-link voltage was proposed in Ref. [27], in which it was pointed out that a small-signal instability occurred when this VSG provided an inertial response. Nevertheless, the mechanism of instability and the stabilization control method were not discussed. Based on Ref. [27], a VS control strategy for the Type-IV WT was proposed in Ref. [28], in which the mechanism of instability mentioned in Ref. [27] was analyzed and a stabilization control method in the GSC was proposed to increase the system electrical damping. However, Sang [28] only analyzed the stability of a single WT but ignored the stability of a wind farm composed of multiple VS controlled WTs under weak grid conditions. Although Wu et al. [26] explored the stability of multiple VSGs in weak grids by only considering the intersection between multiple VSGs and the weak grid, but simplifying the analysis process and ignoring the intersection between multiple VSGs.

Although the VS control and the stabilization control make the Type-IV WT operate stably under the weak grid condition and have the ability to provide inertial response [28], the applicability for the wind farm, especially with respect to stability, needs to be further evaluated and clarified. Therefore, this paper analyzes the stability of a wind farm composed of multiple VS controlled Type-IV WTs considering the internal interaction, i.e., the interaction among WTs and the external interaction, i.e., the interaction between the wind farm and the weak grid. First, it proposes the control structure of the VS controlled WT and the topological structure of the wind farm. Then, it builds the model of the VS controlled wind farm. After that, it analyzes the stability of the wind farm. Finally, it proposes a machine-side stabilization method and conducts simulations based on PSCAD/EMTDC.

2 VS control structure and wind farm topology

In Ref. [28], a type of VS control strategy for the Type-IV WT was proposed. The control structure of the VS controlled WT is shown in Fig. 1, where the machine-side converter (MSC) still adopts the vector control strategy based on rotor flux orientation, the GSC adopts the inertia synchronization control (ISynC) strategy proposed in Ref. [28], PMSG is the permanent magnet synchronous generator, SPWM is sinusoidal pulse width modulation, PI is the proportional integral controller, and MPPT is maximum power point tracking. The per-unit DC-link voltage {\bar{u}}_{\mathrm{dc}} is the input to an integral controller, and the output of the controller is utilized as the phase of the modulation voltage of the GSC. The output reactive power of the GSC can be controlled by adjusting the amplitude of the modulation voltage {\bar{U}}_{\mathrm{t}}, where the subscript t means the modulation voltage. It can be seen from Fig. 1 that since the physical inertia of the DC-link capacitor is directly used for grid synchronization, this synchronization method of the GSC is named ISynC. Known from Ref. [28], the ISynC method can instantaneously mirror the dynamics of grid frequency to the dynamics of the DC-link voltage. Due to this merit, the inertia of WT can be extracted and transmitted to the grid through measuring the DC-link voltage. The corresponding control block is shown in Fig. 1 and is denoted as the inertia transmission control loop. Therefore, the inertial response function is achieved in an autonomous manner. The inertia transmission coefficient K_C is a controlled variable which reflects the inertial response capability of WT when grid frequency fluctuates. The larger the inertia transmission coefficient K_C, the more inertia response will be provided under the same condition of grid frequency fluctuation.

Fig.1 Control structure of voltage-source-controlled WT.

Full size|PPT slide

Although the VS control strategy was demonstrated to be well applied to a single WT, as mentioned before, its applicability for a wind farm, particularly from the perspective of stability impact, has not yet been well studied. Therefore, the following analysis will be devoted to this issue, where the small-signal stability of a VS controlled wind farm as depicted in Fig. 2 will be investigated. In detail, the wind farm contains n feeders, each of which contains M WTs. WT₁₁–WT_1M are connected to feeder 1, and WT_N1–WT_NM are connected to feeder N. {\bar{Z}}_{\mathrm{L}\mathrm{11}}–{\overline{Z}}_{\mathrm{L}NM} are the line impedances between WTs in the wind farm. All of the feeders are connected to the bus of the wind farm, i.e., the point of common connection (PCC), and then merged into the grid via the step-up transformer T. The grid is represented by a VS cascaded with the inner impedance {\bar{Z}}_{\mathrm{s}}, and {\bar{Z}}_{\mathrm{Line}} is the line impedance. The above subscript L and Line means the line in the wind farm and the line in the grid respectively, and the subscript s means the power source.

Fig.2 Topological structure of the VS controlled wind farm under study.

Full size|PPT slide

3 Impedance modeling of the VS controlled wind farm

In this paper, the small-signal stability of the VS controlled wind farm is studied by using the impedance-based method, where the impedance modeling of WT is first presented. The linearized model of the output impedance of the VS controlled WT from the perspective of the AC output side is given in Fig. 3, where H_in is the transfer function matrix from the DC-link voltage to the inertial power reference, the subscript “in” means inertial power, H_ss is the transfer function matrix from the machine-side power deviation to the current reference, the subscript “ss” means machine-side power deviation, H₁ is the transfer function matrix from the machine-side current reference to the actual output current, H₂ is the transfer function matrix from the machine-side current reference to the machine-side output voltage, H_mL is the transfer function matrix from the machine-side current to the machine-side output voltage, the subscript “mL” means the machine-side current, U_s0 is the transfer function matrix from the machine-side output voltage to the machine-side output power, the subscript “s0” means the machine-side power, I_s0 is the transfer function matrix from the machine-side output voltage to the machine-side output power, U_m is the transfer function matrix from the dc-link voltage to the output voltage of the GSC, {\bar{Z}}_{\mathrm{f}}^{-\mathrm{1}} is the transfer function matrix of the filter of GSC, U_g0 is the transfer function matrix from the grid-side current to the grid-side output power, I_p0 is the transfer function matrix from the grid-side voltage to the grid-side output power, and K_dc is the transfer function matrix from the DC-link power to the DC-link voltage.

Fig.3 Linearized model of the output impedance of WT with VS control.

Full size|PPT slide

Based on the model in Fig. 3, the expression of the output impedance of WT {\bar{Z}}_{\mathrm{WT}} with VS control can be obtained as

(1){\bar{Z}}_{\mathrm{WT}}={[U_{\mathrm{m}}{K}_{\mathrm{dc}}{I}_{\mathrm{p0}}+(\mathrm{1}-K_{\mathrm{dc}}{K}_{\mathrm{m}})I_{\mathrm{2}}]}^{-\mathrm{1}}\left[(\mathrm{1}-K_{\mathrm{dc}}{K}_{\mathrm{m}}){\bar{Z}}_{\mathrm{f}}+U_{\mathrm{m}}{K}_{\mathrm{dc}}{U}_{\mathrm{g0}}+U_{\mathrm{m}}{K}_{\mathrm{dc}}{I}_{\mathrm{p0}}{\bar{Z}}_{\mathrm{f}}\right],

where I₂ is the second order identity matrix.

When studying the interaction between the wind farm and the grid, i.e., the external interaction stability, the grid-connected wind farm system in Fig. 2 is divided into the wind farm subsystem and the grid subsystem.

Taking the wind farm bus as the dividing line, Fig. 4 gives the division diagram of the wind farm subsystem and the grid subsystem, where WT and the grid are represented by a VS cascaded with the impedance, respectively. With respect to the grid sub-system, the impedance {\bar{Z}}_{\mathrm{g}} where the subscript “g” means the grid is the sum of the grid inner impedance {\bar{Z}}_{\mathrm{s}}, the line impedance {\bar{Z}}_{\mathrm{Line}}, and the leakage reactance of the transformer of the wind farm. With respect to the wind farm subsystem, based on the inner line impedance and the calculated output impedance {\bar{Z}}_{\mathrm{WT}} of the VS-controlled WT, the equivalent impedance {\bar{Z}}_{\mathrm{WF}} where the subscript “WF” means that the wind farm of the wind farm in Fig. 4 can be derived according to the series and parallel calculation principle.

Fig.4 Diagram of the wind farm subsystem and the grid subsystem.

Full size|PPT slide

When studying the interaction between the WTs inside the wind farm, i.e., the internal interaction stability, the system in Fig. 2 is divided into two subsystems with the AC output side of one WT as the boundary. For a wind farm with n feeders and M units per feeder, there are N× M ways to divide subsystems for the internal interaction stability analysis. Taking WT WT₁₃ as an example, Fig. 5 demonstrates the division diagram of the subsystem of WT WT₁₃ and the subsystem of the remaining WTs and the grid. In Fig. 5, the impedance of the WT WT₁₃ subsystem is {\bar{Z}}_{\mathrm{WT13}}. With respect to the subsystem of the remaining WTs and the grid, the equivalent impedance {\bar{Z}}_{\mathrm{E}\mathrm{13}} where the subscript “E” means that the remaining WTs and the grid in Fig. 5 can also be obtained according to the series and parallel calculation principle.

Fig.5 Diagram of the subsystem of WT WT₁₃ and the subsystem of the remaining WTs and the grid.

Full size|PPT slide

4 Stability analysis of VS controlled wind farm

4.1 Stability analysis method and quantitative indexes of the wind farm

Applying the Thevenin’s theorem to Figs. 4 and 5, the equivalent circuit diagram for analyzing the stability of the grid-connected wind farm system can be obtained in Fig. 6, where the subsystems are all represented by an equivalent VS in series with an impedance, {\left[\mathrm{\Delta }{\bar{u}}_{\mathrm{WF}d}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\Delta }{\bar{u}}_{\mathrm{WF}q}\right]}^{\mathrm{T}}is the equivalent voltage vector of the wind farm, {\left[\mathrm{\Delta }{\bar{e}}_{\mathrm{g}d}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\Delta }{\bar{e}}_{\mathrm{g}q}\right]}^{\mathrm{T}} is the voltage vector of the grid, {\left[\mathrm{\Delta }{\bar{i}}_{\mathrm{WF}d}\mathrm{\hspace{0.17em}}\mathrm{\Delta }{\bar{i}}_{\mathrm{WF}q}\right]}^{\mathrm{T}} is the output current vector, {\left[\mathrm{\Delta }{\bar{u}}_{\mathrm{13}d}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\Delta }{\bar{u}}_{\mathrm{13}q}\right]}^{\mathrm{T}} is the voltage vector of WT13, {\left[\mathrm{\Delta }{\bar{u}}_{\mathrm{E}d}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\Delta }{\bar{u}}_{\mathrm{E}q}\right]}^{\mathrm{T}} is the equivalent voltage vector of the remaining WTs and the grid, and {\left[\mathrm{\Delta }{\bar{i}}_{\mathrm{13}d}\mathrm{\hspace{0.17em}}\mathrm{\Delta }{\bar{i}}_{\mathrm{13}q}\right]}^{\mathrm{T}} is the output current vector of WT13.

Fig.6 Equivalent circuit diagram for analyzing the stability of the grid-connected wind farm system.

Full size|PPT slide

4.1.1 Quantitative index for measuring the external interaction

When studying the interaction between the wind farm and the grid, i.e., the external interaction, the output current vector {\left[\mathrm{\Delta }{\bar{i}}_{\mathrm{WF}d}\mathrm{\hspace{0.17em}}\mathrm{\Delta }{\bar{i}}_{\mathrm{WF}q}\right]}^{\mathrm{T}} in Fig. 6(a) can be expressed as

(2)\left[\begin{array}{l}\mathrm{\Delta }{\bar{i}}_{\mathrm{WF}d}\\ \mathrm{\Delta }{\bar{i}}_{\mathrm{WF}q}\end{array}\right]={\left({\bar{Z}}_{\mathrm{WF}}+{\bar{Z}}_{\mathrm{g}}\right)}^{-\mathrm{1}}\left(\left[\begin{array}{l}\mathrm{\Delta }{\bar{u}}_{\mathrm{WF}d}\\ \mathrm{\Delta }{\bar{u}}_{\mathrm{WF}q}\end{array}\right]-\left[\begin{array}{l}\mathrm{\Delta }{\bar{e}}_{\mathrm{g}d}\\ \mathrm{\Delta }{\bar{e}}_{\mathrm{g}q}\end{array}\right]\right).

The characteristic equation f₁(s) of Eq. (2) is

(3)f_{\mathrm{1}}(s)=\det \left({\bar{Z}}_{\mathrm{WF}}+{\bar{Z}}_{\mathrm{g}}\right)=\mathrm{0.}

According to Eq. (3), the closed-loop poles λ₁₁, λ₁₂, ..., λ_1k can be obtained. The quantitative index ζ₁ for measuring the external interaction is the minimum damping ratio of these above closed-loop poles, which can be expressed as

(4){\zeta }_{\mathrm{1}}=\underset{h=\mathrm{1}\to k}{\min }\left[-{\displaystyle \frac{\mathrm{real}({\lambda }_{\mathrm{1}h})}{\left|{\lambda }_{\mathrm{1}h}\right|}}\right].

4.1.2 Quantitative index for measuring the internal interaction

When studying the interaction between WT WT₁₃ and other WTs, the output current vector {\left[\mathrm{\Delta }{\bar{i}}_{\mathrm{13}d}\mathrm{\hspace{0.17em}}\mathrm{\Delta }{\bar{i}}_{\mathrm{13}q}\right]}^{\mathrm{T}} of WT₁₃ in Fig. 6(b) can be expressed as

(5)\left[\begin{array}{l}\mathrm{\Delta }{\bar{i}}_{\mathrm{13}d}\\ \mathrm{\Delta }{\bar{i}}_{\mathrm{13}q}\end{array}\right]={\left({\bar{Z}}_{\mathrm{WT13}}+{\bar{Z}}_{\mathrm{E}\mathrm{13}}\right)}^{-\mathrm{1}}\left(\left[\begin{array}{l}\mathrm{\Delta }{\bar{u}}_{\mathrm{13}d}\\ \mathrm{\Delta }{\bar{u}}_{\mathrm{13}q}\end{array}\right]-\left[\begin{array}{l}\mathrm{\Delta }{\bar{u}}_{\mathrm{E}d}\\ \mathrm{\Delta }{\bar{u}}_{\mathrm{E}q}\end{array}\right]\right).

The characteristic equation f₂₁₃(s) of Eq. (5) is

(6)f_{\mathrm{213}}(s)=\det \left({\bar{Z}}_{\mathrm{WT13}}+{\bar{Z}}_{\mathrm{E13}}\right)=\mathrm{0.}

According to Eq. (6), the closed-loop poles λ₂₁₃₁, λ₂₁₃₂, ..., λ_213k can be obtained. The quantitative index ζ₂₁₃ for measuring the interaction between WT₁₃ and the remaining WTs and the grid is the minimum damping ratio of these above closed-loop poles, which can be expressed as

(7){\zeta }_{\mathrm{213}}=\underset{h=\mathrm{1}\to k}{\min }\left[-{\displaystyle \frac{\mathrm{real}({\lambda }_{\mathrm{213}h})}{\left|{\lambda }_{\mathrm{213}h}\right|}}\right].

For any WT_ij (1≤i≤N, 1≤j≤M), according to the calculation method in Eqs. (5)–(7), the quantitative index for measuring the interaction between WT WT_ij and the remaining WTs and the grid, i.e., the damping ratio ζ_2ij can be obtained. Therefore, the quantitative index ζ₂ for measuring the internal interaction of the wind farm is the minimum value of these above damping ratios ζ_2ij (1≤i≤N, 1≤j≤M), i.e.,

(8){\zeta }_{\mathrm{2}}\mathrm{=}\underset{\begin{array}{l}i=\mathrm{1}\to N\\ j=\mathrm{1}\to M\end{array}}{\min }({\zeta }_{\mathrm{2}ij}).

4.1.3 Quantitative index for measuring the stability of the wind farm

According to Eqs. (4) and (8), after deriving the external interaction index ζ₁ and the internal interaction ζ₂, the quantitative index ζ for measuring the stability of the wind farm is the smaller value between ζ₁ and ζ₂, i.e.,

(9)\zeta =\min ({\zeta }_{\mathrm{1}},\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}{\zeta }_{\mathrm{2}}).

In Eq. (9), when ζ is greater than zero, the grid-connected wind farm system operates stably. In contrast, when ζ is smaller than zero, the grid-connected wind farm system becomes unstable. Furthermore, according to Eq. (9), the small-disturbance dominant instability mode of the grid-connected wind farm system can be identified. When ζ is smaller than zero and ζ₁ is smaller than ζ₂, the dominant instability mode of the grid-connected wind farm system is the interaction between the wind farm and the grid, i.e., the external interaction. When ζ is smaller than zero and ζ₂ is smaller than ζ₁, the dominant instability mode of the grid-connected wind farm system is the interaction between the WTs inside the wind farm, i.e., the internal interaction.

If the wind farm operates unstably, according to Eqs. (4), (8) and (9), the negative damping ratios ζ₁ or ζ_2ij (1≤i≤N, 1≤j≤M) can be found out, which contributes to locating the weak points in the grid-connected wind farm system, and proposing a targeted stabilization control strategy.

4.2 An example of wind farm stability analysis

The grid-connected wind farm system with 3 feeders and each feeder with 5 WTs is taken as an example to analyze its operation stability under weak grid conditions. Table 1 lists the electrical parameters of the WT rated at 2 MW, and Table 2 gives the control parameters. The inductance and resistance per kilometer of the lines between WTs in the wind farm are 1.23 mH/km and 0.17 Ω/km, respectively, and the distance between WTs is 0.7 km.

Tab.1 Electrical parameters of a 2 MW WT

Symbol	Description	Value
SB	Base power value/MW	2
UB	Base value of AC phase voltage/kV	0.563
UdcB	Base value of DC-link voltage/kV	1.1
ωBm	Base value of stator angular frequency/(rad·s−1)	84.6
ωBg	Base value of grid angular frequency/(rad·s−1)	314
fN	Rated frequency of PMSG/Hz	13.47
P	Pole pairs of PMSG	42
ψr	Magnetic flux linkage of rotor/(p.u.)	0.896
Ls	Synchronous inductance of PMSG/(p.u.)	0.5495
Rs	Stator resistance of PMSG/(p.u.)	0.00387
HWT	Inertia constant of WT and PMSG/s	4
HC	Inertia time constant of DC-link capacitor/ms	3.6
udc0	steady-state DC-link voltage/(p.u.)	1.0
eg	Equivalent grid phase voltage/(p.u.)	1.0
fs	Switching frequency/kHz	2

Tab.2 Control parameters of a 2 MW WT

Symbol	Description	Value
T	Filter time constant/s	0.1
kpc	Proportional gain of MSC current controller	2.6
kic	Integral gain of MSC current controller	520
kps	Proportional gain of MSC power controller	0.05
kis	Integral gain of MSC power controller	10

Figure 7 illustrates the relationship between the damping ratios ζ₁, ζ₂, ζ and K_C with no stabilization control method, where the wind farm contains 15 WTs, the rated capacity of WT is 2 MW, the short circuit capacity at the PCC is 90 MW, and the SCR at the PCC is 3. In Fig. 7, when no inertial response function is provided, i.e., the inertia transmission coefficient K_C is 0, the wind farm with the VS control can operate stably in a weak grid condition with an SCR value of 3. With the increase of inertia transmission coefficient K_C, both the external interaction index ζ₁ and internal interaction index ζ₂ decrease. It should be noted that the value of ζ₂ is smaller than or equal to that of ζ₁ throughout the range of K_C, and the quantitative index ζ for measuring the stability of the wind farm is equal to ζ₂. When K_C is bigger than 0.475, ζ is smaller than 0, which means that the wind farm operates unstably and the dominant instability mode of the wind farm is the internal interaction.

Fig.7 Damping ratios ζ₁, ζ₂, ζ versus K_C with no stabilization control method.

Full size|PPT slide

The conventional stability analysis method for multiple VS controlled converters (i.e., VSGs) in Ref. [26] only considers the external interaction mode. If the stability analysis method in Ref. [26] is adopted to study the stability of the VS controlled wind farm in this paper, the corresponding quantitative index ζ for measuring the stability of the wind farm in Fig. 7 is ζ₁. Apparently, it can be seen from Fig. 7 that the critical unstable value of K_C adopting the analysis method in Ref. [26] is 0.575, which is bigger than the critical unstable value 0.475 with the analysis method in this paper. Therefore, the stability analysis result adopting the presented stability analysis method is more accurate than that of the stability analysis method in Ref. [26].

This study indicates that under VS control, if WTs have to provide a large inertial response to the grid, i.e., with a large inertia transmission coefficient K_C, the stability margin of the wind farm will be reduced, having the risk of triggering instability. To solve this issue, the stabilization control strategy should be added.

5 Stabilization control methods

5.1 Stabilization method by modifying MSC control

In Ref. [28], a stabilization method in the GSC was proposed to improve the stability of the WT under VS control. However, due to the limitation of the modulation ratio of GSC, the stabilization method in Ref. [28] cannot increase the damping indefinitely, and instability still occurs when WT provides a stronger inertial response. Therefore, in this paper, another stabilization control strategy is proposed in the control loop of MSC. Figure 8 exhibits the control block diagram of the stabilization method in MSC.

Fig.8 Control block diagram of stabilization method in MSC.

Full size|PPT slide

It can be seen from Fig. 8 that the proposed stabilization method adds a three-stage low-pass filter to the original inertia transmission control loop of MSC in Fig. 1. The added stabilization controller in MSC has different effects at different time scales. On the one hand, the controller can adjust the phase of machine-side power -\mathrm{\Delta }{\bar{P}}_{\mathrm{m}} in a small time scale to make the corresponding machine-side damping power coefficient D_m larger than 0, which improves the stability of WT. On the other hand, in a large time scale, the controller does not affect the transmission of grid frequency signals, ensuring the quality of the inertial response.

The impedance-based stability analysis in Sections 3 and 4 can provide the numerical analysis results of the VS controlled wind farm, but it cannot reveal the mechanism of instability and direct the design of stabilization control method. The “complex power coefficient method” judges the stability of WT according to the value of the decomposed damping power coefficient, i.e., the positive damping power coefficient corresponds to the stability while the negative damping power coefficient corresponds to instability. According to the analysis based on the “complex power coefficient method” in Ref. [28], the machine-side complex power with no stabilization control is represented as -\mathrm{\Delta }{\bar{P}}_{\mathrm{m}}, and the machine-side complex power with the stabilization control in MSC is represented as -\mathrm{\Delta }{\bar{P}}_{\mathrm{m}\mathrm{2}}. The relationship between -\mathrm{\Delta }{\bar{P}}_{\mathrm{m2}} and -\mathrm{\Delta }{\bar{P}}_{\mathrm{m}} is expressed as

(10)-\mathrm{\Delta }{\bar{P}}_{\mathrm{m2}}={\displaystyle \frac{\mathrm{1}}{{(T_{\mathrm{2}}s+\mathrm{1})}^{\mathrm{3}}}}\left(-\mathrm{\Delta }{\bar{P}}_{\mathrm{m}}\right)=K_{\mathrm{m}\mathrm{2}}\mathrm{\Delta }\delta +D_{\mathrm{m2}}s\mathrm{\Delta }\delta ,

where K_{\mathrm{m2}} is the machine-side synchronous power coefficient with stabilization control in MSC, and D_{\mathrm{m2}} is machine-side damping power coefficient with stabilization control in MSC.

Fig.9 Vector diagram of -\mathrm{\Delta }{\bar{P}}_{\mathrm{m2}} with stabilization control in MSC.

Full size|PPT slide

In Fig. 7, when K_C exceeds 0.475, instability occurs in the wind farm and the oscillation frequency is 302 rad/s. At this oscillation frequency, the lag phase φ₂ of a low-pass filter with a time constant T₂ of 0.1 s is close to 90 degrees. According to Eq. (10), the vector diagram of -\mathrm{\Delta }{\bar{P}}_{\mathrm{m}\mathrm{2}} with stabilization control in MSC is given in Fig. 9. As shown in Fig. 9, in the initial state without the stabilization control strategy, the machine-side power vector -\mathrm{\Delta }{\bar{P}}_{\mathrm{m}} is in the fourth quadrant. Therefore, the value of the decomposed machine-side damping power coefficient D_m is negative, which indicates the VS controlled WT operates unstably. After the proposed machine-side stabilization control strategy is added, the machine-side power vector -\mathrm{\Delta }{\bar{P}}_{\mathrm{m}} is adjusted to the first quadrant, and the corresponding machine-side damping power coefficient D_{\mathrm{m2}} is corrected to a positive value. Thus, the proposed stabilization control strategy in this paper overcomes the shortcomings of instability caused by increasing the inertial response capability.

5.2 An example of wind farm stability analysis with stabilization control

Figure 10 shows the curve of the damping ratio ζ with the change of inertia transmission coefficient K_C after adding the stabilization control proposed in Ref. [28] or in this paper, where the wind farm contains 15 WTs, the rated capacity of WT is 2 MW, the short circuit capacity at the PCC is 90 MW, and the SCR at the PCC is 3. In Fig. 10(a), the grid-side stabilization control method proposed in Ref. [28] is added, and the grid-side stabilization control coefficient K_PSS is 3. When the inertia transmission coefficient K_C is bigger than 2.7, the quantitative index ζ is smaller than 0, which means the wind farm operates unstably. In Fig. 10(b), the machine-side stabilization control method proposed in this paper is added, and the time constant T₂ is 0.1 s. When K_C increases to 100, the value of the quantitative index ζ stays around 0.1. Compared with the grid-side stabilization control in Ref. [28], it can be seen from Fig. 10 that the proposed machine-side stabilization control method can guarantee the stable operation of the VS controlled wind farm with a bigger inertia transmission coefficient.

Fig.10 Curve of the damping ratio ζ with the change of K_C.

Full size|PPT slide

Although the proposed machine-side stabilization control in the MSC makes the VS controlled wind farm have a wider stable range, the value of the quantitative index ζ is relatively small, i.e., 0.1. The comprehensive stabilization control strategy including the stabilization method in the GSC [28] and the proposed stabilization method in the MSC, can greatly improve the stability of the VS controlled wind farm under weak grid conditions.

Fig.11 Curve of the damping ratio ζ with the change of K_C after adding the comprehensive stabilization control.

Full size|PPT slide

Figure 11 shows the curve of the damping ratio ζ with the change of inertia transmission coefficient K_C after adding the comprehensive stabilization control, where the wind farm contains 15 WTs, the rated capacity of WT is 2 MW, the short circuit capacity at the PCC is 90 MW, the SCR at the PCC is 3, the grid-side stabilization control coefficient K_PSS is 1.57, and the time constant T₂ of the proposed stabilization controller in MSC is 0.1 s. In Fig. 11, when the inertia transmission coefficient K_C increases to 100, the quantitative index ζ for measuring the stability of the wind farm still stays above 0.2. Comparing Fig. 11 with Figs. 10 and 7, it can be seen that the comprehensive stabilization control strategy can enhance the stability of the grid-connected wind farm system in a weak grid condition when providing inertial response.

5.3 Stability performance of VS controlled wind farm under weak grid conditions

Generally, WTs in the same wind farm adopt the same control parameters. Therefore, the output impedance {\bar{Z}}_{\mathrm{WT}} of the WT can be considered approximately the same. The value of line impedance between WTs is small, which has little effect on the equivalent impedance of the wind farm. For a wind farm with n WTs, when studying the external interaction, neglecting the line impedances {\bar{Z}}_{\mathrm{L}ij} between WTs, the equivalent impedance {\bar{Z}}_{\mathrm{WF}} of the wind farm in Fig. 4 can be approximately derived as

(11){\bar{Z}}_{\mathrm{WF}}={\displaystyle \frac{{\bar{Z}}_{\mathrm{WT}}}{n}}.

When studying the internal interaction, taking the AC output side of any WT as the boundary, neglecting the line impedances between WTs, the equivalent impedance {\bar{Z}}_{\mathrm{E}} of the remaining WTs and the grid can be approximately derived as

(12){\bar{Z}}_{\mathrm{E}}={\left({\left({\displaystyle \frac{{\bar{Z}}_{\mathrm{WT}}}{n-\mathrm{1}}}\right)}^{-\mathrm{1}}+{\left({\bar{Z}}_{\mathrm{g}}\right)}^{-\mathrm{1}}\right)}^{-\mathrm{1}}.

According to the definition of SCR in Ref. [16], the SCR k_SCR at the PCC of the wind farm with n WTs can be expressed as

(13)k_{\mathrm{SCR}}={\displaystyle \frac{S_{\mathrm{SC}}}{n\cdot S_{\mathrm{N}}}},

where S_{\mathrm{SC}} is the short circuit capacity at the PCC and S_{\mathrm{N}} is the rated capacity of a single WT.

Fig.12 Three-dimensional damping ratio diagram ζ with the change of K_C, n and k_SCR

Full size|PPT slide

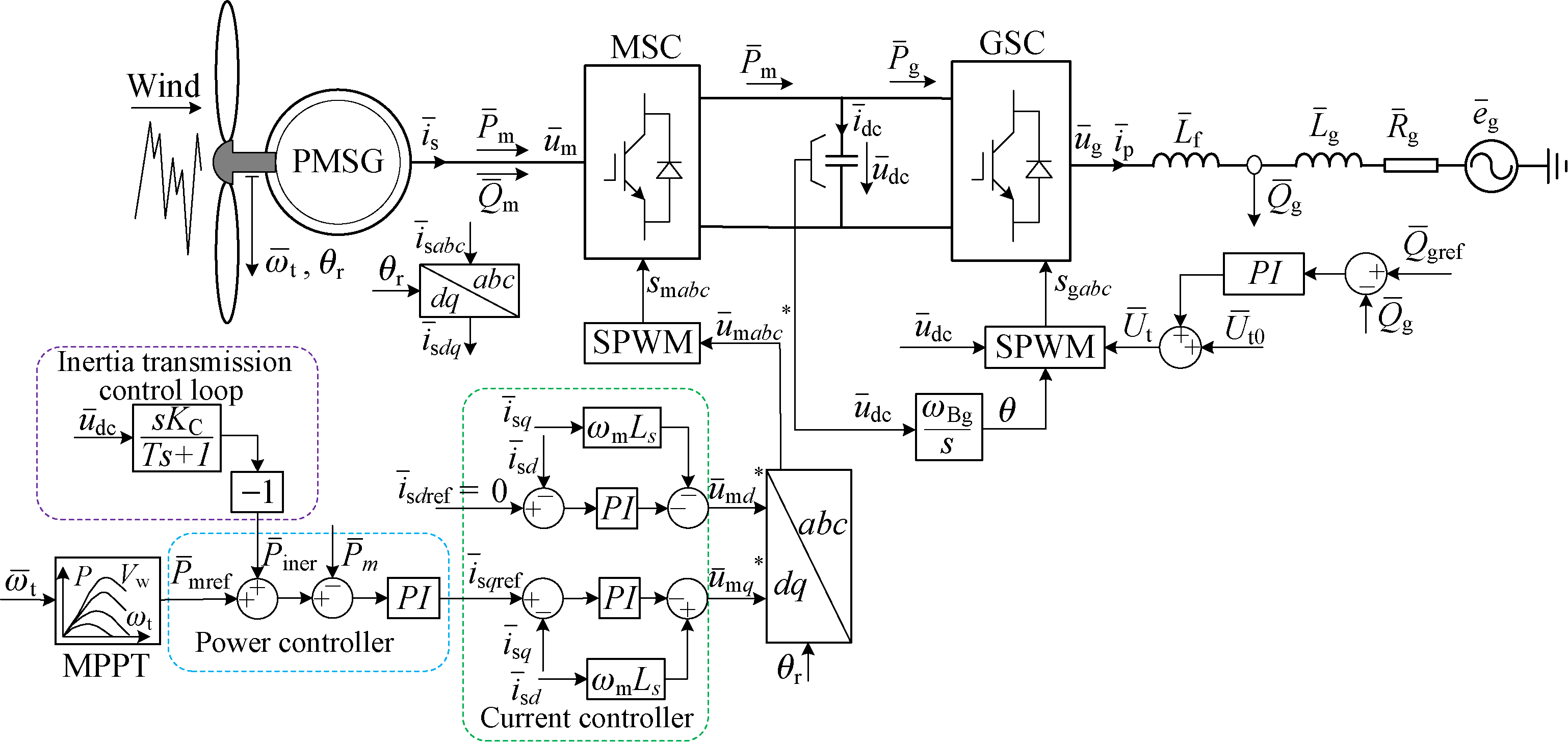
Figure 12 shows the three-dimensional damping ratio diagram ζ with the change of K_C and n, where the rated capacity of WT is 2 MW and the short circuit capacity at the PCC is 200 MW. In Fig. 12(a), without stabilization control, when the n of WTs is constant, with the increase of the inertia transmission coefficient K_C from 0 to 2, the quantitative index ζ for measuring the stability of the wind farm decreases rapidly to below 0, corresponding to the instability of the wind farm. When K_C is constant, as the n of WTs increases to 80 and the corresponding k_SCR decreases to 1.25, the quantitative index ζ decreases gradually. In Fig. 12(b), with the grid-side stabilization control method in Ref. [28], where K_PSS is 1.57, the quantitative index ζ for measuring the stability of the wind farm drops quickly below 0 with the increase of K_C and n. Comparing Fig. 12(b) with 12(a), it can be seen that the inertia transmission coefficient K_C corresponding to critical stability increases, which indicates that the grid-side stabilization control method in Ref. [28] can expand the stable range of WT to a certain degree. However, the grid-side stabilization control method in Ref. [28] still has a limited effect. In Fig. 12(c), the comprehensive stabilization control is added, where K_PSS is 1.57 and T₂ is 0.1 s. As K_C increases from 0 to 60 and the n of WTs increases to 80 (corresponding to the reduced k_SCR of 1.25), the quantitative index ζ still stays greater than 0. Comparing Fig. 12(c) with Figs. 12(a) and 12(b), it can be seen that the proposed comprehensive stabilization control strategy greatly improves the weak-grid connection capability of the VS controlled wind farm.

6 Simulation and verification

To verify the effectiveness of the proposed stabilization control strategy and analysis results, time-domain simulations are conducted in PSCAD/EMTDC. The topological structure of the wind farm is shown in Fig. 2, where the wind farm contains 3 feeders and each feeder contains 5 WTs. The electrical and control parameters of WT can be referred to in Tables 1 and 2.

6.1 Verification of stability analysis and stabilization control

Figure 13 shows simulation waveforms of instability when increasing the inertia transmission coefficient K_C without stabilization control, where the number of WTs is 15, the rated capacity of WT is 2 MW, and the short circuit capacity at the PCC is 90 MW, i.e., the corresponding k_SCR is 3. In Fig. 13, when K_C is 0.48, the wind farm operates stably. When K_C increases to 0.49, the DC-link voltage {\bar{u}}_{\mathrm{dc13}} and output active power {\bar{P}}_{\mathrm{g}\mathrm{13}} of WT₁₃ oscillate and diverge gradually, and the output power {\bar{P}}_{\mathrm{farm}} of the wind farm oscillates as well. In Fig. 13, the critical unstable value of inertia transmission coefficient K_C is 0.49, which is close to the theoretical critical unstable value of 0.475 in Fig. 7. In addition, the oscillation amplitude of the output power {\bar{P}}_{\mathrm{g}\mathrm{13}} of WT₁₃ is much larger than that of the output power {\bar{P}}_{\mathrm{farm}} of the wind farm, which illustrates that the interaction mode is the interaction between the WTs inside the wind farm, i.e., the internal interaction. The simulation result is consistent with the theoretical analysis results.

Fig.13 Simulation waveforms when increasing K_C without stabilization control.

Full size|PPT slide

Fig.14 Simulation waveforms when increasing K_C after adding comprehensive stabilization control.

Full size|PPT slide

Figure 14 shows simulation waveforms when increasing the inertia transmission coefficient K_C after adding the comprehensive stabilization control, where the wind farm contains 15 WTs, the rated capacity of WT is 2 MW, the short circuit capacity at the PCC is 90 MW, the SCR at the PCC is 3, the grid-side stabilization control coefficient K_PSS is 1.57, and the time constant T₂ of the proposed stabilization controller in MSC is 0.1 s. In Fig. 14, when the inertia transmission coefficient K_C increases from 60.00 to 60.02, the DC-link voltage {\bar{u}}_{\mathrm{dc13}} and output active power {\bar{P}}_{\mathrm{g}\mathrm{13}} of WT WT₁₃ fluctuate slightly and recover, and the output power {\bar{P}}_{\mathrm{farm}} of the wind farm reduces and then recovers. After entering the steady-state, {\bar{u}}_{\mathrm{dc13}}, {\bar{P}}_{\mathrm{g13}}, and {\bar{P}}_{\mathrm{farm}} are all stable without distortion. It can be seen from Fig. 14 that the proposed comprehensive stabilization control strategy can ensure the stable operation of the VS controlled wind farm with a strong inertia transmission capability under weak grid conditions, which demonstrates the effectiveness of the proposed comprehensive stabilization strategy.

6.2 Verification of inertial response function under weak grid conditions

Figure 15 shows the simulation waveforms of the inertial response of the wind farm after adding the proposed comprehensive stabilization control, where the wind farm contains 15 WTs, the rated capacity of WT is 2 MW, the short circuit capacity at the PCC is 90 MW, the SCR at the PCC is 3, the grid-side stabilization control coefficient K_PSS is 1.57, the time constant T₂ of the proposed stabilization controller in MSC is 0.1 s, and the inertia transmission coefficient K_C is 30. In Fig. 15(a), when the grid frequency f_g decreases to 0.01 p.u., the DC-link voltage {\bar{u}}_{\mathrm{dc13}}of WT₁₃ decreases to 0.01 p.u. accordingly, and the speed {\bar{\omega }}_{\mathrm{t13}}of WT₁₃ decreases to 0.03 p.u. and recovers. The output active power {\bar{P}}_{\mathrm{g13}} of WT₁₃ increases to 0.15 p.u. and recovers, and the output power {\bar{P}}_{\mathrm{farm}} of the wind farm increases to 2.3 p.u. and then recovers. In Fig. 15(b), a similar situation occurs when the grid frequency increases. The simulation results in Fig. 15 suggest that with the applied inertia transmission control and the comprehensive stabilization control, the VS controlled wind farm cannot only operate stably under weak grid conditions but also fulfill the capability of providing the inertial response, verifying the correctness of the theoretical analysis and the feasibility of the proposed control strategy.

Fig.15 Simulation waveforms of the inertial response of the wind farm after adding the comprehensive stabilization control.

Full size|PPT slide

7 Conclusions

This paper investigated the stability of a VS control method applied to the Type-IV wind farm under weak grid conditions. Different from existing studies which only consider the interaction between the wind farm and the weak grid (denoted by external interaction), this paper also focuses on the interaction between WTs in the wind farm (denoted by internal interaction). The stability performance is assessed by using a quantification index of stability margin. Based on this approach, the negative impact of the inherent inertial response function of VS control on the stability margin of the overall system has been revealed and identified, and the dominant instability mode turns out to be more relevant to the interactions among the WTs within the wind farm rather than the typical grid-wind farm interaction. Therefore, careful attention needs to be paid to the stability issue when VS control is responsible for the inertial response. To alleviate this issue, a stabilization control method is proposed to enhance the stability of the VS controlled wind farm while fulfilling the inertial response.

Besides, the proposed machine-side stabilization method in this paper can overcome the shortcomings of the grid-side stabilization method in Ref. [28], which is limited by the modulation ratio of the GSC. After adding the proposed stabilization control strategy, the VS controlled wind farm can operate stably under extremely weak grid conditions (e.g., tested with the SCR value of 1.25), and provide a considerable inertial response to the grid.

Overall, this paper may shed light on the further development and improvement of VS control in particular from the stability perspective. It may also provide reference for stability analysis and stabilization control of wind farms under the control scheme similar to VS control (such as VSG control, droop control, etc.).

Acknowledgments

This work was supported in part by the National Key R&D Plan of China (Grant No. 2018YFB1501300), and in part by the Key Laboratory of Control of Power Transmission and Conversion (SJTU), Ministry of Education (2021AC03).

References

1 Krautz H J, Lisk A, Posselt J, Impact of renewable energies on the operation and economic situation of coal fired power stations: actual situation of coal fired power stations in Germany. Frontiers in Energy, 2017, 11(2): 119–125

2 Chen X, Wu W, Gao N, Finite control set model predictive control for LCL-filtered grid-tied inverter with minimum sensors. IEEE Transactions on Industrial Electronics, 2020, 67(12): 9980–9990

3 Li J, Liu G, Zhang S. Smoothing ramp events in wind farm based on dynamic programming in energy internet. Frontiers in Energy, 2018, 12(4): 550–559

4 Deng F, Chen Z, Khan M R, Fault detection and localization method for modular multilevel converters. IEEE Transactions on Power Electronics, 2015, 30(5): 2721–2732

5 Heidari A, Esmaeel Nezhad A, Tavakoli A, A comprehensive review of renewable energy resources for electricity generation in Australia. Frontiers in Energy, 2020, 14(3): 510–529

6 Kundur P.Power System Stability and Control. New York: McGraw-Hill, Inc, 1994

7 Xi J, Geng H, Zou X. Decoupling scheme for virtual synchronous generator controlled wind farms participating in inertial response. Journal of Modern Power Systems and Clean Energy, 2021, 9(2): 347–355

8 Huang S, Wu Q, Bao W, Hierarchical optimal control for synthetic inertial response of wind farm based on alternating direction method of multipliers. IEEE Transactions on Sustainable Energy, 2021, 12(1): 25–35

9 Diaz F G A, Mombello E E, Venerdini G D G. Calculation of leakage reactance in transformers with constructive deformations in low voltage foil windings. IEEE Transactions on Power Delivery, 2018, 33(6): 3205–3210

10 Sun Y, Ye H, Sun X, Wind power fluctuation mitigation based low-frequency oscillation. Journal of Engineering (Stevenage, England), 2017, 2017(13): 1299–1306

11 Lyu J, Cai X, Amin M, Sub-synchronous oscillation mechanism and its suppression in MMC-based HVDC connected wind farms. IET Generation, Transmission & Distribution, 2018, 12(4): 1021–1029

12 Egea-Alvarez A, Fekriasl S, Gomis-Bellmunt O. Advanced vector control for voltage source converters connected to weak grids. In: 2016 IEEE Power and Energy Society General Meeting, Boston, USA, 2016

13 Davari M, Mohamed Y A R I. Robust vector control of a very weak-grid-connected voltage-source converter considering the phase-locked loop dynamics. IEEE Transactions on Power Electronics, 2017, 32(2): 977–994

14 Zhang C, Cai X, Rygg A, Sequence domain SISO equivalent models of a grid-tied voltage source converter system for small-signal stability analysis. IEEE Transactions on Energy Conversion, 2018, 33(2): 741–749

15 Zhang C, Cai X, Li Z, Properties and physical interpretation of the dynamic interactions between voltage source converters and grid: electrical oscillation and its stability control. IET Power Electronics, 2017, 10(8): 894–902

16 Sang S, Gao N, Cai X, A novel power-voltage control strategy for the grid-tied inverter to raise the rated power injection level in a weak grid. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(1): 219–232

17 Zhou J Z, Ding H, Fan S, Impact of short-circuit ratio and phase-locked-loop parameters on the small-signal behavior of a VSC-HVDC converter. IEEE Transactions on Power Delivery, 2014, 29(5): 2287–2296

18 Chen X, Zhang Y, Wang S, Impedance-phased dynamic control method for grid-connected inverters in a weak grid. IEEE Transactions on Power Electronics, 2017, 32(1): 274–283

19 Peña-Alzola R, Liserre M, Blaabjerg F, LCL-filter design for robust active damping in grid-connected converters. IEEE Transactions on Industrial Informatics, 2014, 10(4): 2192–2203

20 Wang Y, Meng J, Zhang X, Control of PMSG-based wind turbines for system inertial response and power oscillation damping. IEEE Transactions on Sustainable Energy, 2015, 6(2): 565–574

21 Xu G, Xu L. Improved use of WT kinetic energy for system frequency support. IET Renewable Power Generation, 2017, 11(8): 1094–1100

22 Xiong X, Wu C, Blaabjerg F. An improved synchronization stability method of virtual synchronous generators based on frequency feedforward on reactive power control loop. IEEE Transactions on Power Electronics, 2021, 36(8): 9136–9148

23 Chen M, Zhou D, Blaabjerg F. Active power oscillation damping based on acceleration control in paralleled virtual synchronous generators system. IEEE Transactions on Power Electronics, 2021, 36(8): 9501–9510

24 Yazdani S, Davari M, Ferdowsi M, Internal model power synchronization control of a PV-based voltage-source converter in weak-grid and islanded conditions. IEEE Transactions on Sustainable Energy, 2021, 12(2): 1360–1371

25 Harnefors L, Rahman F M M, Hinkkanen M, Reference-feedforward power-synchronization control. IEEE Transactions on Power Electronics, 2020, 35(9): 8878–8881

26 Wu W, Zhou L, Chen Y, Sequence-impedance-based stability comparison between VSGs and traditional grid-connected inverters. IEEE Transactions on Power Electronics, 2019, 34(1): 46–52

27 Cvetkovic I, Boroyevich D, Burgos R, Modeling of a virtual synchronous machine-based grid-interface converter for renewable energy systems integration. In: 2014 IEEE 15th Workshop on Control and Modeling for Power Electronics, Santander, Spain, 2014

28 Sang S, Zhang C, Cai X, Control of a type-IV wind turbine with the capability of robust grid-synchronization and inertial response for weak grid stable operation. IEEE Access: Practical Innovations, Open Solutions, 2019, 7: 58553–58569