A comprehensive review and analysis of solar forecasting techniques

Abstract

In the last two decades, renewable energy has been paid immeasurable attention to toward the attainment of electricity requirements for domestic, industrial, and agriculture sectors. Solar forecasting plays a vital role in smooth operation, scheduling, and balancing of electricity production by standalone PV plants as well as grid interconnected solar PV plants. Numerous models and techniques have been developed in short, mid and long-term solar forecasting. This paper analyzes some of the potential solar forecasting models based on various methodologies discussed in literature, by mainly focusing on investigating the influence of meteorological variables, time horizon, climatic zone, pre-processing techniques, air pollution, and sample size on the complexity and accuracy of the model. To make the paper reader-friendly, it presents all-important parameters and findings of the models revealed from different studies in a tabular mode having the year of publication, time resolution, input parameters, forecasted parameters, error metrics, and performance. The literature studied showed that ANN-based models outperform the others due to their nonlinear complex problem-solving capabilities. Their accuracy can be further improved by hybridization of the two models or by performing pre-processing on the input data. Besides, it also discusses the diverse key constituents that affect the accuracy of a model. It has been observed that the proper selection of training and testing period along with the correlated dependent variables also enhances the accuracy of the model.

Key words： forecasting techniques; hybrid models; neural network; solar forecasting; error metric; support vector machine (SVM)

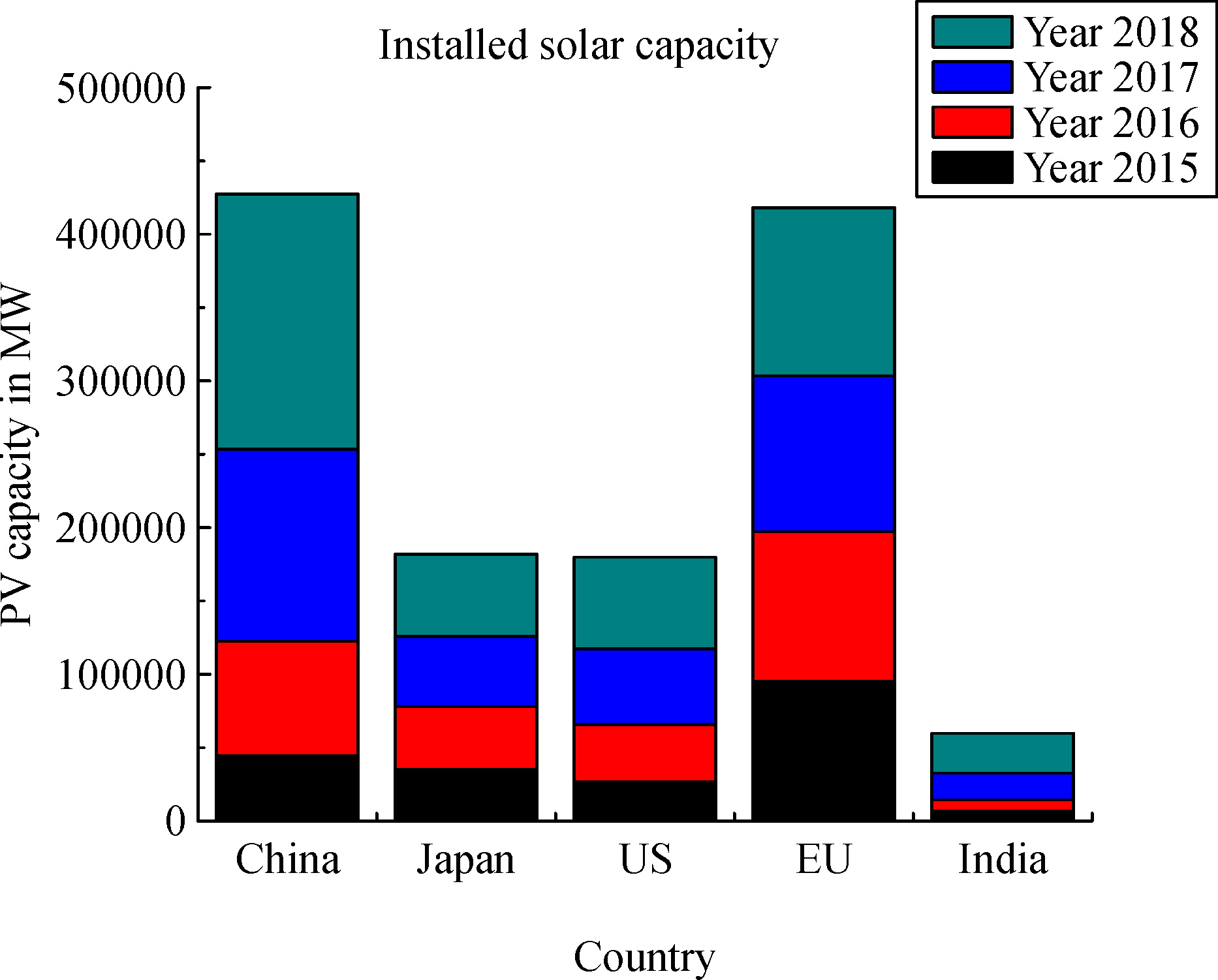
1 Introduction

All over the world, the expansion in demand of energy and availability of limited resources (fossil fuels), encouraged us to move toward the use of alternative forms of energy [1] such as solar [2], biomass [3], geothermal [4], wind, ocean energy [5], etc. These alternate sources provide a potential solution to meet this huge demand for energy, of which, solar energy becomes the most promising renewable source of energy that is freely available on the earth’s surface and can be converted into electricity [6]. According to the report of IEA 2018, the number, size, and electricity production of PV plants have been increased all over the world with a cumulative generation capacity of up to 500 GW [7]. Almost every year approximately 1.5 × 10¹⁸ KWh/a of solar energy has been received by the earth’s surface which is nearly multiples of ten thousand of the present consumption throughout the globe. Lhasa (China) receives the highest annual mean daily global solar radiation among all Asian countries of about 20.2 MJ/(m²·d) [8] whereas, India only receives an 18 MJ/(m²·d) [9]. In 2018, China was the top player of the solar market with a 10.8 GW PV installation whereas India took the second position in annual installed capacity followed by the US [10]. In India, as an example of developing countries, the renewable energy sector is growing exponentially in the last two decades. India has even set up a separate ministry for renewable energy source named Ministry of New and Renewable Energy (MNRE) who determines to generate 175 GW of energy at the end of 2022 using renewable sources of energy with a 100 GW of electricity from solar only [11]. According to the report produced by the Indian government in 2019, the 80GW mark has been crossed with 25 GW of generation only from the sun [12]. The installed solar PV capacity of five major countries/regions (China, Japan, US, India, and EU) is shown in Fig. 1 using the bar graph.

Fig.1 Installed solar PV capacity (MW) of five countries from 2015 to 2018 (adapted with permission from Refs. [7,10,13–15]).

Full size|PPT slide

Forecasting of solar components to estimate the power output of a photovoltaic (PV) systems is a challenging task as it depends on meteorological and geographical characteristics. The forecast of solar radiation is the forecast of the components of solar radiation like direct normal radiation, diffuse horizontal radiation, and global horizontal radiation [16]. However, the measurement of such components is very intricate at several geographical locations due to climatic and geographical conditions of a particular site [17]. These types of sites require a forecasting model to estimate these components using time series data of neighborhood sites [18]. Modeling of solar forecasting models requires predicting the precise information about the solar radiation components to decide whether or not to set a plant at a new location. There are even various places on the earth where the measurement of solar radiation is not only a typical task but also sometimes a difficult one due to cost, maintenance, and calibration of the measuring devices [19]. Many countries have grid inter-connectivity to solar plants and provide the opportunity to sell excessively produced electricity, which opens the doors to make money by the common man [20]. A large number of researchers tend to work with the sizing, modeling, structure, controller, battery, and physical parts of the solar PV cell to efficiently convert solar radiation into electricity whereas many of them opt to work with the planning of solar PV power plants [6].The scheduling and planning of PV power plants is a critical task as both are performed under variable meteorological conditions that may result in the poor balancing of load demand and power generation which further results in the penalty on power producer [21]. Each country has its schemes and policies to boost up its solar market [22]. A large deviation from promised generation results in financial penalties on the producers, which vary from country to country and state to state [23]. But the excess produced power using different renewable sources may lead to the concept of negative pricing in the electricity market. This phenomenon of negative pricing usually occurs in the middle of the day where all renewable generators are supplying their energies [24]. It is the direct signal to either reduce the supply or increase the demand. However, solar and other renewable resources are not to be set to produce 65% of the demanded electricity including the peak hours. Yet, the low level of flexibility in conventional plants enhances the chance of negative price hours [25]. The demand of the consumers/customers is relatively dynamic in behavior. Therefore, the demand side management tool helps to ensure the reliability in the complex dynamic of consumptions. As per the report of Agora Energiewende, the negative price hour will increase from 64 h in 2013 to more than 1000 h by 2020. But the use of information and communication technology (ICT) provides progress in grid integrated renewable energy generation systems [25]. An appropriate, accurate, and flexible forecasting technique along with the dynamic pricing scheme can also provide a promising solution to defeat issues of the negative price hour. Therefore, it is highly appreciable to develop an optimum model to precisely predict the solar radiation components for real as well as offline data [26].

Several researchers already conducted reviews on solar forecasting with consideration of the ANN and hybrid-based techniques. This paper comprehensively examines diverse types of solar irradiation forecasting techniques and potential models developed based on pre-processing techniques, data set used, training and testing period, and accuracy evaluation metrics. The primary intention of the paper is to classify and review the various endogenous and exogenous data-based techniques reported in the literature. First, it introduces the solar growth and requirement of forecasting techniques along with the cumulative PV installed capacity of different countries worldwide. Next, it discusses the various forecasting techniques along with the data set used, and presents a proper dedicated investigation on potential and the latest studies with the outcome-based representation of the table containing Ref. No., year of publication (YOP), study area, latitude (Lat.)/longitude (Long.), time resolution, training period, testing period, input variables, output variables, technique, and error metrics. Then, it details the error metrics used to measure the performance of the forecasting models, and discusses different conventional statistical assessment metrics, conventional metrics, and other latest metrics. After that, it focuses on the factor influencing the solar irradiation forecasting considering the different time horizon, air pollution, samples, climatic conditions, geographical locations. Finally, it describes the sources to obtain the data set for training, testing, and validation of the designed model.

2 Forecasting techniques

Forecasting solar irradiation components is the process of predicting the different components of solar irradiations like global horizontal irradiance (GHI), direct normal irradiance (DNI), and diffuse horizontal irradiance (DHI) for a specific PV site in advance. However, forecasting such components in advance for a specific location is not an easy task as is prone to the effect of variable climatic conditions. This section covers the important techniques to design forecasting models for the prediction of solar irradiation components. Different methods have been discussed in the literature for solar forecasting, which can broadly be classified based on data sets, model structure, and operation. The different types of data set-based techniques and structure-based techniques are shown in Fig. 2.

Fig.2 Types of forecasting techniques based on data processed and their structure.

Full size|PPT slide

2.1 Forecasting techniques based on data sets

The selection of the data set for a specific geographical location has a significant impact on the accuracy of solar forecasting results [27,28]. To collect the data, different instrument needs to be installed on the target location to observe different meteorological and solar irradiation components, but the aging, inaccurate behavior, and shadow of the instruments during sunrise and sunset hours, dust, raindrops, cloud coverage, etc., induce the errors in the recorded data. The forecasting models based on the data sets can be classified into three main categories as the time series data set-based ones, the structural data set-based ones, and the hybrid data set-based ones.

The performance of the time series data set-based models is dependent on the historical data vector of solar irradiation as an input and is independent of the internal state of the model [29–32].

The structural data set-based models are operated based on meteorological and geographical data sets. Some statistical functions are used to create the relation between the meteorological and geographical data to forecast solar irradiation [32].

The hybrid data set-based models combine the features of both the aforesaid models. The main aim of combining this data set is to enhance the accuracy of the forecast. Based on the correlation and regression theory, the relevant meteorological and geographical variables are used along with the historical time series to predict future values [33].

2.2 Forecasting techniques based on structure, operation, and utilization

Several models are available in the literature based on their structure, operation, and utilization. Broadly, these models can be classified into three categorizations named statistical [34], physical [35] and hybrid models [36,37]. These models were designed with various techniques including intelligent techniques for forecasting, regression, support vector machines(SVM), an advanced regression technique, Markov chain, wavelet transform based intelligence techniques, mathematical techniques, and numerical weather prediction (NWP).

2.2.1 Regression models

Regression models are the models that are based on the technique to develop the mathematical association between dependent and independent variables [38]. However, numerous models have been designed by researchers based on the simple linear regression and multiple linear-regression techniques but autoregressive models are much popular than the simple and multiple linear regression. These autoregressive models measure the correlation between the response and predictor variables [6]. Moreover, different categories have already been formed based on linearity/nonlinearity and stationarity/non-stationarity of the time series such as autoregressive (AR), moving average (MA), autoregressive and moving average (ARMA), autoregressive integrated and moving average (ARIMA), seasonal autoregressive integrated moving average (SARMIA), autoregressive integrated and moving average with explanatory variables (ARIMAX) [39] etc. Yule et al. (1921) proposed two new approaches for analysis of stationarity in 1992, where the first was called MA and the second called AR [40]. Of all models, ARIMA is the most popular model that creates the relationship between forecasted outputs to the actual measured output.

ARIMA is the statistical method of forecasting which is the advance and generalized form of the autoregressive and the moving average algorithm. This method is an extension of the ARMA method [41]. An ARMA method is the combination of AR and MA and used to find the correlation between the input and the output time series using the coefficient p and q. Here the coefficient p is for AR and q for MA. Mathematically, AR can be represented as [6,21]

(1)y_t=c+{\displaystyle \sum _{i=\mathrm{1}}^p{\phi }_i{y}_{t-\mathrm{1}}+{\epsilon }_t=c}+{\phi }_{\mathrm{1}}{y}_{t-\mathrm{1}}+{\phi }_{\mathrm{2}}{y}_{t-\mathrm{1}}+\mathrm{............}+{\phi }_p{y}_{t-p}+{\epsilon }_t.

where the operator y_t is the actual value; {\epsilon }_t is represented as random error; {\phi }_i is model parameters for different time periods t = 1, 2, 3…; and c and p are the constant term and order of the model respectively. Equation (1) indicates that the predicted value is in a linear relation with the p past value with some error and constant terms.

MA can be expressed using past values as dependent variables as in Eq. (2).

(2)y_t=\mu +{\displaystyle \sum _{j=\mathrm{1}}^q{\theta }_j{\epsilon }_{t-j}+{\epsilon }_t=\mu }+{\theta }_{\mathrm{1}}{\epsilon }_{t-\mathrm{1}}+{\theta }_{\mathrm{2}}{\epsilon }_{t-\mathrm{2}}+\mathrm{.............}+{\theta }_q{\epsilon }_{t-q}+{\epsilon }_t.

where q is the order of the model, \muis the mean of time series, and{\theta }_jis model parameter.

Combining Eqs. (1) and (2), AR and MA becomes the ARMA model which can mathematically be expressed as

(3)y_t=c+{\displaystyle \sum _{t=\mathrm{1}}^p{\phi }_i{y}_{t-\mathrm{1}}}+{\displaystyle \sum _{j=\mathrm{1}}^q{\phi }_j{y}_{t-j}}+{\epsilon }_t.

where p is for AR and q is for MA.

To solve the ARMA model, the Lag operator denoted by Lwhich is L_{y_t} = L_{y_{t-\mathrm{1}}}andhas to be considered. The AR (p) model be represented as {\epsilon }_t^{}=\phi (L)y_t

(4)\phi (L)=\mathrm{1}-{\displaystyle \sum _{i=\mathrm{1}}^p{\phi }_i{L}^i}.

(5)\mathrm{MA}(q)={\epsilon }_t=\theta (L){\epsilon }_t.

(6)\theta (L)=\mathrm{1}-{\displaystyle \sum _{j=\mathrm{1}}^q{\theta }_j{L}^j}.

(7)\mathrm{ARMA}(p,q)=\phi (L)y_t=\theta (L){\epsilon }_t.

The ARIMA model is the analytical method to establish the relation using the differencing method. ARIMA uses the three main steps for forecasting i.e., model identification, estimation of parameters, and diagnostic checking. Although due to the advanced knowledge of statistical methods, ARIMA is somewhat typical for the users but the latest version of MATLAB makes it easier with the ‘Econometric Modeler app’ available in the MATLAB 2018 and 2019 [42]. Unlike ARMA, this method adds one more coefficient d, called differencing operator i.e., (p, d, and q). The mathematical expression for ARIMA is

(8)\phi (L){(\mathrm{1}-L)}^d{y}_t=\theta (L){\epsilon }_t.

The basic condition for applying this method is that the series must be a stationary series. The autocorrelation and partial autocorrelation techniques are used to find the type of stationarity in the series. The selection of the parameters of the model in the case of ARIMA is one of the crucial tasks. The accurate parameters for the model is generally selected by calculating the Akaike Information criteria (AIC) and Bayesian Information Criteria (BIC) of the data sets [43].

Fig.3 Hierarchy of ARIMA for forecasting (adapted with permission from Ref. [6]).

Full size|PPT slide

The autocorrelation and partial autocorrelation functions are generally used in regression-based models to forecast solar irradiation [44–46]. Atique et al. developed an ARIMA based model to predict the daily solar radiation for a given PV panel. The model was designed by using a very simple and sophisticated statistical technique. The input data first transformed from non-stationary time series data into stationary data by analyzing autocorrelation function (ACF) and partial autocorrelation function (PACF). The proper model parameters were selected and their goodness of fit was checked by a different test like AIC, BIC, corrected Akaike Information Criterion (AICc), and sum of squared error (SSE). The mean absolute percentage error (MAPE) obtained for this model was 17.70% [44]. Alsharif et al. [45] developed a model for the prediction of daily and monthly global solar radiation using a seasonal autoregressive integrated moving average (SARIMA) model. The time series non-stationary data was first transformed into stationary data by analyzing the ACF and PACF, which identified the model parameters p and q using Phillips-Perron test that is a non-parametric test, also known as the pp-test that were used to obtain the first difference stationary of data. The root mean square error (RMSE) and R² for daily global solar forecasting was 104.26% and 68% respectively but 33.18%and 79% respectively for the monthly solar radiation model with ARIMA (4, 1, 1) [45]. Shadab et al. [46] discussed the estimation of monthly solar radiation using SARIMA. The SARIMA model was simulated using the Box-Jenkins approach which was a reiterative process. This approach has four steps: model order identification using ACF and PACF, parameters estimation based on the least square method, model validation to examine the suitability of model, and forecasting. The seasonality in the time series data set was analyzed by the ACF and PACF to transform the data into stationary. Differencing operators, AR, and MA coefficient were selected in a way to operate with the highest accuracy prediction. The study used 34 years of satellite data for modeling the SARIMA based process. The AIC and BIC factor were used for selecting the best model among different designed ARIMA models. The results showed that ARIMA (1, 0, 1) × (0, 1, 2)₁₂ provided the lowest AIC and BIC with the lowest MPE of 1.402 [46]. The multi-step ahead estimation of solar radiation using the ARMA and ARIMA model was determined by Colak et al. The study obtained the p and q coefficients of ARMA and ARIMA for the goodness of fit model using the log-likelihood function (LLF). The performance of the model was evaluated using the parameters MAPE up to the 3-step ahead and compared with the smart persistence model. The MAPE of the 1-step ahead prediction for ARMA(1, 2) and ARIMA(2, 2, 2) was 18.11% and7.87% respectively while that of the 2-step ahead prediction was 43.24% and 16.06% respectively for the ARMA(1, 2) and ARIMA(2, 2, 2) model, and that for the 3-step ahead was 71.67%and 32.07% for ARMA(1, 2) and ARIMA(2, 2, 2) respectively [47].

Doorga et al. [48] discussed the modified sayigh universal formula (refer to Appendix) for the prediction of global solar radiation. Eleven different regression models based on sunshine, temperature, and hybrid parameters were analyzed. The modified form of the sayigh universal formula for relative humidity was used for the selected location. This formula which estimated the global solar radiation by assuming GSR was very sensitive to relative humidity. It detected the variations in global solar radiation by calculating trends of relative humidity after averaging all target sites. The MAPE and RMSE values were used for the evaluation of the models which were 5.07% and 0.96 (MJ/(m²·d)) respectively for the modified sayigh model for the data set from 1961 to 1990 and 7.49 and 1.57 (MJ/(m²·d)) respectively from the data set from 2011 to 2016 [48]. However, Trapero et al. [49] proposed a frequency domain-based approach to estimate the short-term solar irradiation. A univariate dynamic harmonic regression model was established to forecast the global and direct normal irradiance. The model offered the self-adaptation of prediction based on the single-step recursive algorithm. The potential parameter bias problem was efficiently reduced in simultaneous estimation. The relative mean bias error (rMBE) and relative root mean square error (rRMSE) obtained for GHI was 0.21% and 29.66% respectively in the case of dynamic harmonic regression (DHR) whereas for direct normal irradiance (DNI), it was 3.82% and 46.79% respectively in the case of DHR [49]. Suthar et al. [50] empirically evaluated the various regression models to predict global solar radiation by considering air pollution index (API) as an input parameter. They included an extra parameter i.e., API to the A-P regression model but selected the other location-based parameters using a correlation coefficient, and determined that the exponential quadratic regression model performed better with RMSE of 3.08 for sunshine and API as inputs.

Therefore, regression-based models are more simplistic ones to form the relation between dependent and independent variables but the autoregressive models, ARIMA and SARIMA, are much popular over simple and multiple linear regression techniques. The seasonality in the time series data was eliminated by the transformation of non-stationarity data to stationarity which makes the process a little bit complex but the accuracy of the autoregressive models is improved.

2.2.2 Markov chain

The Markov chain follows a stochastic process which performs very short-term wind and solar irradiance forecasting [51]. The process of Markov chain is basically dependent on the adjacent states i.e., the present state parameters depend on the previous one; similarly, the next state parameters is dependent on the present state [52] as demonstrated in Fig. 4.

Fig.4 Markov process for three states (adapted with permission from Ref. [6]).

Full size|PPT slide

This process is represented by a series of finite random numbers. Let \{X_n\mathrm{\hspace{0.17em}},\mathrm{\hspace{0.17em}}n=\mathrm{0},\mathrm{1},\mathrm{2},.n.\}

The series for the present state i at the nth time can be represented as

(9)X_n=i.

However, the probability of the next state in j is P_{ij}

\mathrm{i}.\mathrm{e}.,\mathrm{\hspace{0.17em}}P\{X_{n+\mathrm{1}}=j\mathrm{\hspace{0.17em}}|X_n=i,\mathrm{\hspace{0.17em}}{X}_{n-\mathrm{1}}=i_{n-\mathrm{1}},\mathrm{.............},\mathrm{\hspace{0.17em}}{X}_{\mathrm{1}}=i_{\mathrm{1}},X_o=i_o\}=P_{ij}.

This equation suggests that the next state is dependent on the present state of the series.

Based on the literature available, the hidden Markov model (HMM) and the Markov transition model were used by the majority of researchers to predict the solar irradiation components [54–56]. Hacaooglue et al. discussed the Mycielski approach to forecast solar radiation for the short-time horizon based on the sub-array of similar characteristics data. The Mycielski approach used the Markov chain to select the most probable sub-pattern among all sub-patterns. This approach considered the longest matching sub-pattern for solar prediction. The model estimated that the RMSE, MABE, and R² are 13.49, 10.7554%, and 0.08320 respectively [57]. The genetic algorithm with HMM was used by Eniola et al. where the genetic algorithm optimized the model functioning with or without the correction factor to adapt to the HMM-GA. The nRMSE and MAPE obtained from this model were 2.33% and 6.27% respectively [54]. However, Bharadwaj et al. [55] forecasted solar irradiation by using the generalized fuzzy model (GFM) with HMM. They used a data vector pattern for the clustering to find a similarity index to reduce the problem associated with distance functions. The training of the cluster was performed by GFM which is a function approximation model to properly tune these clusters. The input combinations of day number, temperature, sunshine hour, relative humidity, and atmospheric pressure provided a RMSE and MPE of 7.9124 and 3.4255 respectively [55]. Wibun et al. [56] discussed solar radiation estimation using the Markov transition method (MTM) for an hourly time horizon. The input data set was categorized into six different types of cloud characteristics based on calculations of sky ratio. The probability values calculated by five 1stand 2nd order MTM used to generate the global solar radiation data depend on the sky ratio [56]. Li et al. [58] developed a model based on the discrete-time Markov chain to synthesize the typical solar radiation year (TSRY). The model overcomes the effect of fluctuation and transition in daily solar radiation. The model prepared the data in four categories based on clear sky ratio and then clustered them using the k-means cluster algorithm based on feature vector output. The discrete-time Markov chain model was used to model the transition rules for each and every cluster which was then combined with the samples of clusters. The performance of the model was calculated by percentage average error with the comparison of TMY. The synthesized TSRY has the maximum and minimum percentage average error of 10% and 6% respectively [58].

Therefore, the hidden Markov model and Markov transition model can be used to forecast solar radiation components for a shorter time horizon. They performed better with the optimization techniques like GA and fuzzy logics where the data was clustered using the similarity index.

2.2.3 Numerical weather prediction (NWP)

NWP is a physical model which comprises of a set of partial differential equations for estimating the atmospherically and environmental states of the planet [59]. The local weather station data are generally used to estimate the weather condition even 15days in advance to help agriculture farms, industries, and other services based on weather conditions [21]. The solar irradiance intensity gets reduced from its actual value once it enters the atmosphere due to the influence of aerosols and atmospheric gases [28]. The cloud conditions and the rainfall also affect the solar irradiance reaching the earth surface [60]. These climatic conditions are generally estimated by the NWP models. Many countries use the numerical weather forecast system for the day ahead prediction. For instance, National Center for Medium Range Weather Forecasting (NCMRWF) in India has been using the NWP model, named the T-80 model, since 1994. The United States has 14 stations of SURFRAD/ISIS. The University of Oregon solar radiation monitoring laboratory has cooperative network for renewable resources measurement (CONFRRM), NREL, Solar RGIS etc [61].

Verzijlbergh et al. [62] discussed a stepwise linear regression method to correct the solar prediction output of the numerical weather prediction model. The model output statistics (MOS) routine was used for systematic bias based on the meteorological variables which were generated by the linear regression model by adding variable sequentially. The global forecast system (GFS) model of the National Centers for Environmental Prediction (NCEP) was used as a NWP model and 3h interpolation applied to it. The model was determined by RMSE, mean absolute percentage error (MAE), and continuous ranked probability skill (CRPS) where MOS MLR (multilinear regression) performed better than MOS-P5 [62]. A NWP model with a post-processing technique like step-wise regression and principle component analysis (PCA) was developed by Verbois et al. [63] to obtain the one day ahead accurate forecast. In this model, the stepwise regression was used for selecting the best explanatory variable. The large number of variable inputs in the weather research and forecasting (WRF) and global forecast system (GFS) were reduced by deploying PCA in a manner to be uncorrelated with original levels. The model obtained 169 W/m² of RMSE, 35.7% of rRMSE, 133 W/m² of MAE, 28.1% of rMAE, –14 W/m² of MBE, and –2.9% of rMBE for WRF-solar-PCA [63]. Bakker et al. [64] compared the model output statistical post-processing technique for the probabilistic forecast of NWP for solar global radiation. The model output statistical post-processing method was the regression method including the parametric and the non-parametric method. The NWP data were obtained from HARMONIE-AROME (HA) from 2016 to 2018. The error matrices used for the model evaluation were RMSE, RMSE-SS (skill score), and continuous ranked probability skill score (CRPSS) [64].

2.2.4 Empirical model

The empirical model is one of the techniques to predict the future value of solar irradiance by developing a linear or nonlinear relationship between meteorological and solar variables [8]. Although many empirical models have been developed in the literature, the latest models predict solar irradiance with the help of different meteorological parameters with the consideration of maximum and minimum temperature [16,19]. The first model developed in 1982 by Hargreaves and Samani [65] (refer to Appendix) considered the difference between the maximum and the minimum temperature. Now, many models have been developed by modifying different factors like latitude, longitude, azimuth angle, elevation angle, air particle scattering, content of water vapor, component of O₂, N₂, CO₂, O etc., sunshine hours, maximum temperature, minimum temperature, cloudiness index, clear sky index, and etc [16]. In the case of most empirical models, the main parameter calculated is extraterrestrial solar radiation (H_o) which can be expressed mathematically as [66]

(10)H_{\mathrm{o}}={\displaystyle \frac{\mathrm{24}}{\mathrm{\pi }}}{I}_{\mathrm{sc}}\left(\mathrm{1}+\mathrm{0.033}\cos {\displaystyle \frac{\mathrm{360}n}{\mathrm{365}}}\right)\left(\cos \varphi \cos \delta \sin {\omega }_{\mathrm{s}}+{\displaystyle \frac{\mathrm{2}\mathrm{\pi }{\omega }_{\mathrm{s}}}{\mathrm{360}}}\sin \varphi \sin \delta \right).

where I_sc is solar constant, φ is location latitude, n is the day number in a given year, \delta =\mathrm{Solar}\mathrm{\hspace{0.17em}}\mathrm{declination}=\mathrm{23.45}\sin \left({\displaystyle \frac{\mathrm{360}(n+\mathrm{284})}{\mathrm{365}}}\right),{\omega }_{\mathrm{s}}=\mathrm{Sunrise}\mathrm{\hspace{0.17em}}\mathrm{angle}={\cos }^{-\mathrm{1}}(\tan \delta \tan \tan \varphi ),δ is solar declination, and ω_s is sunrise angle.

Mahajan and Namrata [67] proposed empirical models for the prediction of global solar radiation and mean diffuse solar radiation with consideration of sunshine hours, temperature, and relative humidity calculated the values of prime elements and then used these values for curve fitting. They developed seven empirical models and compared them with the three conventional ones. The least value of MAPE obtained was 2.501% for mean global solar radiation (GSR) and 13.506% for mean daily solar radiation (DSR) whereas RMSE was 0.5875 (MJ/(m²·d)) for mean GSR and 1.115 (MJ/(m²·d)) for mean DSR, and the maximum R² was 0.9802 for mean GSR and 0.943 for mean DSR [67]. Quansah et al. [68] developed an empirical model for prediction of GSR based on sunshine hours and air temperature. They considered the Angstrom-Prescott model for the sunshine hour but Hargreaves-Samani and Chandel models for air temperature. The model developed obtained a MBE value of –0.0102 (MJ/(m²·d)), an MPE value of 0.0585%, and a RMSE value of 0.0338 (MJ/(m²·d)) respectively for sunshine hour models whereas a MBE value of –0.2973 (MJ/(m²·d)), an MPE value of 1.7075%, and an RMSE value of 0.9859 (MJ/(m²·d)) respectively for air temperature empirical models [68]. Ayodele et al. [69] developed an empirical model to predict global solar radiation using the proposed regression coefficient of Angstrom-Prescott model (refer to Appendix), the Garcia model (refer to Appendix), and the Hargreaves-Sammani model (refer to Appendix) for a daily and monthly time horizon. The proposed regression coefficient obtained from the fitting tool was interpolated in these models to obtain a good accuracy in the results. The results showed that the Garcia model with quadratic variation performed the best for the daily average global solar radiation with an RMSE value of 2.70 (MJ/(m²·d)), an MAE value of 1.86 (MJ/(m²·d)), an MAPE value of 9.34%, and an R² value of 0.68, respectively; whereas an RMSE value of 0.0909 (MJ/(m²·d)), an MAPE value of 0.0733 (MJ/(m²·d)), an MAPE value of 0.5174% and an R² value of 0.9974 respectively for monthly average daily global solar radiation [69]. Bailek et al. [70] discussed 35-empirical models to obtain the accurate diffuse solar radiation by finding the appropriate regression coefficients. Three categories of the model were created based on sunshine duration, clearness index and sunshine duration, and clearness index model. The regression coefficient was found for the good fitness in the model by a diffuse fraction and diffuse transmittance. The accuracy of all the models was evaluated using MPE, RMSE, U₉₅ (uncertainty factor), R and t-statistics method (TS) and compared with the performance of eight models discussed in the literature. They showed that the clearness index and sunshine-based model performed better than others in terms of correlation [70].

Therefore, these models are designed based on observation and experiments. Relative humidity, temperature, and sunshine hours are the three main components used in most of the models to forecast global solar radiations and its components. However, different models have been generated by modifying the basics mathematical equations as in Sayigh formula and modified sayigh formula (refer to Appendix), Garcia models (refer to Appendix) etc. and the accuracy achieved by these models are at a satisfactory level.

2.2.5 Artificial neural network

The concept of the artificial neural network (ANN) was first proposed in 1943 by the McCulloch and pits [71]. Different forms of parallel processing and pattern recognition analysis are performed by the neuron in the human brain [72]. The same phenomenon can be applied to solve the nonlinear mathematical problems in pattern recognition, forecasting, image processing, etc. This technique-based model has to be trained repeatedly to obtain the best value to weight to map the input and the output [73]. The basic ANN structure, illustrated in Fig. 5, has three main phases, the input layer, the hidden layer, and the output layer [74]. The ANN uses different algorithms like the Levenberg-Marquardt (LM) algorithm, the scaled conjugate gradient, and the Pola-Ribiere conjugate gradient to predict the output variables [75,76]. Moreover, various combinations of input parameters [77] and characteristics-based cluster of input data were also used by Yu et al. [78] for prediction.

Fig.5 Architecture of ANN (adapted with permission from Ref. [32]).

Full size|PPT slide

Three models of multi-layer perceptron (MLP) with back-propagation, unity gain, and regression network were designed by Kumar et al. [79] to estimate the daily global solar radiation (DGSR). The MAPE obtained by this model for all three algorithms was 14.84%, 14.68%, and 16.32% respectively [79]. Moreover, Notton et al. [80] used the pre-processing technique to estimate the 1–6 h ahead GHI and DNI using ANN. The RMSE obtained by this model for GHI prediction varied from 126.65 to157.27 (Wh/m²), while the nRMSE varied from 28.08% to 34.85%. The model obtained MAE for h + 4, h + 5, h+ 6 varied from 112.60 to118.59 (Wh/m²) and nMAE for h + 4, h + 5, h + 6 varied from 24.16% to 26.28% [80]. Similarly, the ANN with the variational input delay methodology was used by Rodriguez et al. [81] to forecast the solar irradiance. This approach selected appropriate neurons and kept them constant with variation in the input delay to obtain the good accuracy of the ANN model. The RMSE obtained for sunny, partially cloudy, and cloudy days by this model was 0.03%, 0.49%, and 0.64% respectively [81]. Jahani et al. (2019) compared empirical, ANN, and ANN with the GA model to forecast the GSR for the location of Iran. The GA used in the model for the optimization of accuracy reduced the prediction error. This model attained a more prediction accuracy by ANN+ GA than conventional ANN and empirical models with an RMSE value of 0.92 J/(cm²·d), an MBE value of 38.4 J/(cm²·d), and an R² value of185.5 J/(cm²·d), respectively [82]. In the same way, the future values of solar irradiance using ANN and fuzzy logic along with the error correction method was predicted by Sivaneasan et al. [83]. The fuzzy logic was employed on the input data to preprocess whereas the error correction method was applied on the past values to correct the error acquired by the back propagation algorithm. Three models, i.e., ANN, ANN with fuzzy pre-process, and ANN with fuzzy pre-processing along with error correction were compared to evaluate the better model. The MAPE obtained for these three models was 46.3%, 43.1%, and 29.6% respectively [83]. Bou-Rabee et al. (2017) estimated solar radiation by using the gradient descent method and the LM back propagation algorithm. The accuracy of this model was determined by the MAPE which was 86.3% for the gradient descent method and 85.6% for LM [75]. The deterministic and probabilistic forecast of 72h ahead power generation for a PV plant using combination of ANN and the analog ensemble technology was discussed by Cervone et al. [84]. Three different sites of Italy were selected for model testing where the forecast was composed of five variables: three variables were obtained from deterministic forecast provided by RAMS and two were from computations. The performance of the model was evaluated by the RMSE, correlation, and bias where ANN+ Analog Ensemble for deterministic forecast provided an RMSE of 8.90% and a correlation of 9.30 [84]. Chen and Kartini [85] designed a model to forecast 1h ahead solar irradiation using the combination of the k-NN and the ANN technique. The k-NN was used as a pre-processing technique applied to the input data. The model performance was determined by MABE (W/m²) and RMSE (W/m²). The RMSE for k-NN-ANN was 242 W/m² and MABE was 42 W/m² whereas RMSE and MABE for k-NN were 251 W/m² and 44 W/m² respectively [85]. Li et al. [86] compared two forecasting design techniques, ANN and support vector regression(SVR), for solar PV energy. The ANN model was explored as a feed-forward neural network having input parameters of time, historical time lag solar PV power, meteorological parameters, and PV power as an output. The performance of the ANN and SVM was determined by MBE (KWh), MAE (KWh), and RMSE (KWh) for 15 min, 1 h, and 24h ahead forecast. The RMSE of 15 min, 1 h, and 24 h was 42.15, 63.62, and 182.64 (kWh) respectively for ANN whereas the MAE was 34.57, 50.77, and 126.32 respectively for ANN, while the MBE was 0.49, 0.50, and 0.03 respectively for ANN [86]. Six ANN models with different combinations of inputs were created by Koca et al. [77] to predict solar radiation. The first ANN model was created by selecting latitude, longitude, altitude, and month as input variables while the second model used average cloudiness as an extra input variable. The third model had the average temperature along with the latitude, longitude, and month whereas the fourth and fifth model used the average humidity and the average wind velocity respectively in place of average temperature. The sixth ANN model used latitude, longitude, altitude, month, average cloudiness, and sunshine duration as the input variable to predict solar radiation. A minimum RMSE and R² of 0.0358 and 0.9974 was obtained respectively [77]. Vakili et al. [87] developed two models for forecasting GSR. To observe the impact of particulate matter on the accuracy of the model, two combinations of various meteorological variables including particulate matters and without particulate matters were prepared and applied on the neural network. The model evaluation was performed by MAPE, RMSE, and R² which were 3.13, 0.077, and 0.97 respectively for the model having particulate matter as an input variable which showed its importance as a function for a better accuracy in the prediction of GSR [87].

The 3 h ahead forecasting of wind and solar using the different algorithms of ANN was performed by Hossain et al. [88]. The data set of six years was used in the forecast process where a small sample of the data of four months were used in training and the data of one month were used in the testing of the model. A correlation coefficient R of 0.9489 was obtained for the wind energy but a correlation coefficient R of 0.96399 was obtained for solar energy [88]. Sozen et al. [76] developed a model for solar radiation forecasting using ANN for the 12 cities of Turkey. The scaled conjugate gradients (SCG), the Pola-Ribiere conjugate gradient (CGP), and the Levenberg-Marquardt (LM) algorithm were used on the data for learning of the model. The MAPE obtained for the SCG algorithm was less than 6.78% whereas R² was 99.7768 [76]. The model for short-term forecasting with a 5 min horizon using the ANN-based algorithm was prepared by Izgi et al. [89]. The designed model was trained using the LM back-propagation algorithm and evaluated by RMSE and correlation coefficient using 45 to 50 iterations. The stable power prediction for the targeted location was the best for the month of April, only between the 5–35 min time horizon and for the August between the 3–40 min [89]. Alam et al. [90] predicted the hourly and daily diffuse solar radiation using the ANN model in four different stations in India, Ahmadabad, Nagpur, Mumbai, and Vishakhapatnam. They discussed eight different models developed using the different combinations of input variables based on the correlation between input variables. The RMSE and MBE were calculated for all targeted locations of India where the maximum RMSE obtained was 4.5% among all sites [90].

Therefore, the models based on ANN can be used to solve nonlinear problems. The ANN models were used to forecast all type of time horizons with a satisfactory level. The training data of two to three years proved the best to use for the learning of model. However, the different meteorological input parameters provide different results for different sites. As a result, a better selection of input parameters according to the selected geographical area can enhance the accuracy of the model. The LM algorithm was used by most of the researchers which prove to be better than others.

2.2.6 SVM

The SVM is a type of machine learning with statistical learning introduced by Cortes and Vapnik in 1995 [91]. This particular method is first developed for pattern recognition and nowadays eagerly used for different technologies like image retrieval, fault diagnosis, regression, computation, and forecasting, etc [92]. The time series is used to train the model which is as simple as that of neural network and there is no problem of curve over fitting, strucking to local minima in SVM [93]. It maps the input vector (x_{\mathrm{1}}+x_{\mathrm{2}}+x_{\mathrm{3}}+\mathrm{.....}+x_n) to the output (y_{\mathrm{1}}+y_{\mathrm{2}}+y_{\mathrm{3}}+\mathrm{......}+y_n) using the mapping function \phi. The SVM equation can be expressed as [6]

(11)y_i={\displaystyle \sum _{j=\mathrm{1}}^n{w}_j{\phi }_{ij}+b},

where y is output function, w is weight, and b is bias. Different forms of kernel functions have been used in the SVM such as linear, polynomial, radial basis function, and sigmoid etc [94]. The basic architecture of a SVM classifier is depicted in Fig. 6.

Fig.6 Basic structure of SVM (adapted from Ref. [95] under CC BY).

Full size|PPT slide

Jimenez-Perez et al. [96] developed a model to forecast hourly global solar radiation using the SVR and support vector clustering technique. The k-mean was used to cluster the data according to the distribution of the proposed variable. Four different models were designed using techniques such as DT+ ANN, DT+ SVM-R, SVM-C+ ANN, and SVM-C+ SVM-R and were evaluated using the rMAE, RMSE and S. The combination of SVM-C+ SVM-R performed better than others with a rMAE, RMSE, S of 15.2%, 22.9%, and 3.9% respectively [96]. An LS-SVM based model was used for short-term solar power prediction (SPP) for 1445 locations in the United States [97]. In this model, the meteorological inputs were first normalized based on transitivity and then applied to different models like SVM, AR, and RBFNN. It is shown that SVM>RBFNN>AR model [97]. Shi et al. [98] designed a model based on SVM to predict the solar PV power output by dividing the historical and weather data into four categories based on cloudy, clear sky, rainy, and foggy days. These four categories were then applied to the four different SVM models having different radial basis kernel functions. The RMSE and MRE obtained for the cloudy model was 1.824 (MW) and 12.42% respectively, for foggy days was 2.52 (MW) and 8.16% respectively, for rainy days was 2.48 (MW) and 9.12% respectively, and for sunny days was 1.57 (MW) and 4.85% respectively [98]. Similarly, a model for solar irradiation forecasting was developed by Jang et al. [99] based on satellite image and SVM along with the prediction of the amount of clouds at the target site. The atmosphere motion vector scheme was used to extract the motion vector information from the images collected by the satellite. The cloud and solar irradiation vector data were then applied to the SVM. The RMSE, MRE, and R²obtained for the SVM model was of 44.1390 (W/m²), 7.7329%, and 09420 respectively [99].

Fan et al. [100] observed the effect of air quality index (AQI) and six other air pollutants in the prediction of global and diffuse solar radiation. The SVM model was used in practice for sunshine and temperature-based input parameters. Different combinations of air pollutants were employed to prepare the ranking of most influencing air pollutant using RMSE. The AQI was recognized as the most influencial parameter for both predictions (GSR and DSR) whereas the combination of PM₁₀, PM _2.5, and O₃ was also the most influencial variable which improved the RMSE by 22.2% over the conventional SVM without air pollutants as input [100]. However, Ma et al. (2019) considered only AQI along with climatology parameters to estimate the DSR using the SVR model. The Pearson’s coefficient was used as a feature selection technique to select the only variable with a strong correlation [101].

Therefore, SVM performs better with data categorization. Several studies categorize the data according to their characteristics as doShi et al. [98]. The k-means and Pearson’s coefficient could be used as feature selection techniques and the inclusion of AQI and air pollutants as input variables also increase the model accuracy.

2.2.7 Deep learning

As per literature, deep learning becomes an active and promising area of research in the field of forecasting [102]. Various deep learning algorithms have been implemented in different studies to forecast solar irradiance or PV power output but the most commonly used deep learning algorithms are recurrent neural network (RNN), long short-term memory (LSTM), convolution neural network (CNN), and gated recurrent unit (GRU) [103]. The advancement in the conventional feed-forward network is known as RNN where the past output is used as inputs to each node. This network applied a nonlinear function to the weighted sum of the input sequence. If y_t is the output of a RNN network at time t, it can be expressed as [104]

(12)y_t=\sigma ({\omega }_{\mathrm{o}}{h}_t),

where h_t=\tanh ({\omega }_t{x}_t+W{h}_{t-\mathrm{1}}) is hidden state; ω_tand W are the input and previous hidden state weight matrix; and h_{t-\mathrm{1}} is previous hidden state matrix.

The combination of three gates i.e., inputs, outputs, and forget gate with internal memory is used in each unit of LSTM. These units process the data and determine whether to keep or forget the memory. The important features of the input sequence are recognized by LSTM unit while GRU is also performing the same operation as LSTM but with less complexity and more efficiently. Figure 7 presents the architecture of RNN, LSTM, and GRU.

In the case of LSTM, the input gate passes the current information according Eq. (13).

(13)i_t=\sigma (x_t{\omega }_t^i+h_{t-\mathrm{1}}{W}^i).

The forget gate decides which information from previous state needs to be forgotten and expressed as

(14)f_t=\sigma (x_t{\omega }^f+h_{t-\mathrm{1}}{W}^f).

whereas the internal state that needs to pass is declared as the output gate and expressed as

(15)o_t=\sigma (x_t{\omega }^{\mathrm{o}}+h_{t-\mathrm{1}}{W}^{\mathrm{o}}).

The internal memory elements can be calculated by using

(16)\widetilde{C_t}=\tanh (x_t{\omega }^{\mathrm{g}}+h_{t-\mathrm{1}}{W}^{\mathrm{g}}),

(17)C_t=\sigma (f_t\times C_{t-\mathrm{1}}+i_{t-\mathrm{1}}\widetilde{C_t}),

(18)h_t=\tanh (C_t)\times o_t.

However, the hidden state of GRU can be expresses mathematically as

(19)h_t=(\mathrm{1}-z_t)\times h_{t-\mathrm{1}}+z{}_t\times \tilde{h},

where, \tilde{h}=\tanh (x_t{\omega }^{\mathrm{h}}+(r_t\times h_{t-\mathrm{1}})W^{\mathrm{h}}),r_t=\sigma (x_t{\omega }^{\mathrm{r}}+h_{t-\mathrm{1}}{W}^{\mathrm{r}}),z_t=\sigma (x_t{\omega }^{\mathrm{z}}+h_{t-\mathrm{1}}{W}^{\mathrm{z}}).

Fig.7 Architecture of deep learning.

Full size|PPT slide

Qing et al. [105] developed the LSTM network to forecast the hourly day-ahead solar irradiance. They used the weather data set of the island of Cape Verde, Santiago to perform the forecasting. They compared the designed model with the BPNN and the persistence method based on different sizes of data sets. The model accuracy was improved by 18.34% using LSTM with the data of 2 years. However, with the training data of 9 years and a validation of 1 year, it showed a 42.9% improvement in RMSE [105]. Although the 2, 6, and 24 h ahead forecasting was performed by Chandola et al. [106] using LSTM for four locations in Thar-desert, the MAPE obtained ranged from 6.79% to10.47%; whereas the RMSE ranged from 0.099 to0.181 for different targeted locations [106]. However, Wang et al. [107] proposed a gated recurrent unit network-based PV output power forecasting for short time horizon. The model used the Pearson coefficient to extract the input variables that affect PV forecasting. The k-means cluster algorithm was also employed to reduce the training time by clustering the sets based on the same features. Each cluster then was applied to the GRU network to forecast the PV output power. The performance of the proposed model was evaluated using RMSE with comparison to other models like LSTM, BO, SVM, and ARIMA. An average RMSE of 0.036 was obtained by GRU-based network which was better than the above-said models [107]. Yu et al. used LSTM and the k-means algorithm for short-term solar irradiation prediction in complicated weather conditions. They divided the days into three categories on their clearness index named sunny, cloudy, and mixed days. Based on the clear sky index, the LSTM method was applied to the input data and then all the values were ensemble to obtain the final GHI prediction. The proposed model outperformed CNN and SVM with RMSE varying from 41.37 to 66.69 (W/m²), MAE varying from 30.19 to 46.04 (W/m²), and R² varying from 0.95 to 0.97 [78]. However, Sodsong et al. [108] predicted short-term solar PV power using multiple GRUs. The numbers of GRU networks were connected in a cascade structure to improve the nRMSE. The output of the first network becomes the input to the succeeding network and so on until the nRMSE approaches to a minimum value. The model accuracy was then compared with the SVR, KNN, and conventional GRU in terms of nRMSE. The model outperforms others with a nRMSE of 9.64% using three networks connections [108].

Deep learning is an effective technology in contemporary research and used by several researchers for forecasting solar components. The forecasting of short to long-time horizon can be performed favorably by this technique with a better accuracy than others. The LSTM proves to be better than ARIMA, ANN, SVM, and other standalone models. However, k-means algorithms along with LSTM have increased the accuracy in complicated weather conditions but the GRU also improves the RMSE by more than 40%.

2.2.8 Hybrid models

The hybrid models are the most widely used models to forecast solar irradiation with a more increased accuracy than the isolated models. There are several factors which a model has to consider to perform with a more accuracy which are usually not considers by the standalone models [109]. The hybrid method is the combination of two or more techniques to generate the forecast. There are a number of models based on the linear and nonlinear methods. The hybrid model might be a combination of two or more linear models, a combination of two or more nonlinear models, and a combination of linear and nonlinear models.

Based on the literature, various pre-processing, post-processing, and optimization techniques are used to create the hybrid models, including ANFIS+ ANN, ECMWF+ ANN, SVM+ RBF+ WT, GA+ CNN, PSO+ CNN, WMIM+ ELM, LSTM+ CNN, LASSO+ ANN, WT+ ELM, CNN+ GRU, WT+ PSO+ FFNN, k-means+ RBFNN, LM-ANN, WT+ NNMFOA+ GMDHMFOA, Fuzzy+ ANN, DFT+ PCA+ Elman, k-mean+ NAR as ANN as a major part of forecasting model [32,110–126].

The ANN and ANFIS (artificial neuro-fuzzy inference system) model was developed by Kumar et al. [110] to estimate solar PV power generation. The ANFIS was the combination of neural network and the fuzzy inference system (FIS) that properly tune the fuzzy inference system by applying the neural learning functions. Kumar et al. showed that ANN had less error than ANFIS in forecast [110]. Guermouiet al [127]. proposed a weighted Gaussian process regression (WGPR) model for 10- steps ahead solar radiation component forecasting. Two architectures of WGPR with cascade and parallel configuration were proposed for estimating the GHR and DHR. The WGPR model was used to select the optimum input parameters to obtain the accurate estimation of solar radiation components. The performance of these models was determined by RMSE, rRMSE, and r², where WGPR-CFA out performed WGPR-PFA for DHR and GHR [127]. Aguiar et al. [119] developed three models of forecasting with three different techniques to obtain less error in the forecasting results. The models designed in the study were ANN with grounded data (ANN), ANN with grounded and satellite data (ANN+ Sat), ANN with ground and European Centre for Medium-range Weather Forecasts (ECMWF) data (ANN+ ECMWF), and ANN with ENMWF and satellite data (ANN+ ECMWF+ Sat). The best RMSE range obtained in this was from 83.58 to 147.88% for ANN+ ECMWF+ Sat [119].

Shamshirband et al. [120] developed a hybrid model using SVM and wavelet transform to predict the DSR for Kerman, Iran. The discrete wavelet transform was used in the model to decompose the input time series, each of which was then applied to the individual SVM model. The mode developed l was compared with the hybrid structure of SVM and RBF (SVM-RBF), ANN and the 3rd-degree empirical model. The SVM+ WT model outperforms the other hybrid models with a MABE of 0.5757 (MJ/m²), a RMSE of 0.6940 (MJ/m²), and a R² of 0.9631 [120]. Moreover, Huang et al. [125] used WT to decompose the input series whereas Lan et al. [117] used discrete fourier transform (DFT) to convert the time domain series into the frequency domain where the crucial frequency components were collected by PCA. The output series of both methods were applied to the elman neural network (ENN) and obtained a RMSE of 25.83(W/m²) by WT+ ENN and a MAE of 118.67%, 89.29%, 39.46 and 49.82% respectively for spring, summer, autumn, winter by DFT-PCA-Elman [117,125]. The PV output power estimation using the neural network ensemble technique was performed by Raza et al. (2018). The neural network ensemble technique combines the output of different neural networks. The discrete wavelet transform was applied on the time series data with PSO to optimize the model performance. The method proposed outperforms the others in terms of an error variance of 0.2847 for summer, 0.2645 for autumn, 0.3103 for winter, and 0.1723 for spring [111].

Bouzgou et al. used the extreme learning machine (ELM) along with wrapper mutual information methodology (WMIM) to forecast GSR whereas Cornejo-Bueno et al. compared it with the support vector regression and Gaussian process, and used WMIM with ELM to select the appropriate input variables for training and testing the phase of model. They obtained an MAPE of 7.4%–10.77% for 1–6 steps ahead forecast for ELM+ WMIM and when compared with the support vector regression and Gaussian process, the RMSE was 60.61 (W/m²) for ELM [118,122]. Furthermore, Benali et al. performed a comparison of beam normal, global horizontal radiation, and diffuse horizontal solar radiation using the three different methods, i.e., smart persistence, artificial neural network, and the random forest method [112]. They used the clear sky index parameter to improve the forecasting accuracy by transforming the historical time series solar data into the stationary data. The results revealed the random forest forecast was better with nRMSE varying from 19.65% to 27.78% for GHI, 34.11% to 49.08% for BNI, and 35.08% to49.14% for DHI [112]. Behrang et al. (2010) also compared six models of RBF and MLP based on different combinations of meteorological inputs to estimate the GSR [32]. The k-fold cross-validation was used by Mellit et al. [115] to validate the capability of the neural based forecaster. The maximum value of r obtained for sunny days was 94.14% and the minimum RMSE was 32.98% whereas MAE and MBE were 2.75% and –23.25% respectively for this model [115]. Huang et al. [124] used the Jaya based algorithm to optimize the BRT parameters to predict the solar irradiation based on boosted regression trees, ANN, SVM, and the least absolute shrinkage and selection operator (LASSO). They provided a RMSE of 18.4%, 24.3%, 27.9% and 30.6% respectively for the time horizon of 30 min, 60 min, 90 min, and 120 min forecast [124].

Elminir et al. [113] estimated the solar radiation components for the location of Helwan, Egypt in different spectral bands with the help of LM-ANN. The normal radiation of different bands was measured with the help of the band pass filter method. The lowest RMSE obtained were 5.02%, 7.46%, and 3.97% for IR, U.V. and global isolation respectively [113]. A method for short-term forecast of solar irradiation using ANN with statistical features was proposed by Wang et al. [128]. The random effect of weather conditions on the ANN inputs was reduced by proper selection of input parameters using statistical features. By statistical features, the 3rd order difference of solar irradiance was taken as the input whereas the maximum temperature of a day was considered as the weather changing characteristic index. The combination of Gauss-Newton and gradient descent algorithm was used for learning of the model. The evaluation of the model was performed by MAPE, RMSE, and MABE where MAPE was 9.09% for sunny and 26.70% for cloudy, RMSE was 42.29 W/m² for sunny and 84.65 W/m² for cloudy and MABE was 31.10 W/m² for sunny and 64.60 W/m² for cloudy days [128]. Antonopoulos et al. (2019) discussed the forecasting of daily solar radiation by considering the empirical equations of the Hargreaves, ANN, and multilinear regression models. The RMSE and r values used for the evaluation of models showed a RMSE and r values of 3.344 and 1 respectively for station 1 with MLR having input combinations of Ra, TD,\sqrt{TD}, RH_av and 3.166 and 1 for station-2 with ANN inputs combinations of Ra, TD,\sqrt{TD}, and RH_av [19]. Heydari et al. designed a model for prediction of wind and solar power using modified fruit fly optimization in association with neural network. Two other models were also proposed in the paper by MFOA, one being the point prediction of energy consumption model GMDHMFOA and the other, the renewable energy prediction interval model (WT-NNMFOA-GMDHMFOA). The proposed GMDHMFOA model has a RMSE of 0.017868, a MAPE of 1.7275, a MAE of 0.015095, and a r² of 0.99649 [114]. Wang et al. [41] proposed an adaptive learning hybrid model (ALHM) for estimation of solar intensity. The ALHM model was integrated with the time-varying linear model and the GA-BP model to obtain useful information from the data. The proposed ALHM model keeps improving the forecasting performance automatically by capturing the linear, the temporal and the nonlinear relationship in input data. The MAPE achieved by the model was 13.68% [41].

Besides ANN based hybridization, many researchers also used other techniques such as HGWO+ RF, EMD+ SVR, Ramp Rate+ NWP, WT+ SVM, SARIMA+ RVFL, Firefly+ SVM, k-means+ regression techniques, WT+ PSO+ SVM, GA+ SVM to predict the solar components [129–141]. Liu et al. discussed the autoregressive arithmetic average model for different standalone techniques to predict the PV system output. The prediction by various standalone methods was ensemble and opted to the best result generated by any of the models or made an average of the result if the results of each model were the same. The auto-recursive method was used to automatically update the weight of the SVM, MLP, and MARS standalone model. It was concluded that the ensemble averaging outperformed the others on every testing data sets i.e., ensemble averaging>SVM>MLP>MARS [142]. Three models to predict the daily diffuse solar radiation using SVM with firefly algorithm, Copula based nonlinear quantile regression (CNQR) and different combinations of empirical models were implemented by Liu et al. [138]. Different copulas were tested to select the optimal parameter for the model in CNQR for predicting solar radiation. The performance of the model was evaluated by the RMSE, R², MABE, and MBE for four locations which shows SVM>CNQR>empirical model [138]. Moreover, Basurto et al. [141] designed a hybrid intelligent system to predict solar energy using the clustering and regression technique. They clustered the input data to prepare sub groups using the k-means clustering algorithm and then applied it to MLP, least square SVM (LS-SVM), and RBFN. They also compared the results and performance of the model with those of Bayesian regularization (BR), scaled conjugate gradient (SCG), batch training with bias and weight learning rules (RB), gradient descent with adaptive rates and momentous (GDX), and the LM algorithm and found that the performance of the clustered data by the k-means algorithm using RBFN and MLP was better than that of others [141]. Eseye et al. [132] developed a model for solar PV power forecasting using a combination of wavelet, PSO and the SVM model. This model attained a MAPE of 4.22% for 24 h ahead forecasting for the given location [132]. Feng et al. [143] developed an optimized cross-validated clustering (OCCUR) method for selection of a suitable cluster of the time series data for GHI forecasting. The input data was clustered using the OCCUR method based on the k-means algorithm. The category of the cluster was recognized by SVM classification named SVM-PR classification. The recognized classification was then applied to the two-layer-based machine learning model such as ANN, SVM, GBM, and RF [143]. Deventer et al. [133] proposed a genetic algorithm (GA) based SVM for PV power forecasting. The GA was used to optimize the SVM forecast where SVM classified the historical weather data using SVM classifiers. The RMSE and MAPE for the GA-SVM was 11.226% and 1.7052% respectively for the designed models [133].

Zhang et al. [130] used the post-processing technique—Hilbert Huang transform (HHT) EMD to decompose the output data instead of the cubic spline curve (CSC). They predicted the solar power output using the hybrid design of the SVR model and used the improved feature selection algorithm to select the best input for the next processing. They based the proposed model design on the SVR with PSO optimization to improve the accuracy of the model. They found that the proposed algorithm performed better than the other benchmarks with an average nRMSE (%) of 0.95 and an average MAPE (%) of 14.55 [130]. Furthermore, Kushwaha et al. [137] proposed a method to forecast the solar radiation for a short-time horizon using the hybridization of seasonal autoregressive integrated moving averaging (SARIMA) and the random vector functional link (RVFL) neural network. They used the random vector functioning link neural network to obsolete the problem of strucking in local minima and maxima while updating biases. This percentage change in MAPE, RMSE, MASE, and r² for the proposed model were obtained to be 6.376, 3.497, 6.452 and –0.649 respectively [137]. Monjoly et al. [144] proposed a hybrid approach to forecast GSR. They analyzed different multi-scale decomposition techniques such as EMD, ensemble EMD, and WT. This hybrid approach automatically selected the algorithm according to the time scale component of decomposition. The NN model worked for the short-time scale component and the autoregressive model worked for the long-time scale component. They found that the wavelet decomposition hybrid method performed better with a rMBE of 0.04%, a rMAE of 5.34%, a rRMSE of 7.90%, and a skill of 71.94% [144].

A hybrid method for 3 h ahead estimation of solar power using the principal component analysis, k-means algorithm, and differential evolution gray wolf optimization (HGWO) random forest was proposed by Liu et al. [129] and used for optimization and updating of wolf position by continuous cross mutation process. The results showed that PCA+ K-means+ HGWO+ RF outperforms in terms of RMSE varying from 8.88 to 9.92 and MAE varying from 4.76 to 5.80 [129]. Dong et al. [134] predicted the GSR on an hourly basis using the ensemble method. The ensemble method combined the different sub-results to obtain the final result using the firefly algorithm based on the thresholding rule and the accelerated gradient method. The input data set was first divided into different subspaces using the random subspace (RS) method and then suitable covariate was obtained from each subspace using the square root smoothly clipped absolute deviation (SRSCAD) method. The performance of the model was determined by MAPE, RMSE, Theil inequality coefficient (TIC), computation cost, and correlation coefficient which was 0.066, 20.21 W/m², 0.06, 3.40S, 0.98 respectively [134]. Abuella et al. deployed a technique to adjust the ramp rate occurred in the solar prediction by combining the 24 h ahead forecast obtained from NWP and 1 h ahead forecast obtained from the persistence method. The random forest forecast method was used to combine both of the outputs obtained from NWP and persistence where the ramp rates of both forecast were added up and the accuracy of the prediction was increased by the two loss functions [135]. Two novel stochastic models to forecast the solar radiation and the PV power were developed by Dong et al. [136]. The features of solar energy and PV power were extracted by the filter based-stochastic state space model where the Kalman filtering mechanism was implemented to obtain system parameters and state variables. The nRMSE obtained for solar radiation varied from 7.43% to 26.13% for Gaussian uncertain bias with a 1–50 min time horizon whereas the MAPE for solar radiation varied from 5.72% to 25.73% for Gaussian uncertain bias for a 1–50 min time horizon [136].

Srivastava et al. [140] discussed 1 to 6 day ahead prediction of solar PV plant power output using MARS, CART, the M5 model, and the random forest (RF) model. The performance of the RF was found to be better than that of the M5, MARS and the CART model. However, in cloudy days, the forecasting results have more errors [140]. The real time sky images were used by Caldas et al. (2019) to forecast1–10 min ahead solar irradiance. The real time images captured by the camera were directly used for the prediction of solar irradiance while the previous images were used for the estimation of mean motion of the clouds. The mean bias deviation (MBD), mean absolute deviation (MAD), and root mean square deviation (RMSD) were used to determine the performance of the model where the proposed model outperforms the smart persistence model with a forecasting skill of 11.4% [131]. A k-means cluster based NAR network was used by Benmouiza et al. [145] to estimate the hourly GSR. The k-means clustering algorithm was used to prepare the cluster of the same characteristic unlabeled data and then applied to the nonlinear autoregressive (NAR) network having a good auto-regression property for nonlinear data. To choose the number of suitable clusters, the silhouette function was used. This model obtained a RMSE and a nRMSE of 60.24 Wh/m² and 0.1985 respectively [145].

Deep learning techniques were also used in several studies where CNN, LSTM, and GRU were used for solar irradiation forecasting in hybrid configurations. Zhou et al. [139] developed a method to forecast PV power using LSTM along with the attention mechanism which observes and selects the optimal forecasted output from LSTM. They used two LSTM networks, one for PV power output forecast and the other for temperature forecast. They found that the proposed method performed better than other available models for the time horizon of 7.5 min to 60 min ahead [139]. Dong et al. [121] used the CNN framework to simply forecast the output variables and GA/PSO to optimize the forecasted variables whereas Ghimire et al. [146] used CNN for the input pattern recognition with different filter configurations. Furthermore, Chen et al. [116] used fuzzy logic to classify the temperature and sky information and neural network to achieve a good accuracy. This method achieved a MAPE of 6.03% –9.65% which was very low compared to that of the statistical, fuzzy, and neural algorithms [116]. Liu et al. [126] developed a model to forecast solar irradiation using deep neural networks (DNN) by considering the spatial and temporal variation. They proposed a combination of CNN and GRU to handle the large dimensions of spatial and temporal variations with training loss functions. The model proposed used the convolution in the GRU network instead of using the convention multiplications for spatiotemporal forecasting. This model achieved a mean of defined error metrics RMSE, MEA, and Nash-Sutcliffe efficiency (NSE) for the ConvGRU-VB of 69.5, 34.8, and 0.929 respectively [126]. Jiang et al. [147] proposed a hybrid DNN named Resnet TL to estimate the hourly GSR using CNN and MLP. They used CNN to extract the spatial pattern from the geostationary satellite observations where these patterns along with external attributes were fed to MLP to estimate GSR and obtained a RMSE of 0.30 MJ/m² for hourly GSR, a RMSE of 1.92 MJ/m² for daily, and a RMSE of 1.08 MJ/m² for monthly GSR [147]. Alkandari et al. [148] combined the machine learning and theta statistical methods to forecast solar power. They used the novel Auto-GRU model as a machine learning model while used four different approaches of simple averaging approach, weighted averaging, linear and nonlinear approach, and inverse approach to combine the prediction of MLSHM members. Besides, they used nMAE and nMSE to calculate the accuracy of the model which showed that the Theta-MLSHM performed better than the individual machine learning model [148].

In summary, numerous hybrid models have been proposed by several researchers. However, it is very hard to select an appropriate model among all models for a particular problem as each model is developed for different regions, for different set of input variables, for different environmental conditions, for different training data, and used different error matrices. But the performance of wavelet transform (WT) is better than that of empirical model decomposition (EMD) for the pre-processing of the data whereas GA/PSO can optimize the results better than others. The attention mechanism along with LSTM can be used to forecast an ultra-short time horizon, which performs with a better accuracy. The large spatial and temporal variations in the data can be handled by the hybridizations of CNN and GRU. Therefore, in general, the hybrid structure of deep learning models performed better than others.

Tab.1 Summary of investigated studies

Ref.	YOP	Region/place	Lat/Long	Time ahead	Training period	Testing period	Input variable	Output variable	Technique	Error parameters	Error/%
[76]	2005	Turkey	36°/42°		4 years, train 9 station	3 station	Lat, Long, Al, M, MSD, Tm	SR	ANN with SCG, CGP, LM	MAPE, R2	MAPE<6.78%, R2 = 99.7768%
[113]	2005	Helwan, Egypt			1 year	1 year	RH, T, WS, WD, CC	UV, IR, GI	ANN	RMSE	RMSE: IR= 5.02%, UR= 7.46%, GI= 3.97%
[90]	2009	India: Ahmadabad, Nagpur, Mumbai, Vishakhapatnam			10 stations in India	10 stations in India	Lat, Long, Al, t, M, T, RH, R, WS, LW	CI	ANN-FFBP	RMSE	RMSE= 4.5%
[32]	2010	Dezful, Iran	32°.16′N 48°.25′ E	24 h	1398 d	214 d	DATm, RH, SD, E WS	DGSR	MLP, RBF	MAPE	MAPE= 5.21%
[77]	2011	Mediterrane, Anatolia, Turkey	36°.43′ –37°.46′ /30°.17′ –36°.55′		1 year	1 year	Lat, Long, Al, M, CC, Ta, Ha, WSa, SD	SR	ANN	R2, RMSE	RMSE= 0.0358, R2 = 0.9974
[88]	2012	Central Queensland, Australia	23°.38′/150°.58′	3 h	4 m	1 m	AT, WS, WD, SR, RH, R, VWSP, WS, WD, WG, E,	WE, SE	ANN	R	R = 0.96399
[89]	2012	Istanbul	-	3–40 min	1 m	1 m	SI, AT,CT	PVo	ANN-LMBP	RMSE,R2	Stable forecast 3–40 min, Augest, stable 5–35 min forecast, April
[98]	2012	South China		1 d	Historic	10 m	Weather+ Historic	Solar PV power	SVM	RMSE, MRE	RMSE= 2.10 MW, MRE= 8.64%
[128]	2012	China		24–72 h	80% of data	20% of data	3rd order difference of SI, Tm day, normalized discrete difference, Ta	SR	ANN with statistical parameter selection	RMSE, MAPE, MABE	MAPE= 9.09%–26.7%, RMSE= 42.29–84.65 (W/m2), MABE= 31.10–64.6 (W/m2)
[97]	2013	US		1–6 h	1 year	1 year	Meteorological variables	Solar power	SVM, RBFNN AR	MAE, MAPE, R2	SVM>RBFNN>AR
[55]	2013	Gurgaon, India			750 d	165 d	AT, RH, AP, WS, WD, SR	SR	HMM and GFM	RMSE, MAPE	RMSE= 7.9124, MAPE= 3.4255
[116]	2013	NEA, Singapore		1 h–1 d	17280 data	4320 data	T, SKI, SR	SR	Fuzzy and ANN	MAPE	MAPE= 6.03%–9.65%
[145]	2013	Algeria, Oran		Hourly	2.6 years	6 m	Time series	GSR	k-means cluster and NAR	RMSE, nRMSE	RMSE= 60.24 (W/m2), nRMSE= 0.1985
[68]	2014	Owabi, Ghana,	6°.45′ N/1°.43′ W		11 m	Monthly	T, RH, AP, R, DR, SMP, SHF, WS	GSR	Sunshine and air temperature based empirical model	MBE, MPE, RMSE	Sunshine: MPE= 0.0585%, MBE= -0.0102 (MJ/(m2·d)), RMSE= 0.0338 (MJ/(m2·d))
											Air temp: MPE= 1.707%, MBE= –2.973(MJ/(m2·d)), RMSE= 0.985(MJ/(m2·d))
[47]	2015			1–3 step ahead			Time series	SR	ARMA, ARIMA with LLF	MAPE	ARMA_MAPE= 71.67%, ARIMA_MAPE= 32.07%
[49]	2015	Spain	38°.67′ N/4°.15′ W	1–24 h	1 year	Monthly	Aggregated hourly SR	DHI and DNI	DHR	rMBE, rRMSE	GHI: rMBE= 0.21, rRMSE= 29.66
											DNI: rMBE= 3.82, rRMSE= 46.79
[62]	2015			1 h to 1 d	1 year	1 year	NWP, meteorological	SI	Multi/step linear regression	RMSE, MAE	MOS-MLR>MOSP5
[86]	2016	Florida		15 m, 1h, 24 h			t, time lag, PM energy MT	PV energy	ANN and SVR	RMSE, MAE, MBE	ANN>SVR
[87]	2016	Tehran, Iran	51°.23′ N/35°.44′ E		1 year	1 year	Molde-1: Tmax, Tmin, RH, WS, PM, Model-2: Tmax, Tmin, RH, WS,	GSR	ANN	MAPE, RMSE, R2	MAPE= 3.13, RMSE= 0.077, R2 = 0.97
[96]	2016	Malaga, Spain	36°.42′ N/4°.28′ W		4 years	4 years	AT, RH, AP, GHI	GSR	DT and ANN, DT and SVM, -R, SVM-C and SVM-R, SVM-C and ANN	rMAE, RMSE, S%	rMAE= 15.2%, RMSE= 22.9%, S= 43.9%
[99]	2016	North East Asia		60 min	4 years		Satellite image	SI	AVM+ SVM	RMSE, MRE, R2	RMSE= 44.1390 (W/m2), MRE= 7.7329%, R2 = 0.9420
[56]	2016	Nakhon Pathom station, Thailand	13°.81′ N/100°.04′ E	Hourly	3 years	1 year	GSR, DSR, Al, CI, ESR	GSR	Markov transition matrix	RMSD	Second order>First order
[69]	2016	Ibadan	7°.4′ N/3°.5′ E		9 years	Daily and monthly	daily avg. GSR daily SD, daily avg. Tmax, daily avg.Tmin	Daily and monthly vg. GSR,	Angstrom Prescott model, Garcia model, Hargreaves-Sammani model	RMSE, MAE, MAPE, R2	Daily avg. GSR RMSE= 2.70 (MJ/(m2·d)), MAE= 1.86(MJ/(m2·d)), MAPE= 9.34%, R2 = 0.68
											Monthly avg. GSR RMSE= 0.0909 (MJ/(m2·d)), MAE= 0.0733(MJ/(m2·d)), MAPE= 0.5174%, R2 = 0.9974
[119]	2016	Gran Canaria Island (Spain)	28°.75′ /–16°	1 to 6 h	1 year		Meteorological data, NWP, Satellite data	GHI	ANN, ANN and SATANN and ECMWF, ANN and ECMWF and NWP	RMSE, % skill	RMSE= 83.58%–147.88%, %S= 9.67%–35.19%
[120]	2016	Kerman, Iran	25°.55′–32°/ 30°.29′–57°.06′		5 years	2 years	CI	GHI	SVM and WT	MABE, RMSE, R	MABE= 0.5757 (MJ/m2), RMSE= 0.69 (MJ/m2), R = 0.96
[75]	2017	Kuwait: Wafra, Kuwait, International Airport, Abdaly, Rabyah, Sulaibiya			3 years	1 year	Time series data	SR	Gradient descent algo, LM algo	MAPE	GDE MAPE= 86.3, LM MAPE= 85.6
[79]	2017	10 cities, India		Hourly	90% of 2 years	10% of 2 years	Tmin, Tmax, Tavg, WS, RH, P, ESR, SD	DGSR	ANN and unity feedback, RBF and LR	MAPE	Average MAPE= 14.84%–16.32%
[83]	2017	Singapore	1°.34′ N, 103°.96′ E		3 m	1 m	T, DP, WD, WS, WG, irradiance (clear sky), error (BP)	SI	FF-ANN, BP-ANN, Fuzzy preprocessing, Error correction of past 5 min output	MAPE	ANN and Fuzzy and error correction= 29.6%, ANN and Fuzzy= 43.1%, ANN= 46.3%
[84]	2017	Italy: Lombardy, Calabria, Sicily		72 h ahead	2 years	3 m to 1 year	GHI, CC, T, Azimuth Elevation	Solar power	Analog ensemble and ANN	RMSE	RMSE= 8.09%
[85]	2017	9 plants in Taipei, China		60 min	4 h with 5 min interval		Past GSI, T, RH,WS, WD	GSI	K-NN and ANN	RMSE, MABE	RMSE= 242 (W/m2), MABE= 42 (W/m2)
[50]	2017	9 cities in Indian	NA	Hourly, Montly	data sets of 7 cities	data set of 2 cities	SD, API, Lat/Long	DGSR`	Linear, quadratic, explinear, expquadratic regression	RMSE, MAPE, r	RMSE= 3.08 (W/m2), MAPE= 0.1342%, R = 0.3790
[57]	2017	Afyonkarahisarand Antalya, Turkey		Hourly	75% of 4 years	25% of 4 years	Time series	GSR	Mycielski-Markov	RMSE, MABE, R2	RMSE= 13.49(W/m2), MABE= 10.7554%, R2 = 0.8320
[58]	2017	Fort Peck, Montana, desert Rock, Navada, Bondville, Illinois Penn State Univ, Pensylvania	48°.30′ N/105°.10′ W 36°.62′ N/116°.01′ W 40°.05′ N/88°.37′ W 40°.72′ N/77°.93′ W	Seasonal			Historical data	TSRY	Discrete Markov chain	% average error	Max % Error= 10%, Min % Error= 6%
[70]	2017	Adrar, Ghardaïa, Tamanrasset, Algeria	27°.88′/–0.27′ 32°.36′/ 3°.81′ 22°.78′/ 5°.51′		3 years	3 years	SD, AT, RH	DSR	Sunshine based empirical, CI based sunshine and clearness	MPE, RMSE, U95, R, t-statistics	Sunshine and clearness index>All
[144]	2017	Le-Raizet, France	16°.26′ N/ 61°.5′ W	1 h	1 year	1 year	Time series	GSR	WD-hybrid, EEMD-hybrid, EMD-hybrid	rRMSE, rMBE, rMAE	rRMSE= 3.80%–8.31%, rMBE= –2.06%–0.02%, rMAE= 2.76%–6.64%
[28]	2018	12 locations, Iran		1 d ahead	70%	30%	M, atmosphere insolation, AP, AT, Tmax, Tmin, RH, WS, Lat, long	DGSR	GMDH, ANFIS, ANFIS-PSO, ANFIS-GA, ANFIS-ACO	RMSE, MAPE	GMDH>MLFFNN>ANFIS-PSO>ANFIS-GA>ANFIS-ACO>ANFIS
[81]	2018	Data Euskalmet			Six years	Seasonal	SI, AP, RH, AT	SI	ANN with delays	RMSE	RMSE= 0.03%–1.64,
[41]	2018	UMASS Trace Repository		5 min to 2 days	2 years	2 m	T, RH, DP, WS, P	SI	TMLM and GABP and ALHM	MAPE	MAPE= 8.66%
[100]	2018	Beijing, China		1 d	2 years	1 year	MSD, Tmax, Tmin, PM2.5, PM10, SO2, NO2, CO, O3, AQI	GSR, DSR	SVM	RMSE_DSR, RMSE_GSR	RMSE_DSR= 1.432 MJ/(m2·d), RMSE_GSR= 2.947 MJ/(m2·d)
[63]	2018	Singapore	2°/140°	1 d	2 years	1 year	NWP	SI	NWP and PCA	RMSE, rMSE, MAE, rMAE, MBE, rMBE	RMSE= 169 (W·m2), rRMSE= 35.7%, MAE= 193 (W/m2), rMAE= 28.1% MBE= –14 (W/m2), rMBE= 2.9%
[105]	2018	Santiago, Cape Verde	NA	1 d	2 years and 10 years	6 m, 1 year	M, day, t, T, DP, RH, V, WS	GHI	LSTM	RMSE	RMSE= 76.245 (W/m2)
[107]	2018	Global Energy Forecasting Competiton 2014 and ECMRWF			2 years and 8 d	1 m and 10 d	Time series, T, CC TCLW, IW, SP, RH, UWC, SSRD, STRD, GHI, P	PV power	k-means and GRU	RMSEavg	RMSEavg = 0.036
[110]	2018	Kalipi, Andhra-Pradesh, India	13°.99′ / 77°.45′		1 year	Day	GHI, DHI, T, P, WS, AP, SD, RH, Surface Temp.	PV power	ANN ANFIS	% Error	ANN>ANFIS
[122]	2018	Tamanrasset (Algeria), Madina(Saudi Arabia)	22°.79′/5°.52′ 24°.55′/39°.70′	5 min to 3 h ahead	Tamanrassrt 11 years, Madina 1 year		Time series	GHI	WMIM and ELM	MAPE	MAPE= 7.4%–10.77
[127]	2018	Ghardaia, Algeria	32°.6′ /3°.8′	10 steps	1 year	1.5 year	D, Tmin, Tmax, RH, P, Max. elevation, declination angle, day duration, SD, sunshine ratio	GHR, DHR	WGPR-CFA, WGPR-PFA	RMSE, r2	RMSEGHR= 3.18 (MJ/m2), r2GHR= 85.85%, RMSEDHR= 5.23 (MJ/m2), r2DHR= 56.21%
[130]	2018	Syracuse		Monthly	1 year	Monthly	Sun angle, SI, T, visibility, CC, RH	Solar power	EMD and PSO and SVR	nRME MAPE	Avg nRMSE= 0.95%, Avg MAPE= 14.55%
[132]	2018	Beijing, China		1 d	1 year	Seasonal	SR, T, CC, RH, AP, WS, SCADA	Solar PV Power	Wavelet-PSO-SVM	MAPE	MAPE= 4.22%
[135]	2018	3 PV site in Australia	149°.06′E/35°.16′ S		2 years		CC, CW, IC, SI, P, AT, WS, RH AP	Ramp events	RF with loss functions	NA	NA
[143]	2018	Colorado	39°.74′/105°.1′	1 h	75% of 1 year	25% of 1 year	GHI, GHIclr, CSI, DNI, DHI, T, RH, AP, WS, WD	GHI	OCCUR and SVM and M3	nRMSE, nMAE	UC-M3>UC-GBM
[19]	2019	AUTH, Central Macedonia, AMIN, West Macedonia	40°.37′ N/22°.57′ E 40°.36′ N/ 21°.39′ E	d	1 year	Daily	Tmax, Tmin, Tavg, Radiation, TD, \sqrt{\mathrm{TD}}, RHavg	Rs	Empirical, ANN, MLR	RMSE, R	For AUTH, RMSE= 3.344 MJ/(m2·d), R= 1; For AMIN, RMSE= 3.166 MJ/(m2·d), R= 1
[78]	2019	Atlanta New York Hawaii	33°.77′/84°.98′ 43°.13′/75°.90′ 19°.33′/155°.58′	1 h to 1d	3 year	1 year	GHI, CSK, GHI, CC, DP, PW, RH, SZA, WS, WD, T	GHI	LSTM	RMSE, MAE, R2	RMSE= 41.37–66.69 (W/m2), MAE= 30.19–46.04 (W/m2), R2 = 0.95–0.97
[80]	2019	Algiers	36°.8′ N/3°.170′ E	5 min	2 years	Monthly	T, RH, WS,WD, P, SD, AP, SZA, ESI	GHI, DNI	ANN	RMSE, nRME, MAE, nMAE	RMSE= 126.65–157.2 (Wh/m2), nRMSE= 28.08%–34.85%, MAE= 112.60–118.59 (Wh/m2), nMAE= 24.96%–26.28%
[44]	2019	Reese Research Center, Lubbock, TX			1 year	30 days	Time series	Daily solar energy	ARIMA	MAPE	MAPE= 17.70%
[45]	2019	Seoul, South Korea	37°.34′ N/126°.5′ E	Monthly and daily	3 years		Time series	Daily and monthly SR	SARIMA	RMSE and R2	Daily: RMSE= 104.26, R2 = 68%; Monthly: RMSE= 33.18, R2 = 79%
[46]	2019	Jamia Millia Islamia, New Delhi	28°.56′ N/77°.28′ E	Monthly	34 years	Monthly	Time series	SR	SARIMA	MPE	MPE= 1.402
[48]	2019	Mauritius	20°.3′ S/57°.6′ E	Monthly	29 years	10 years	SD, T, ER, RH	GSR	Sayigh Universal formula	MAPE, RMSE	MAPE= 5.07%–7.49%, RMSE= 0.96–1.57 MJ/(m2·d)
[101]	2019	6 sites in China		Daily	70% of 3 years	30% of 3 years	Tm, Tmax, Tmin, AP, RH, SD, N WS, AQI	DGSR	SVR	RMSE	RMSE= 0.00036–0.1910 MJ/m2
[54]	2019	Naresuan University, Thailand		1 h	6 m		GSR, AT, WS	PV power	HMM, GA-HMM	MAPE, nRME	nRMSE= 2.33%, MAPE= 6.27%
[64]	2019	Netherland		Hourly	2 year	Seasonal	T, RH, SR, CC, R, aerosols, CSK, CI, lat, long, VIAE, VIO	Deterministic and Proba-bilistic forecast	Parametric regression, Quantile regression, Quantile regression, RF, GBDT	RMSE, RMSE_SS, CRPSS
[67]	2019	Amravati, Maharashtra	20°.93′/77°.77′		5 years		DGSR, ESR, SD, SDmax monthly average DSI, T, RH	GSR, DSR	Empirical model	MAPE, RMSE, R2	GSR: MAPE= 2.50%, RMSE= 0.58 (MJ/m2), R2 = 0.98; MDR: MAPE= 13.506%, RMSE= 1.11 (MJ/m2), R2 = 0.94
[108]	2019	Nanao, Japan	NA		90% of 8735 data points	10% of 8735 data points	GHI, T, WS, WD, Ep, Ei	Solar PV power	GRU	nRMSE	nRMSE= 9.64%
[111]	2019	University of Queensland, Australia		1 d	1 year	Seasonal	PV power, SI, WS, T	PV power	WT and PSO and NNE	Error-variance	Seasonal variations, 0.1723–0.3103
[125]	2019	Kunming, China; Denver, USA	24°.51′/102°.51′ 39°.44′/105°.1′	Monthly	2 years	1 year	Time series	GHI	WT and ENN	RMSE, nRME, FS	RMSE= 25.83 (W/m2), nRMSE= 14.17%, FS= 0.7590
[126]	2019	NSRDB	W97°/N33°W107°/N143°	3 h ahead	1 year	Monthly	GHI, SZA, T, DP, RH, PWWD, WS,	GHI	ConvGRU-VB	RMSE, MEA, NSE	RMSE= 69.5, MEA= 34.8, NSE= 0.929
[112]	2019	Odeillo, France	42°.29′ /2°.01′	1 to 6 h ahead	80% of 3 years	20% of 3 year	SR time series	GHI, BNI, DHI	SP, ANN, RF	nRME, RMSE, MAE, nMAE	nRMSE_GHI= 19.65%–27.78%, nRMSE_BNI= 34.11%–49.08%, nRMSE_DHI= 35.08%–49.14%
[114]	2019	Favignana Island, Italy	37°.55′/12°.19′	Monthly	1 year	Seasonal	WS and solar data	Wind power, solar power	GMDHNNFOA	MAPE, AME, RMSE, R2	MAPE= 1.770%, MAE= 0.015, RMSE= –0.017868
[117]	2019	5 cites in China		1 h to 24 h	1 year	Monthly	Time series	DSR	DFT-PCA-Elman	RMSE, MAE	RMSE= 72.95–191.33, MAE= 39.46–118.67
[118]	2019	Toledo, Spain	39°.53′ N/4°.02′ N	Hourly	80% of each month	20% of each month	Reflectivity, CSK, CI	GSR	ELM	RMSE	RMSE= 60.60 W/m2
[129]	2019	GEFcom2014		1 to 3 step ahead	3 m	10% of data	t, RH, SP, CC, WS, P, T, R, SR	PV power	PCA and k-means and HGWO and RF	RMSE, MAE	RMSE= 8.88%–9.82%, MAE= 4.76%–5.80%
[134]	2019	8 sites in Xinjiang Uygur Autonomous Region, China		1 h	1 year	1 year	SZA, P, T, WD, WS, RH, AP	GSR	RS and SRSCAD and FF	MAPE, RMSE, TIC, CC, R2	MAPE= 0.066, RMSE= 20.21 W/m2, TIC= 0.06, CC= 3.40 s, R2 = 0.98
[137]	2019	IIT Gandhinagar		20 to 60 min	1 year		Time series	SR	SARIMA-RVFL	∆MAPE, ∆R2, ∆ RMSE, ∆MASE	MAPE= 6.376, RMSE= 3.497, MASE= 6.452, R2 = –0.649
[139]	2019	Shaoxing, China	120°.23′ E/29°.72′ N	7.5 min to 60 min	3 years	2 years	PV power, T	PV power output	ALSTM	RMSE, MAPE, MAE	ALSTM>PM>ARIMAX>LSTM>MLP>
[140]	2019	MMMUT, Gorakhpur, India	26°.43′/83°.26′	1 d to 6 d	Monthly	Daily	Tmin, Tmax, Tavg, WS,R, DP, GSR, AP, SZ	Solar PV output	MARS, CART, M5, RF	MBE, RMSE, MAE	RF>M5>MARS>CART
[141]	2019	Galicia, Spain		Monthly	70% of data	30% of 1 year data	Flow, SR, Lower and upper panel T	Solar energy	ML with BR, SCG, RB, GDX, LM algo	NMSE	RBFN, MLP>MLR, MN-LR
[131]	2019	Salto, Uruguay	31°.28′/57°.92′	1 to 10 min			Sky images	GHI	Cloud detection and motion estimation	FS	FS= 11.4%
[133]	2019	Victoria, Australia		Hourly	80% of 278 days	20% of 278 d	PV power, SI, AT	PV power	GASVM	RMSE, MAPE	RMSE= 11.226 W, MAPE= 1.7052%
[142]	2019	Australia		Daily	5 years	Daily, weekly, monthly	WS, T, RH, GHI, DHI, WD	PV output	Ensemble with recursive arithmetic average	RMSE, MAPE, MAE	Ensemble>SVM>MLR>MARS
[146]	2019	Australia		1 d	60743 data points	23 to 5077 data points	Time series	GSR	CNN and LSTM	rRMSE, MAPE, APE	rRMSE= 1.515%, MAPE= 4.672%, APE= 1.233%
[147]	2019	90 stations in China		Hourly	1 year	Hourly, daily, monthly	MTSAT images, long, lat, Al	GSR	CNN and MLP	RMSE	RMSEhourly = 0.30 MJ/m2, RMSEdaily = 1.92 MJ/m2, RMSEmonthly = 1.08 MJ/m2
[148]	2019	Shagaya, Kuwait Cocoa, USA			255 to 330 data points	32 to 38 data points	GHI, GTI, WS, WD, AT, RH, P, CT	Solar power	Theta and MLSHM	nMAE, nMSE	nMAE= 0.0317–0.0877, nMSE= 0.00197–0.0168
[106]	2020	Barmer, Jaisalmer, Bikaner, Jodhpur	25°.75′ N/71°.38′ E 26°.90′ N/70°.90′ E 28°.02′ N/73°.31′ E 26°.23′ N/73°.02′ E	3/6/24 h	70% of 5 years	30% of 5 years	DHI, DNI, DP, WD, RH, T	GSR	LSTM	MAPE, RMSE	MAPE= 6.69%–10.47%, RMSE= 0.099–0.181
[121]	2020	American Meteorological Society 2013–2014			10 years	2 years	P, DLWF, DSWF, AP,P, RH, total column-integrated condensate ULWRs, CC	Solar irradiation	GA/PSO and CNN	MSE, MAE, RS, AER	MSE= 4.268·1012, MAE= 1.5153 (MJ/m2), RS= 70.89%, AER= 0.14208
[136]	2020	Oak Ridge National Laboratory		1 to 50min	1 year		past PV power Past PV+ CC	Solar radiation, PV power	Uncertainty bias and Kalman filter	nRMSE MAPE	nRME= 7.43%–26.13% MAPE= 5.72%–25.75%
[138]	2020	Wuhan, Beijing, Lhasa, and Urumqi, China	30°.37′/114°.08′ 39°.48′/116°.28′ 29°.40′/91°.08′ 43°.47′/87°.39′		10 years	10 years	CI, sunshine ratio, Tavg, RHavg	SR	SVM, CNQR, Empirical model	RMSE, R2, MABE, MBE	SVM>CNQR>Empirical model

Notes: Al—Altitude; AP—Atmospheric pressure; AT—Ambient temperature; CC—Cloud cover; CT—Cell temperature; CSK—Clear sky radiation; CW—Cloud water; DATm—Daily mean air temperature; DGSR —Daily global solar radiation; DLWF—Downward long-wave irradiative flux average; DP—Dew point; DR—Down welling radiation; DSWF—Downward short-wave irradiative flux average; E—Evaporation; Ei = Inverter energy; Ep—Plant energy; GI—Global isolation; GTI—Global tilt irradiance; Ha = Average humidity; IC= Ice contents; Lat—Latitude; Long—Longitude; LW—Long wavelength; M—Month number; MSD—Mean sunshine duration; MT—Meteorological data; MTSAT—Geostationary satellite; N—No. of day; P—Precipitation; PM—Particulate matter; PVo—PV output; R—Rainfall; RH—Relative humidity; Rs— Radiation; SE—Solar energy; SHF—Soil heat flux; SI—Solar irradiance; SKI—Sky information; SMP—Soil matrix potential; SP—Surface pressure; SR—Solar radiation; SSRD—Surface solar radiation down; STRD —Surface thermal radiation down; t—time; SZA—Solar zenith angle; T—Temperature; Ta—Average temperature; Tm—Mean temperature; Tmax—Maximum temperature; Tmin—Minimum temperature; TCLW—Total Coloumn liquid water; ULWRs—Upward long-wave radiation at the surface; VIAE—Vertically integrated Angstrom exponent; VIO—Vertically integrated ozone; WC—Wind components; WD—Wind direction; WE—Wind energy; WG—Wind gust; WS—Wind speed; WSa—Average wind speed

3 Evaluation metrics

Different evaluation metrics have been used by numerous researchers to assess forecasting models. These evaluation metrics are also termed as performance metrics or error metrics which allow a designer to compare different models based on error skills, deviation, median etc. Many researchers adopted some of the standard error metrics whereas others evaluated the models based on different error metrics. The units for different performance metrics are different but generally the unit used for the statistical error of solar radiation is W/m². However, the unit for power is KW or MW.

3.1 Conventional statistical assessment metrics

Correlation coefficient: Correlation coefficient is the parameter to set a relationship between two data sets [138], which is denote by ρ and expressed as

(20)\rho ={\displaystyle \frac{{(\mathrm{conv}(R_{\mathrm{real,}}{R}_{\mathrm{forecast}}))}^{\mathrm{2}}}{\mathrm{var}(R_{\mathrm{real)}}\mathrm{var}(R_{\mathrm{forecast)}}}},

where R_real is the actual value of radiation and R_forecast is the forecasted value of radiation by the model.

The greater the value of correlation coefficient is, the better the model is. The correlation coefficient directly provides the strength and direction of relationship between real and forecasted data set. The ideal value of correlation coefficient is 1.

Determination coefficient: Determination coefficient is denoted by R² and used to extract the information of the correlation between the forecasted and the real values, or it is a measure of the dependency between two data sets [113,122,149].

(21)R^{\mathrm{2}}=\mathrm{1}-{\displaystyle \frac{\mathrm{var}(R_{\mathrm{real}}-R_{\mathrm{forecast}})}{\mathrm{var}(R_{\mathrm{forecast}})}}.

(22)R^{\mathrm{2}}={\displaystyle \frac{n{\displaystyle \sum _{i=\mathrm{1}}^n{R}_{\mathrm{real},i}{R}_{\mathrm{forecast},i}-\left({\displaystyle \sum _{i=\mathrm{1}}^n{R}_{\mathrm{real},i}}\right)\left({\displaystyle \sum _{i=\mathrm{1}}^n{R}_{\mathrm{forecast},i}}\right)}}{\sqrt{n\left({\displaystyle \sum _{i-\mathrm{1}}^n{R}_{\mathrm{real},i}{}^{\mathrm{2}}}\right)-{\left({\displaystyle \sum _{i=\mathrm{1}}^n{R}_{\mathrm{real},i}}\right)}^{\mathrm{2}}}\sqrt{n\left({\displaystyle \sum _{i-\mathrm{1}}^n{R}_{\mathrm{forecast},i}{}^{\mathrm{2}}}\right)-{\left({\displaystyle \sum _{i=\mathrm{1}}^n{R}_{\mathrm{forecast},i}}\right)}^{\mathrm{2}}}}}.

where n is the number of sample data set.

Normalized error: Normalized error is denoted by nE and used for finding the outliers in the result, which is mathematically expressed as

(23)nE={\displaystyle \frac{R_{\mathrm{forecast}}-R_{\mathrm{real}}}{\max (R_{\mathrm{forecast}})}}.

Mean bias error (MBE): MBE metric is used to calculate the average bias in the system or the model. It identifies the overestimation or underestimation in the results provided by the model [128,150].

(24)\mathrm{MBE}={\displaystyle \frac{\mathrm{1}}{n}}{\displaystyle \sum _{i=\mathrm{1}}^n(R_{\mathrm{forecast},i}-R_{\mathrm{real},i})}.

Mean absolute error (MAE): MAE provides the uniform error in the prediction. This is the measure of the difference between two different data sets [150,151].

(25)\mathrm{MAE}={\displaystyle \frac{\mathrm{1}}{n}}{\displaystyle \sum _{i=\mathrm{1}}^n\left|R_{\mathrm{forecast},i}-R_{\mathrm{real},i}\right|}.

Standard deviation error (SDE): SDE is the measure of the deviation from the mean [132].

(26)\mathrm{SDE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{n}}{\sum _{i=\mathrm{1}}^n(R_{\mathrm{forecast},i}-R_{\mathrm{real},i}-MBE)}^{\mathrm{2}}}.

Root mean square error: Root mean square error is the measure of the largest error in the predicted data set [152].

\mathrm{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{n}}{\displaystyle \sum _{i=\mathrm{1}}^n{(R_{\mathrm{forecast},i}-R_{\mathrm{forecast},i})}^{\mathrm{2}}}}.

(27){\mathrm{RMSE}}^{\mathrm{2}}{\mathrm{=MBE}}^{\mathrm{2}}{\mathrm{+SDE}}^{\mathrm{2}}\mathrm{.}

Mean absolute percentage error (MAPE): MAPE is the measure of uniform prediction error in percentage. In simple terms, it is the calculation of MAE in percentage form [151].

(28)\mathrm{MAPE}={\displaystyle \frac{\mathrm{1}}{n}}{\displaystyle \sum _{i=\mathrm{1}}^n\left|{\displaystyle \frac{R_{\mathrm{forecast},i}-R_{\mathrm{real},i}}{R_{\mathrm{real},i}}}\right|}.

Mean deviation absolute percentage error (MdAPE): MdAPE is less affected by the outliers than the MAPE.

(29)\mathrm{MdAPE}=\mathrm{median}\left(\left|\mathrm{100.}{\displaystyle \frac{R_{\mathrm{forecast}}-R_{\mathrm{real}}}{R_{\mathrm{real}}}}\right|\right).

Normalized RMSE: Normalized RMSE is the measure of RMSE on different scales. It is the measure of RMSE and average of forecasted data.

(30)\mathrm{nRMSE}={\displaystyle \frac{\sqrt{{\displaystyle \frac{\mathrm{1}}{n}}{\displaystyle \sum _{i=\mathrm{1}}^n{(R_{\mathrm{forecast},i}-R_{\mathrm{real},i})}^{\mathrm{2}}}}}{\mathrm{avg}(R_{\mathrm{forecast}})}}.

The lesser the value of nRMSE, the better is the performance of the model.

Relative root mean square error (rRMSE): rRMSE is the ratio of the root mean square error of the forecasted value to the mean of actual values.

(31)\mathrm{rRMSE}={\displaystyle \frac{\mathrm{RMSE}}{{\bar{R}}_{\mathrm{real}}}}\times \mathrm{100},

where the performance of the model is evaluated as excellent for rRMSE<10%, good for 10%<rRMSE<20%, fair for 20%<rRMSE<30%, poor for rRMSE>30%.

Clear sky index: Clear sky index is the ratio of measured radiation to the clear sky radiation.

(32)k_t={\displaystyle \frac{R_{\mathrm{real}}}{R_{\mathrm{real(csk)}}}}.

t-statistics: It is measure of the difference between the means of two data sets. The value of t-statistics for a model close to zero is better for any model [8].

(33)t-\mathrm{statistics}={\displaystyle \frac{\mathrm{1}}{n}}\sqrt{{\displaystyle \frac{(n-\mathrm{1}){\mathrm{MBE}}^{\mathrm{2}}}{{\mathrm{RMSE}}^{\mathrm{2}}-{\mathrm{MBE}}^{\mathrm{2}}}}}.

Forecast skill score: Forecast skill score is the measure of prediction accuracy of a model with reference to the accuracy of standard prediction. It can also be defined as the ratio of uncertainty U to the variability V of solar radiation prediction [153].

(34)SS=\mathrm{1}-{\displaystyle \frac{U}{V}},

where

U=\sqrt{{\displaystyle \frac{\mathrm{1}}{n}}{\displaystyle \sum _{t=\mathrm{1}}^n\left\{{\displaystyle \frac{{(R_{\mathrm{forecast},t}-R_{\mathrm{real},t})}^{\mathrm{2}}}{R_{\mathrm{csk},t}}}\right\}}},

V=\sqrt{{\displaystyle \frac{\mathrm{1}}{n}}{\displaystyle \sum _{t=\mathrm{1}}^n{\{\mathrm{\Delta }k(t)\}}^{\mathrm{2}}}},

where R _csk is clear sky radiation and Δk is the step change.

(35)\mathrm{Skill}\mathrm{\hspace{0.17em}}\mathrm{score=}{\displaystyle \frac{\mathrm{Score}\mathrm{\hspace{0.17em}}\mathrm{for}\mathrm{\hspace{0.17em}}\mathrm{the}\mathrm{\hspace{0.17em}}\mathrm{forecast}-\mathrm{Score}\mathrm{\hspace{0.17em}}\mathrm{for\; the}\mathrm{\hspace{0.17em}}\mathrm{standard}\mathrm{\hspace{0.17em}}\mathrm{forecast}}{\mathrm{Prefect}\mathrm{\hspace{0.17em}}\mathrm{score}-\mathrm{score}\mathrm{\hspace{0.17em}}\mathrm{for\; standalone}\mathrm{\hspace{0.17em}}\mathrm{forecast}}}.

3.2 Contemporary metrics

Usually conventional metrics were used by most researcher to evaluate the performance of models. However, other metrics were also adopted lately along with conventional metrics to evaluate the performance of models. In the scenario of inter-connection of solar parks to the grid, any error in the prediction may create the imbalance in the scheduling and operation of the entire system [154]. Therefore, complete information and assessment is the prime concern in developed model with consideration of time scale, geographic locations, climatic conditions, etc. The metrics discussed in this section are termed as cotemporary metrics as they are used in latest literature and are also in the trend although not in all studies. These metrics can be categories into four different category terms as statistical metrics, uncertainty quantification, ramp characterization, and economic metrics.

3.2.1 Statistical metrics

The two different data sets having the same mean and variance but having different distribution of symmetry or skewness and kurtosis cannot be identified and differentiated by the MAPE, MAE and RMSE only. However, it is necessary to use the conventional metrics to analyze the system but the overlooked parameter like skewness, kurtosis, MASE etc. may affect larger systems in real time process. Therefore, the conventional metrics are used in combinations with other metrics called contemporary statistical metrics.

Skew: Skew is the measure of asymmetry in the distribution [150].

(36)\mathrm{Skew}={\displaystyle \frac{N}{(N-\mathrm{1})(N-\mathrm{2})}}{\displaystyle \sum _{i=\mathrm{2}}^N{\left({\displaystyle \frac{nE-n\bar{E}}{\mathrm{SD}}}\right)}^{\mathrm{3}}}.

Kurtosis: Kurtosis is again the measure of distribution [150].

(37)\mathrm{Kurt}=\left\{{\displaystyle \frac{N(N-\mathrm{1})}{(N-\mathrm{1})(N-\mathrm{2})(N-\mathrm{3})}}{\displaystyle \sum _{i=\mathrm{1}}^N{\left({\displaystyle \frac{nE-n\bar{E}}{\mathrm{SD}}}\right)}^{\mathrm{4}}}\right\}{\displaystyle \frac{\mathrm{3}{(N-\mathrm{1})}^{\mathrm{2}}}{(N-\mathrm{2})(N-\mathrm{3})}}.

.

Maximum absolute error (MaxAE): MaxAE is the measure of the largest prediction error.

(38)\mathrm{MaxAE}=\underset{i=\mathrm{1},\mathrm{2},\mathrm{3....}N}{\max }\left|R_{\mathrm{forecast}}-R_{\mathrm{real}}\right|.

The larger the value of MaxAE is, the maximum the impact on the grid operation is.

Mean absolute scaled error (MASE): MASE is a scale free error metric which is less sensitive to outliers [155].

(39)\mathrm{MASE}={\displaystyle \frac{\mathrm{MAE}}{{\displaystyle \frac{\mathrm{1}}{N-\mathrm{1}}}{\displaystyle \sum _{i=\mathrm{2}}^N\left|R_{\mathrm{real},i}-R_{\mathrm{real},i-\mathrm{1}}\right|}}}.

The smaller the value of MASE is, the better the prediction is.

Kolonogorov-Smirnov integral (KSI): KSI is the measure of the difference between two different data sets [150]. The value of KSI is expected to be smaller for a better prediction. The smaller value of KSI interpreted as the real value and forecasted value have similarity. The zero CDF of the two data sets represents the fact that they are similar.

(40)\mathrm{KSI}={\displaystyle {\int }_{x_{\min }}^{x_{\max }}{D}_n\mathrm{d}x}

where D_n is the difference in the two CDFs.

OVER: Unlike KSI, OVER is the measure of similarity on the forecast error between the predicted and the real radiation value [150].

(41)\mathrm{OVER}={\displaystyle {\int }_{R_{\min }}^{R_{\max }}D\mathrm{\hspace{0.17em}}\mathrm{d}R}

where R_min is the minimum radiation, R_max is the maximum radiation, and D is express as

D\mathrm{\hspace{0.17em}}=\mathrm{\hspace{0.17em}}\{\begin{array}{l}{D}_j-V_{\mathrm{c}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{if}\mathrm{\hspace{0.17em}}{D}_j>V_{\mathrm{c}},\\ \mathrm{0}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{\hspace{0.17em}}\mathrm{if}\mathrm{\hspace{0.17em}}{D}_j\le V_{\mathrm{c}},\mathrm{\hspace{0.17em}}\end{array}

where V_c is the critical value and D_j is the difference between the CDFs of the two data sets.

KSD: KDS provides the classification of the output by the combining results of KSI and OVER.

(42)\mathrm{KSD}=W_{\mathrm{1}}\mathrm{KSI}+W_{\mathrm{2}}\mathrm{OVER},

where W₁ and W₂ are the weight parameters.

RIO: RIO provides the information from the distance between the pairs and the CDFs. It can be expressed by using KSD and RMSD.

(43)\mathrm{RIO}={\displaystyle \frac{\mathrm{KSD}\mathrm{\hspace{0.17em}}+\mathrm{\hspace{0.17em}}\mathrm{RMSE}}{\mathrm{2}}}.

Average error rate (AER): AER is the ratio of error rate of forecasting to the total number of observations.

(44)\mathrm{AER}={\displaystyle \frac{{\displaystyle \sum _{i=\mathrm{1}}^N{E}_r(i)}}{N}}.

where E_r={\displaystyle \frac{\left|R_{\mathrm{forecast}}-R_{\mathrm{real}}\right|}{R_{\mathrm{real}}}}, is the error rate of each sample.

Rate of success (RS): RS indicates the percentage of the data with accurate forecast.

(45)\mathrm{RS}={\displaystyle \frac{n}{N}}.

where N is the number of samples, and n is the number of samples with E_r<0.1.

Nash-Sutcliffe efficiency (NSE) [156]: NSE is the measure of forecasting skill of any model.

(46)\mathrm{NSE}=\mathrm{1}-{\displaystyle \frac{{\displaystyle \sum _{i=\mathrm{1}}^N{\left(\overline{R_{\mathrm{forecast}}}-R_{\mathrm{real}}\right)}^{\mathrm{2}}}}{{\displaystyle \sum _{i=\mathrm{1}}^N{\left(R_{\mathrm{forecast}}-\bar{R}\right)}^{\mathrm{2}}}}},

where \bar{R}is the mean of the data in the test data set.

The NSE range lies from –∞ to 1 where the value is close to 1 interpreted as a better prediction results.

Prediction interval normalized average width (PINAW): PINAW is used as a performance metric for a probabilistic forecasting to identify the sharpness of the prediction [29].

(47)\mathrm{PINAW}(\eta )={\displaystyle \frac{\mathrm{1}}{\mathrm{TR}}}{\displaystyle \sum _{t=\mathrm{1}}^T\left(q_{t,\tau -\mathrm{1}-\frac{\mathrm{1}-\eta }{\mathrm{2}}}-q_{t,\tau -\frac{\mathrm{1}-\eta }{\mathrm{2}}}\right)},

where T is the length of time series, H is the nominal coverage ratio, q_t,τ is quintile τ for prediction, R is normalization constant= \left|b-a\right|,b is the maximum of the test data set, and a is the minimum of the test data set.

3.2.2 Uncertainty quantification

Re`nyientropy of uncertainty: This metric was proposed by Zhang et al. (2015) and expressed as [157]

(48)H_{\alpha }(x)={\displaystyle \frac{\mathrm{1}}{\mathrm{1}-\alpha }}{\log }_{\mathrm{2}}{\displaystyle \sum _{i=\mathrm{1}}^N{P}_i^{\alpha }},

where α(α>0andα≠0) is the order of Re`nyi entropy and P_i is the probability density at the ith discrete section of distribution.

The larger the value of Re`nyi entropy is, the more uncertainty is presented in the forecast results.

3.2.3 Ramp characterization

In regards of ramp characterization, Florita et al. [158] proposed a swinging door algorithm which was a simple and flexible method to represent the width of ramp or “door” with the help of threshold parameter (ϵ).

If the value of ϵ is small, it represents many fluctuations; if the value of ϵ is large, there exist larger changes.

Ramp detection index(RDI): RDI is the measure of the ability of a model to forecast ramp in a very short-term prediction [131].

(49)\mathrm{RDI}={\displaystyle \frac{N_{\mathrm{hit}}}{N_{\mathrm{hit}}+N_{\mathrm{miss}}}},

where N_hit is the number of hit counts when the absolute difference between the real value and the predicted value is greater than 0.1 times of R_csk, and N_hit+ N_miss is the total number of ramp occurrence.

Ramp magnitude (RM): Chu et al. (2015) discussed RM in their study to find the ability to forecast ramps. RM is the measure of the normalized difference between the irradiance at present and that after a little time to clear sky irradiance of present time [159].

(50)\mathrm{RM}={\displaystyle \frac{\left|R_{\mathrm{h}}(t)-R_{\mathrm{h}}(t+\Delta t)\right|}{R_{\mathrm{csk}}(t)}}.

RM≥0.5 represents high magnitude ramps, and 0.3>RM<0.5 represents moderate ramps.

3.3 Other metrics

This section covers some other metrics which are not popular in calculating the performance of models.

Uncertainty of 95% (U₉₅): The confidence level which expanded uncertainty of up to 95% is used to express the data on the eccentricity of the model. U₉₅ can be expresses in term of SD and RMSE [70].

(51)U_{\mathrm{95}}=\mathrm{1.96}\sqrt{{(\mathrm{SD}+\mathrm{RMSE})}^{\mathrm{2}}}.

The lower the value of U₉₅ is, the better the model is.

Error: Russo et al. (2014) proposed an error metric to determine the model performance, which is better and more correct than MAE and RMSE [160].

(52)E=\mathrm{100}\sqrt{{\displaystyle \sum _{i=\mathrm{1}}^N\frac{{(R_{\mathrm{real},i}-R_{\mathrm{forecast},i})}^{\mathrm{2}}}{{\sigma }_i^{\mathrm{2}}{N}_i}}}.

Global performance indicator: Despotovic et al. [161] discussed a global indicator to propose the determination of model performance.

(53)\mathrm{GPI}={\displaystyle \sum _{i=\mathrm{1}}^{\mathrm{6}}{\alpha }_j\left(\overline{R_j}-R_{ij}\right)},

where \overline{R_j} is the scaled value median of the ith indicator, R_ij is the scaled value of the jth indicator of the ith model, and

{\alpha }_j=\{\begin{array}{cc}-1& \text{for}j=4{(R)}^2,\\ 1& \text{for otherwise}\text{.}\end{array}

The higher the GPI is, the better the model is.

Continuous ranked probability score (CRPS): CRPS is the method to compare the CDF [62].

(54)\mathrm{CRPS}={\displaystyle \frac{\mathrm{1}}{N}}{\sum _{i=\mathrm{1}}^N{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}(F_i^{R_{\mathrm{forecast}}}(x)-F_i^{R_{\mathrm{real}}}(x))}}^{\mathrm{2}}\mathrm{d}x,

where F_i^{R_{f\mathrm{orecast}}}(x) is the CDF of forecasted R_forecast;F_i^{R_{\mathrm{real}}}(x) is the CDF of observation of the ith ensemble prediction pair; and N is the number of available pairs.

Brier score (BS): BS is used to evaluate the probability forecast [162], which is expressed as

(55)\mathrm{BS}={\displaystyle \frac{\mathrm{1}}{n}}{\displaystyle \sum _{t=\mathrm{1}}^n{\displaystyle \sum _{i=\mathrm{1}}^m{(P_{t,i}-O_{t,i})}^{\mathrm{2}}}},

where P_t,i is the probability of forecast at time t for category i, and 0<O_t,i<1.The lower the value of BS is, the better the forecast by the model is.

CRPS skill score: CRPS skill score is the ranked probability score of forecasted model w.r.t. reference model.

(56)S=\left(\mathrm{1}-{\displaystyle \frac{{\mathrm{CRPS}}_{\mathrm{model}}}{{\mathrm{CRPS}}_{\mathrm{ref}}}}\right)\times \mathrm{100.}

Mean absolute interval deviation (MAID): MAID measures the deviation of forecasted interval from the real interval. Rana et al. (2015) used this metric in their study for interval forecasting [163].

(57)\mathrm{MAID}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}N}}\left\{{\displaystyle \sum _{i=\mathrm{1}}^N\left|U_{\mathrm{real},i,k}^{\mathrm{P}}-U_{\mathrm{forecast},i,k}^{\mathrm{P}}\right|+}\left|L_{\mathrm{real},i,k}^{\mathrm{P}}-L_{\mathrm{forecast},i,k}^{\mathrm{P}}\right|\right\},

where U_{\mathrm{real},i,k}^{\mathrm{P}} and L_{\mathrm{real},i,k}^{\mathrm{P}} are the upper and lower bound of the real k length interval; and U_{\mathrm{forecast},i,k}^{\mathrm{P}} and L_{\mathrm{forecast},i,k}^{\mathrm{P}} are the predicted upper and lower bound of the interval.

A lower value of MAID represents a lower error in forecast.

3.4 Economic metrics

The variation in the forecast ramp makes proportional changes in different metrics like skewness, kurtosis etc. To measure these small changes accurately, economic metrics are used. These economic metrics are also correlating the operative reserves with the solar requirements and the cost. The large adjustments in the ramps interpreted as poor forecasting with large operative reserves result in more cost. Therefore, the accuracy in forecasting is proportional to the lesser requirement of reserves [150].

Potential economic value (PEV): PEV, described by the Bakker et al. is a metric that measures the potential economic impact of forecast. It identifies the events that does not exceed a certain threshold [64].

(58)

where H is the hit alarm, FA is the false alarm, M is the miss frequency, and ORF is the observed relative frequency.

Interval coverage probability (ICP): ICP is the calculation of the probability that the n value of time series P_{t+ 1…,} P_{t+ n,} for the next n-length segment will fall between the upper band U_{\mathrm{real},n,i}^{\mathrm{P}} and the lower band L_{\mathrm{real},n,i}^{\mathrm{P}} of forecast interval, averaged over all values in the data set [6].

(59)\mathrm{ICP}={\displaystyle \frac{\mathrm{1}}{N\cdot n}}{\displaystyle \sum _{i=\mathrm{1}}^N{\displaystyle \sum _{j=i+\mathrm{1}}^{i+n}{C}_j\times \mathrm{100}}},

where N is the number of samples, n is the length of segment/interval, and

C_j=\{\begin{array}{l}\mathrm{1}\mathrm{if}{P}_j\in \left|U_{\mathrm{real},n,i}^{\mathrm{P}},L_{\mathrm{real},n,i}^{\mathrm{P}}\right|,\\ \mathrm{0}\mathrm{otherwise}.\end{array}

Coefficient of variation of MAE and MBE: Almida et al. used the revised MAE metric to evaluate the models which penalize the hourly energy, but used coefficient of variation of MBE to evaluate the models which penalize the daily energy hour [164].

(60)\mathrm{CvMAPE}={\displaystyle \frac{\mathrm{MAE}}{\overline{R_{\mathrm{real}}}}},

(61)\mathrm{CvMBE}={\displaystyle \frac{\mathrm{MBE}}{\overline{R_{\mathrm{real}}}}},

where \overline{R_{\mathrm{real}}} is the mean of real energy.

Confidence interval output: This measure of the model is for evaluating its accuracy and its amplitude. The amplitude calculations give the information about the amount of predicted energy in relation to the real energy and calculated as its area is normalized.

(62)\mathrm{Q1Q}{\mathrm{9}}_{\mathrm{sum}}={\displaystyle \frac{{\displaystyle \sum _{i=\mathrm{1}}^N(Q_{\mathrm{9}i}-Q_{\mathrm{1}i})}}{{\displaystyle \sum _{i=\mathrm{1}}^N{R}_{\mathrm{real},i}}}}.

A larger value of Q1Q9 represents more uncertainty of Quintile.

4 Key findings about factors affecting solar prediction

This section describes the key findings from the literature reviewed about the factors/parameters that directly or indirectly affect the accuracy of model forecasting. In solar forecasting, data granularity, time horizon, geographical location, and climatic conditions vary from place to place. There are a number of factors which should be taken into account in forecasting the solar radiation components with a maximum accuracy and lesser error.

Data granularity: The data collected from any agency with different granularities directly affects the performance of the model. The numbers of studies are proof that the collected data with a smaller interval of time increases the prediction accuracy. Moreover, transforming the minute based interval data into daily average or hourly based data are not a simple task, but real time operation requires a 15 min interval of data for the prediction [165].

Issue of time horizon forecasting: The issue of time horizon is related to the future period for which the model is forecasting. This period may be from 1 min to several hours or days. Based on the literature, there are four categories of time horizon: very short-term forecasting (now-casting or intra-hour forecasting) (performed for 1min to several min ahead) [166], short-term forecasting (performed for 1 h to several hour/day ahead) [167], mid-term forecasting (1 month to 1 year ahead) [168], and long-term forecasting (1 year to several years ahead) [169].

Figure 8 illustrates the four time horizon forecastings with their model classification. Various studies show that the performance of the model increases with short-time ahead forecasting whereas the performance decreases with longer time ahead irrespective of the type of the model and the data granularity.

Fig.8 Time horizon based solar irradiation forecasting models (adapted with permission from Ref. [52]).

Full size|PPT slide

Geographical location: The behaviors of the model varies in accordance with geographical locations [31]. The model performance is directly affected by the areas or locations having certain/uncertain climatic conditions like Leh, India where the cold desert receives the enormous amount of solar radiation which may make the model perform better than the area having most of the cloud in the sky. Five different geographical locations of India with different climatic conditions were discussed by Premalatha et al. who trained and tested two different models with data of different locations. Both the model showed variance in the accuracy which can be interpreted as being affected by different locations [31].

Selection of meteorological parameters: The input data variables might be structural, endogenous and exogenous. Different models act differently on different combinations of inputs parameters. ANN provides importance to meteorological and geographical variables in most of the studies. The increased number of irrelevant meteorological parameters degrades the performance of the model. Therefore, appropriate parameters have to be selected to increase the performance of a model. Behrang et al. developed six models using ANN with different combinations of meteorological variables to predict solar radiation [32]. Similarly, Koca et al. also designed six models with different combinations of meteorological variables. These models provided different output to different combinations of input variable [77].

Air pollution: The anthropogenic/dust pollutants directly attenuate the solar radiation received on the ground, which badly affect the performance in terms of the accuracy of the model. The soiling of PV panels also influences the power production which is commonly due to accumulation and deposition of aerosol particles on PV panels. Therefore, the radiation received at a polluted area on a clear day is less than that at an unpolluted area of that day. Suthar et al. analyzed different regression models to estimate the GSR and to observe the effect of air pollution. They noticed that air pollution straightly affected the prediction accuracy of forecasting models [50]. Similarly, Fan et al. (2018) employed the SVM machine to analyze the single and combined effect of SO₂, CO, NO₂, PM_2.5, PM₁₀, and O₃ [100]. Hence, air pollution is one of the factors that influence the accuracy of a model. The proper selection of air pollutant components can also improve the forecasting accuracy of the model.

Climatic effects: The accuracy of the forecasting model depends on the time variable climate/weather parameters such as temperature, relative humidity, pressure, dew point, wind speed, wind direction etc. More variations in the data sets due to climate variability will lead to more inaccuracy in forecasting. Fouilloy et al. found that the weather variability undeviatingly affected the error in the forecasted values by predicted the solar radiation using different ANN and regression-based techniques [33]. Similarly, Gil et al. proposed that temperature and solar radiation were highly correlated to each other and solar energy increased with the decrease in variability [170].

Night hour and normalization: Solar irradiance is not available at night but grid operators demand the PV output for all time without interruption. Most of the studies were conducted for day time hours by removing the night hours. Even the time just after the sunrise and just before the sunset were also removed from the data set to overcome the effects of false readings (cosine instrumentation error). Therefore, a fair comparison should be necessary for the selected time frame [165].

Model selection: The proper selection of the model according to time horizon, climatic conditions, meteorological variables, and geographical locations is one of the important tasks to achieve a good accuracy in results. For a day-ahead market or the real-time market where one day ahead forecasting is required, the NWP model is preferable. Similarly, the NWP and satellite models are used for the 6–8 h ahead forecasting. Therefore, the understanding of model selection with different parameters provides good results [26].

Pre-processing techniques: The accuracy of the model could also be improved by applying the pre-processing techniques on input data sets. The input data sets collected from any agency for a specific targeted site are highly uncertain and irregular. The pre-processing techniques are used on the data to scale up or scale down the dimension of the data. Many researchers used wavelet transform to decompose input series into different constituent. In the same way, EMD decomposed input series in different frequency series [111,144]. Huang et al. used wavelet transform along with Elman neural network (ENN). WT decomposed input time series data into different subset and then fed the data to the ENN which improved the accuracy of the model [125]. Monjoly et al. used EMD and the WT algorithm to decompose input series [144].

Training and testing period: As per literature, different models were used in different training and testing periods for learning purposes. Some studies used a longer period of data for training whereas other studies used only seasonal data sets which were very difficult to compare. A majority of the studies used one, two, three, and four years of the data set for the training of the models. However, the data of two and three years were found to be suitable and commonly used period for the learning of the models [41,45,56,63,64,70,75,78–80,112,125,135,139,145]. Moreover, the numbers and characteristics of selected input variables also affect the length of training data. Doorga et al. used the data of 29 years with SD, T, ER, and RH as variables whereas Liu et al. used the data of ten years with CI, sunshine ration, T_avg, and RH_avg only [48,138].

Competitive comparison: The improper comparison or unfair comparison of models leads to wrong conclusions and false results. The designed model should be compared against the same category of the model. For example, if the univariate model is compared with the spatio-temporal model, it leads to false and wrong results.

Aggregation of sample results: Many researchers used different sized sample frames for their studies. The aggregation of the sampled frames also affects the performance of the forecast model. The aggregation over a long time (1 h) provides lesser error in the predicted results in comparison with a shorter time (15 to 30 min) which leads to greater error in the results.

5 Conclusions

Solar irradiance is highly dependent on various geographical and climatic parameters. The dynamic behavior of solar irradiance directly influences the reliability of PV integrated systems, energy market, and power utility agencies. Therefore, a highly precise and reliable solar irradiance prediction is required in order to perform smooth operations of the power system. However, accurate forecasting of solar irradiance is one of the challenging tasks to perform where many desperate models have already been designed in the literature. This work is a comprehensive review of potential models with different techniques to come out with significant information. From the study of 170 papers, several important conclusions were drawn as follows:

The forecast time horizon is classified from nowcasting to long-term forecasting. Many of the current researches and industries are converging on next day forecasting. However, long-term forecasting is used for long-time power system planning.

Various types of models have been developed such as statistical, physical, and hybrid models. Hybrid models perform better than standalone ones. However, hybrid models have more complex structures than standalone ones and provide better accuracies as a single structure fails to reach the desired accuracy. The hybrid structure of deep learning models of RNN, CNN, LSTM, and ELM with optimization techniques like PSO, GA, and firefly perform better than isolated models where PSO attains good remarks for accuracy.

The proper selection of pre-processing techniques has a greater impact on the accuracy as it boosts the accuracy level. PCA, WT, and EMD have been used in most studies where WT is much popular among all. Inpre-processing, the reduction of night hours and missing values from the data set is much necessary to perform before learning of the model. However, in latest studies, learning through the calculation of the clear-sky index is also producing better results. The k-means algorithm is also used in many studies to reduce the training time of the model by clustering the data set of the same features.

The selections of input variables are completely user-dependent, but the proper selection of climatological and geographical parameters is also one of the important points to be considered. Latitude, longitude, month number, sunshine hours, wind speed, wind direction, relative humidity, temperature, and air pressure are the most widely used parameters in the case of a model trained on meteorological parameters otherwise the time-lag-based time series should also be used in models to forecast.

The use of training data for a model is, however, an experimental process but the data of two to three years are found to be suitable for model training to get the best results.

The comparison of the performance of different models is very complicated due to different region/place of interest, variation in input-output data availability, variation in climatic conditions, time-horizon, and use of diverse error matrices. But this work provided the main findings and components of the studied models in a tabular form. The key- finding section of the paper directly helps the reader to consider important parameters in developing new forecasting models. Therefore, the hybridization of the models with various combination techniques and correct consideration of pre-processing techniques along with the proper selection of input parameters for a specific location enriches the precision and reliability of solar forecasting.

References

1 Sun S, Wang S, Zhang G, Zheng J. A decomposition-clustering-ensemble learning approach for solar radiation forecasting. Solar Energy, 2018, 163: 189–199

2 Bahaj A S. Means of enhancing and promoting the use of solar energy. Renewable Energy, 2002, 27(1): 97–105

3 Barnes D I. Understanding pulverised coal, biomass and waste combustion–a brief overview. Applied Thermal Engineering, 2015, 74: 89–95

4 Setel A, Gordan I M, Gordan C E. Use of geothermal energy to produce electricity and heating at average temperatures. In: Mediterranean Conference on Power Generation, Transmission, Distribution and Energy Conversion, Belgrade, Serbia, 2016

5 Alhmoud L, Wang B. A review of the state-of-the-art in wind-energy reliability analysis. Renewable & Sustainable Energy Reviews, 2018, 81: 1643–1651

6 Sobri S, Koohi-Kamali S, Rahim N A. Solar photovoltaic generation forecasting methods: a review. Energy Conversion and Management, 2018, 156: 459–497

7 International Energy Agency. Snapshot of global photovoltaic markets. Technical Report IEA PVPS T1–332018, 2018

8 Fan J, Wu L, Zhang F, Cai H, Zeng W, Wang X, Zou H. Empirical and machine learning models for predicting daily global solar radiation from sunshine duration: a review and case study in China. Renewable & Sustainable Energy Reviews, 2019, 100: 186–212

9 Mohanty S, Patra P K, Sahoo S S, Mohanty A. Forecasting of solar energy with application for a growing economy like India: survey and implication. Renewable & Sustainable Energy Reviews, 2017, 78: 539–553

10 International Energy Agency. Snapshot of global PV markets. Photovoltaic Power Systems Technology Collaboration Program Report IEA PVPS T1–35, 2019

11 International Renewable Energy Agency (IRENA).Renewable capacity statistics 2019. Technical Report, Abu Dhabi, 2019

12 Graph G.Annual report by Ministry of New and Renewable Energy. 2017, available at the website of mnre.gov.in

13 Singh R K. India’s renewable energy capacity crosses 80 GW-mark. 2019–07–16, available at website of The Economic Times.

14 Masson G, Brunisholz M. 2015 Snapshot of global photovoltaic markets. IEA PVPS T1–292016, 2016

15 Kalogirou S A. Global photovoltaic markets. In: McEvoy’s Handbook of Photovoltaics . Academic Press, 2016, 1231–1235

16 Nwokolo S C, Ogbulezie J C. A quantitative review and classification of empirical models for predicting global solar radiation in West Africa. Beni-Suef University Journal of Basic and Applied Sciences, 2018, 7(4): 367–396

17 Wang K, Qi X, Liu H. A comparison of day-ahead photovoltaic power forecasting models based on deep learning neural network. Applied Energy, 2019, 251: 113315

18 da Silva Fonseca J G Jr, Oozeki T, Takashima T, . Use of support vector regression and numerically predicted cloudiness to forecast power output of a photovoltaic power plant in Kitakyushu, Japan. Progress in Photovoltaics: Research and Applications, 2012, 20(7): 874–882

19 Antonopoulos V Z, Papamichail D M, Aschonitis V G, . Solar radiation estimation methods using ANN and empirical models. Computers and Electronics in Agriculture, 2019, 160: 160–167

20 Manjili Y S, Vega R, Jamshidi M M. Data-analytic-based adaptive solar energy forecasting framework. IEEE Systems Journal, 2018, 12(1): 285–296

21 Antonanzas J, Osorio N, Escobar R, . Review of photovoltaic power forecasting. Solar Energy, 2016, 136: 78–111

22 Kumar A.KUSUM scheme for solar uptake by farmers: a fineprint. 2019–03–22, available at website of ET EnergyWorld

23 Gigoni L, Betti A, Crisostomi E, . Day-ahead hourly forecasting of power generation from photovoltaic plants. IEEE Transaction on Sustainable Energy, 2018, 9(2): 831–842

24 Stanwell. Negative prices: how they occur, what they mean? 2020–04–16, available at website of Stanwell

25 Götz P, Henkel J, Lenck T, . Negative Electricity Prices: Causes and Effects. Agora Energiewende, 2014.

26 Yang D, Wu E, Kleissl J. Operational solar forecasting for the real-time market. International Journal of Forecasting, 2019, 35(4): 1499–1519

27 Huld T. VMAPS: Software tools and data for the estimation of solar radiation and photovoltaic module performance over large geographical areas. Solar Energy, 2017, 142: 171–181

28 Khosravi A, Nunes R O, Assad M E H, . Comparison of artificial intelligence methods in estimation of daily global solar radiation. Journal of Cleaner Production, 2018, 194: 342–358

29 Munkhammar J, Van der Meer D, Widén J. Probabilistic forecasting of high-resolution clear-sky index time-series using a Markov-chain mixture distribution model. Solar Energy, 2019, 184: 688–695

30 Fan J, Chen B, Wu L, . Evaluation and development of temperature-based empirical models for estimating daily global solar radiation in humid regions. Energy, 2018, 144: 903–914

31 Premalatha N, Valan Arasu A. Prediction of solar radiation for solar systems by using ANN models with different back propagation algorithms. Journal of Applied Research and Technology, 2016, 14(3): 206–214

32 Behrang M A, Assareh E, Ghanbarzadeh A, . The potential of different artificial neural network (ANN) techniques in daily global solar radiation modeling based on meteorological data. Solar Energy, 2010, 84(8): 1468–1480

33 Fouilloy A, Voyant C, Notton G, . Solar irradiation prediction with machine learning: forecasting models selection method depending on weather variability. Energy, 2018, 165: 620–629

34 Mazorra-Aguiar L, Díaz F. Solar radiation forecasting with statistical models. In: Wind Field and Solar Radiation Characterization and Forecasting: A Numerical Approach for Complex Terrain, Springer Verlag, 2018: 171–200

35 Dolara A, Leva S, Manzolini G. Comparison of different physical models for PV power output prediction. Solar Energy, 2015, 119: 83–99

36 Liu Y, Shimada S, Yoshino J, . Ensemble forecasting of solar irradiance by applying a mesoscale meteorological model. Solar Energy, 2016, 136: 597–605

37 Yadav H K, Pal Y, Tripathi M M. A novel GA-ANFIS hybrid model for short-term solar PV power forecasting in Indian electricity market. Journal of Information and Optimization Science, 2019, 40(2): 377–395

38 Reilly P M. Probability and statistics for engineers and scientists. Canadian Journal of Statistics, 1978, 6(2): 283–284

39 Wan C, Zhao J, Song Y, . Photovoltaic and solar power forecasting for smart grid energy management. CSEE Journal of Power Energy Systems, 2015, 1(4): 38–46

40 Yule G U. On the time-correlation problem, with especial reference to the variate–difference correlation method. Journal of the Royal Statistical Society, 1921, 84(4): 497

41 Wang Y, Wang C, Shi C, . Short-term cloud coverage prediction using the ARIMA time series model. Remote Sensing Letters, 2018, 9(3): 274–283

42 MATLAB. Works India-Econometric Modeler App Overview. 2019–12–20, available at website of MathWorks India

43 sekulima E B, El Moursi M S, Al Hinai A, . Wind speed and solar irradiance forecasting techniques for enhanced renewable energy integration with the grid: a review. IET Renewable Power Generation, 2016, 10(7): 885–989

44 Atique S, Noureen S, Roy V, . Forecasting of total daily solar energy generation using ARIMA: a case study. In: 9th Annual Computing and Communication Workshop Conference, Las Vegas, NV, USA, 2019, 114–119

45 Alsharif M H, Younes M K, Kim J. Time series ARIMA model for prediction of daily and monthly average global solar radiation: the case study of Seoul, South Korea. Symmetry, 2019, 11(2): 240

46 Shadab A, Said S, Ahmad S. Box–Jenkins multiplicative ARIMA modeling for prediction of solar radiation: a case study. International Journal of Energy Water Resources, 2019, 3: 0123456789

47 Colak I, Yesilbudak M, Genc N, . Multi-period prediction of solar radiation using ARMA and ARIMA models. In: IEEE 14th International Conference Machine Learning and Applications, Miami, FL, USA, 2015, 1045–1049

48 Doorga J, Rughooputh S, Boojhawon R. Modelling the global solar radiation climate of Mauritius using regression techniques. Renewable Energy, 2019, 131: 861–878

49 Trapero J R, Kourentzes N, Martin A. Short-term solar irradiation forecasting based on dynamic harmonic regression. Energy, 2015, 84: 289–295

50 Suthar M, Singh G K, Saini R P. Effects of air pollution for estimating global solar radiation in India. International Journal of Sustainable Energy, 2017, 36(1): 20–27

51 Bright J M, Smith C J, Taylor P G, . Stochastic generation of synthetic minutely irradiance time series derived from mean hourly weather observation data. Solar Energy, 2015, 115: 229–242

52 Voyant C, Notton G, Kalogirou S, . Machine learning methods for solar radiation forecasting: a review. Renewable Energy, 2017, 105: 569–582

53 Gurarie E.Introduction to stochastic processes: Markov chains. 2019–11–22, available at website of Department of Mathematics, University of Washington

54 Eniola V, Suriwong T, Sirisamphanwong C, . Hour-ahead forecasting of photovoltaic power output based on hidden Markov model and genetic algorithm. International Journal of Renewable Energy Research, 2019, 9(2): 933–943

55 Bhardwaj S, Sharma V, Srivastava S, . Estimation of solar radiation using a combination of hidden Markov model and generalized fuzzy model. Solar Energy, 2013, 93: 43–54

56 Wibun A, Chaiwiwatworakul P. An estimation of Thailand’s hourly solar radiation using Markov transition matrix method. Applied Mechanics and Materials, 2016, 839: 29–33

57 Hocaoglu F O, Serttas F. A novel hybrid (Mycielski-Markov) model for hourly solar radiation forecasting. Renewable Energy, 2017, 108: 635–643

58 Li S, Ma H, Li W. Typical solar radiation year construction using k-means clustering and discrete-time Markov chain. Applied Energy, 2017, 205: 720–731

59 Mengaldo G, Wyszogrodzki A, Diamantakis M, . Current and emerging time-integration strategies in global numerical weather and climate prediction. Archives of Computational Methods in Engineering, 2019, 26(3): 663–684

60 Yadav A, Chandel S. Solar radiation prediction using artificial neural network techniques: a review. Renewable & Sustainable Energy Reviews, 2014, 33: 772–781

61 Das S, Ashrit R, Iyengar G, . Skills of different mesoscale models over Indian region during monsoon season: forecast errors. Journal of Earth System Science, 2008, 117(5): 603–620

62 Verzijlbergh R A, Heijnen P W, De Roode S R, . Improved model output statistics of numerical weather prediction based irradiance forecasts for solar power applications. Solar Energy, 2015, 118: 634–645

63 Verbois H, Huva R, Rusydi A, . Solar irradiance forecasting in the tropics using numerical weather prediction and statistical learning. Solar Energy, 2018, 162: 265–277

64 Bakker K, Whan K, Knap W, . Comparison of statistical post-processing methods for probabilistic NWP forecasts of solar radiation. Solar Energy, 2019, 191: 138–150

65 Hargreaves G H, Samani Z A. Estimating potential evapotranspiration. Journal of the Irrigation and Drainage Division, 1982, 108(3): 225–230

66 Besharat F, Dehghan A A, Faghih A R. Empirical models for estimating global solar radiation: a review and case study. Renewable & Sustainable Energy Reviews, 2013, 21: 798–821

67 Mahajan B Y, Namrata K. Performance evaluation of developed empirical models for predicting global solar radiation in western region of India. International Journal of Renewable Energy Research, 2019, 9(3): 1135–1143

68 Quansah E, Amekudzi L K, Preko K, . Empirical models for estimating global solar radiation over the Ashanti Region of Ghana. Journal of Solar Energy, 2014, 2014: 1–6

69 Ayodele T R, Ogunjuyigbe A S O. Performance assessment of empirical models for prediction of daily and monthly average global solar radiation: the case study of Ibadan, Nigeria. International Journal of Ambient Energy, 2017, 38(8): 803–813

70 Bailek N, Bouchouicha K, Al-Mostafa Z, . A new empirical model for forecasting the diffuse solar radiation over Sahara in the Algerian Big South. Renewable Energy, 2018, 117: 530–537

71 Fausett L V. Fundamentals of Neural Networks: Architectures, Algorithms, and Applications. Prentice-Hall, Inc., USA, 1994

72 Ghanbarzadeh A, Noghrehabadi A R, Assareh E, . Solar radiation forecasting based on meteorological data using artificial neural networks. In: 7th IEEE International Conference of Industrial Informatics, Cardiff, Wales, UK, 2009: 227–231

73 Elsheikh A H, Sharshir S W, Abd Elaziz M, . Modeling of solar energy systems using artificial neural network: a comprehensive review. Solar Energy, 2019, 180: 622–639

74 Samara S, Natsheh E. Modeling the output power of heterogeneous photovoltaic panels based on artificial neural networks using low cost microcontrollers. Heliyon, 2018, 4(11): e00972

75 Bou-Rabee M, Sulaiman S A, Saleh M S, . Using artificial neural networks to estimate solar radiation in Kuwait. Renewable & Sustainable Energy Reviews, 2017, 72: 434–438

76 Sözen A, Arcaklioǧlu E, Özalp M, . Forecasting based on neural network approach of solar potential in Turkey. Renewable Energy, 2005, 30(7): 1075–1090

77 Koca A, Oztop H F, Varol Y, . Estimation of solar radiation using artificial neural networks with different input parameters for Mediterranean region of Anatolia in Turkey. Expert Systems with Applications, 2011, 38(7): 8756–8762

78 Yu Y, Cao J, Zhu J. An LSTM short-term solar irradiance forecasting under complicated weather conditions. IEEE Access : Practical Innovations, Open Solutions, 2019, 7: 145651–145666

79 Kumar N, Sinha U K, Sharma S P. Prediction of daily global solar radiation using neural networks with improved gain factors and RBF Networks. International Journal of Renewable Energy Research, 2017, 7(3): 1235–1244

80 Notton G, Voyant C, Fouilloy A, . Some applications of ANN to solar radiation estimation and forecasting for energy applications. Applied Sciences (Basel, Switzerland), 2019, 9(1): 209

81 Rodríguez F, Fleetwood A, Galarza A, . Predicting solar energy generation through artificial neural networks using weather forecasts for microgrid control. Renewable Energy, 2018, 126: 855–864

82 Jahani B, Mohammadi B. A comparison between the application of empirical and ANN methods for estimation of daily global solar radiation in Iran. Theoretical and Applied Climatology, 2019, 137(1-2): 1257–1269

83 Sivaneasan B, Yu C Y, Goh K P. Solar forecasting using ANN with fuzzy logic pre-processing. Energy Procedia, 2017, 143: 727–732

84 Cervone G, Clemente-Harding L, Alessandrini S, . Short-term photovoltaic power forecasting using artificial neural networks and an analog ensemble. Renewable Energy, 2017, 108: 274–286

85 Chen C R, Kartini U T. K-nearest neighbor neural network models for very short-term global solar irradiance forecasting based on meteorological data. Energies, 2017, 10(2): 186

86 Li Z, Rahman S M, Vega R, . A hierarchical approach using machine learning methods in solar photovoltaic energy production forecasting. Energies, 2016, 9(1): 55

87 Vakili M, Sabbagh-Yazdi S R, Khosrojerdi S, . Evaluating the effect of particulate matter pollution on estimation of daily global solar radiation using artificial neural network modeling based on meteorological data. Journal of Cleaner Production, 2017, 141: 1275–1285

88 Hossain R, Ooa A M T, Alia A B M S. Historical weather data supported hybrid renewable energy forecasting using artificial neural network (ANN). Energy Procedia, 2012, 14: 1035–1040

89 İzgi E, Öztopal A, Yerli B, . Short-mid-term solar power prediction by using artificial neural networks. Solar Energy, 2012, 86(2): 725–733

90 Alam S, Kaushik S C, Garg S N. Assessment of diffuse solar energy under general sky condition using artificial neural network. Applied Energy, 2009, 86(4): 554–564

91 Awad M, Khanna R. Support vector machines for classification. In: Efficient Learning Machines, Apress, Berkeley, CA, 2015, 39–66

92 Zendehboudi A, Baseer M A, Saidur R. Application of support vector machine models for forecasting solar and wind energy resources: a review. Journal of Cleaner Production, 2018, 199: 272–285

93 Srivastava N, Hinton G, Krizhevsky A, . Dropout: a simple way to prevent neural networks from overfitting. Journal of Machine Learning Research, 2014, 15: 1929–1958

94 Zhang W, Chen J. Relief feature selection and parameter optimization for support vector machine based on mixed kernel function. International Journal of Performability Engineering, 2018, 14(2): 280–289

95 Ruiz-Gonzalez R, Gomez-Gil J, Gomez-Gil F J, . An SVM-based classifier for estimating the state of various rotating components in agro-industrial machinery with a vibration signal acquired from a single point on the machine chassis. Sensors (Switzerland), 2014, 14(11): 20713–20735

96 Jiménez-Pérez P F, Mora-López L. Modeling and forecasting hourly global solar radiation using clustering and classification techniques. Solar Energy, 2016, 135: 682–691

97 Zeng J, Qiao W. Short-term solar power prediction using a support vector machine. Renewable Energy, 2013, 52: 118–127

98 Shi J, Lee W J, Liu Y, . Forecasting power output of photovoltaic systems based on weather classification and support vector machines. IEEE Transactions on Industry Applications, 2012, 48(3): 1064–1069

99 Jang H S, Bae K Y, Park H S, . Solar power prediction based on satellite images and support vector machine. IEEE Transaction on Sustainable Energy, 2016, 7(3): 1255–1263

100 Fan J, Wu L, Zhang F, . Evaluating the effect of air pollution on global and diffuse solar radiation prediction using support vector machine modeling based on sunshine duration and air temperature. Renewable & Sustainable Energy Reviews, 2018, 94: 732–747

101 Ma M, Zhao L, Deng S, . Estimation of horizontal direct solar radiation considering air quality index in China. Energy Procedia, 2019, 158: 424–430

102 Gensler A, Henze J, Sick B, . Deep Learning for solar power forecasting–an approach using AutoEncoder and LSTM neural networks. In: 2016 IEEE International Conference on Systems Man and Cybernetics, Budapest, 2016, 2858–2865

103 Suresh V, Janik P, Rezmer J, . Forecasting solar PV output using convolutional neural networks with a sliding window algorithm. Energies, 2020, 13(3): 723

104 Aslam M, Lee J M, Kim H S, . Deep learning models for long-term solar radiation forecasting considering microgrid installation: a comparative study. Energies, 2019, 13(1): 147

105 Qing X, Niu Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy, 2018, 148: 461–468

106 Chandola D, Gupta H, Tikkiwal V A, . Multi-step ahead forecasting of global solar radiation for arid zones using deep learning. Procedia Computer Science, 2020, 167: 626–635

107 Wang Y, Liao W, Chang Y. Gated recurrent unit network-based short-term photovoltaic forecasting. Energies, 2018, 11(8): 2163

108 Sodsong N, Yu K M, Ouyang W. Short-term solar PV forecasting using gated recurrent unit with a cascade model. In: 1st IEEE International Conference on Artificial Intelligence in Information and Communication, Okinawa, Japan, 2019, 292–297

109 Xie Y. Values and limitations of statistical models. Research in Social Stratification and Mobility, 2011, 29(3): 343–349

110 Kumar K R, Kalavathi M S. Artificial intelligence based forecast models for predicting solar power generation. Materials Today: Proceedings, 2018, 5(1): 796–802

111 Raza M Q, Nadarajah M, Li J, . An ensemble framework for day-ahead forecast of PV output power in smart grids. IEEE Transactions on Industrial Informatics, 2019, 15(8): 4624–4634

112 Benali L, Notton G, Fouilloy A, . Solar radiation forecasting using artificial neural network and random forest methods: application to normal beam, horizontal diffuse and global components. Renewable Energy, 2019, 132: 871–884

113 Elminir H K, Areed F F, Elsayed T S. Estimation of solar radiation components incident on Helwan site using neural networks. Solar Energy, 2005, 79(3): 270–279

114 Heydari A, Garcia D A, Keynia F, . A novel composite neural network based method for wind and solar power forecasting in microgrids. Applied Energy, 2019, 251: 113353

115 Mellit A, Pavan A M A. 24-h forecast of solar irradiance using artificial neural network: application for performance prediction of a grid-connected PV plant at Trieste, Italy. Solar Energy, 2010, 84(5): 807–821

116 Chen S X, Gooi H B, Wang M Q. Solar radiation forecast based on fuzzy logic and neural networks. Renewable Energy, 2013, 60: 195–201

117 Lan H, Zhang C, Hong Y Y, . Day-ahead spatiotemporal solar irradiation forecasting using frequency-based hybrid principal component analysis and neural network. Applied Energy, 2019, 247: 389–402

118 Cornejo-Bueno L, Casanova-Mateo C, Sanz-Justo J, . Machine learning regressors for solar radiation estimation from satellite data. Solar Energy, 2019, 183: 768–775

119 Aguiar L M, Pereira B, Lauret P, . Combining solar irradiance measurements, satellite-derived data and a numerical weather prediction model to improve intra-day solar forecasting. Renewable Energy, 2016, 97: 599–610

120 Shamshirband S, Mohammadi K, Khorasanizadeh H, . Estimating the diffuse solar radiation using a coupled support vector machine-wavelet transform model. Renewable & Sustainable Energy Reviews, 2016, 56: 428–435

121 Dong N, Chang J F, Wu A G, . A novel convolutional neural network framework based solar irradiance prediction method. International Journal of Electrical Power & Energy Systems, 2020, 114: 105411

122 Bouzgou H, Gueymard C A. Fast short-term global solar irradiance forecasting with wrapper mutual information. Renewable Energy, 2019, 133: 1055–1065

123 Ghimire S, Deo R C, Downs N J,. Global solar radiation prediction by ANN integrated with European Centre for medium range weather forecast fields in solar rich cities of Queensland Australia. Journal of Cleaner Production, 2019, 216: 288–310

124 Huang C, Wang L, Lai L L. Data-driven short-term solar irradiance forecasting based on information of neighboring sites. IEEE Transactions on Industrial Electronics, 2019, 66(12): 9918–9927

125 Huang X, Shi J, Gao B, . Forecasting hourly solar irradiance using hybrid wavelet transformation and Elman model in smart grid. IEEE Access : Practical Innovations, Open Solutions, 2019, 7: 139909–139923

126 Liu Y, Qin H, Zhang Z, . Ensemble spatiotemporal forecasting of solar irradiation using variational Bayesian convolutional gate recurrent unit network. Applied Energy, 2019, 253: 113596

127 Guermoui M, Melgani F, Danilo C. Multi-step ahead forecasting of daily global and direct solar radiation: a review and case study of Ghardaia region. Journal of Cleaner Production, 2018, 201: 716–734

128 Wang F, Mi Z, Su S, . Short-term solar irradiance forecasting model based on artificial neural network using statistical feature parameters. Energies, 2012, 5(5): 1355–1370

129 Liu D, Sun K. Random forest solar power forecast based on classification optimization. Energy, 2019, 187: 115940

130 Zhang W, Dang H, Simoes R. A new solar power output prediction based on hybrid forecast engine and decomposition model. ISA Transactions, 2018, 81: 105–120

131 Caldas M, Alonso-Suárez R. Very short-term solar irradiance forecast using all-sky imaging and real-time irradiance measurements. Renewable Energy, 2019, 143: 1643–1658

132 Eseye A T, Zhang J, Zheng D. Short-term photovoltaic solar power forecasting using a hybrid Wavelet-PSO-SVM model based on SCADA and meteorological information. Renewable Energy, 2018, 118: 357–367

133 VanDeventer W, Jamei E, Thirunavukkarasu G S, . Short-term PV power forecasting using hybrid GASVM technique. Renewable Energy, 2019, 140: 367–379

134 Dong Y, Jiang H. Global solar radiation forecasting using square root regularization-based ensemble. Mathematical Problems in Engineering, 2019, 2019: 9620945

135 Abuella M, Chowdhury B. Forecasting of solar power ramp events: a post-processing approach. Renewable Energy, 2019, 133: 1380–1392

136 Dong J, Olama M M, Kuruganti T, . Novel stochastic methods to predict short-term solar radiation and photovoltaic power. Renewable Energy, 2020, 145: 333–346

137 Kushwaha V, Pindoriya N M. A SARIMA-RVFL hybrid model assisted by wavelet decomposition for very short-term solar PV power generation forecast. Renewable Energy, 2019, 140: 124–139

138 Liu Y, Zhou Y, Chen Y, . Comparison of support vector machine and copula-based nonlinear quantile regression for estimating the daily diffuse solar radiation: a case study in China. Renewable Energy, 2020, 146: 1101–1112

139 Zhou H, Zhang Y, Yang L, . Short-term photovoltaic power forecasting based on long short term memory neural network and attention mechanism. IEEE Access : Practical Innovations, Open Solutions, 2019, 7: 78063–78074

140 Srivastava R, Tiwari A N, Giri V K. Solar radiation forecasting using MARS, CART, M5, and random forest model: a case study for India. Heliyon, 2019, 5(10): e02692

141 Basurto N, Arroyo A, Vega R, . A hybrid intelligent system to forecast solar energy production. Computers & Electrical Engineering, 2019, 78: 373–387

142 Liu L, Zhan M, Bai Y. A recursive ensemble model for forecasting the power output of photovoltaic systems. Solar Energy, 2019, 189: 291–298

143 Feng C, Cui M, Hodge B M, . Unsupervised clustering-based short-term solar forecasting. IEEE Transaction on Sustainable Energy, 2019, 10(4): 2174–2185

144 Monjoly S, André M, Calif R, . Hourly forecasting of global solar radiation based on multiscale decomposition methods: a hybrid approach. Energy, 2017, 119: 288–298

145 Benmouiza K, Cheknane A. Forecasting hourly global solar radiation using hybrid k-means and nonlinear autoregressive neural network models. Energy Conversion and Management, 2013, 75: 561–569

146 Ghimire S, Deo R C, Raj N, . Deep solar radiation forecasting with convolutional neural network and long short-term memory network algorithms. Applied Energy, 2019, 253: 113541

147 Jiang H, Lu N, Qin J, . A deep learning algorithm to estimate hourly global solar radiation from geostationary satellite data. Renewable & Sustainable Energy Reviews, 2019, 114: 109327

148 AlKandari M, Ahmad I. Solar power generation forecasting using ensemble approach based on deep learning and statistical methods. Applied Computing and Informatics, 2016, (in press)

149 Durrani S P, Balluff S, Wurzer L, . Photovoltaic yield prediction using an irradiance forecast model based on multiple neural networks. Journal of Modern Power Systems and Clean Energy, 2018, 6(2): 255–267

150 Zhang J, Hodge B M, Florita A, . Metrics for evaluating the accuracy of solar power forecasting. In: 3rd International Workshop on Integration of Solar Power into Power Systems, London, England, 2013, 17436

151 Willmott C J, Matsuura K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Climate Research, 2005, 30(1): 79–82

152 Lauret P, Voyant C, Soubdhan T, . A benchmarking of machine learning techniques for solar radiation forecasting in an insular context. Solar Energy, 2015, 112: 446–457

153 Coimbra C F M, Kleissl J, Marquez R. Overview of solar-forecasting methods and a metric for accuracy evaluation. In: Kleissl J, ed. Solar Energy Forecasting and Resource Assessment. Academic Press, 2013,171–194

154 Crabtree G, Misewich J, Ambrosio R, . Integrating renewable electricity on the grid. In: AIP Conference Proceedings, 2011, 1401: 387–405

155 Hyndman R J, Koehler A B. Another look at measures of forecast accuracy. International Journal of Forecasting, 2006, 22(4): 679–688

156 Pereira R M, Silva Santos C, Rocha A. Solar irradiance modelling using an offline coupling procedure for the weather research and forecasting (WRF) model. Solar Energy, 2019, 188: 339–352

157 Zhang J, Zhang Y, Yu C S. Rényi entropy uncertainty relation for successive projective measurements. Quantum Information Processing, 2015, 14(6): 2239–2253

158 Florita A, Hodge B M, Orwig K. Identifying wind and solar ramping events. In: IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 2013, 147–152

159 Chu Y, Pedro H T C, Li M, . Real-time forecasting of solar irradiance ramps with smart image processing. Solar Energy, 2015, 114: 91–104

160 Russo M, Leotta G, Pugliatti P M, . Genetic programming for photovoltaic plant output forecasting. Solar Energy, 2014, 105: 264–273

161 Despotovic M, Nedic V, Despotovic D, . Review and statistical analysis of different global solar radiation sunshine models. Renewable & Sustainable Energy Reviews, 2015, 52: 1869–1880

162 Alessandrini S, Delle Monache L, Sperati S, . An analog ensemble for short-term probabilistic solar power forecast. Applied Energy, 2015, 157: 95–110

163 Rana M, Koprinska I, Agelidis V G. 2D-interval forecasts for solar power production. Solar Energy, 2015, 122: 191–203

164 Almeida M P, Perpiñán O, Narvarte L. PV power forecast using a nonparametric PV model. Solar Energy, 2015, 115: 354–368

165 Paulescu M, Paulescu E. Short-term forecasting of solar irradiance. Renewable Energy, 2019, 143: 985–994

166 Voyant C, Notton G. Solar irradiation nowcasting by stochastic persistence: a new parsimonious, simple and efficient forecasting tool. Renewable & Sustainable Energy Reviews, 2018, 92: 343–352

167 Jiang F, Jiang Y, Zhi H, . Artificial intelligence in healthcare: past, present and future. Stroke and Vascular Neurology, 2017, 2(4): 230–243

168 Wang H B, Xiong J N, Zhao C Y. The mid-term forecast method of solar radiation index. Chinese Astronomy and Astrophysics, 2015, 39(2): 198–211 doi:10.1016/j.chinastron.2015.04.010

169 Yang D. A guideline to solar forecasting research practice: reproducible, operational, probabilistic or physically-based, ensemble, and skill (ROPES). Journal of Renewable and Sustainable Energy, 2019, 11(2): 022701

170 Gil V, Gaertner M A, Gutierrez C, Impact of climate change on solar irradiation and variability over the Iberian Peninsula using regional climate models. International Journal of Climatology, 2018, 39(3): 1733–1747doi: 10.1002/joc.5916