

Frontiers of Mathematics in China >
Multiscale mathematical models for biological systems
Copyright
Life activities are extremely complex phenomena in nature. From molecular signaling regulation to multi-cellular tissue formation and so on, the biological system consists of multiple temporal, spatial and functional scales. Multiscale mathematical models have extensive applications in life science research due to their capacity of appropriately simulating the complex multiscale biological systems. Many mathematical methods, including deterministic methods, stochastic methods as well as discrete or rule-based methods, have been widely used for modeling biological systems. However, the models at single scale are not sufficient to simulate complex biological systems. Therefore, in this paper we give a survey of two multiscale modeling approaches for biological systems. One approach is continuous stochastic method that couples ordinary differential equations and stochastic differential equations; Another approach is hybrid continuous-discrete method that couples agent-based model with partial differential equations. We then introduce the applications of these multiscale modeling approaches in systems biology and look ahead to the future research.
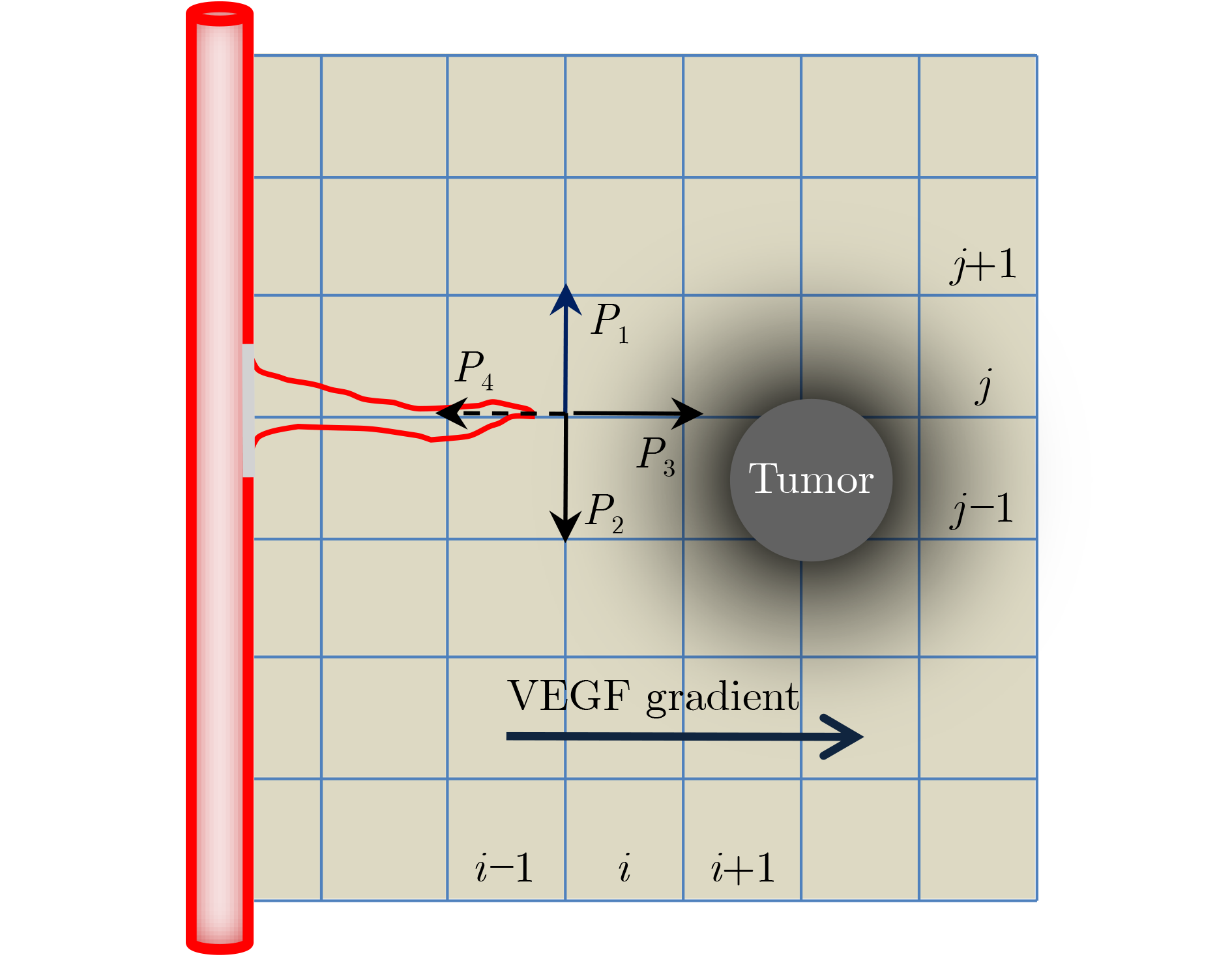
Xiaoqiang SUN , Jiguang BAO . Multiscale mathematical models for biological systems[J]. Frontiers of Mathematics in China, 2023 , 18(2) : 75 -94 . DOI: 10.3868/S140-DDD-023-0011-X
| 1 |
Aldridge B B, Burke J M, Lauffenburger D A.
|
| 2 |
AlonU. An Introduction to Systems Biology: Design Principles of Biological Circuits. Boca Raton: Chapman & Hall/CRC, 2006
|
| 3 |
Anderson A R A. A hybrid mathematical model of solid tumour invasion: the importance of cell adhesion. Math Med Biol J IMA 2005; 22(2): 163–186
|
| 4 |
Anderson A R A, Chaplain M A J. Continuous and discrete mathematical models of tumor-induced angiogenesis. Bull Math Biol 1998; 60(5): 857–899
|
| 5 |
Ballesta A, Lopez J, Popgeorgiev N.
|
| 6 |
Bonabeau E. Agent-based modeling: Methods and techniques for simulating human systems. Proc Nat Acad Sci USA 2002; 99(Suppl 3): 7280–7287
|
| 7 |
ChapmanS J. Multiscale mathematical modelling in medicine and biology. In: Proceedings of the 18th World IMACS Congress and MODSIM09 International Congress on Modelling and Simulation: Interfacing Modeling and Simulation with Mathematcial and Computational Sciences, Anderssen R S, Bradock R D and Newham L T H eds. Cairns, Australia, 2009, 13–22
|
| 8 |
Checa S, Prendergast P J. A mechanobiological model for tissue differentiation that includes angiogenesis: a lattice-based modeling approach. Ann Biomed Eng 2009; 37(1): 129–145
|
| 9 |
Checa S, Prendergast P J. Effect of cell seeding and mechanical loading on vascularization and tissue formation inside a scaffold: a mechano-biological model using a lattice approach to simulate cell activity. J Biomech 2010; 43(5): 961–968
|
| 10 |
Cheng J, Zhang J, Wu Z.
|
| 11 |
ChopardBDroz M. Cellular Automata Modeling of Physical Systems. Cambridge: Cambridge University Press, 1998
|
| 12 |
Chou T C. Derivation and properties of Michaelis-Menten type and Hill type equations for reference ligands. J Theor Biol 1976; 59(2): 253–276
|
| 13 |
Dada J O, Mendes P. Multi-scale modelling and simulation in systems biology. Inter Biol 2011; 3(2): 86–96
|
| 14 |
Ellis P M, Morzycki W, Melosky B.
|
| 15 |
Garfinkel A, Tintut Y, Petrasek D.
|
| 16 |
Geris L, Reed A A C, Vander Sloten J.
|
| 17 |
Geris L, Vander Sloten J, Van Oosterwyck H. In silico biology of bone modelling and remodelling: regeneration. Phil Trans Royal Soc A: Math Phys Eng Sci 2009; 367(1895): 2031–2053
|
| 18 |
Geris L, Vander Sloten J, Van Oosterwyck H. Connecting biology and mechanics in fracture healing: an integrated mathematical modeling framework for the study of nonunions. Biomech Model Mechanobiol 2010; 9(6): 713–724
|
| 19 |
Gierer A, Meinhardt H. A theory of biological pattern formation. Kybernetik 1972; 12(1): 30–39
|
| 20 |
Gillespie D T. Exact stochastic simulation of coupled chemical reactions. J Phys Chem 1977; 81(25): 2340–2361
|
| 21 |
Gillespie D T. Stochastic simulation of chemical kinetics. Annu Rev Phys Chem 2007; 58(1): 35–55
|
| 22 |
Gordeladze J O, Reseland J E, Duroux-Richard I.
|
| 23 |
Higham D J. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev 2001; 43(3): 525–546
|
| 24 |
Kansal A R, Torquato S, Harsh IV G R.
|
| 25 |
Karplus M, Petsko G A. Molecular dynamics simulations in biology. Nature 1990; 347(6294): 631–639
|
| 26 |
Katare S, Bhan A, Caruthers J M.
|
| 27 |
Kauffman S A. Metabolic stability and epigenesis in randomly constructed genetic nets. J Theor Biol 1969; 22(3): 437–467
|
| 28 |
KitanoH. Foundations of Systems Biology. Cambridge, MA: MIT Press, 2001
|
| 29 |
KlebanerF C. Introduction to Stochastic Calculus with Applications, 2nd ed. Singapore: Imperial College Press, 2005
|
| 30 |
Klepeis J L, Lindorff-Larsen K, Dror R O.
|
| 31 |
KlippELiebermeister WWierlingC,
|
| 32 |
Komarova S V, Smith R J, Dixon S J.
|
| 33 |
Komori T. Regulation of bone development and maintenance by Runx2. Front Biosci 2008; 13(3): 898–903
|
| 34 |
Lee J M, Gianchandani E P, Eddy J A.
|
| 35 |
Legewie S, Blüthgen N, Herzel H. Mathematical modeling identifies inhibitors of apoptosis as mediators of positive feedback and bistability. PLoS Comput Biol 2006; 2(9): e120
|
| 36 |
Lemaire V, Tobin F L, Greller L D.
|
| 37 |
Liang J, Qian H. Computational cellular dynamics based on the chemical master equation: a challenge for understanding complexity. J Comput Sci Tech 2010; 25(1): 154–168
|
| 38 |
Liang W, Zheng Y, Zhang J.
|
| 39 |
Lovett M, Lee K, Edwards A.
|
| 40 |
Macklin P, McDougall S, Anderson A R.
|
| 41 |
Michaelis L, Menten M L. Die kinetik der invertinwirkung. Biochem Z 1913; 49: 333–369
|
| 42 |
MortonK WMayers D F. Numerical Solution of Partial Differential Equations: An Introduction. Cambridge: Cambridge University Press, 2005
|
| 43 |
Neumann L, Pforr C, Beaudouin J.
|
| 44 |
Nguyen L H, Annabi N, Nikkah M.
|
| 45 |
NicolisGPrigogine I. Self-organization in Nonequilibrium Systems: From Dissipative Structures to Order Through Fluctuations. New York: John Wiley & Sons, 1977
|
| 46 |
ØksendalB K. Stochastic Differential Equations: An Introduction with Applications, 5th ed. New York: Springer-Verlag, 2003, 61–72
|
| 47 |
Patel A A, Gawlinski E T, Lemieux S K.
|
| 48 |
Pivonka P, Zimak J, Smith D W.
|
| 49 |
Pivonka P, Zimak J, Smith D W.
|
| 50 |
Rejniak K A, Anderson A R A. Hybrid models of tumor growth. Wiley Interdiscip Rev: Syst Biol Med 2011; 3(1): 115–125
|
| 51 |
Sandino C, Checa S, Prendergast P J.
|
| 52 |
Sanz-Herrera J A, Garcia-Aznar J, Doblare M. Micro-macro numerical modelling of bone regeneration in tissue engineering. Comput Meth Appl Mech Eng 2008; 197(33): 3092–3107
|
| 53 |
Sanz-Herrera J A, Garcia-Aznar J, Doblare M. Simulation of bone remodelling and bone ingrowth within scaffolds. Key Eng Mater 2008; 377: 225–273
|
| 54 |
Sanz-Herrera J A, García-Aznar J M, Doblaré M. A mathematical approach to bone tissue engineering. Phi Trans Roy Soc A: Math Phys Eng Sci 2009; 367(1895): 2055–2078
|
| 55 |
Schlatter R, Schmich K, Avalos Vizcarra I.
|
| 56 |
Stokes C L, Lauffenburger D A. Analysis of the roles of microvessel endothelial cell random motility and chemotaxis in angiogenesis. J Theor Biol 1991; 152(3): 377–403
|
| 57 |
Sun W, Lal P. Recent development on computer aided tissue engineering—a review. Comput Meth Prog Biomed 2002; 67(2): 85–103
|
| 58 |
Sun X Q, Bao J G, Nelson K C.
|
| 59 |
Sun X Q, Bao J G, Shao Y Z. Mathematical modeling of therapy-induced cancer drug resistance: connecting cancer mechanisms to population survival rates. Sci Rep 2016; 6(1): 22498
|
| 60 |
Sun X Q, Hu B. Mathematical modeling and computational prediction of cancer drug resistance. Briefings Bioinf 2018; 19(6): 1382–1399
|
| 61 |
Sun X Q, Kang Y Q, Bao J G.
|
| 62 |
Sun X Q, Su J, Bao J G.
|
| 63 |
Sun X Q, Zhang J, Nie Q. Inferring latent temporal progression and regulatory networks from cross-sectional transcriptomic data of cancer samples. PLoS Comput Biol 2021; 17(3): e1008379
|
| 64 |
Sun X Q, Zhang J, Zhao Q.
|
| 65 |
Wang Z H, Zhang L, Sagotsky J.
|
| 66 |
Zhang J, Guan M G, Wang Q L.
|
| 67 |
Zhang J J, Zhu W B, Wang Q L.
|
| 68 |
Zhang L, Athale C A, Deisboeck T S. Development of a three-dimensional multiscale agent-based tumor model: simulating gene-protein interaction profiles, cell phenotypes and multicellular patterns in brain cancer. J Theor Biol 2007; 244(1): 96–107
|
| 69 |
Zhang L, Chen L L, Deisboeck T S. Multi-scale, multi-resolution brain cancer modeling. Mathe Comp Simul 2009; 79(7): 2021–2035
|
| 70 |
Zhang L, Wang Z H, Sagotsky J A.
|
| 71 |
Zheng X, Wise S M, Cristini V. Nonlinear simulation of tumor necrosis, neo-vascularization and tissue invasion via an adaptive finite-element/level-set method. Bull Math Biol 2005; 67(2): 211–259
|
| 72 |
Zheng Y J, Bao J G, Zhao Q Y.
|
/
| 〈 |
|
〉 |